Assessment and Validation of Shallow Groundwater Vulnerability to Contamination Based on Fuzzy Logic and DRASTIC Method for Sustainable Groundwater Management in Southeast Hungary
Abstract
1. Introduction
2. Methodology
2.1. Introduction of Study Area
2.2. DRASTIC Model
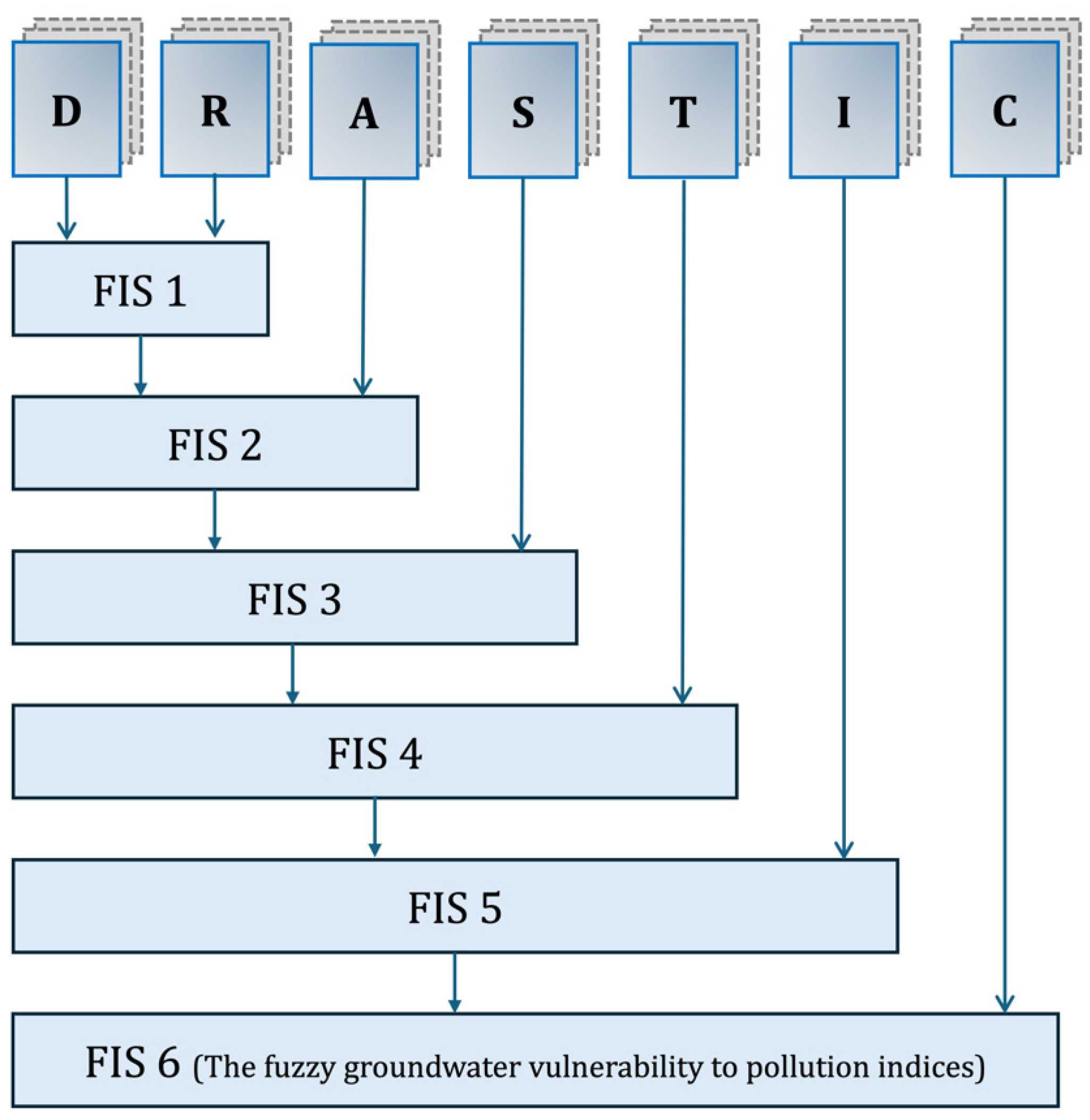
2.3. Hierarchical Fuzzy Inference System (FIS)
- a is the starting point of the trapezoid where the membership value starts to increase from 0.
- b is the point where the membership function reaches a value of 1, starting the flat “top” of the trapezoid.
- c is the point where the flat “top” of the trapezoid ends and the membership value starts to decrease.
- d is the ending point of the trapezoid where the membership function value returns to 0.
2.3.1. FIS1: Groundwater Depth vs. Recharge Rate
2.3.2. FIS2: FIS1 vs. Aquifer Media
2.3.3. FIS3: FIS2 vs. Soil Media
2.3.4. FIS4: FIS3 vs. Topography
2.3.5. FIS5: FIS4 vs. Impact of Vadose Zone
2.3.6. FIS6: FIS5 vs. Hydraulic Conductivity
2.4. Model Validation
3. Results
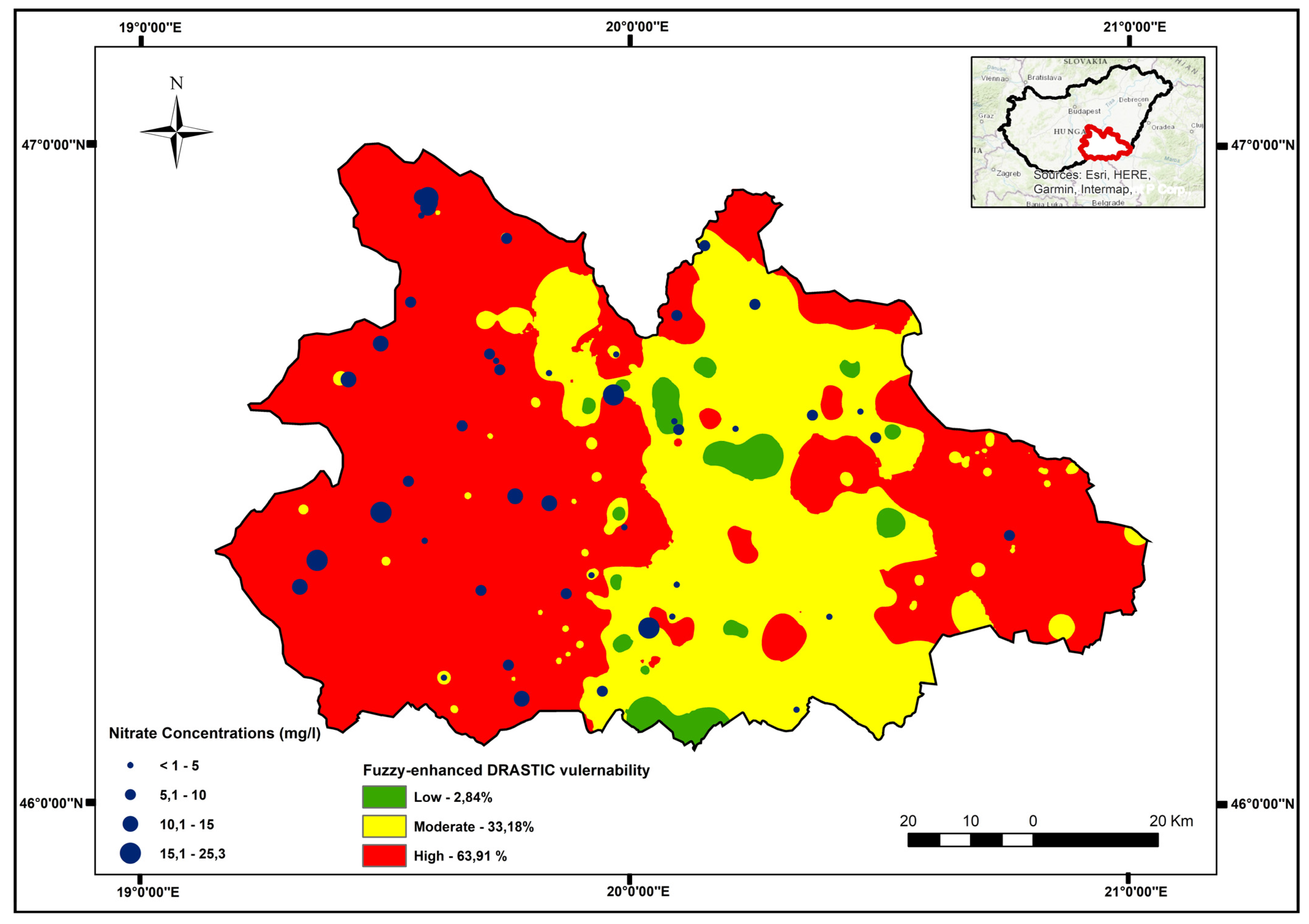
3.1. Fuzzy-Enhanced DRASTIC Model
3.2. Validation of the Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DEM | Digital Elevation Model |
| FGWVI | Fuzzy Groundwater Vulnerability Index |
| FIS | Fuzzy Inference System |
| FL | Fuzzy Logic |
| GHP | Great Hungarian Plain |
| GIS | Geographic Information System |
| MF | Membership Function |
| VH | Very High |
| H | High |
| M | Moderate |
| L | Low |
| VL | Very Low |
References
- Denizman, C. Land use changes and groundwater quality in Florida. Appl. Water Sci. 2018, 8, 134. [Google Scholar] [CrossRef]
- Sukmawati Rukmana, B.T.; Bargawa, W.S.; Cahyadi, T.A. Assessment of Groundwater Vulnerability Using GOD Method. IOP Conf. Ser. Earth Environ. Sci. 2020, 477, 012020. [Google Scholar] [CrossRef]
- Li, P.; Karunanidhi, D.; Subramani, T.; Srinivasamoorthy, K. Sources and Consequences of Groundwater Contamination. Arch. Environ. Contam. Toxicol. 2021, 80, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Ghouili, N.; Jarraya-Horriche, F.; Hamzaoui-Azaza, F.; Zaghrarni, M.F.; Ribeiro, L.; Zammouri, M. Groundwater vulnerability mapping using the Susceptibility Index (SI) method: Case study of Takelsa aquifer, Northeastern Tunisia. J. Afr. Earth Sci. 2021, 173, 104035. [Google Scholar] [CrossRef]
- Raisa, S.S.; Sarkar, S.K.; Sadiq, M.A. Advancing groundwater vulnerability assessment in Bangladesh: A comprehensive machine learning approach. Groundw. Sustain. Dev. 2024, 25, 101128. [Google Scholar] [CrossRef]
- Bordbar, M.; Rezaie, F.; Bateni, S.M.; Jun, C.; Kim, D.; Busico, G.; Moghaddam, H.K.; Paryani, S.; Panahi, M.; Valipour, M. Global Review of Modification, Optimization, and Improvement Models for Aquifer Vulnerability Assessment in the Era of Climate Change. Curr. Clim. Chang. Rep. 2023, 9, 45–67. [Google Scholar] [CrossRef]
- Jain, H. Groundwater vulnerability and risk mitigation: A comprehensive review of the techniques and applications. Groundw. Sustain. Dev. 2023, 22, 100968. [Google Scholar] [CrossRef]
- Zhang, Q.; Shan, Q.; Chen, F.; Liu, J.; Yuan, Y. Groundwater Vulnerability Assessment and Protection Strategy in the Coastal Area of China: A GIS-Based DRASTIC Model Approach. Appl. Sci. 2023, 13, 10781. [Google Scholar] [CrossRef]
- Goyal, D.; Haritash, A.K.; Singh, S.K. A comprehensive review of groundwater vulnerability assessment using index-based, modelling and coupling methods. J. Environ. Manag. 2021, 296, 113161. [Google Scholar] [CrossRef]
- Barbulescu, A. Assessing groundwater vulnerability: DRASTIC and DRASTIC-like methods: A review. Water 2020, 12, 1356. [Google Scholar] [CrossRef]
- Rama, F.; Busico, G.; Arumi, J.L.; Kazakis, N.; Colombani, N.; Marfella, L.; Hirata, R.; Kruse, E.E.; Sweeney, P.; Mastrocicco, M. Assessment of intrinsic aquifer vulnerability at continental scale through a critical application of the drastic framework: The case of South America. Sci. Total Environ. 2022, 823, 153748. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, A.H.; Tat, V.M.H. Groundwater pollution vulnerability assessment using a modified DRASTIC model in Ho Chi Minh City, Vietnam. Irrig. Drain. 2024, 73, 1453–1469. [Google Scholar] [CrossRef]
- Baki, A.M.; Ghavami, S.M. A modified DRASTIC model for groundwater vulnerability assessment using connecting path and analytic hierarchy process methods. Environ. Sci. Pollut. Res. 2023, 30, 111270–111283. [Google Scholar] [CrossRef] [PubMed]
- Kirlas, M.C.; Karpouzos, D.K.; Georgiou, P.E.; Katsifarakis, K.L. A comparative study of groundwater vulnerability methods in a porous aquifer in Greece. Appl. Water Sci. 2022, 12, 16. [Google Scholar] [CrossRef]
- Noori, R.; Ghahremanzadeh, H.; Kløve, B.; Adamowski, J.F.; Baghvand, A. Modified-DRASTIC, modified-SINTACS and SI methods for groundwater vulnerability assessment in the southern Tehran aquifer. J. Environ. Sci. Health Part A Tox. Hazard. Subst. Environ. Eng. 2019, 54, 89–100. [Google Scholar] [CrossRef]
- Jenifer, M.A.; Jha, M.K. Comparative evaluation of GIS-based models for mapping aquifer vulnerability in hard-rock terrains. Environ. Earth Sci. 2018, 77, 7821. [Google Scholar] [CrossRef]
- Neshat, A.; Pradhan, B.; Pirasteh, S.; Shafri, H.Z.M. Estimating groundwater vulnerability to pollution using a modified DRASTIC model in the Kerman agricultural area, Iran. Environ. Earth Sci. 2014, 71, 3119–3131. [Google Scholar] [CrossRef]
- Sener, E.; Davraz, A. Assessment of groundwater vulnerability based on a modified DRASTIC model, GIS and an analytic hierarchy process (AHP) method: The case of Egirdir Lake basin (Isparta, Turkey). Hydrogeol. J. 2013, 21, 701–714. [Google Scholar] [CrossRef]
- Javadi, S.; Kavehkar, N.; Mousavizadeh, M.H.; Mohammadi, K. Modification of DRASTIC model to map groundwater vulnerability to pollution using nitrate measurements in agricultural areas. J. Agric. Sci. Technol. 2011, 13, 239–249. [Google Scholar]
- Taghavi, N.; Niven, R.K.; Kramer, M.; Paull, D.J. Comparison of DRASTIC and DRASTICL groundwater vulnerability assessments of the Burdekin Basin, Queensland, Australia. Sci. Total Environ. 2023, 858, 159945. [Google Scholar] [CrossRef]
- Mfonka, E.H.; Ngoupayou, Z.N.; Ndjigui, P.D.; Kpoumie, A.; Zammouri, M.; Ngouh, A.N.; Mouncherou, O.F.; Rakotondrabe, F.; Rasolomanana, F. A GIS-based DRASTIC and GOD models for assessing alterites aquifer of three experimental watersheds in Foumban (Western-Cameroon). Groundw. Sustain. Dev. 2018, 7, 250–264. [Google Scholar] [CrossRef]
- Das, B.; Pal, S.C. Assessment of groundwater vulnerability to over-exploitation using MCDA, AHP, fuzzy logic and novel ensemble models: A case study of Goghat-I and II blocks of West Bengal, India. Environ. Earth Sci. 2020, 79, 8843. [Google Scholar] [CrossRef]
- Dixon, B. Applicability of neuro-fuzzy techniques in predicting ground-water vulnerability: A GIS-based sensitivity analysis. J. Hydrol. 2005, 309, 17–38. [Google Scholar] [CrossRef]
- Duhalde, D.J.; Arumí, J.L.; Oyarzún, R.A.; Rivera, D.A. Fuzzy-based assessment of groundwater intrinsic vulnerability of a volcanic aquifer in the Chilean Andean Valley. Environ. Monit. Assess. 2018, 190, 6758. [Google Scholar] [CrossRef]
- Jafari, S.M.; Nikoo, M.R. Developing a fuzzy optimization model for groundwater risk assessment based on improved DRASTIC method. Environ. Earth Sci. 2019, 78, 8090. [Google Scholar] [CrossRef]
- Nobre, R.C.M.; Rotunno Filho, O.C.; Mansur, W.J.; Nobre, M.M.M.; Cosenza, C.A.N. Groundwater vulnerability and risk mapping using GIS, modeling and a fuzzy logic tool. J. Contam. Hydrol. 2007, 94, 277–292. [Google Scholar] [CrossRef]
- Saranya, T.; Saravanan, S. A comparative analysis on groundwater vulnerability models—Fuzzy DRASTIC and fuzzy DRASTIC-L. Environ. Sci. Pollut. Res. 2022, 29, 86005–86019. [Google Scholar] [CrossRef]
- Nourani, V.; Maleki, S.; Najafi, H.; Baghanam, A.H. A fuzzy logic-based approach for groundwater vulnerability assessment. Environ. Sci. Pollut. Res. 2023, 31, 18010–18029, in press. [Google Scholar] [CrossRef]
- Iqbal, J.; Pathak, G.; Gorai, A.K. Development of hierarchical fuzzy model for groundwater vulnerability to pollution assessment. Arab. J. Geosci. 2015, 8, 2713–2728. [Google Scholar] [CrossRef]
- Saranya, T.; Saravanan, S. Evolution of a hybrid approach for groundwater vulnerability assessment using hierarchical fuzzy-DRASTIC models in the Cuddalore Region, India. Environ. Earth Sci. 2021, 80, 9479. [Google Scholar] [CrossRef]
- Dhanya, C.T.; Kumar, D.N. Data Mining for Evolving Fuzzy Association Rules for Predicting Monsoon Rainfall of India. J. Intell. Syst. 2009, 18, 193. [Google Scholar] [CrossRef]
- Khan, Q.; Liaqat, M.U.; Mohamed, M.M. A comparative assessment of modeling groundwater vulnerability using DRASTIC method from GIS and a novel classification method using machine learning classifiers. Geocarto Int. 2022, 37, 5832–5850. [Google Scholar] [CrossRef]
- Pinke, Z.; Decsi, B.; Kozma, Z.; Vári, Á.; Lövei, G.L. A spatially explicit analysis of wheat and maize yield sensitivity to changing groundwater levels in Hungary, 1961–2010. Sci. Total Environ. 2020, 715, 136555. [Google Scholar] [CrossRef] [PubMed]
- Gribovszki, Z.; Kalicz, P.; Balog, K.; Szabó, A.; Tóth, T.; Csáfordi, P.; Metwaly, M.; Szalai, S. Groundwater uptake of different surface cover and its consequences in great Hungarian plain. Ecol. Process. 2017, 6, 106. [Google Scholar] [CrossRef]
- Barreto, S.; Bártfai, B.; Engloner, A.; Liptay, Á.Z.; Madarász, T.; Vargha, M. Water in Hungary; Status overview for the National Water Programme of the Hungarian Academy of Sciences: Budapest, Hungary, 2017. [Google Scholar]
- Mezősi, G. The Physical Geography of Hungary; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- ICPDR—International Commission for the Protection of the Danube River. Journey to a Balanced Tisza Basin. An Introduction to the Integrated Tisza River Basin Management Plan. 2011. Available online: https://www.icpdr.org/sites/default/files/Tisa_04082011.pdf (accessed on 23 October 2024).
- National Water Directorate General of Hungary—OFV. MÁSODIK FELÜLVIZSGÁLATA MAGYARORSZÁG VÍZGYŰJTŐ—GAZDÁLKODÁSI TERVE—2021 TERVEZET, Budapest, Hungary. 2021. Available online: https://vizeink.hu/wp-content/uploads/2021/05/VGT3_II_Vitaanyag.pdf (accessed on 23 October 2024).
- Szöllősi-Nagy, A. On climate change, hydrological extremes and water security in a globalized world. Sci. Secur. 2022, 2, 504–509. [Google Scholar] [CrossRef]
- Rossi, L.; Wens, M.; De Moel, H.; Cotti, D.; Siemons, A.-S.S.; Hagenlocher, M.; Van Loon, A.; Maetens, W.; Masante, D.; Toreti, A.; et al. European Drought Risk Atlas; Publications Office of the European Union: Luxembourg, 2023. [Google Scholar] [CrossRef]
- Demiroǧlu, M.; Dowd, J. The utility of vulnerability maps and GIS in groundwater management: A case study. Turkish J. Earth Sci. 2014, 23, 80–90. [Google Scholar] [CrossRef]
- Aller, L.; Bennett, T.; Lehr, J.H.; Petty, R.J.; Hackett, G. DRASTIC: A Standardized Method for Evaluating Ground Water Pollution Potential Using Hydrogeologic Settings; NWWA/EPA-600/2-87-035; US Environmental Protection Agency: Washington, DC, USA, 1987. [Google Scholar]
- Tahmassebipoor, N.; Rahmati, O.; Noormohamadi, F.; Lee, S. Spatial analysis of groundwater potential using weights-of-evidence and evidential belief function models and remote sensing. Arab. J. Geosci. 2016, 9, 79. [Google Scholar] [CrossRef]
- Gesim, N.A.; Okazaki, T. Assessment of groundwater vulnerability to pollution using DRASTIC model and fuzzy logic in Herat City, Afghanistan. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 181–188. [Google Scholar] [CrossRef]
- Rezaei, F.; Safavi, H.R.; Ahmadi, A. Groundwater vulnerability assessment using fuzzy logic: A case study in the Zayandehrood aquifers, Iran. Environ. Manag. 2013, 51, 267–277. [Google Scholar] [CrossRef]
- Selvaraj, A.; Saravanan, S.; Jennifer, J.J. Mamdani fuzzy-based decision support system for prediction of groundwater quality: An application of soft computing in water resources. Environ. Sci. Pollut. Res. 2020, 27, 25535–25552. [Google Scholar] [CrossRef]
- Fannakh, A.; Farsang, A. DRASTIC, GOD, and SI approaches for assessing groundwater vulnerability to pollution: A review. Environ. Sci. Eur. 2022, 34, 77. [Google Scholar] [CrossRef]
- Piscopo, G. Groundwater Vulnerability Map Explanatory Notes: Castlereagh Catchment; Tech. Rep.; NSW Department of Land and Water Conservation: Parramatta, NSW, Australia, 2001; pp. 1–35. [Google Scholar]
- Farsang, A.; Károly, B.; Boudewijn, V.L. Az Öntözés Talajtani Feltételei, Lehetőségei és Körülményei az Ativizig Működési Területén—Soil Conditions, Possibilities and Circumstances of Irrigation in Ativizig’s Operating Area; Technical Report; K&K Mérnöki Iroda Kft.: Csongrád, Hungary, 2017. [Google Scholar]
- Oroji, B. Groundwater vulnerability assessment with using GIS in Hamadan–Bahar plain, Iran. Appl. Water Sci. 2019, 9, 1082. [Google Scholar] [CrossRef]
- Tomer, T.; Katyal, D.; Joshi, V. Sensitivity analysis of groundwater vulnerability using DRASTIC method: A case study of National Capital Territory, Delhi, India. Groundw. Sustain. Dev. 2019, 9, 100271. [Google Scholar] [CrossRef]
- Dizaji, A.R.; Hosseini, S.A.; Rezaverdinejad, V.; Sharafati, A. Groundwater contamination vulnerability assessment using DRASTIC method, GSA, and uncertainty analysis. Arab. J. Geosci. 2020, 13, 5650. [Google Scholar] [CrossRef]
- Jesiya, N.P.; Gopinath, G. A Customized Fuzzy-AHP-GIS-based DRASTIC-L model for intrinsic groundwater vulnerability assessment of urban and peri-urban phreatic aquifer clusters. Groundw. Sustain. Dev. 2019, 8, 654–666. [Google Scholar] [CrossRef]
- Cashman, P.M.; Preene, M. Groundwater Lowering in Construction: A Practical Guide to Dewatering. Environ. Eng. Geosci. 2021, 20, 406–407. [Google Scholar] [CrossRef]
- Hasan, M.; Islam, M.A.; Hasan, M.A.; Alam, M.J.; Peas, M.H. Groundwater vulnerability assessment in Savar Upazila of Dhaka District, Bangladesh—A GIS-based DRASTIC modeling. Groundw. Sustain. Dev. 2019, 9, 100220. [Google Scholar] [CrossRef]
- Fannakh, A.; Károly, B.; Farsang, A.; Ben Ali, M. Evaluation of index-overlay methods for assessing shallow groundwater vulnerability in southeast Hungary. Appl. Water Sci. (In press)
- Kvålseth, T.O. Cautionary Note about R2. Am. Stat. 1985, 39, 279–285. [Google Scholar] [CrossRef]
- Nadiri, A.A.; Sedghi, Z.; Khatibi, R.; Gharekhani, M. Mapping vulnerability of multiple aquifers using multiple models and fuzzy logic to objectively derive model structures. Sci. Total Environ. 2017, 593, 75–90. [Google Scholar] [CrossRef]
- Afshar, A.; Mariño, M.A.; Ebtehaj, M.; Moosavi, J. Rule-Based Fuzzy System for Assessing Groundwater Vulnerability. J. Environ. Eng. 2007, 133, 532–540. [Google Scholar] [CrossRef]
- Podgorski, J.; Kracht, O.; Araguas-Araguas, L.; Terzer-Wassmuth, S.; Miller, J.; Straub, R.; Kipfer, R.; Berg, M. Groundwater vulnerability to pollution in Africa’s Sahel region. Nat. Sustain. 2024, 7, 558–567. [Google Scholar] [CrossRef]



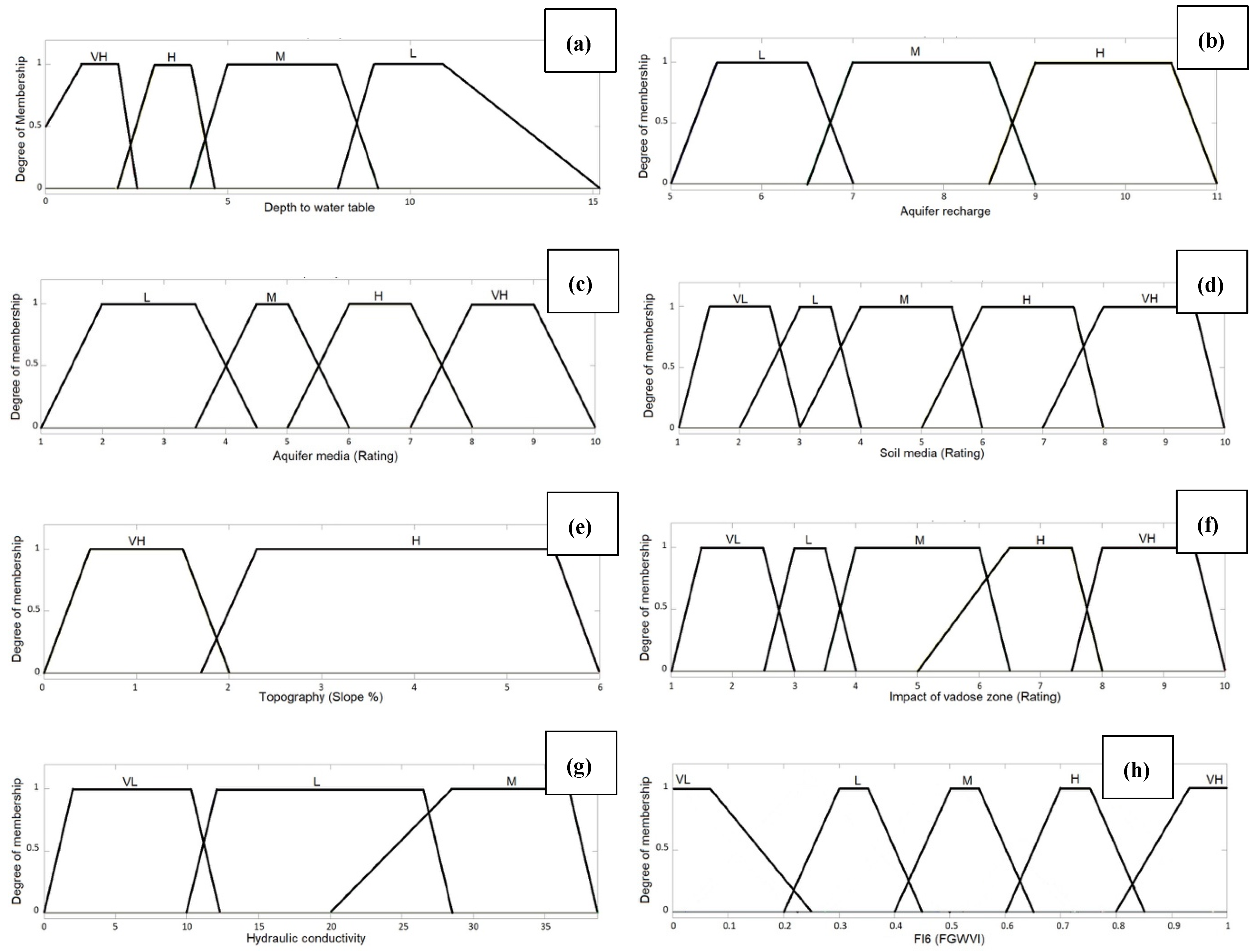


| DRASTIC Parameters | Fuzzy Membership Function | ||
|---|---|---|---|
| Layers | Attribute values | Category | |
| Depth to groundwater table (mbs *) | <1.5 | Very high | MF1 |
| 1.5–4.6 | High | MF2 | |
| 4.6–9.1 | Moderate | MF3 | |
| 9.1–15.2 | Low | MF4 | |
| >15.2 | Very Low | ||
| Aquifer Recharge | See Table 2 | See Table 2 | |
| Aquifer media | Sand and gravel | Very high | MF1, MF2 |
| Massive sandstone | High | MF3 | |
| Metamorphic/igneous | Moderate | MF4, MF5 | |
| Soil media | Sand | Very high | MF1 |
| Sandy loam | High | MF2 | |
| Loamy sand | Moderate | MF3 | |
| Sandy clay/clay loam/sandy clay loam | Low | MF4 | |
| Clay | Very low | MF5 | |
| Topography (slope, %) | <2% | Very high | MF1 |
| 2–6% | High | MF2 | |
| Impact of vadose zone | Sand and gravel | Very high | MF1 |
| Sand/sandy silt | High | MF2 | |
| Sand and silty with clay | Moderate | MF3 | |
| Silty Clay | Low | MF4 | |
| Clay | Very low | MF5 | |
| Hydraulic conductivity (m/day) | >81.5 | Very high | MF1 |
| 40.8–81.5 | High | MF2 | |
| 28.5–40.8 | Moderate | MF3 | |
| 12.3–28.5 | Low | MF4 | |
| 4.1–12.3 | Very low | MF5 | |
| Slope (%) | Rainfall (mm) | Soil Permeability (cm/s) | Net Recharge | ||||
|---|---|---|---|---|---|---|---|
| Range | Rating | Range | Rating | Range | Rating | Range | Rating |
| <2 | 4 | <500 | 1 | High | 5 | 11–13 | 10 |
| 2–10 | 3 | 500–700 | 2 | Mod–high | 4 | 9–11 | 8 |
| 10–33 | 2 | 700–850 | 3 | Moderate | 3 | 7–9 | 5 |
| >33 | 1 | >850 | 4 | Slow | 2 | 5–7 | 3 |
| Very slow | 1 | 3–5 | 1 | ||||
| FIS1 | ||||||
| THEN FIS1 | IF Aquifer recharge | |||||
| AND depth to water table | L | M | H | |||
| L | VL | L | M | |||
| M | L | M | H | |||
| H | M | M | VH | |||
| VH | M | H | VH | |||
| FIS2 | ||||||
| THEN FIS2 | IF Aquifer type | |||||
| AND FIS1 | L | M | H | VH | ||
| VL | VL | L | M | M | ||
| L | VL | L | M | M | ||
| M | L | M | H | H | ||
| H | M | M | VH | VH | ||
| VH | M | H | VH | VH | ||
| FIS3 | ||||||
| THEN FIS3 | IF Soil media | |||||
| AND FIS2 | VL | L | M | H | VH | |
| VL | VL | VL | L | M | M | |
| L | VL | VL | L | M | M | |
| M | L | L | M | H | H | |
| H | M | M | M | VH | VH | |
| VH | M | M | H | VH | VH | |
| FIS4 | ||||||
| THEN FIS4 | IF Topography (slope) | |||||
| AND FIS3 | H | VH | ||||
| VL | M | M | ||||
| L | M | M | ||||
| M | M | H | ||||
| H | VH | VH | ||||
| VH | VH | VH | ||||
| FIS5 | ||||||
| THEN FIS5 | IF Impact of vadose zone | |||||
| AND FIS4 | VL | L | M | H | VH | |
| VL | VL | VL | L | M | M | |
| L | VL | VL | L | M | H | |
| M | L | L | M | H | H | |
| H | M | M | H | VH | VH | |
| VH | M | M | H | VH | VH | |
| FIS6 | ||||||
| THEN FIS6 | IF Hydraulic conductivity | |||||
| AND FIS5 | VL | L | M | |||
| VL | VL | VL | L | |||
| L | VL | VL | L | |||
| M | L | L | M | |||
| H | L | M | H | |||
| VH | M | M | H | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fannakh, A.; Károly, B.; Fannakh, M.; Farsang, A. Assessment and Validation of Shallow Groundwater Vulnerability to Contamination Based on Fuzzy Logic and DRASTIC Method for Sustainable Groundwater Management in Southeast Hungary. Water 2025, 17, 739. https://doi.org/10.3390/w17050739
Fannakh A, Károly B, Fannakh M, Farsang A. Assessment and Validation of Shallow Groundwater Vulnerability to Contamination Based on Fuzzy Logic and DRASTIC Method for Sustainable Groundwater Management in Southeast Hungary. Water. 2025; 17(5):739. https://doi.org/10.3390/w17050739
Chicago/Turabian StyleFannakh, Abdelouahed, Barta Károly, Mhamed Fannakh, and Andrea Farsang. 2025. "Assessment and Validation of Shallow Groundwater Vulnerability to Contamination Based on Fuzzy Logic and DRASTIC Method for Sustainable Groundwater Management in Southeast Hungary" Water 17, no. 5: 739. https://doi.org/10.3390/w17050739
APA StyleFannakh, A., Károly, B., Fannakh, M., & Farsang, A. (2025). Assessment and Validation of Shallow Groundwater Vulnerability to Contamination Based on Fuzzy Logic and DRASTIC Method for Sustainable Groundwater Management in Southeast Hungary. Water, 17(5), 739. https://doi.org/10.3390/w17050739






