Optimization of 3D Borehole Electrical Resistivity Tomography (ERT) Measurements for Real-Time Subsurface Imaging
Abstract
1. Introduction
- The flow can be adjusted in real-time to force the delivery of the grout, when grout does not flow as designed.
- Delivery can be evaluated in the short term. If necessary, a part of the target area can be treated immediately (rather than waiting for leaks to spring).
- (Non-real-time): At a later point in time, the grout barrier can be located and evaluated and expanded or repaired if necessary.
2. Principles of Electrical Resistivity Tomography
3. Laboratory Test
- (1)
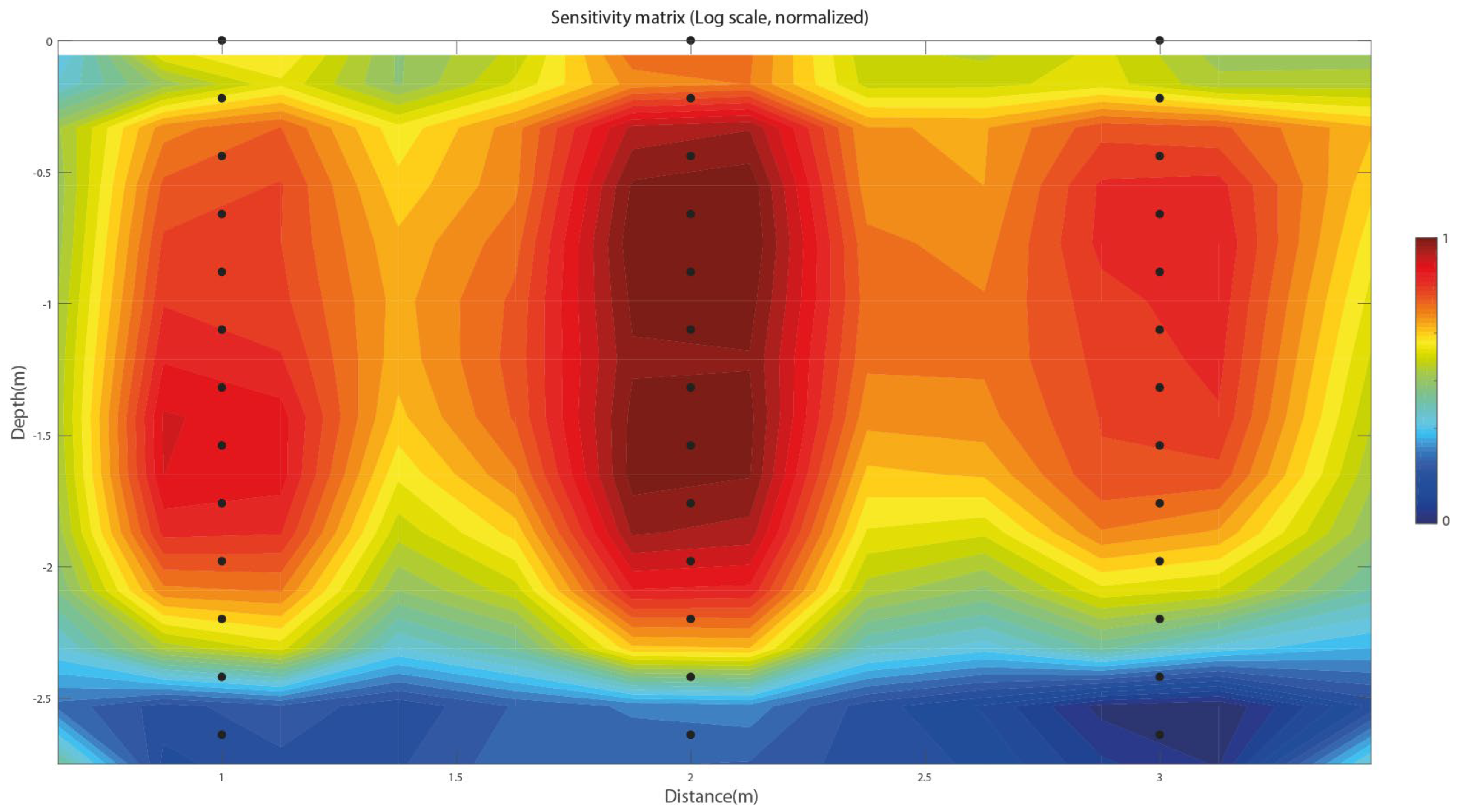
- Numerical modeling to evaluate the optimum array (Section 4.1).
- (2)
- Evaluate the results with real data, collected from a tank filled with water. In the water-filled tank (Section 4.2), we placed a layer of sandbags (Section 4.4). We replaced a few of the sandbags with iron-grout sandbags and evaluated the performance of the reduced arrays.
- (3)
- We show the grout experiment data and results (Section 5).
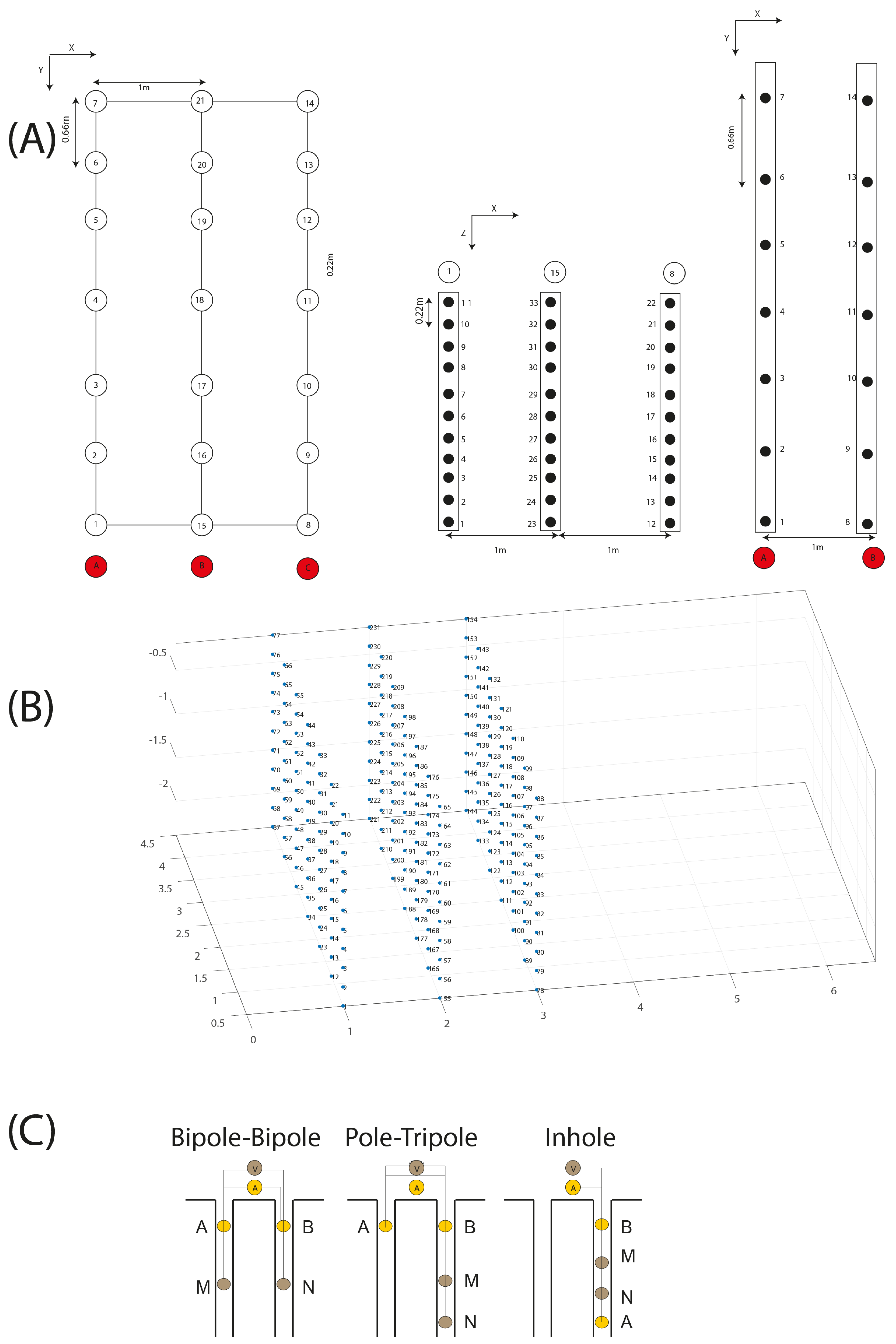
Details of the Lab Setup
4. Optimization in Water Tank
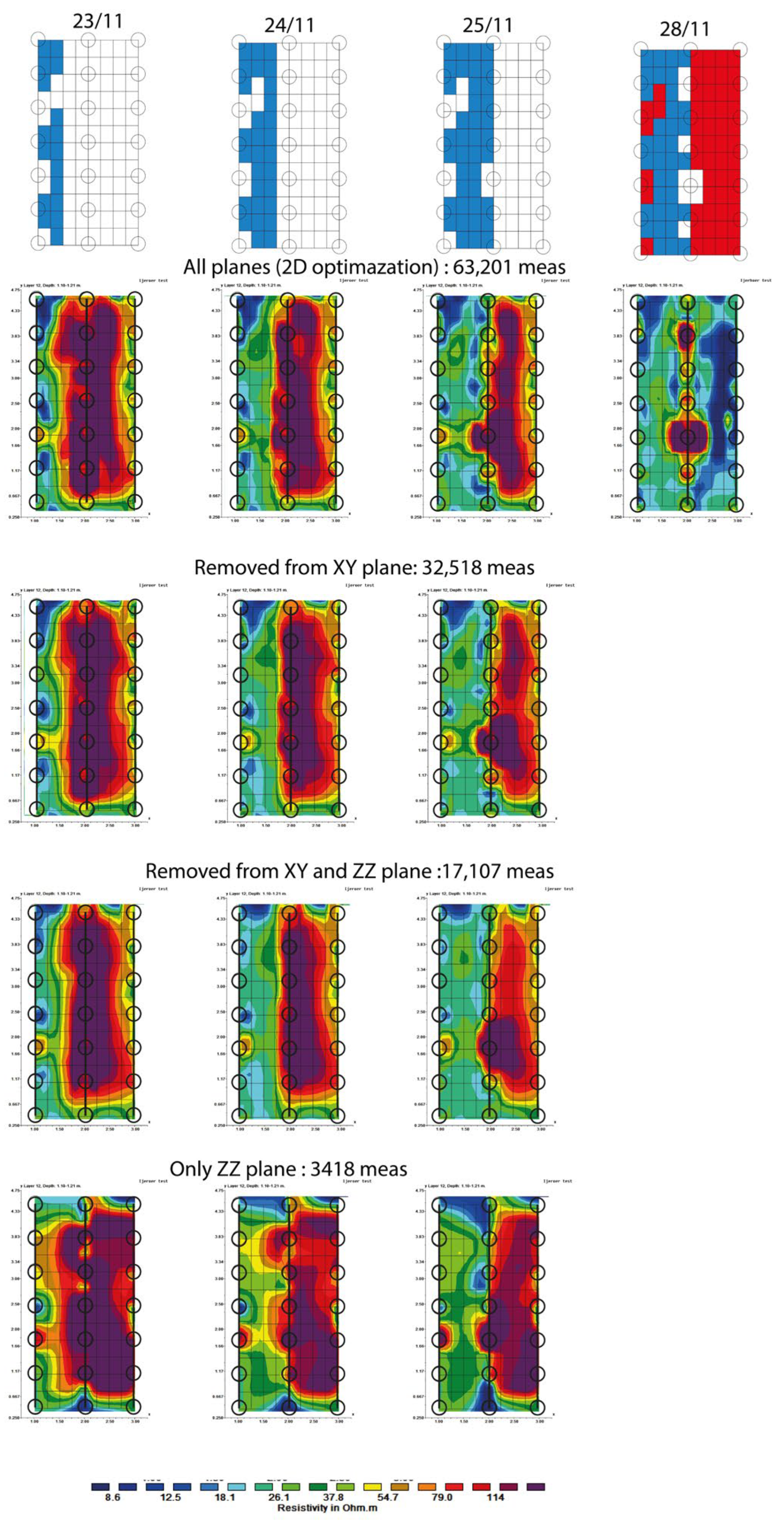
4.1. Optimization in 2D Planes (Numerical Modeling)
4.2. Lab Test (Evaluation with Real Data)
4.3. Effects of Additional Equipment
4.4. Sandbag Tests—Results
- (a)
- On the XZ plane, for instance, between 1 and 15 boreholes (i.e., row A and B) and also between 15 and 8 (i.e., row B and C).
- (b)
- On the XY plane, in two directions, for instance, 1 and 16 and 2 and 15.
- (c)
- On the ZZ plane, for instance, between A and B and also between B and C.
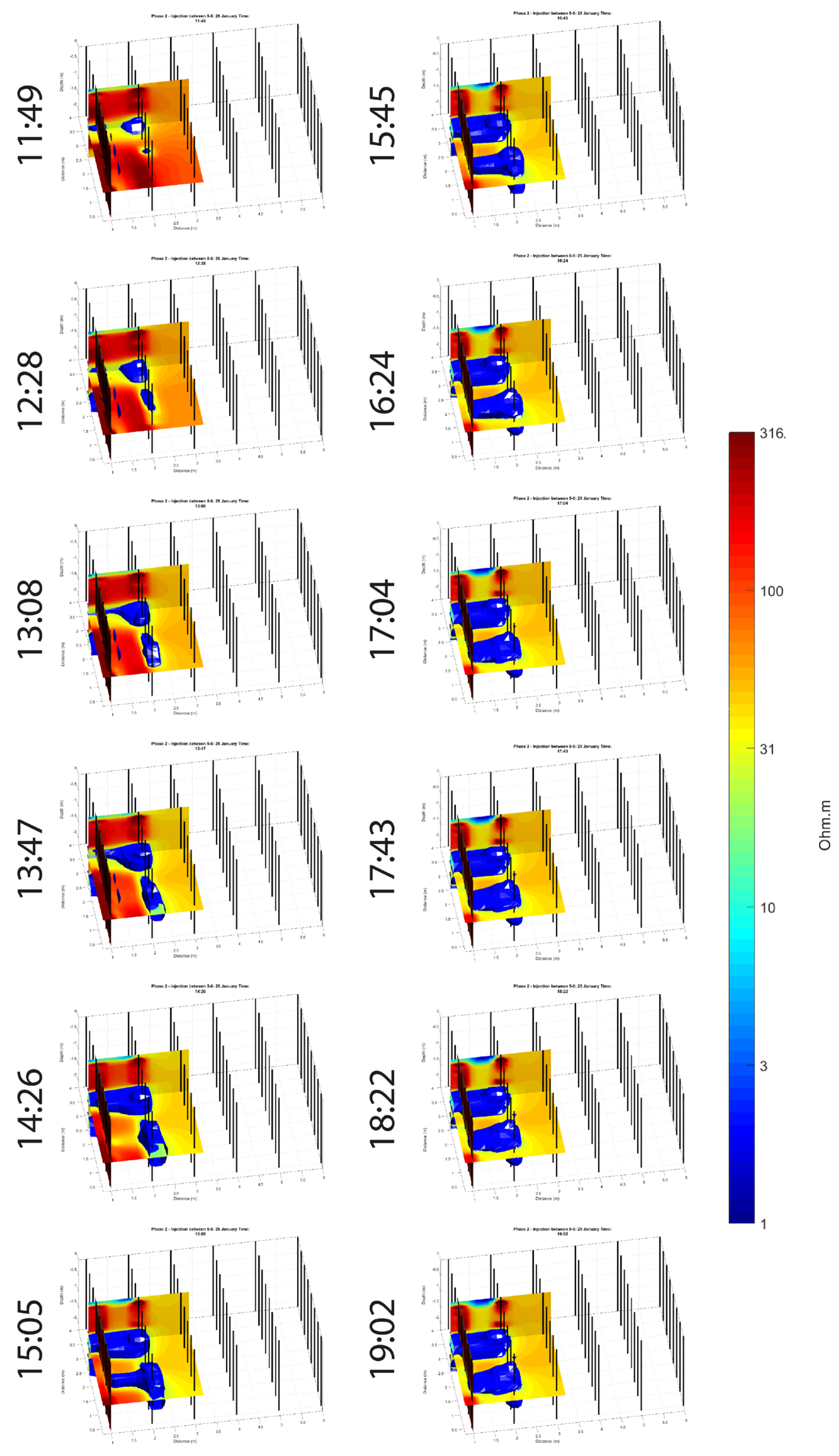
5. Injection Test—Results
- A-1-2-B;
- B-3-4-C;
- C-5-6-D.
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Q.; Li, Q.; Wu, J.; Li, X.; Li, H.; Cheng, Y. Wellhead Stability During Development Process of Hydrate Reservoir in the Northern South China Sea: Evolution and Mechanism. Processes 2025, 13, 1630. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Cao, H.; Wu, J.; Wang, F.; Wang, Y. The Crack Propagation Behaviour of CO2 Fracturing Fluid in Unconventional Low Permeability Reservoirs: Factor Analysis and Mechanism Revelation. Processes 2025, 13, 159. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers (USACE). Grouting Technology Manual; EM 1110-2-3506; USACE: Washington, DC, USA, 1995.
- Chambers, J.E.; Gunn, D.A.; Wilkinson, P.B.; Meldrum, P.I.; Haslam, E.; Holyoake, S.; Kirkham, M.; Kuras, O.; Merritt, A.; Wragg, J. 4D electrical resistivity tomography monitoring of soil moisture dynamics in an operational railway embankment. Near Surf. Geophys. 2014, 12, 61–72. [Google Scholar] [CrossRef]
- Uhlemann, S.; Chambers, J.; Falck, W.E.; Tirado Alonso, A.; Fernández González, J.L.; Espín de Gea, A. Applying Electrical Resistivity Tomography in Ornamental Stone Mining: Challenges and Solutions. Minerals 2018, 8, 491. [Google Scholar] [CrossRef]
- Uhlemann, S.S.; Chambers, J.E.; Meldrum, P.I.; Wilkinson, P.B.; Gunn, D.A.; Hutchinson, D.; Swift, R.; Dijkstra, T.A.; Kuras, O. Imaging of Moisture Dynamics within an Operational Railway Cutting—The Effects of Vegetation. 2016. Available online: https://www.earthdoc.org/content/papers/10.3997/2214-4609.201602050 (accessed on 27 May 2025).
- De Lange, W.; Vink, J.P. A Method to Create a Horizontal Resistance Layer by Injection of a Viscous Fluid: PLAID. Ground Water 2018, 56, 541–546. [Google Scholar] [CrossRef] [PubMed]
- Revil, A.; Karaoulis, M.; Johnson, T.; Kemna, A. Review: Some low-frequency electrical methods for subsurface characterization and monitoring in hydrogeology. Hydrogeol. J. 2012, 20, 617–658. [Google Scholar] [CrossRef]
- Loke, M.H.; Chambers, J.E.; Rucker, D.F.; Kuras, O.; Wilkinson, P.B. Recent developments in the direct-current geoelectrical imaging method. J. Appl. Geophys. 2013, 95, 135–156. [Google Scholar] [CrossRef]
- Stummer, P.; Maurer, H.; Green, A. Experimental design: Electrical resistivity data sets that provide optimum subsurface information. Geophysics 2004, 69, 120–129. [Google Scholar] [CrossRef]
- Wilkinson, P.B.; Meldrum, P.I.; Chambers, J.E.; Kuras, O.; Ogilvy, R.D. Improved strategies for the automatic selection of optimized sets of Electrical Resistivity Tomography measurement configurations. Geophys. J. Int. 2006, 167, 1119–1126. [Google Scholar] [CrossRef]
- Wilkinson, P.B.; Chambers, J.E.; Lelliott, M.; Wealthall, G.P.; Ogilvy, R.D. Extreme sensitivity of crosshole electrical resistivity tomography measurements to geometric errors. Geophys. J. Int. 2008, 173, 49–62. [Google Scholar] [CrossRef]
- Wilkinson, P.B.; Loke, M.H.; Meldrum, P.I.; Chambers, J.E.; Kuras, O.; Gunn, D.A.; Ogilvy, R.D. Practical aspects of applied optimized survey design for electrical resistivity tomography. Geophys. J. Int. 2012, 189, 428–440. [Google Scholar] [CrossRef]
- Furman, A.; Ferré, T.P.A.; Warrick, A.W. Optimization of ERT surveys for monitoring transient hydrological events using perturbation sensitivity and genetic algorithms. Vadose Zone J. 2004, 3, 1230–1239. [Google Scholar] [CrossRef]
- Hennig, T.; Weller, A. Two-dimensional object-oriented focusing of geoelectrical multi-electrode measurements. In Proceedings of the 11th Meeting of the EAGE Near Surface Geophysics Conference, Palermo, Italy, 4–7 September 2005. [Google Scholar]
- Athanasiou, E.N.; Tsourlos, P.I.; Vargemezis, G.N. Optimizing electrical resistivity array configurations for hydrogeological studies. In Proceedings of the TIAC’07 International Conference on Technology of Seawater Intrusion in Coastal Aquifers, Almeria, Spain, 16–19 October 2007. [Google Scholar]
- Wilkinson, P.B.; Uhlemann, S.; Meldrum, P.I.; Chambers, J.E.; Carrière, S.; Oxby, L.S.; Loke, M.H. Adaptive time-lapse optimized survey design for electrical resistivity tomography monitoring. Geophys. J. Int. 2015, 203, 755–766. [Google Scholar] [CrossRef]
- Tsakiribaloglou, K.; Tsourlos, P.; Vargemezis, G.; Tsokas, G. An Algorithm for the Adaptive Optimization of ERT Measurements. In Proceedings of the Near Surface Geoscience 2016-22nd European Meeting of Environmental and Engineering Geophysics, Barcelona, Spain, 4–8 September 2016. [Google Scholar]
- Loke, M.H. Res2Dinv ver. 3.59 for Windows XP/Vista/7: Rapid 2-D Resistivity & IP Inversion Using the Least-Squares Method; Geoelectrical Imaging 2D & 3D; Geotomo Software: Gelugor, Malaysia, 2010. [Google Scholar]
- Kim, J.-H.; Yi, M.J.; Park, S.G.; Kim, J.G. 4-D inversion of DC resistivity monitoring data acquired over a dynamically changing earth model. J. Appl. Geophys. 2009, 68, 522–532. [Google Scholar] [CrossRef]
- Karaoulis, M.; Revil, A.; Tsourlos, P.; Werkema, D.D.; Minsley, B.J. IP4DI: A software for time-lapse 2D/3D DC-resistivity and induced polarization tomography. Comput. Geosci. 2013, 54, 164–170. [Google Scholar] [CrossRef]
- Tsourlos, P.; Jochum, B.; Supper, R.; Ottowitz, D.; Kim, J.H. Optimizing Geoelectrical Arrays for Special Geoelectrical Monitoring Instruments. In Proceedings of the Near Surface Geoscience 2016-22nd European Meeting of Environmental and Engineering Geophysics, Barcelona, Spain, 4–8 September 2016. [Google Scholar]
- Athanasiou, E. Development of Algorithms Producing Optimum Strategies for Measuring and Inverting Electrical Resistivity Tomography (ERT) Data. Ph.D. Thesis, Aristotle University of Thessaloniki, Thessaloniki, Greece, 2009. [Google Scholar]
- Slater, L.; Binley, A.; Versteeg, R.; Cassiani, G.; Birken, R.; Sandberg, S. A 3D ERT study of solute transport in a large experimental tank. J. Appl. Geophys. 2002, 49, 211–229. [Google Scholar] [CrossRef]
- Karaoulis, M.; Pauw, P.; Nivorlis, A.; Tsourlos, P. Evaluating data compression of ERT time-lapse measures in a DUNEA extraction well. Gelmon, 2025; in press. [Google Scholar]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karaoulis, M. Optimization of 3D Borehole Electrical Resistivity Tomography (ERT) Measurements for Real-Time Subsurface Imaging. Water 2025, 17, 1695. https://doi.org/10.3390/w17111695
Karaoulis M. Optimization of 3D Borehole Electrical Resistivity Tomography (ERT) Measurements for Real-Time Subsurface Imaging. Water. 2025; 17(11):1695. https://doi.org/10.3390/w17111695
Chicago/Turabian StyleKaraoulis, Marios. 2025. "Optimization of 3D Borehole Electrical Resistivity Tomography (ERT) Measurements for Real-Time Subsurface Imaging" Water 17, no. 11: 1695. https://doi.org/10.3390/w17111695
APA StyleKaraoulis, M. (2025). Optimization of 3D Borehole Electrical Resistivity Tomography (ERT) Measurements for Real-Time Subsurface Imaging. Water, 17(11), 1695. https://doi.org/10.3390/w17111695





