Developing Machine Learning Models for Optimal Design of Water Distribution Networks Using Graph Theory-Based Features
Abstract
1. Introduction
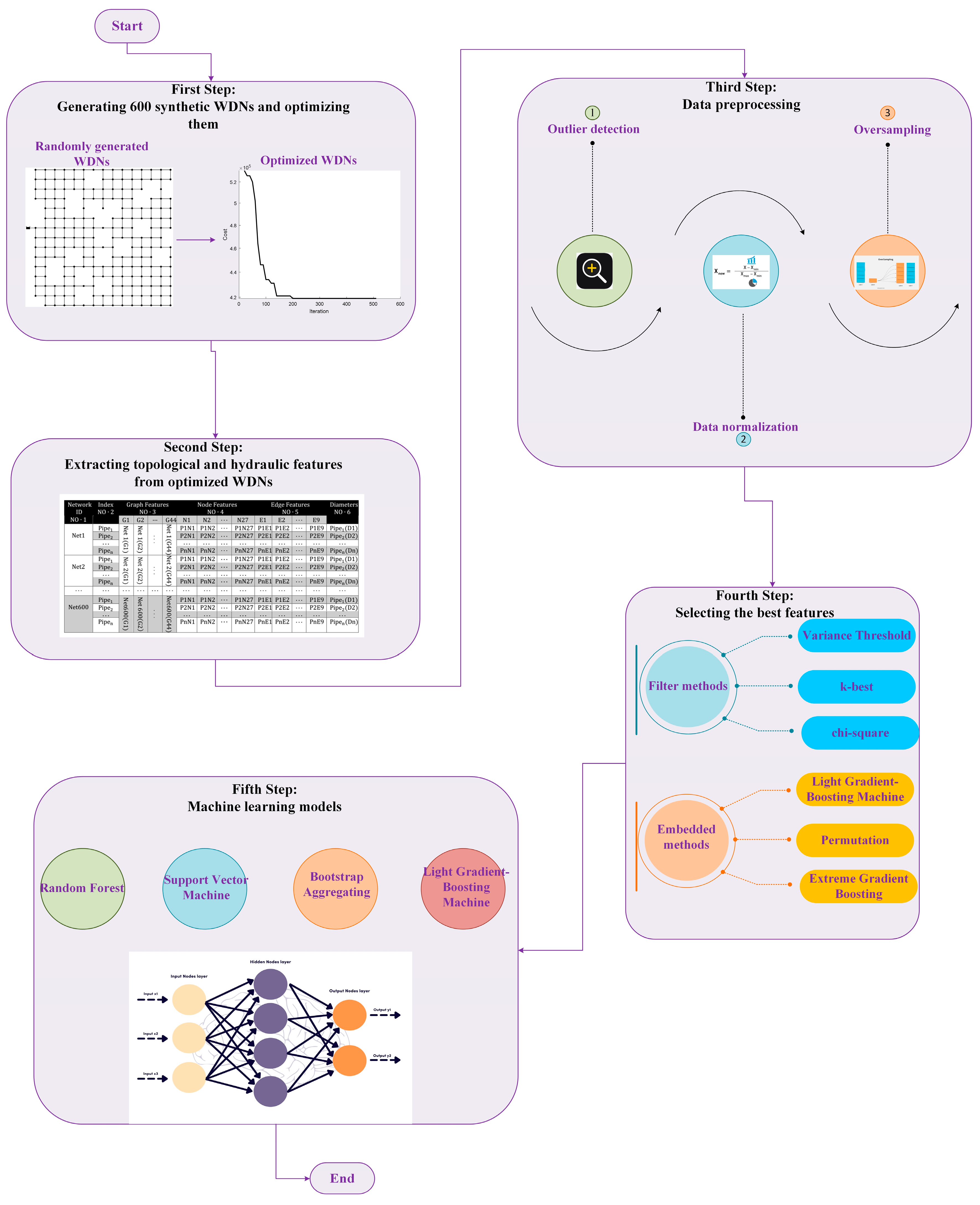
2. Methodology
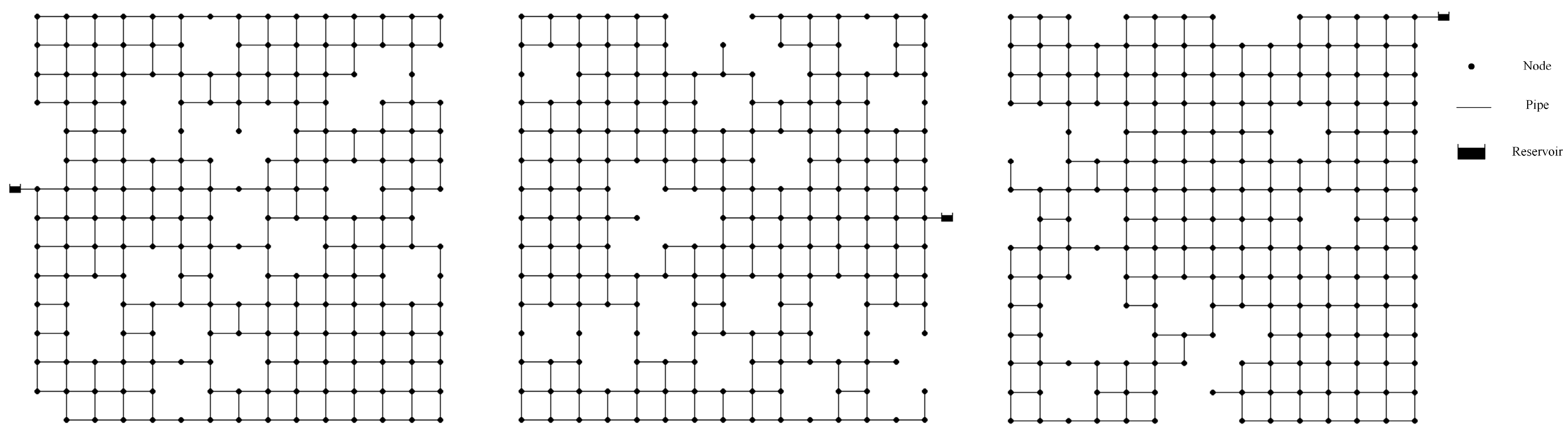
2.1. Synthetic Water Distribution Network Generation
- Number of nodes: Between 16 and 141 nodes
- Number of pipes: Between 24 and 252 pipes
- Pipe lengths: Between 20 and 100 m
- Hazen-Williams friction coefficient: In the 80 to 130 range
- Reservoir head height: Between 20 and 90 m
- Number of loops: Between 9 and 112 loops
2.2. Water Distribution Network Optimization
2.3. Topological and Hydraulic Features
- Node and overall network graph features are assigned to pipes.
- For each pipe, the average of features from connecting nodes is calculated and assigned as a descriptive feature.
- Features derived from the overall network graph are uniformly applied to all pipes within that network, aiding in network differentiation during the learning process.
- Undirected graphs are used for features such as square clustering coefficient, node eccentricity, and pipe length index.
- Directed graphs are necessary for features like degree of centrality and shortest path from the reservoir to nodes.
- Some features, including node closeness centrality index and betweenness centrality indices, require examination of both directed and undirected graphs.
2.4. Database Preparation
- Outlier Data Detection: Identifying and handling outliers is crucial, as these anomalous values can significantly impact model training, reducing accuracy and generalizability. In this study, outliers are defined as data points whose distance from the same dataset’s mean exceeds four times the standard deviation. Once identified, outliers are removed from the final database.
- Data Normalization: Normalization is performed using the Min-max normalization method. This step is vital for (1) aligning features with different scales and (2) preventing the disproportionate impact of varying value ranges (e.g., pipe lengths vs. node pressures) on machine learning model performance.
2.5. Feature Selection Methods
- 1.
- Chi2
- 2.
- Var
- Kb
- 4.
- LGB
- 5.
- Per
- 6.
- Xg
2.6. Machine Learning Models
2.6.1. Regression in Machine Learning
- 1.
- Random Forest (RF)
- 2.
- SVM
- 3.
- BAG
- 4.
- LGB
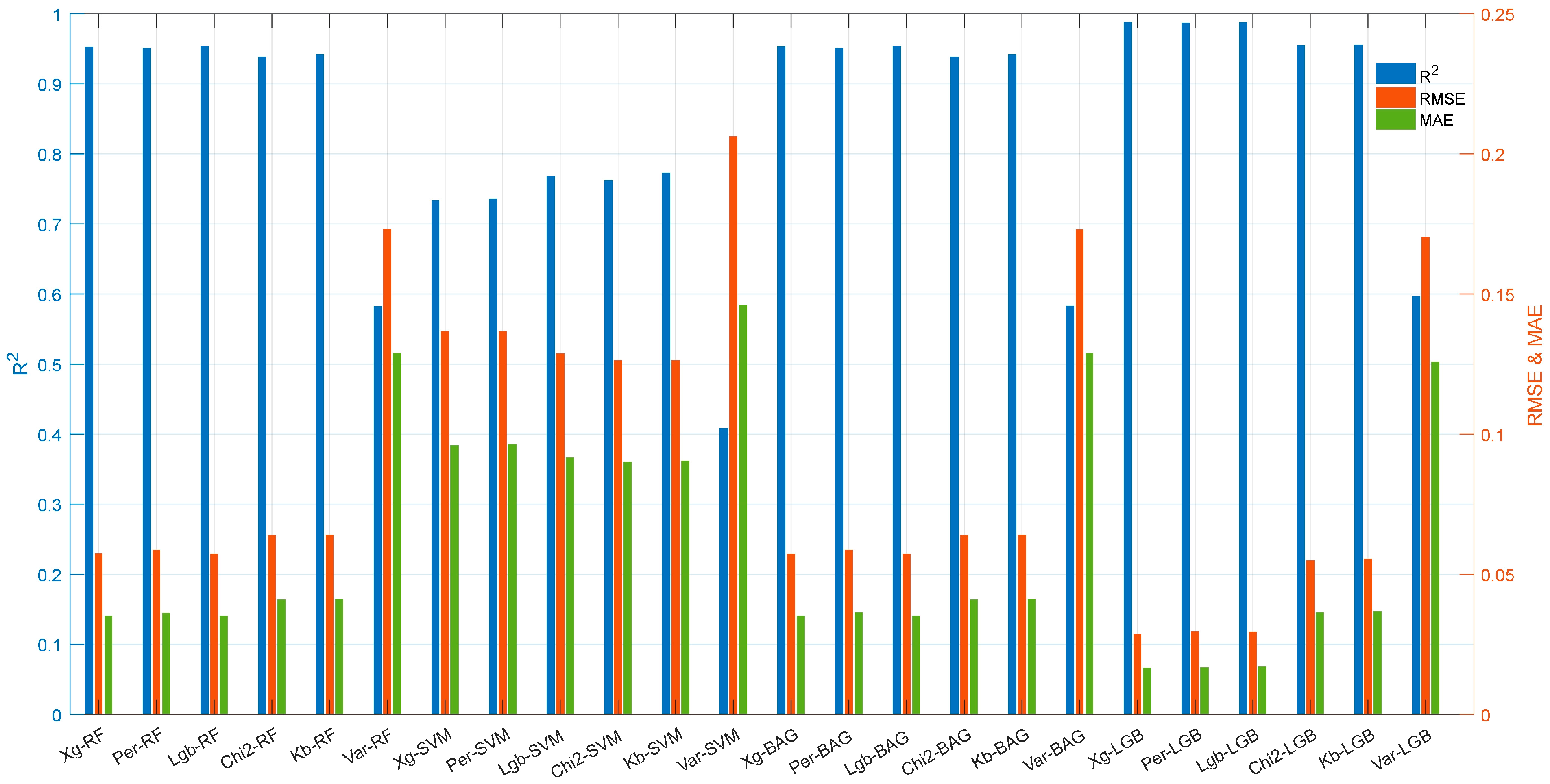
2.6.2. Model Evaluation
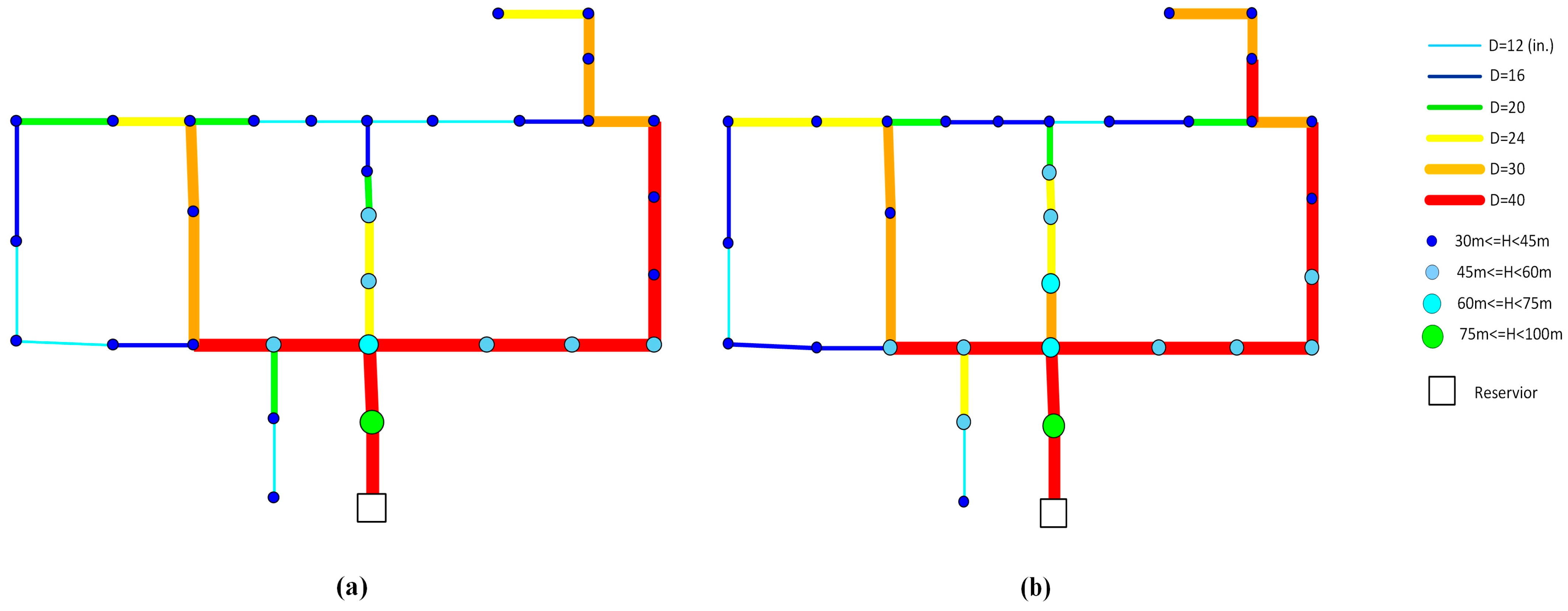
2.6.3. Hanoi WDN
- Minimum pressure head at demand nodes: 30 m
- Hazen-Williams coefficient for all pipes: 130
3. Results and Discussion
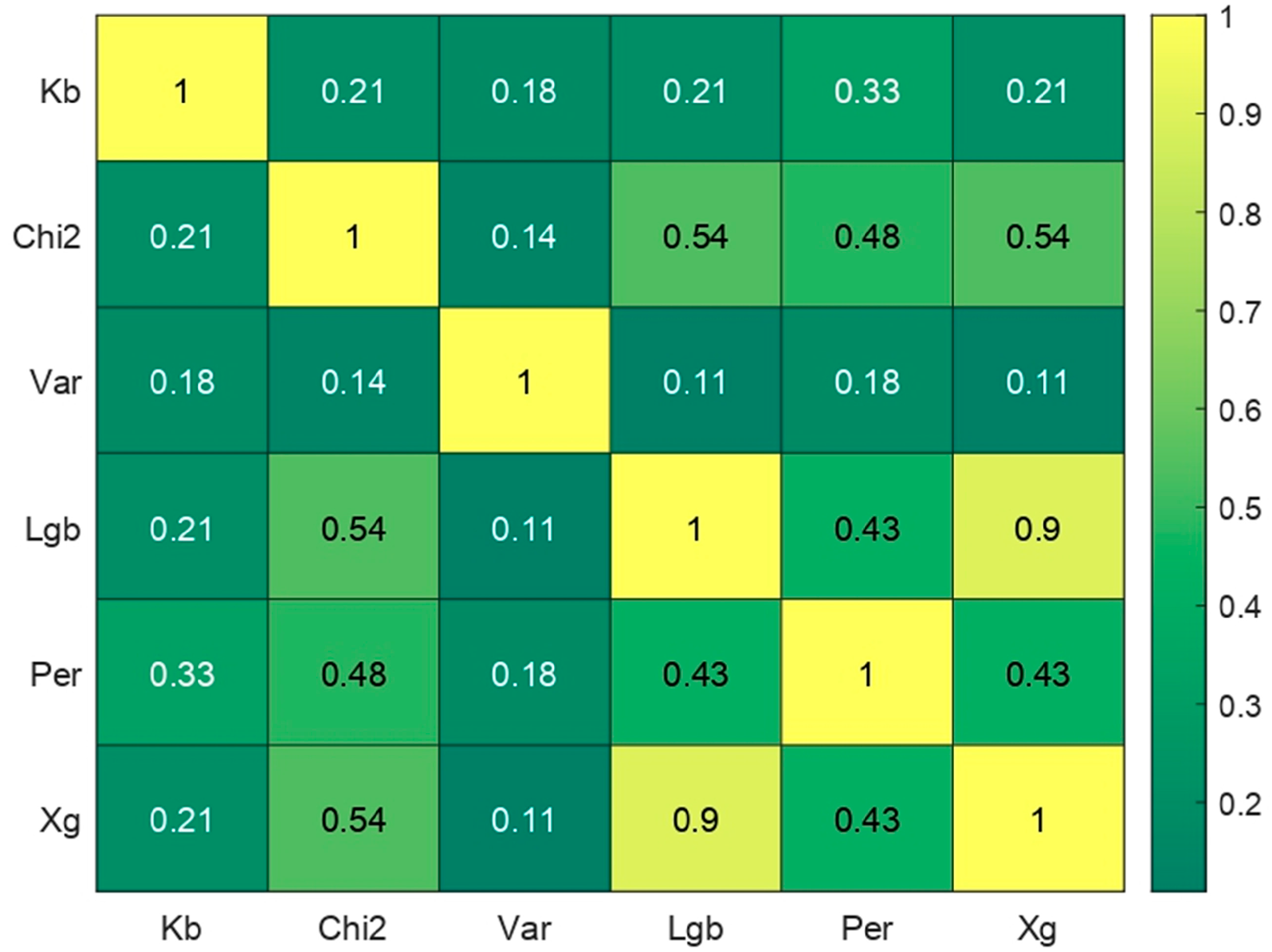
- Node-related features dominate in four methods (Xg, Per, LGB, and Chi2)
- Overall network graph properties are most prominent in two methods (Kb and Var)
- N5 and N7 (weighted node centrality degrees) consistently rank in the top quartile for most methods, except Var
- Features that use pipe resistance (R) as a weighted criterion show greater importance than those based on pipe length.
- Node features: 50% on average
- Pipe features: 26% on average
- Graph features: 24% on average
- Filter methods (e.g., Kb and Var) tend to select more overall network graph features.
- Embedded methods (e.g., Xg, Per, LGB) primarily select node and pipe features.
- Top features from each selection method are paired with corresponding optimal diameters.
- These feature sets are used as inputs for four machine learning models.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Index | Features Name | |||
| Node Centrality Degree | ||||
| Output Degree of Directed Graph Nodes | ||||
| Input Degree of Directed Graph Nodes | ||||
| Internal Weighted Centrality Degree for Weighted Multiplication of Input Edge Lengths by Input Degree in the Directed Graph | ||||
| Internal Weighted Centrality Degree for Weighted Multiplication of Resistance Index (R) of Input Edges by Input Degree in the Directed Graph | ||||
| External Weighted Centrality Degree for Weighted Multiplication of Input Edge Lengths by Input Degree in the Directed Graph | ||||
| External Weighted Centrality Degree for Weighted Multiplication of Resistance Index (R) of Input Edges by Input Degree in the Directed Graph | ||||
| Average Diameter of Tubes Connected to Node | ||||
| Minimum Weighted Length Distance from Reservoir to Node in the Directed Graph | ||||
| Minimum Weighted Resistance Distance from Reservoir to Node in the Directed Graph | ||||
| Node Clustering Coefficient in the Undirected Graph | ||||
| Weighted Length Closeness Centrality Index in the Undirected Graph | ||||
| Weighted Resistance Closeness Centrality Index in the Undirected Graph | ||||
| Weighted Length Closeness Centrality Index in the Directed Graph | ||||
| Weighted Resistance Closeness Centrality Index in the Directed Graph | ||||
| Weighted Length Betweenness Centrality Index in the Undirected Graph | ||||
| Weighted Resistance Betweenness Centrality Index in the Undirected Graph | ||||
| Weighted Length Betweenness Centrality Index in the Directed Graph | ||||
| Weighted Resistance Betweenness Centrality Index in the Directed Graph | ||||
| Weighted Length Eigenvector Centrality Index in the Undirected Graph | ||||
| Weighted Length Eigenvector Centrality Index in the Directed Graph | ||||
| Weighted Resistance Eigenvector Centrality Index in the Directed Graph | ||||
| Subgraph Centrality Index in the Undirected Graph | ||||
| Weighted Length Node Eccentricity Index in the Undirected Graph | ||||
| Weighted Resistance Node Eccentricity Index in the Undirected Graph | ||||
| Consumption Flow Rates at Nodes | ||||
| Pressure at Nodes | ||||
| Pipe Roughness Index | ||||
| Pipe Diameter Index | ||||
| Pipe Length Index | ||||
| Weighted Length Edge Betweenness Centrality Index in the Undirected Graph | ||||
| Weighted Resistance Edge Betweenness Centrality Index in the Undirected Graph | ||||
| Weighted Length Edge Betweenness Centrality Index in the Directed Graph | ||||
| Weighted Resistance Edge Betweenness Centrality Index in the Directed Graph | ||||
| Flow Velocity Index in Pipe | ||||
| Energy Loss Index per Pipe Length | ||||
| Average Minimum Weighted Length Distance from Reservoir to Node in the Overall Directed Graph | ||||
| Average Minimum Weighted Resistance Distance from Reservoir to Node in the Overall Directed Graph | ||||
| Graph Diameter of Weighted Length Type in Overall Undirected Graph | ||||
| Graph Diameter of Weighted Resistance Type in the Overall Undirected Graph | ||||
| Graph Radius of Weighted Length Type in the Overall Undirected Graph | ||||
| Graph Radius of Weighted Resistance Type in the Overall Undirected Graph | ||||
| Graph Efficiency in the Overall Undirected Graph | ||||
| Average Closeness Centrality Index of Weighted Length Type in the Overall Undirected Graph | ||||
| Average Closeness Centrality Index of Weighted Resistance Type in the Overall Undirected Graph | ||||
| Average Closeness Centrality Index of Weighted Length Type in the Overall Directed Graph | ||||
| Average Closeness Centrality Index of Weighted Resistance Type in the Overall Directed Graph | ||||
| Average Betweenness Centrality Index of Weighted Length Type in the Overall Undirected Graph | ||||
| Average Betweenness Centrality Index of Weighted Resistance Type in the Overall Undirected Graph | ||||
| Average Betweenness Centrality Index of Weighted Length Type in the Overall Directed Graph | ||||
| Average Betweenness Centrality Index of Weighted Resistance Type in the Overall Directed Graph | ||||
| Dominance of Central Point of Weighted Length Type in the Overall Undirected Graph | ||||
| Dominance of Central Point of Weighted Resistance Type in the Overall Undirected Graph | ||||
| Dominance of Central Point of Weighted Length Type in Overall Directed Graph | ||||
| Dominance of Central Point of Weighted Resistance Type in the Overall Directed Graph | ||||
| Average Graph Degree in the Overall Undirected Graph | ||||
| Average Output Degree in the Overall Directed Graph | ||||
| Maximum Degree in the Overall Undirected Graph | ||||
| Maximum Input Degree in the Overall Directed Graph | ||||
| Maximum Output Degree in the Overall Directed Graph | ||||
| Average Node Square Clustering Coefficient in the Overall Undirected Graph | ||||
| Algebraic Connectivity Index in the Overall Undirected Graph | ||||
| Algebraic Connectivity Index of Weighted Length Type in the Overall Undirected Graph | ||||
| Algebraic Connectivity Index of Weighted Resistance Type in the Overall Undirected Graph | ||||
| Spectral Difference of the Overall Undirected Graph | ||||
| Number of Edges in the Overall Undirected Graph | ||||
| Density of the Overall Undirected Graph | ||||
| Density of the Overall Directed Graph | ||||
| Mesh Coefficient of Overall Undirected Graph | ||||
| Sum of Input Degrees of Dead-End Nodes in the Overall Directed Graph | ||||
| Normalized Minimum Cut between Reservoir and First Node with Other Nodes in the Overall Undirected Graph | ||||
| Normalized Minimum Cut of Weighted Length Type between Reservoir and First Node with Other Nodes in the Overall Undirected Graph | ||||
| Normalized Minimum Cut of Weighted Resistance Type between Reservoir and First Node with Other Nodes in Overall Undirected Graph | ||||
| Normalized Minimum Cut between Terminal Node and Other Nodes in the Overall Undirected Graph | ||||
| Normalized Minimum Cut of Weighted Length Type between Terminal Node and Other Nodes in the Overall Undirected Graph | ||||
| Normalized Minimum Cut of Weighted Resistance Type between Terminal Node and Other Nodes in the Overall Undirected Graph | ||||
| Total Network Length in the Overall Graph | ||||
| Overall Network Resistance Index in the Overall Undirected Graph | ||||
| Water Level in Reservoir in the Overall Graph | ||||
| Total Input Flow to Network in the Overall Graph | ||||
Appendix B
Appendix B.1. Whale Optimization Algorithm (WOA)
- (1)
- Prey Encircling (Exploitation Phase)
- (2)
- Bubble-Net Attacking (Local Search Phase)
- (3)
- Searching for Prey (Exploration Phase)
| Optimization Algorithm | Hyperparameter | Tuning Range of Hyperparameter Values | Optimal Hyperparameter Values |
|---|---|---|---|
| WOA | Number of Whales | 20–50 | 30 |
| Number of Iterations | 50–200 | 100 |
Appendix B.2. Artificial Neural Networks (ANNs)
| Pipe Number | Predicted Diameters | ||
|---|---|---|---|
| Pipe Diameters from [101] (In) | Commercial Pipe Diameters from Xg-LGB Model (In) | Commercial Pipe Diameters from ANN-WOA Model (In) | |
| 1 | 40 | 40 | 40 |
| 2 | 40 | 40 | 40 |
| 3 | 40 | 40 | 40 |
| 4 | 40 | 40 | 40 |
| 5 | 40 | 40 | 40 |
| 6 | 40 | 40 | 40 |
| 7 | 40 | 40 | 40 |
| 8 | 40 | 40 | 40 |
| 9 | 30 | 30 | 40 |
| 10 | 30 | 40 | 30 |
| 11 | 30 | 30 | 30 |
| 12 | 24 | 30 | 20 |
| 13 | 16 | 20 | 20 |
| 14 | 12 | 16 | 16 |
| 15 | 12 | 12 | 16 |
| 16 | 16 | 20 | 20 |
| 17 | 20 | 24 | 24 |
| 18 | 24 | 24 | 30 |
| 19 | 24 | 30 | 30 |
| 20 | 40 | 40 | 40 |
| 21 | 20 | 24 | 24 |
| 22 | 12 | 12 | 16 |
| 23 | 40 | 40 | 40 |
| 24 | 30 | 30 | 40 |
| 25 | 30 | 30 | 30 |
| 26 | 20 | 20 | 24 |
| 27 | 12 | 16 | 16 |
| 28 | 12 | 16 | 12 |
| 29 | 16 | 16 | 20 |
| 30 | 12 | 16 | 16 |
| 31 | 12 | 12 | 12 |
| 32 | 16 | 16 | 16 |
| 33 | 20 | 24 | 20 |
| 34 | 24 | 24 | 24 |
References
- Swamee, P.K.; Sharma, A.K. Design of Water Supply Pipe Networks; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Gupta, I. Linear programming analysis of a water supply system. AIIE Trans. 1969, 1, 56–61. [Google Scholar] [CrossRef]
- Karmeli, D.; Gadish, Y.; Meyers, S. Design of optimal water distribution networks. J. Pipeline Div. 1968, 94, 1–10. [Google Scholar] [CrossRef]
- Schaake, J.C., Jr.; Lai, D. Linear Programming and Dynamic Programming Application to Water Distribution Network Design; M.I.T. Hydrodynamics Laboratory: Cambridge, MA, USA, 1969. [Google Scholar]
- Su, Y.-C.; Mays, L.W.; Duan, N.; Lansey, K.E. Reliability-based optimization model for water distribution systems. J. Hydraul. Eng. 1987, 113, 1539–1556. [Google Scholar] [CrossRef]
- Duan, N.; Mays, L.W.; Lansey, K.E. Optimal reliability-based design of pumping and distribution systems. J. Hydraul. Eng. 1990, 116, 249–268. [Google Scholar] [CrossRef]
- Samani, H.M.; Taghi Naeeni, S. Optimization of water distribution networks. J. Hydraul. Res. 1996, 34, 623–632. [Google Scholar] [CrossRef]
- Murphy, L.; Simpson, A. Pipe optimization using genetic algorithms. Res. Rep. 1992, 93, 95. [Google Scholar]
- Savic, D.A.; Walters, G.A. Genetic algorithms for least-cost design of water distribution networks. J. Water Resour. Plan. Manag. 1997, 123, 67–77. [Google Scholar] [CrossRef]
- Simpson, A.R.; Dandy, G.C.; Murphy, L.J. Genetic algorithms compared to other techniques for pipe optimization. J. Water Resour. Plan. Manag. 1994, 120, 423–443. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M. Low level hybrid procedure for the multi-objective design of water distribution networks. Procedia Eng. 2014, 70, 369–378. [Google Scholar] [CrossRef][Green Version]
- Farmani, R.; Walters, G.A.; Savic, D.A. Trade-off between total cost and reliability for Anytown water distribution network. J. Water Resour. Plan. Manag. 2005, 131, 161–171. [Google Scholar] [CrossRef]
- Farmani, R.; Walters, G.; Savic, D. Evolutionary multi-objective optimization of the design and operation of water distribution network: Total cost vs. reliability vs. water quality. J. Hydroinform. 2006, 8, 165–179. [Google Scholar] [CrossRef]
- Prasad, T.D.; Park, N.-S. Multiobjective genetic algorithms for design of water distribution networks. J. Water Resour. Plan. Manag. 2004, 130, 73–82. [Google Scholar] [CrossRef]
- Riyahi, M.M.; Bakhshipour, A.E.; Haghighi, A. Probabilistic warm solutions-based multi-objective optimization algorithm, application in optimal design of water distribution networks. Sustain. Cities Soc. 2023, 91, 104424. [Google Scholar] [CrossRef]
- Todini, E. Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Elshaboury, N.; Marzouk, M. Prioritizing water distribution pipelines rehabilitation using machine learning algorithms. Soft Comput. 2022, 26, 5179–5193. [Google Scholar] [CrossRef]
- Jafari, S.M.; Nikoo, M.R.; Bozorg-Haddad, O.; Alamdari, N.; Farmani, R.; Gandomi, A.H. A robust clustering-based multi-objective model for optimal instruction of pipes replacement in urban WDN based on machine learning approaches. Urban Water J. 2023, 20, 689–706. [Google Scholar] [CrossRef]
- Maußner, C.; Oberascher, M.; Autengruber, A.; Kahl, A.; Sitzenfrei, R. Explainable artificial intelligence for reliable water demand forecasting to increase trust in predictions. Water Res. 2025, 268, 122779. [Google Scholar] [CrossRef]
- Namdari, H.; Haghighi, A.; Ashrafi, S.M. Short-term urban water demand forecasting; application of 1D convolutional neural network (1D CNN) in comparison with different deep learning schemes. Stoch. Environ. Res. Risk Assess. 2023, 1–16. [Google Scholar] [CrossRef]
- Baziar, M.; Behnami, A.; Jafari, N.; Mohammadi, A.; Abdolahnejad, A. Machine learning-based Monte Carlo hyperparameter optimization for THMs prediction in urban water distribution networks. J. Water Process Eng. 2025, 73, 107683. [Google Scholar] [CrossRef]
- Magini, R.; Moretti, M.; Boniforti, M.A.; Guercio, R. A machine-learning approach for monitoring water distribution networks (WDNS). Sustainability 2023, 15, 2981. [Google Scholar] [CrossRef]
- Pandian, C.; Alphonse, P. Evaluating water pipe leak detection and localization with various machine learning and deep learning models. Int. J. Syst. Assur. Eng. Manag. 2025, 1–13. [Google Scholar] [CrossRef]
- Ayati, A.H.; Haghighi, A. Multiobjective wrapper sampling design for leak detection of pipe networks based on machine learning and transient methods. J. Water Resour. Plan. Manag. 2023, 149, 04022076. [Google Scholar] [CrossRef]
- Pei, S.; Hoang, L.; Fu, G.; Butler, D. Real-time multi-objective optimization of pump scheduling in water distribution networks using neuro-evolution. J. Water Process Eng. 2024, 68, 106315. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Macmillan London: London, UK, 1976; Volume 290. [Google Scholar]
- Hamam, Y.; Brameller, A. Hybrid method for the solution of piping networks. Proc. Inst. Electr. Eng. 1971, 118, 1607–1612. [Google Scholar] [CrossRef]
- Kesavan, H.K.; Chandrashekar, M. Graph-theoretic models for pipe network analysis. J. Hydraul. Div. 1972, 98, 345–364. [Google Scholar] [CrossRef]
- Riyahi, M.M.; Bakhshipour, A.E.; Giudicianni, C.; Dittmer, U.; Haghighi, A.; Creaco, E. An Analytical Solution for the Hydraulics of Looped Pipe Networks. Eng. Proc. 2024, 69, 4. [Google Scholar]
- Sitzenfrei, R. A graph-based optimization framework for large water distribution networks. Water 2023, 15, 2896. [Google Scholar] [CrossRef]
- Jung, D.; Yoo, D.G.; Kang, D.; Kim, J.H. Linear model for estimating water distribution system reliability. J. Water Resour. Plan. Manag. 2016, 142, 04016022. [Google Scholar] [CrossRef]
- Alzamora, F.M.; Ulanicki, B.; Zehnpfund. Simplification of Water Distribution Network Models. In Proceedings of the 2nd International Conference on Hydroinformatic, Zurich, Switzerland, 9–13 September 1996. [Google Scholar]
- Giudicianni, C.; di Nardo, A.; Oliva, G.; Scala, A.; Herrera, M. A dimensionality-reduction strategy to compute shortest paths in urban water networks. arXiv 2019, arXiv:1903.11710. [Google Scholar]
- Satish, R.; Hajibabaei, M.; Dastgir, A.; Oberascher, M.; Sitzenfrei, R. A graph-based method for identifying critical pipe failure combinations in water distribution networks. Water Supply 2024, 24, 2353–2366. [Google Scholar] [CrossRef]
- Ostfeld, A. Water distribution systems connectivity analysis. J. Water Resour. Plan. Manag. 2005, 131, 58–66. [Google Scholar] [CrossRef]
- Yazdani, A.; Jeffrey, P. Robustness and vulnerability analysis of water distribution networks using graph theoretic and complex network principles. In Water Distribution Systems Analysis 2010; American Society of Civil Engineers: Reston, VA, USA, 2010; pp. 933–945. [Google Scholar]
- Yazdani, A.; Otoo, R.A.; Jeffrey, P. Resilience enhancing expansion strategies for water distribution systems: A network theory approach. Environ. Model. Softw. 2011, 26, 1574–1582. [Google Scholar] [CrossRef]
- Ulusoy, A.-J.; Stoianov, I.; Chazerain, A. Hydraulically informed graph theoretic measure of link criticality for the resilience analysis of water distribution networks. Appl. Netw. Sci. 2018, 3, 1–22. [Google Scholar] [CrossRef]
- Oberascher, M.; Minaei, A.; Sitzenfrei, R. Graph-Based Genetic Algorithm for Localization of Multiple Existing Leakages in Water Distribution Networks. J. Water Resour. Plan. Manag. 2025, 151, 04024059. [Google Scholar] [CrossRef]
- Rajeswaran, A.; Narasimhan, S.; Narasimhan, S. A graph partitioning algorithm for leak detection in water distribution networks. Comput. Chem. Eng. 2018, 108, 11–23. [Google Scholar] [CrossRef]
- Di Nardo, A.; Giudicianni, C.; Greco, R.; Herrera, M.; Santonastaso, G.F. Applications of graph spectral techniques to water distribution network management. Water 2018, 10, 45. [Google Scholar] [CrossRef]
- Sitzenfrei, R.; Satish, R.; Rajabi, M.; Hajibabaei, M.; Oberascher, M. Graph-Based Methodology for Segment Criticality Assessment and Optimal Valve Placements in Water Networks. In Proceedings of the EGU General Assembly 2025, Vienna, Austria, 27 April–2 May 2025. [Google Scholar]
- Riyahi, M.M.; Giudicianni, C.; Haghighi, A.; Creaco, E. Coupled multi-objective optimization of water distribution network design and partitioning: A spectral graph-theory approach. Urban Water J. 2024, 21, 745–756. [Google Scholar] [CrossRef]
- Tzatchkov, V.G.; Alcocer-Yamanaka, V.H.; Bourguett Ortíz, V. Graph theory based algorithms for water distribution network sectorization projects. In Proceedings of the Water Distribution Systems Analysis Symposium 2006, Cincinnati, OH, USA, 27–30 August 2006; pp. 1–15. [Google Scholar]
- Deuerlein, J.W. Decomposition model of a general water supply network graph. J. Hydraul. Eng. 2008, 134, 822–832. [Google Scholar] [CrossRef]
- Price, E.; Ostfeld, A. Graph theory modeling approach for optimal operation of water distribution systems. J. Hydraul. Eng. 2016, 142, 04015061. [Google Scholar] [CrossRef]
- Price, E.; Ostfeld, A. Optimal pump scheduling in water distribution systems using graph theory under hydraulic and chlorine constraints. J. Water Resour. Plan. Manag. 2016, 142, 04016037. [Google Scholar] [CrossRef]
- Marini, G.; Fontana, N.; Maio, M.; Di Menna, F.; Giugni, M. A novel approach to avoiding technically unfeasible solutions in the pump scheduling problem. Water 2023, 15, 286. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Sayed, S.; Abdoulhalik, A.; Moutari, S.; Oyedele, L. Applications of machine learning to water resources management: A review of present status and future opportunities. J. Clean. Prod. 2024, 441, 140715. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, S.; Xin, K.; Tang, Z.; Chu, X.; Fu, G. Network embedding: The bridge between water distribution network hydraulics and machine learning. Water Res. 2025, 273, 123011. [Google Scholar] [CrossRef] [PubMed]
- Coelho, M.; Austin, M.A.; Mishra, S.; Blackburn, M. Teaching Machines to Understand Urban Networks: A Graph Autoencoder Approach. Int. J. Adv. Netw. Serv. 2020, 13, 70–81. [Google Scholar]
- Arsene, C.; Al-Dabass, D.; Hartley, J. Decision support system for water distribution systems based on neural networks and graphs. In Proceedings of the 2012 UKSim 14th International Conference on Computer Modelling and Simulation, Cambridge, UK, 28–30 March 2012; pp. 315–323. [Google Scholar]
- Kang, J.; Park, Y.-J.; Lee, J.; Wang, S.-H.; Eom, D.-S. Novel leakage detection by ensemble CNN-SVM and graph-based localization in water distribution systems. IEEE Trans. Ind. Electron. 2017, 65, 4279–4289. [Google Scholar] [CrossRef]
- Barros, D.; Zanfei, A.; Menapace, A.; Meirelles, G.; Herrera, M.; Brentan, B. Leak detection and localization in water distribution systems via multilayer networks. Water Res. X 2025, 26, 100280. [Google Scholar] [CrossRef]
- Komba, G. A Novel Leak Detection Algorithm Based on SVM-CNN-GT for Water Distribution Networks. Indones. J. Comput. Sci. 2025, 14. [Google Scholar] [CrossRef]
- Amali, S.; Faddouli, N.-e.E.; Boutoulout, A. Machine learning and graph theory to optimize drinking water. Procedia Comput. Sci. 2018, 127, 310–319. [Google Scholar] [CrossRef]
- Li, Z.; Liu, H.; Zhang, C.; Fu, G. Real-time water quality prediction in water distribution networks using graph neural networks with sparse monitoring data. Water Res. 2024, 250, 121018. [Google Scholar] [CrossRef]
- Liy-González, P.-A.; Santos-Ruiz, I.; Delgado-Aguiñaga, J.-A.; Navarro-Díaz, A.; López-Estrada, F.-R.; Gómez-Peñate, S. Pressure Interpolation in Water Distribution Networks by Using Gaussian Processes: Application to Leak Diagnosis. Processes 2024, 12, 1147. [Google Scholar] [CrossRef]
- Cheng, M.; Li, J. Optimal sensor placement for leak location in water distribution networks: A feature selection method combined with graph signal processing. Water Res. 2023, 242, 120313. [Google Scholar] [CrossRef] [PubMed]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G.F.; Simone, A. Water distribution system clustering and partitioning based on social network algorithms. Procedia Eng. 2015, 119, 196–205. [Google Scholar] [CrossRef]
- Han, R.; Liu, J. Spectral clustering and genetic algorithm for design of district metered areas in water distribution systems. Procedia Eng. 2017, 186, 152–159. [Google Scholar] [CrossRef]
- Chen, T.Y.-J.; Guikema, S.D. Prediction of water main failures with the spatial clustering of breaks. Reliab. Eng. Syst. Saf. 2020, 203, 107108. [Google Scholar] [CrossRef]
- Grammatopoulou, M.; Kanellopoulos, A.; Vamvoudakis, K.G.; Lau, N. A Multi-step and Resilient Predictive Q-learning Algorithm for IoT with Human Operators in the Loop: A Case Study in Water Supply Networks. arXiv 2020, arXiv:2006.03899. [Google Scholar]
- Xia, W.; Wang, S.; Shi, M.; Xia, Q.; Jin, W. Research on partition strategy of an urban water supply network based on optimized hierarchical clustering algorithm. Water Supply 2022, 22, 4387–4399. [Google Scholar] [CrossRef]
- Chen, R.; Wang, Q.; Javanmardi, A. A Review of the Application of Machine Learning for Pipeline Integrity Predictive Analysis in Water Distribution Networks. Arch. Comput. Methods Eng. 2025, 1–29. [Google Scholar] [CrossRef]
- Rossman, L.A.; Woo, H.; Tryby, M.; Shang, F.; Janke, R.; Haxton, T. EPANET 2.2 User Manual; Water Infrastructure Division, Center for Environmental Solutions and Emergency Response, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2020. [Google Scholar]
- Kyriakou, M.S.; Demetriades, M.; Vrachimis, S.G.; Eliades, D.G.; Polycarpou, M.M. Epyt: An epanet-python toolkit for smart water network simulations. J. Open Source Softw. 2023, 8, 5947. [Google Scholar] [CrossRef]
- Makaremi, Y.; Haghighi, A.; Ghafouri, H.R. Optimization of pump scheduling program in water supply systems using a self-adaptive NSGA-II; a review of theory to real application. Water Resour. Manag. 2017, 31, 1283–1304. [Google Scholar] [CrossRef]
- Zheng, A.; Casari, A. Feature Engineering for Machine Learning: Principles and Techniques for Data Scientists; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2018. [Google Scholar]
- Venkatesh, B.; Anuradha, J. A review of feature selection and its methods. Cybern. Inf. Technol 2019, 19, 3–26. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Probst, P.; Boulesteix, A.-L.; Bischl, B. Tunability: Importance of hyperparameters of machine learning algorithms. J. Mach. Learn. Res. 2019, 20, 1–32. [Google Scholar]
- Injadat, M.; Moubayed, A.; Nassif, A.B.; Shami, A. Systematic ensemble model selection approach for educational data mining. Knowl.-Based Syst. 2020, 200, 105992. [Google Scholar] [CrossRef]
- Liu, H.; Setiono, R. Chi2: Feature selection and discretization of numeric attributes. In Proceedings of the 7th IEEE International Conference on Tools with Artificial Intelligence, Herndon, VA, USA, 5–8 November 1995; pp. 388–391. [Google Scholar]
- Khomytska, I.; Bazylevych, I.; Teslyuk, V.; Karamysheva, I. The chi-square test and data clustering combined for author identification. In Proceedings of the 2023 IEEE 18th International Conference on Computer Science and Information Technologies (CSIT), Lviv, Ukraine, 19–21 October 2023; pp. 1–5. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Fida, M.A.F.A.; Ahmad, T.; Ntahobari, M. Variance threshold as early screening to Boruta feature selection for intrusion detection system. In Proceedings of the 2021 13th International Conference on Information & Communication Technology and System (ICTS), Surabaya, Indonesia, 20–21 October 2021; pp. 46–50. [Google Scholar]
- Desyani, T.; Saifudin, A.; Yulianti, Y. Feature selection based on naive bayes for caesarean section prediction. IOP Conf. Ser. Mater. Sci. Eng. 2020, 879, 012091. [Google Scholar] [CrossRef]
- Ye, Y.; Liu, C.; Zemiti, N.; Yang, C. Optimal feature selection for EMG-based finger force estimation using LightGBM model. In Proceedings of the 2019 28th IEEE International Conference on Robot and Human Interactive Communication (RO-MAN), New Delhi, India, 14–18 October 2019; pp. 1–7. [Google Scholar]
- Hua, Y. An efficient traffic classification scheme using embedded feature selection and lightgbm. In Proceedings of the 2020 Information Communication Technologies Conference (ICTC), Nanjing, China, 29–31 May 2020; pp. 125–130. [Google Scholar]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
- Hsieh, C.-P.; Chen, Y.-T.; Beh, W.-K.; Wu, A.-Y.A. Feature selection framework for XGBoost based on electrodermal activity in stress detection. In Proceedings of the 2019 IEEE International Workshop on Signal Processing Systems (SiPS), Nanjing, China, 20–23 October 2019; pp. 330–335. [Google Scholar]
- Alsahaf, A.; Petkov, N.; Shenoy, V.; Azzopardi, G. A framework for feature selection through boosting. Expert Syst. Appl. 2022, 187, 115895. [Google Scholar] [CrossRef]
- Riyahi, M.M.; Rahmanshahi, M.; Ranginkaman, M.H. Frequency domain analysis of transient flow in pipelines; application of the genetic programming to reduce the linearization errors. J. Hydraul. Struct. 2018, 4, 75–90. [Google Scholar]
- Han, J.; Pei, J.; Tong, H. Data Mining: Concepts and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2022. [Google Scholar]
- Messenger, R.; Mandell, L. A modal search technique for predictive nominal scale multivariate analysis. J. Am. Stat. Assoc. 1972, 67, 768–772. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random forests. In Ensemble Machine Learning: Methods and Applications; Springer: New York, NY, USA, 2012; pp. 157–175. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Scholkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Ben-Hur, A.; Weston, J. A user’s guide to support vector machines. In Data Mining Techniques for the Life Sciences; Springer: New York, NY, USA, 2009; pp. 223–239. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Gaikwad, D.P.; Thool, R.C. Intrusion detection system using bagging ensemble method of machine learning. In Proceedings of the 2015 International Conference on Computing Communication Control and Automation, Pune, India, 26–27 February 2015; pp. 291–295. [Google Scholar]
- Tüysüzoğlu, G.; Birant, D. Enhanced bagging (eBagging): A novel approach for ensemble learning. Int. Arab J. Inf. Technol. 2020, 17, 515–528. [Google Scholar]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Fujiwara, O.; Khang, D.B. A two-phase decomposition method for optimal design of looped water distribution networks. Water Resour. Res. 1990, 26, 539–549. [Google Scholar] [CrossRef]
- Kadu, M.S.; Gupta, R.; Bhave, P.R. Optimal design of water networks using a modified genetic algorithm with reduction in search space. J. Water Resour. Plan. Manag. 2008, 134, 147–160. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
| Application | Machine Learning Model | Features Used | Dataset | Reference |
|---|---|---|---|---|
| Rehabilitation/Design of WDN | Feed-Forward Neural Network (FFNN) | Length, material, age, diameter, depth, and wall thickness | Real-world WDN (Shaker Al-Bahery WDN) | [17] |
| Rehabilitation/Design of WDN | Hybrtid based model (GLR-LR-RBFNN-SVR-ANFIS-FFNN) | Age, pipe depth, number of failures, diameter, and length | Real-world WDN (Gorgan WDN) | [18] |
| Water demand forecasting | Six machine learning models (LS, DT, KNN, SVR, RF, and RNN) | Air temperature, water consumption, precipitation, | The Battle of Water Demand Forecasting (WDSA-CCWI-2024) dataset | [19] |
| Water demand forecasting | One-Dimensional convolutional neural network (1D CNN) | Hourly water demand dat | Real-world WDN (Shiraz WDN) | [20] |
| WDN monitoring | XGBoost | Free residual chlorine concentration (FRC), Total Organic Carbon (TOC), pH, and distance from water treatment plants (WTPs) | Real-world WDN (Maragheh WDN) | [21] |
| WDN monitoring | Artificial neural network (ANN) | Pressure values, demand values, and number of users. | The benchmark network (Fossolo WDN) | [22] |
| Pump operation | Artificial neural network (ANN) | Water levels in tanks | The benchmark network (Anytown network) | [25] |
| WDN analysis and management | KNN, SVM, and RF | Demand variations and structural relationships | The benchmark network (M town) | [50] |
| Leak detection | RF | Structure and network attribute | Two case studies | [51] |
| Leak detection | SVM-CNN | Flow rate, pressure, and tempreture | Real-world WDN | [55] |
| Failure prediction | Gradient Boosted Trees (GBTs), and RF | 19 features such as pipe diameter, pipe material, pipe length, pipe age, etc. | Real-world WDN | [62] |
| Failure prediction | Reinforcement learning algorithm based on Q-learning | Location ID, time to repair, and cost | Arlington County’s water network | [63] |
| Failure prediction | Random Forest-Hierarchical Clustering (RF-HC) | Time-domain features of flow data (Peak value, mean, variance, Form factor, etc.) | Real-world WDN | [64] |
| Diameter Number | Diameter (mm) | Cost of Pipes (€/m) | Diameter Number | Diameter (mm) | Cost of Pipes (€/m) |
|---|---|---|---|---|---|
| 1 | 16 | 10.34 | 11 | 125 | 35.38 |
| 2 | 20 | 11.18 | 12 | 160 | 48.84 |
| 3 | 25 | 12.22 | 13 | 200 | 66.80 |
| 4 | 32 | 13.69 | 14 | 250 | 95.25 |
| 5 | 40 | 15.36 | 15 | 315 | 141.83 |
| 6 | 50 | 17.45 | 16 | 400 | 216.60 |
| 7 | 63 | 20.17 | 17 | 500 | 327.50 |
| 8 | 75 | 22.67 | 18 | 600 | 438.40 |
| 9 | 90 | 25.81 | 19 | 800 | 660.20 |
| 10 | 110 | 30.89 | 20 | 1000 | 882.00 |
| Network ID No. 1 | Index No. 2 | Graph Features No. 3 | Node Features No. 4 | Edge Features No. 5 | Diameters No. 6 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G1 | G2 | … | G44 | N1 | N2 | … | N27 | E1 | E2 | … | E9 | |||
| Net 1 | Pipe1 | Net 1(G1) | Net 1(G2) | … | Net 1(G44) | P1N1 | P1N2 | … | P1N27 | P1E1 | P1E2 | … | P1E9 | Pipe1(D1) |
| Pipe2 | P2N1 | P2N2 | … | P2N27 | P2E1 | P2E2 | … | P2E9 | Pipe2(D2) | |||||
| … | … | … | … | … | … | … | … | … | … | |||||
| Pipen | PnN1 | PnN2 | … | PnN27 | PnE1 | PnE2 | … | PnE9 | Pipen(Dn) | |||||
| Net 2 | Pipe1 | Net 2(G1) | Net 2(G2) | … | Net 2(G44) | P1N1 | P1N2 | … | P1N27 | P1E1 | P1E2 | … | P1E9 | Pipe1(D1) |
| Pipe2 | P2N1 | P2N2 | … | P2N27 | P2E1 | P2E2 | … | P2E9 | Pipe2(D2) | |||||
| … | … | … | … | … | … | … | … | … | … | |||||
| Pipen | PnN1 | PnN2 | … | PnN27 | PnE1 | PnE2 | … | PnE9 | Pipen(Dn) | |||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| Net 600 | Pipe1 | Net 600(G1) | Net 600(G2) | … | Net 600(G44) | P1N1 | P1N2 | … | P1N27 | P1E1 | P1E2 | … | P1E9 | Pipe1(D1) |
| Pipe2 | P2N1 | P2N2 | … | P2N27 | P2E1 | P2E2 | … | P2E9 | Pipe2(D2) | |||||
| … | … | … | … | … | … | … | … | … | … | |||||
| Pipen | PnN1 | PnN2 | … | PnN27 | PnE1 | PnE2 | … | PnE9 | Pipen(Dn) | |||||
| Optimization Algorithm | Hyperparameter | Tuning Range of Hyperparameter Values | Optimal Hyperparameter Values |
|---|---|---|---|
| GA | Population Size | [5–20] × Number Of Pipes | 12 × Number Of Pipes |
| Mutation Probability | 0.01–0.015 | 0.06 | |
| Crossover Probability | 0.6–0.95 | 0.85 | |
| Number of Iterations | 100–600 | 400 |
| Index | Graph Features | Node Features | Edge Features | Diameters (mm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G1 | G2 | … | G44 | N1 | N2 | … | N27 | E1 | E3 | … | E9 | ||
| 0 | 379 | 407 | … | 3749 | 2.50 | 0.50 | … | 11.80 | 87 | 31 | … | 0.01 | 200 |
| 1 | 379 | 407 | … | 3749 | 2.50 | 1.00 | … | 11.90 | 108 | 71 | … | 0.00 | 600 |
| 2 | 379 | 407 | … | 3749 | 3.50 | 1.50 | … | 13.70 | 112 | 94 | … | 0.04 | 125 |
| 3 | 379 | 407 | … | 3749 | 3.00 | 1.00 | … | 11.90 | 112 | 22 | … | 0.00 | 500 |
| 4 | 379 | 407 | … | 3749 | 3.50 | 1.50 | … | 14.20 | 111 | 23 | … | 0.20 | 200 |
| 5 | 379 | 407 | … | 3749 | 2.50 | 1.00 | … | 15.20 | 114 | 29 | … | 0.22 | 50 |
| 6 | 379 | 407 | … | 3749 | 3.00 | 1.50 | … | 18.70 | 111 | 21 | … | 0.03 | 160 |
| 7 | 379 | 407 | … | 3749 | 3.00 | 1.50 | … | 18.90 | 111 | 22 | … | 0.00 | 800 |
| 8 | 379 | 407 | … | 3749 | 2.50 | 1.50 | … | 18.70 | 96 | 92 | … | 0.00 | 400 |
| 9 | 379 | 407 | … | 3749 | 3.50 | 2.00 | … | 18.50 | 96 | 78 | … | 0.00 | 315 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 85,735 | 484 | 507 | … | 3672 | 3.00 | 0.50 | … | 28.80 | 120 | 46 | … | 0.00 | 250 |
| 85,736 | 484 | 507 | … | 3672 | 3.00 | 1.50 | … | 36.50 | 118 | 54 | … | 0.30 | 40 |
| 85,737 | 484 | 507 | … | 3672 | 3.00 | 1.50 | … | 45.00 | 106 | 63 | … | 0.03 | 250 |
| 85,738 | 484 | 507 | … | 3672 | 3.00 | 1.00 | … | 46.30 | 87 | 38 | … | 0.02 | 315 |
| 85,739 | 484 | 507 | … | 3672 | 3.00 | 1.50 | … | 52.20 | 88 | 49 | … | 0.22 | 90 |
| 85,740 | 484 | 507 | … | 3672 | 3.00 | 1.50 | … | 58.80 | 91 | 40 | … | 0.06 | 315 |
| 85,741 | 484 | 507 | … | 3672 | 3.00 | 1.50 | … | 63.80 | 92 | 89 | … | 0.08 | 315 |
| 85,742 | 484 | 507 | … | 3672 | 3.00 | 2.00 | … | 68.20 | 83 | 45 | … | 0.03 | 1,000 |
| 85,743 | 484 | 507 | … | 3672 | 3.00 | 2.00 | … | 70.20 | 90 | 35 | … | 0.01 | 800 |
| 85,744 | 484 | 507 | … | 3672 | 2.00 | 1.50 | … | 35.80 | 89 | 63 | … | 0.09 | 800 |
| Index | Graph Features | Node Features | Edge Features | Diameters (mm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G1 | G2 | … | G44 | N1 | N2 | … | N27 | E1 | E3 | … | E9 | ||
| 0 | 0.23 | 0.04 | … | 0.41 | 0.25 | 0.00 | … | 0.13 | 0.17 | 0.14 | … | 0.01 | 0.19 |
| 1 | 0.23 | 0.04 | … | 0.41 | 0.25 | 0.20 | … | 0.14 | 0.70 | 0.64 | … | 0.00 | 0.59 |
| 2 | 0.23 | 0.04 | … | 0.41 | 0.75 | 0.40 | … | 0.16 | 0.80 | 0.92 | … | 0.07 | 0.11 |
| 3 | 0.23 | 0.04 | … | 0.41 | 0.50 | 0.20 | … | 0.14 | 0.80 | 0.02 | … | 0.00 | 0.49 |
| 4 | 0.23 | 0.04 | … | 0.41 | 0.75 | 0.40 | … | 0.16 | 0.77 | 0.04 | … | 0.38 | 0.19 |
| 5 | 0.23 | 0.04 | … | 0.41 | 0.25 | 0.20 | … | 0.17 | 0.85 | 0.11 | … | 0.44 | 0.03 |
| 6 | 0.23 | 0.04 | … | 0.41 | 0.50 | 0.40 | … | 0.22 | 0.77 | 0.01 | … | 0.06 | 0.15 |
| 7 | 0.23 | 0.04 | … | 0.41 | 0.50 | 0.40 | … | 0.22 | 0.77 | 0.02 | … | 0.00 | 0.80 |
| 8 | 0.23 | 0.04 | … | 0.41 | 0.25 | 0.40 | … | 0.22 | 0.40 | 0.90 | … | 0.01 | 0.39 |
| 9 | 0.23 | 0.04 | … | 0.41 | 0.75 | 0.60 | … | 0.21 | 0.40 | 0.73 | … | 0.00 | 0.30 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 85736 | 0.55 | 0.05 | … | 0.39 | 0.50 | 0.40 | … | 0.42 | 0.95 | 0.42 | … | 0.56 | 0.02 |
| 85737 | 0.55 | 0.05 | … | 0.39 | 0.50 | 0.40 | … | 0.52 | 0.65 | 0.54 | … | 0.06 | 0.24 |
| 85738 | 0.55 | 0.05 | … | 0.39 | 0.50 | 0.20 | … | 0.54 | 0.17 | 0.22 | … | 0.04 | 0.30 |
| 85739 | 0.55 | 0.05 | … | 0.39 | 0.50 | 0.40 | … | 0.61 | 0.20 | 0.36 | … | 0.44 | 0.07 |
| 85740 | 0.55 | 0.05 | … | 0.39 | 0.50 | 0.40 | … | 0.68 | 0.27 | 0.25 | … | 0.12 | 0.30 |
| 85741 | 0.55 | 0.05 | … | 0.39 | 0.50 | 0.40 | … | 0.74 | 0.30 | 0.86 | … | 0.17 | 0.30 |
| 85743 | 0.55 | 0.05 | … | 0.39 | 0.50 | 0.60 | … | 0.82 | 0.25 | 0.19 | … | 0.15 | 0.80 |
| 85744 | 0.55 | 0.05 | … | 0.39 | 0.00 | 0.40 | … | 0.41 | 0.22 | 0.54 | … | 0.17 | 0.80 |
| Hyperparameter Tuning with Grid Search | Embedded Methods | ||
|---|---|---|---|
| Xg | LGB | Per | |
| n-estimators | 1350 | 1500 | 1500 |
| eta | 0.250 | - | - |
| gamma | 0.002 | - | - |
| Max-depth | 15 | 12 | 12 |
| Num-leaves | - | 45 | 45 |
| Learning-rate | - | 0.011 | 0.011 |
| Methods | Kb | Chi2 | Var | LGB | Per | Xg |
|---|---|---|---|---|---|---|
| Selected Features | N5 | N5 | E1 | E9 | N5 | E9 |
| N7 | N7 | E3 | E8 | N7 | N5 | |
| E5 | E5 | G43 | N5 | E3 | E8 | |
| N8 | N8 | G44 | N7 | E9 | N7 | |
| E9 | N17 | G7 | E3 | E1 | E1 | |
| E3 | E9 | G20 | E1 | E5 | E3 | |
| E1 | N15 | G21 | N8 | E8 | N8 | |
| G42 | N19 | G23 | E5 | N8 | N10 | |
| N23 | E8 | G30 | N10 | N10 | E5 | |
| G12 | N18 | G31 | N6 | N6 | N6 | |
| G8 | N2 | G32 | N4 | N3 | N26 | |
| G4 | N10 | G35 | N17 | N17 | N4 | |
| G17 | N3 | G36 | N26 | N1 | E6 | |
| G13 | N13 | G39 | E4 | N23 | E7 | |
| G10 | N6 | G41 | N19 | N25 | N17 | |
| G41 | E3 | N1 | N9 | N4 | N20 | |
| G6 | N4 | N2 | E6 | G25 | N15 | |
| G18 | N14 | N5 | N18 | G3 | E4 | |
| G27 | N22 | N7 | E7 | G2 | N9 | |
| G2 | E1 | N23 | N20 | G10 | N19 | |
| Node features percentage | 20 | 75 | 25 | 60 | 55 | 60 |
| Pipe features percentage | 20 | 25 | 10 | 40 | 25 | 40 |
| Over all graph features percentage | 60 | 0.0 | 65 | 0.0 | 20 | 0.0 |
| Hyperparameter Tuning with Grid Search | Ensemble Model | |||
|---|---|---|---|---|
| RF | SVM | BAG | LGB | |
| n-estimators | 250 | - | 140 | 1500 |
| Max-depth | 30 | - | - | - |
| Min-samples-split | 10 | - | - | 12 |
| Max-samples | - | - | 0.7000 | - |
| Max-features | - | - | 0.7500 | - |
| C | - | 1.0000 | - | - |
| kernel | - | ‘rbf’ | - | - |
| gamma | - | - | 0.0001 | - |
| Num-leaves | - | - | - | 45 |
| Learning-rate | - | - | - | 0.0110 |
| Pipe Number | Predicted Diameters | Node Number | Pressure Head from [101] (m) | Pressure Head from Xg-LGB Model (m) | ||
|---|---|---|---|---|---|---|
| Pipe Diameters from [101] (in) | Continuous Pipe Diameters from Xg-LGB Model (in) | Commercial Pipe Diameters from Xg-LGB Model (in) | ||||
| 1 | 40 | 38.9 | 40 | 1 | 100.00 | 100.00 |
| 2 | 40 | 36.9 | 40 | 2 | 97.08 | 97.14 |
| 3 | 40 | 40.7 | 40 | 3 | 60.82 | 61.67 |
| 4 | 40 | 40.3 | 40 | 4 | 56.38 | 57.39 |
| 5 | 40 | 39.9 | 40 | 5 | 50.88 | 52.09 |
| 6 | 40 | 39.5 | 40 | 6 | 45.13 | 46.56 |
| 7 | 40 | 39.1 | 40 | 7 | 43.81 | 45.29 |
| 8 | 40 | 40.0 | 40 | 8 | 42.28 | 43.83 |
| 9 | 30 | 33.7 | 30 | 9 | 41.09 | 42.69 |
| 10 | 30 | 35.4 | 40 | 10 | 37.61 | 39.40 |
| 11 | 30 | 34.9 | 30 | 11 | 36.01 | 39.01 |
| 12 | 24 | 27.4 | 30 | 12 | 34.83 | 37.85 |
| 13 | 16 | 18.2 | 20 | 13 | 30.53 | 36.44 |
| 14 | 12 | 14.0 | 16 | 14 | 32.06 | 37.81 |
| 15 | 12 | 13.0 | 12 | 15 | 30.96 | 37.66 |
| 16 | 16 | 18.4 | 20 | 16 | 31.13 | 38.17 |
| 17 | 20 | 22.1 | 24 | 17 | 39.28 | 45.01 |
| 18 | 24 | 24.4 | 24 | 18 | 50.04 | 51.52 |
| 19 | 24 | 28.2 | 30 | 19 | 57.13 | 60.16 |
| 20 | 40 | 40.0 | 40 | 20 | 49.59 | 51.41 |
| 21 | 20 | 23.4 | 24 | 21 | 40.04 | 47.56 |
| 22 | 12 | 13.1 | 12 | 22 | 34.76 | 42.40 |
| 23 | 40 | 39.2 | 40 | 23 | 43.42 | 45.98 |
| 24 | 30 | 34.6 | 30 | 24 | 37.73 | 41.44 |
| 25 | 30 | 34.4 | 30 | 25 | 34.07 | 38.72 |
| 26 | 20 | 21.4 | 20 | 26 | 30.51 | 36.67 |
| 27 | 12 | 14.1 | 16 | 27 | 30.32 | 36.69 |
| 28 | 12 | 14.6 | 16 | 28 | 38.05 | 39.30 |
| 29 | 16 | 17.6 | 16 | 29 | 30.08 | 36.26 |
| 30 | 12 | 14.5 | 16 | 30 | 30.58 | 36.26 |
| 31 | 12 | 13.0 | 12 | 31 | 30.90 | 36.47 |
| 32 | 16 | 17.6 | 16 | 32 | 31.81 | 36.74 |
| 33 | 20 | 23.9 | 24 | |||
| 34 | 24 | 26.8 | 24 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahrami Chegeni, I.; Riyahi, M.M.; Bakhshipour, A.E.; Azizipour, M.; Haghighi, A. Developing Machine Learning Models for Optimal Design of Water Distribution Networks Using Graph Theory-Based Features. Water 2025, 17, 1654. https://doi.org/10.3390/w17111654
Bahrami Chegeni I, Riyahi MM, Bakhshipour AE, Azizipour M, Haghighi A. Developing Machine Learning Models for Optimal Design of Water Distribution Networks Using Graph Theory-Based Features. Water. 2025; 17(11):1654. https://doi.org/10.3390/w17111654
Chicago/Turabian StyleBahrami Chegeni, Iman, Mohammad Mehdi Riyahi, Amin E. Bakhshipour, Mohamad Azizipour, and Ali Haghighi. 2025. "Developing Machine Learning Models for Optimal Design of Water Distribution Networks Using Graph Theory-Based Features" Water 17, no. 11: 1654. https://doi.org/10.3390/w17111654
APA StyleBahrami Chegeni, I., Riyahi, M. M., Bakhshipour, A. E., Azizipour, M., & Haghighi, A. (2025). Developing Machine Learning Models for Optimal Design of Water Distribution Networks Using Graph Theory-Based Features. Water, 17(11), 1654. https://doi.org/10.3390/w17111654







