Numerical Investigation of Subcooled Boiling Flow and Patterns’ Transitions in a High-Heat-Flux Rectangular Small Channel
Abstract
1. Introduction
2. Methodology
2.1. Grid Geometry and Boundary Conditions
2.2. Fluid Properties
2.3. Numerical Model
2.3.1. Governing Equations
2.3.2. Turbulence Equation
2.3.3. Phase Change Model
2.4. Solution Methods
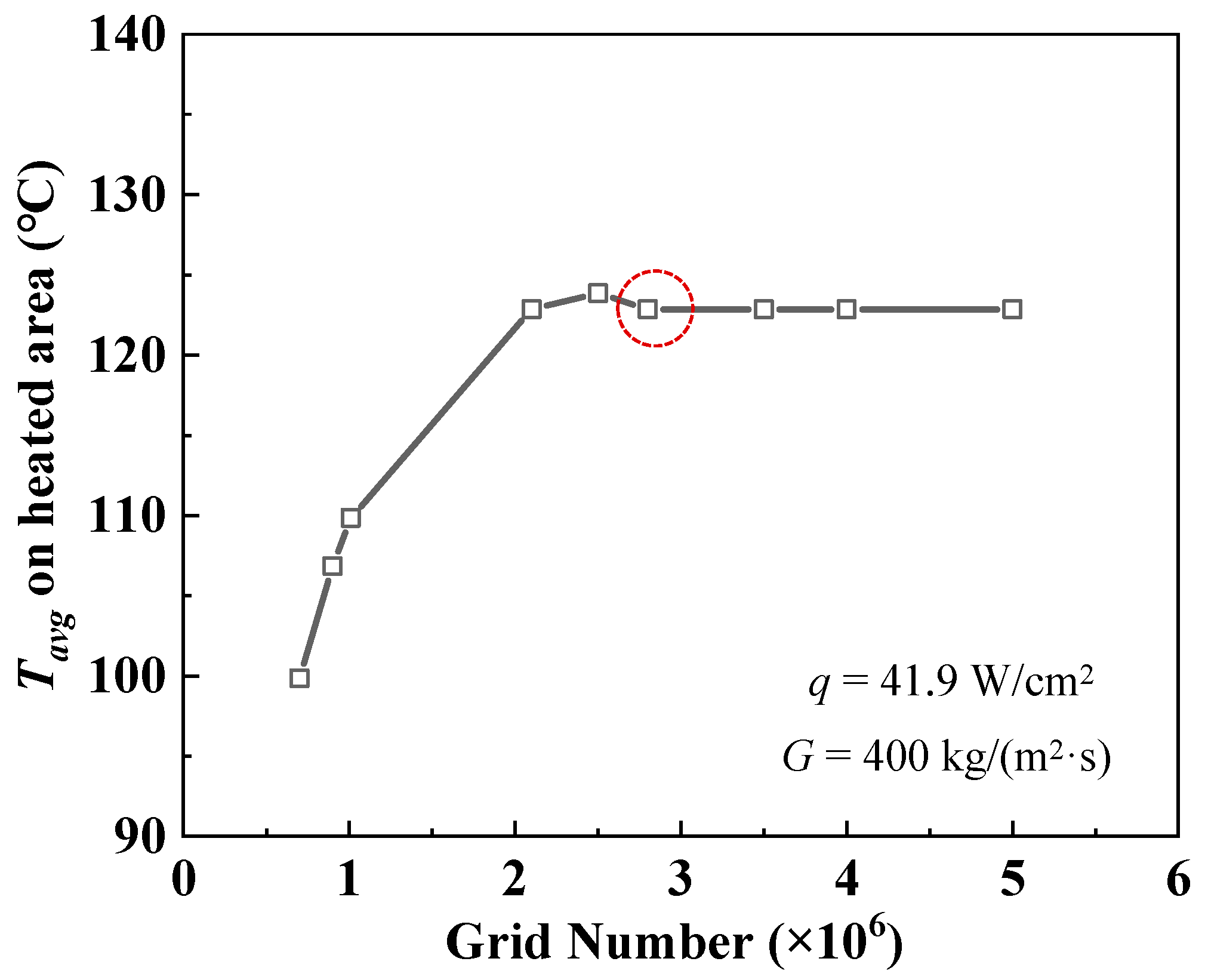
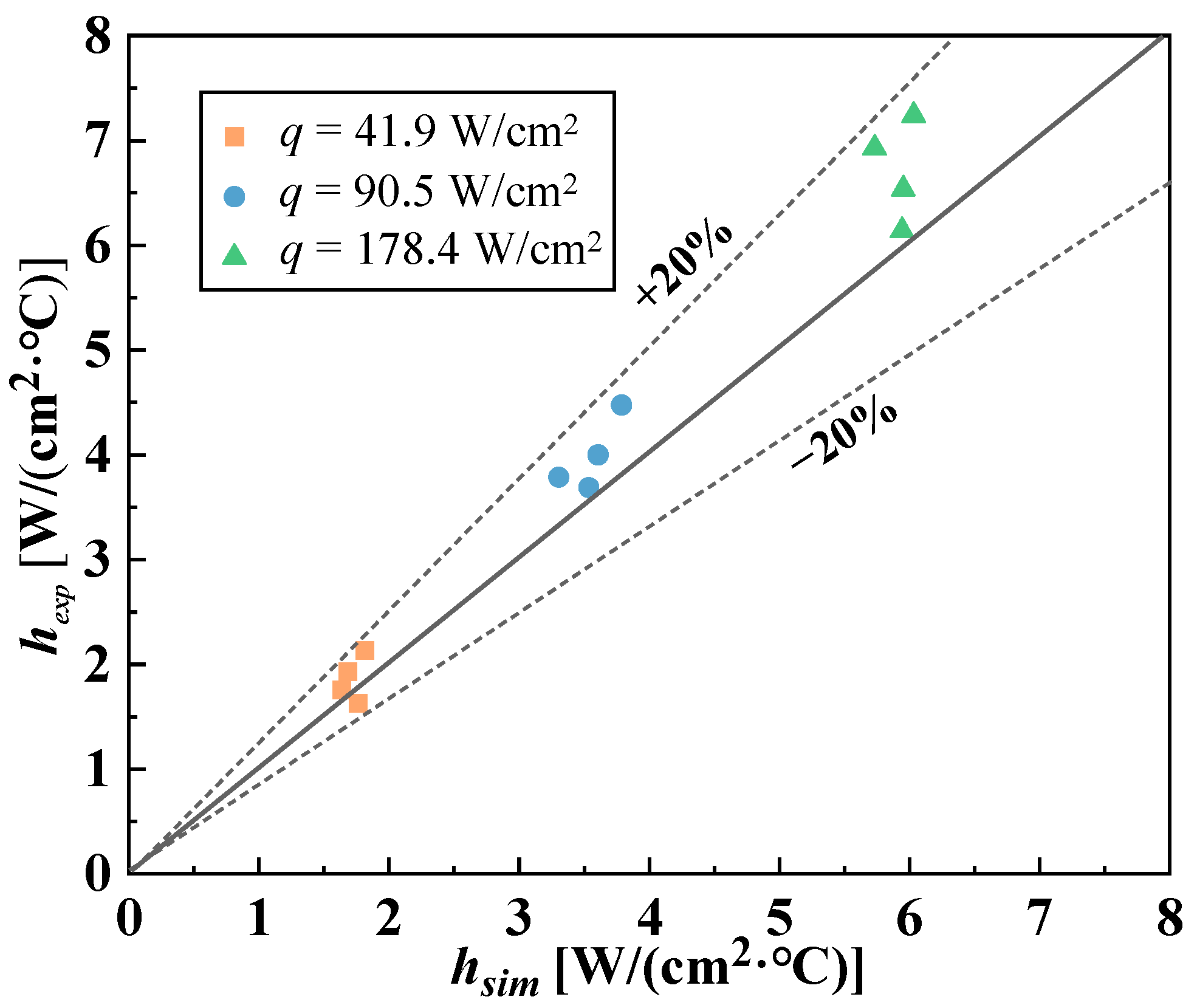
2.5. Validation of Grid Independence and Numerical Model
3. Results and Discussion
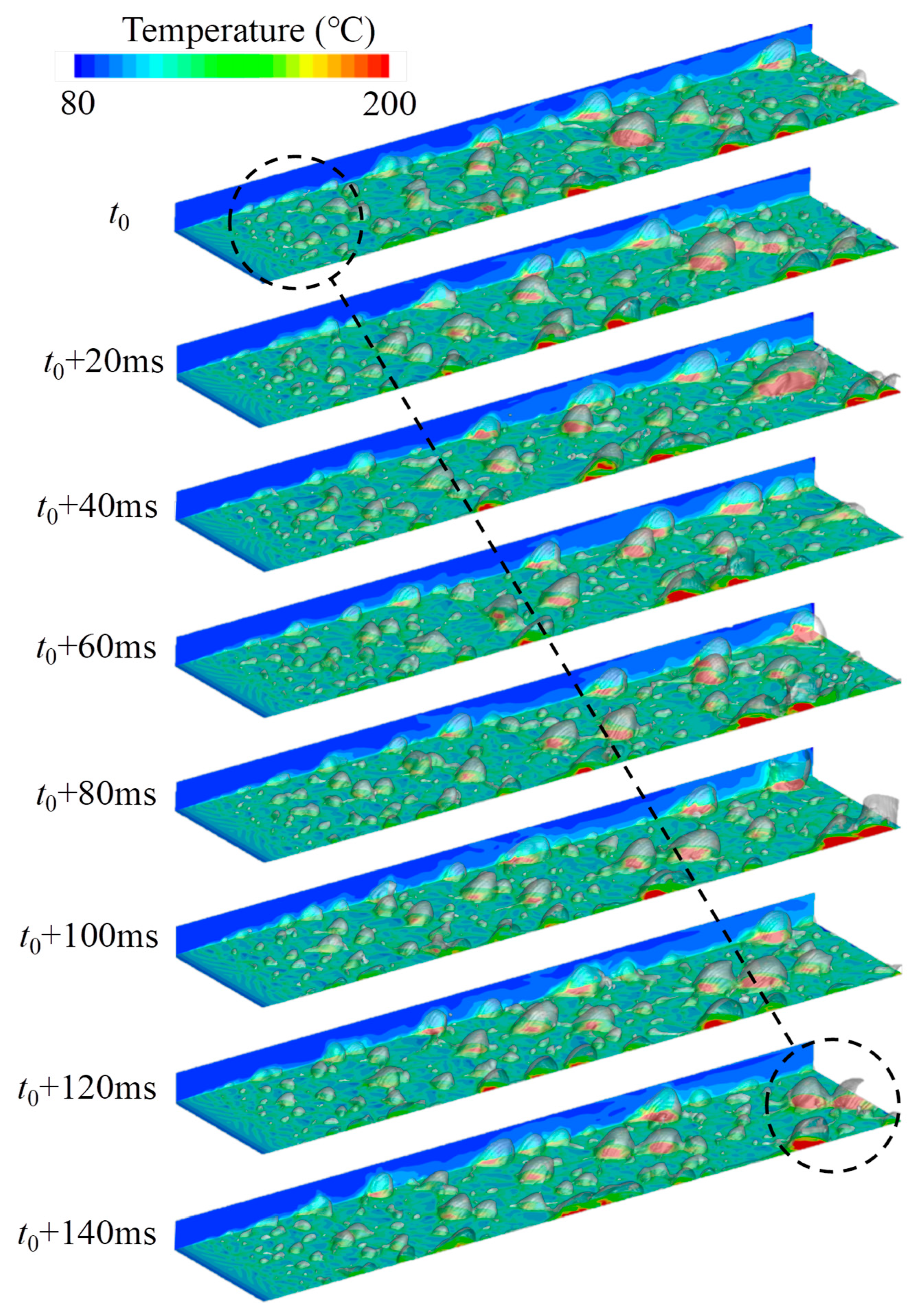
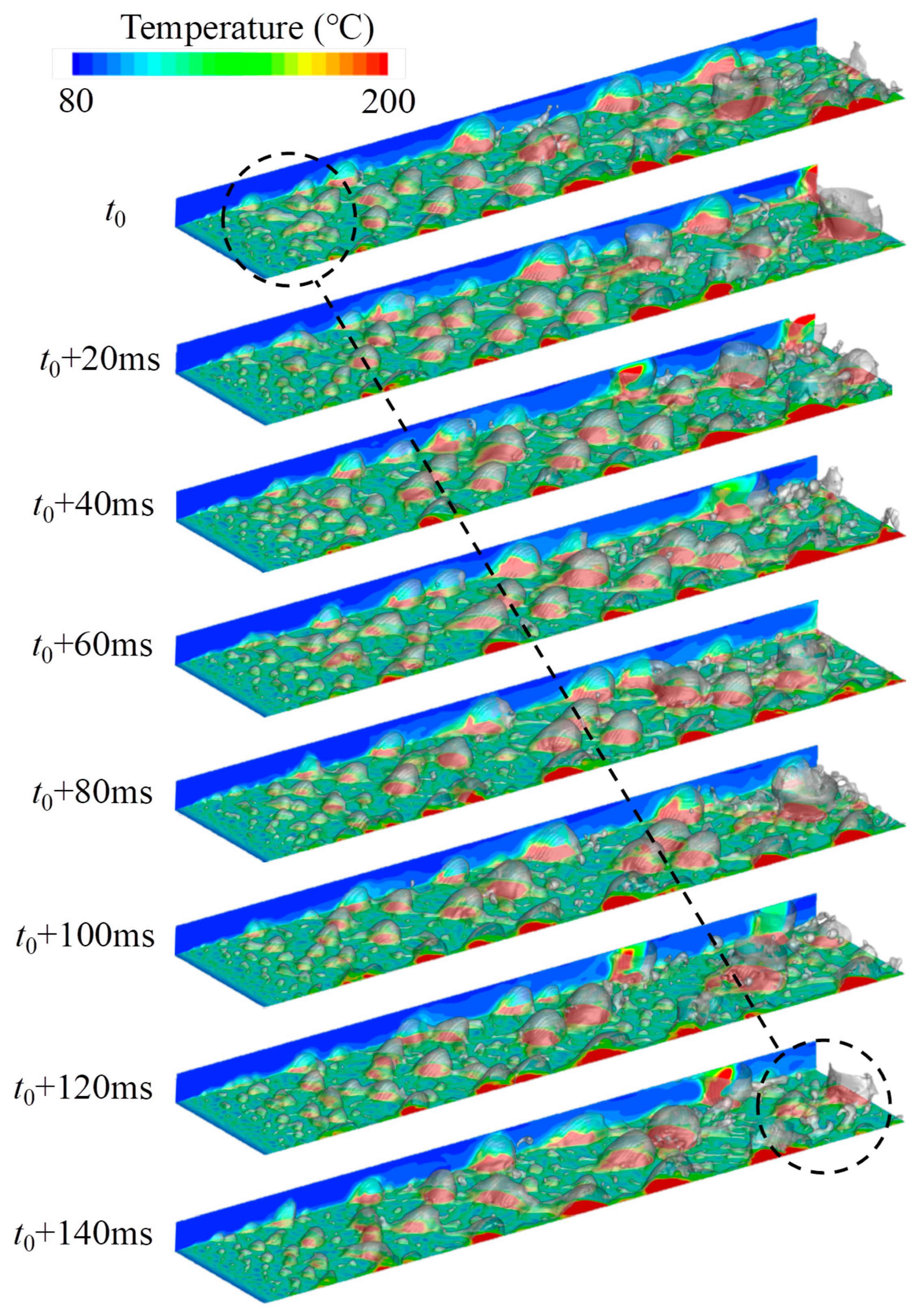
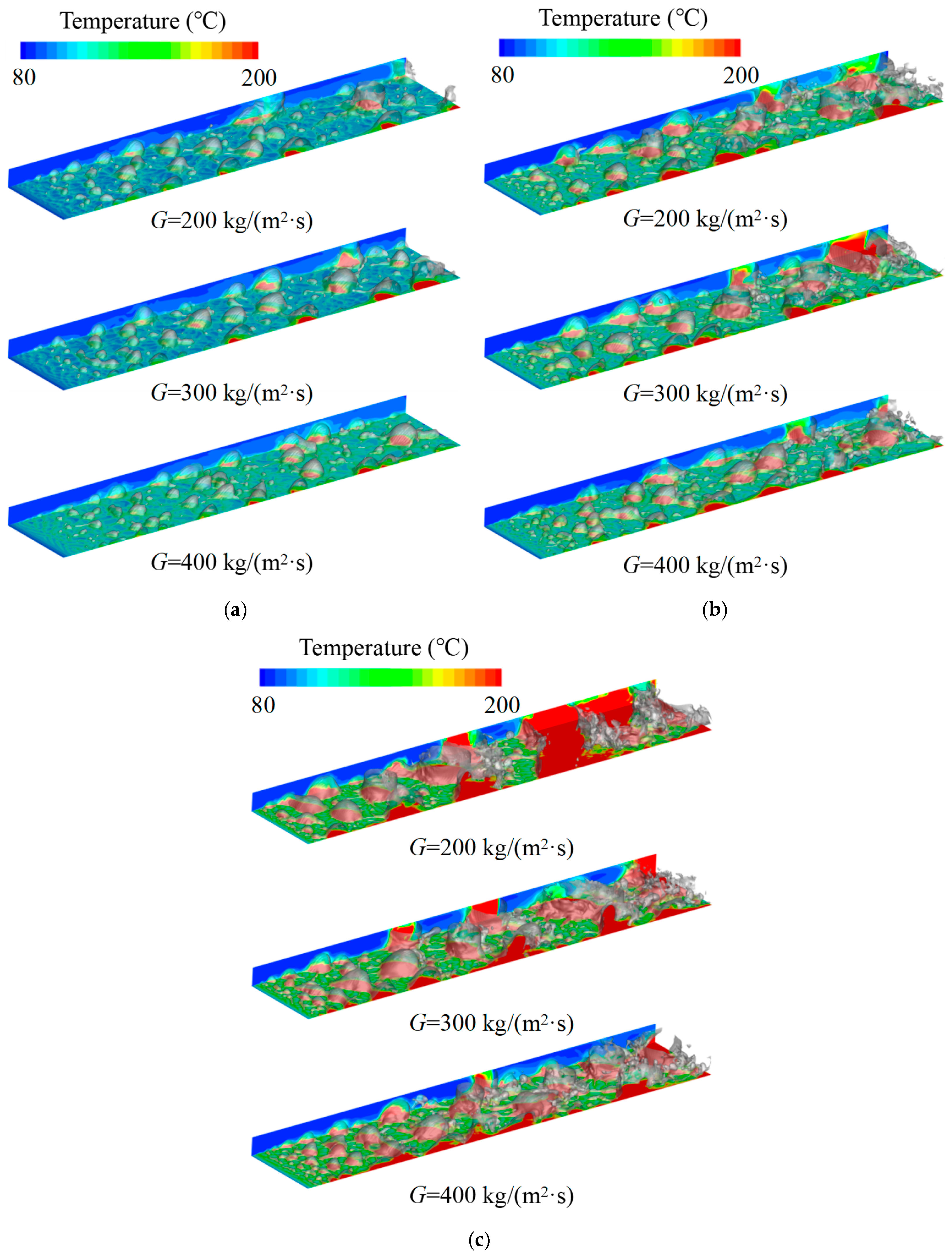
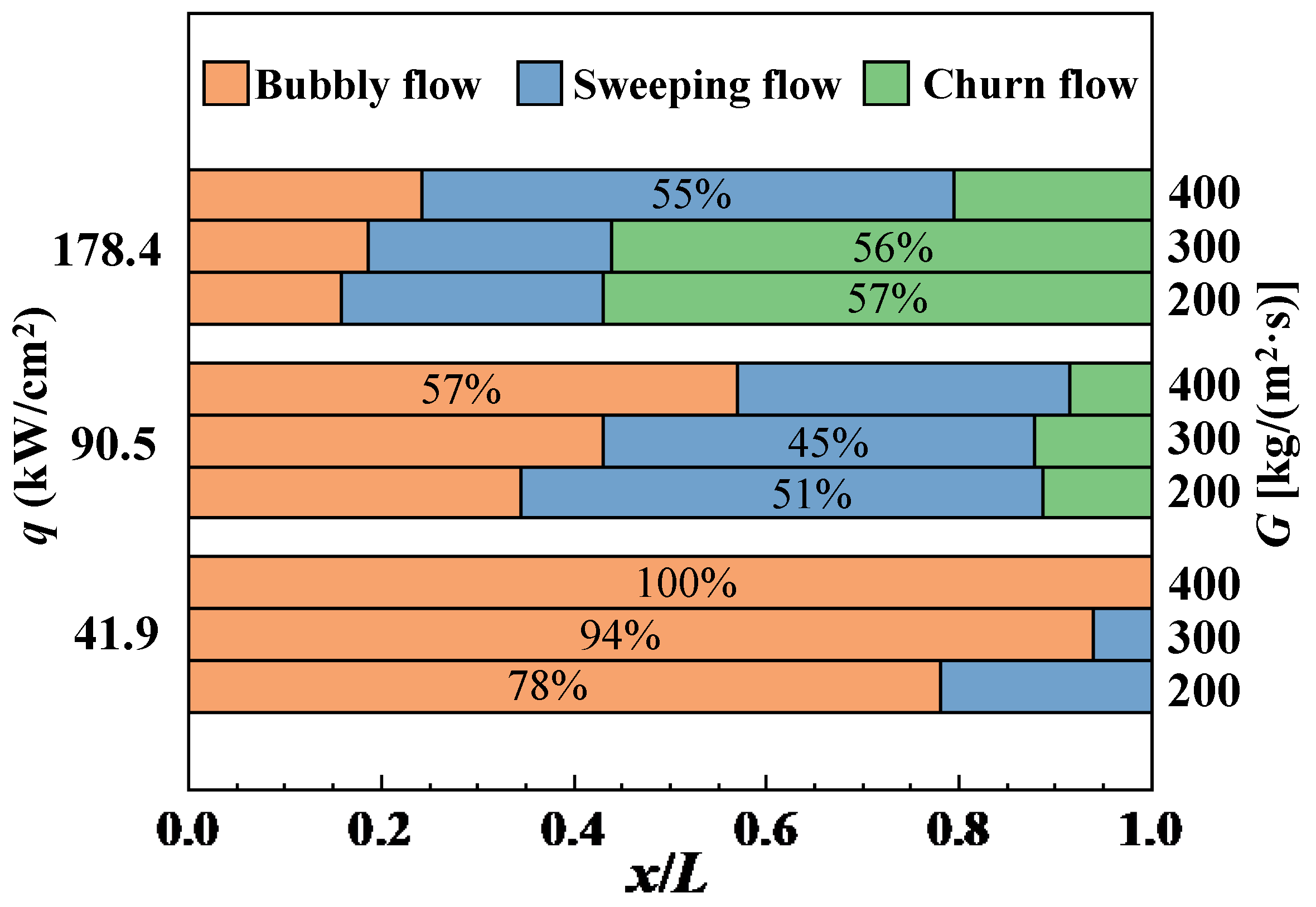
3.1. Boiling Flow Patterns Under Different Conditions
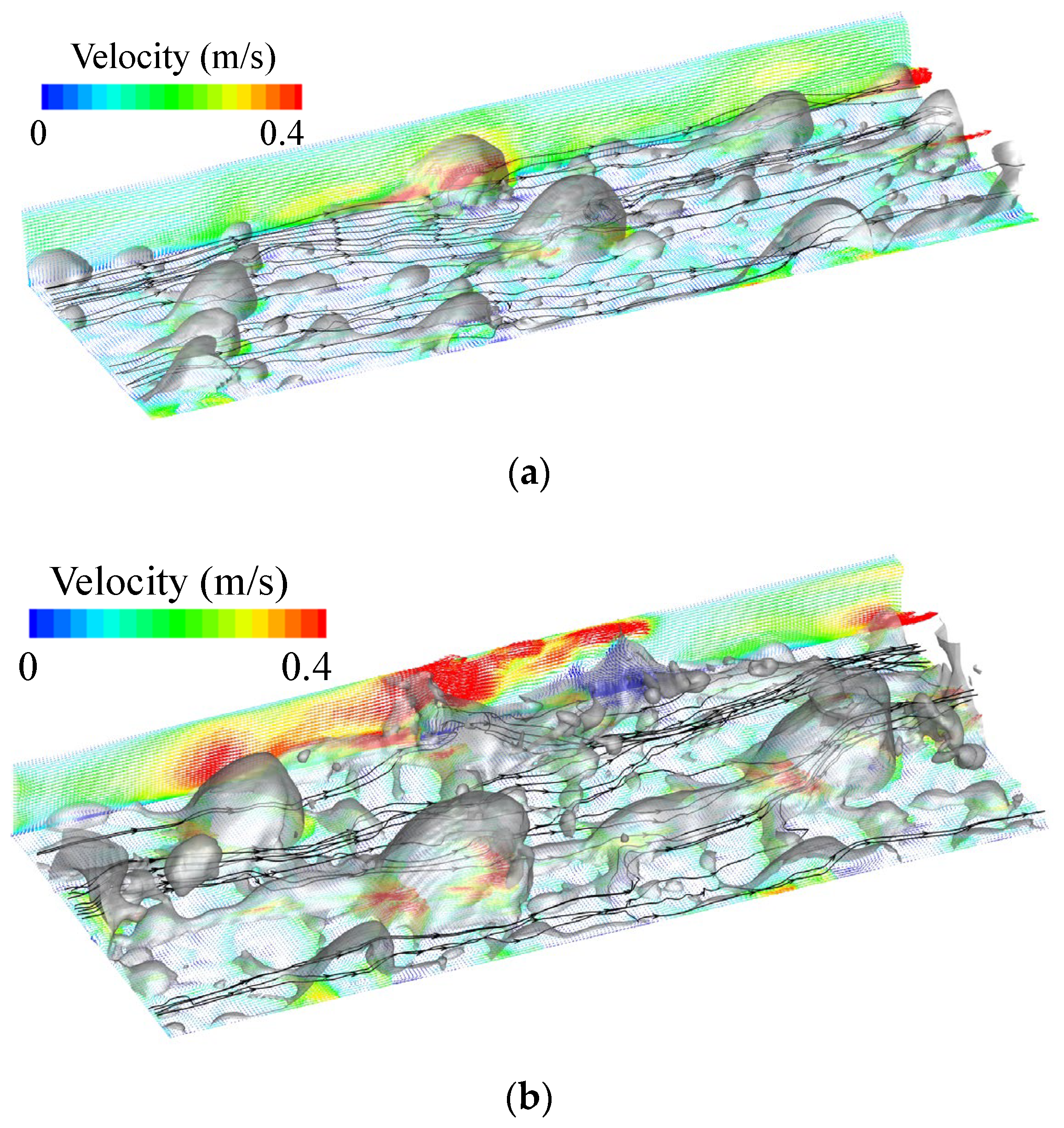
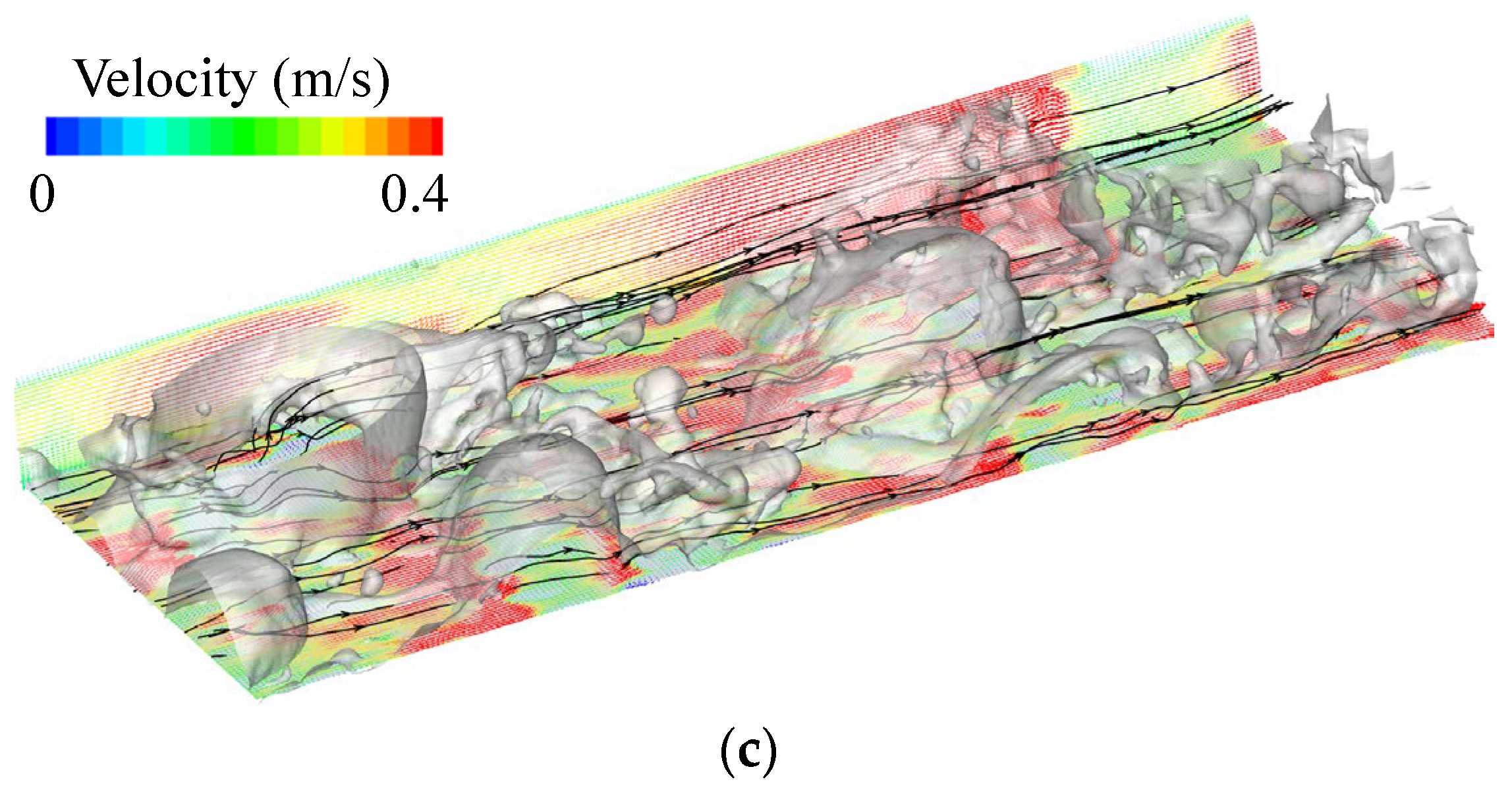
3.2. Flow Characteristics Around Bubbles Under Typical Boiling Flow Pattern
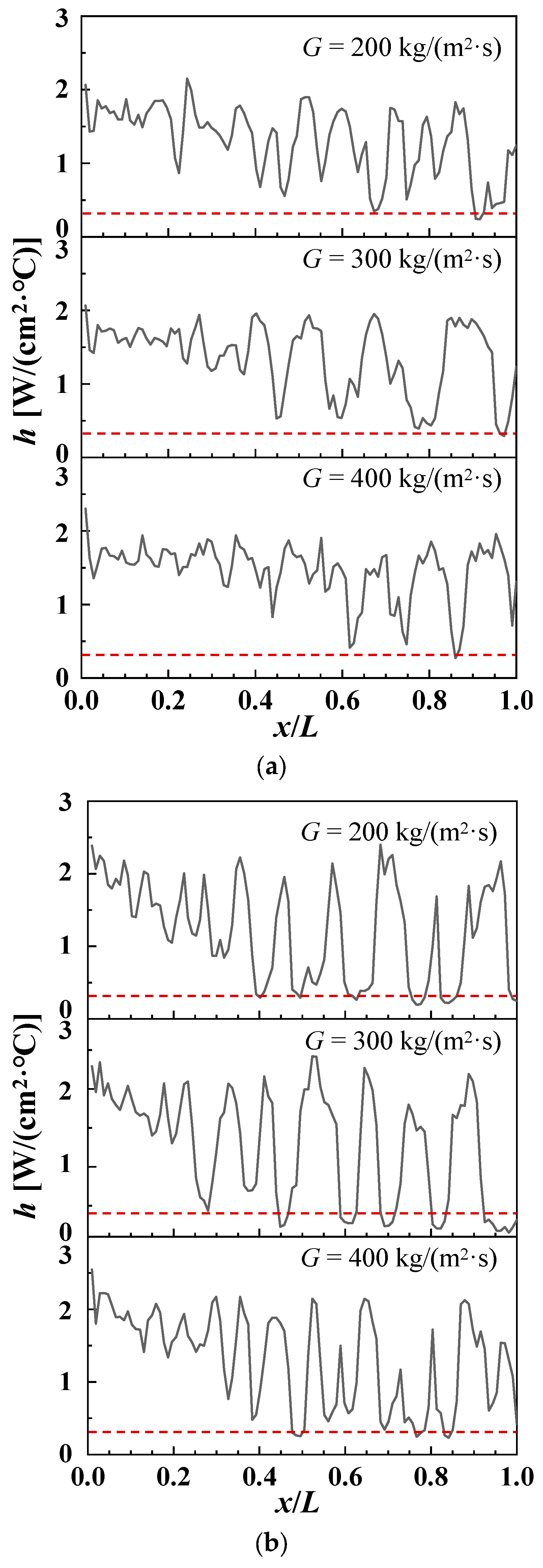
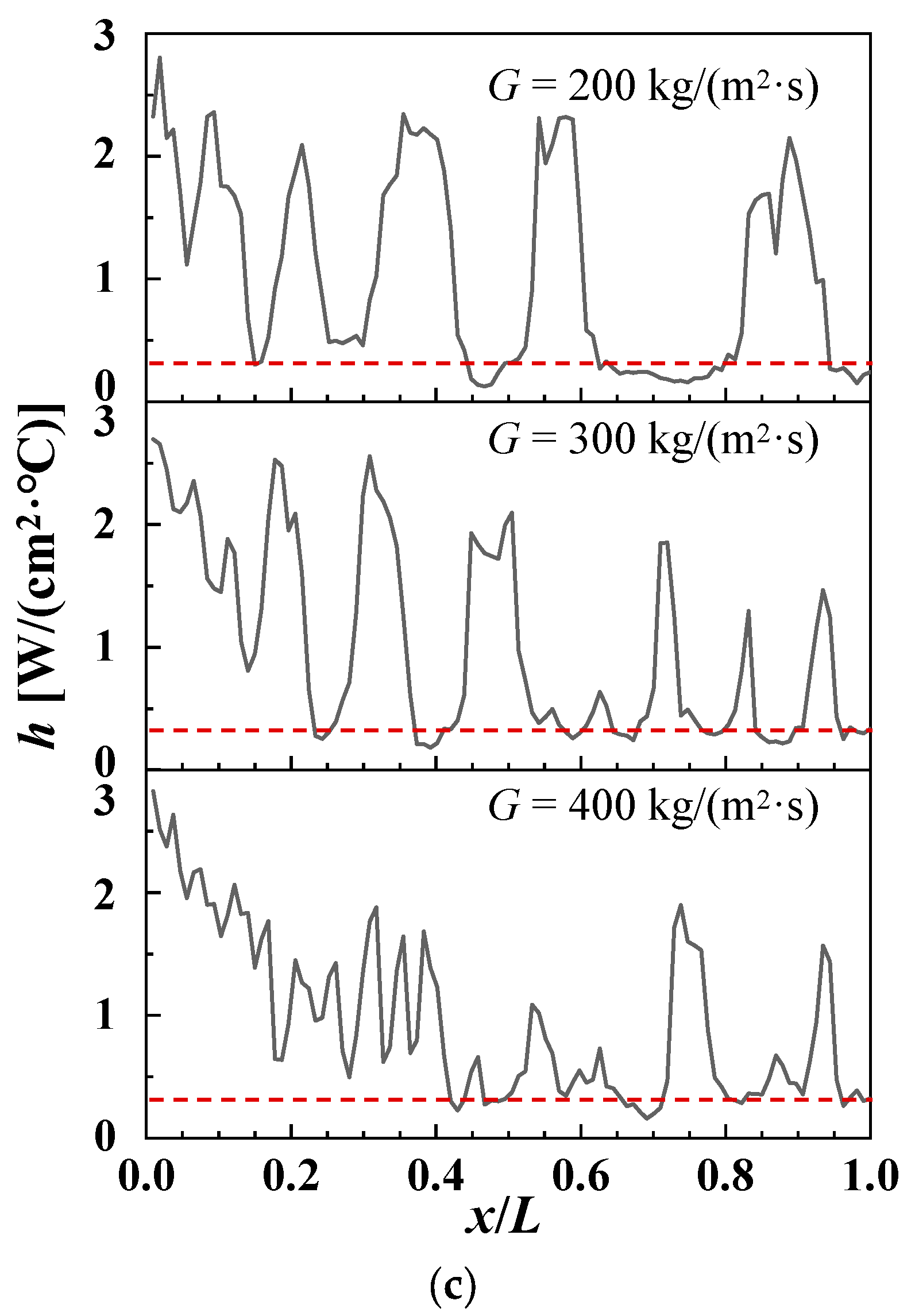
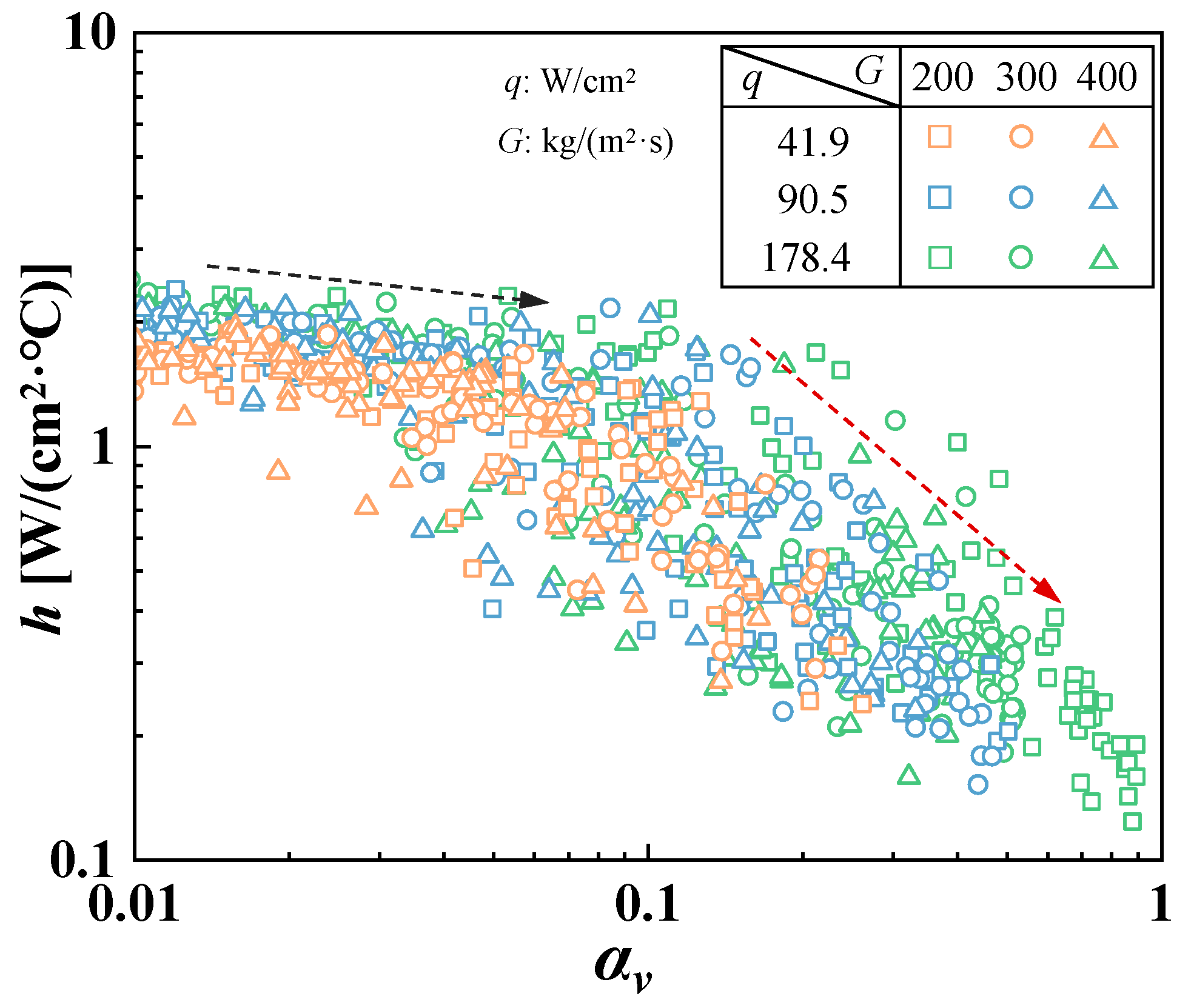
3.3. Characterization of Local Boiling Flow Patterns
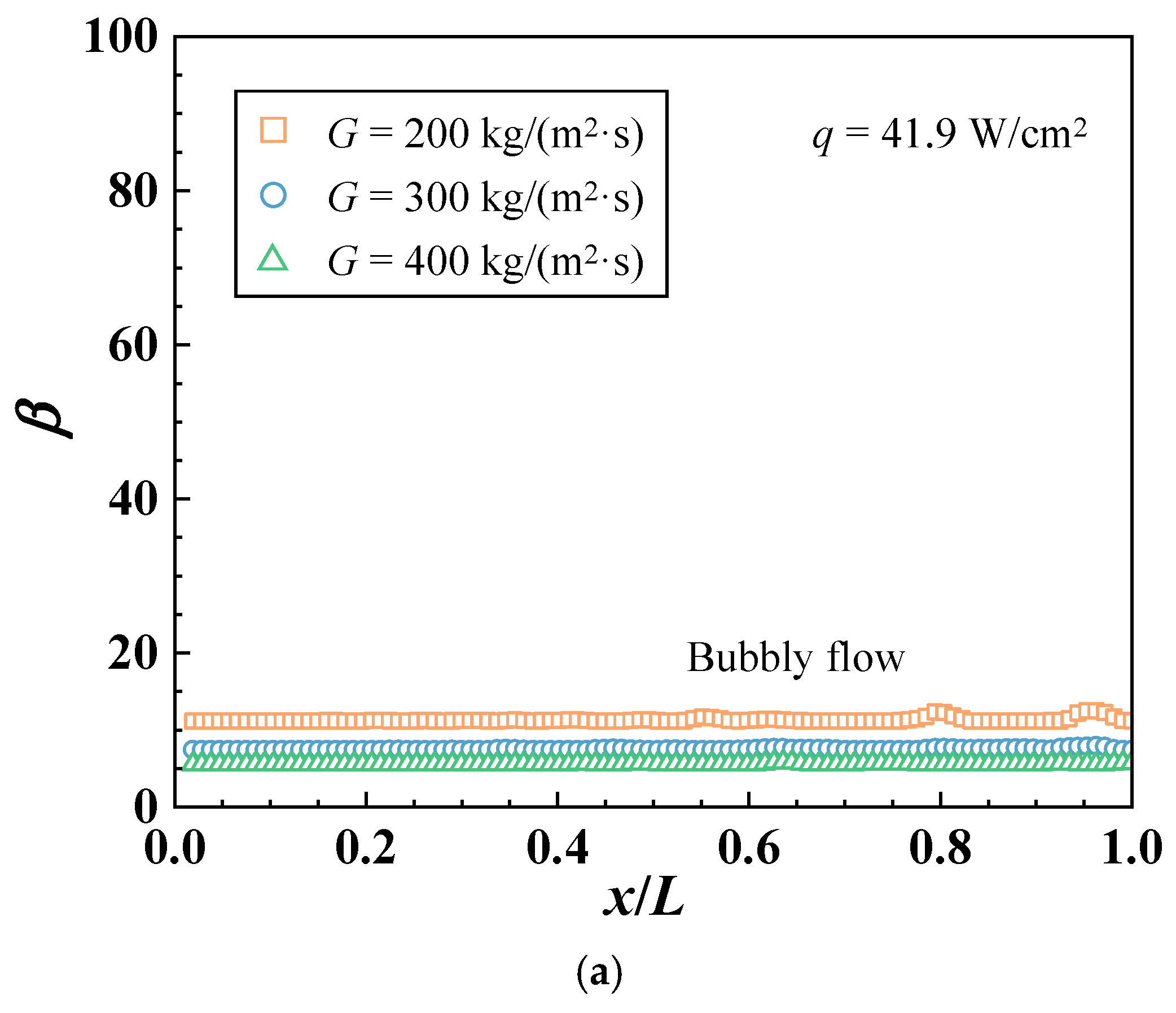
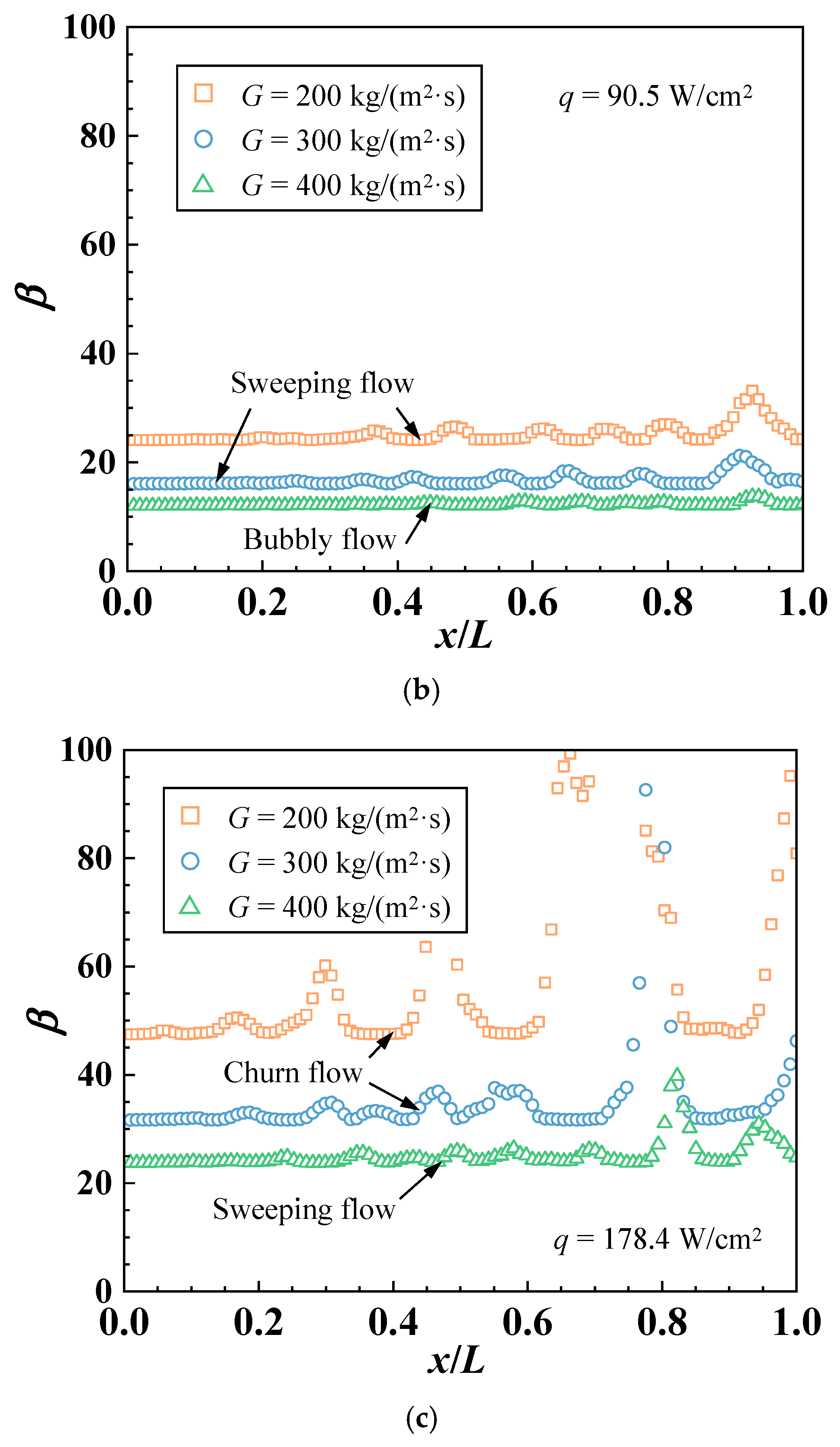
3.4. Characterization of Dominant Boiling Flow Pattern
4. Conclusions
- (1)
- The model accurately captures boiling behavior, with average heat transfer coefficient predictions deviating within ±20% of experimental results.
- (2)
- Multiple flow regimes coexist under high-heat flux. Increased heat flux accelerates bubble nucleation and coalescence, while reduced mass flux promotes earlier slug formation and upstream flow regime transitions, resulting in thermal performance degradation.
- (3)
- The local vapor volume fraction effectively identifies flow regime transitions, with critical values of 0.2 and 0.4 marking the transitions from bubbly to sweeping and sweeping to churn flows, respectively.
- (4)
- A dimensionless parameter β is introduced to classify dominant boiling flow regimes, with transition ranges of 12–16 and 24–32 corresponding to bubbly-to-sweeping and sweeping-to-churn regimes, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Roman symbols | W | channel width, m | |
| Bo | boiling number | x | axial position, m/vapor quality |
| cp | isobaric specific heat, J/(kg·K) | ||
| Dh | hydraulic diameter, m | Greek symbols | |
| E | internal energy, J | α | volume fraction |
| Fvol | converted volumetric force, N | β | dimensionless parameter |
| g | gravitational acceleration, m/s2 | ρ | density, kg/m3 |
| G | mass flux, kg/(m2·s) | κ | curvatures, 1/m |
| h | heat transfer coefficient, W/(m2·K) | φ | thermophysical properties |
| H | channel height, m | σ | surface tension, N/m |
| ilv | latent heat of vaporization, J/kg | μ | dynamic viscosity, Pa·s |
| L | channel length, m | λ | thermal conductivity, W/(m·K) |
| p | pressure, Pa | ||
| q | heat flux, W/m2 | Subscripts | |
| rl | evaporation coefficient, 1/s | avg | averaged value |
| rv | condensation coefficient, 1/s | sat | saturation point |
| S | source term/slip ratio | l | liquid phase |
| t | time, s | v | vapor phase |
| t0 | initial time, s | exp | experimental data |
| T | temperature, K | sim | simulation results |
| u | velocity, m/s | ||
References
- Joshi, S.N.; Dede, E.M. Two-phase jet impingement cooling for high heat flux wide band-gap devices using multi-scale porous surfaces. Appl. Therm. Eng. 2017, 110, 10–17. [Google Scholar] [CrossRef]
- Bertsch, S.S.; Groll, E.A.; Garimella, S.V. Effects of heat flux, mass flux, vapor quality, and saturation temperature on flow boiling heat transfer in microchannels. Int. J. Multiph. Flow 2009, 35, 142–154. [Google Scholar] [CrossRef]
- Qu, W.; Mudawar, I. Flow boiling heat transfer in two-phase micro-channel heat sinks-I. Experimental investigation and assessment of correlation methods. Int. J. Heat Mass Tran. 2003, 46, 2755–2771. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Grande, W.J. Evolution of microchannel flow passages-thermohydraulic performance and fabrication technology. Heat Transfer Eng. 2003, 24, 3–17. [Google Scholar] [CrossRef]
- Jiang, L.; Wong, M.; Zohar, Y. Forced Convection Boiling in a Microchannel Heat Sink. J. Microelectromech. Syst. 2001, 10, 80–87. [Google Scholar] [CrossRef]
- Yin, L.; Xu, R.; Jiang, P.; Cai, H.; Jia, L. Subcooled flow boiling of water in a large aspect ratio microchannel. Int. J. Heat Mass Tran. 2017, 112, 1081–1089. [Google Scholar] [CrossRef]
- Ma, D.; Pang, L.; Wu, H. Numerical investigation on boiling heat transfer in a rectangular channel under sub-atmospheric environment. Therm. Sci. Eng. Prog. 2023, 46, 102182. [Google Scholar] [CrossRef]
- Xie, L.; Hu, B.; Xu, Y.; Lin, M.; Wang, Q. Experimental study on flow boiling heat transfer in rigid-tail rib-channel under rolling motion conditions. Appl. Therm. Eng. 2025, 258, 124468. [Google Scholar] [CrossRef]
- Li, Q.; Fu, X.; Lin, Z.; Liu, X.; Zhao, B.; Cai, W. Analysis of complex methane transcritical flow and heat transfer mechanism in PCHE Zigzag channel. Int. J. Therm. Sci. 2025, 210, 109678. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, J.; Zhang, Z.; Li, J.; Zhang, G.; Han, F. Gradient distribution surface texture for enhancing the surface heat transfer performance of the mini-channel. Appl. Therm. Eng. 2025, 270, 126237. [Google Scholar] [CrossRef]
- Zhang, Z.; Cui, K.; Zhao, H.; Han, T.; He, K.; Yan, X. Experimental investigation into flow boiling heat transfer in ribbed micro-channel with porous-decorated sidewalls. Int. J. Therm. Sci. 2025, 214, 109883. [Google Scholar] [CrossRef]
- Song, W.; Li, W.; Lin, S.; Ye, H.; Li, G. Experimental and numerical investigation of flow pattern evolution and flow-induced vibrations in an M-shaped subsea jumper under gas-liquid two-phase flow conditions. Ocean Eng. 2025, 327, 120964. [Google Scholar] [CrossRef]
- Shu, Q.; Mo, D.-M.; Hu, Y.-P.; Wu, C.-M.; Li, Y.-R. Formation mechanism and evolution of flow patterns for thermal convection in an inner cylinder-heated annular pool. Int. Commun. Heat Mass Transfer 2024, 158, 107963. [Google Scholar] [CrossRef]
- Sun, C.; Dai, R.; Tao, L.; Huang, L.; Gu, S.; Zhang, Y.; Gu, Z. Experimental study on the relationship between the flow pattern and heat transfer characteristics of flow boiling in a vertical upward rectangular narrow channel. Int. J. Heat Mass Tran. 2025, 242, 126844. [Google Scholar] [CrossRef]
- Brutin, D.; Tadrist, L. Pressure drop and heat transfer analysis of flow boiling in a minichannel: Influence of the inlet condition on two-phase flow stability. Int. J. Heat Mass Tran. 2004, 47, 2365–2377. [Google Scholar] [CrossRef]
- Katiyar, G.; Karagadde, S.; Saha, S.K.; Sharma, A. Numerical modelling of bubble growth in microchannel using level set method. Int. J. Heat Mass Tran. 2016, 101, 719–732. [Google Scholar] [CrossRef]
- Wang, Q.; Cao, J.; Su, D.; Li, M.; Dang, C.; Liu, X.; Song, R.; Li, J. Numerical simulation of R134a flow boiling heat transfer in a horizontal mini-channel under various gravity levels. Int. J. Heat Mass Tran. 2024, 235, 126141. [Google Scholar] [CrossRef]
- Wang, G.; Cheng, P. Subcooled flow boiling and microbubble emission boiling phenomena in a partially heated microchannel. Int. J. Heat Mass Tran. 2009, 52, 79–91. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, X.; Liu, Y.; Mubarak, S.; Wang, S. Experimental study of flow boiling characteristics in minigap channels over a wide heat flux range. Int. J. Heat Mass Tran. 2023, 201, 123567. [Google Scholar] [CrossRef]
- He, J.; Hou, Q.; Yang, X.; Duan, H.; Lin, L. Isolated slug traveling in a voided line and impacting at an end orifice. Phys. Fluids 2024, 36, 027105. [Google Scholar] [CrossRef]
- Tan, X.; Han, X.; Li, X.; Meng, Z.; Zhang, F.; Li, L.; Li, T.; Peng, X.; Yuan, H. Modeling the water transport in water invasion channel with water invasion unit numerical simulation based on intelligent proxies. Phys. Fluids 2025, 37, 023330. [Google Scholar] [CrossRef]
- Song, Y.; Huang, G.; Yin, J.; Wang, D. Three-dimensional reconstruction of bubble geometry from single-perspective images based on ray tracing algorithm. Meas. Sci. Technol. 2024, 36, 016010. [Google Scholar] [CrossRef]
- Yin, L.; Jiang, P.; Xu, R.; Wang, W.; Jia, L. Visualization of flow patterns and bubble behavior during flow boiling in open microchannels. Int. Commun. Heat Mass Transfer 2017, 85, 131–138. [Google Scholar] [CrossRef]
- Gu, S.; Tao, L.; Jin, C.; Ju, Y.; Zhao, X. Study of flow pattern transition criterion and heat transfer characteristics in vertical rectangular narrow channel for steam heating. Int. J. Heat Mass Tran. 2024, 220, 124877. [Google Scholar] [CrossRef]
- Revellin, R.; Dupont, V.; Ursenbacher, T.; Thome, J.R.; Zun, I. Characterization of diabatic two-phase flows in microchannels: Flow parameter results for R-134a in a 0.5 mm channel. Int. J. Multiph. Flow 2006, 32, 755–774. [Google Scholar] [CrossRef]
- Wilmarth, T.; Ishii, M. Two-phase flow regimes in narrow rectangular vertical and horizontal channels. Int. J. Heat Mass Tran. 1994, 37, 1749–1758. [Google Scholar] [CrossRef]
- Chalgeri, V.S.; Jeong, J.H. Flow regime transition criteria for vertical downward two-phase flow in rectangular channel. Nucl. Eng. Technol. 2022, 54, 546–553. [Google Scholar] [CrossRef]
- Viggiano, B.; Skjæraasen, O.; Schümann, H.; Tutkun, M.; Cal, R.B. Characterization of flow dynamics and reduced-order description of experimental two-phase pipe flow. Int. J. Multiph. Flow 2018, 105, 91–101. [Google Scholar] [CrossRef]
- Oliveira, J.D.; Copetti, J.B.; Indrusiak, M.L.S.; Souza, R.R.; Lima, R. On the nature of flow patterns and pressure drop fluctuations during flow boiling. Int. J. Multiph. Flow 2021, 144, 103793. [Google Scholar] [CrossRef]
- Da Riva, E.; Del Col, D.; Garimella, S.V.; Cavallini, A. The importance of turbulence during condensation in a horizontal circular minichannel. Int. J. Heat Mass Tran. 2012, 55, 3470–3481. [Google Scholar] [CrossRef]
- Zhang, J.; Li, W.; Minkowycz, W. Numerical simulation of condensation for R410A at varying saturation temperatures in mini/micro tubes. Numer. Heat Transf. Part A Appl. 2016, 69, 464–478. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, X.; Ye, P. Numerical and experimental investigation of two phase flow during boiling in a coiled tube. Int. J. Heat Mass Tran. 2008, 51, 1003–1016. [Google Scholar] [CrossRef]
- Liu, H.; Tang, J.; Sun, L.; Mo, Z.; Xie, G. An assessment and analysis of phase change models for the simulation of vapor bubble condensation. Int. J. Heat Mass Tran. 2020, 157, 119924. [Google Scholar] [CrossRef]
- Chalgeri, V.S.; Jeong, J.H. Flow patterns of vertically upward and downward air-water two-phase flow in a narrow rectangular channel. Int. J. Heat Mass Tran. 2019, 128, 934–953. [Google Scholar] [CrossRef]
- Hibiki, T.; Mishima, K. Flow regime transition criteria for upward two-phase flow in vertical narrow rectangular channels. Nucl. Eng. Des. 2001, 203, 117–131. [Google Scholar] [CrossRef]
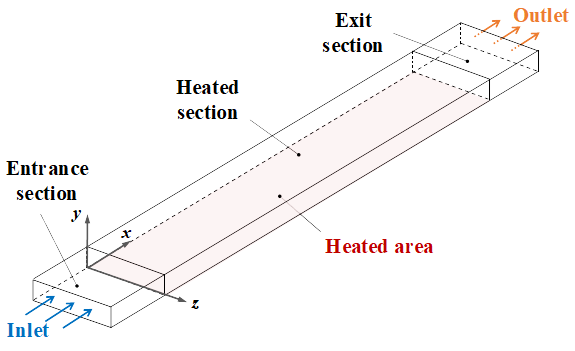
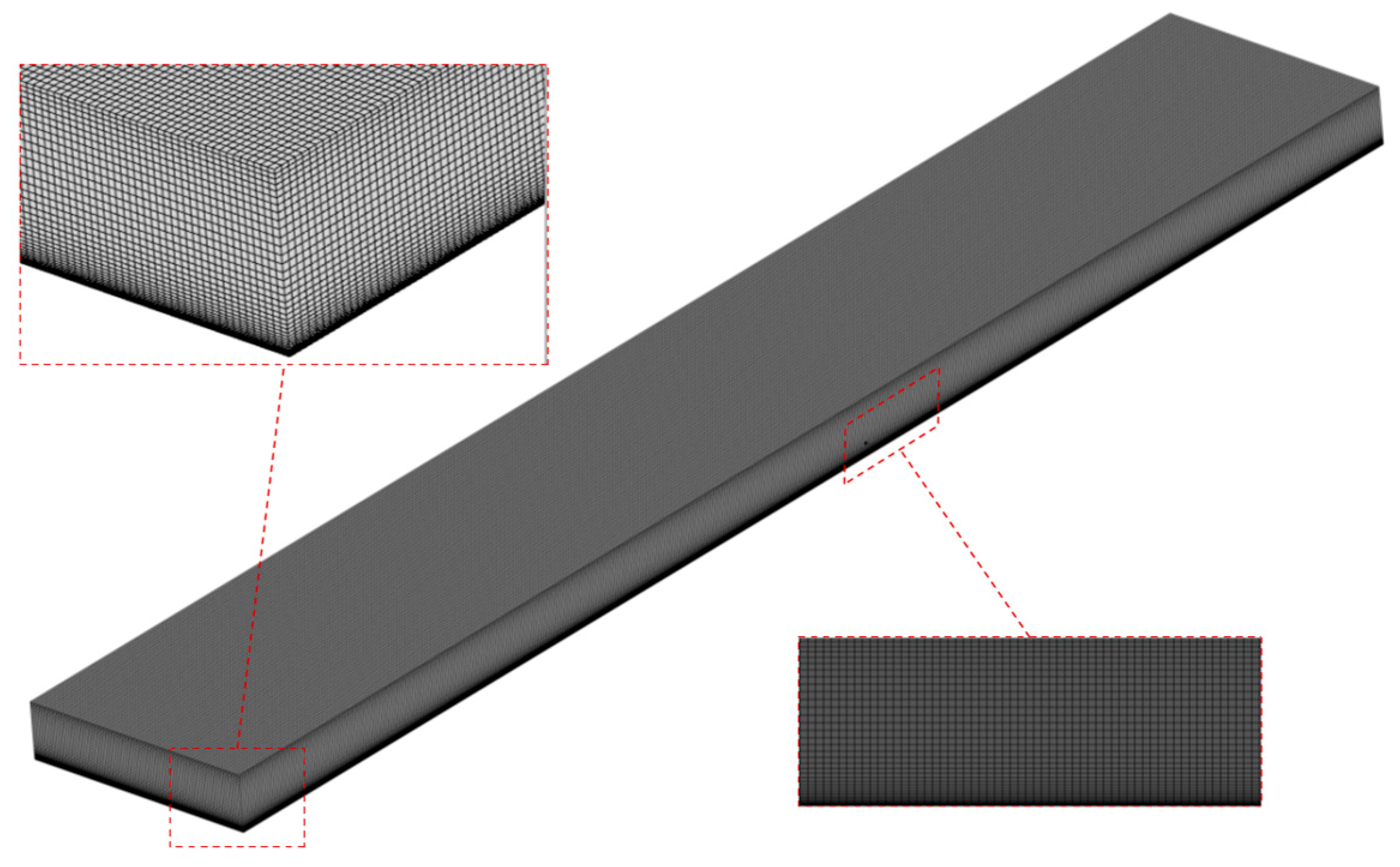


| Parameters | Symbol | Unit | Value |
|---|---|---|---|
| Inlet temperature | Tin | ℃ | 80 |
| Outlet pressure | pout | kPa | 101.325 |
| Mass flux | G | kg/(m2·s) | 200/300/400 |
| Heat flux | q | W/cm2 | 41.9/90.5/178.4 |
| Item | Content |
|---|---|
| Transient formulation | First-order implicit |
| Gradient | Least-square cell based |
| Pressure–velocity coupling | Coupled |
| Pressure | PRSETO! |
| Momentum and energy | Bounded Central Differencing |
| Max iterations | 20 |
| Time step | 10−5 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Wang, X.; Liu, Y.; Li, L. Numerical Investigation of Subcooled Boiling Flow and Patterns’ Transitions in a High-Heat-Flux Rectangular Small Channel. Water 2025, 17, 1580. https://doi.org/10.3390/w17111580
Wu X, Wang X, Liu Y, Li L. Numerical Investigation of Subcooled Boiling Flow and Patterns’ Transitions in a High-Heat-Flux Rectangular Small Channel. Water. 2025; 17(11):1580. https://doi.org/10.3390/w17111580
Chicago/Turabian StyleWu, Xianyang, Xiao Wang, Yang Liu, and Linmin Li. 2025. "Numerical Investigation of Subcooled Boiling Flow and Patterns’ Transitions in a High-Heat-Flux Rectangular Small Channel" Water 17, no. 11: 1580. https://doi.org/10.3390/w17111580
APA StyleWu, X., Wang, X., Liu, Y., & Li, L. (2025). Numerical Investigation of Subcooled Boiling Flow and Patterns’ Transitions in a High-Heat-Flux Rectangular Small Channel. Water, 17(11), 1580. https://doi.org/10.3390/w17111580









