Different Sensitivities of Earthquake-Induced Water Level Responses and the Influencing Factors in Fault Zones: Insights from the Dachuan-Shuangshi Fault
Abstract
1. Introduction
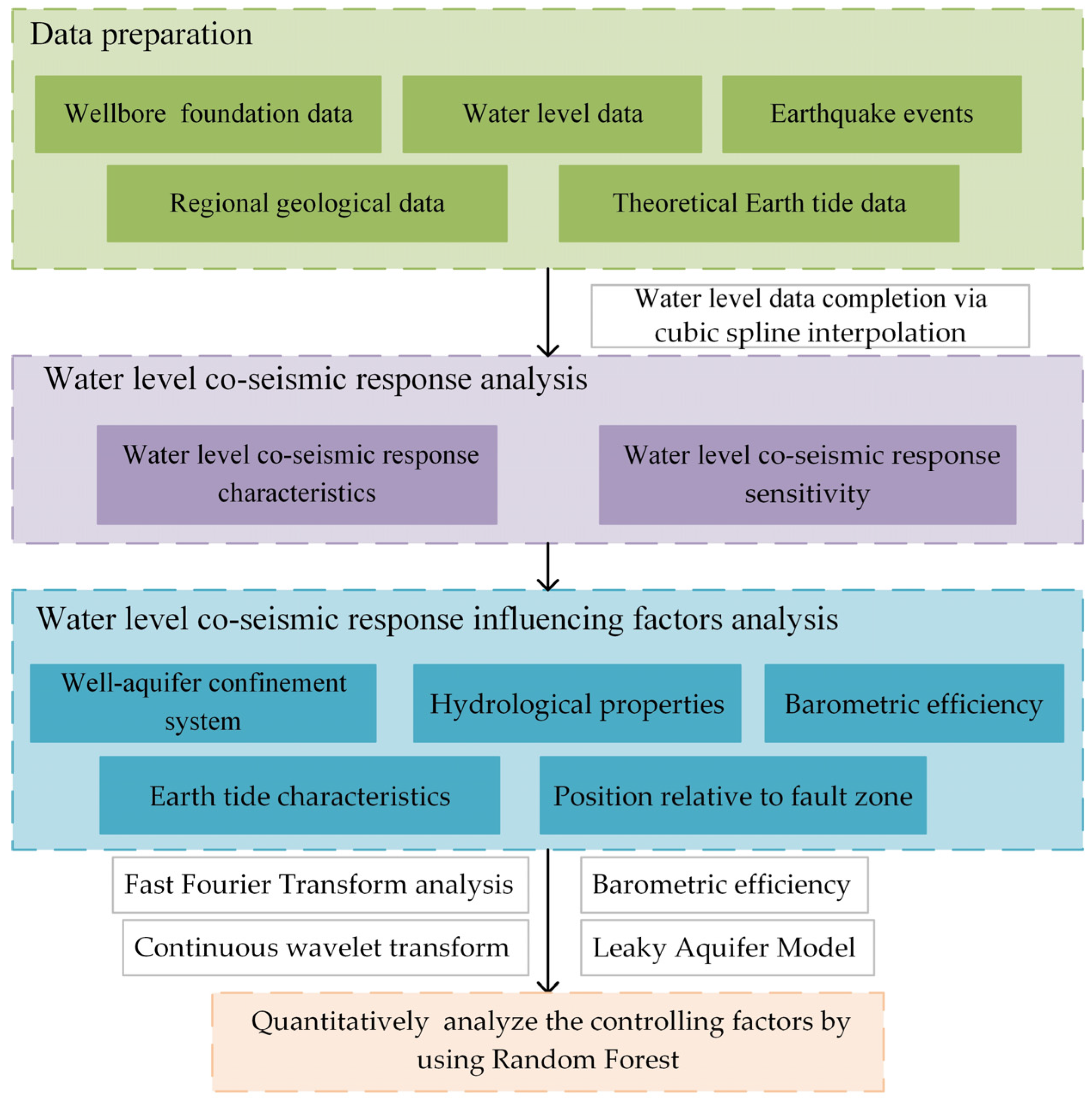
2. Materials and Methods
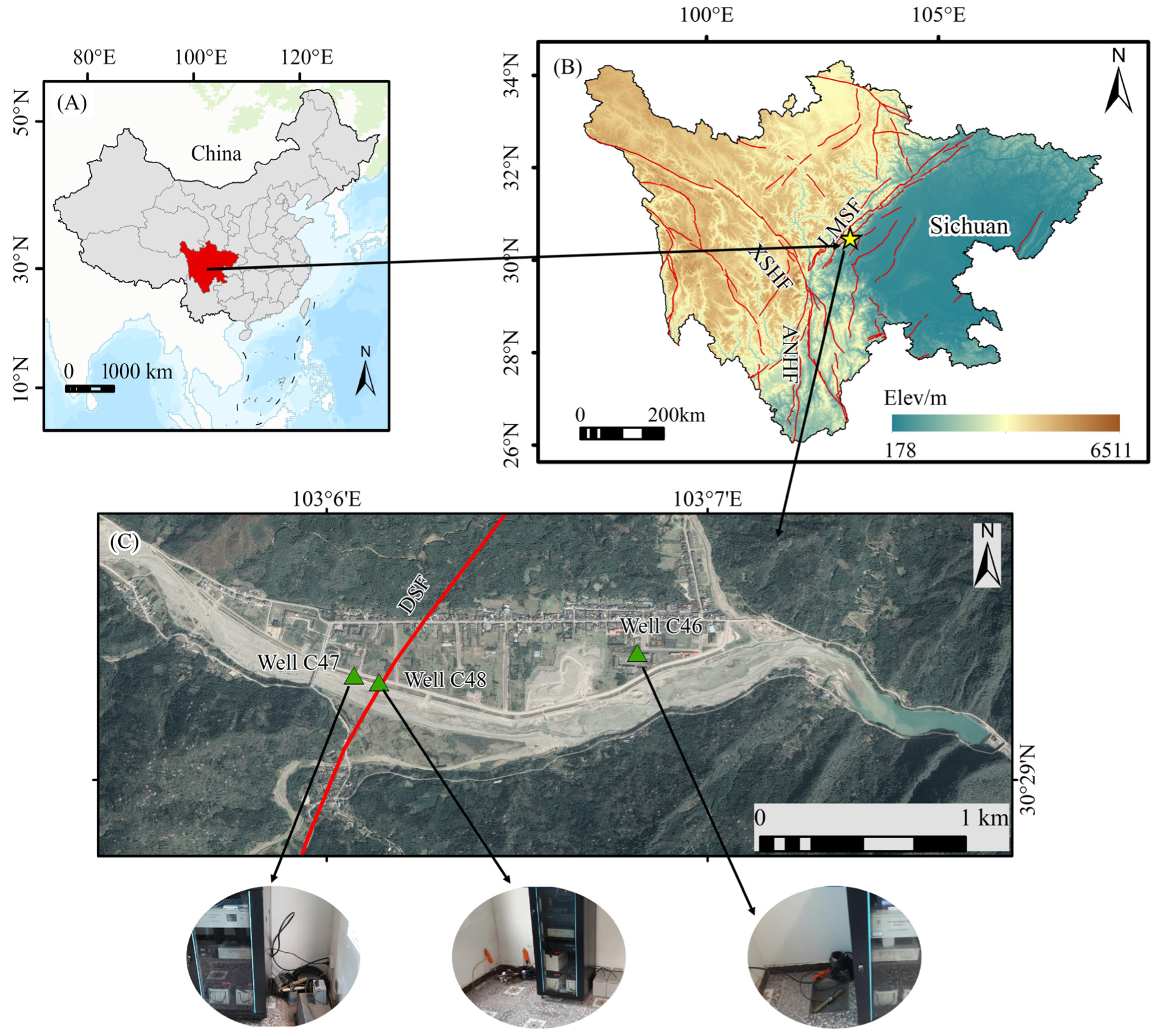
2.1. Study Area Background
2.2. Data Sources
2.2.1. Water Level Data
2.2.2. Earthquake Events
2.3. Methods
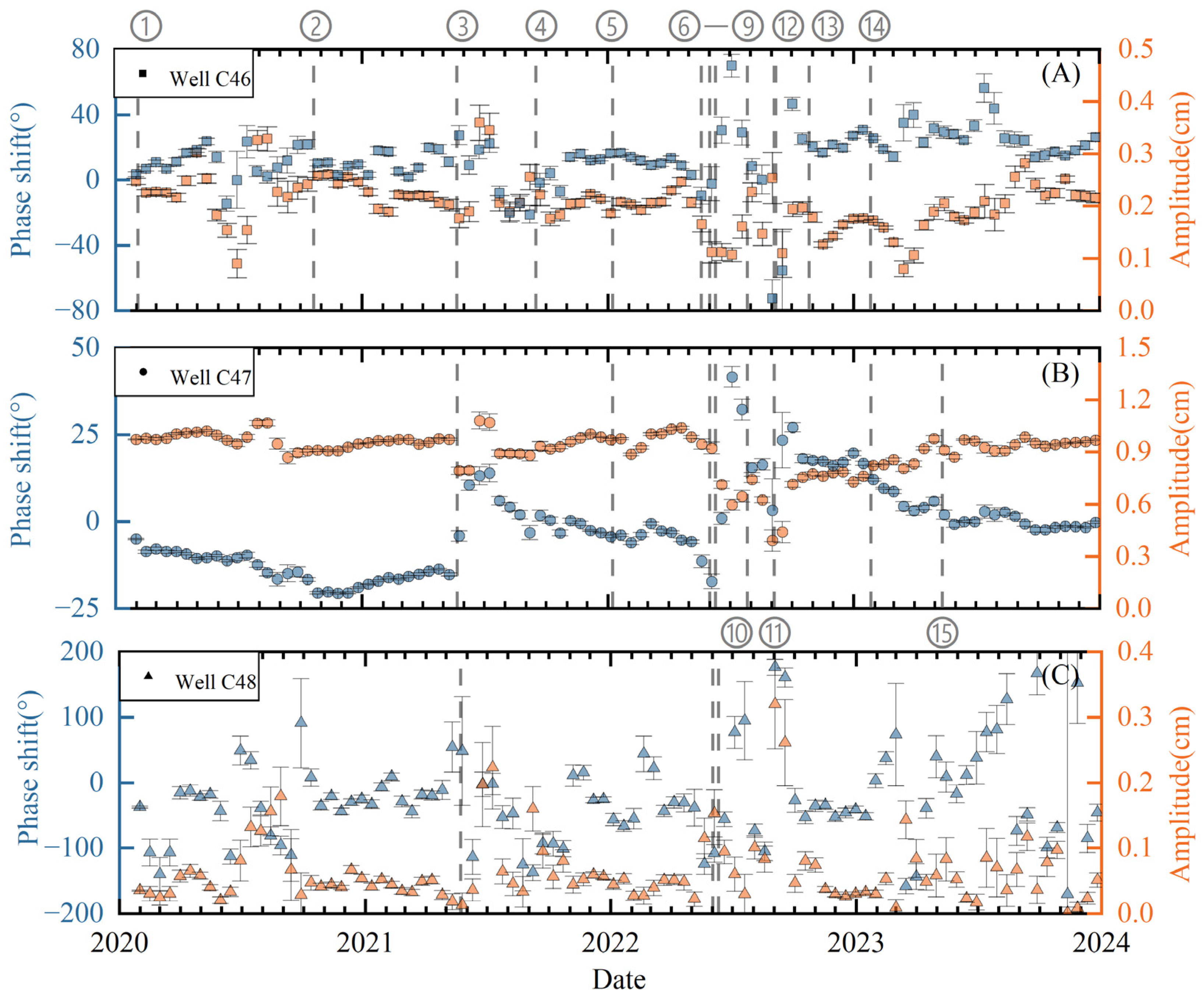
2.3.1. Well–Aquifer Confinement Based on Tidal Response
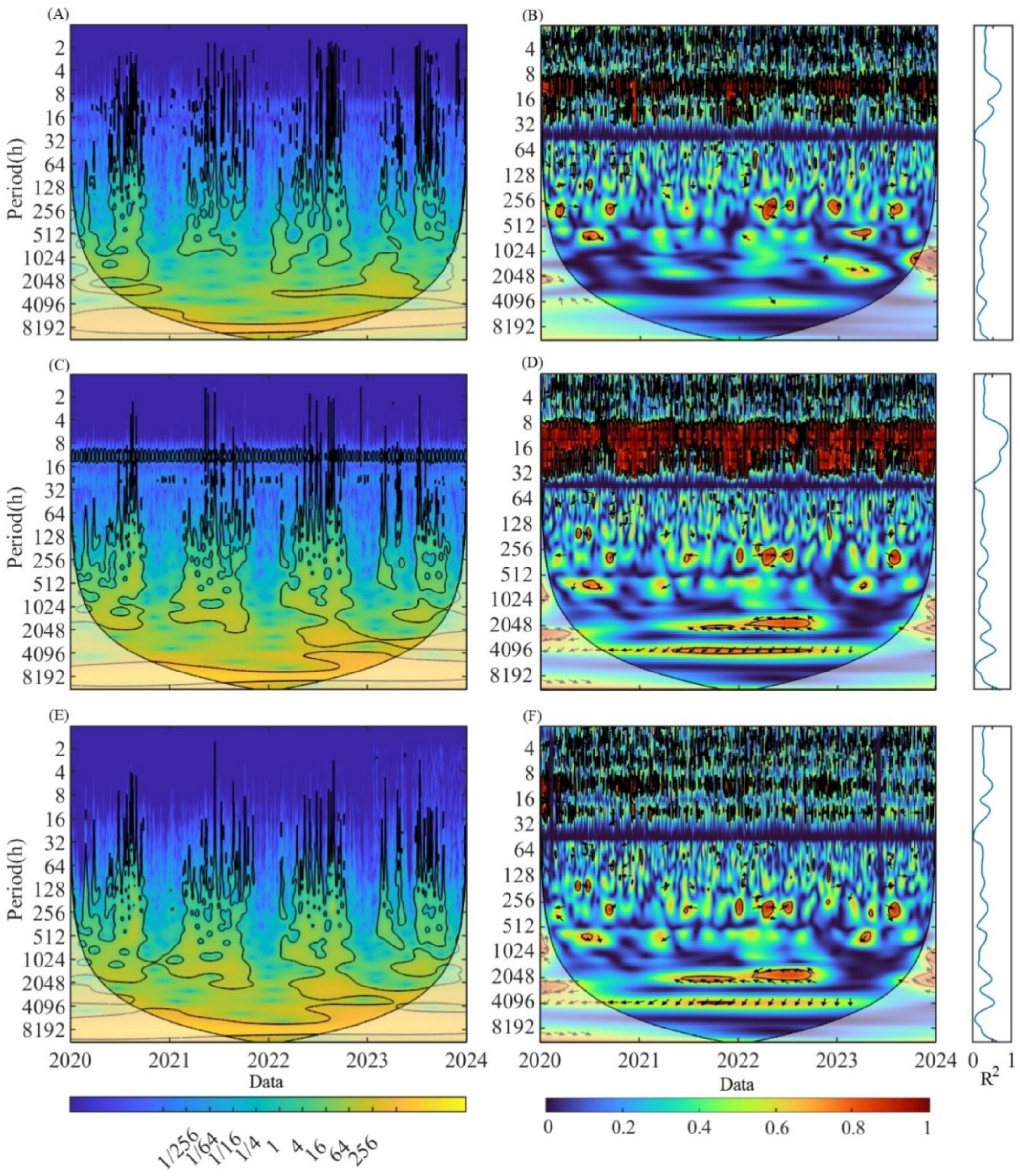
2.3.2. Continuous Wavelet Coherence
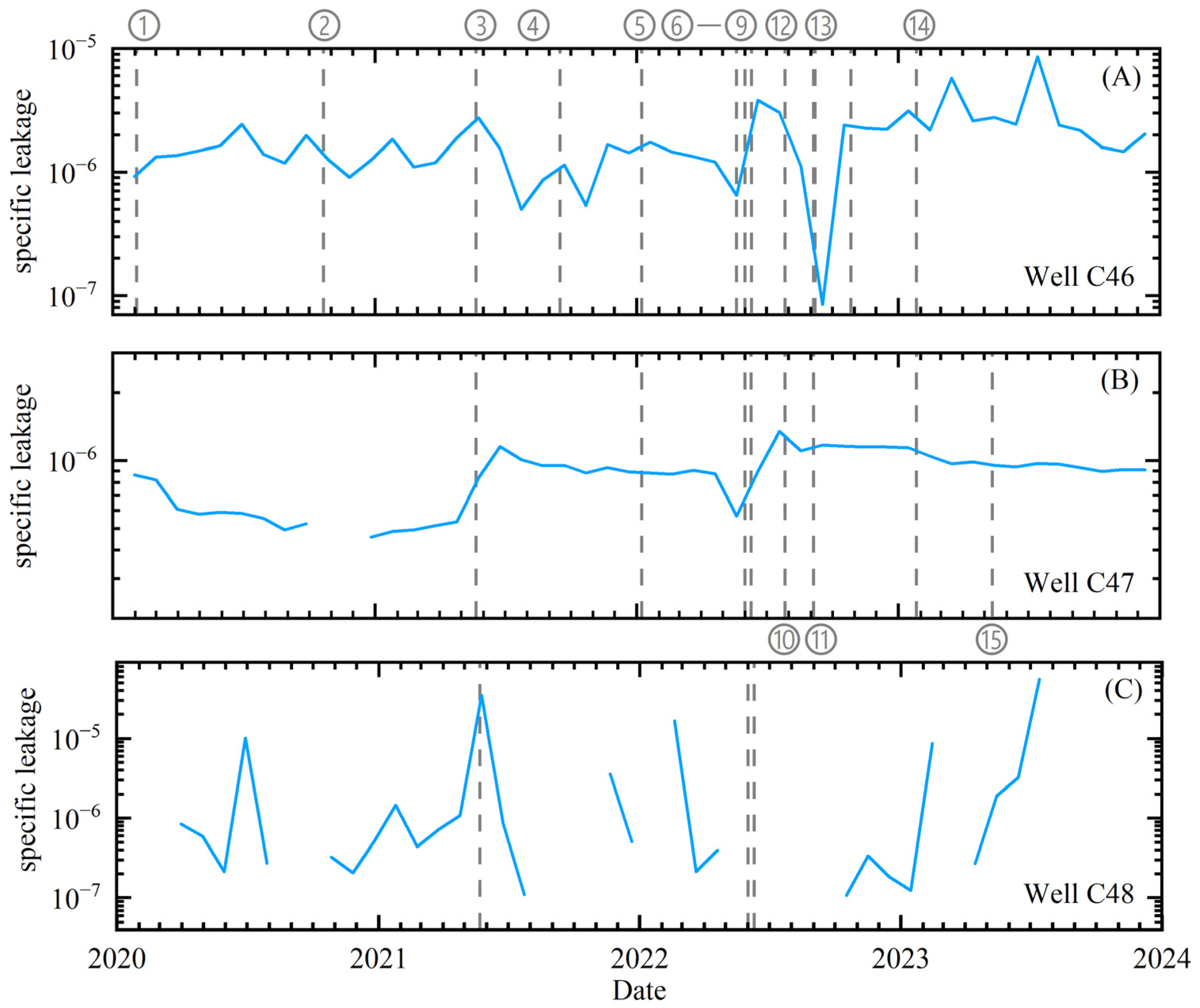
2.3.3. Leaky Aquifer Model
2.3.4. Barometric Efficiency
2.3.5. Random Forest
3. Results and Discussion
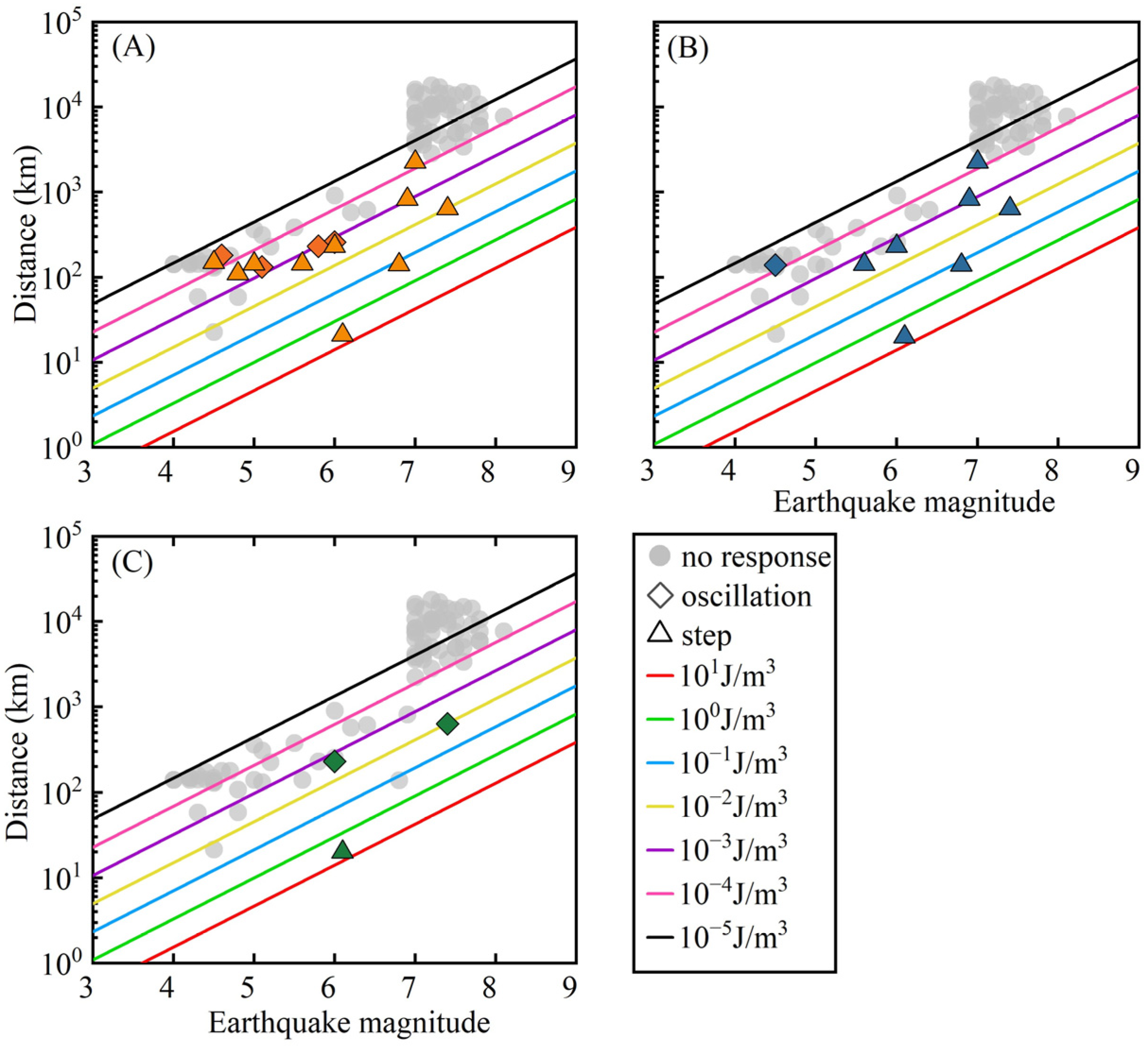
3.1. Response to Earthquakes
3.2. Co-Seismic Response Sensitivity
3.3. Water Level Co-Seismic Response Mechanism
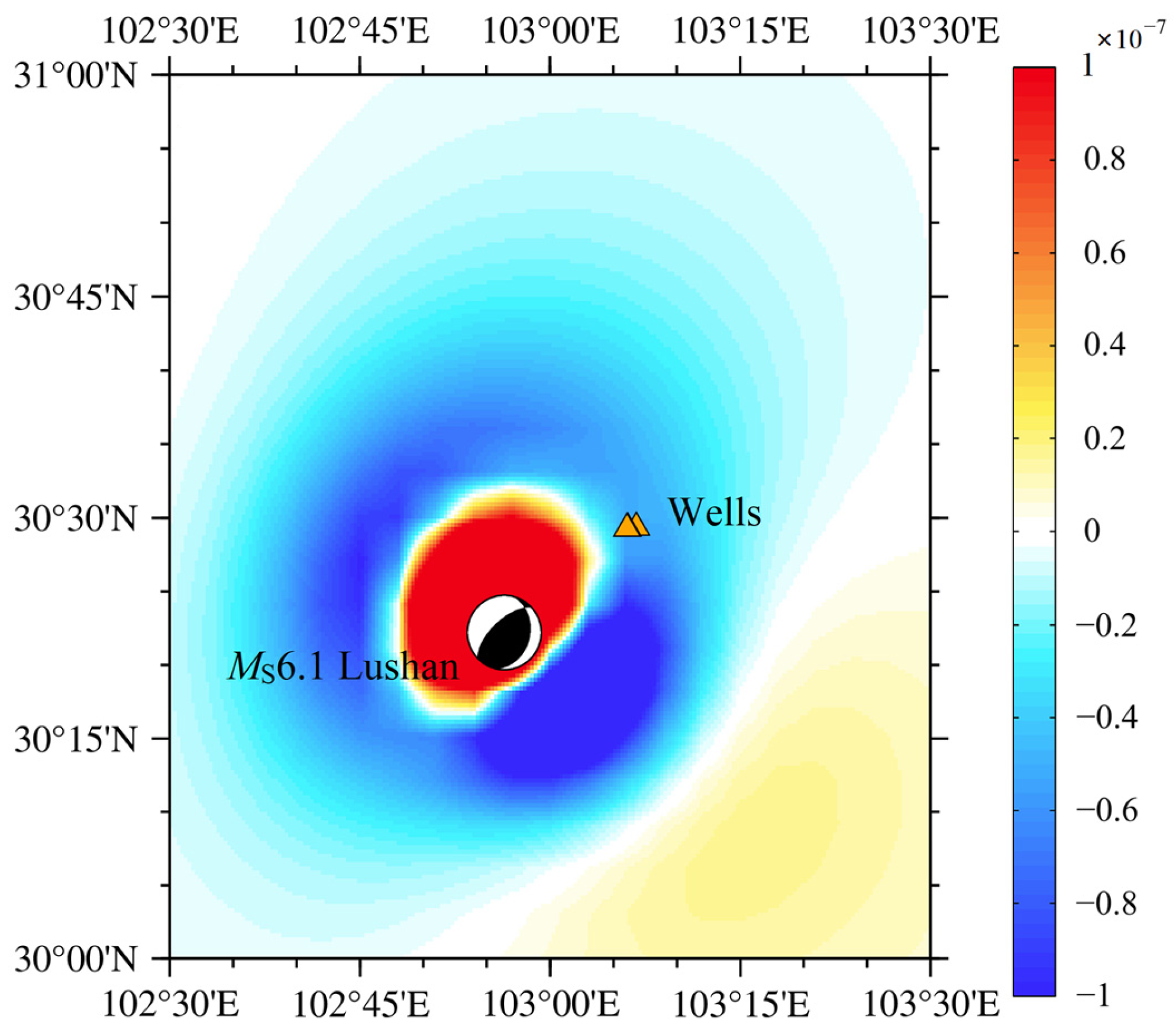
3.3.1. The Near-Field Region
3.3.2. The Mid-To-Far-Field Region
3.4. Factors Influencing Response Sensitivity
3.4.1. Influence of the Well–Aquifer Confinement System
3.4.2. Influence of the Characteristics of the Earth’s Tides
3.4.3. Influence of Hydrological Properties
3.4.4. Influence of Barometric Efficiency
3.4.5. Influence of Position Relative to the Fault Zone
3.5. Importance Analysis of Influencing Factors
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Manga, M.; Wang, C.-Y. Earthquake hydrology. Treatise Geophys. 2007, 4, 293–320. [Google Scholar]
- Wang, C.-Y.; Manga, M. Earthquakes influenced by water. In Water and Earthquakes; Springer: Berlin/Heidelberg, Germany, 2021; pp. 61–82. [Google Scholar]
- He, A.; Singh, R.P. Groundwater level response to the Wenchuan earthquake of May 2008. Geomat. Nat. Hazards Risk 2019, 10, 336–352. [Google Scholar] [CrossRef]
- Lai, G.; Jiang, C.; Han, L.; Sheng, S.; Ma, Y. Co-seismic water level changes in response to multiple large earthquakes at the LGH well in Sichuan, China. Tectonophysics 2016, 679, 211–217. [Google Scholar] [CrossRef]
- Sun, X.; Wang, G.; Yang, X. Coseismic response of water level in Changping well, China, to the Mw 9.0 Tohoku earthquake. J. Hydrol. 2015, 531, 1028–1039. [Google Scholar] [CrossRef]
- Skelton, A.; Andrén, M.; Kristmannsdóttir, H.; Stockmann, G.; Mörth, C.-M.; Sveinbjörnsdóttir, Á.; Jónsson, S.; Sturkell, E.; Guðrúnardóttir, H.R.; Hjartarson, H.; et al. Changes in groundwater chemistry before two consecutive earthquakes in Iceland. Nat. Geosci. 2014, 7, 752–756. [Google Scholar] [CrossRef]
- Chi-Yuen, W.; Michael, M. New streams and springs after the 2014 Mw6.0 South Napa earthquake. Nat. Commun. 2015, 6, 7597. [Google Scholar]
- Yan, X.; Shi, Z.; Zhou, P.; Zhang, H.; Wang, G. Modeling Earthquake-Induced Spring Discharge and Temperature Changes in a Fault Zone Hydrothermal System. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019344. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, G.; Lin, X.; Li, R.; Lu, S.; Jiao, Y.; Qiu, D.; Meng, G.; Wang, Q. The Complexity of Moisture Sources Affects the Altitude Effect of Stable Isotopes of Precipitation in Inland Mountainous Regions. Water Resour. Res. 2024, 60, e2023WR036084. [Google Scholar] [CrossRef]
- Li, R.; Zhu, G.; Lu, S.; Meng, G.; Chen, L.; Wang, Y.; Huang, E.; Jiao, Y.; Wang, Q. Effects of cascade hydropower stations on hydrologic cycle in Xiying river basin, a runoff in Qilian mountain. J. Hydrol. 2025, 646, 132342. [Google Scholar] [CrossRef]
- Fan, X.; Scaringi, G.; Korup, O.; West, A.J.; Westen, C.J.; Tanyas, H.; Hovius, N.; Hales, T.C.; Jibson, R.W.; Allstadt, K.E.; et al. Earthquake-Induced Chains of Geologic Hazards: Patterns, Mechanisms, and Impacts. Rev. Geophys. 2019, 57, 421–503. [Google Scholar] [CrossRef]
- Shrestha, B.R.; Khanal, N.R.; Smadja, J.; Fort, M. Geo-hydrological hazards induced by Gorkha Earthquake 2015: A Case of Pharak area, Everest Region, Nepal. Geogr. J. Nepal 2020, 13, 91–106. [Google Scholar] [CrossRef]
- Fan, X.; Westen, C.J.v.; Korup, O.; Gorum, T.; Xu, Q.; Dai, F.; Huang, R.; Wang, G. Transient water and sediment storage of the decaying landslide dams induced by the 2008 Wenchuan earthquake, China. Geomorphology 2012, 171–172, 58–68. [Google Scholar] [CrossRef]
- Cui, P.; Dang, C.; Zhuang, J.-Q.; You, Y.; Chen, X.-Q.; Scott, K.M. Landslide-dammed lake at Tangjiashan, Sichuan province, China (triggered by the Wenchuan Earthquake, May 12, 2008): Risk assessment, mitigation strategy, and lessons learned. Environ. Earth Sci. 2012, 65, 1055–1065. [Google Scholar] [CrossRef]
- Hong-jian, Z.; Xi, W.; Yi, Y. Risk Assessment of Disaster Chain: Experience from Wenchuan Earthquake-induced Landslides in China. J. Mt. Sci. 2015, 12, 1169–1180. [Google Scholar]
- Jacquemond, L.; Godano, M.; Cappa, F.; Larroque, C. Interplay Between Fluid Intrusion and Aseismic Stress Perturbations in the Onset of Earthquake Swarms Following the 2020 Alex Extreme Rainstorm. Earth Space Sci. 2024, 11, e2024EA003528. [Google Scholar] [CrossRef]
- Mansouri Daneshvar, M.R.; Freund, F.T. Survey of a relationship between precipitation and major earthquakes along the Peru-Chilean trench (2000–2015). Eur. Phys. J. Spec. Top. 2021, 230, 335–351. [Google Scholar] [CrossRef]
- Nie, W.; Tian, C.; Song, D.; Liu, X.; Wang, E. Disaster process and multisource information monitoring and warning method for rainfall-triggered landslide: A case study in the southeastern coastal area of China. Nat. Hazards 2024, 121, 2535–2564. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, G.; Manga, M.; Wang, C.-Y. Mechanism of co-seismic water level change following four great earthquakes–insights from co-seismic responses throughout the Chinese mainland. Earth Planet. Sci. Lett. 2015, 430, 66–74. [Google Scholar] [CrossRef]
- Lai, G.; Ge, H.; Xue, L.; Brodsky, E.E.; Huang, F.; Wang, W. Tidal response variation and recovery following the Wenchuan earthquake from water level data of multiple wells in the nearfield. Tectonophysics 2014, 619–620, 115–122. [Google Scholar] [CrossRef]
- Yan, R.; Wang, G.; Ma, Y.; Shi, Z.; Song, J. Local groundwater and tidal changes induced by large earthquakes in the Taiyuan Basin, North China from well monitoring. J. Hydrol. 2020, 582, 124479. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, G. Hydrological response to multiple large distant earthquakes in the Mile well, China. J. Geophys. Res. Earth Surf. 2014, 119, 2448–2459. [Google Scholar] [CrossRef]
- Yi, L.C.; Yeeping, C.; Yu, C.P.; Chia, C.Y.; Lin, T.T. Impacts of hydrogeological characteristics on groundwater-level changes induced by earthquakes. Hydrogeol. J. 2018, 26, 451–465. [Google Scholar]
- Wang, C.Y.; Doan, M.L.; Xue, L.; Barbour, A.J. Tidal response of groundwater in a leaky aquifer—Application to Oklahoma. Water Resour. Res. 2018, 54, 8019–8033. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Manga, M. Streamflow and water well responses to earthquakes. Science 2003, 300, 2047–2049. [Google Scholar] [CrossRef]
- Sun, X.; Xiang, Y.; Shi, Z. Changes in permeability caused by two consecutive earthquakes—Insights from the responses of a well-aquifer system to seismic waves. Geophys. Res. Lett. 2019, 46, 10367–10374. [Google Scholar] [CrossRef]
- Manga, M.; Beresnev, I.; Brodsky, E.E.; Elkhoury, J.E.; Elsworth, D.; Ingebritsen, S.E.; Mays, D.C.; Wang, C.Y. Changes in permeability caused by transient stresses: Field observations, experiments, and mechanisms. Rev. Geophys. 2012, 50, 1–24. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, Z.; Wang, G.; Yan, X.; Liu, C.; Sun, X.; Ma, Y.; Wen, D. Different sensitivities of earthquake-induced water level and hydrogeological property variations in two aquifer systems. Water Resour. Res. 2021, 57, e2020WR028217. [Google Scholar] [CrossRef]
- Bense, V.; Gleeson, T.; Loveless, S.; Bour, O.; Scibek, J. Fault zone hydrogeology. Earth-Sci. Rev. 2013, 127, 171–192. [Google Scholar] [CrossRef]
- Yan, R.; Wang, G.; Shi, Z. Sensitivity of hydraulic properties to dynamic strain within a fault damage zone. J. Hydrol. 2016, 543, 721–728. [Google Scholar] [CrossRef]
- Sun, X.; Xiang, Y.; Shi, Z.; Hu, X.; Zhang, H. Sensitivity of the response of well-aquifer systems to different periodic loadings: A comparison of two wells in Huize, China. J. Hydrol. 2019, 572, 121–130. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, G.; Yan, R.; Wang, B.; Yu, H.; Yu, C.; Yue, C.; Wang, Y. Relationship between earthquake-induced hydrologic changes and faults. Water 2021, 13, 2795. [Google Scholar] [CrossRef]
- Fronzi, D.; Mirabella, F.; Cardellini, C.; Caliro, S.; Palpacelli, S.; Cambi, C.; Valigi, D.; Tazioli, A. The role of faults in groundwater circulation before and after seismic events: Insights from tracers, water isotopes and geochemistry. Water 2021, 13, 1499. [Google Scholar] [CrossRef]
- Xiang, Y.; Sun, X.; Gao, X. Different coseismic groundwater level changes in two adjacent wells in a fault-intersected aquifer system. J. Hydrol. 2019, 578, 124123. [Google Scholar] [CrossRef]
- Nalmpantis, C.; Vrakas, D. Machine learning approaches for non-intrusive load monitoring: From qualitative to quantitative comparation. Artif. Intell. Rev. 2019, 52, 217–243. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, Y.; Ritzwoller, M.H.; Zheng, X.; Xiong, X.; Li, Z. Crustal structure of the northeastern Tibetan plateau, the Ordos block and the Sichuan basin from ambient noise tomography. Earthq. Sci. 2010, 23, 465–476. [Google Scholar] [CrossRef]
- Zhang, L.; Fu, L.; Liu, A.; Chen, S. Simulating the strong ground motion of the 2022 MS6. 8 Luding, Sichuan, China Earthquake. Earthq. Sci. 2023, 36, 283–296. [Google Scholar] [CrossRef]
- Chen, L.; Ran, Y.; Wang, H.; Li, Y.; Ma, X. The Lushan Ms 7.0 earthquake and activity of the southern segment of the Longmenshan fault zone. Chin. Sci. Bull. 2013, 58, 3475–3482. [Google Scholar] [CrossRef]
- Rahi, K.A.; Halihan, T. Identifying aquifer type in fractured rock aquifers using harmonic analysis. Groundwater 2013, 51, 76–82. [Google Scholar] [CrossRef]
- Qu, S.; Shi, Z.; Wang, G.; Xu, Q.; Zhu, Z.; Han, J. Using water-level fluctuations in response to Earth-tide and barometric-pressure changes to measure the in-situ hydrogeological properties of an overburden aquifer in a coalfield. Hydrogeol. J. 2020, 28, 1465–1479. [Google Scholar]
- Qi, Z.; Shi, Z.; Rasmussen, T.C. Time-and frequency-domain determination of aquifer hydraulic properties using water-level responses to natural perturbations: A case study of the Rongchang Well, Chongqing, southwestern China. J. Hydrol. 2023, 617, 128820. [Google Scholar] [CrossRef]
- Tamura, Y.; Sato, T.; Ooe, M.; Ishiguro, M. A procedure for tidal analysis with a Bayesian information criterion. Geophys. J. Int. 1991, 104, 507–516. [Google Scholar] [CrossRef]
- Liu, W.; Shi, Z.; Lyu, S.; Qi, Z.; Yang, P. Comparison of the Methods of Barometric Efficiency Estimation by Water Level:An Application to Gaoda Well in Yunnan. J. Seismol. Res. 2024, 47, 191–199. [Google Scholar]
- Zhang, H.; Shi, Z.; Wang, G.; Sun, X.; Yan, R.; Liu, C. Large earthquake reshapes the groundwater flow system: Insight from the water-level response to earth tides and atmospheric pressure in a deep well. Water Resour. Res. 2019, 55, 4207–4219. [Google Scholar] [CrossRef]
- Song, Y.; Gu, H.; Li, H.; Chi, B. Comparison Analysis of Co-Seismic Response Characteristics of Groundwater Level at Two Sides of Fault: A Case Study of Dahuichang Observation Wells in the Middle of Babaoshan Fault in Beijing. J. Jilin Univ. (Earth Sci. Ed.) 2016, 46, 1815–1822. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, J.; Zhang, G.; Jing, J. Response of water level of confined well to dynamic process of barometric pressure. Chin. J. Geophys. 1989, 32, 539–549. [Google Scholar]
- Clark, W.E. Computing the barometric efficiency of a well. J. Hydraul. Div. 1967, 93, 93–98. [Google Scholar] [CrossRef]
- Roeloffs, E.A. Hydrologic precursors to earthquakes: A review. Pure Appl. Geophys. 1988, 126, 177–209. [Google Scholar] [CrossRef]
- Wang, C.Y.; Manga, M. Hydrologic responses to earthquakes and a general metric. Geofluids 2010, 10, 206–216. [Google Scholar] [CrossRef]
- Kopylova, G.; Boldina, S. Seismo-Hydrogeodynamic Effects in Groundwater Pressure Changes: A Case Study of the YuZ-5 Well on the Kamchatka Peninsula. Water 2023, 15, 2174. [Google Scholar] [CrossRef]
- Kopylova, G.; Boldina, S. Effects of seismic waves in water level changes in a well: Empirical data and models. Izv. Phys. Solid Earth 2020, 56, 530–549. [Google Scholar] [CrossRef]
- Freed, A.M. Earthquake triggering by static, dynamic, and postseismic stress transfer. Annu. Rev. Earth Planet. Sci. 2005, 33, 335–367. [Google Scholar] [CrossRef]
- Okada, Y. Surface Deformation due to Shear and Tensile Faults in a Half Space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar] [CrossRef]
- Chia, Y. Changes of Groundwater Level due to the 1999 Chi-Chi Earthquake in the Choshui River Alluvial Fan in Taiwan. Bull. Seismol. Soc. Am 2001, 91, 1062–1068. [Google Scholar] [CrossRef]
- Jónsson, S.; Segall, P.; Pedersen, R.; Björnsson, G. Post-earthquake ground movements correlated to pore-pressure transients. Nature 2003, 424, 179–183. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Wang, G.C.; Manga, M.; Wang, C.Y. Continental-scale water-level response to a large earthquake. Crustal Permeability 2012, 15, 324–333. [Google Scholar]
- King, C.Y.; Azuma, S.; Igarashi, G.; Ohno, M.; Saito, H.; Wakita, H. Earthquake-related water-level changes at 16 closely clustered wells in Tono, central Japan. J. Geophys. Res. Atmos. 1999, 1041, 13073–13082. [Google Scholar] [CrossRef]
- Bonini, M. Investigating earthquake triggering of fluid seepage systems by dynamic and static stresses. Earth-Sci. Rev. 2020, 210, 103343. [Google Scholar] [CrossRef]
- Zhao, D.; Zeng, Y.; Sun, X.; Mei, A. Rock Damage and aquifer property estimation from water level fluctuations in wells induced by seismic waves: A case study in X10 Well, Xinjiang, China. Shock. Vib. 2021, 2021, 2137978. [Google Scholar] [CrossRef]
- He, A.; Singh, R.P.; Sun, Z.; Ye, Q.; Zhao, G. Comparison of regression methods to compute atmospheric pressure and earth tidal coefficients in water level associated with Wenchuan Earthquake of 12 May 2008. Pure Appl. Geophys. 2016, 173, 2277–2294. [Google Scholar] [CrossRef]
- He, A.; Deng, W.; Singh, R.P.; Lyu, F. Characteristics of hydroseismograms in Jingle well, China. J. Hydrol. 2020, 582, 124529. [Google Scholar] [CrossRef]
- Zhang, W.; Li, M.; Yang, Y.; Rui, X.; Lu, M.; Lan, S. Implications of groundwater level changes before near field earthquakes and its influencing factors–several earthquakes in the vicinity of the Longmenshan-Anninghe fault as an example. Front. Earth Sci. 2025, 13, 1541346. [Google Scholar] [CrossRef]
- Xue, L.; Brodsky, E.E.; Erskine, J.; Fulton, P.M.; Carter, R. A permeability and compliance contrast measured hydrogeologically on the San Andreas Fault. Geochem. Geophys. Geosystems 2016, 17, 858–871. [Google Scholar] [CrossRef]
- Husseini, M.I.; Jovanovich, D.B.; Randall, M.; Freund, L. The fracture energy of earthquakes. Geophys. J. Int. 1975, 43, 367–385. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, D.; Xu, Y.; Zhang, X. Comparative Analysis of Water Level Coseismic Response Characteristics in Sichuan Fluid Network. Earthquake 2024, 44, 55–72. [Google Scholar]
- Weaver, K.C.; Arnold, R.; Holden, C.; Townend, J.; Cox, S.C. A probabilistic model of aquifer susceptibility to earthquake-induced groundwater-level changes. Bull. Seismol. Soc. Am. 2020, 110, 1046–1063. [Google Scholar] [CrossRef]





| MS | 4.0~5.0 | 5.1~6.0 | 6.1~7.0 | 7.1~8.0 | ≥8.0 |
|---|---|---|---|---|---|
| Frequency | 21 | 6 | 18 | 44 | 1 |
| ID | Date and Time | Earthquake | MS | Water Well Stations | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Well C46 | Well C47 | Well C48 | ||||||||||
| EP | Amp | Res | EP | Amp | Res | EP | Amp | Res | ||||
| 1 | 2020/2/3 0:05 | qingbaijiang | 5.1 | 132 | 1.9 | oscillation | - | - | - | - | - | - |
| 2 | 2020/10/21 12:04 | beichuan | 4.6 | 181 | 1.3 | oscillation | - | - | - | - | - | - |
| 3 | 2021/5/22 2:04 | maduo | 7.4 | 639 | 113.8 | step fall | 639 | 118.9 | step fall | 639 | 1 | Oscillation |
| 4 | 2021/9/16 4:33 | luxian | 6 | 258 | 1.9 | oscillation | - | - | - | - | - | - |
| 5 | 2022/1/8 1:45 | menyuan | 6.9 | 828 | 8.9 | gradual fall | 828 | 1 | gradual rise | - | - | - |
| 6 | 2022/5/20 8:36 | hanyuan | 4.8 | 110 | 20.1 | gradual fall | - | - | - | - | - | - |
| 7 | 2022/6/1 17:00 | lushan | 6.1 | 21 | 308.1 | step rise–step fall | 20 | 220.8 | step fall–gradual rise | 20 | 13.1 | step rise |
| 8 | 2022/6/10 0:03 | maerkang | 5.8 | 233 | 2.8 | oscillation | - | - | - | - | - | - |
| 9 | 2022/6/10 1:28 | maerkan | 6 | 231 | 7 | step fall | 231 | 2.4 | step fall | 231 | 2 | oscillation |
| 10 | 2022/7/27 8:43 | Philippines | 7 | 2268 | 4.6 | step rise | 2269 | 7.8 | step rise | - | - | - |
| 11 | 2022/9/5 12:52 | luding | 6.8 | 141 | 73.6 | step fall | 140 | 21.5 | step fall | - | - | - |
| 12 | 2022/9/7 2:42 | shimian | 4.5 | 150 | 2.9 | step rise | - | - | - | - | - | - |
| 13 | 2022/10/22 13:17 | luding | 5 | 143 | 4.9 | step fall | - | - | - | - | - | - |
| 14 | 2023/1/26 3:49 | luding | 5.6 | 143 | 25.2 | step fall | 142 | 2.4 | gradual rise | - | - | - |
| 15 | 2023/5/12 2:34 | luding | 4.5 | - | - | - | 139 | 1.1 | oscillation | - | - | - |
| Magnitude Division | Seismic Events | Water Well Stations | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Well C46 | Well C47 | Well C48 | ||||||||
| Response Times | Ratio (%) | Maximum Distance (km) | Response Times | Ratio (%) | Maximum Distance (km) | Response Times | Ratio (%) | Maximum Distance (km) | ||
| 4 ≤ MS < 5 | 19 | 3 | 15.79 | 181 | 1 | 5.26 | 139 | 0 | 0 | - |
| 5 ≤ MS < 6 | 8 | 4 | 50 | 233 | 1 | 12.50 | 142 | 0 | 0 | - |
| 6 ≤ MS < 7 | 8 | 5 | 62.5 | 828 | 4 | 50 | 828 | 2 | 25 | 231 |
| 7 ≤ MS < 8 | 54 | 2 | 3.7 | 2268 | 2 | 3.7 | 2269 | 1 | 1.85 | 639 |
| MS ≥ 8 | 1 | 0 | 0 | - | 0 | 0 | - | 0 | 0 | - |
| Variable | Regression Coefficients | |||||
|---|---|---|---|---|---|---|
| Unstandardized Coefficients | Unstandardized Coefficients | t | Sig | |||
| B | Std. Error | Beta | ||||
| constant | −0.271 | 0.772 | −0.351 | 0.732 | ||
| 0.715 | 0.147 | 0.924 | 4.870 | 0.000 ** | ||
| −1.249 | 0.295 | −0.804 | −4.239 | 0.001 ** | ||
| constant | −1.645 | 1.569 | −1.048 | 0.342 | ||
| −1.151 | 0.435 | −0.797 | −2.648 | 0.046 * | ||
| 0.849 | 0.290 | 0.881 | 2.925 | 0.033 * | ||
| Data | Water Well Stations | ||
|---|---|---|---|
| Bp C46 | Bp C47 | Bp C48 | |
| Average value | 0.87 | 2.33 | −0.73 |
| Hydraulic Parameters | Aquifer Confinement | Fault Architecture | Tidal Characteristics | Barometric Efficiency |
|---|---|---|---|---|
| 0.4 | 0.24 | 0.17 | 0.13 | 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Gu, H.; Zhao, D.; Rui, X.; Zhang, X.; Huang, X. Different Sensitivities of Earthquake-Induced Water Level Responses and the Influencing Factors in Fault Zones: Insights from the Dachuan-Shuangshi Fault. Water 2025, 17, 1568. https://doi.org/10.3390/w17111568
Zhang J, Gu H, Zhao D, Rui X, Zhang X, Huang X. Different Sensitivities of Earthquake-Induced Water Level Responses and the Influencing Factors in Fault Zones: Insights from the Dachuan-Shuangshi Fault. Water. 2025; 17(11):1568. https://doi.org/10.3390/w17111568
Chicago/Turabian StyleZhang, Ju, Hongbiao Gu, Deyang Zhao, Xuelian Rui, Xiaoming Zhang, and Xiansi Huang. 2025. "Different Sensitivities of Earthquake-Induced Water Level Responses and the Influencing Factors in Fault Zones: Insights from the Dachuan-Shuangshi Fault" Water 17, no. 11: 1568. https://doi.org/10.3390/w17111568
APA StyleZhang, J., Gu, H., Zhao, D., Rui, X., Zhang, X., & Huang, X. (2025). Different Sensitivities of Earthquake-Induced Water Level Responses and the Influencing Factors in Fault Zones: Insights from the Dachuan-Shuangshi Fault. Water, 17(11), 1568. https://doi.org/10.3390/w17111568








