Abstract
This review examines various methods for the design and optimization of horizontal-axis hydrokinetic turbines. A detailed analysis is presented of the results from numerical and experimental studies on small axial hydrokinetic turbines optimized through different methodologies. The influence of individual components of the flow passage on the turbine’s efficiency is emphasized. The energy performance of the studied turbines is compared with that of modern commercial hydrokinetic turbines. It is demonstrated that Computational Fluid Dynamics (CFD) can be used to optimize the geometry of the flow passage, achieving a higher power coefficient compared to commercial hydrokinetic turbines. All of this contributes to the future development of more efficient axial hydrokinetic turbines suitable for operation at lower flow velocities.
1. Introduction
Hydropower is one of the inexhaustible, reliable, and stable sources of renewable energy. Hydropower plants operate with high efficiency, generating large amounts of electricity over long periods while maintaining the stability of the energy system. The optimization of the working process involves both numerical and physical experiments aimed at developing new, more efficient water turbines. Most contemporary numerical models for turbine design are based on a number of assumptions, often significantly neglecting certain aspects of the actual flow characteristics within the passage section. This necessitates validation of the results using a specialized laboratory test rig, in accordance with the IEC 60193 standard. Data from these studies enable the prediction of the power curves of the hydro unit within its operating range and provide a basis for validating the numerical models used in the design of individual components of the turbine’s flow passage.
This review focuses on small axial hydrokinetic turbines with a maximum power output of up to 5 kW, which achieve higher efficiency at lower flow velocities, making them suitable for operation in weak to moderate river currents. Their compact size facilitates installation and maintenance, making them well suited to meet the energy needs of small- to medium-sized households.
To date, several review papers examine the performance and efficiency of axial hydrokinetic turbines, as well as broader aspects related to various types of hydrokinetic systems. In their review, Vicente H. Aristizábal-Tique et al. [1] focus on the hydrokinetic potential of water resources. They present a comparative analysis of the main types of hydrokinetic turbines (axial and vertical), highlighting their advantages and disadvantages. The examples discussed refer to actual hydrokinetic systems implemented in different countries around the world. The authors emphasize the necessity of conducting a preliminary techno-economic analysis of the site intended for the construction of a hydrokinetic power plant.
Zhibin Zhou et al. [2] provided a detailed systematic review of hydrokinetic turbines with a capacity exceeding 500 kW. Their study focused on structural design solutions for installation, resistance to wave forces and corrosion, ease of access for maintenance and repair, the selection of appropriate materials for marine environments, and the optimization of both production and operational costs.
C.M. Niebuhr et al. [3] present a detailed analysis of hydrokinetic turbines installed in diffusers and profiled channels open to the atmosphere. Their focus is on optimizing the geometry of the turbine’s flow section and the optimal positioning of the runner. The goal is to increase energy efficiency and reduce the hydraulic losses of the hydro unit.
In their review, Pankaj Kumar Yadav et al. [4] summarize key internal parameters of turbines, such as blade solidity, tip–speed ratio, and blade angle of attack. They conduct a comparative analysis of various types of vertical hydrokinetic turbines, including Gorlov, Darrieus, and Savonius turbines. The authors highlight the main drawbacks of these systems—namely, low starting torque and reduced efficiency at lower flow velocities. Nevertheless, they emphasize the significant potential of hydrokinetic turbines to provide affordable and clean energy.
Mancilla et al. [5] present a detailed review on the development and research of horizontal hydrokinetic turbines. The review focuses on the design features of the flow passage, structural loading, numerical modeling, and the influence of various internal parameters on efficiency (such as the number of blades, blade pitch angle, and flow velocity). The review is primarily centered on the efficiency of bare turbines, while shrouded turbines are only briefly discussed.
Ibrahim et al. [6] highlight the environmental advantages of hydrokinetic turbines, as well as their application in areas without access to the national power grid. The review covers equipment corrosion, installation challenges, and the impact of turbines on aquatic environments. The main contribution of the article lies in the detailed classification and comparative analysis of hydrokinetic energy technologies, as well as the issues that arise during their implementation.
To date, there is no published comparative review of small axial hydrokinetic turbines optimized using different methodologies and their commercially available counterparts. Furthermore, critical analysis reveals that existing reviews primarily focus on large-scale hydrokinetic systems or theoretical models, with insufficient experimental validation of the results. The present review addresses this gap by comparing synthesis, analysis, and numerical optimization data of small hydrokinetic turbines with real-world data from commercially available models. The findings will support the design of efficient, low-cost hydrokinetic systems suitable for rural and remote areas, thereby contributing to the expansion of decentralized renewable energy generation.
The aim of this review is, on the one hand, to analyze and compare the output power and power coefficient of small axial hydrokinetic turbines optimized using various methodologies by different researchers with the power curves of commercially available low-power axial hydrokinetic turbines. On the other hand, it seeks to provide a better understanding of the influence of flow passage components on the efficiency of these turbines.
2. State of Art
Hydrokinetic turbines are divided into two main types: those with a horizontal axis and those with a vertical axis. Vertical kinetic turbines are more suitable for extracting energy from water flows with variable speed and direction. Their main disadvantage is low efficiency, which is due to the trajectory of the blade movement relative to the flow. During one rotation, the blades change their position relative to the flow, which alters their angle of attack and generates a variable torque. The operating area of vertical kinetic turbines can be divided into active and passive regions. When the blades enter the active region, they generate positive torque, while in the passive region, they generate negative torque. One way to improve their efficiency is to shield the passive area with a barrier. According to laboratory studies, the power output of the turbine can be increased by approximately 30% [7,8,9]. Horizontal kinetic turbines are preferred because they can achieve higher efficiency [6]. Their blades maintain a constant angle of attack, which ensures more efficient conversion of kinetic energy.
The efficiency of the wind and hydrokinetic turbines is measured by the power coefficient Cp, which express the ratio between the extracted mechanical power Pext. and the kinetic power of the flow Pflow:
where T (Nm) is the torque of the turbine, ω (rad/s)—its the angular velocity, ρ is the density of the air/water (kg/m3), Sr (m2) is the swept area of the rotor (m2), and Cw (m/s) is the flow velocity in front of the rotor. Since Pflow depend on the flow velocity, it is common practice to use specially profiled hydrodynamic channels (Figure 1). These channels operate on the Venturi principle [10]. By constricting the cross-section in the working area, they locally increase the flow velocity in front of the turbine. In axial hydrokinetic turbines, the rotor can be places in diffuser-shaped housing, which achieves a similar result (Figure 2). In the first version, the rotor was placed in front of the diffuser entrance (a). Later, a straight cylindrical part (shroud) was added, which stabilizes the flow through the rotor (b). Subsequently, a brim diffuser was added, which increases the pulling force through the flow passage due to the vortices formed after brim (c) and (d). The last variant (e) is a curved shroud and diffuser, optimized according to the flow pattern. With these diffusers, the values of Cp can even exceed the Betz limit [11], which represents the theoretical maximum of 0.59.
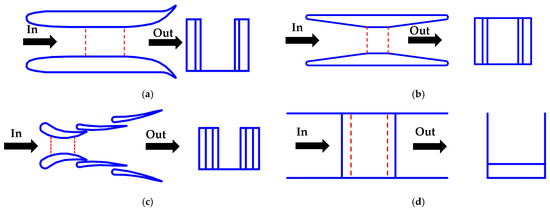
Figure 1.
Different channel modifications (a) Hybrid (curvilinear), (b) hybrid (rectilinear), (c) multi hydrofoil diffuser, (d) channel bed modifications (bed lifting) [8,9]. The black arrow indicates the flow direction. The working region is enclosed by red dashed lines.
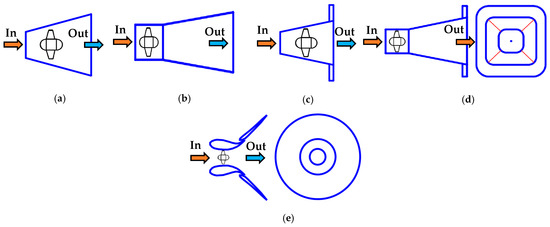
Figure 2.
Different shapes of housing for axial hydrokinetic turbines: (a) diffuser, (b) shroud and diffuser, (c) diffuser with brim, (d) shroud and diffuser with brim, and (e) curved shroud with diffuser [6]. The arrows indicates flow direction.
2.1. Synthesis and Analysis Methods
To assess the energy potential of free-flowing currents, it is necessary to have the turbine’s power curve, which shows the dependence of the maximum power coefficient on the flow velocity. Much of the research is focused on optimizing the geometry of the rotor with the aim of achieving a higher power coefficient, rather than studying the power curve of the turbine. When conducting laboratory experiments, it is essential to adhere to the laws of similarity outlined in international standards. This is important to ensure the correspondence between the power curves of the model and the full-scale (natural) turbine in the corresponding operating conditions.
The optimization of kinetic turbines is typically performed in the following sequence: synthesis, numerical analysis, and validation on a laboratory test bench or under field conditions. Optimization is achieved through iterative synthesis and analysis of different geometry variations of the flow passage. The numerical analysis evaluates the synthesized geometry, providing initial information on the torque, power, and power coefficient of the turbine. The influence of both external parameters (such as velocity and pressure) and internal parameters (such as the number of blades, chord length, blade and diffuser shape, etc.) on the operating process and its efficiency is examined. If the obtained results meet the technical requirements, the production of a real prototype and its physical testing are undertaken.
The methods for synthesizing the rotor of kinetic turbines can be analytical, numerical, or experimental. Analytical methods use mathematical equations that describe the interaction between the flow and the forces acting on the blades. One of the most commonly used analytical methods is based on the Blade Element Momentum Theory (BEMT) [12]. The number of blades, the chord length, the flow velocity, and the rotation speed of the rotor are specified. The rotor is represented as a rotating annular disc, which is divided into n cylindrical rotating sections. Two adjacent cylindrical rotating sections form an annular rotating section. The relative flow velocity in the midpoint of each rotating annular section is the vector sum of the free-flow velocity and the peripheral velocity of the midpoint of the current rotating annular section. Tangential and normal forces are calculated in each annular section based on the number of blades, the coefficients of the selected blade profile, the selected angle of attack, and the calculated relative velocity. The pitch angle of the blades in each annular section is calculated by the difference between the flow angle and the angle of attack. The contour of the blades is obtained by connecting their individual segments, and the torque of the rotor is obtained by integration of the torque into each blade segment. If the results meet the technical requirements, the process proceeds to the design and/or fabrication of a real prototype. If the results meet the technical requirements, the process proceeds to the design and/or fabrication of a real prototype.
Numerical methods use iterative numerical solutions, making them more complex. One example is the method of singularities [13,14]. In this method, the number of blades, chord length, flow velocity, and rotor rotation speed are specified. The space between the blades is divided into n concentric cylindrical sections. Each of these sections is unfolded into a plane, forming a rectangular-shaped surface. It is assumed that, in each individual section, the blades are subjected to a uniform flow structure. In the method of singularities, the velocity at each point in the flow (including around the blade profile) can be calculated using Biot–Savart’s law. The method of singularities provides reliable results at small angles of attack, when there is no flow separation from the blade surface—but this does not fully correspond to real conditions. In order to optimize the blades for actual operation, the method of singularities can be combined with methods for analyzing the flow through the blade cascade (Table 1).

Table 1.
Numerical methods used for analyzing the flow pattern through the blade cascade of the turbine rotor.
Experimental synthesis methods are empirical methods based on experimental research and observations. Various real prototypes are created using rapid prototyping methods (3D printing, stereolithography, molding and casting, CNC machining) [22,23]. Experimental data are used to develop empirical formulas that describe the influence of the geometry of the flow part (rotor and/or diffuser) on the operational characteristics and efficiency of the turbine. Experimental methods usually provide more accurate results but require significant costs for conducting research and producing prototypes, which makes them more expensive compared to numerical methods that are faster and more cost effective. During physical experiments in a laboratory hydrodynamic channel, the ratio between the turbine cross-section and the channel cross-section must be kept below 0.25 [24,25]. This ratio, known as the blockage coefficient, can alter the velocity in the measurement section and affect the obtained results.
Turbine optimization is carried out through the sequential synthesis and analysis of different variants of the geometry of the flow passage. The influence of external parameters (speed and pressure) and internal parameters (number of blades, chord length, blade and diffuser shape, etc.) on the operating performance and efficiency of the working process is examined. If the obtained results meet the technical specifications, the production of a real prototype and its physical testing is initiated.
2.2. CFD Modeling of Axial Hydrokinetic Turbines
In recent years, emphasis has been placed primarily on numerical studies using Computational Fluid Dynamics (CFD), a computational approach used to calculate and analyze flows [26,27]. CFD simulations allow scientists and engineers to analyze the distribution of temperature, pressure, velocity, and turbulence at every point in the studied area. The influence of the shape of different streamlined bodies on the pressure distribution along their surface is also examined. CFD describes the movement of fluids through mathematical equations of the Navier–Stokes equations. The main advantage of the CFD approach over physical experiments is the lower cost and the reduced time required to conduct the experiment [28].
According to the relevant studies, to achieve reliable results in the creation of the CFD numerical model, some recommendations must be followed: the rotor should be positioned at a distance of 5 to 20 times the main diameter from the surrounding walls of the computational domain [29], 2–5 times the main diameter from the inlet section [30,31], and 10–20 times the main diameter from the outlet section [32,33]. This is carried out to avoid the influence of surrounding walls, which can cause acceleration of the flow through the turbine (blockage effect), and to ensure that the turbulent flow has enough space to fully develop after the rotor. Undeveloped turbulent flow may affect the accuracy of the calculated flow parameters in the surrounding space, creating incorrect velocity and pressure distributions. In this case, the boundary conditions of Velocity inlet and Pressure Outlet are recommended. The surrounding walls are defined as fictitious (e.g., boundary condition Symmetry for Fluent or free-slip wall for CFX), allowing the turbine to operate under open flow conditions without being influenced by the surrounding walls. The mesh around the blades should be sufficiently fine to ensure higher accuracy in the calculation of tangential stresses and the development of the boundary layer. In the model settings, the y+ coefficient is often used, which defines the dimensionless distance normal to the surface of the body to the geometric center of the first cell layer. In specialized literature, recommended values of y+ are provided, depending on the choice of the turbulence model, as shown in Table 2.
The CFD simulations of hydrokinetic turbines are usually performed with the turbulence models k-ω SST [34], Large Eddy Simulation (LES) [35,36], and Detached Eddy Simulation (DES) [37,38]. The k-ω SST model can accurately determine the point of separation of the flow along the blade contour. This model is a hybrid and combines the advantages of the k-ε and k-ω models. In the near-wall region, it works like k-ω, calculating the boundary layer, while outside, it works like k-ε, calculating the eddies of the flow.
LES is more accurate in modeling eddy-dominated flows. It requires more memory and computational time. DES is a hybrid turbulence model that combines Reynolds Averaged Navier–Stokes equations (RANS) and LES. In the boundary layer region, the model calculates the boundary layer with RANS equations, and outside it calculates the eddies using the DES turbulence model method. It requires fewer computing resources and time than LES. Spalart–Allmaras is more suitable for simulating the flow through wind turbines. It uses the least memory, but the calculations are of lower accuracy [39].
The k-ε Standard, k-ε Realizable, and k-ε RNG use pre-defined empirical functions to predict the behavior of the boundary layer in the wall region [40], but these empirical functions cannot calculate the flow separation along the blade contour with sufficient accuracy. They are more suitable for predicting the behavior of turbulent jets, and flows in pipeline systems. K-ω Standard can calculate the boundary layer and the separation point along the blade contour, but is more unstable in the far-field region.
The accuracy of the results also depends on the parameters of the numerical mesh. Usually, the mesh is refined in the studied area, where higher accuracy of the studied quantities is required. The refinement step is controlled by the growth rate parameter. Another important parameter is the orthogonal quality of the numerical mesh. The greater the orthogonality of the cells, the more accurate the results of the numerical study will be. Ideally, the cells of the generated mesh should be rectangular. In practice, this is impossible due to the complexity of the studied geometry. The skewness parameter monitors the deformations of the cells (twisting and bending), which can lead to inaccurate results. The aspect ratio is a parameter that refers to the ratio between the longest and shortest sides of a cell. This parameter must change smoothly between neighboring cells, otherwise, it will lead to a poor approximation of the studied quantities. Each CFD solver has its own recommended parameter values. Some of them are shown in Table 3.

Table 2.
Recommended y+ values for various turbulence models.
Table 2.
Recommended y+ values for various turbulence models.
| Turbulence Model | y+ Range | Description and Application |
|---|---|---|
| Spalart–Allmaras (SA) | 0.5–2 [39] | Requires fine near-wall resolution. Used in aerodynamics and external flows. |
| k-ε Standard | 30–300 [40] | Uses wall functions; not suitable for low y+. Best for industrial flows. |
| k-ε RNG | 30–100 [40] | Improved near-wall performance but still uses wall functions. |
| k-ε Realizable | 30–100 [40] | Better for separated flows; still relies on wall functions. |
| k-ω Standard | 1–5 [34] | Resolves boundary layers well; good for near-wall effects. |
| k-ω SST | 0.5–2 [34] | Ideal for resolving boundary layers accurately; used in aerospace and turbomachinery. |
| Reynolds Stress Model (RSM) | <1 [41] | Requires full boundary layer resolution; no wall functions. Used in highly anisotropic turbulence. |
| Large Eddy Simulation (LES) | ≈1 [36,37] | Requires extremely fine mesh near walls; used for highly unsteady flows. |
| Detached Eddy Simulation (DES) | ≈1 [38,39] | Hybrid RANS-LES; requires fine mesh in boundary layers but coarser mesh elsewhere. |
| Smagorinsky Model (LES) | ≈1 [38] | Requires fine mesh; used for high-Re turbulent flows. |
| Wall-Modeled LES (WMLES) | 30–100 [38] | Coarser mesh than LES, but still provides good accuracy. |
| Direct Numerical Simulation (DNS) | ≈0.1 [42] | Fully resolves turbulence; requires extreme computational power. |

Table 3.
Recommended values of the geometric parameters of the mesh.
Table 3.
Recommended values of the geometric parameters of the mesh.
| Parameter | Fluent | CFX | OpenFOAM | STAR-CCM+ | Autodesk Flow Simulation |
|---|---|---|---|---|---|
| Aspect ratio | <5 (wall layers) [43] | <10 [44] | <10 [45] | <20 [46] | <10 [47] |
| Skewness | <0.85 [43] | <0.85 [44] | <0.85 [45] | <0.85 [46] | <0.85 [47] |
| Orthogonality | >0.1 [43] | >0.1 [44] | >0.1 [45] | >0.1 [46] | >0.1 [47] |
| Growth rate | <1.2 [43] | <1.2 [44] | <1.3 [45] | <1.3 [46] | <1.3 [47] |
2.3. Summary of Research and Optimization of Hydrokinetic Turbines
Table 4, Table 5, Table 6 and Table 7 present results from studies of the rotor solidity on the power factor by various authors. Most of these optimizations were carried out using the CFD simulations, the BEM method, and experimental approaches.

Table 4.
Summary of the obtained power coefficient by Mukherji et al. [48].

Table 5.
Summary of the obtained power coefficient by Chihaia et al. [49].

Table 6.
Summary of the obtained power coefficient by Antonio et al. [50].

Table 7.
Summary of the obtained power coefficient by Patel et al. [51].
Mukherji et al. [48] performed a numerical optimization of the blade cascade density—σ, by varying the number of blades and their chord. The rotor was synthesized using the BEM methodology, and the analysis was carried out with the Fluent 12.1 solver at a flow velocity of 2 m/s. The turbine rotor has a main diameter of D1 = 2 m. Numerical experiments were conducted with 2, 3, and 4 untwisted blades with a pitch angle of φr = 10 deg, and a chord length lr = 0.15, 0.167, 0.2, and 0.3 m. The results are shown in Table 4. The highest power coefficient (0.41) was achieved with three blades, at a blade cascade density of 0.095 and a chord length of 0.063 m. However, no information is provided regarding the blade profile name or the distribution of the thickness function along the camber line. Moreover, the results were not validated through a physical experiment.
Chihaia et al. [49] and Antonio et al. [50] optimize axial rotors with a main diameter of 0.6 m 0.2 m. The geometry of the rotors was synthesized using the QBlade [52] and XFoil [53] programs with the BEM method. The optimization was carried out by varying the blade cascade density (i.e., the number of blades, chord length, and pitch angle) at a water flow velocity of 2 m/s. Chihaia et al. [49] achieved the highest power coefficient of 0.4 with three blades, while adjusting the pitch angle along the span increased the coefficient to 0.45 (Table 5). Antonio et al. [50] obtained a power coefficient of 0.41 with three blades. A standard NACA 4415 airfoil profile was used (Table 6).
Patel et al. [51] conduct a physical experiment to investigate the impact of the number of blades with a chord length of 65 mm, and a pitch angle of 110°, on the efficiency of an axial hydrokinetic turbine placed in a cylindrical casing, with a flow rate of 1.91 L/s. A standard NACA 0012 airfoil profile was used for the blades. According to the data presented in Table 7, the highest power coefficient of 0.45 was achieved with four blades.
The results from the studies show that the highest efficiency is achieved with three or four blades in bare runner configurations. When the rotor is placed in a shroud, the optimal number of blades is four.
The data from the remaining studies are summarized in Table 8 (bare turbines) and Table 9 (shrouded turbines). In the first column, the study number is indicated; in the second column, the names of the researchers; in the third column, the established maximum power coefficient; and in the subsequent columns, the methods used for the synthesis and/or analysis of the turbine characteristics, the airfoil used, the flow velocity, the rotor distance from surrounding walls in the CFD model, the dimensions of the channel measurement section where the physical experiments were conducted, the main rotor diameter, the blockage coefficient (which should be below 0.25 to prevent flow acceleration around the rotor due to the constriction of the measurement section [24,25]), and the optimized parameters are indicated. The data are also visualized in Figure 3. in bar chart format. Most of these studies are numerical (the blue bars) and have not been validated with physical experiments. The calculated values of Cp can be used only for a comparative analysis of the accuracy of the numerical method applied, by evaluating the deviation (error) from actual values that can be determined experimentally.
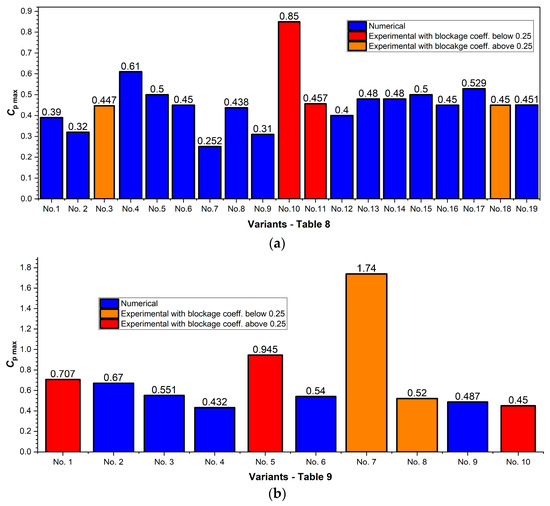
Figure 3.
Comparison of the maximum power coefficient (Cp max) obtained from numerical and experimental studies: (a) bare turbines and (b) shrouded turbines. Numerical data are represented in blue, while experimental data with high and low blockage coefficient with orange and red.
According to Figure 3a, nearly half of the studies on bare turbines achieved Cp values in the range of 0.45–0.48. These include No. 3, 6, 8, 11, 13, 14, 16, 18, and 19. The studies were conducted at flow velocities Cw ranging from 1 to 3.5 m/s, which indicates that the turbine efficiency remains relatively stable across this velocity interval (Table 8). The optimization parameters are blade profile, pitch angle and chord length across the span (column 12). The reference value of Cp = 0.45 is defined based on the physical experiments from studies No. 3 and 18 (orange bars), which were performed under free-flow conditions (blockage coefficient < 0.25). The absolute error of the numerical studies within this interval, relative to the reference Cp, was in the range of 0.03–0.05, while the relative error was in the range of 6.7–11%. CFD simulations indicate rotors synthesized using the BEM method reach Cp values of 0.44–0.48 (No. 6, 13, 14, and 19). The remaining numerical studies (No. 1, 2, 4, 5, 15, and 17) exhibit larger deviations from the reference value of 0.45, which may be attributed to incorrect CFD settings (boundary conditions or turbulence model), blade profile, or incorrectly selected initial values of optimization parameters. Assuming the numerical model settings are correct, the use of variable pitch blades can improve the power coefficient by 0.16, relative to the accepted reference value (No. 4). Optimizing the blade swept angles can improve the efficiency by 0.08 (No. 17), while optimizing the skew and wake angles (No. 11) does not improve the performance.
According to Table 8 and Figure 3a, Patel et al. [54] (No. 10, indicated with red bar) achieved the highest Cp of 0.85 through a physical experiment. They optimized the tip filled radius of the blades, which increased the power coefficient by 0.5. Vogel et al. [55] (No. 4) reported a Cp of 0.610 using modified BEM model that accounts for the blockage effect of the rotor. The results were compare with OpenFOAM solver v.2.3.1. and SST k-ω turbulence model. The reported values are unusually high for a bare axial hydrokinetic turbine, which may be caused by the high blockage coefficient (0.569) of the measurement section in the test rig. Vogel et al. [55] did not provide additional data for the CFD model, and this prevents a more accurate assessment.
The lowest Cp values were found in Wang et al.’s study [56] (0.252—No. 7) and Abutunis et al.’s study [57] (0.320—No. 2) using BEM, NN (MLP). Wang et al. [56] used the CFD method with the ANSYS Fluent solver v.14.5 and the k-ω SST turbulence model, while Abutunis et al. [57] used a Neural Network (MLP) model for their analysis. The rotor’s positioning in the CFD model is within the recommended range, which eliminates the flow acceleration and overprediction of the torque.
As shown in Table 8, the most effective blade profiles are SG6043 and NACA63-8xx. Romero et al. [58] (No. 11), Eriamiatoe et al. [59] (No. 16), and Hanzla et al. [60] (No. 18) use the SG6043 profile. They obtained power coefficients between 0.450 and 0.457. Payne et al. (No. 5) and Wang et al. [56] (No. 19) use NACA63-8xx series. They report values of Cp in the range of 0.451–0.500. The data in Table 8 confirm that there is no significant difference in power coefficient between three-bladed and four-bladed rotors. The choice of the blade number depends on the strength considerations and the operational conditions of the turbine.
Table 9 and Figure 3b present the results from the optimization of shrouded turbines. Analogously, the numerical studies are shown in blue, while the experimental ones are marked in orange for low blockage coefficients and red for high blockage coefficients. According to Table 9, column 7 computational domain geometries used in the CFD models are within acceptable limits, which ensures the development of free-stream conditions. As a reference value of Cp, 0.52 can be chosen (No 9—Figure 3b). The numerical results from studies No. 3, 6, and 9 yield values close to this reference, with absolute errors of 0.03–0.033 and relative errors of 5.77–6.34%. The optimization parameters in these studies include shaft diameter and diffuser shape. Song et al. [61] (No. 3) increased Cp max by 0.003 after removing the shaft and the front fairing of the rotor. Parka et al. [62] (No. 6) raised Cp from 0.45 to 0.54 after optimizing the length of the diffuser. Mancillia et al. [30] (No. 9) increased Cp from 0.285 to 0.487 by optimizing a diffuser with two inlets through the second inlet, which has an annular cross-section, with additional flow introduced, thereby increasing the kinetic energy through the turbine rotor. Nishi et al. [63] (No. 1), Chihaia et al. [64] (No. 5), and Gish et al. [65] (No. 10) reported Cp values of 0.707, 0.945, and 0.45, respectively, based on physical experiments conducted at blockage coefficients of 0.282 and 0.349. These studies focused on the optimization of the diffuser shape and the rotor position inside the diffuser. Nishi et al. [63] optimized the brim placed at the outlet section of the diffuser, investigating its effect on the velocity profile. The power coefficient was increased from 0.580 to 0.707. Chihaia et al. [64] increased the power coefficient from 0.42 to 0.945 by changing the rotor position inside the diffuser. The power coefficients of studies No. 1 and No. 5 exceed the reference value by approximately 34.6% and 55.6%, while the value from study No. 10 coincides with the typical power coefficient of a bare turbine~0.45, after the optimization of the diffuser shape.
Reinecke et al. [66] (No. 7), through CFD and a physical optimization of the diffuser shape, achieved the highest power coefficient. The blockage coefficient of the hydrodynamic channel was found to be 0.012, which guarantees conditions for free flow; values of 0.43–1.74 were found with four variables and a Support Vector Regression (SVR) algorithm trained on 110 data points. The variables define the coordinates of the points along the diffuser contour. Wang et al. [67] (No. 4) reported the lowest Cp value of 0.432. They optimized a diffuser shaped like a Ventury nozzle. The gain of Cp is around 0.11. Tampier et al. [68] (No.2) optimized the diffuser by shaping its wall in the form of an airfoil profile. The power coefficient increased from 0.436 to 0.670. This result was achieved using an asymmetric NACA airfoil with an angle of attack of 16°. According to Table 9, the most effective hydrofoils are MEL021 and MEL031 (No. 1), achieving Cp of 0.707, followed by Sandia MHKF1 (No. 2), achieving Cp of 0.670, and NACA4412 (No. 10), achieving Cp of 0.45. The most plausible results are those of J. Reinecke et al. [66] (No. 7) and Góralczyk et al. [69] (No. 8), as they validated their CFD results with physical experiments under free-flow conditions, where the blockage coefficient of the channel is below 0.25.

Table 8.
Summary of optimizations for bare axial hydrokinetic turbines.
Table 8.
Summary of optimizations for bare axial hydrokinetic turbines.
| No. | Author(s) | Power Coefficient (Cp) | Method Used | Blade Profile | Water Velocity (m/s) | Rotor Position in the CFD Domain (m) | Dimensions of the Measurement Section (m) | Rotor Main Diameter (m) | Blockage Coeff. | Blade Number | Optimized Parameters |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Pucci et al. [70] | 0.390 | BEM, CFD comparisons | Wortmann-FX 63-137 | 1.0–1.5 | Inlet dist. 10D1 Outlet dist. 20D1 Wall dist. 4D1 | Not mentioned | 0.900 | - | 3 | Blade pitch angles and chord lengths |
| 2 | Abutunis et al. [57] | 0.320 | BEM, NN (MLP) | Eppler 395 | 0.5–1.0 | Not mentioned | Not mentioned | Not mentioned | - | 3 | |
| 3 | Zhu et al. [71] | 0.447 | BEM, CFD (SST k-ω), NSGA-II, RBF-NN, experiment | Not mentioned | 3.5 | Inlet dist. 5D1 Outlet dist. 10D1 | 0.600 × 0.600 × 1.000 | 5.400 (CFD) 0.240 (exp) | 0.126 | 4 | |
| 4 | Vogel et al. [55] | 0.610 | BEM, CFD (OpenFOAM, SST k-ω) | Not mentioned | 2.2 | Not mentioned | - | 20.000 | - | 3 | Dynamic pitch angle range |
| 5 | Payne et al. [72] | 0.500 | BEM, CFD | NACA 63-8XX series | 0.8 | Not mentioned | - | 1.200 | - | 3 | Blade profile pitch angles, and chord lengths |
| 6 | Nigam et al. [73] | 0.450 | BEM, ANSYS Fluent | E817 (hub), S832 (blade) | 2 | Not mentioned | - | 2.000 | - | 3 | |
| 7 | Wang et al. [56] | 0.252 | CFD (ANSYS Fluent, k-ω SST) | NACA 4412 | 0.8 | Inlet dist. 2D1 Outlet dist. 5D1 | - | 2.000 | - | 3 | |
| 8 | Chica et al. [74] | 0.438 | BEM, CFD (ANSYS CFX, k-ε) | NREL S822 | 1.5 | Not mentioned | - | 1.360 | - | 3 | |
| 9 | Chen et al. [75] | 0.310 | BEM, Wilson’s optimization | Not mentioned | 0.8–2.2 | Not mentioned | - | 3.700 | - | 3 | Blade profile pitch angles, and chord lengths |
| 10 | Patel et al. [54] | 0.850 | Experimental | Not mentioned | 1.9 | Not mentioned | 0.101 × 1.000 | 0.086 | 0.569 | 4 | Tip fillet radius, blade number |
| 11 | Romero et al. [58] | 0.457 | CFD (ANSYS Fluent, k-ω SST), experiment | SG 6043 | 1.5 | Inlet dist. 2.5D1 Outlet dist. 6.25D1 Wall dist. 5D1 | 0.31 × 0.5 × 8.000 | 1.600 (CFD) 0.240 (exp.) | 0.292 | 3 | Skew and wake angles of the blades |
| 12 | Arribas et al. [76] | 0.400 | BEM | NACA 4415, NACA 23015 | 1.5–3.0 | Not mentioned | - | 0.400 | - | 2, 3 and 4 | Blade profile. pitch angles, chord lengths, blade number |
| 13 | Sale et al. [77] | 0.480 | BEM, Genetic Algorithm | NACA 44XX, Risø-A1-XX | 1.0–2.5 | Not mentioned | - | 5.000 | - | 3 | |
| 14 | Chadras et al. [78] | 0.480 | CFD (ANSYS CFX, k-ω SST) | NREL S822 | 1 | Not mentioned | - | 0.800 | - | 3 | Blade swept angles |
| 15 | Li et al. [79] | 0.500 | BEM, ANN, Genetic Algorithm, CFD (Fine/Turbo, Spalart-Allmaras) | NACA 63-418 | 2 | Not mentioned | - | 3.700 | - | 3 | Blade pitch angles and chord lengths |
| 16 | Eriamiatoe et al. [59] | 0.450 | CFD (ANSYS CFX, k-ω SST) | SG6043 | 2 | Not mentioned | - | 2.000 | - | 3 | |
| 17 | Gemaque et al. [80] | 0.529 | Extended BEM | SG6040 | 1 | Not mentioned | - | 0.800 | - | 4 | Blades swept angles |
| 18 | Hanzla et al. [60] | ~0.450 | Experimental | SG6043 | 1 | - | 0.610 × 0.610 × 1.980 | 0.280 | 0.165 | 3 | Blade shape |
| 19 | Wang et al. [81] | 0.451 | BEM, CFD (ANSYS Fluent, URANS, DES) | NACA 63-8XX | 3.4 | Not mentioned | - | 15.200 | - | 3 | Blade number, pitch angles, and chord lengths |

Table 9.
Summary of optimizations for shrouded axial hydrokinetic turbines.
Table 9.
Summary of optimizations for shrouded axial hydrokinetic turbines.
| No. | Authors | Power Coefficient (CP) | Method Used | Blade Profile | Water Velocity (m/s) | Rotor Position in the CFD Domain (m) | Dimensions of the Measurement Section (m) | Rotor Main Diameter (m) | Blockage Coeff. | Blade Num | Optimized Parameters |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Nishi et al. [63] | 0.707 | CFD (ANSYS CFX 15.0) + Experiment | MEL021, MEL031 | 1.50 (CFD), 1.72 (Exp) | Inlet dist. 10D1 Outlet dist. 15D1 Wall dist. 10D1 | 0.570 × 1.900 | 0.342 | 0.282 | 3 | Blade number, profile, diffuser shape |
| 2 | Tampier et al. [68] | 0.670 | CFD (STAR-CCM+) | Sandia MHKF1 | 2 | Inlet dist. 5D1 Outlet dist. 5D1 Wall dist. 7D1 | - | 2.000 | - | 3 | Rotor position in the diffuser |
| 3 | Song et al. [61] | 0.551 | CFD (ANSYS Fluent) | Not mentioned | 1.5 | Inlet dist. 5D1 Outlet dist. 15D1 Wall dist. 5D1 | - | 2.000 | - | 3 | Diameter of the shaft |
| 4 | Wang et al. [67] | 0.432 | CFD (ANSYS Fluent) | Not mentioned | 2 | Inlet dist. 19.92D1 Outlet dist. 33.2D1 Wall dist. 9.6D1 | - | 0.250 | - | 4 | Diffuser shape |
| 5 | Chihaia et al. [64] | 0.945 | Experimental | Not mentioned | 0.9 | - | 0.300 × 0.300 | 0.200 | 0.349 | 4 | Diffuser shape and rotor position |
| 6 | Parka et al. [62] | 0.540 | CFD (OpenFOAM, DAFoam) | Not mentioned | 1.4 | Inlet dist. 11.4D1 Outlet dist. 19D1 Wall dist. 5.4D1 | - | 0.440 | - | 3 | Diffuser shape |
| 7 | J. Reinecke [66] | 1.740 | CFD (ANSYS Fluent) + Experiment | Not mentioned | 1.5 | - | 4.600 × 9.300 × 90.000 | 0.800 | 0.012 | 3 | Diffuser shape |
| 8 | Góralczyket al. [69] | 0.520 | CFD (Vortex Lattice Method), experiment | Not mentioned | 3.4 | Not mentioned | 0.425 × 0.425 | 0.148 | 0.095 | 5 | Rotor position in the diffuser |
| 9 | Cardona-Mancilla et al. [30] | 0.487 | CFD (ANSYS CFX 18.2) | NREL S822 | 1.5 | Inlet dist. 0.55D1 Outlet dist. 4.875D1 Wall dist. 1.6D1 | - | 0.800 | - | 3 | Diffuser shape |
| 10 | Gish et al. [65] | 0.450 | CFD (SolidWorks FlowSim), experiment | NACA 4412 | 0.61–1.52 | Not mentioned | Not mentioned | 0.265 | - | 3 | Diffuser shape |
Table 10 sorts the examined hydrokinetic turbines from Table 8 and Table 9, according to the theoretical flow velocity of different rivers. The first column presents the theoretical flow velocity range of different rivers, and the second and third columns show the turbines from Table 8 and Table 9, which fit in. The indices of the researchers who achieved a higher power coefficient through numerical and/or physical experiments in real free-flow conditions are bolded. These are Hanzla et al. [60] (No. 18, Table 8) and J. Reinecke et al. [66] (No. 8, Table 9). The data show that most of the experiments were conducted at real flow velocities, but only two of them were performed in free-flow conditions.

Table 10.
Comparison of river flow velocities and corresponding experimental conditions of the examined turbines.
To achieve the goal set in this paper, we will compare the power coefficients achieved from the various optimizations of the flow passage of axial hydrokinetic turbines with those of some commercial small-scale axial hydrokinetic turbines.
2.4. Specifications of the Commercial Turbines
There is a lack of extensive data regarding the power curves of the hydrokinetic turbines. Figure 4, Figure 5 and Figure 6 present the main parameters of some of the commercial small-scale hydrokinetic turbines. The turbine rotors of Smart Duofloat/Monofloat (Figure 3) are attached inside a cylindrical casing that resembles a diffuser. The floating construction keeps the runner submerged at a certain depth. The generator is placed inside the rear fairing of the turbine. A debris protection system is placed in front of the runner. Its purpose is to prevent fish from entering between the turbine blades. According to the power curve presented in Figure 4c, the turbine can generate electrical power from 0.220 to 5 kW. The cut-in speed is 0.7 m/s [86] and the rated speed is 2.8 m/s [86]. The Guinard Energies axial kinetic turbine (Figure 5) has a similar construction. The turbine is attached to a supporting frame, which keeps the runner submerged. The maximum output power is 3.5 kW [87] at a rated speed of 3 m/s [87] (Figure 5c). The runner of the Smart Freestream turbine (Figure 6) is attached inside a rectangular supporting frame. Its parameters are similar to the Duofloat/Monofloat turbine, but in this case, the maximum obtained power is at 3.1 m/s [88].
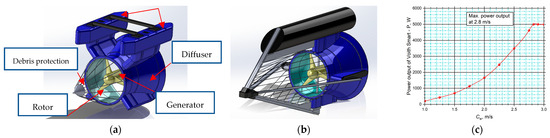
Figure 4.
Smart (a) Duofloat and (b) Monofloat, axial kinetic turbine [3,86] with parameters: N = 90–230 min−1, Pef = 5 kW, D1 = 1 m, and nominal current speed 2.8 m/s. (c) Power curve of the Smart hydrokinetic turbine [3,86].
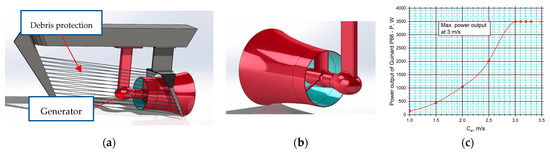
Figure 5.
Guinard Energies. Axial kinetic turbine [3,87] with parameters Pef = 130–3500 W, D1 = 0.660 m. Nominal current speed 3 m/s. (a) Components of the Guinard Energies turbine, (b) axial look into the fan shroud, (c) power curve of the Guinard Energies turbine [3,87].
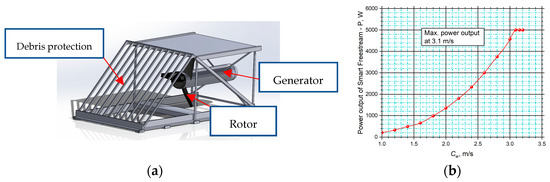
Figure 6.
Smart Freestream, axial kinetic turbine [3,88] with parameters: Pef = 5 kW, D1 = 1 m, and nominal current speed 3.1 m/s. (a) Components of Smart Freestream turbine, (b) power curve of the Smart Freestream turbine [3,88].
3. Results
To assess the effect of the optimization, we will compare the obtained power coefficients, presented in Table 8 and Table 9, with those of the commercial hydrokinetic turbines, presented in Figure 4, Figure 5 and Figure 6. The data are sorted in Table 11 and Table 12. The first two columns show the index number and the authors’ names. The remaining columns present the obtained maximum Cp, the flow velocity at which the experiments were conducted, the rotor’s main diameter, blade number, and the calculated power coefficients of the hydrokinetic turbines Voith, Genuard P66, and Smart Freestream. The bold rows indicate the authors conducting physical experiments in free-flow conditions.

Table 11.
Summary of optimizations for bare axial hydrokinetic turbines.

Table 12.
Summary of optimizations for shrouded axial hydrokinetic turbines.
Among the commercial turbines, Genuard P66 demonstrates the highest Cp values (0.857–0.879) at lower flow velocities (0.8–1.5 m/s). In second place is Voith Duofloat, with Cp values ranging from 0.514 to 0.635 at flow velocities ranging from 1.5 to 3.5 m/s. The least efficient is Smart Freestream, with Cp values between 0.425 and 0.45 at flow velocities ranging from 1.5 to 1.9 m/s. The calculations indicate that each of these turbines is optimized for a specific velocity range.
According to Table 11, the power coefficient of the examined bare turbines ranges from 0.252 to 0.529 for flow velocities between 0.8 and 3.5 m/s. The commercial turbines achieve higher values of Cp. The power coefficient of Hanzla et al. [60] exceeds those of Voith Duofloat and Smart Freestream at flow velocity of 1 m/s, while Zhu et al. [71] surpasses that of Smart Freestream at flow velocity of 3.5 m/s. According to Table 12, the power coefficient of the examined shrouded turbines ranges from 0.199 to 1.740 for flow velocities between 0.9 and 1.72 m/s. The experiments of J. Reinecke et al. [66] (Cp = 1.740) were conducted at free-flow conditions, which make them more reliable. The obtained power coefficient exceeds those of Voith Duofloat, Genuard P66, and Smart Freestream at a flow velocity of 1.5 m/s. These results show that the optimized turbines with contemporary numerical methods can achieve higher efficiency than commercial turbines. The data are also visualized in Figure 7.
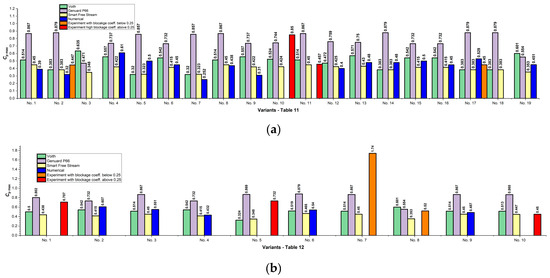
Figure 7.
Assessment of the maximum power coefficient (Cp max) from numerical and experimental studies relative to commercial turbines: (a) bare turbines and (b) shrouded turbines. Numerical results are shown in blue, experimental results with low blockage coefficient in orange, and those with high blockage coefficient in red. The power coefficient of Voith, Genuard P66, and Smart Freestream are represented in green, purple, and yellow.
4. Discussion
Based on the analysis and comparative review presented in this study, several key observations and practical conclusions emerge. Most reviews on this topic focus on hydropower potential, the main parameters of hydrokinetic turbines, and various methods for improving their efficiency, maintenance, and installation. This review provides a comparison between the performance results of various optimized hydrokinetic turbines and the actual energy characteristics of contemporary commercial turbines. The analysis demonstrates that optimizing the flow passage components—such as the rotor, shroud, and diffuser—can significantly enhance the efficiency of axial hydrokinetic turbines. Most experiments have been conducted in hydrodynamic channels with high blockage ratios, which do not comply with free-stream flow conditions. For instance, Vogel et al. [55] achieved a power coefficient (Cp) greater than 0.6 at a blockage ratio of 0.569. Among researchers conducting only numerical simulations, Cp values differ from those obtained through physical testing. For turbines without shrouds, physical experiments show Cp values ranging from 0.35 to 0.45, while numerical simulations report values between 0.3 and 0.61. For shrouded turbines, experimental Cp values range from 0.450 to 1.740, whereas numerical values fall between 0.199 and 0.607. Experimental validation is essential to confirm the accuracy of numerical results.
The Blade Element Momentum (BEM) method is frequently used in the optimization process due to its simple and easily applicable algorithm. When combined with modern numerical techniques—such as the panel method, vortex lattice method, and Computational Fluid Dynamics (CFD)—it enables the characterization of individual blade profiles, thereby extending the capabilities of the BEM method in predicting rotor power curves.
The results presented in this study can be effectively applied to the future design and optimization of axial hydrokinetic turbines. For instance, using the aforementioned numerical methods, the blade profile can be further optimized by refining profiles from the SG4063 and NACA 63-8XX series. The shape of the diffuser can also be improved for better performance at lower flow velocities. J. Reinecke et al. [66], for example, achieved a Cp value of 1.740 using an optimization approach that combined metamodeling via Support Vector Regression (SVR), Computational Fluid Dynamics (CFD), and Design of Experiments (DoE). SVR enables the prediction of the effects of various turbine geometric configurations on the power curves. These conclusions are particularly valuable for the design of low-power, decentralized energy systems in remote areas, where high efficiency at low flow velocities is essential. This highlights the practical value of turbine geometry optimization using modern numerical methods.
Considering the power coefficients of the partially optimized turbines discussed, it becomes clear that modern methods for the synthesis and analysis of axial hydrokinetic turbines can achieve significantly higher Cp values compared to those of commercially available turbines. To achieve better efficiency, all influencing parameters (such as the maximum blade thickness, thickness distribution along the blade length, chord, number of blades, and diffuser shape) must be simultaneously optimized for the specific operating conditions. In some cases, synthesized rotors without a shroud even outperform the efficiency of market turbines with a shroud. For example, Hanzla et al. [60] achieved a Cp value of 0.45 following a physical experiment. The highest power coefficient (1.740) was achieved by J. Reinecke et al. [66] with a shrouded turbine. Both experiments were conducted in a hydrodynamic channel under free-stream conditions, ensuring the reliability of the experiments. The Cp value of 1.740 obtained is significantly higher than that of the small-power turbines currently available, regardless of whether they include the entire hydro unit or just the rotor
Future work should focus on the development of multi-objective optimization methods that integrate both hydrodynamic and structural criteria. Moreover, the validation of simulation outcomes through field-scale experimental studies in natural riverine environments is crucial for ensuring their practical applicability.
5. Conclusions
This review presented some of the key methods for the synthesis, analysis, and optimization of hydrokinetic turbines, as well as the conditions under which physical and numerical CFD studies should be conducted. The main contribution of this paper is the comparison of results from various numerical and physical experiments conducted by researchers in this field, confirming the impact of optimized flow passage components (blades, diffuser, blade cascade solidity) on the efficiency of the unit. It is evident that the greatest influence on operational efficiency is exerted by the blade cascade solidity and the diffuser geometry. For example, J. Reinecke et al. [66] achieved a Cp value of 1.740 after optimizing the diffuser, while Zhu et al. [71] achieved a Cp value of 0.447 with a four-blade rotor. The data clearly show that the Cp values obtained through numerical studies are generally higher than those observed in real-world applications. In CFD simulations, this may be due to the incorrect selection of turbulence models, boundary conditions, flow velocity profile, computational domain size, or rotor positioning relative to the inlet and outlet. In numerical and analytical methods, such deviations may arise from simplified models that do not account for flow separation and vortex formation in the inter-blade channel, as well as the impact of rotor blade cascade solidity on efficiency. However, numerical methods can be indicative in optimizing individual components of the flow passage of hydrokinetic turbines. However, to confirm their reliability, the data must be validated through physical experiments under conditions that ensure free-stream flow.
Author Contributions
Conceptualization, R.I.; methodology, R.I.; software, G.T.; validation, K.K., R.I. and B.Z.; formal analysis, G.T.; investigation, R.I.; resources, R.I.; data curation, K.K.; writing—original draft preparation, R.I.; writing—review and editing, R.I.; visualization, R.I. and B.Z; supervision, G.T.; project administration, G.T.; funding acquisition, G.T and K.K. All authors have read and agreed to the published version of the manuscript.
Funding
This study is financed by the European Union-Next Generation EU, through the National Recovery and Resilience Plan of the Republic of Bulgaria, project № BG-RRP-2.004-0005 and by the project KΠ-06-H67/8 “Development of a fluid-structural methodology for the study and modernization of HYDRAulic turbomachines, through the TECHnologies of virtual prototyping—HydraTech”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aristizábal-Tique, V.; Villegas-Quiceno, A.P.; Arbeláez-Pérez, O.F.; Colmenares-Quintero, R.F.; Vélez-Hoyos, F.J. Development of riverine hydrokinetic energy systems in Colombia and other world regions: A review of case studies. DYNA 2021, 88, 256–264. [Google Scholar]
- Zhou, Z.; Benbouzid, M.; Charpentier, J.; Scuiller, F.; Tang, T. Developments in large marine current turbine technologies—A review. Renew. Sustain. Energy Rev. 2017, 71, 852–858. [Google Scholar] [CrossRef]
- Niebuhra, C.M.; Dijka, M.; Nearyb, V.S.; Bhagwanc, J.N. A review of hydrokinetic turbines and enhancement techniques for canal installations: Technology, applicability and potential. Renew. Sustain. Energy Rev. 2019, 113, 109240. [Google Scholar] [CrossRef]
- Yadav, K.P.; Kumar, A.; Jaiswal, S. A critical review of technologies for harnessing the power from flowing water using a hydrokinetic turbine to fulfill the energy need. Energy Rep. 2023, 9, 2102–2117. [Google Scholar] [CrossRef]
- Mancilla, C.C.; Río, J.S.; Arrieta, E.C.; Zuluaga, D.H. Horizontal axis hydrokinetic turbines: A literature review. Tecnol. Cienc. Agua 2018, 9, 180–197. [Google Scholar] [CrossRef]
- Ibrahim, W.I.; Mohamed, M.R.; Ismail, R.M.T.R.; Leung, P.K.; Xing, W.W.; Shah, A.A. Hydrokinetic energy harnessing technologies: A review. Energy Rep. 2021, 7, 2021–2042. [Google Scholar] [CrossRef]
- Iliev, R.; Tsalov, T. Investigation of a cross-flow wind turbine with a hybrid frontal guiding device. Earth Environ. Sci. 2024, 1380, 012001. [Google Scholar] [CrossRef]
- Iliev, R. Investigation of a cross-flow wind turbine with frontal deflector. Earth Environ. Sci. 2024, 1380, 012002. [Google Scholar] [CrossRef]
- Matias, I.J.T.; Danao, L.A.M.; Abuan, B.E. Numerical Investigation on the Effects of Varying the Arclength of a Windshield on the Performance of a Highway Installed Banki Wind Turbine. Fluids 2021, 6, 285. [Google Scholar] [CrossRef]
- Monchwe, T.B. Bernoulli’s principle and the Venturi effect. South Afr. J. Anaesth. Analg. 2023, 29, S42–S44. [Google Scholar]
- Lecanu, P.N.; Mouazé, D.; Bréard, J. Theoretical calculation of wind (Or water) turbine considering kinetic and potential energy to exceed the Betz limit. HoS 2023. [Google Scholar]
- Ledoux, J.; Riffo, S.; Salomon, J. Analysis of the Blade Element Momentum Theory. SIAM J. Appl. Math. 2021, 81, 2596–2621. [Google Scholar] [CrossRef]
- Kravtsoff, F.; Schvallinger, M.; Ottavy, X. A CFD-Based Throughflow Solver Using Cascade Potential Theory for Axial Compressor Flow Modeling. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: Houston, TX, USA, 2023. [Google Scholar]
- Anderson, J.D. Computational Fluid Dynamics: The Basics with Applications; McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory, 8th ed.; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- White, F.M. Viscous Fluid Flow, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Lancaster, J.M. Panel Methods in Computational Fluid Dynamics; Elsevier Science: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter; Report No. 496; National Advisory Committee for Aeronautics (NACA): Washington, DC, USA, 1935. [Google Scholar]
- Anthoine, L.; Delyon, B. Vortex Lattice Method for the Prediction of the Aerodynamic Forces on a Wing; AIAA: Reston, VA, USA, 1986; Volume 23, pp. 719–724. [Google Scholar]
- Miele, A.; Russo, G. Aerodynamic Shape Optimization: The Vortex Lattice Method; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Todorov, G.; Obretenov, V.; Kamberov, K.; Ivanov, T.; Tsalov, T.; Zlatev, B. Concept and Physical Prototyping of Micro Hydropower System Using Vertical Crossflow Turbine. In Proceedings of the 6th International Symposium on Environment-Friendly Energies and Applications (EFEA), Sofia, Bulgaria, 24–26 March 2021; pp. 1–4. [Google Scholar]
- Todorov, G.; Kamberov, K.; Semkov, M. Improvement of undershot water wheel performance through virtual prototyping. AIP Conf. Proc. 2021, 2333, 110011. [Google Scholar]
- Anthoine, J.; Olivari, D.; Portugaels, D. Wind-tunnel blockage effect on drag coefficient of circular cylinders. Wind. Struct. 2009, 12, 541–551. [Google Scholar] [CrossRef]
- Investigation of Blockage Correction Methods for Full-Scale Wind Tunnel Testing of Trucks. KTH. Available online: https://www.diva-portal.org/smash/get/diva2:893809/FULLTEXT01.pdf (accessed on 13 March 2025).
- López, S. Emerging Trends in Computational Fluid Dynamics. Fluid Mech. 2023, 10, 276. [Google Scholar]
- Vinuesa, R.; Brunton, S. Emerging trends in machine learning for computational fluid dynamics. Comput. Sci. Eng. 2022, 24, 33–41. [Google Scholar] [CrossRef]
- Ji, G.; Dong, J. Computational Fluid Dynamics—Recent Advances, New Perspectives and Applications; IntechOpen: London, UK, 2023. [Google Scholar]
- Badshah, M.; VanZwieten, J.; Badshah, S.; Khalil, S.J. A CFD study of blockage ratio and boundary proximity effects on the performance of a tidal turbine. IET Renew. Power Gener. 2019, 13, 744–749. [Google Scholar] [CrossRef]
- Cardona-Mancilla, C.; Sierra-Del Rio, J.; Hincapié-Zuluaga, D.; Chica, E. A Numerical Simulation of Horizontal Axis Hydrokinetic Turbine with and without Augmented Diffuser. Int. J. Renew. Energy Res. 2018, 8, 1833–1839. [Google Scholar]
- Ren, H.W.; Saat, F.A.Z.M.; Anuar, F.S.; Wahap, M.A.A.; Tokit, E.M.; Tuan, T.B. Computational Fluid Dynamics Study of Wake Recovery for Flow Across Hydrokinetic Turbine at Different Depth of Water. CFD Lett. 2021, 13, 62–76. [Google Scholar] [CrossRef]
- Du, X.; Tan, J.; Yuan, P.; Si, X.; Liu, Y.; Wang, S. Research on the blockage correction of a diffuser-augmented hydrokinetic turbine. Ocean Eng. 2023, 280, 114470. [Google Scholar] [CrossRef]
- Salunkhe, S.; Fajri, O.; Bhushan, S.; Thompson, D.; O’Doherty, D.; O’Doherty, T.; Mason-Jones, A. Validation of Tidal Stream Turbine Wake Predictions and Analysis of Wake Recovery Mechanism. J. Mar. Sci. Eng. 2019, 7, 362. [Google Scholar] [CrossRef]
- Menter, F.R. Zonal Two Equation Kappa-Omega Turbulence Models for Aerodynamic Flows. In AIAA Fluid Dynamics Conference (No. AIAA Paper 93-2906); AIAA: Reston, VA, USA, 1993. [Google Scholar]
- Piomelli, U. Large-eddy simulation: Achievements and challenges. Prog. Aerosp. Sci. 1999, 35, 335–362. [Google Scholar] [CrossRef]
- Lesieur, M.; Metais, O. New trends in large-eddy simulations of turbulence. Annu. Rev. Fluid Mech. 1996, 28, 45–82. [Google Scholar] [CrossRef]
- Spalart, P.R. Comments on the Feasibility of LES for Wings and on the Hybrid RANS/LES Approach. In Proceedings of the First AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997; pp. 137–147. [Google Scholar]
- Spalart, P.R. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Kostić, C. Review of the Spalart-Allmaras Turbulence Model and its Modifications to Three-Dimensional Supersonic Configurations. Sci. Tech. Rev. 2015, 65, 43–49. [Google Scholar] [CrossRef]
- Shahed, R.; Mohammadian, A.; Gildeh, A. A comparison of standard k–ε and realizable k–ε turbulence models in curved and confluent channels. Environ. Fluid Mech. 2018, 19, 543–568. [Google Scholar] [CrossRef]
- Wronski, T.; Schönnenbeck, C.; Zouaoui-Mahzoul, N.; Brillard, A. Numerical simulation through Fluent of a cold, confined and swirling airflow in a combustion chamber. Eur. J. Mech.-B/Fluids 2022, 96, 173–187. [Google Scholar] [CrossRef]
- Doran, P. Direct Numerical Simulation. In Bioprocess Engineering Principles, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 201–254. [Google Scholar]
- ANSYS Fluent User’s Guide. Available online: https://www.ansys.com (accessed on 13 March 2025).
- Ansys CFX Solver Modeling Guide. Available online: https://dl.cfdexperts.net/cfd_resources/Ansys_Documentation/CFX/Ansys_CFX-Solver_Modeling_Guide.pdf (accessed on 13 March 2025).
- OpenFOAM User Guide. Available online: https://www.openfoam.com/documentation/ (accessed on 13 March 2025).
- STAR-CCM+ User Guide. Available online: https://www.plm.automation.siemens.com (accessed on 13 March 2025).
- Autodesk Flow Simulation Technical Documentation. Available online: https://help.autodesk.com (accessed on 13 March 2025).
- Subhra Mukherji, S.; Kolekar, N.; Banerjee, A.; Mishra, R. Numerical investigation and evaluation of optimum hydrodynamic performance of a horizontal axis hydrokinetic turbine. J. Renew. Sustain. Energy 2011, 3, 063105. [Google Scholar] [CrossRef]
- Chihaia, R.; Oprina, G.; Nicolaie, S.; El-Leathey, A.; Babutanu, C.; Nedelcu, A. Assessing the blade chord length influence on the efficiency of a horizontal axis hydrokinetic turbine. In Proceedings of the 2016 International Conference on Hydraulics and Pneumatics—HERVEX, Baile Govora, Romania, 9–11 November 2016. [Google Scholar]
- Antonio, C.P.; Brasil, J.; Mendes, R.C.F.; Wirrig, T.; Noguera, R.; Oliveira, T.F. On the design of propeller hydrokinetic turbines: The effect of the number of blades. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 253. [Google Scholar]
- Patel, C.; Rathod, V.; Patel, V. Effect of blade count on the performance of shrouded axial flow turbines. Sustain. Energy Technol. Assess. 2024, 65, 103779. [Google Scholar] [CrossRef]
- Q Blade. Available online: https://qblade.org/ (accessed on 13 March 2025).
- X Foil. Available online: https://xfoil.com/?srsltid=AfmBOopY_QIFCmOMJOhpL4XPap72ehTwyoz6MOpYDwsKZCVCaEbh7k1v (accessed on 13 March 2025).
- Patel, C.; Rathod, V.; Patel, V. Experimental Investigations of Hydrokinetic Turbine Providing Fillet at the Leading Edge Corner of the Runner Blades. J. Appl. Fluid Mech. 2022, 16, 865–876. [Google Scholar]
- Vogel, C.R.; Willden, R.H.J.; Houlsby, G.T. Blade element momentum theory for a tidal turbine. Ocean Eng. 2018, 169, 215–226. [Google Scholar] [CrossRef]
- Wang, W.; Yin, R.; Yan, Y. Design and prediction hydrodynamic performance of horizontal axis micro-hydrokinetic river turbine. Renew. Energy 2019, 133, 91–102. [Google Scholar] [CrossRef]
- Abutunis, A.; Hussein, R.; Chandrashekhara, K. A neural network approach to enhance blade element momentum theory performance for horizontal axis hydrokinetic turbine application. Renew. Energy 2019, 136, 1281–1293. [Google Scholar] [CrossRef]
- Romero-Menco, F.; Betancour, J.; Velásquez, L.; Rubio-Clemente, A.; Chica, E. Horizontal-axis propeller hydrokinetic turbine optimization by using the response surface methodology: Performance effect of rake and skew angles. Ain Shams Eng. J. 2024, 15, 102596. [Google Scholar] [CrossRef]
- Eriamiatoe, S.; Udo, U. Optimization of Horizontal Axis Hydrokinetic Turbine Performances using Computational Fluid Dynamics (CFD). IOSR J. Mech. Civ. Eng. 2020, 17, 1–6. [Google Scholar]
- Hanzla, M.; Banerjee, A. Spectral behavior of a horizontal axis tidal turbine in elevated levels of homogeneous turbulence. Appl. Energy 2024, 380, 124842. [Google Scholar] [CrossRef]
- Song, K.; Yang, B. A Comparative Study on the Hydrodynamic-Energy Loss Characteristics between a Ducted Turbine and a Shaftless Ducted Turbine. J. Mar. Sci. Eng. J. Mar. Sci. Eng. 2021, 9, 930. [Google Scholar] [CrossRef]
- Parka, J.; Knighta, B.G.; Liao, Y.; Manganob, M.; Pacinib, B.; Makia, K.J.; Martinsb, A.J.R.R.; Suna, J.; Pana, Y. CFD-based Design Optimization of Ducted Hydrokinetic Turbines. Sci. Rep. 2023, 13, 17968. [Google Scholar] [CrossRef]
- Nishi, Y.; Inagaki, T.; Li, Y.; Hirama, S.; Kikuchi, N. Study on Performance Improvement of an Axial Flow Hydraulic Turbine with a Collection Device. Int. J. Fluid Mach. Syst. 2016, 9, 47–55. [Google Scholar] [CrossRef]
- Chihaia, R.; El-Leathey, L.; Cîrciumaru, G.; Tănase, N. Increasing the energy conversion efficiency for shrouded hydrokinetic turbines using experimental analysis on a scale model. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2019. [Google Scholar]
- Gish, L.A.; Hawbaker, G. Experimental and Numerical Study on Performance of Shrouded Hydrokinetic Turbines. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016. [Google Scholar]
- Reinecke, J. Effect of a Diffuser on the Power Production of Ocean Current Turbines. Ph.D. Thesis, University of Stellenbosch, Stellenbosch, South Africa, 2011. [Google Scholar]
- Wang, B.; Yu, Y.; Niu, X. A parametric analysis of the performance of a horizontal axis tidal current turbine for improving flow-converging effect. Ocean Eng. 2024, 291, 116481. [Google Scholar] [CrossRef]
- Tampier, G.; Troncoso, C.; Zilic, F. Numerical analysis of a diffuser-augmented hydrokinetic turbine. Ocean Eng. 2017, 145, 138–147. [Google Scholar] [CrossRef]
- Góralczyk, A.; Adamkowski, A. Model of a ducted axial-flow hydrokinetic turbine—Results of experimental and numerical examination. Pol. Marit. Res. 2018, 25, 113–122. [Google Scholar] [CrossRef]
- Pucci, M.; Garbo, C.D.; Bellafiore, D.; Zanforlin, S.; Umgiesser, G. A BEM-Based Model of a Horizontal Axis Tidal Turbine in the 3D Shallow Water Code SHYFEM. J. Mar. Sci. Eng. 2022, 10, 1864. [Google Scholar] [CrossRef]
- Zhu, F.; Ding, L.; Huang, B.; Bao, M.; Liu, J. Blade design and optimization of a horizontal axis tidal turbine. Ocean Eng. 2020, 195, 106652. [Google Scholar] [CrossRef]
- Payne, G.S.; Stallard, T.; Martinez, R. Design and manufacture of a bed supported tidal turbine model for blade and shaft load measurement in turbulent flow and waves. Renew. Energy 2017, 107, 312–326. [Google Scholar] [CrossRef]
- Nigama, S.; Bansal, S.; Nema, T.; Sharma, V.; Singh, R.K. Design and Pitch Angle Optimisation of Horizontal Axis Hydrokinetic Turbine with Constant Tip Speed Ratio. MATEC Web Conf. 2016, 95, 06004. [Google Scholar] [CrossRef]
- Chica, E.; Perez, F.; Rubio-Clemente, A.; Agudelo, S. Design of a hydrokinetic turbine. Energy Sustain. 2015, 195, 137–148. [Google Scholar]
- Chen, J.; Wang, X.; Li, H.; Jiang, C.; Bao, L. Design of the Blade under Low Flow Velocity for Horizontal Axis Tidal Current Turbine. J. Mar. Sci. Eng. 2020, 8, 989. [Google Scholar] [CrossRef]
- Arribas, F.P. Hydrodynamic design of rotor blades of marine current turbines. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019. [Google Scholar]
- Sale, D. Hydrodynamic Optimization Method and Design Code for Stall-Regulated Hydrokinetic Turbine Rotors; No. NREL/CP-500-45021; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Chandras, P.; Sharma, L.; Chatterjee, D. Numerical prediction of the performance of axialflow hydrokinetic turbine. In Proceedings of the MARINE: V International Conference on Computational Methods in Marine Engineering, Hamburg, Germany, 29–31 June 2013. [Google Scholar]
- Li, Z.; Li, G.; Du, L.; Guo, H.; Yuan, W. Optimal design of horizontal axis tidal current turbine blade. Ocean Eng. 2023, 271, 113666. [Google Scholar] [CrossRef]
- Gemaque, M.L.A.; Vaz, J.R.P.; Saavedra, O.R. Optimization of Hydrokinetic Swept Blades. Sustainability 2022, 14, 13968. [Google Scholar] [CrossRef]
- Wang, P.; Wang, L.; Zhang, Q.; Zhu, F.; Huang, B. A model for predicting the unsteady hydrodynamic characteristics on the blades of a horizontal axis tidal turbine. Appl. Math. Model. 2024, 127, 506–528. [Google Scholar] [CrossRef]
- Saupi, A.F.M.; Mailah, N.F.; Radzi, M.A.M.; Mohamad, K.B.; Ahmad, S.Z.; Soh, A.C. An Illustrated Guide to Estimation of Water Velocity in Unregulated River for Hydrokinetic Performance Analysis Studies in East Malaysia. Water 2018, 10, 1330. [Google Scholar] [CrossRef]
- Kos, Ž. Ðurin, B.; Dogan, D.; Kranj. Hydro-Energy Suitability of Rivers Regarding Their Hydrological and Hydrogeological Characteristics. Water 2021, 13, 1777. [Google Scholar] [CrossRef]
- Oladeji, A.S.; Akorede, M.F.; Mohammed, A.A.; Adeogun, A.G.; Salami, A.W. Investigation of small hydropower potential of river oshininkwara. Arid. Zone J. Eng. Technol. Environ. 2020, 16, 321–336. [Google Scholar]
- Kayastha, R.; Kayastha, R.B.; Shrestha, K.L.; Gurung, S. Hydropower potential of the Marsyangdi River and Bheri River basins of Nepal and their sensitivity to climate variables. Proc. IAHS 2024, 387, 53–58. [Google Scholar] [CrossRef]
- Smart Hydro Power. Available online: https://www.smart-hydro.de (accessed on 13 March 2025).
- Guinard Energies. Available online: https://www.guinard-energies.bzh/en/our-products/p66-hydrokinetic-turbine-3-5-kw/ (accessed on 13 March 2025).
- Smart Hydro Power. Available online: https://smart-hydro.de/wp-content/uploads/2015/12/Datasheet_SMART_Freestream.pdf (accessed on 13 March 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).