Progressive Linear Programming Optimality Method Based on Decomposing Nonlinear Functions for Short-Term Cascade Hydropower Scheduling
Abstract
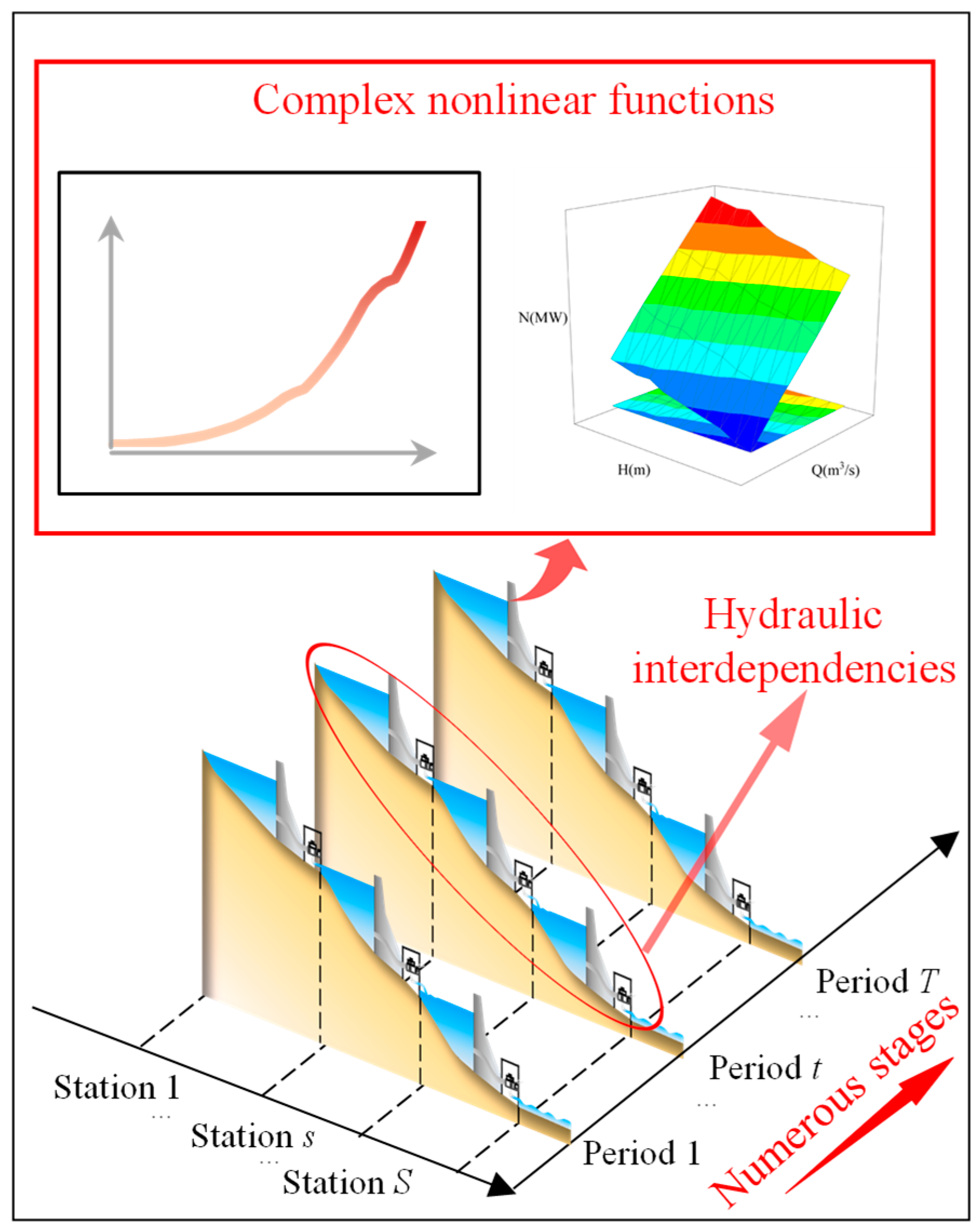
1. Introduction
2. Model Formulation
2.1. Objective Function
2.2. Constraints
2.2.1. Linear Constraints
- The continuity water balance constraint:
- 2.
- The complex hydraulic connection:
- 3.
- The ecological flow constraint:
- 4.
- The shipping water level constraint:
- 5.
- The forebay water level constraints:
- 6.
- The power water release constraints:
- 7.
- The power output constraints:
- 8.
- The power output ramp-up and ramp-down constraints:
- 9.
- The initial and final forebay water level constraints:
2.2.2. Nonlinear Constraints
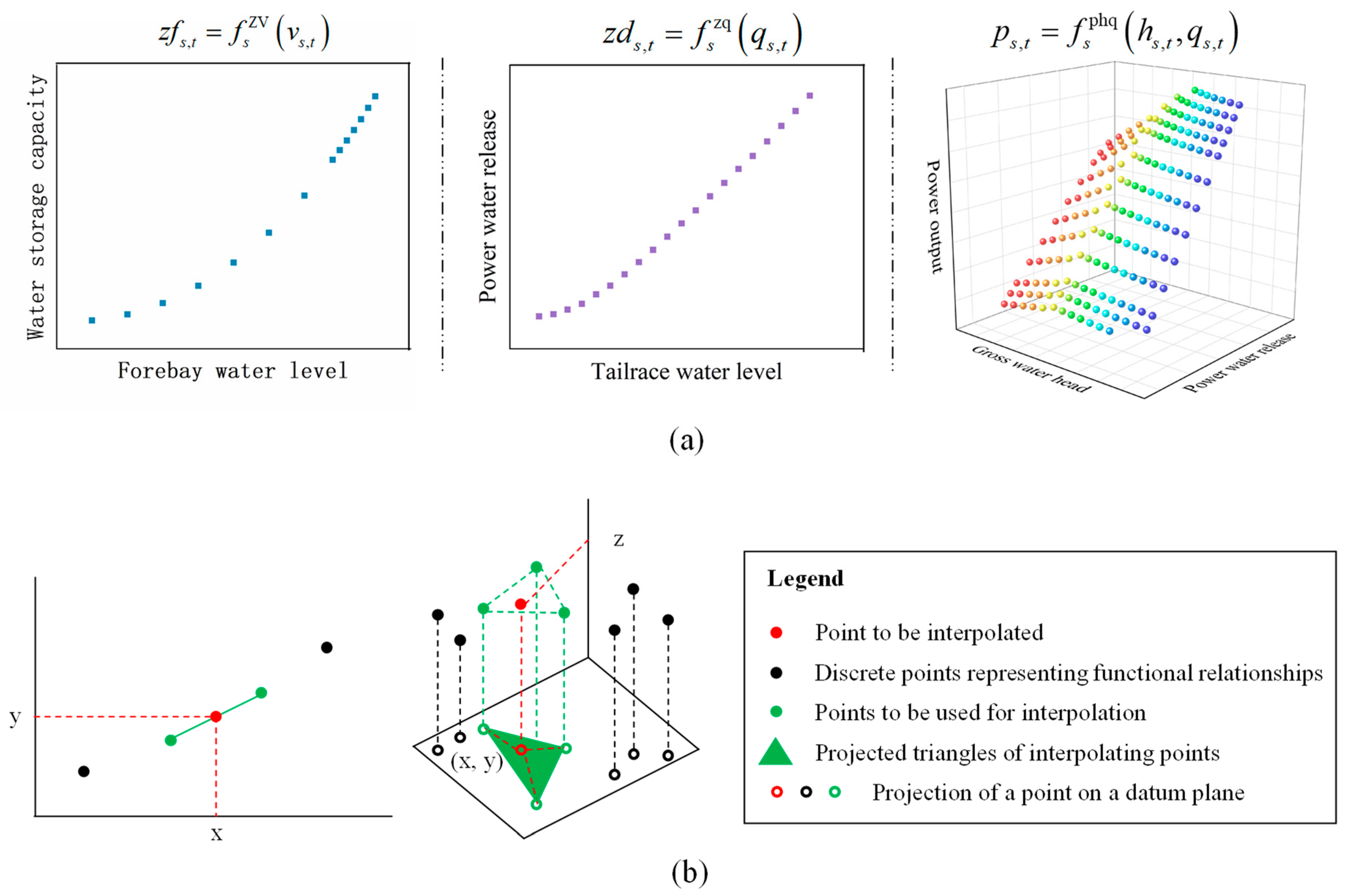
- The relationship between head loss and power water release:
- 2.
- The functional relationship between the forebay water level and water storage:
- 3.
- The functional relationship of the tailrace water level and power water release:
- 4.
- The hydropower output formula:where can be calculated by the following formula:
2.3. Reduction of Model Nonlinearities
3. Methods
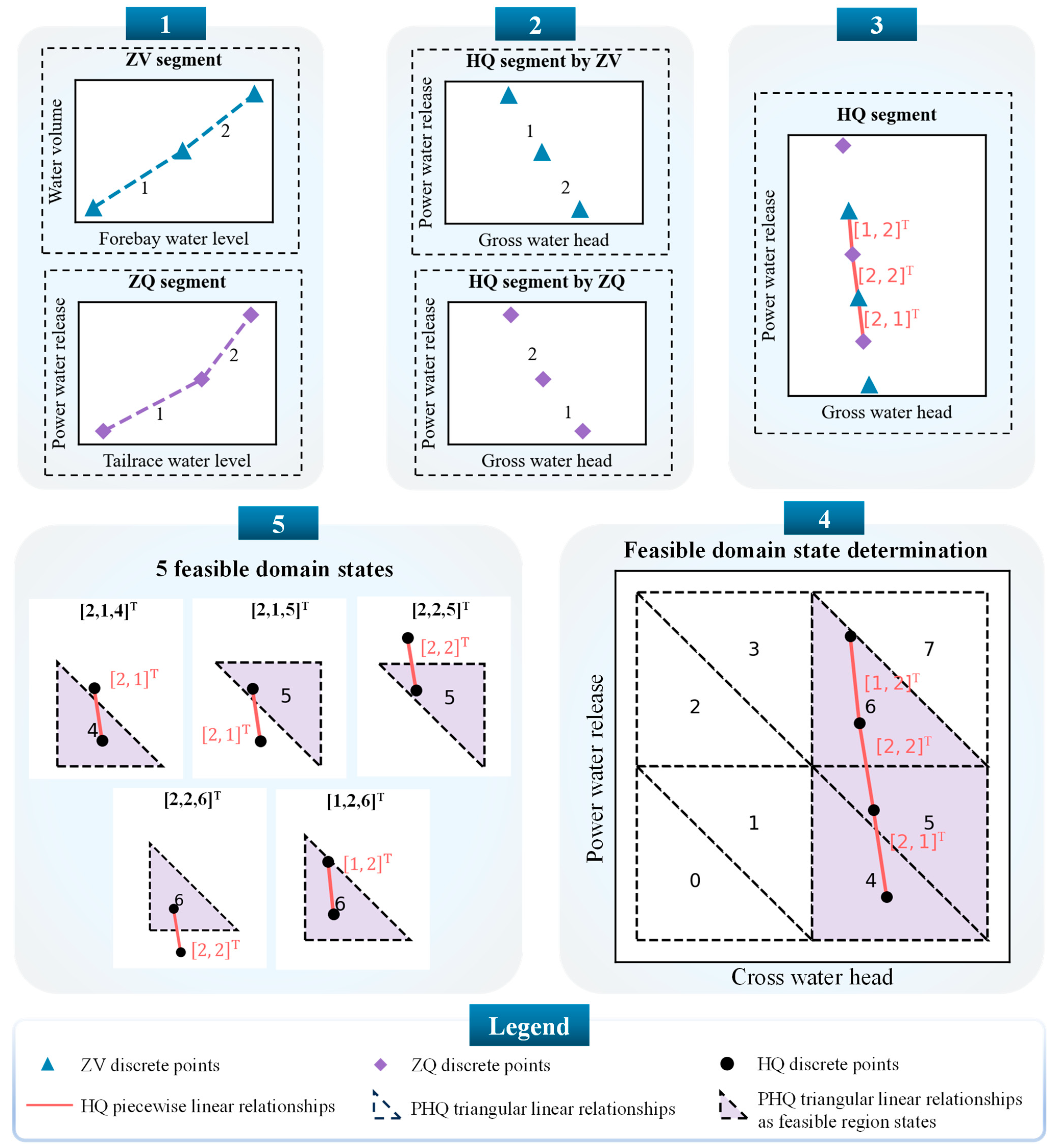
3.1. Partitioning Feasible Domains Coupled with NLF Characteristics
3.1.1. NLFs of Hydropower Stations
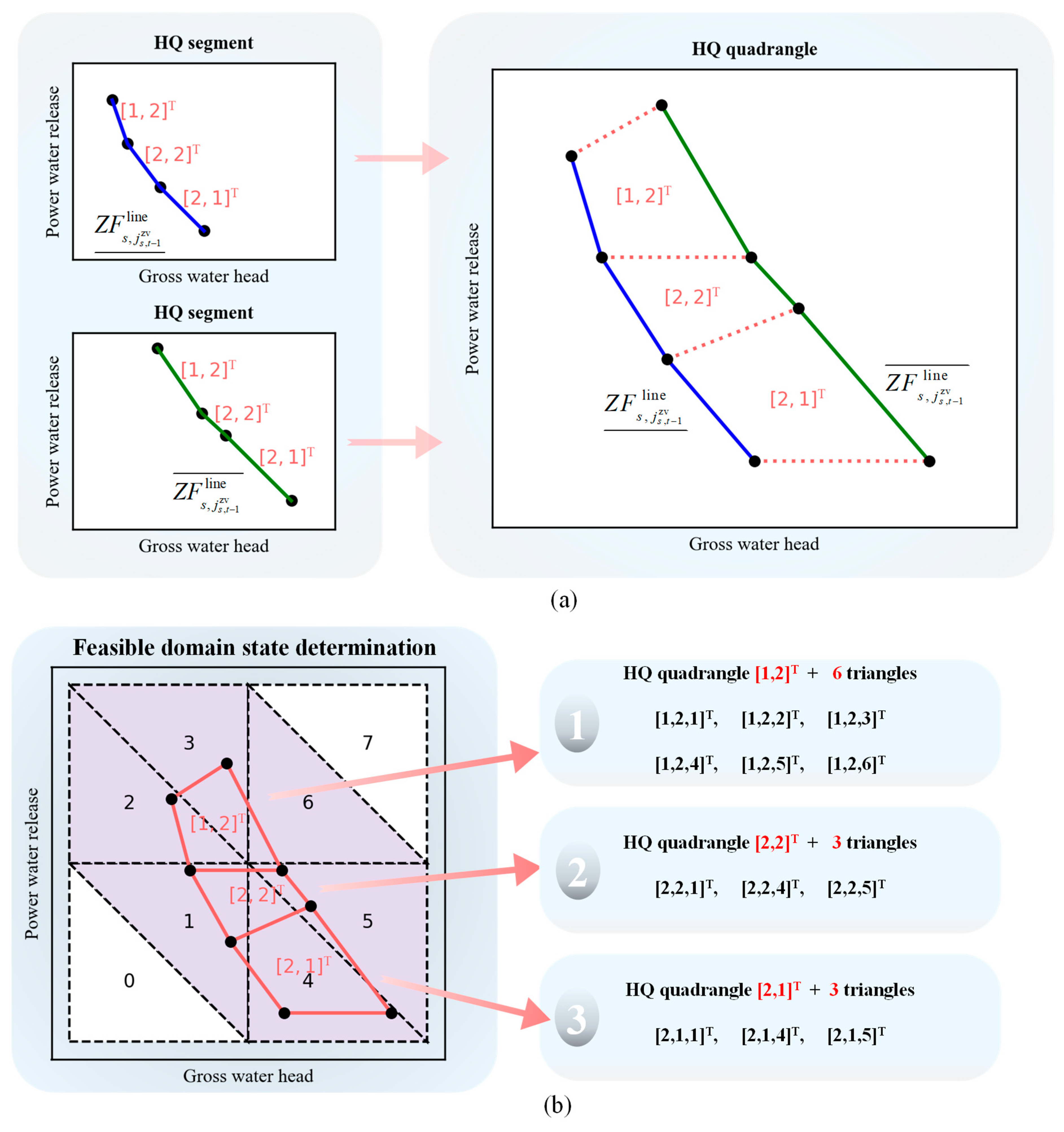
3.1.2. Partitioning the Feasible Domains of One Hydropower Station
3.1.3. Combinatorial Subdomains of Cascade Hydropower Stations
3.2. Algorithm
3.2.1. Progressive Optimality Principle
3.2.2. Progressive Linear Programming Optimality Algorithm
3.3. Dimensionality Reduction Strategy
3.3.1. Feasible Domain State Dynamic Acquisition Method Based on Optimization Logic
3.3.2. Feasible Variable Ranges Obtained via the VBCLP
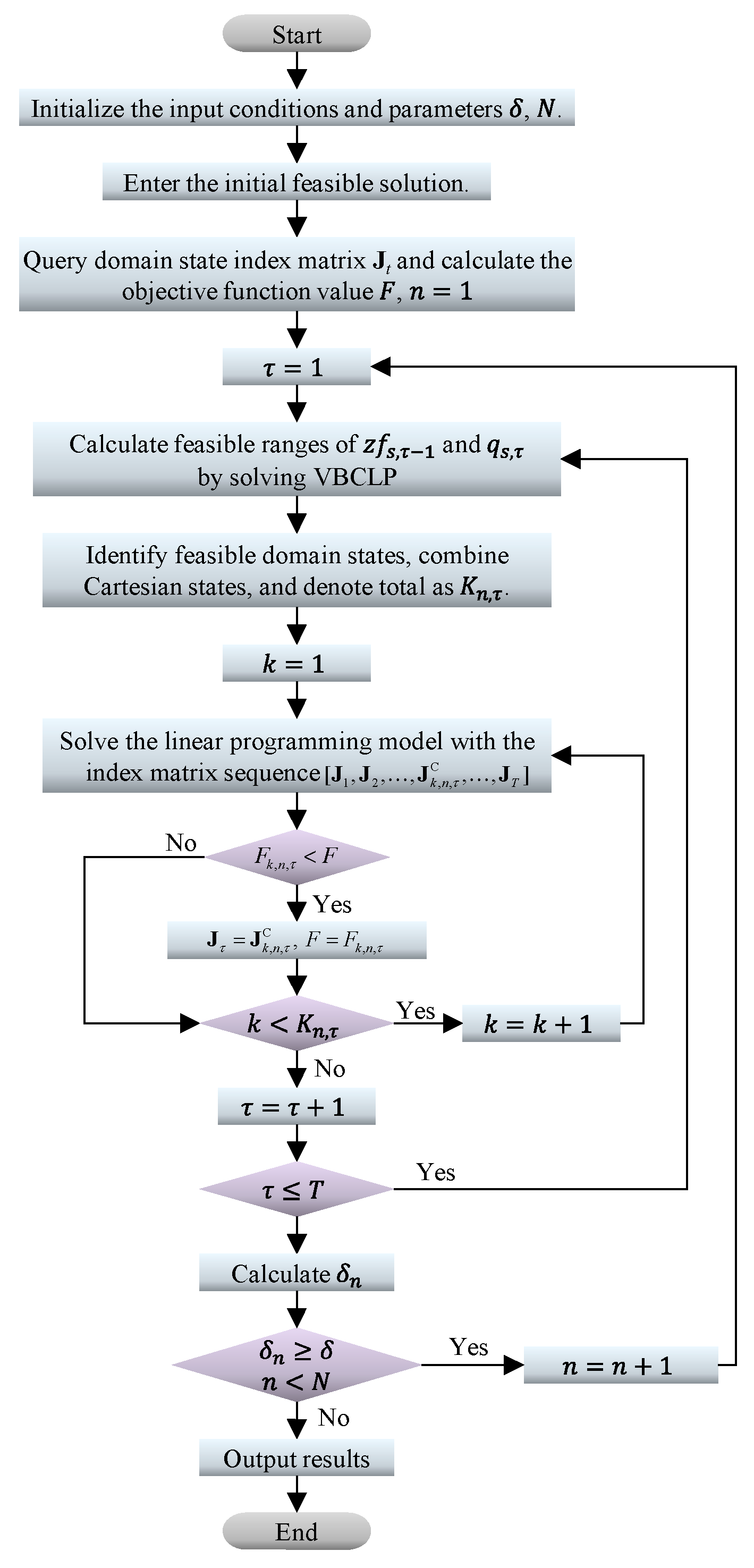
3.4. PLPOMDNF Solution Process
- Initialize the input conditions of each hydropower station in the cascade and the parameters of the PLPOMDNF, including and .
- Enter the initial feasible solution.
- Query the combinatorial domain state index matrix , calculate the objective function value according to the initial feasible solution, and recode. Set .
- Set the stage variable .
- Calculate the feasible ranges of the initial water level and power water release for each station in period by solving the VBCLP, which should be calculated times.
- Identify the feasible domain state of each station and then combine all states in a Cartesian fashion, resulting in a total of states.
- Set .
- The combinatorial domain state index matrix is for periods and for other periods. Solve the linear programming model with the index matrix sequence . If the new objective function is better, set and .
- If , set and return to step 8; otherwise, go to step 10.
- Set . If , return to step 5; otherwise, go to step 11.
- Calculate . If and , set and return to step 4; otherwise, go to step 12.
- End the calculation and output the result.
4. Case Study and Discussion
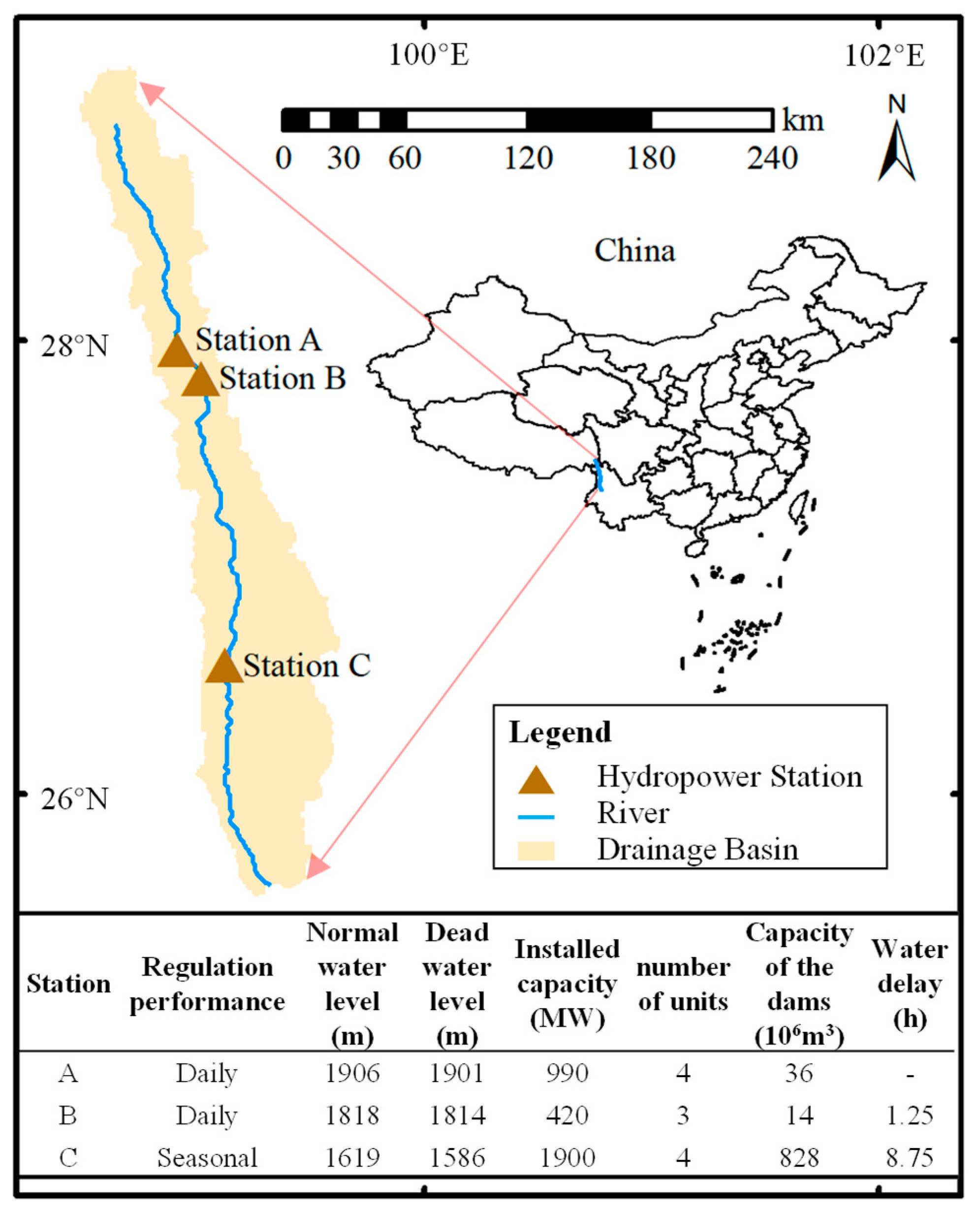
4.1. Introduction to Research Objects
4.2. Comparison of Different Solution Methods
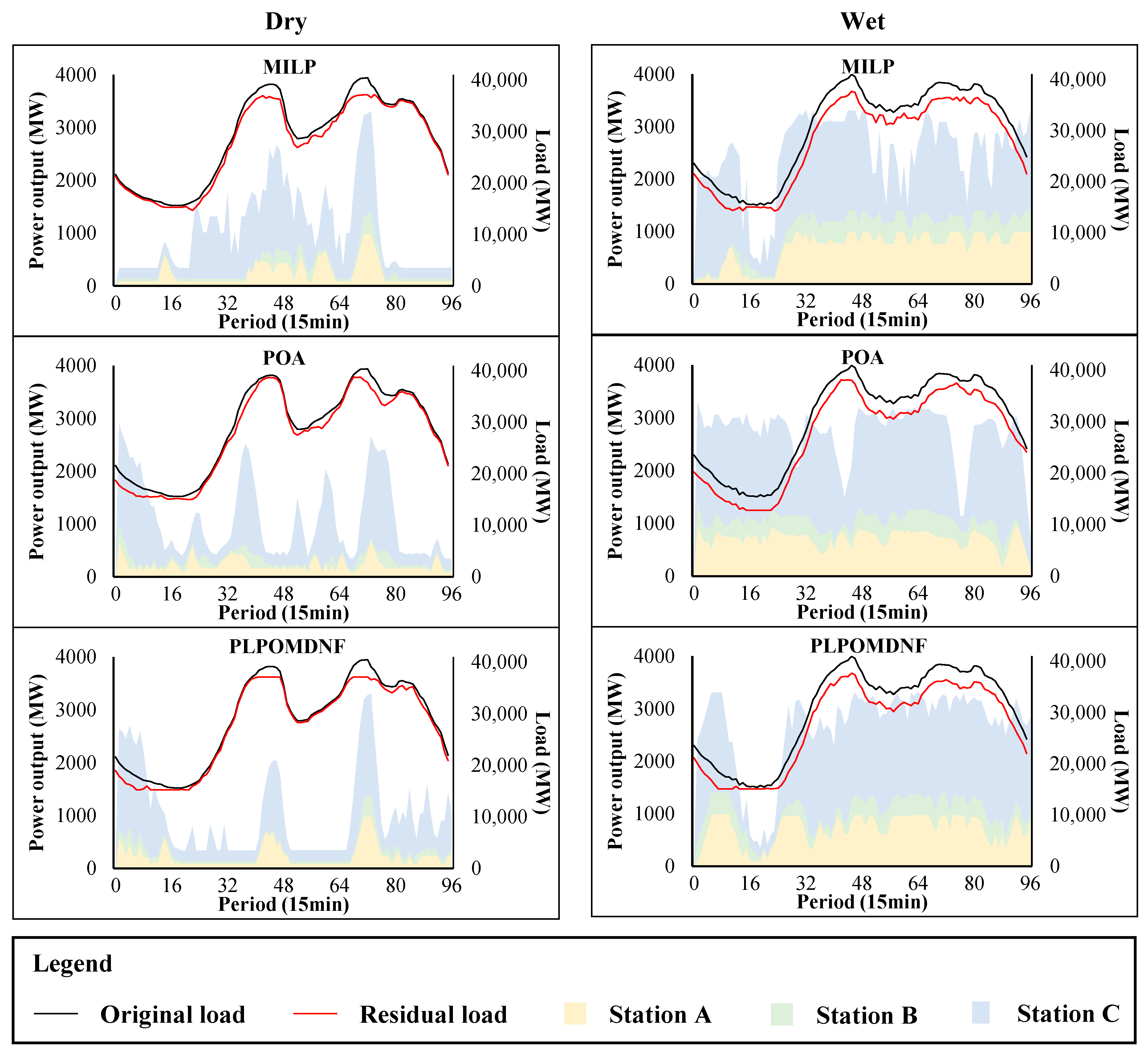
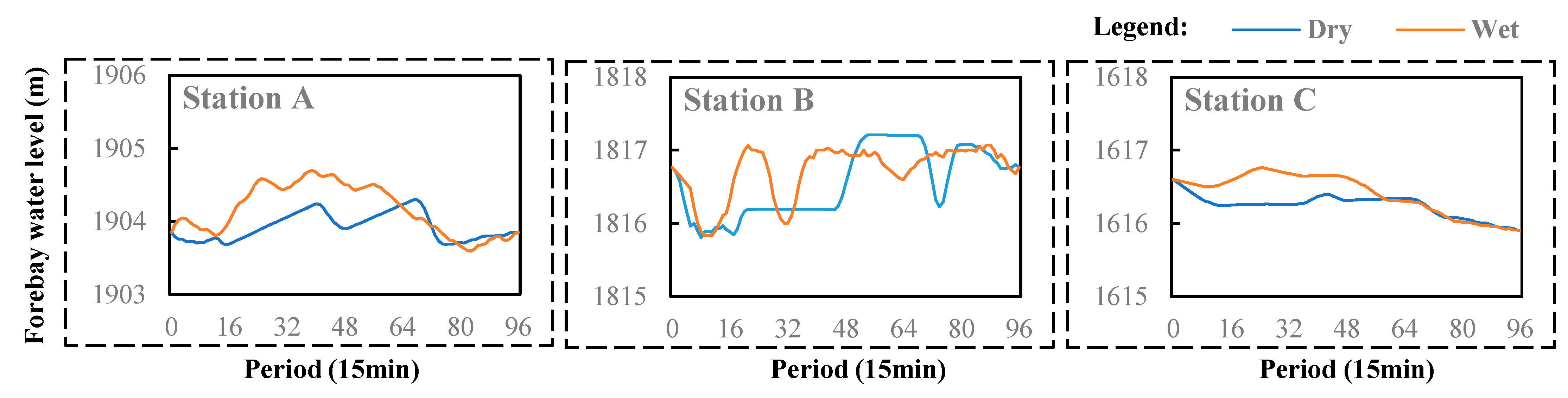
4.3. Analysis of Result Rationality
4.4. Effectiveness of the Dimensionality Reduction Strategy
5. Conclusions
- Significant fluctuations in daily hydropower station forebay water levels introduce errors that cannot be ignored when approximating NLFs. Compared with the commonly used MILP, which introduces large integers for approximations of NLFs, coupling NLF characteristics with their decomposition prevents the introduction of errors and results in more precise outcomes. The power output errors during both the wet and dry seasons can be controlled within 5 MW.
- Compared with the common POA, the PLPOMDNF converges faster within a single iteration and achieves superior final objectives, indicating that the use of continuous domain states provides adjustability for non-optimization stages, ensuring strong convergence of the algorithm. Typically, after two iterations, the objective function value of PLPOMDNF surpasses the final objective function value of POA.
- The feasible domain state dynamic acquisition method using variable bounds obtained through the VBCLP successfully reduces the number of states in each stage, demonstrating that the proposed dimensionality reduction strategy lowers the solution complexity by avoiding unnecessary computations. The method reduces the number of domain states during the wet and dry seasons by 91.8% and 88.2%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Indexes: | |
| Index of time periods. | |
| Index of hydropower stations. | |
| Index of directly upstream stations. | |
| Index of the segment in for station at the end of period . | |
| Index of the segment in for station during period . | |
| Index of the triangular plane in for station during period . | |
| Index of the hydropower station under calculation. | |
| Index of the time period under calculation. | |
| Index of iterations. | |
| Sets: | |
| Set of time periods. | |
| Set of hydropower stations. | |
| Set of hydropower stations without upstream stations. | |
| Set of hydropower stations with upstream stations. | |
| Set of directly upstream hydropower stations of station . | |
| Set of states during period . | |
| Vectors and matrices: | |
| Vector of the index for domain states of station during period . | |
| Matrix of the index for combinatorial domain states of all stations during period . | |
| Matrix of the index for the combinatorial domain state during computational period at iteration . | |
| Constants: | |
| Load demand of the power grid during period (MW). | |
| Duration of a time period (s). | |
| Natural inflow into station during period (m3/s). | |
| Number of water delay periods between station and its direct downstream station. | |
| Instantaneous ecological flow requirement of station (m3/s). | |
| Shipping water level requirement of station (m). | |
| , | Lower and upper boundaries of the forebay water level of station , respectively (m). |
| Lower and upper boundaries of the power water release of station , respectively (m3/s). | |
| , | Lower and upper boundaries of the power output of station , respectively (MW). |
| Maximum allowable variation in the output of station (MW). | |
| , | Forebay water levels at the beginning and end of the scheduling cycle of station , respectively (m). |
| Number of time periods in the scheduling cycle. | |
| , | Lower and upper boundaries of the forebay water level corresponding to ZV segment of station , respectively (m). |
| , | Lower and upper boundaries of the water storage corresponding to ZV segment of station , respectively (m3). |
| , | Lower and upper boundaries of the tailrace water level corresponding to ZQ segment of station , respectively (m). |
| , | Lower and upper boundaries of the power water release corresponding to ZQ segment of station , respectively (m3/s). |
| , | Water heads corresponding to the three vertices of PHQ triangle of station (m). |
| , | Power water release corresponding to the three vertices of PHQ triangle of station (m3/s). |
| , | Power output corresponding to the three vertices of PHQ triangle of station (MW). |
| Precision for terminating iterations. | |
| Maximum number of iterations. | |
| Number of combinatorial domain states for period at iteration . | |
| Variables: | |
| Objective function value of the short-term optimal scheduling model (MW). | |
| Residual load of the power grid during period (MW). | |
| Power output of station during period (MW). | |
| , | Auxiliary variables for linearization (MW). |
| Water storage of station at the end of period (m3). | |
| Total inflow into station during period (m3/s). | |
| Power water release from station during period (m3/s). | |
| Tailrace water level of station during period (m). | |
| Forebay water level of station at the end of period (m). | |
| Net water head of station during period (m). | |
| Head loss of station during period (m). | |
| Gross water head of station during period (m). | |
| , , | Weight coefficients of the three vertices in the PHQ triangular interpolation for station during period . |
| State of period . | |
| Unchanged state of period . | |
| Objective function value of the variable boundary calculation linear programming model | |
| , | Lower and upper boundaries of a variable, which can be either or for station in period . |
| Objective function value corresponding to combinatorial domain state in period for iteration . | |
| Improvement of the objective function value at iteration n. | |
| Functions | |
| Head loss of station as a function of power water release of the station. | |
| Forebay water level of station as a function of water storage of the station. | |
| Tailrace water level of station as a function of power water release of the station. | |
| Power output of station as a function of net water head and power water release of the station. | |
| Power output of station as a function of gross water head and power water release of the station. | |
| Gross water head of station as a function of power water release of the station with as a parameter. | |
| Abbreviations | |
| MILP | mixed integer linear programming |
| POA | progressive optimality algorithm |
| STOSCHS | short-term optimal scheduling of cascade hydropower stations |
| NLF | nonlinear function |
| PLPOMDNF | progressive linear programming optimality method based on decomposing nonlinear functions |
| VBCLP | variable boundary calculation linear programming |
References
- Rosinska, W.; Jurasz, J.; Przestrzelska, K.; Wartalska, K.; Kazmierczak, B. Climate change’s ripple effect on water supply systems and the water-energy nexus—A review. Water Resour. Ind. 2024, 32, 100266. [Google Scholar] [CrossRef]
- Perera, A.T.D.; Nik, V.M.; Chen, D.L.; Scartezzini, J.L.; Hong, T.Z. Quantifying the impacts of climate change and extreme climate events on energy systems. Nat. Energy 2020, 5, 150–159. [Google Scholar] [CrossRef]
- Bhatti, B.A.; Hanif, S.; Alam, J.; Mitra, B.; Kini, R.; Wu, D. Using energy storage systems to extend the life of hydropower plants. Appl. Energy 2023, 337, 120894. [Google Scholar] [CrossRef]
- Sterl, S.; Vanderkelen, I.; Chawanda, C.J.; Russo, D.; Brecha, R.J.; van Griensven, A.; van Lipzig, N.P.M.; Thiery, W. Smart renewable electricity portfolios in West Africa. Nat. Sustain. 2020, 3, 710–719. [Google Scholar] [CrossRef]
- Wan, W.H.; Wang, H.; Zhao, J.S. Hydraulic Potential Energy Model for Hydropower Operation in Mixed Reservoir Systems. Water Resour. Res. 2020, 56, e2019WR026062. [Google Scholar] [CrossRef]
- Jamali, S.; Jamali, B. Cascade hydropower systems optimal operation: Implications for Iran’s Great Karun hydropower systems. Appl. Water Sci. 2019, 9, 66. [Google Scholar] [CrossRef]
- Li, X.; Wei, J.H.; Li, T.J.; Wang, G.Q.; Yeh, W.W.G. A parallel dynamic programming algorithm for multi-reservoir system optimization. Adv. Water Resour. 2014, 67, 1–15. [Google Scholar] [CrossRef]
- Zhao, T.T.G.; Zhao, J.S.; Yang, D.W. Improved Dynamic Programming for Hydropower Reservoir Operation. J. Water Resour. Plan. Manag. 2014, 140, 365–374. [Google Scholar] [CrossRef]
- Zhao, Q.K.; Cai, X.M.; Li, Y. Algorithm Design Based on Derived Operation Rules for a System of Reservoirs in Parallel. J. Water Resour. Plan. Manag. 2020, 146, 5. [Google Scholar] [CrossRef]
- Jia, Z.B.; Shen, J.J.; Cheng, C.T.; Zhang, Y.; Lyu, Q. Optimum day-ahead clearing for high proportion hydropower market considering complex hydraulic connection. Int. J. Electr. Power Energy Syst. 2022, 141, 108211. [Google Scholar] [CrossRef]
- Liao, S.L.; Liu, Z.W.; Liu, B.X.; Wu, X.Y.; Cheng, C.T.; Su, H.Y. Short-Term Hydro Scheduling Considering Multiple Units Sharing a Common Tunnel and Crossing Vibration Zones Constraints. J. Water Resour. Plan. Manag. 2021, 147, 10. [Google Scholar] [CrossRef]
- Liu, B.X.; Lund, J.R.; Liao, S.L.; Jin, X.Y.; Liu, L.J.; Cheng, C.T. Optimal power peak shaving using hydropower to complement wind and solar power uncertainty. Energy Convers. Manag. 2020, 209, 112628. [Google Scholar] [CrossRef]
- Lima, R.M.; Marcovecchio, M.G.; Novais, A.Q.; Grossmann, I.E. On the Computational Studies of Deterministic Global Optimization of Head Dependent Short-Term Hydro Scheduling. IEEE Trans. Power Syst. 2013, 28, 4336–4347. [Google Scholar] [CrossRef]
- Shen, J.J.; Chen, G.Z.; Cheng, C.T.; Wei, W.; Zhang, X.F.; Zhang, J. Modeling of Generation Scheduling for Multiple Provincial Power Grids Using Peak-Shaving Indexes. J. Water Resour. Plan. Manag. 2021, 147, 9. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, C.T.; Shen, J.J.; Cao, R.; Yeh, W.W.G. Optimization of Large-Scale Daily Hydrothermal System Operations with Multiple Objectives. Water Resour. Res. 2018, 54, 2834–2850. [Google Scholar] [CrossRef]
- Cheng, C.T.; Wang, J.Y.; Wu, X.Y. Hydro Unit Commitment With a Head-Sensitive Reservoir and Multiple Vibration Zones Using MILP. IEEE Trans. Power Syst. 2016, 31, 4842–4852. [Google Scholar] [CrossRef]
- Fang, Z.; Liao, S.L.; Zhao, H.Y.; Cheng, C.T.; Liu, B.X.; Wang, H.; Li, S.S. An MILP model based on a processing strategy of complex multisource constraints for the short-term peak shaving operation of large-scale cascaded hydropower plants. Renew. Energy 2024, 231, 120932. [Google Scholar] [CrossRef]
- Su, C.G.; Wang, P.L.; Yuan, W.L.; Cheng, C.T.; Zhang, T.H.; Yan, D.H.; Wu, Z.N. An MILP based optimization model for reservoir flood control operation considering spillway gate scheduling. J. Hydrol. 2022, 613, 128483. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.V.; Ferreira, A.R.; Simonovic, S.P. Fuzzy multiobjective models for optimal operation of a hydropower system. Water Resour. Res. 2013, 49, 3180–3193. [Google Scholar] [CrossRef]
- Wu, X.; Shen, X.J.; Wei, C.J.; Xie, X.M.; Li, J.S. A Hybrid Particle Swarm Optimization-Genetic Algorithm for Multiobjective Reservoir Ecological Dispatching. Water Resour. Manag. 2024, 38, 2229–2249. [Google Scholar] [CrossRef]
- Qiu, R.J.; Wang, D.; Singh, V.P.; Wang, Y.K.; Wu, J.C. Integration of deep learning and improved multi-objective algorithm to optimize reservoir operation for balancing human and downstream ecological needs. Water Res. 2024, 253, 121314. [Google Scholar] [CrossRef] [PubMed]
- Azizipour, M.; Ghalenoei, V.; Afshar, M.H.; Solis, S.S. Optimal Operation of Hydropower Reservoir Systems Using Weed Optimization Algorithm. Water Resour. Manag. 2016, 30, 3995–4009. [Google Scholar] [CrossRef]
- Azizipour, M.; Sattari, A.; Afshar, M.H.; Goharian, E. Incorporating reliability into the optimal design of multi-hydropower systems: A cellular automata-based approach. J. Hydrol. 2022, 604, 127227. [Google Scholar] [CrossRef]
- Zhao, T.T.G.; Cai, X.M.; Lei, X.H.; Wang, H. Improved Dynamic Programming for Reservoir Operation Optimization with a Concave Objective Function. J. Water Resour. Plan. Manag. 2012, 138, 590–596. [Google Scholar] [CrossRef]
- Chai, F.X.; Peng, F.; Zhang, H.P.; Zang, W.B. Stable Improved Dynamic Programming Method: An Efficient and Accurate Method for Optimization of Reservoir Flood Control Operation. Water Resour. Manag. 2023, 37, 5635–5654. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Liao, S.L. Hydropower system operation optimization by discrete differential dynamic programming based on orthogonal experiment design. Energy 2017, 126, 720–732. [Google Scholar] [CrossRef]
- Fang, Z.; Liao, S.L.; Cheng, C.T.; Zhao, H.Y.; Liu, B.X.; Su, H.Y. Parallel improved DPSA algorithm for medium-term optimal scheduling of large-scale cascade hydropower plants. Renew. Energy 2023, 210, 134–147. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Wu, X.Y. Peak operation of hydropower system with parallel technique and progressive optimality algorithm. Int. J. Electr. Power Energy Syst. 2018, 94, 267–275. [Google Scholar] [CrossRef]
- Liao, S.L.; Liu, H.; Liu, B.X.; Liu, T.; Li, C.H.; Su, H.Y. Solution framework for short-term cascade hydropower system optimization operations based on the load decomposition strategy. Energy 2023, 277, 127685. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Liao, S.L.; Fang, Z.; Liu, B.X.; Ma, X.Y.; Lu, J. Short-term peak-shaving operation of “N-reservoirs and multicascade” large-scale hydropower systems based on a decomposition-iteration strategy. Energy 2024, 288, 129834. [Google Scholar] [CrossRef]
- Cheng, C.T.; Wang, S.; Chau, K.W.; Wu, X.Y. Parallel discrete differential dynamic programming for multireservoir operation. Environ. Model. Softw. 2014, 57, 152–164. [Google Scholar] [CrossRef]
- Liu, P.; Cai, X.M.; Guo, S.L. Deriving multiple near-optimal solutions to deterministic reservoir operation problems. Water Resour. Res. 2011, 47, W08506. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. China’s large-scale hydropower system: Operation characteristics, modeling challenge and dimensionality reduction possibilities. Renew. Energy 2019, 136, 805–818. [Google Scholar] [CrossRef]
- Optimization Gurobi. Gurobi Optimizer Reference Manual. 2020. Available online: http://www.gurobi.com (accessed on 1 December 2020).

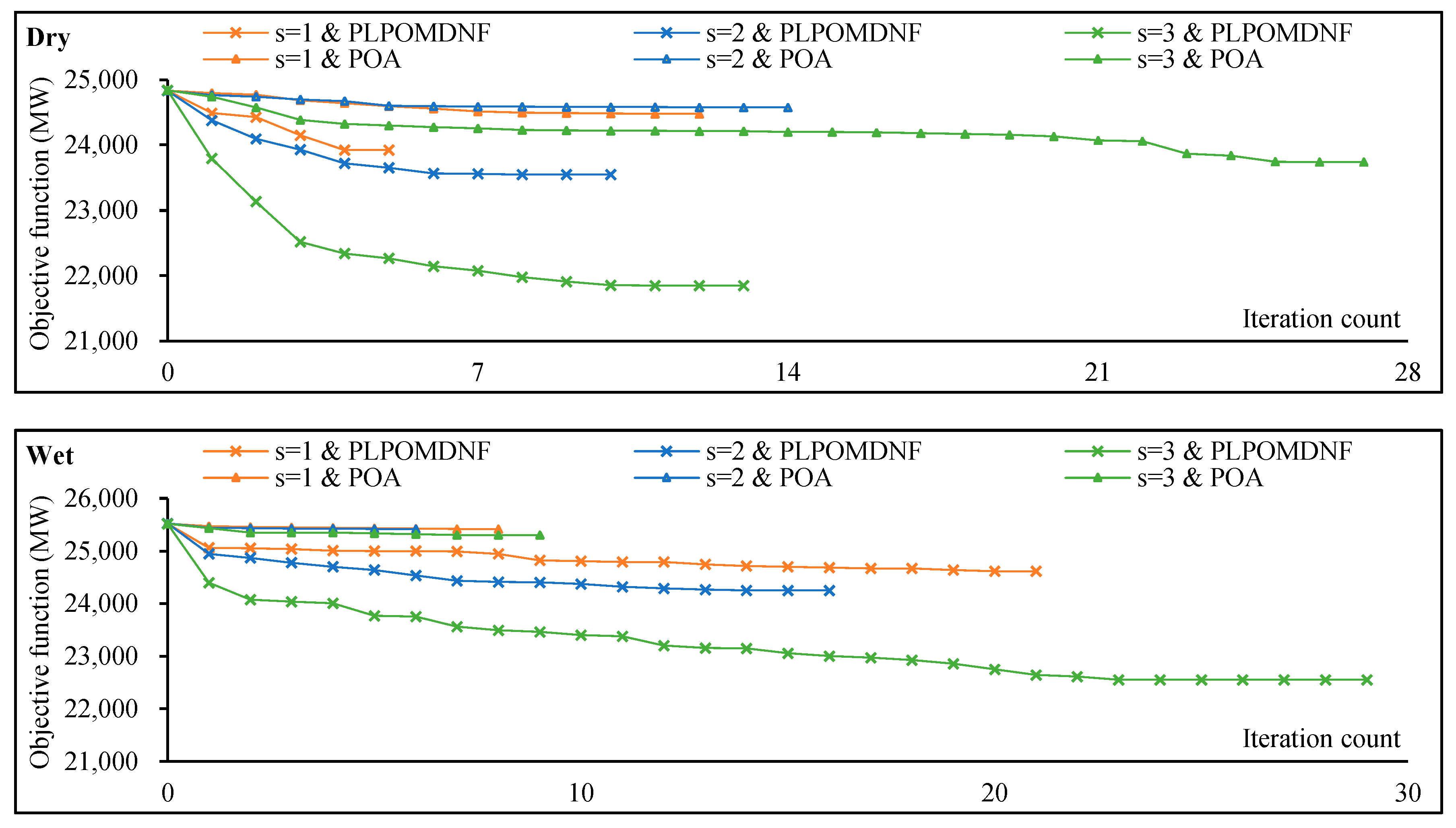


| Season | Number of Stations | Method | Iteration Count | Peak–Valley Difference (MW) | Improvement of PLPOMDNF (MW) | ||
|---|---|---|---|---|---|---|---|
| Original Load | Residual Load | Reduction | |||||
| Dry | 1 | MILP | - | 24,822 | 23,926 | 896 | 7 |
| POA | 12 | 24,475 | 347 | 556 | |||
| PLPOMDNF | 5 | 23,919 | 903 | - | |||
| 2 | MILP | - | 23,557 | 1265 | 10 | ||
| POA | 14 | 24,573 | 249 | 1026 | |||
| PLPOMDNF | 10 | 23,547 | 1275 | - | |||
| 3 | MILP | - | 22,462 | 2360 | 612 | ||
| POA | 27 | 23,739 | 1083 | 1889 | |||
| PLPOMDNF | 13 | 21,850 | 2972 | - | |||
| Wet | 1 | MILP | - | 25,520 | 24,625 | 895 | 8 |
| POA | 8 | 25,418 | 102 | 801 | |||
| PLPOMDNF | 21 | 24,617 | 903 | - | |||
| 2 | MILP | - | 24,255 | 1265 | 8 | ||
| POA | 6 | 25,420 | 100 | 1173 | |||
| PLPOMDNF | 16 | 24,247 | 1273 | - | |||
| 3 | MILP | - | 23,383 | 2137 | 521 | ||
| POA | 9 | 25,301 | 219 | 2439 | |||
| PLPOMDNF | 19 | 22,862 | 2658 | - | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Fang, Z.; Zhang, Z.; Liu, Y.; Xu, Y.; Wang, T.; Yang, Y. Progressive Linear Programming Optimality Method Based on Decomposing Nonlinear Functions for Short-Term Cascade Hydropower Scheduling. Water 2025, 17, 1441. https://doi.org/10.3390/w17101441
Lu J, Fang Z, Zhang Z, Liu Y, Xu Y, Wang T, Yang Y. Progressive Linear Programming Optimality Method Based on Decomposing Nonlinear Functions for Short-Term Cascade Hydropower Scheduling. Water. 2025; 17(10):1441. https://doi.org/10.3390/w17101441
Chicago/Turabian StyleLu, Jia, Zhou Fang, Zheng Zhang, Yaxin Liu, Yang Xu, Tao Wang, and Yuqi Yang. 2025. "Progressive Linear Programming Optimality Method Based on Decomposing Nonlinear Functions for Short-Term Cascade Hydropower Scheduling" Water 17, no. 10: 1441. https://doi.org/10.3390/w17101441
APA StyleLu, J., Fang, Z., Zhang, Z., Liu, Y., Xu, Y., Wang, T., & Yang, Y. (2025). Progressive Linear Programming Optimality Method Based on Decomposing Nonlinear Functions for Short-Term Cascade Hydropower Scheduling. Water, 17(10), 1441. https://doi.org/10.3390/w17101441






