A Comparative Analysis on the Vibrational Behavior of Two Low-Head Francis Turbine Units with Similar Design
Abstract
1. Introduction
2. Field Test Design
2.1. Researched Turbine Units
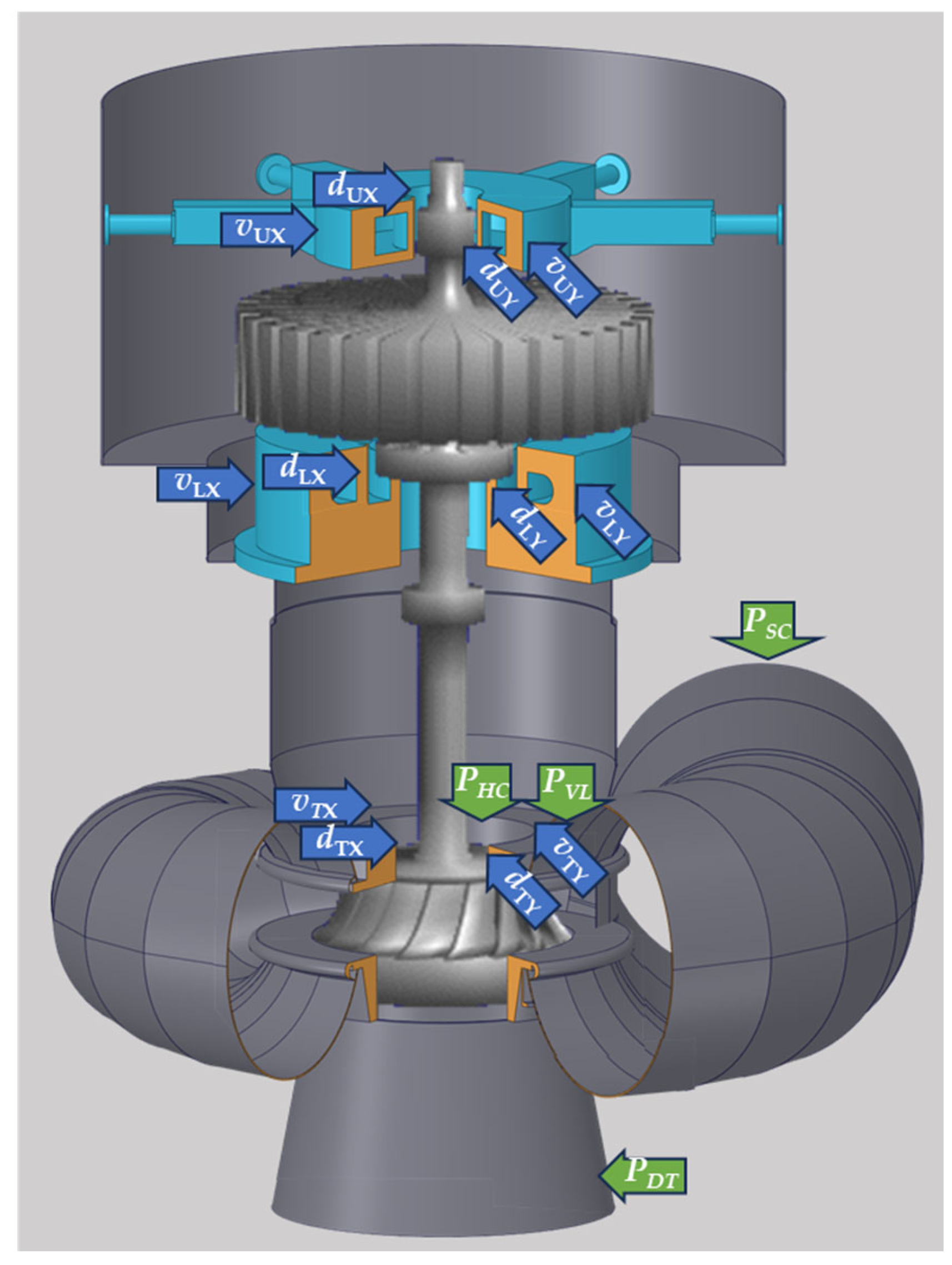
2.2. Measurement Setup
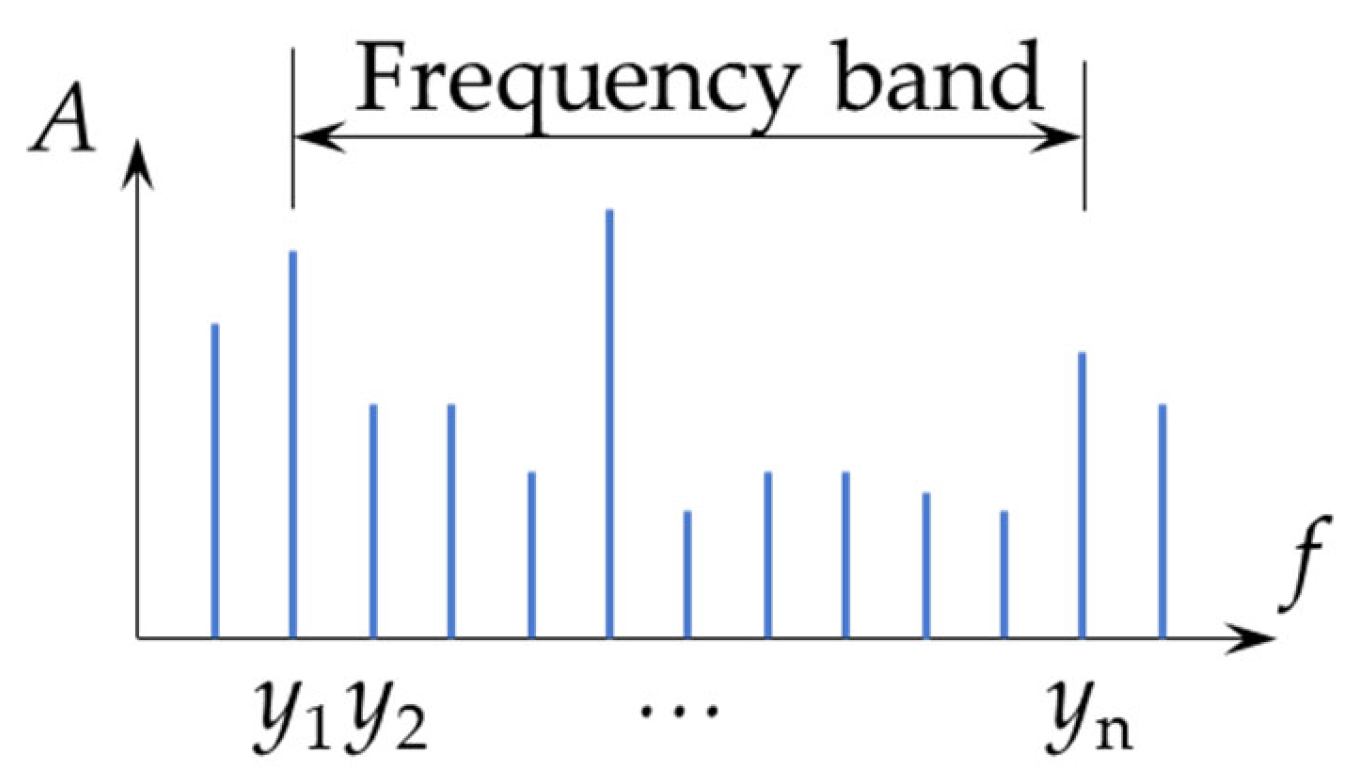
2.3. Signal Processing Methodology
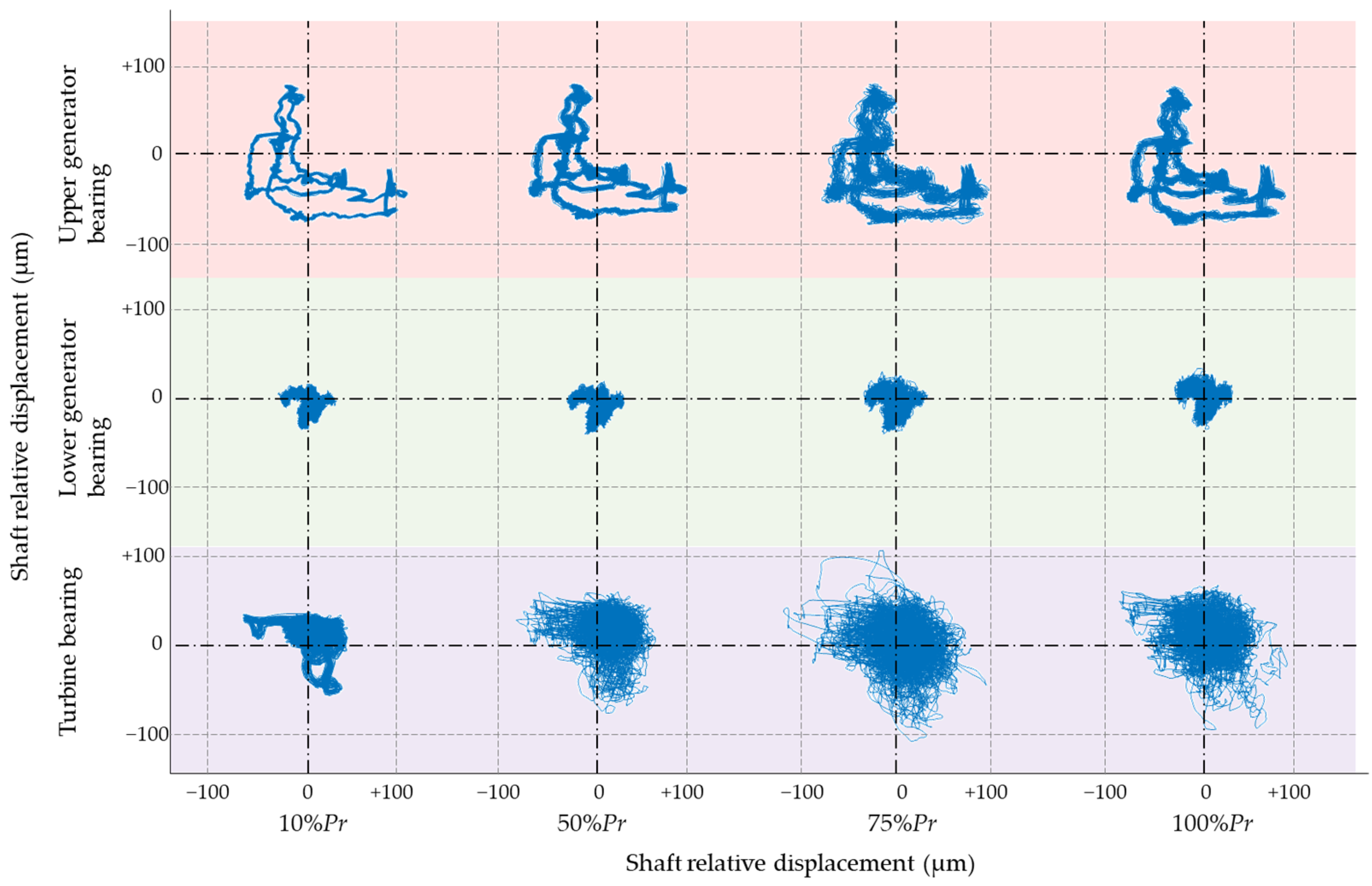
3. Machine Behavior Comparison
3.1. Pressure and Pressure Pulsation Comparison
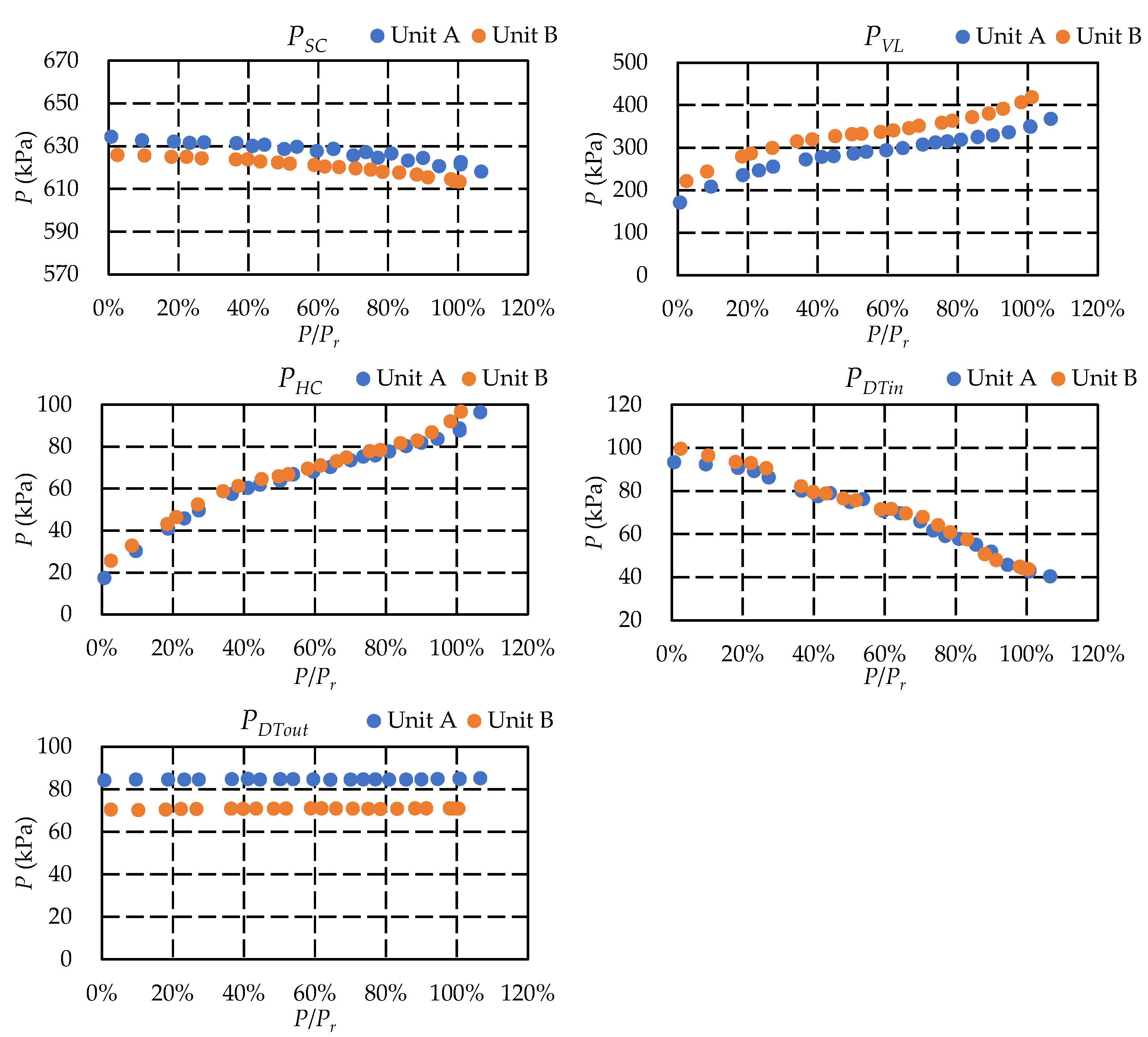
3.1.1. Pressure Comparison
3.1.2. Vibration Behavior Comparison
3.2. Discussion and Outlook
3.2.1. Discussion
3.2.2. Outlook
4. Conclusions
- (1)
- The design of the spiral casing has a great influence on the pressure in the runner inlet, which is significant for the performance of the machine.
- (2)
- The amplitude of pressure pulsation is lower at deep-low load conditions and rated operating conditions, and is higher at part load condition. The pressure pulsation directly causes the variation of vibration.
- (3)
- The intensity of vibration caused by RSI difference can reach 10 times difference between two similar hydraulic turbine units with different designs. Greater attention should be given to the design of the inlet of the runner and the guide vanes.
- (4)
- Even with similar designs, installation error can result in significant differences in vibration behavior hidden behind the same overall vibration levels.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Energy Agency. World Energy Outlook 2023; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Li, J.; Chen, S.; Wu, Y.; Wang, Q.; Liu, X.; Qi, L.; Lu, X.; Gao, L. How to Make Better Use of Intermittent and Variable Energy? A Review of Wind and Photovoltaic Power Consumption in China. Renew. Sustain. Energy Rev. 2021, 137, 110626. [Google Scholar] [CrossRef]
- Pommeret, A.; Schubert, K. Optimal Energy Transition with Variable and Intermittent Renewable Electricity Generation. J. Econ. Dyn. Control 2022, 134, 104273. [Google Scholar] [CrossRef]
- Jing, Z.; Wang, Y.; Chang, J.; Wang, X.; Zhou, Y.; Li, L.; Tian, Y. Benefit Compensation of Hydropower-Wind-Photovoltaic Complementary Operation in the Large Clean Energy Base. Appl. Energy 2024, 354, 122040. [Google Scholar] [CrossRef]
- Pereira, J.G., Jr.; Vagnoni, E.; Favrel, A.; Landry, C.; Alligné, S.; Nicolet, C.; Avellan, F. Prediction of Unstable Full Load Conditions in a Francis Turbine Prototype. Mech. Syst. Signal Process. 2022, 169, 108666. [Google Scholar] [CrossRef]
- Zobeiri, A.; Kueny, J.-L.; Farhat, M.; Avellan, F. Pump-Turbine Rotor-Stator Interactions in Generating Mode: Pressure Fluctuation in Distributor Channel. In Proceedings of the 23rd IAHR Symposium on Hydraulic Machinery and Systems, Yokohama, Japan, 18–21 October 2006. [Google Scholar]
- Rodriguez, C.G.; Mateos-Prieto, B.; Egusquiza, E. Monitoring of Rotor-Stator Interaction in Pump-Turbine Using Vibrations Measured with on-Board Sensors Rotating with Shaft. Shock Vib. 2014, 2014, 276796. [Google Scholar] [CrossRef]
- Linlin, G. Numerical Investigation and Modelling of the Unsteady Behavior and Erosion Power of Cloud Cavitation. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2021. [Google Scholar]
- Kumar, P.; Saini, R.P. Study of Cavitation in Hydro Turbines—A Review. Renew. Sustain. Energy Rev. 2010, 14, 374–383. [Google Scholar] [CrossRef]
- Gohil, P.P.; Saini, R.P. Investigation into Cavitation Damage Potentiality Using Pressure Pulsation Phenomena in a Low Head Francis Turbine for Small Hydropower Schemes. Ocean Eng. 2022, 263, 112230. [Google Scholar] [CrossRef]
- Abu-Nab, A.K.; Hakami, A.M.; Abu-Bakr, A.F. Charged Cavitation Multibubbles Dynamics Model: Growth Process. Mathematics 2024, 12, 569. [Google Scholar] [CrossRef]
- Favrel, A.; Müller, A.; Landry, C.; Yamamoto, K.; Avellan, F. Study of the Vortex-Induced Pressure Excitation Source in a Francis Turbine Draft Tube by Particle Image Velocimetry. Exp. Fluids 2015, 56, 215. [Google Scholar] [CrossRef]
- Maika, N.; Lin, W.; Khatamifar, M. A Review of Gravitational Water Vortex Hydro Turbine Systems for Hydropower Generation. Energies 2023, 16, 5394. [Google Scholar] [CrossRef]
- Favrel, A.; Müller, A.; Landry, C.; Gomes, J.; Yamamoto, K.; Avellan, F. Dynamics of the Precessing Vortex Rope and Its Interaction with the System at Francis Turbines Part Load Operating Conditions. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2017; Volume 813, p. 12023. [Google Scholar]
- Müller, A.; Bullani, A.; Dreyer, M.; Roth, S.; Favrel, A.; Landry, C.; Avellan, F. Interaction of a Pulsating Vortex Rope with the Local Velocity Field in a Francis Turbine Draft Tube. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2012; Volume 15, p. 32040. [Google Scholar]
- Moraga, G.; Egusquiza, M.; Valentín, D.; Valero, C.; Presas, A. Analysis of the Mode Shapes of Kaplan Runners. Appl. Sci. 2022, 12, 6708. [Google Scholar] [CrossRef]
- Zhao, Q.; Luo, Y.; Zhai, L.; Cao, J.; Cao, J.; Xu, Y.; Zhao, Y. Failure Analysis on the Bolt Connecting the Head-Cover and Stay Ring in Pumped Storage Unit: Part I—Experimental Study. Eng. Fail. Anal. 2023, 153, 107557. [Google Scholar] [CrossRef]
- Valentín, D.; Valero, C.; Egusquiza, M.; Presas, A. Failure Investigation of a Solar Tracker Due to Wind-Induced Torsional Galloping. Eng. Fail. Anal. 2022, 135, 106137. [Google Scholar] [CrossRef]
- Valero, C.; Egusquiza, M.; Egusquiza, E.; Presas, A.; Valentin, D.; Bossio, M. Extension of Operating Range in Pump-Turbines. Influence of Head and Load. Energies 2017, 10, 2178. [Google Scholar] [CrossRef]
- Egusquiza, E.; Valero, C.; Estévez, A.; Guardo, A.; Coussirat, M. Failures Due to Ingested Bodies in Hydraulic Turbines. Eng. Fail. Anal. 2011, 18, 464–473. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z. Computational Model for Investigating the Influence of Unbalanced Magnetic Pull on the Radial Vibration of Large Hydro-Turbine Generators. ASME. J. Vib. Acoust. 2012, 134, 051013. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Deering, J.; Kampschulte, M.; Yu, B.; Grandfield, K.; Mele, E.; Biehl, C.; Krombach, G.A.; Heiss, C. Resonance Vibration Interventions in the Femur: Experimental-Numerical Modelling Approaches. J. Mech. Behav. Biomed. Mater. 2021, 124, 104850. [Google Scholar] [CrossRef]
- Zhao, W.; Egusquiza, E.; Valero, C.; Egusquiza, M.; Valentín, D.; Presas, A. A Novel Condition Monitoring Methodology Based on Neural Network of Pump-Turbines with Extended Operating Range. In Proceedings of the 16th IMEKO TC10 Conference, Berlin, Germany, 3–4 September 2019; p. 4. [Google Scholar]
- Zhao, W.; Huang, X.; Yang, M.; Yang, H.; Bi, H.; He, Q.; Wang, Z. Flow-Induced Dynamic Behavior of Head-Cover Bolts in a Prototype Pump-Turbine during Load Rejection. Machines 2022, 10, 1130. [Google Scholar] [CrossRef]
- Trivedi, C. A Review on Fluid Structure Interaction in Hydraulic Turbines: A Focus on Hydrodynamic Damping. Eng. Fail. Anal. 2017, 77, 1–22. [Google Scholar] [CrossRef]
- Kahraman, G.; Özdemir, O. Mathematical Modeling of Vibration Failure Caused by Balancing Effect in Hydraulic Turbines. Mech. Based Des. Struct. Mach. 2023, 51, 1489–1500. [Google Scholar] [CrossRef]
- Casanova, F. Failure Analysis of the Draft Tube Connecting Bolts of a Francis-Type Hydroelectric Power Plant. Eng. Fail. Anal. 2009, 16, 2202–2208. [Google Scholar] [CrossRef]
- Presas, A.; Egusquiza, E.; Valero, C.; Valentin, D.; Seidel, U. Feasibility of Using PZT Actuators to Study the Dynamic Behavior of a Rotating Disk Due to Rotor-Stator Interaction. Sensors 2014, 14, 11919–11942. [Google Scholar] [CrossRef] [PubMed]
- Presas, A.; Valentin, D.; Egusquiza Montagut, M.; Bossio, M.; Egusquiza, E.; Valero, C. Optimized Use of Sensors to Detect Critical Full Load Instability in Large Hydraulic Turbines. Proceedings 2017, 1, 822. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, R.; Yu, A.; Lu, L.; Luo, X. Suppression of Vortex Rope Oscillation and Pressure Vibrations in Francis Turbine Draft Tube Using Various Strategies. J. Hydrodyn. 2021, 33, 534–545. [Google Scholar] [CrossRef]
- Agarwal, A.; Mthembu, L. Finite Element Investigation of the Vibration Characteristics of Francis Turbine Vanes. In Emerging Trends in Mechanical and Industrial Engineering: Select Proceedings of ICETMIE 2022; Springer: Berlin/Heidelberg, Germany, 2023; pp. 945–960. [Google Scholar]




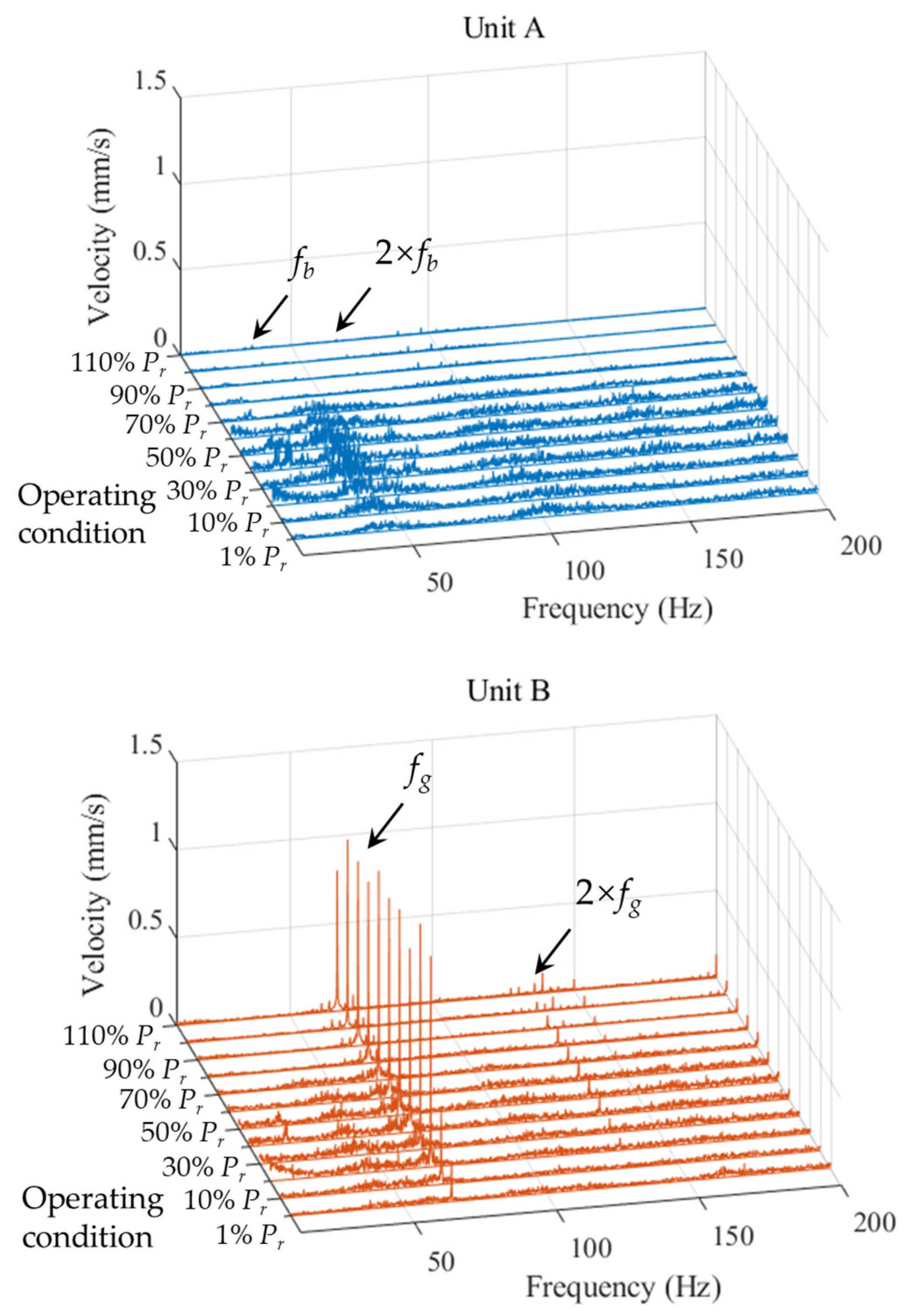
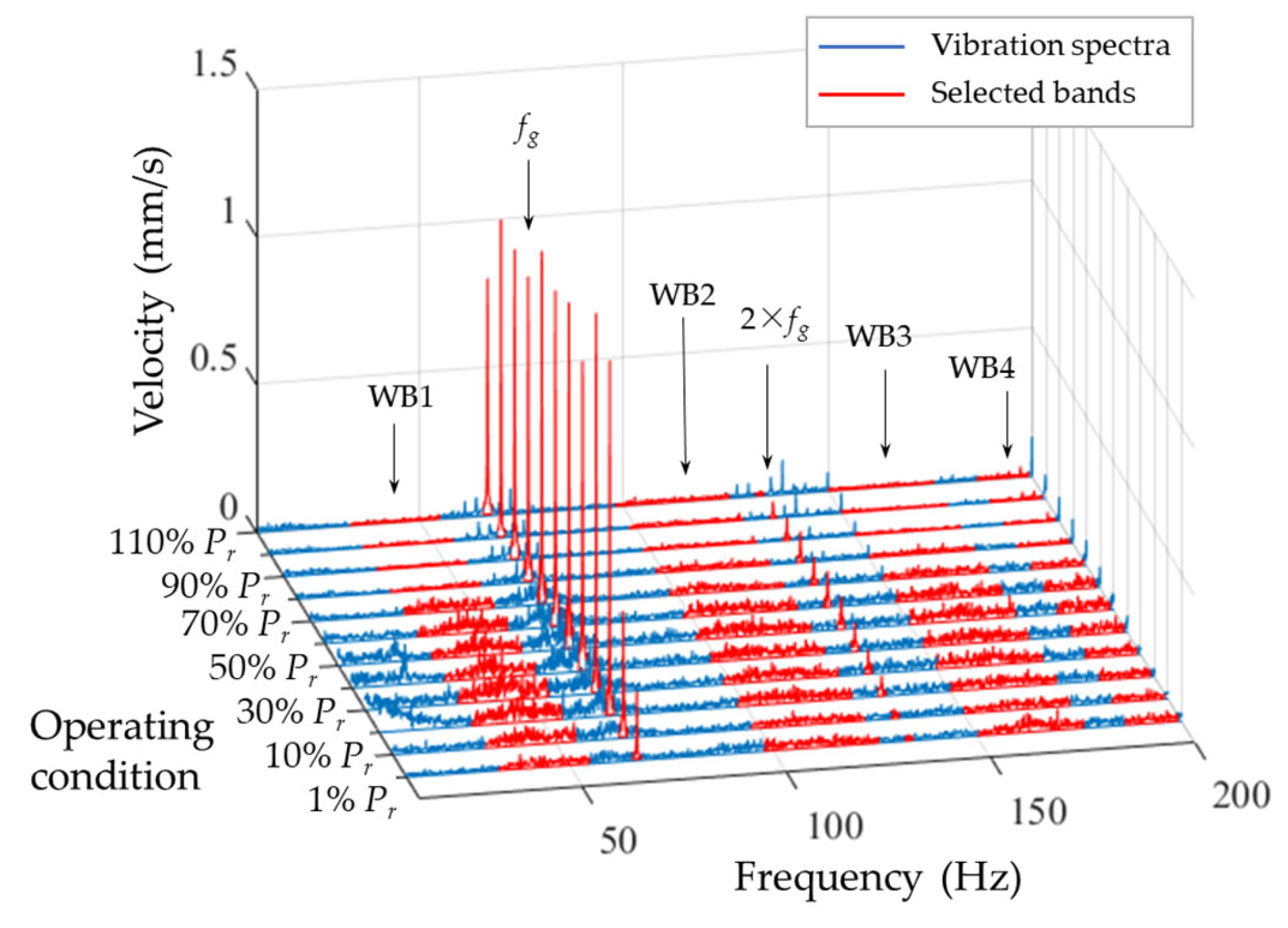

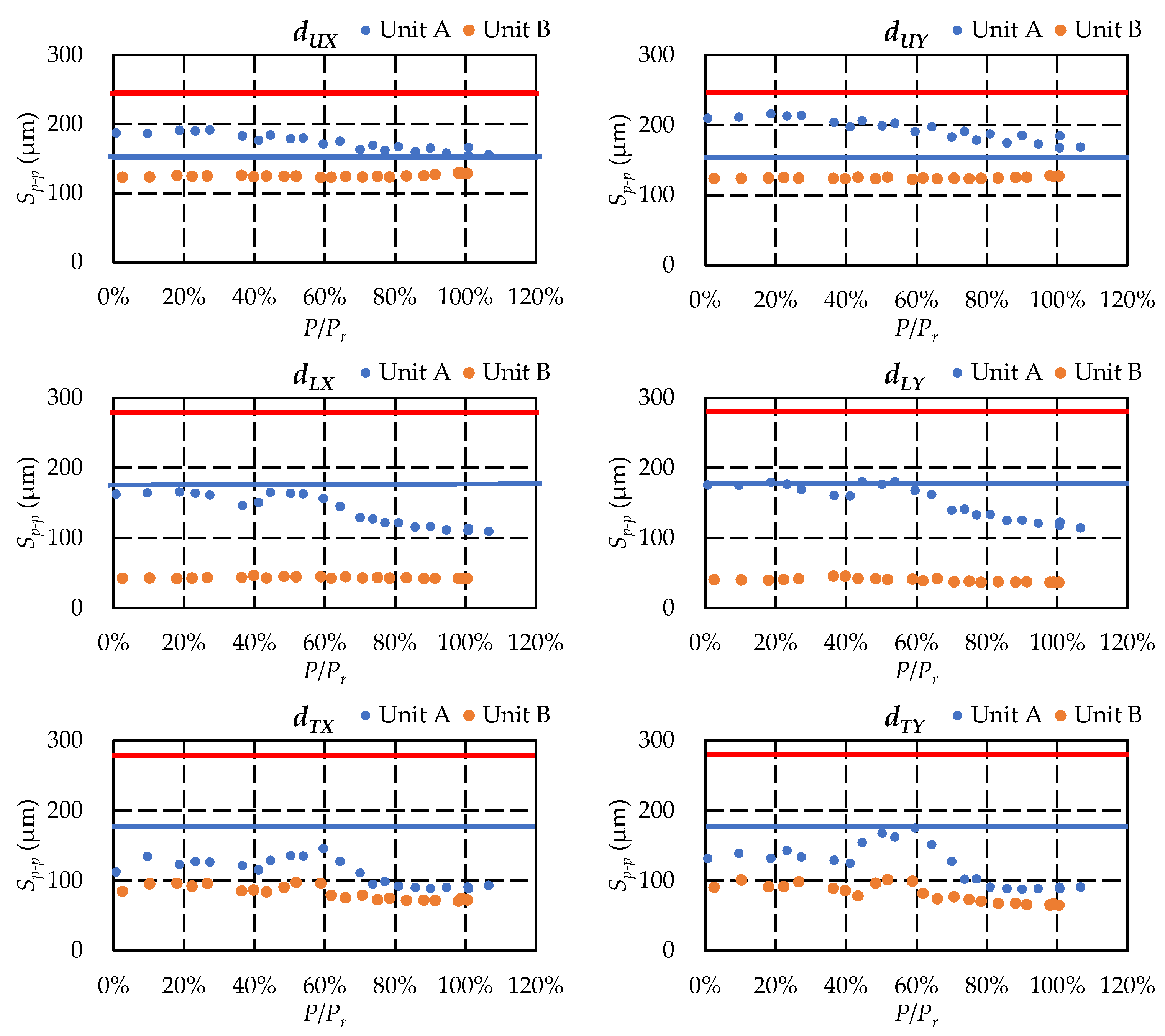
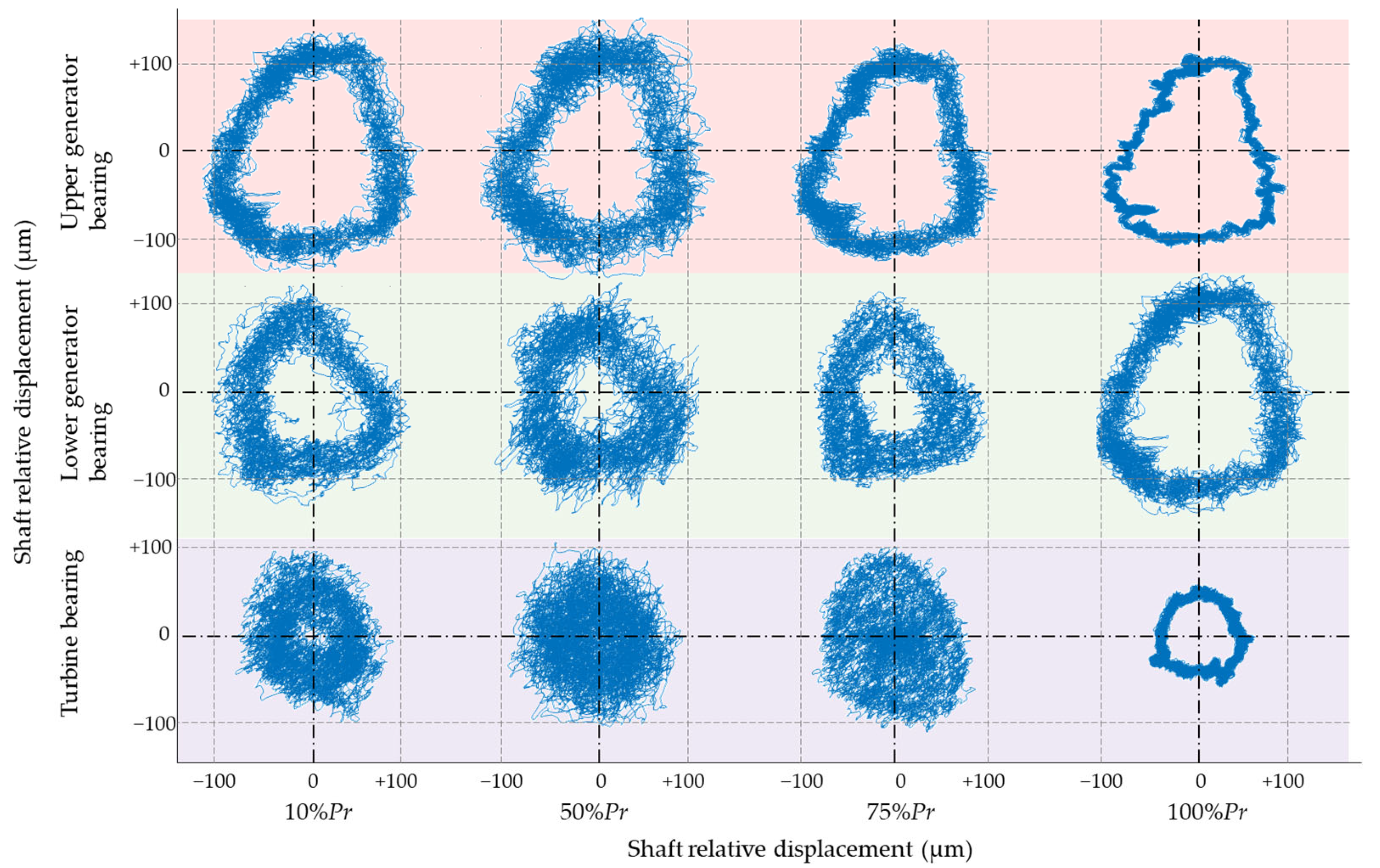
| Structure Parameter | Value |
|---|---|
| Runner diameter | 3.5 m |
| Number of blades Zb | 13 |
| Number of guide vanes Zg | 24 |
| Rated head Hr | 54.5 m |
| Rated speed n | 166.7 rpm |
| Rated rotating frequency ff | 2.78 Hz |
| Rated output Pr | 44.6 MW |
| Blade passing frequency fb | 36.11 Hz |
| Best efficiency | 94.14% |
| Band name | Center Frequency | Band Width |
|---|---|---|
| fg | fg | ±1.00 Hz |
| 2 × fg | 2 × fg | ±1.00 Hz |
| WB1 | 41.55 Hz | 8.75 Hz |
| WB2 | 100.30 Hz | 13.90 Hz |
| WB3 | 153.50 Hz | 8.60 Hz |
| WB4 | 190.45 Hz | 9.55 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Deng, J.; Jin, Z.; Xia, M.; Wang, G.; Wang, Z. A Comparative Analysis on the Vibrational Behavior of Two Low-Head Francis Turbine Units with Similar Design. Water 2025, 17, 113. https://doi.org/10.3390/w17010113
Zhao W, Deng J, Jin Z, Xia M, Wang G, Wang Z. A Comparative Analysis on the Vibrational Behavior of Two Low-Head Francis Turbine Units with Similar Design. Water. 2025; 17(1):113. https://doi.org/10.3390/w17010113
Chicago/Turabian StyleZhao, Weiqiang, Jianhua Deng, Zhiqiang Jin, Ming Xia, Gang Wang, and Zhengwei Wang. 2025. "A Comparative Analysis on the Vibrational Behavior of Two Low-Head Francis Turbine Units with Similar Design" Water 17, no. 1: 113. https://doi.org/10.3390/w17010113
APA StyleZhao, W., Deng, J., Jin, Z., Xia, M., Wang, G., & Wang, Z. (2025). A Comparative Analysis on the Vibrational Behavior of Two Low-Head Francis Turbine Units with Similar Design. Water, 17(1), 113. https://doi.org/10.3390/w17010113








