Abstract
A set of experimental field single-borehole dilution tests were completed in the Motril–Salobreña detrital aquifer (Spain) in a sector with coarse material in four different moments under variable hydrological conditions. The comparative study of the tracer washing, and the temperature profile patterns for the tests carried out in two wells located hundreds of m from each other, revealed the presence of ascending vertical flows in one of the wells (not detected by other means) that compromises the reliability of the tracer test. The values of both the apparent horizontal velocity and hydraulic conductivity obtained in the affected well were less than half of those estimated in the well not affected by the upward vertical flows. The repetition of the test eight times during different seasons showed that the hydraulic conductivity calculated from the apparent horizontal velocity can vary; therefore, to approximate to a representative hydraulic conductivity value, using this method is recommended to carry out tests under different hydrological conditions and average the results. The difference generated by the changes in conditions for the specific setting of the study area was 25%. Taking this into account, it was considered that an approximation to the more representative value would be an average under variable hydrological conditions, resulting in a horizontal velocity of 6.7 m/d and hydraulic conductivity of 337 m/d. This information is critical for the management of the aquifer as it has strategic resources against droughts that are becoming more frequent in the Mediterranean area.
1. Introduction
Single-borehole dilution tests (SBDTs) have been widely used as an alternative or complementary method to pumping tests to estimate groundwater flow velocity [1,2,3,4,5,6,7,8,9,10,11,12] and, to a lesser extent, hydraulic conductivity in aquifers [13,14,15]. In addition, [12,16,17,18] used this method to estimate hydrodynamic dispersion.
A SBDT consists of introducing a tracer into a borehole and measuring the tracer concentration over time. According to [3], if there is a steady flow and the tracer is homogeneously distributed throughout the dilution volume, an apparent dilution rate, , results according to the following:
where is the borehole volume [M3], A is the cross-section of the borehole perpendicular to the direction of the undisturbed ground water flow [L2], t is the time after the beginning of the measurement, C0 is the tracer concentration in the borehole at the beginning of the measurement (t = 0) [M/L3], C* is the initial tracer concentration in the groundwater, and C is the tracer concentration at time t.
Halevy et al. [2] indicated that solute dilution in the borehole not only results from groundwater flow, but also potentially affects other processes, which may in turn affect the extent of the tracer dilution, for example, the presence of convection due to density contrasts in the tracer from poor mixing or a large vertical variation in temperature, the presence of natural vertical currents in the well generated by communication between the various aquifers with different heads, or the artificial mixing or intrinsic diffusion of the tracer due to different concentrations in the well. Thus, the dilution rate will be defined as follows:
where is the groundwater Darcy velocity, is the apparent velocity caused by the density convection, is the apparent velocity caused by vertical flows, is the apparent flow rate caused by artificial mixing, is the apparent velocity caused by the tracer’s molecular diffusion, and is the correction factor that considers the distortion of the flow net in the aquifer due to the physical interference of the borehole.
In aquifers with medium-to-high hydraulic conductivity and with a dominant horizontal flow, to avoid high tracer concentrations and ensure good initial mixing, the effects that can alter the tracer washout can be disregarded [2], thereby leading to the following equation:
Therefore, it is assumed that the dilution rate in the borehole is simply a consequence of the horizontal ground waterflow. Thus, groundwater flow velocity can be calculated after combining Equation (1) with Equation (3), as follows:
This equation has been used for aquifers with different lithologies, for example, in fissured aquifers such as granite [19,20], shale [21], shale–limestone sequences [17,22,23], carbonate formations [24,25], and fractured mudstones and sandstones [26]. Numerous studies have also applied this technique to detrital aquifers [8,12,13,27,28,29,30,31,32].
A variety of tracers have also been used in SBDTs, such as radioisotopes, isotopes dyes [3,30,31], and fluorescent dyes [6,9,20,23], salts, brines [24,33,34,35], and deionized water [36,37].
The main sources of estimation error of the horizontal velocity from SBDTs are derived from (1) a non-uniform distribution of the tracer following its injection into the borehole, (2) a significant diffusive mass flux, and (3) a vertical flow within or outside of the screened well [5]. In the first case, the problem can be mitigated by excluding the early test periods from the dilution analysis because, in these initial measurements, the tracer mixing is likely poor [7]. Regarding the effect of the diffusive mass flux, if the hydraulic conductivity reaches a sufficiently high value, the advective flux becomes significantly higher than the diffusive flux and the diffusion effect can be disregarded [11]. However, when detecting vertical flows, the effect on the dilution processes is very important, and the value of velocity may even be several orders of magnitude higher than an estimate of the velocity obtained using the Darcy formula [7]. Maurice et al. [38] proposed simulated tracer profiles through numerical modeling resulting from SBDTs under various conditions with the presence of vertical flows.
The information provided by SBDT, groundwater velocity and hydraulic conductivity is useful in many hydrogeological circumstances to develop groundwater flow models, estimate groundwater inputs to aquifer systems or develop management plans. In this study, a study area for which this knowledge is essential for the adequate management of water resources has been selected. The Motril–Salobreña aquifer is a strategic system for water supply on the coast of Granada, where the local economy is based on the cultivation of tropical fruits (cherimoya, avocado, and mango, among others) and beach tourism. This coastal aquifer has abnormally higher water resources compared to other nearby coastal systems because the aquifer is recharged by the Guadalfeo River, which is fed by the snow melting of Sierra Nevada (3482 m). Considering the good water quality of the Motril–Salobreña aquifer, the authorities have included this aquifer in Drought Emergency Response Plans to ensure water supply during periods of drought that frequently hit the Mediterranean region. However, the correct inclusion of the resources of the Motril–Salobreña aquifer in Emergency Response Plans requires an exact groundwater balance for a correct distribution of the groundwater resources. Accordingly, almost all water inlets and outlets are well established in the aquifer, except for the underground inlets and outlets from other aquifer units in the northern sector. The estimation of this component of groundwater balance requires assessing the aquifer parameters as accurately as possible. Previous studies using pumping tests show very high values of hydraulic conductivity, at 1000 m/d, of the aquifer [39] that can represent an overestimation of the groundwater input and hence generate a water problem for the use of groundwater resources under drought conditions.
The main objective of this study is to determine the hydraulic conductivity in a key sector of the coastal detrital Motril–Salobreña aquifer to estimate its recharge. In this area, there are two boreholes specifically drilled for the estimation of groundwater inputs to the aquifer. Pumping tests, which are most used to determine the hydraulic conductivity of an aquifer, would be difficult to interpret in this case due to the recharge effect of the Guadalfeo River, which is located just a few meters from both wells. In this case, SBDT is the most appropriate method for its determination because, in principle, all the premises are met to apply the method proposed by [2]. The experiments were repeated under different hydrological conditions to determine the effect on the results obtained and assess the reliability of the parameters obtained.
2. Hydrogeological Context
The Motril–Salobreña aquifer is formed by quaternary-age sediments transported by the Guadalfeo River, which crosses the west sector of the aquifer in the north–south direction (Figure 1). The Guadalfeo is a loser river about 500 m downstream of the study area based on differential gauging experiments but also, as shown by previous studies, using numerical modeling techniques, such as heat [40] or mass [41] transport models. The river flows through a valley carved into a Triassic-age permeable carbonate massif (Escalate carbonate aquifer), which feeds the alluvial fill. Metapelitic materials of low permeability are found under the carbonates and alluvial fill at 10s of meters of depths [42].
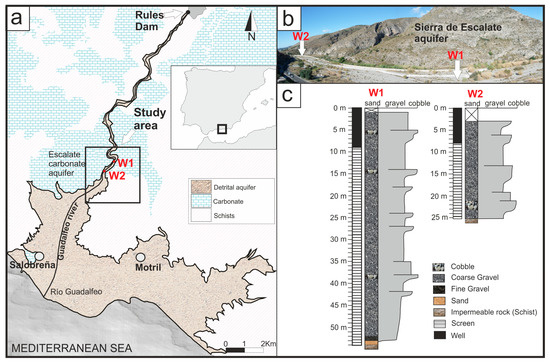
Figure 1.
(a) Location of the Motril–Salobreña aquifer, Rules Dam, and wells. (b) Detailed location of W1 and W2 wells at Guadalfeo´s alluvial. (c) The lithological core of the two wells, W1 and W2.
The Guadalfeo River is regulated by the Rules Dam, which is located 17 km upstream of its mouth. The discharge of the river as it flows through the Motril–Salobreña aquifer mostly depends on the volume of water released at the dam, which ranged between 900 and 170 m3/d when the tests were performed (Figure 2).
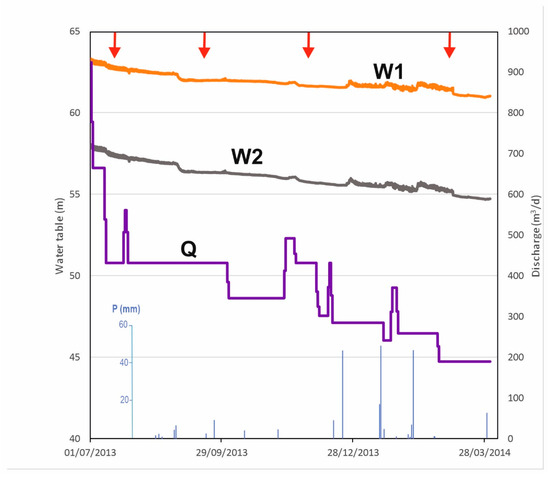
Figure 2.
Water table in the two wells, W1 and W2, the discharge in the Guadalfeo River (Q) downstream Rules Dam, and precipitation in Motril. The red arrows indicate the times when the SBDTs were conducted.
The recharge sources of the aquifer are precipitation, Guadalfeo River infiltration, irrigation return flow, underground inflow from the Escalate carbonate aquifer and underground inflow from the alluvial fill of the Guadalfeo River [42]. This last recharge source has been assessed by different authors, ranging from 25 Mm3/year [43] to 15.5 Mm3/year [44] when applying Darcy’s law. In more recent studies, this input ranged from 3 Mm3/year [45,46] to 4.6 Mm3/year [41]. These large differences between studies indicated the need for a more specific study due to the lack of data necessary for the calculation of the underground flow through this section of the alluvial plain, and particularly the lack of data on hydraulic conductivity.
The tests were performed in two research boreholes located in the alluvial plain of the Guadalfeo River (W1 at 64.49 m a.s.l. and W2 at 61.59 m a.s.l.), just before the fluvio-deltaic plain that forms the main aquifer (Figure 1). W1 is located farther north and has a total depth of 54 m and W2 of 25 m. W1 and W2 are 550 m apart in the direction of the groundwater flow. The lithology logs showed layers of gravel and conglomerates with grain sizes larger than 5 cm and, to a lesser extent, sand levels. Both boreholes cross the entire thickness of the alluvial aquifer until reaching the impermeable substrate (schists and phyllites rocks).
The variation in the water tables measured in W1 and W2 indicated that groundwater recession occurred during the year when the tests were performed (Figure 2). The water level almost continuously dropped 2.3 m in W1 from 63.3 m a.s.l. in July 2013 to 61.0 m a.s.l. in March 2014. The same trend was observed in W2, in which the water level dropped 3.3 m from 58.0 m a.s.l. to 54.7 m a.s.l. on the same dates. Only short episodes of water level rise occurred in January and February 2014, which did not break the trend of a widespread decline. The same dynamics were observed in the discharge of the Guadalfeo River, which decreased during the study period from 900 to 200 m3/d. The hydraulic gradient, however, shows an increasing trend over the period studied, with values of 0.0099 in July 2013, 0.0103 in September 2013, 0.108 in December 2013, and 0.0114 in March 2014. This increase in hydraulic gradient is related to the faster decrease in piezometric level occurring in W1 relative to W2.
3. Materials and Methods
3.1. Single-Borehole Dilution Tests (SBDTs)
3.1.1. Field Procedure
In total, eight SBDTs were completed at four different times in the two wells, W1 and W2 (Figure 1). Both wells were designed with a metal screen throughout the entire hole (except the shallowest 10 m with blank casing) and without a gravel pack surrounding the well since the lithology was mainly gravels and boulders.
Since the diameter of the wells was 350 mm for W1 and 300 mm for W2, it was not possible to use packers to isolate sections, and the test was carried out along the entire depth of the well.
In each test, and before injecting the tracer, the depth of the water table was measured, and the temperature and total dissolved solids (TDSs) were vertically recorded—meter by meter—using a downhole KLL-Q-2-type probe (SEBA Hydrometrie). The probe provides the TDS value via an automatic conversion from the water’s electrical conductivity.
Brine from the Meliones hypersaline spring located in the Málaga province (150 g/L of mainly sodium chloride) was injected using a funnel and a hose with a length according to the depth of each well: 25 m in W1 and 50 m in W2. When the hose was filled (3.5 L in W2 and 8.5 L in W1), it was removed from the well at a constant speed to leave a homogeneous amount of brine throughout the well. Then, 5 or 10 min after injecting the tracer, a new TDS record was started using the same equipment and measuring at the same depths.
The TDS in the groundwater were recorded at every meter of depth over time for 4 or 5 h, until reaching a value as close as possible to the original value of the TDS prior to the injection of the brine. In well W1, five or six vertical TDS profiles were measured in each test, whereas six or seven vertical TDS profiles were measured in W2. Consecutive profiles were measured by slowly lowering the sensor to avoid causing turbulence, leaving it at the bottom of the well during the rest interval, and alternately raising the probe during the second profile to avoid causing excessive changes in the water due to the movement of the sensor inside the well. In total, four dilution tests were performed in each well on 30 July 2013, 27 September 2013, 4 December 2013, and 6 March 2014 to collect a wide range of data under different hydrological conditions (Figure 2).
3.1.2. Hydraulic Conductivity Calculation
Hydraulic conductivity was obtained from Darcy’s law, dividing the Darcy velocity () by the hydraulic gradient (i). To estimate the value of the at each depth of measurement, first the value of the apparent dilution rate () was assessed via least squares fitting the experimental values of the TDS concentration measured throughout the test (disregarding the initial values measured in the first profile before injecting saltwater) to an exponential function derived from Equation (1), as follows:
where t is the time from the beginning of the measurements, V is the dilution volume in the well, A is the cross-section of the dilution volume perpendicular to the direction of the undisturbed groundwater flow (cross-section of the well at its central point), C0 is the tracer concentration at the start of the measurements (immediately after injecting the tracer), and C is the tracer concentration at time t. The A/V ratio is equivalent to 2/πr, and r is the radius of the well where the tracer is injected. The data recorded until the first 10 m of depth were not considered for estimating K because the screen starts at a depth of 10 m.
Considering that in this section of the Motril–Salobreña aquifer, the groundwater flow should, in principle, be mostly horizontal and that the effects of the density convection, the tracer’s molecular diffusion, and the turbulences caused by the measuring sensor on the apparent dilution rate are negligible, the Darcy velocity () in the aquifer is proportional to the apparent dilution rate (), which can be corrected by dividing it by a correction coefficient α according to Equation (3).
Data found in the literature on this subject were used to estimate α. Drost et al. [3] proposed different values for the correction factor, α, depending on the well geometry and hydraulic conductivities. In the absence of a filter pack, the following equation would be used to calculate α:
where is the inside radius of the filter screen, the outside radius of the filter screen, is the hydraulic conductivity of the filter screen, and is the hydraulic conductivity of the aquifer.
The well casing thickness was 3 mm for W1 and W2; therefore, the following conditions could be considered: = ; in addition, the good connection between the well and the aquifer (based on the coarse lithology) allowed for to also be considered equal to , thus obtaining a value of α very close to 2, which is similar to other studies that applied the same correction factor value for similar characteristics of the well–aquifer relation [7,8,9,14,46,47].
At each depth of measurement in W1 and W2, four exponential functions were fitted to the concentration data measured during each dilution test (Figure 3). An average value of was obtained for each depth of measurement in W1 and W2 from the four tests performed. From these values, and from considering the α coefficient and the average hydraulic gradient calculated from the water table measured between W1 and W2 in the four tests, the values of hydraulic conductivity at each depth were calculated.
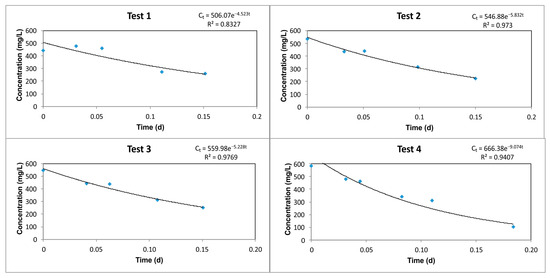
Figure 3.
Exponential function adjusted with concentration versus time in W1 at a 12 m depth.
3.2. Temperature Logs
The predominant groundwater flow pattern in the environment of each well was analyzed with temperature logs recorded at every meter of depth during the SBDTs. The patterns of these logs were analyzed at four different seasons. This distribution provides information on whether the location is a groundwater recharge or discharge zone of the aquifer, which can be applied to gaining or losing rivers [48], or more generally to the presence or not of vertical flows [40,49,50]. Normally, wide elongated profiles refer to recharge areas and compressed ones reveal upward flows in the discharge zones [48].
4. Results
4.1. Concentration Logs
The vertical distribution of the initial TDS in wells W1 and W2 before introducing the tracer (baseline TDS) was homogeneous throughout the column, except for the first few meters of depth (until −10 m in W1 and until −9 m in W2), in which less saline water is usually found, that is related to the presence of a blank casing in the well (Figure 4). There is little variation in the natural salinity of the water from one test to another. Well W1 has 405 mg/L, while well W2 ranges from 312 mg/L in the first test to 414 mg/L in the last test.
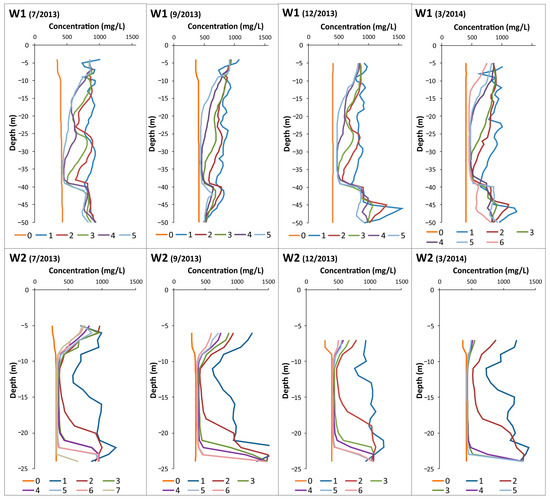
Figure 4.
TDS logs in every SBDT at W1 and W2. Line 0 corresponds to the initial tracer concentration in the groundwater before the tracer injection. The numbers are sequential profiles measured at regular time intervals.
After injecting the brine, the tracer was washed out relatively quick in both cases (after 3 h in W2 and after 4 h in W1, with only 10% and 15% of the tracer left, respectively); the washout rate in W2 was generally higher than that in W1.
The tracer washout was not homogeneous. In W2, the decrease in the tracer concentration was extremely fast from −10 to −20 m, and from the second measurement, the tracer was almost entirely washed out, while in W1, it was a more homogenous process. In W2, in the central area of the well, the tracer concentration gradually decreases; however, in W1, from approximately −40 to −25 m (from −40 to −10 m in March), the salinity peaks are shifted upward from one measurement to the other.
4.2. Darcy Velocity and Hydraulic Conductivity
The calculated values of varied both vertically in the well and between tests (Table 1 and Table 2). Vertical variations in the wells are related to differences in the lithology of the crossed materials, which will increase or decrease the flow. Velocity differences over time are related to the increased or decreased groundwater flow when the test was performed, which will be reflected in the hydraulic gradient values estimated at each time.

Table 1.
Apparent horizontal velocity () and hydraulic conductivity (K) estimated in the four PDTs, and average and calculated K at W1. α is the corrector factor and i is the hydraulic gradient.

Table 2.
Apparent horizontal velocity () and hydraulic conductivity (K) estimated in the four PDTs, and average and calculated K at W2. α is the corrector factor and i is the hydraulic gradient.
At W1 (Table 1, Figure 5), the average values calculated throughout the column varied between 0.7 and 4.4 m/d, with the lowest values between 40 and 44 m depth, where almost no tracer washout was detected (Figure 4). Higher values were found at depths ranging from −17 to −37 m. The varied from one time of the year to another, ranging between 2.2 and 3.1 m/d (mean of 2.6 m/d).
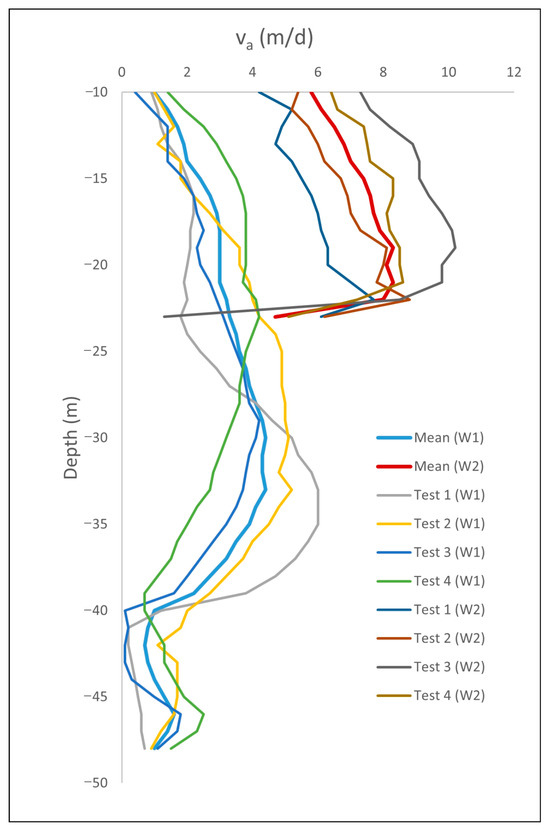
Figure 5.
Average apparent velocity in W1 and W2.
Considerably higher values were recorded in W2 (mean velocity 6.7 m/d), more than twice than in W1 (Table 2, Figure 5). The varied between 4.7 and 8.3 m/d throughout the vertical profile, although the lowest values were found in the deepest part of the well. In the rest of the column, the values were higher. The varies even more than in W1 from one time of year to another, as reflected by the different values calculated in each of the tests, which ranged between 5.4 and 8 m/d.
W2 showed an increasing trend of values estimated during the four tests performed following the same trend as the hydraulic gradients found (Table 1), except for the fourth test, although the differences found both in the hydraulic gradient and the of tests 3 and 4 are very small, so the error of the method can justify the breaking of the trend. This trend cannot be established in W1 where the distribution of values does not follow a defined pattern.
The hydraulic conductivity values estimated from ranged from 47 to 207 m/d throughout the vertical profile (mean value 126 m/d) in W1. However, for W2, the estimated K values are quite higher, ranging from 222 to 391 m/d (mean value 337 m/d). These K values would be in the range corresponding to the clean sands and gravels [51] found in the lithological columns of the drillings. Similarly to the apparent velocity estimated in W1 and W2, the K in W2 is more than double that in W1.
4.3. Temperature Logs
The temperature logs showed a clear difference between W1 and W2 (Figure 6). In W1, the logs have a shallow narrow fringe (only 5 m deep) that varies up to 5 °C in temperature throughout the study period. From −10 m until −25 m, the temperature varies less than 2 °C, and from −30 m on down, the temperature is constant all year round. This type of temperature log has been attributed to the presence of an upward vertical flow that appears in groundwater discharge zones [40,48,49,51]. Considering that in this case, the Guadalfeo River in this sector of the aquifer is not a gaining stream because the river stage was higher than the water table measured in W1, groundwater upward flow inside the well without discharge to the river could explain the pattern. However, in W2, the temperature variation is recorded throughout the entire depth of the well. The thermal oscillation throughout the study period is up to 7 °C higher than in W1, and the shape of the logs indicated the absence of vertical upward flow.
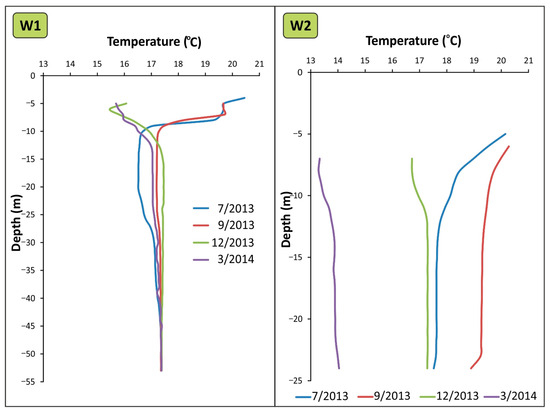
Figure 6.
Groundwater temperature logs in W1 and W2.
5. Discussion
The application of SBDT and temperature logs has showed the differences in the hydrogeological behavior between the two wells located in the north–western sector of the Motril–Salobreña aquifer, even though they are only 550 m apart. The initial logs (without tracer effects) already indicate a much more uniform behavior in W1 than in W2. In W2, the conductivity values varied over time, showing a more dynamic groundwater flow. However, this effect is not observed in W1, where the groundwater salinity remained constant.
The temperature logs also highlighted a different flow pattern between the two wells. In W1, the water temperature throughout the column is homogeneous along the time, except for the first 5 meters, indicating the presence of an upward vertical flow. However, in W2, the temperature varies widely throughout the water column over time, indicating the absence of these upward vertical flows.
The application of SBDT requires the absence of vertical flows or, at least, a clear predominance of horizontal flow over vertical flow. In the case of W1, the possibility of vertical upward flows was initially unknown, which was later revealed by the temperature logs and the tracer washout patterns. The relative importance of these vertical flows in relation to the horizontal flows would be needed to assess whether they significantly affect the washout of the injected tracer during the tests and the reliability of the obtained results. The shapes of the washout curves in W1 (Figure 7) showed that the concentration curves’ peaks shifted upward; but in W2 (Figure 8), the successive tracer concentration curves gradually decrease, maintaining the shape of the curves, which indicates a cross-flow (flow that enters and exits the well horizontally). Both the temperature logs and the concentration curves indicated that W2 would be suitable to conduct SBDT while W1 was affected by vertical flow, preventing the use of this technique to measure hydraulic conductivity and groundwater flow. Nevertheless, for both W1 and W2, the tracer is quickly and almost completely washed out, thereby confirming that the horizontal flow prevails in both cases.
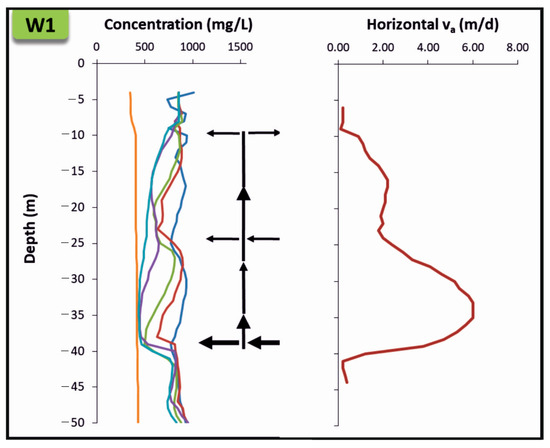
Figure 7.
Comparative results of the concentration logs for the SBDT (July 2013) and the apparent horizontal velocity (July 2013) at W1. Black arrows indicate the magnitude and direction of the flow in the well according to the model proposed by Maurice et al. [38].
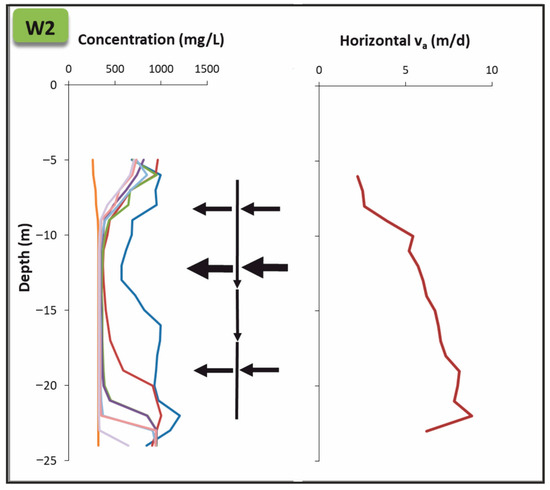
Figure 8.
Comparative results of the concentration logs for the SBDT (September 2013), the vertical flow, and the apparent horizontal velocity (September 2013). Black arrows indicate the magnitude and direction of the flow in the well according to the model proposed by Maurice et al. [38].
According to previous studies on vertical flows [38], the following conclusions can be inferred in W1: a cross-flow is present at −40 m, which causes a nick-point or step in the concentration curves where the lowest are recorded; another weaker cross-flow is found at −25 m, which is not detectable in all tests, and an outflow is present at −10 m. These supposed water inflows and their subsequent upward displacements are consistent with the information provided by the temperature logs, which reveals the existence of vertical upward flows (Figure 7).
The upward vertical flow in W1 would explain why the estimated values of the apparent velocity and hydraulic conductivity are significantly lower in W1 (about one-fifth lower than those in W2), although the lithological columns are very similar. Accordingly, the limited correlation found between the apparent velocities estimated in W1 and the measured hydraulic gradient values indicates the existence of other factors, in this case, the vertical upward flow, that affected to the horizontal velocity estimation in W1.
In W2 (Figure 8), the fast tracer washout in almost the entire column of the well, generated horizontal apparent velocities higher than 5 m/d at a depth of 10 m. In this location the horizontal apparent velocities show a higher correlation with the hydraulic gradient (Table 1) than in the previous case, in line with conditions under which horizontal flows prevail.
In W2, the values of varied up to 25% depending on the time at which the test was carried out, from which it follows that it is convenient to carry out tests at various times to obtain an average value that compensates for seasonal variations.
From a practical perspective, the temperature logs have been useful as indicators of the suitability of the SDBT in an area where, in principle, a vertical upward flow is not expected. This has implications for the management of the water resources in Motril–Salobreña aquifer as this allowed for prioritizing the groundwater flow and hydraulic conductivity obtained in W2 over W1. During the completion of SBDT, it is possible to monitor temperature without any additional cost as often, the measuring devices of salinity measure also temperature, a simple procedure as elaborating temperature logs would a system to determine the presence of vertical flows that can generate errors in the interpretation and calculation of the results.
6. Conclusions
The use of single-borehole dilution tests is a common tool for the quantification of groundwater flow and hydraulic properties. As it is a practical tool, they are often conducted under variable hydrological conditions that can affect the interpretation and validity of the results. The analysis of eight SBDTs in two wells located in the north sector of the Motril–Salobreña aquifer made it possible to discuss the implication of using different sets of data for estimating the value of the hydraulic conductivity, and assess the influence of the hydrological situation on the obtained results.
The different tracer washing patterns found in the two wells indicated hydrodynamic differences in both cases. In W1, the variation in the concentration profiles with an upward shift in the peaks indicated potentially the presence of upward vertical flows; however, in W2, the gradual decrease in the concentration with no vertical shift in the TDS maxima from one log to another shows the predominance of horizontal flow. The temperature logs confirmed the differences in the behaviors of the two wells. These results highlight the potential of using temperature logs as quick and easy to obtain indicators of the suitability of conducting SBDTs when there is no available information about the flow pattern in the region to be studied.
The apparent velocities estimated in W2 are higher (6.7 m/d, mean value of all depths in the four tests) than those estimated in W1 (2.6 m/d, mean value of all depths in the four tests). Consequently, the calculated values of the hydraulic conductivity are also much higher in W2, over two-fold higher (337 m/d, mean value of all depths in the four tests) than those in W1 (126 m/d, mean value of all depths in the four tests). Because the upward vertical flows of W1 alter the tracer dilution rate, the K estimated in W2, at 337 m/d, was considered the most accurate value for this area of the Motril–Salobreña aquifer.
Because the estimated K values vary up to 25% depending on the time of the test and, therefore, the hydrological situation, it is recommended when applying this technique to carry out several tests under different hydrogeological conditions to compensate for the seasonal variations.
Author Contributions
Conceptualization: M.L.C., M.L.-C., B.D.L.T. and C.D.; Methodology: M.L.C., M.L.-C., B.D.L.T., A.M.B.-C. and C.D.; Formal Analysis: M.L.C., M.L.-C. and C.D.; Investigation: M.L.C., M.L.-C., B.D.L.T., A.M.B.-C. and C.D.; Resources: M.L.C., M.L.-C. and C.D.; Writing—original draft preparation: M.L.C. and C.D.; Writing—review and editing: M.L.C., M.L.-C., B.D.L.T., A.M.B.-C. and C.D.; Visualization: M.L.C., A.M.B.-C. and C.D.; Supervision: M.L.C., M.L.-C. and C.D.; Project Administration: M.L.C., M.L.-C. and C.D.; Funding Acquisition: M.L.C., M.L.-C. and C.D. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by project CGL2016-77503-R, which was funded by the Ministerio de Economía y Competitividad (Government of Spain) with FEDER funds of the European Union, by the research group RNM-369 of Junta de Andalucía and by Marie Curie International Outgoing Fellowship under grant agreement (624496) and the Next-Generation EU funding Programa María Zambrano Sénior (REF: MZSA03). This study has also been supported by grant PCM_00018 funded by Consejería de Universidad, Investigación e Innovación and Gobierno de España and Unión Europea—NextGenerationEU, the grants PID2022-137711OB-I00 and PCI2024-153503 funded by MICIU/AEI/10.13039/501100011033 and co-financed by EU.
Data Availability Statement
No new data were created.
Acknowledgments
We thank Sánchez-Úbeda, Pulido-Bosch and Ángel Perandrés for participating in the field work.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Correction Statement
This article has been republished with a minor correction to the Funding statement. This change does not affect the scientific content of the article.
References
- Ogilvi, N.A. Electrolytic method for determination of the ground water filtration velocity. Bull. Sci. Technol. News 1958, 4, 23–44. (In Russian) [Google Scholar]
- Halevy, E.; Moser, H.; Zellhofer, O.; Zuber, A. Borehole dilution techniques: A critical review. In Proceedings of the Symposium on Isotopes in Hydrology; IAEA: Vienna, Austria, 1967; pp. 531–564. [Google Scholar]
- Drost, W.; Klotz, D.; Koch, A.; Moser, H.; Neumaier, F.; Rauert, W. Point dilution methods of investigating ground water flow by means of radioisotopes. Water Resour. Res. 1968, 4, 125–146. [Google Scholar] [CrossRef]
- Grisak, G.E.; Merrit, W.F.; Williams, D.W. Fluoride borehole dilution apparatus for groundwater velocity measurements. Canadian Geotech. J. 1977, 14, 554–561. [Google Scholar] [CrossRef]
- Klotz, D.; Moser, H.; Trimborn, P. Single borehole techniques: Present status and examples of recent applications. In Proceedings of the Symposium on Isotopes in Hydrology; IAEA: Vienna, Austria, 1978; pp. 159–175. [Google Scholar]
- Lewis, D.C.; Kritz, G.J.; Burgy, R.H. Tracer dilution sampling technique to determine hydraulic conductivity of fractured rock. Water Resour. Res. 1966, 2, 533–542. [Google Scholar] [CrossRef]
- Michalski, A. Conductive slug tracing as a single-well test technique for heterogeneous and fractured formations. In Proceedings of the Conference on New Field Techniques for Quantifying the Physical and Chemical Properties, Dallas, TX, USA, 20–23 March 1989; pp. 247–263. [Google Scholar]
- Sottani, A.; Del Prà, A. Groundwater velocity measurements with the single point dilution method (SPDM) in a sample site of the High Venetian Plain (Galliera V.–northern Italy). In Proceedings of International Meeting of Young Researchers in Applied Geology; Politecnico di Torino: Turin, Italy, 1995. [Google Scholar]
- Pitrak, M.; Mares, S.; Kobr, M. A simple borehole dilution technique in measuring horizontal ground water flow. Ground Water 2007, 45, 89–92. [Google Scholar] [CrossRef] [PubMed]
- Williams, A.; Bloomfield, J.; Griffiths, K.; Butler, A. Characterising the vertical variations in hydraulic conductivity within the Chalk aquifer. J. Hydrol. 2006, 330, 53–62. [Google Scholar] [CrossRef]
- Bernstein, A.; Adar, E.; Yakirevich, A.; Nativ, R. Dilution tests in a low-permeability fractured aquifer: Matrix diffusion effect. Ground Water 2007, 45, 235–241. [Google Scholar] [CrossRef] [PubMed]
- Piccinini, L.; Fabbri, P.; Pola, M. Point dilution tests to calculate groundwater velocity: An example in a porous aquifer in northeast Italy. Hydrol. Sci. J. 2016, 61, 1512–1523. [Google Scholar] [CrossRef]
- Newcomer, D.R.; Hall, S.H.; Vermeul, V.R. Use of improved hydrologic testing and borehole geophysical logging methods for aquifer characterization. Winter 1996, 16, 67–72. [Google Scholar] [CrossRef]
- Rollinson, J.; Rees-White, T.; Beaven, R.B.; Barker, J.A. A single borehole dilution technique to measure the hydrogeological properties of a saturated landfilled waste. In Proceedings of the Waste 2010, Stratford-upon-Avon, UK, 27–28 September 2010. [Google Scholar]
- Maldaner, C.H.; Quinn, P.M.; Cherry, J.A.; Parker, B.L. Improving estimates of groundwater velocity in a fractured rock borehole using hydraulic and tracer dilution methods. J. Contam. Hydrol. 2018, 214, 75–86. [Google Scholar] [CrossRef]
- Fujinawa, K. Asymptotic solutions to the convection-dispersion equation and Powell’s optimization method for evaluating groundwater velocity and dispersion coefficients from observed data of single dilution tests. J. Hydrol. 1983, 62, 333–353. [Google Scholar] [CrossRef]
- Canul-Macario, C.; González-Herrera, R.; Sánchez-Pinto, I.; Graniel-Castro, E. Contribution to the evaluation of soute transport properties in a karstic aquifer (Yucatan, Mexico). Hydrogeol. J. 2019, 27, 1683–1691. [Google Scholar] [CrossRef]
- Doummar, J.; Margane, A.; Geyer, T.; Sauter, M. Monitoring transient groundwater fluxes using the Finite Volume Point Dilution Method. J. Contam. Hydrol. 2018, 218, 10–18. [Google Scholar]
- Gustafsson, E.; Andersson, P. Groundwater flow conditions in a low-angle fracture zone at Finnsjön, Sweden. J. Hydrol. 1991, 126, 79–111. [Google Scholar] [CrossRef]
- Gutiérrez, M.G.; Guimerà, J.; Yllera de Llano, A.; Hernández-Benitez, A.; Humm, J.; Saltink, M. Tracer test at El Berrocal site. J. Contam. Hydrol. 1997, 26, 179–188. [Google Scholar] [CrossRef]
- Sanford, W.E.; Moore, G.K. Measurement of specific discharge with point-dilution tests in the fractured rocks of Eastern Tennessee. In Proceedings of Extended Abstracts, American Water Resources Association 1994 Annual Spring Symposium in Nashville, Tennessee; A.A. Balkema Publishers: Cape Town, South Africa, 1994; pp. 449–453. [Google Scholar]
- Jardine, P.M.; Sanford, W.E.; Gwo, J.P.; Reedy, O.C.; Hicks, C.S.; Riggs, J.S.; Bailey, W.B. Quantifying diffusive mass transfer in fractured shale bedrock. Water Resour. Res. 1999, 35, 2015–2030. [Google Scholar] [CrossRef]
- Novakowski, K.S.; Lapcevic, P.A.; Voralek, J.; Bickerton, G. Preliminary interpretation of tracer experiments conducted in a discrete rock fracture under conditions of natural flow. Geophys. Res. Lett. 1995, 22, 1417–1420. [Google Scholar] [CrossRef]
- Moore, Y.H.; Stoesell, R.K.; Easley, D.H. Fresh-water/ sea-water relationship within a ground-water flow system, northern coast of the Yucatan Peninsula. Ground Water 1992, 30, 343–350. [Google Scholar] [CrossRef]
- Novakowski, K.; Bickerton, G.; Lapcevic, P.; Voralek, J.; Ross, N. Measurements of groundwater velocity in discrete rock fractures. J. Contam. Hydrol. 2006, 82, 44–60. [Google Scholar] [CrossRef]
- Riemann, K.; Van Tonder, G.; Dzanga, P. Interpretation of single-well tracer tests using fractional-flow dimensions. Part 2: A case study. Hydrogeol. J. 2002, 10, 357–367. [Google Scholar] [CrossRef]
- Hall, S.H. Single well tracer tests in aquifer characterization. Ground Water Monitor. Remed. 1993, 13, 118–124. [Google Scholar] [CrossRef]
- Ronen, D.; Magaritz, M.; Paldor, N.; Bachmat, Y. The behaviour of groundwater in the vicinity of the water table evidenced by specific discharge profiles. Water Resour. Res. 1986, 22, 1217–1224. [Google Scholar] [CrossRef]
- Ronen, D.; Magaritz, M.; Molz, F.J. Comparison between natural and forced gradient tests to determine the vertical distribution of horizontal transport properties of aquifers. Water Resour. Res. 1991, 27, 1309–1314. [Google Scholar] [CrossRef]
- Ronen, D.; Berkowitz, B.; Magaritz, M. Vertical heterogeneity in horizontal components of specific discharge: Case study analysis. Ground Water 1993, 31, 33–40. [Google Scholar] [CrossRef]
- Wurzel, P. Updated radioisotope studies in Zimbabwean ground waters. Ground Water 1983, 21, 597–605. [Google Scholar] [CrossRef]
- Flynn, R.M.; Schnegg, P.A.; Costa, R.; Mallen, G.; Zwahlen, F. Identification of zones of preferential groundwater tracer transport using a mobile downhole fluorometer. Hydrogeol. J. 2005, 13, 366–377. [Google Scholar] [CrossRef]
- Hatfield, K.; Annable, M.; Cho, J.; Raom, P.S.C.; Klammler, H. A direct passive method for measuring water and contaminant fluxes in porous media. J. Contam. Hydrol. 2004, 75, 155–181. [Google Scholar] [CrossRef] [PubMed]
- West, L.J.; Odling, N.E. Characterization of a multilayer aquifer using open well dilution tests. Ground Water 2007, 45, 74–84. [Google Scholar] [CrossRef]
- Shafer, J.M.; Brantley, D.T.; Waddell, M.G. Variable-density flow and transport simulation of wellbore brine displacement. Ground Water 2010, 48, 122–130. [Google Scholar] [CrossRef]
- Tsang, C.F.; Hufschmied, P.; Hale, F.V. Determination of fracture inflow parameters with a borehole fluid conductivity logging method. Water Resour. Res. 1990, 26, 561–578. [Google Scholar] [CrossRef]
- Paillet, F.L.; Pedler, W.H. Integrated borehole logging methods for wellhead protection applications. Eng. Geol. 1996, 42, 155–165. [Google Scholar] [CrossRef]
- Maurice, L.; Barker, J.A.; Atkinson, T.C.; Williams, A.T.; Smart, P.L. A tracer methodology for identifying ambient flows in boreholes. Ground Water 2011, 49, 227–238. [Google Scholar] [CrossRef] [PubMed]
- Benavente, J.; Cardenal, J.; Cruz San Julián, J.J. Exploitation effects in the Guadalfeo alluvial aquifer (Escalate Canyon area, Granada, Southeastern Spain). In Proceedings of the XXIII Conference A.I.H “Aquifer Overexploitation” (Puerto de la Cruz), Canary Islands, Spain, April 1991; pp. 499–502. [Google Scholar]
- Duque, C.; Calvache, M.L.; Engesgaard, P. Investigating river-aquifer relations using water temperature in an anthropized environment (Motril-Salobreña aquifer). J. Hydrol. 2010, 381, 121–133. [Google Scholar] [CrossRef]
- Calvache, M.L.; Ibáñez, P.; Duque, C.; López-Chicano, M.; Martín-Rosales, W.; González-Ramón, A.; Rubio, J.C.; Viseras, C. Numerical modelling of the potential effects of a dam on a coastal aquifer in S. Spain. Hydrol. Process. 2009, 23, 1268–1281. [Google Scholar] [CrossRef]
- Duque, C.; Calvache, M.L.; Pedrera, A.; Martín-Rosales, W.; López-Chicano, M. Combined time domain electromagnetic soundings and gravimetry to determine marine intrusion in a detrital coastal aquifer (Southern Spain). J. Hydrol. 2008, 349, 536–547. [Google Scholar] [CrossRef]
- CHSE-IRYDA. Estudio de Viabilidad de la Ampliación de la Zona Regable de Motril-Salobreña Hasta la Cota 300, Unpublished. 1984.
- ITGE. Investigación Hidrogeológica para Apoyo a la Gestión Hidrológica en la Cuenca del río Guadalfeo (Cuenca Sur de España, Granada), 1988.
- García-Aróstegui, J.L.; Heredia, J.; Murillo, J.M.; Rubio Campos, J.C.; González-Ramón, A.; López-Geta, J.A. Contribución desde la modelización del flujo subterráneo al conocimiento del acuífero del río Verde (Granada. Proceedings of V Simposio sobre el agua en Andalucía, IGME, Almería 2001.
- Gaspar, E. Modern Trends in Tracer Hydrology; CRC Press: Boca Raton, FL, USA, 1987; Volume II. [Google Scholar]
- Cook, P.G.; Dighton, J.C. Inferring ground water flow in fractured rock from dissolved radon. Ground Water 1999, 37, 606–610. [Google Scholar] [CrossRef]
- Taniguchi, M.; Sharma, M.L. Determination of groundwater recharge using the change in soil temperature. J. Hydrol. 1993, 148, 219–229. [Google Scholar] [CrossRef]
- Calvache, M.L.; Duque, C.; Gomez-Fontalva, J.M.; Crespo, F. Processes affecting groundwater temperature patterns in a coastal aquifer. Int. J. Environ. Technol. 2011, 8, 223–236. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice Hall: Hoboken, NJ, USA, 1979. [Google Scholar]
- Taniguchi, M.; Sharma, M.L. Solute and heat transport experiments for estimating recharge rate. J. Hydrol. 1990, 119, 57–69. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).