Abstract
Climate change and human activities exert significant impact on the mechanism of runoff generation and confluence. Comprehending the reasons of runoff change is crucial for the sustainable development of water resources. Taking the Upper Shule River as the research area, the M-K test and the moving t test were used to diagnose the runoff mutation time. Furthermore, the slope changing ratio of cumulative quantity method (SCRCQ), climate elasticity method, and Budyko equation were utilized to quantitatively evaluate the impacts and contribution rates of climate change and human activities. The following results were obtained: (1) The Upper Shule River experienced a significant increase in runoff from 1972 to 2021, with 1998 marking the year of abrupt change. (2) The runoff sensitivity showed a downward trend from 1972 to 2021. The main factor affecting the decrease in runoff sensitivity was the characteristic parameters of underlying surface (n), followed by precipitation (P), while the influence of potential evapotranspiration (ET0) was the weakest. (3) The response of runoff changes to runoff sensitivity and influencing factors were 90.32% and 9.68%, respectively. (4) The results of three attribution methods indicated that climate change was the primary factor causing the alteration of runoff in the Upper Shule River. The research results supplement the hydrological change mechanisms of the Upper Shule River and provide a scientific basis for future water resources management and flood control measures.
1. Introduction
Precipitation and evapotranspiration, as main factors of the climate change, have caused profound influence on runoff depth, peak and duration [1,2,3]. Human activities can significantly impact the mechanism of runoff generation [4]. For instance, changes in land use, reservoir construction, and reforestation can cause alterations in runoff [5]. The literature reports that precipitation is the dominant factor on runoff changes in the Yangtze River, Margalla Hills River, and Pearl River, whereas human activities are the cause of runoff changes in the Liaohe River, Haihe River, Yellow River, Songhuajiang River, and Huaihe River [6,7,8]. Thus, the influencing mechanism of runoff change is different for each river. Significant changes in runoff may increase frequency of extreme droughts and floods [9], posing significant challenges to water resource management and flood mitigation. Therefore, identifying the mechanisms of runoff changes is crucial to optimize the management of regional water resources and measures for flood prevention and mitigation.
The scientific understanding of the mechanisms of runoff changes is an important issue that hydrologists are working on. Up to now, the runoff attribution analysis methods can be broadly categorized as hydrological models, statistical analysis methods, and conceptual methods [10]. Statistical analysis methods represented by the double-mass curve method and the slope changing ratio of cumulative quantity (SCRCQ) method are simple in calculation and require less data, but they lack a physical mechanism and cannot adequately simulate changes in hydrological processes [11]. Hydrological models represented by the soil and water assessment tool (SWAT) and the variable infiltration capacity (VIC) have strong physical mechanisms and high analytical accuracy. However, the data needs to be very accurate, and the process of calibrating is also very complicated [12,13]. Conceptual methods represented by the Budyko equation have advantages of both hydrological models and statistical analysis methods. The Budyko equation is the most popular method for conducting runoff change attribution analysis [14,15,16]. Compared with hydrological models and statistical analysis methods, the Budyko equation is easy to implement with low data requirements, and its structure can effectively reduce model sensitivity and uncertainty [17,18].
Runoff in the Upper Shule River has changed dramatically as the environment has changed [19,20,21], which has had a negative impact on the development of oasis agriculture in the middle and lower reaches [22]. Previous studies on the causes of runoff change in the upper Shule River have focused mainly on runoff composition and meteorological factors [23,24,25]. For example, He et al. [26] divided data from 1960–2012 into two research periods with 1997 as the break point and used the Budyko equation to carry out a response analysis of runoff variation in the Upper Shule River. The results indicated equal impacts of precipitation (P) and the characteristic parameters of underlying surface change (n) on runoff change. Wei et al. [27] analysed the impacts of LULC (land use changes) and climate change on water yield from 2001 to 2019 in the upstream regions of the Shule River Basin using the Integrated Valuation of Ecosystem Services and Tradeoffs (InVEST) model. The results revealed that climate warming has a positive impact on water yield. Apparently, the impacts of climate change and human activities on runoff change in the Upper Shule River are still unclear. Thus, exploring the main influencing factors of runoff change in the Upper Shule River using a rational method is urgent.
In summary, domestic and foreign scholars have conducted various forms of research on runoff and have achieved certain research results in terms of the variation characteristics, influencing factors, and research methods of runoff. However, studies on runoff drivers are mainly focused on the identification results of the runoff change attribution directly based on a single method, which is uncertain. Furthermore, the previous studies mainly reveal the impact of influencing factors on runoff change and lack attention to runoff sensitivity change and its influence on runoff change, especially in the Shule River Basin, which has experienced a severe water shortage. Although the existing research has preliminarily understood the evolution law of runoff, the mechanism of runoff change still needs to be further explored. Thus, the objectives of this study are (1) to detect the mutation time of runoff change by using Mann–Kendall (M-K) test and the moving t test; (2) to examine runoff sensitivity change and determine runoff sensitivity contributions to runoff variation based on the improved Budyko equation; and (3) to identify the impacts of driving forces on runoff change based on the SCRCQ method, climate elasticity method, and Budyko equation. The results of this study are expected to provide a comprehensive understanding of the process of runoff variation in the Upper Shule River and provide a reference for determining the driving forces of runoff change in areas lacking data.
2. Materials and Methods
2.1. Study Area
The Shule River is located in the arid inland regions of northwest China and Qinghai-Tibet Plateau (92°11′–98°30′ E, 38°00′–42°48′ N), with a standard continental drought climate [28,29]. The area of the Shule River Basin is 4.13 × 104 km2, which is the second largest river in the Hexi Corridor of Gansu Province. The main sources of recharge in the Shule River basin are seasonal snow, glacial meltwater, and rainfall, with large seasonal and interannual changes, and more than half of the annual water volume comes from the flood season [19]. Water resources in the Shule River Basin mainly originate from the Qilian Mountain area, and the change in runoff in the upper reaches directly influence the exploitation and utilization of water resources in the middle and lower reaches. Therefore, the area above the Changmabao hydrological station (96°51′ E, 39°49′ N), which covers 10,961 km2, was selected as the study area (Figure 1). The permafrost cover is 83% and the glacier area is 5% of the catchment area [30]. The main vegetation types in the Upper Shule River are alpine meadows, alpine grasslands, and desert grasslands, and the vegetation coverage is generally 40–80% [31,32]. Furthermore, dominated by the typical continental arid climate, the Upper Shule River is a typical water-shortage area with mean annual precipitation is 209.2 mm, annual mean temperature of about 1.73 °C, and potential evapotranspiration of up to 400 mm per year.
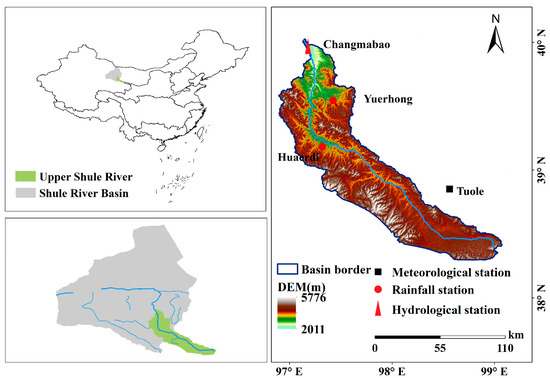
Figure 1.
Location of the Upper Shule River and hydrological station river network.
2.2. Data Sources
In this study, hydro-meteorological data from 1972 to 2021, including monthly and annual precipitation time series, mean temperature, potential evapotranspiration, and runoff, were analysed. Monthly runoff, precipitation, and temperature data series during 1972–2021 from the Changmabao hydrological station and Yuerhong rainfall station were collected from the Gansu Hydrological Station. Notably, the collected precipitation data included rainfall and snowfall. All the original runoff data used in this paper are complete. The land use data, spatial distribution of population data and daily data from the Tuole meteorological station were obtained from the Data Center for Resources and Environmental Sciences, Chinese Academy of Sciences (https://www.resdc.cn/ (accessed on 12 October 2022)). The quality of the meteorological data was firmly controlled before its release. The missing data accounted for less than 1% of the total data and were processed using the 10–year moving average method. Potential evapotranspiration was calculated via the Thornthwaite method [33]. The methodological framework of this research is shown in Figure 2.
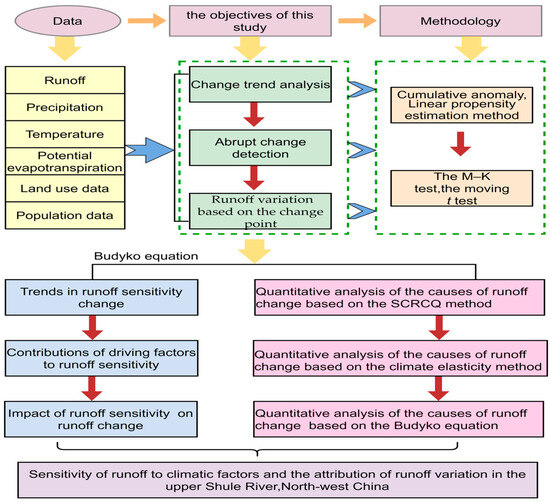
Figure 2.
The methodological framework of this research.
2.3. Methods
2.3.1. Diagnosis of Mutation Time
The M-K test is broadly applied in trend analysis and mutation test of hydrological elements [34]. A trend is determined based on the range of values (Z) for a trend test. The Z is calculated as follows:
represents an upward trend; otherwise, represents a downward trend. When , the significance level is greater than 95% [35]. In the mutation analysis, the statistical values and are determined by the time series. If and both vary within the confidence interval of , the intersection of the two statistical values is the mutation time. The statistical index is calculated based on the following equation:
The test statistics , , and are calculated using the following formulas:
is the backwards sequence and is calculated like with an inverse time series.
Runoff has complex characteristics, such as nonlinearity and randomness, which lead to uncertainty in determining the abrupt change time when based on only one method. Therefore, the moving t test was used as an auxiliary method to detect the year of abrupt change in runoff [36].
2.3.2. Methods of Runoff Variation Attribution Analysis
- (1)
- Budyko equation
When using the Budyko equation for the attribution analysis of runoff change, in addition to precipitation (P), potential evapotranspiration (ET0), and the characteristic parameters of underlying surface change (n), the sensitivity of runoff to P, ET0, and n (runoff sensitivity) are also related to runoff change. In this study, the runoff responses to P, ET0, and n were considered direct effects of drivers on runoff change, and the responses of runoff sensitivity (, , ) to runoff change were considered as the indirect effects of drivers. Focusing on the changes in runoff sensitivity, the improved Budyko formula was used to further understand the mechanism of runoff change from the direct and indirect effects of influencing factors.
- Budyko equation
In this paper, the Budyko equation is used to analyse the mechanism of runoff change [37,38]. The expression obtained by combining the water balance equation is given as follows:
where ∆S is the change in water storage, and this study assumed that ; n is the characteristic parameters of underlying surface, which was calculated by Equation (7).
- b.
- Sensitivity equations
- c.
- Influence analysis of P, ET0, and n on runoff sensitivity
The influences of P, ET0, and n on are expressed as follows:
where , , and are the changes in caused by P, ET0, and n, respectively.
Then, contributions of P, ET0, and n to are expressed as follows:
where , , and are the influences of P, ET0, and n, respectively, on .
By repeating the steps in (c), ,, , , , can be estimated (Equations (11)–(13)). Then, , , , , can also be estimated (Equations (14)–(16)).
- d.
- Calculation of the runoff response to P, ET0 and n
The runoff change caused by each factor is expressed as follows:
Then, the variation in runoff directly caused by driving factors is expressed as follows:
- e.
- Calculation of , and contributions to runoff change
From Equation (17), the runoff changes caused by , and are expressed as follows:
Then, the contributions of runoff sensitivity (indirect effects) and driving factors (direct effects) to runoff change are as follows:
where and are the influences of runoff sensitivity and driving factors on runoff change, respectively.
- (2)
- The slope changing ratio of cumulative quantity (SCRCQ) method
For the SCRCQ method [39,40], the sum of the degree of influence from all contributors that cause changes in runoff is one. Therefore, according to the ratio of the cumulative slope change rate of each contributor to the cumulative slope change rate of runoff, the impact of each contributor on runoff change can be determined. At present, many scholars use this method to identify the reasons for runoff change [41,42]. The equations are as follows:
The impact of human activities is expressed as follows:
where , , and are the slopes of the cumulative R, P, and ET0 before and after the mutation, respectively. , , and are the influences of P, ET0, and n, respectively, on runoff change.
- (3)
- Climate elasticity method
The climate elasticity method mainly reflects the sensitivity of runoff to climate change through the climate elasticity coefficient [43,44]. Combining the Budyko equation and the water balance equation, the actual evapotranspiration of the basin is a function of the drying index (). The following equations are used to calculate the elasticity coefficients:
where is the actual evapotranspiration function.
Then, runoff change caused by climate change is calculated as follows:
The corresponding contributions are expressed as follows:
where , and are the variations in R, P, and ET0, respectively, between the baseline and post-baseline periods.
3. Results
3.1. Runoff Change in the Upper Shule River from 1972 to 2021
3.1.1. Temporal Variation of Runoff Depth
The annual average runoff depth was 101.0 mm, and the Cv (coefficient of variation) was 0.29. The maximum annual runoff depth was 159.1 mm, which occurred in 2017. The minimum annual runoff depth was 54.5 mm, which occurred in 1976. The annual runoff depth passed the 0.05 significance test based on the M-K test, with an overall significant increase at a rate of 14.29 mm/10a (Figure 3a). Before 1998, the cumulative anomaly of the annual average runoff showed a decreasing trend. After 1998, the cumulative anomaly of the annual average runoff showed an increasing trend (Figure 3b). The results showed that the annual runoff depth of the Upper Shule River may have changed in 1998.
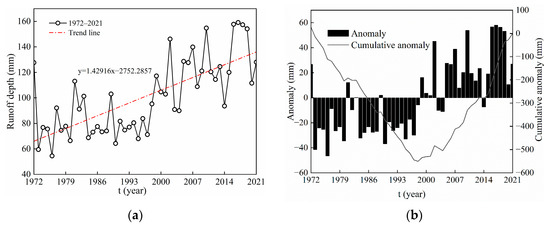
Figure 3.
Temporal variation in annual runoff from 1972 to 2021 in the Upper Shule River. (a) Trend analysis of runoff change by linear tendency estimate method. (b) Trend analysis of runoff change by cumulative anomaly method.
3.1.2. Breakpoint of Runoff
Figure 4 shows mutation analysis of annual runoff depth based on the two methods. According to the M-K test (Figure 4a), the intersections between UF and UB were within the 95% confidence interval, indicating that 1998 was the variation time of annual runoff depth. According to the moving t test (Figure 4b), the study area had a significant breaking point from the 1990s to 2010s. Therefore, the mutation of the runoff depth occurred in 1998 in the Upper Shule River from 1972 to 2021, which may be related to global warming in the late 1990s.
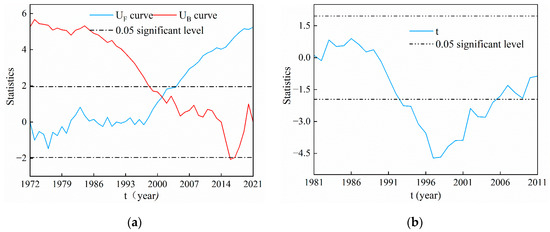
Figure 4.
Detection of mutations of annual runoff depth in the Upper Shule River from 1972 to 2021. (a) Abrupt change time determined by the M-K test; (b) Abrupt change time determined by the moving t test.
3.1.3. Variations in the Annual Runoff Depth Based on the Change Point
The annual runoff depth from 1972 to 2021 was divided into two stages based on the change point: 1972 to 1998 (baseline period) and 1999 to 2021 (post-baseline period). As shown in Figure 5, there was a difference in the annual runoff depth change between the two periods. In the baseline period, the annual runoff depth showed a decreasing trend, while in the post-baseline period, the annual runoff depth showed an increasing trend. The annual mean runoff depth in the post-baseline period was 44.4 mm, which is greater than the annual mean runoff depth in the baseline period.
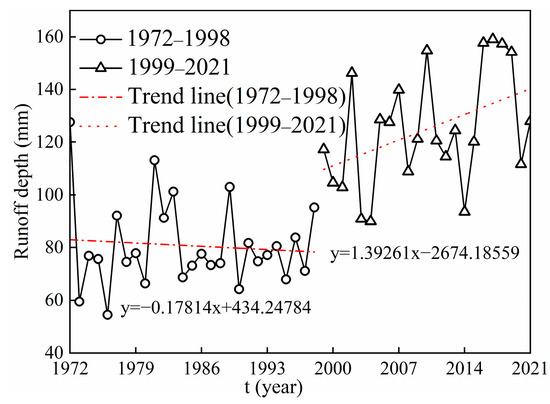
Figure 5.
Variations in the annual runoff depth based on the change point in the Upper Shule River.
3.2. Impact of Runoff Sensitivity to Climate Change and Human Activities (Runoff Sensitivity) on Runoff Change
3.2.1. Runoff Sensitivity Change Trend and Attribution Analysis in the Upper Shule River from 1972 to 2021
The improved Budyko equation was used to calculate runoff sensitivity (, , ). As shown in Table 1, , , and decreased slowly, with change rates of −0.0044/yr, −0.0044/yr, and −0.0031/yr, respectively, and values ranging from 2.12 to 2.46, 1.12 to 1.46, and 0.37 to 0.59, respectively. Figure 6 shows the effects of P, ET0, and n on the changes in runoff sensitivity (, , ). The main contributor to runoff sensitivity was n, followed by P and then ET0. Notably, P, ET0, and n had approximately the same effects on , , and , respectively. Additionally, , so that the effects of P, ET0, and n had the same effect on .

Table 1.
Runoff sensitivity to precipitation (), potential evapotranspiration (), and characteristic parameters of underlying surface change () in the Upper Shule River between 1972 and 2021.
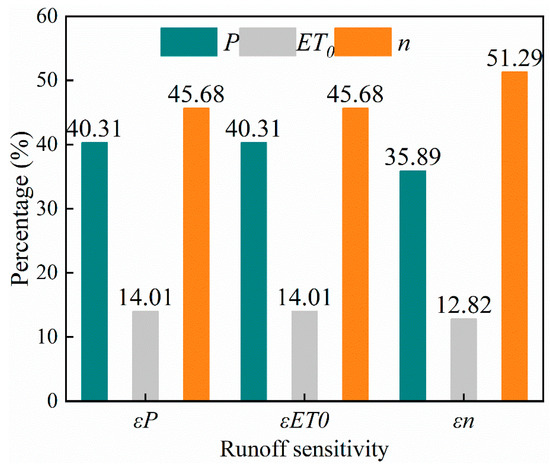
Figure 6.
Contributions of precipitation (P), potential evapotranspiration (ET0), and characteristic parameters of underlying surface (n) to changes in runoff sensitivity in the Upper Shule River from 1972 to 2021.
3.2.2. Contributions of Runoff Sensitivity to Runoff Change in the Upper Shule River
Based on Equations (18) and (19), and characteristic values of hydrological parameters in the baseline and post-baseline periods (Table 2), the values caused by runoff sensitivity (, , ) and driving factors (P, ET0, n) were calculated to be 0.0369 and 0.0040, respectively. Thus, the contributions of runoff sensitivity (indirect effects of P, ET0, and n) and driving factors (direct effects of P, ET0, and n) to runoff change were 90.32% and 9.68%, respectively. Therefore, the runoff change was mainly caused by the indirect effects of P, ET0, and n in the Upper Shule River.

Table 2.
Characteristic values of hydrological parameters in the baseline and post-baseline periods.
3.3. Attribution Analysis of Runoff Change
3.3.1. Quantitative Analysis of the Causes of Runoff Change Based on the SCRCQ Method
Figure 7 shows the slopes of the linear relationships of the cumulative annual runoff depth (SRb and SRa), cumulative annual precipitation (SPb and SPa), and cumulative annual potential evapotranspiration (SEb and SEa) before and after the mutation. The SRb and SRa of the cumulative annual runoff depth in the baseline and post-baseline periods were 79.91 mm/yr and 125.89 mm/yr, respectively. The SPb and SPa of the cumulative annual precipitation in the baseline and post-baseline periods were 196.36 mm/yr and 233.09 mm/yr, respectively. The SEb and SEa of the cumulative annual potential evapotranspiration in the baseline and post-baseline periods were 386.42 mm/yr and 409.93 mm/yr, respectively. The results indicated that the annual runoff depth, precipitation, and potential evapotranspiration showed increasing trends during the whole period. The sum of the changes in P and ET0 was less than the change in R, indicating that the runoff generation and confluence processes were also affected by non-climatic factors.

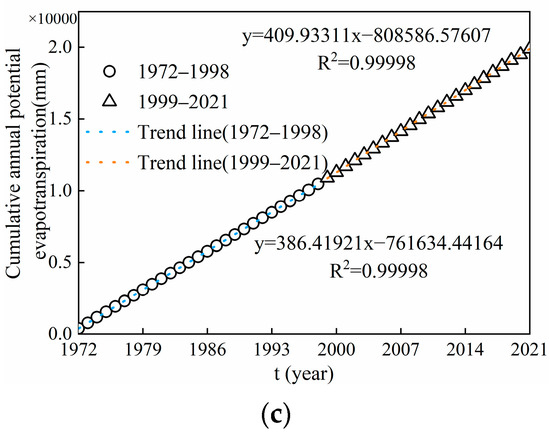
Figure 7.
Relationships between year and cumulative hydrological elements in the Upper Shule River from 1972 to 2021. (a) Relationship between year and cumulative runoff; (b) relationship between year and cumulative precipitation; (c) relationship between year and cumulative potential evapotranspiration.
Based on the results in Table 3 and the principle of the SCRCQ method, the impacts of P and ET0 on R were 32.52% and 10.57%, respectively, which indicated that the contributions of climatic and human factors to the runoff change were 43.09% and 56.91%, respectively. In conclusion, the impacts of climatic and human factors on runoff change have generally been the same in the past 50 years.

Table 3.
Slope of accumulative meteorological elements in the Upper Shule River from 1972 to 2021.
3.3.2. Quantitative Analysis of the Causes of Runoff Change Based on the Climate Elasticity Method
During the baseline period, the mean values of P, ET0 and, R in the Upper Shule River were 195.6 mm, 388.9 mm, and 80.6 mm, respectively. During the post-baseline period, the mean values of P, ET0, and R were 225.1 mm, 410.1 mm, and 125.0 mm, respectively. The results indicated that the mean values of annual precipitation, annual potential evapotranspiration and annual runoff depth increased by 29.5 mm, 21.2 mm, and 44.4 mm, respectively. According to Equations (25)–(27), the drying index of the Upper Shule River was 1.90, the actual evaporation function was 0.8851, and the sensitivity of the annual runoff depth to precipitation () and potential evapotranspiration () were 2.67 and –1.67, respectively (Table 4). The results showed that a 1% increase in precipitation would lead to a 2.67% increase in runoff depth, whereas a 1% increase in potential evapotranspiration would lead to a 1.1% decrease in runoff depth. Hence, precipitation and potential evapotranspiration caused the runoff depth to increase by 29.3 mm, whereas human activities caused the runoff depth to increase by 15.1 mm. In summary, the effects of climatic and human factors on runoff variation were 66.13% and 33.86%, respectively, which indicated that climate change was the main factor driving runoff change in the Upper Shule River.

Table 4.
Calculation results of the relevant parameters based on the climate elasticity method.
3.3.3. Quantitative Analysis of the Causes of Runoff Change Based on the Budyko Equation
Based on the Budyko equation and the relevant parameters (Table 5), the effects of P, ET0, and n on R were 83.88%, –17.87%, and 33.99%, respectively. Thus, the impacts of climatic and human factors on runoff variation were 66.01% and 33.99%, respectively. The climate change was the main cause of runoff variation in the Upper Shule River.

Table 5.
Characteristic values of hydrological element parameters based on the Budyko equation.
4. Discussion
4.1. Attribution of Runoff Change
The runoff in the Upper Shule River Basin is important to the economic and social development of the arid regions in the middle and lower reaches [19,20,21]. The runoff in the Upper Shule River showed a significant increasing trend from 1972 to 2021, and climate change was the dominant influencing factor on runoff change, which was consistent with previous studies [26,27]. Some researchers pointed out that runoff sensitivity (, and ) are greater in areas with a drier climate [45]. In this study, the values of , and range from 2.12 to 2.46, 1.12 to 1.46, and 0.37 to 0.59, respectively, which indicated that runoff sensitivity to climate change were greater than human activities. The literature reported that runoff is becoming gradually less sensitive to the climate conditions and underlying surface changes [46], which was consistent with our results.
The main climatic factors influencing change in runoff are precipitation, temperature, and potential evapotranspiration. Under the background of climate change from warm and dry to warm and wet [47], the change trend of annual precipitation increased from −11.6 mm/10a (baseline period) to 15.82 mm/10a (post-baseline period), the change trend of annual mean temperature decreased from 0.35 °C/10a (baseline period) to 0.11 °C/10a (post-baseline period), and the change trend of annual potential evapotranspiration decreased from 4.74 mm/10a (baseline period) to 0.24 mm/10a (post-baseline period) (Figure 8). The temperature, precipitation, and potential evapotranspiration all increased in the study area during the entire study period. However, the increase in precipitation alleviated the melting of glaciers caused by the increase in temperature, so the influence of precipitation on runoff was greater than that of temperature. This finding is consistent with the conclusion that precipitation was the main reason for the increase in runoff in most basins in China [48,49]. In addition to climate change, human activities have also played a significant role in runoff change in the Upper Shule River.
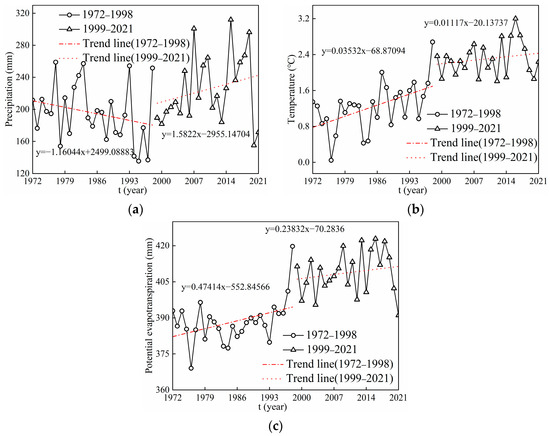
Figure 8.
Variation trends in annual meteorological parameters in the Upper Shule River during the baseline period and post-baseline period. (a) Temporal variation in precipitation. (b) Temporal variation in temperature. (c) Temporal variation in potential evapotranspiration.
The dominant land use types of Upper Shule River were unused land and grassland. There were two main trends of land use changes during 1990–2015: the decrease in grassland and the increase in unused land (23 km2 and 22 km2, respectively) (Table 6). However, the area changes in grassland coverage and unused land were only 0.26% and 0.16%, respectively, which contributed a small part to the increase in runoff. The literature reports that the area of grassland decreased, and the area of unused land increased, which promoted an increase in runoff [6]. Furthermore, the population density in the Upper Shule River was low during 1990–2015 (Figure 9). The changes in population density and the land use types indicated that human activities were not dominant in the Upper Shule River.

Table 6.
Land use changes in the Upper Shule River from 1990 to 2015 (km2).
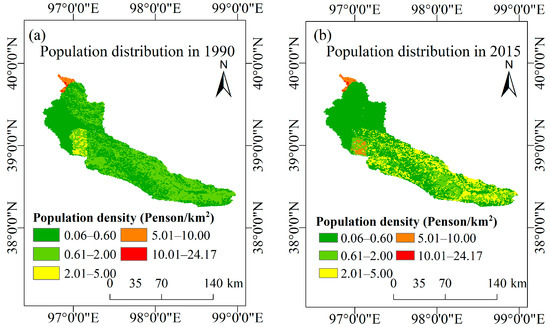
Figure 9.
Spatial distribution of population density in the Upper Shule River from 1990 to 2015.
4.2. Comparison of the Results from Different Attribution Methods
Table 7 shows the results of quantifying the causes of runoff change based on three methods. According to the SCRCQ method, human activities were considered the main influencing factors on runoff change. The method revealed that potential evapotranspiration caused runoff to increase, contributing 10.57% to runoff change. In contrast, the climate elasticity method and the Budyko equation showed that P was the main contributor to runoff change, and the potential evapotranspiration caused runoff to decrease. Watershed water storage (ΔS) is regarded as a constant when analysing the attribution of runoff change based on the Budyko equation. At this time, the human activities causing runoff change were mainly attributed to changes in land/vegetation cover [50]. The literature reported that it may take more than 10 years for watersheds in semi-arid and arid regions to reach steady states [51]. The n values under the three conditions based on the 11-, 15-, and 31-year sliding average data of R, P, and ET0, respectively, were calculated (Figure 10). The mean values and slopes of n exhibited little change under the different moving windows. The results indicated that the step size of the sliding average of n had little effect on its long-term trend. Therefore, the Upper Shule River was generally in a steady-state condition. Thus, the contribution of quantitative influencing factors to runoff change based on the Budyko equation is reliable. The relevant contributions of the Budyko equation and the climate elasticity method were basically the same (Table 7). Overall, the consistent results of contribution quantification are helpful for clarifying the mechanism of runoff increase in the study area. The quantitative results showed that climate change was the dominant driver on runoff change.

Table 7.
Comparison of contributions to runoff change based on different calculation methods in the Upper Shule River during 1972–2021.
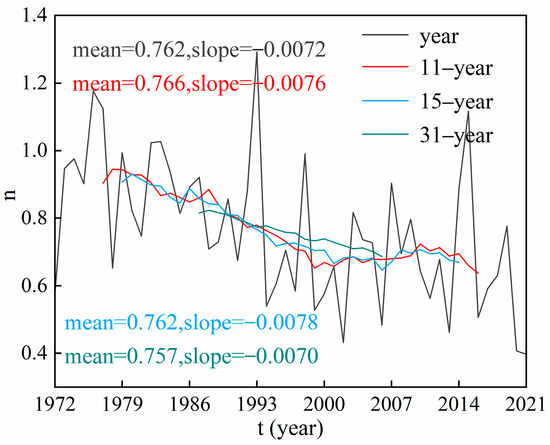
Figure 10.
Trends in the 11-, 15-, and 31-year moving averages of characteristic parameters of underlying surface (n) in the Upper Shule River from 1972 to 2021. The unit of slope of n is yr−1.
Studies have shown that the contribution of climate change to runoff change is related to elevation [52]. The Upper Shule River is an alpine area. Rising temperatures have increased the supply of glacial snowmelt and snow to rivers with global warming [53]. Studies have indicated that the hydrological processes in high-elevation areas are primarily controlled by water volume [52]. As altitude increases, snowfall transitions to rainfall, and precipitation also rises. Of the three methods, the contribution of human activities estimated by the SCRCQ method was relatively large. The limited meteorological data availability in the study area is due to the presence of only one meteorological station and the resulting lack of statistical precipitation data. Therefore, it is necessary to supplement the analysis data with remote sensing data in the future to gain a more accurate understanding of the runoff change mechanism in the Upper Shule River.
5. Conclusions
Based on previous studies, this study adopted different methods to decompose the causes of runoff change in the Upper Shule River. Focusing on the changes in runoff sensitivity, the direct and indirect effects of driving factors on runoff change are discussed. The major conclusions are summarized as follows:
(1) The annual runoff depth experienced a significant abrupt change in 1998. Before 1998, the annual runoff depth showed a downward trend. After 1998, the runoff depth showed an upward trend.
(2) The runoff sensitivity changed with a downward trend. n was the main contributor to the change in runoff sensitivity, followed by P, with ET0 having the weakest effect.
(3) The SCRCQ method, climate elasticity method, and Budyko equation were used to determine the causes of runoff change. The results showed that climate change was the main influencing factor on runoff change in the Upper Shule River.
(4) The increase in runoff in the Upper Shule River was mainly caused by the indirect influence of driving factors (changes in runoff sensitivity).
In summary, this paper integrated the direct and indirect impacts of P, ET0, and n on runoff change and used different runoff change attribution methods to compare and verify the results. This study will provide a useful reference for water resources allocation against climate warming in the Upper Shule River basin. However, the lack of sufficient meteorological data may adversely affect the results of attribution analysis. Meanwhile, the different mechanisms of the methodologies may make the findings of this study are only applicable to the Upper Shule River. Therefore, future research should focus on innovating and optimizing runoff attribution research methods and comprehensively exploring the complex relationship between runoff and environmental changes.
Author Contributions
Conceptualization, L.J.; methodology, L.J.; resources, Z.N.; supervision, R.Z.; validation, Y.M. and R.Z.; visualization, Y.M. and R.Z.; writing—original draft, L.J. and Z.N.; writing—review and editing, Z.N. and L.J.; data curation, L.J.; formal analysis, L.J.; and software, L.J. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Key R&D Plan of Gansu Province (21YF5FA094; 22YF7GA107), and the Water Conservancy Science Experimental Research and Technology Promotion Program Project of Gansu Province, China (Gansu Province Water Resources Department Construction Management Division No. 71 of 2021). We also thank the reviewers for their comments, which greatly improved the quality of the paper.
Data Availability Statement
The land use data and the spatial distribution of population data were sourced from the Data Center for Resources and Environmental Sciences, Chinese Academy of Sciences (https://www.resdc.cn (accessed on 12 October 2022)). The data are available from the corresponding author upon reasonable request.
Acknowledgments
Thank you to the reviewers for the comments, which greatly improved the quality of the paper.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Zhang, Y.; Chiew, F.H.; Peña-Arancibia, J.; Sun, F.; Li, H.; Leuning, R. Global variation of transpiration and soil evaporation and the role of their major climate drivers. J. Geophys. Res. Atmos. 2017, 122, 6868–6881. [Google Scholar] [CrossRef]
- Lu, X.; Zang, C.; Burenina, T. Study on the variation in evapotranspiration in different period of the Genhe River Basin in China. Phys. Chem. Earth Parts A/B/C 2020, 120, 102902. [Google Scholar] [CrossRef]
- Dong, H.; Huang, S.; Fang, W.; Leng, G.; Wang, H.; Ren, K.; Zhao, J.; Ma, C. Copula-based non-stationarity detection of the precipitation-temperature dependency structure dynamics and possible driving mechanism. Atmos. Res. 2021, 249, 105280. [Google Scholar] [CrossRef]
- He, Y.; Song, J.; Hu, Y.; Tu, X.; Zhao, Y. Impacts of different weather conditions and land use change on runoff variations in the Beiluo River Watershed, China. Sustain. Cities Soc. 2019, 50, 101674. [Google Scholar] [CrossRef]
- Sun, X.; Dong, Q.; Zhang, X. Attribution analysis of runoff change based on Budyko-type model with time-varying parameters for the Lhasa River Basin, Qinghai–Tibet Plateau. J. Hydrol. Reg. Stud. 2023, 48, 101469. [Google Scholar] [CrossRef]
- Bai, X.; Zhao, W. Impacts of climate change and anthropogenic stressors on runoff variations in major river basins in China since 1950. Sci. Total Environ. 2023, 898, 165349. [Google Scholar] [CrossRef]
- Shahid, M.; Rahman, K.U.; Balkhair, K.S.; Nabi, A. Impact assessment of land use and climate changes on the variation of runoff in Margalla Hills watersheds, Pakistan. Arab. J. Geosci. 2020, 13, 239. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, G.; Tian, P.; Mu, X.; Tian, X.; Feng, J.; Bai, Y. Runoff changes in the major river basins of China and their responses to potential driving forces. J. Hydrol. 2022, 607, 127536. [Google Scholar] [CrossRef]
- Mo, C.; Lai, S.; Yang, Q.; Huang, K.; Lei, X.; Yang, L.; Yan, Z.; Jiang, C. A comprehensive assessment of runoff dynamics in response to climate change and human activities in a typical karst watershed, southwest China. J. Environ. 2023, 332, 117380. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Miao, C.; Zhang, X.; Yang, T.; Duan, Q. Detecting the quantitative hydrological response to changes in climate and human activities. Sci. Total Environ. 2017, 586, 328–337. [Google Scholar] [CrossRef]
- Chu, H.; Wei, J.; Qiu, J.; Li, Q.; Wang, G. Identification of the impact of climate change and human activities on rainfall-runoff relationship variation in the Three-River Headwaters region. Ecol. Indic. 2019, 106, 105516. [Google Scholar] [CrossRef]
- Bao, S.; Yang, W.; Wang, X.; Li, H. Quantifying Contributions of Climate Change and Local Human Activities to Runoff Decline in the Second Songhua River Basin. Water 2020, 12, 67–74. [Google Scholar] [CrossRef]
- Xue, D.; Zhou, J.; Zhao, X.; Liu, C.; Wei, W.; Yang, X.; Li, Q.; Zhao, Y. Impacts of climate change and human activities on runoff change in a typical arid watershed, NW China. Ecol. Indic. 2021, 121, 107013. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, D.; Jayawardena, A.W.; Xu, X.; Yang, H. Hydrological change driven by human activities and climate variation and its spatial variability in Huaihe Basin, China. Hydrol. Sci. J. 2016, 61, 1370–1382. [Google Scholar] [CrossRef]
- Ning, T.; Li, Z.; Liu, W. Separating the impacts of climate change and land surface alteration on runoff reduction in the Jing River catchment of China. Catena 2016, 147, 80–86. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Fu, J.; Chen, Z.; Ning, Z.; Liu, Y. Quantifying the relative contribution of climate variability and human activities impacts on baseflow dynamics in the Tarim River Basin, Northwest China. J. Hydrol. Reg. Stud. 2021, 36, 100853. [Google Scholar] [CrossRef]
- Ni, Y.; Lv, X.; Yu, Z.; Wang, J.; Ma, L.; Zhang, Q. Intra-annual variation in the attribution of runoff evolution in the Yellow River source area. Catena 2023, 225, 107032. [Google Scholar] [CrossRef]
- Saha, A.; Joseph, J.; Ghosh, S. Climate controls on the terrestrial water balance: Influence of aridity on the basin characteristics parameter in the Budyko framework. Sci. Total Environ. 2020, 739, 139863. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Zhang, C. Holocene millennial-scale erosion and deposition processes in the middle reaches of inland drainage basins, arid China. Environ. Earth Sci. 2016, 75, 1–15. [Google Scholar] [CrossRef]
- Chang, Y.; Ding, Y.; Zhao, Q.; Zhang, S. Remote estimation of terrestrial evapotranspiration by Landsat 5 TM and the SEBAL model in cold and high-altitude regions: A case study of the upper reach of the Shule River Basin, China. Hydrol. Process. 2017, 31, 514–524. [Google Scholar] [CrossRef]
- Wang, S.; Ding, Y.; Iqbal, M. Defining Runoff Indices and Analyzing Their Relationships with Associated Precipitation and Temperature Indices for Upper River Basins in the Northwest Arid Region of China. Water 2017, 9, 618. [Google Scholar] [CrossRef]
- Lang, Y.; Meng, C. Runoff optimization and control for basin water allocation. Water Supply 2022, 22, 2630–2643. [Google Scholar] [CrossRef]
- Qin, J.; Ding, Y.; Han, T.; Liu, Y. Identification of the Factors Influencing the Baseflow in the Permafrost Region of the Northeastern Qinghai-Tibet Plateau. Water 2017, 9, 666. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, S.; Zhao, Q.; Zhang, S.; Zhang, X. Projected glacier meltwater and river run-off changes in the Upper Reach of the Shule River Basin, north-eastern edge of the Tibetan Plateau. Hydrol. Process. 2019, 33, 1059–1074. [Google Scholar] [CrossRef]
- Wu, Q.; Ma, S.; Zhang, Z.; Wang, G.; Zhang, S. Evaluation of nine precipitation products with ground-based measurements during 2001 to 2013 in alpine Upper Reach of Shule River Basin, northeastern edge of the Tibetan Plateau. Theor. Appl. Climatol. 2021, 144, 1101–1117. [Google Scholar] [CrossRef]
- He, Y.; Jiang, X.; Wang, N.; Zhang, S.; Ning, T.; Zhao, Y.; Hu, Y. Changes in mountainous runoff in three inland river basins in the arid Hexi Corridor, China, and its influencing factors. Sustain. Cities Soc. 2019, 50, 101703. [Google Scholar] [CrossRef]
- Wei, P.; Chen, S.; Wu, M.; Deng, Y.; Xu, H.; Jia, Y.; Liu, F. Using the InVEST model to assess the impacts of climate and land use changes on water yield in the upstream regions of the Shule River Basin. Water 2021, 13, 1250. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Q.; Pu, T. Assessment of water stress level about global glacier-covered arid areas: A case study in the Shule River Basin, northwestern China. J. Hydrol. Reg. Stud. 2021, 37, 100895. [Google Scholar] [CrossRef]
- Ma, L.; Bo, J.; Li, X.; Fang, F.; Cheng, W. Identifying key landscape pattern indices influencing the ecological security of inland river basin: The middle and lower reaches of Shule River Basin as an example. Sci. Total Environ. 2019, 674, 424–438. [Google Scholar] [CrossRef]
- Zhou, J.; Ding, Y.; Wu, J.; Liu, F.; Wang, S. Streamflow generation in semi-arid, glacier-covered, montane catchments in the upper Shule River, Qilian Mountains, northeastern Tibetan plateau. Hydrol. Process. 2021, 35, e14276. [Google Scholar] [CrossRef]
- Wu, J.; Li, H.; Zhou, J.; Tai, S.; Wang, X. Variation of Runoff and Runoff Components of the Upper Shule River in the Northeastern Qinghai–Tibet Plateau under Climate Change. Water 2021, 13, 3357. [Google Scholar] [CrossRef]
- Jiang, Y.; Du, W.; Chen, J.; Sun, W. Spatiotemporal Variations in Snow Cover and Hydrological Effects in the Upstream Region of the Shule River Catchment, Northwestern China. Remote Sens. 2021, 13, 3212. [Google Scholar] [CrossRef]
- Yang, Q.; Ma, Z.; Zheng, Z.; Duan, Y. Sensitivity of potential evapotranspiration estimation to the Thornthwaite and Penman–Monteith methods in the study of global drylands. Adv. Atmos. Sci. 2017, 34, 1381–1394. [Google Scholar] [CrossRef]
- Kadioglu, M. Trends in surface air temperature data over Turkey. Int. J. Climatol. 1997, 17, 511–520. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, X.; Yang, G.; Yao, J.; Liao, N. Impacts of climate change and human activities on water resources in the Ebinur Lake Basin, Northwest China. J. Arid Land 2021, 13, 581–598. [Google Scholar] [CrossRef]
- Li, Y.; Cai, Y.; Li, Z.; Wang, X.; Fu, Q.; Liu, D.; Sun, L.; Xu, R. An approach for runoff and sediment nexus analysis under multi-flow conditions in a hyper-concentrated sediment river, Southwest China. J. Contam. Hydrol. 2020, 235, 103702. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, B.J. Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model. J. Hydrol. 1999, 216, 99–110. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; Lei, Z.; Sun, F. New analytical derivation of the mean annual water-energy balance equation. Water Resour. Res. 2008, 44, 893–897. [Google Scholar] [CrossRef]
- Meng, F.; Liu, T.; Huang, Y.; Luo, M.; Bao, A.; Hou, D. Quantitative Detection and Attribution of Runoff Variations in the Aksu River Basin. Water 2016, 8, 338. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, X.; Peng, W.; Liu, X.; Dong, F.; Huang, A.; Wang, W. Changes in Runoff Volumes of Inland Terminal Lake: A Case Study of Lake Daihai. Earth Space Sci. 2021, 8, e2021EA001954. [Google Scholar] [CrossRef]
- Cheng, Q.; Zuo, X.; Zhong, F.; Gao, L.; Xiao, S. Runoff variation characteristics, association with large-scale circulation and dominant causes in the Heihe River Basin, Northwest China. Sci. Total Environ. 2019, 688, 361–379. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.; Xu, M.; Kang, S.; Wu, H. Impacts of climate change and human activities on runoff changes in the Ob River Basin of the Arctic region from 1980 to 2017. Theor. Appl. Climatol. 2022, 148, 1663–1674. [Google Scholar] [CrossRef]
- Ma, H.; Yang, D.; Tan, S.K.; Gao, B.; Hu, Q. Impact of climate variability and human activity on streamflow decrease in the Miyun Reservoir catchment. J. Hydrol. 2010, 389, 317–324. [Google Scholar] [CrossRef]
- Sun, X.; Peng, Y.; Zhou, H.; Zhang, X. Responses of Streamflow to Climate Variability and Hydraulic Project Construction in Wudaogou Basin, Northeast China. J. Hydrol. Eng. 2016, 21, 05016016. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Wang, C.; Zhao, W. Runoff sensitivity increases with land use/cover change contributing to runoff decline across the middle reaches of the Yellow River basin. J. Hydrol. 2021, 600, 126536. [Google Scholar] [CrossRef]
- Ni, Y.; Yu, Z.; Lv, X.; Qin, T.; Yan, D.; Zhang, Q.; Ma, L. Spatial difference analysis of the runoff evolution attribution in the yellow river basin. J. Hydrol. 2022, 612, 128149. [Google Scholar] [CrossRef]
- Wu, X.; Hao, Z.; Hao, F.; Zhang, X. Variations of compound precipitation and temperature extremes in China during 1961-2014. Sci. Total Environ. 2019, 663, 731–737. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ye, A.; Zhang, Y.; Yang, F. The quantitative attribution of climate change to runoff increase over the Qinghai-Tibetan Plateau. Sci. Total Environ. 2023, 897, 165326. [Google Scholar] [CrossRef]
- Shen, Q.; Cong, Z.; Lei, H. Evaluating the impact of climate and underlying surface change on runoff within the Budyko framework: A study across 224 catchments in China. J. Hydrol. 2017, 554, 251–262. [Google Scholar] [CrossRef]
- Xu, X.; Yang, D.; Yang, H.; Lei, H. Attribution analysis based on the Budyko hypothesis for detecting the dominant cause of runoff decline in Haihe basin. J. Hydrol. 2014, 510, 530–540. [Google Scholar] [CrossRef]
- Han, J.; Yang, Y.; Roderick, M.L.; McVicar, T.R.; Yang, D.; Zhang, S.; Beck, H.E. Assessing the Steady-State Assumption in Water Balance Calculation Across Global Catchments. Water Resour. Res. 2020, 56, e2020WR027392. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Fu, J.; Wei, J. Spatiotemporal heterogeneity and attributions of streamflow and baseflow changes across the headstreams of the Tarim River Basin, Northwest China. Sci. Total Environ. 2023, 856, 159230. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Li, B.; Fan, Y.; Sun, C.; Fang, G. Hydrological and water cycle processes of inland river basins in the arid region of Northwest China. J. Arid. Land 2019, 11, 161–179. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).