The Enhanced Adsorption Capacity of Ziziphus jujuba Stones Modified with Ortho-Phosphoric Acid for Organic Dye Removal: A Gaussian Process Regression Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Adsorbent Preparation
2.3. Biosorption Study
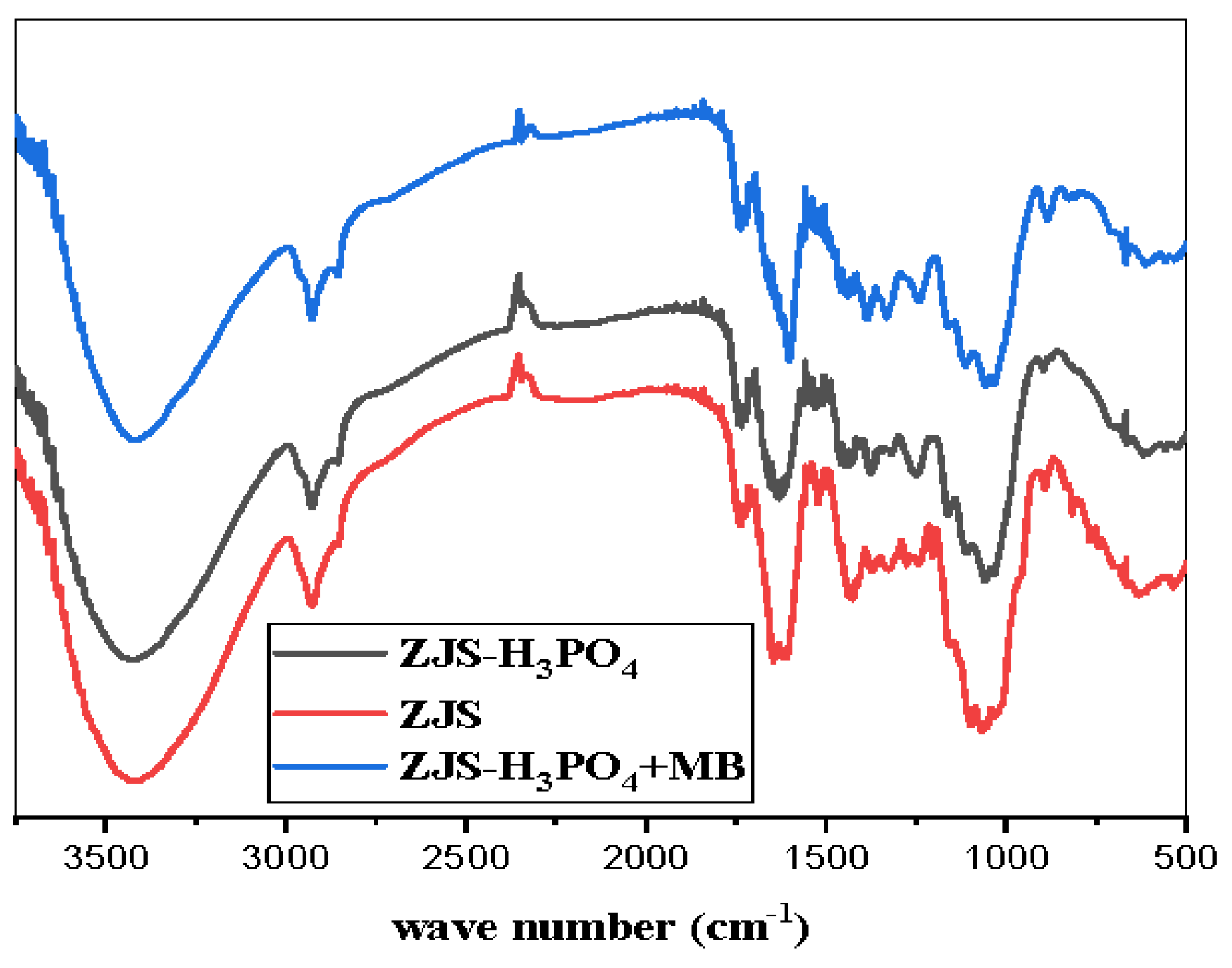
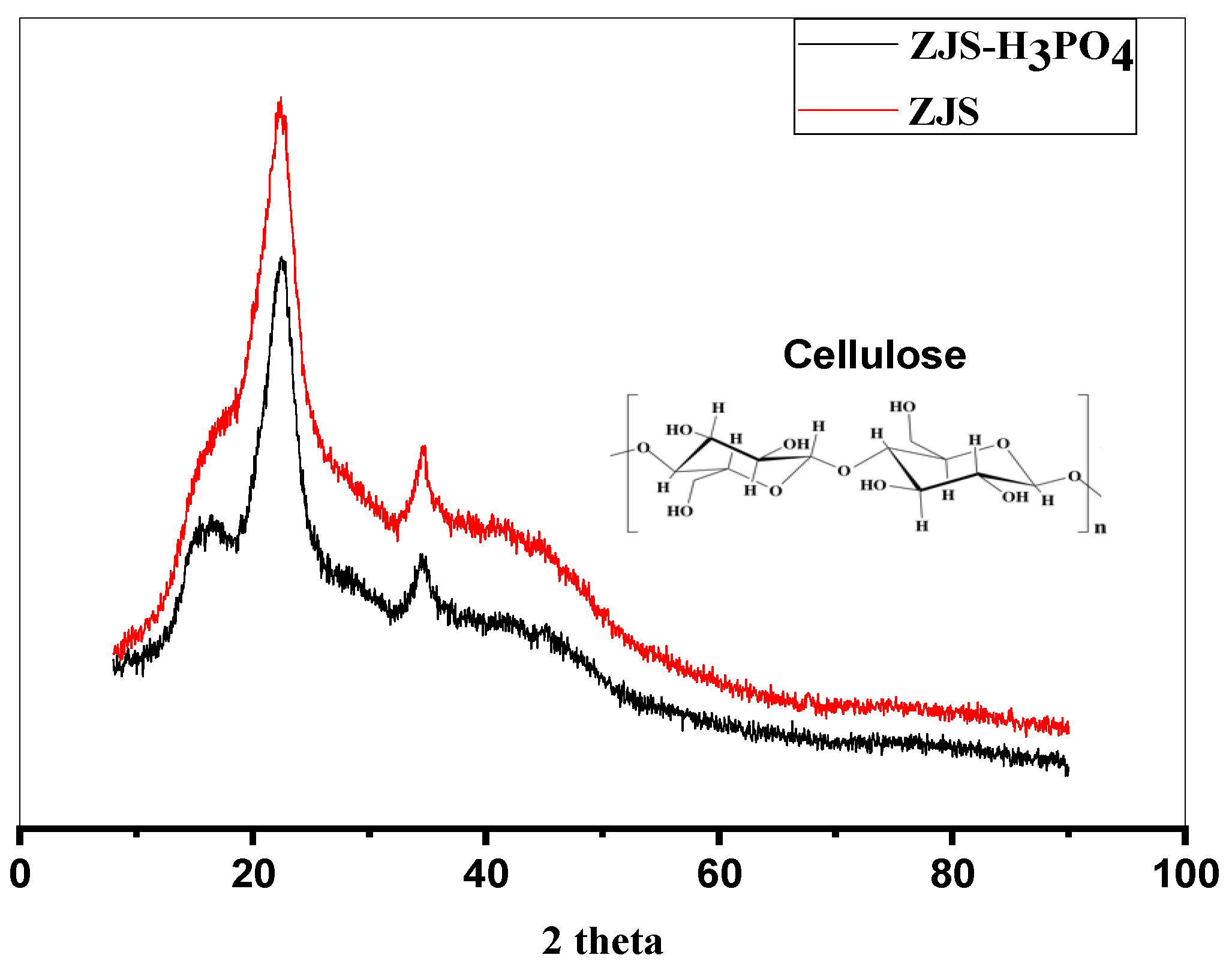
2.4. Characterization
2.5. Biosorption Isotherms
2.6. Modeling the Equilibrium
2.7. Modeling the Biosorption Kinetics
2.8. Statistical Models
2.9. Gaussian Process Regression
3. Results and Discussions
3.1. Material Characterization
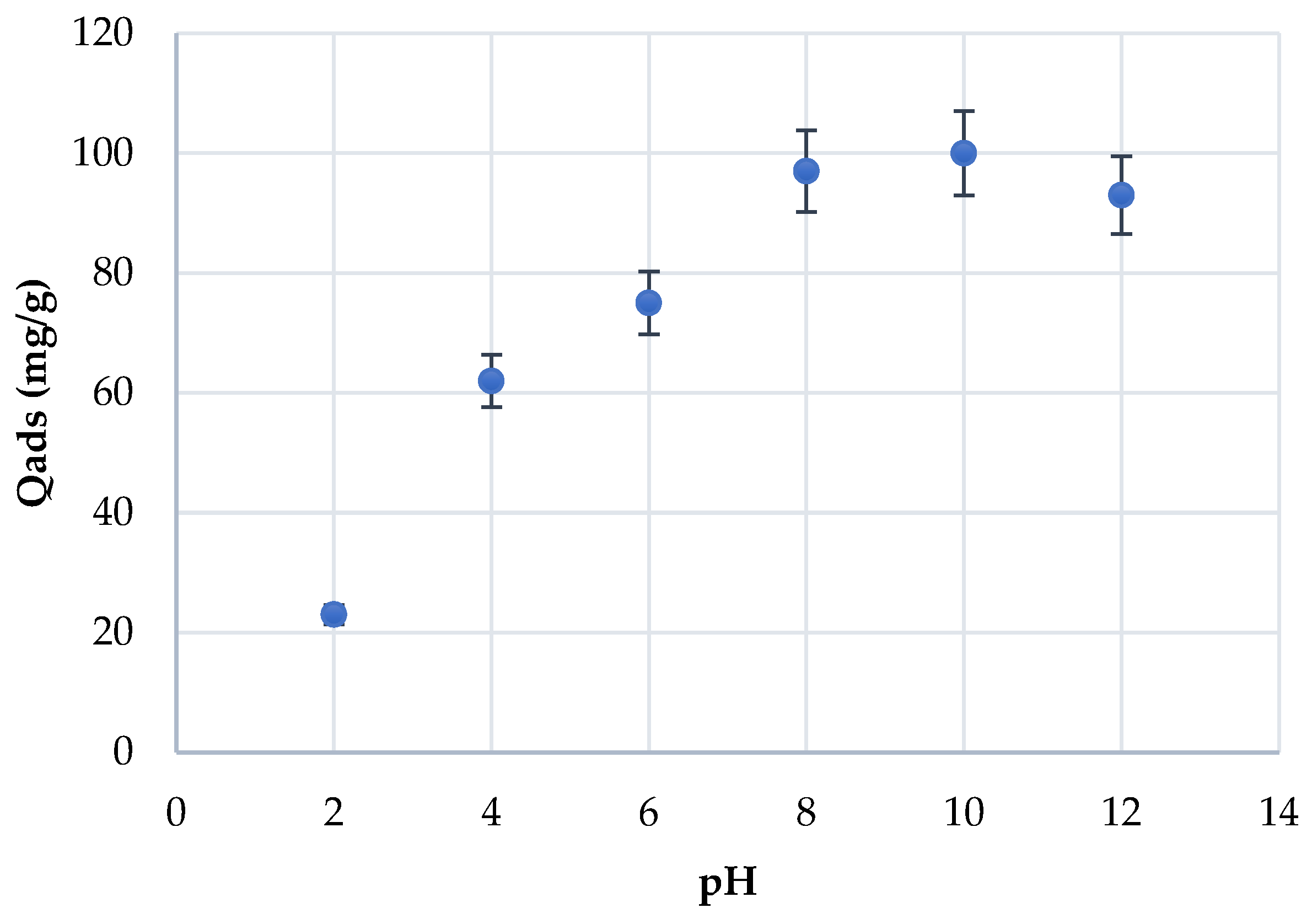
- The material surface functional groups are protonated by excess H+ protons when the pH is below pHPZC.
- The ZJS-H3PO4 surface functional groups are deprotonated by excess OH- ions in the solution when the pH exceeds pHPZC.
3.2. Effect of the pH
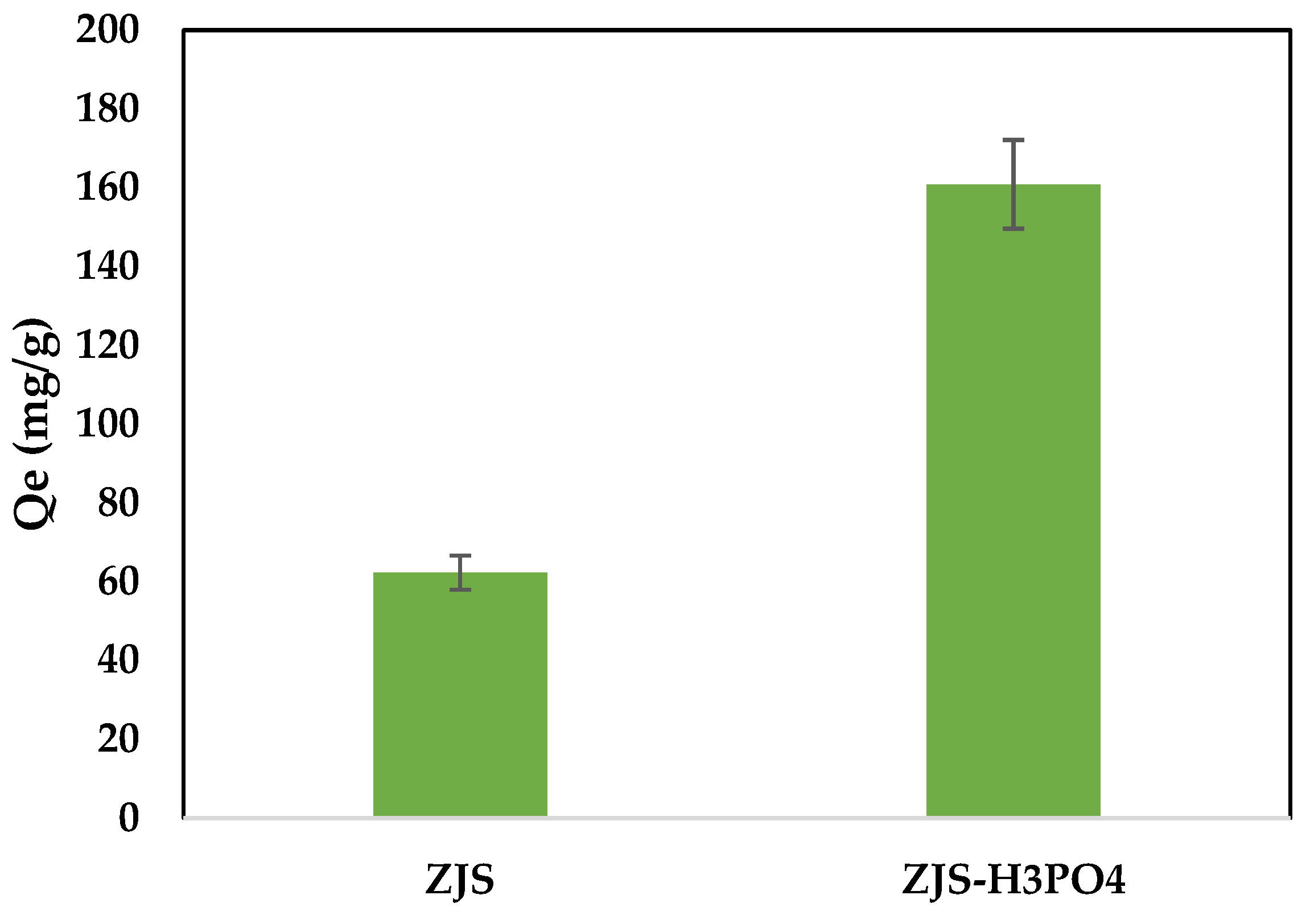
3.3. The Effect of H₃PO₄ Treatment Processes on the Modification of Ziziphus jujuba Stones for MB Adsorption Capacity
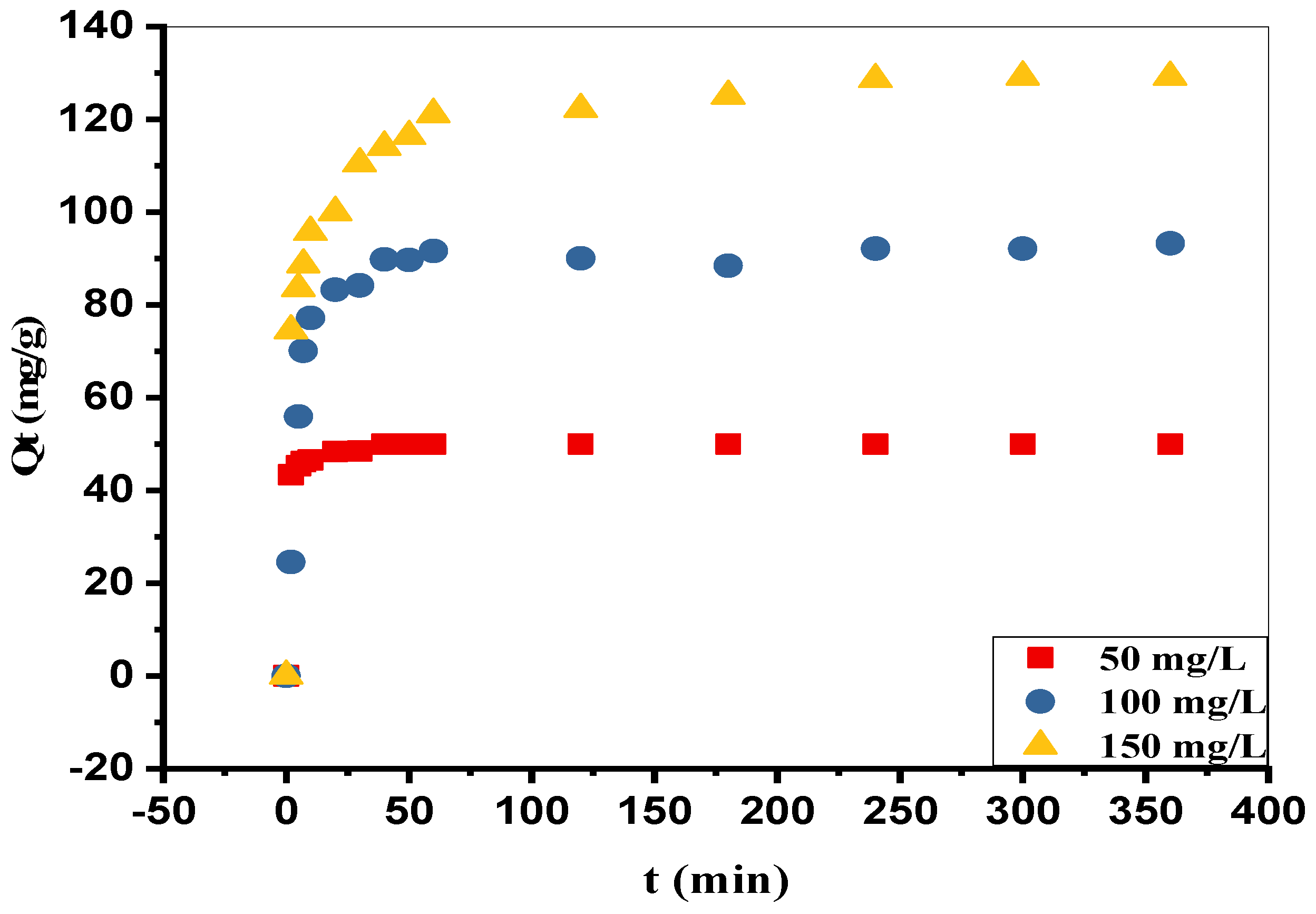
3.4. Effect of the Contact Time and the Initial Concentration
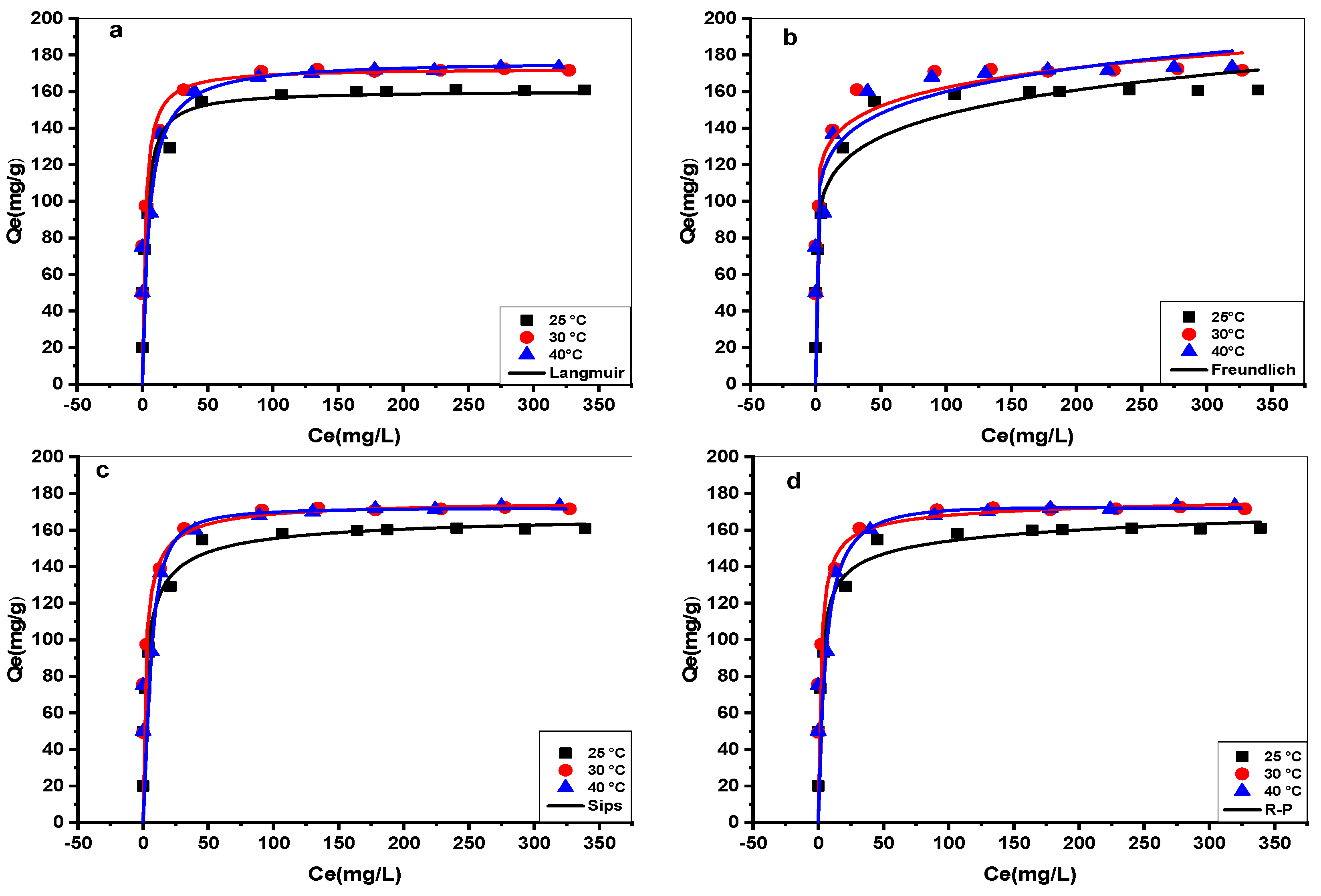
3.5. Isotherms Modeling
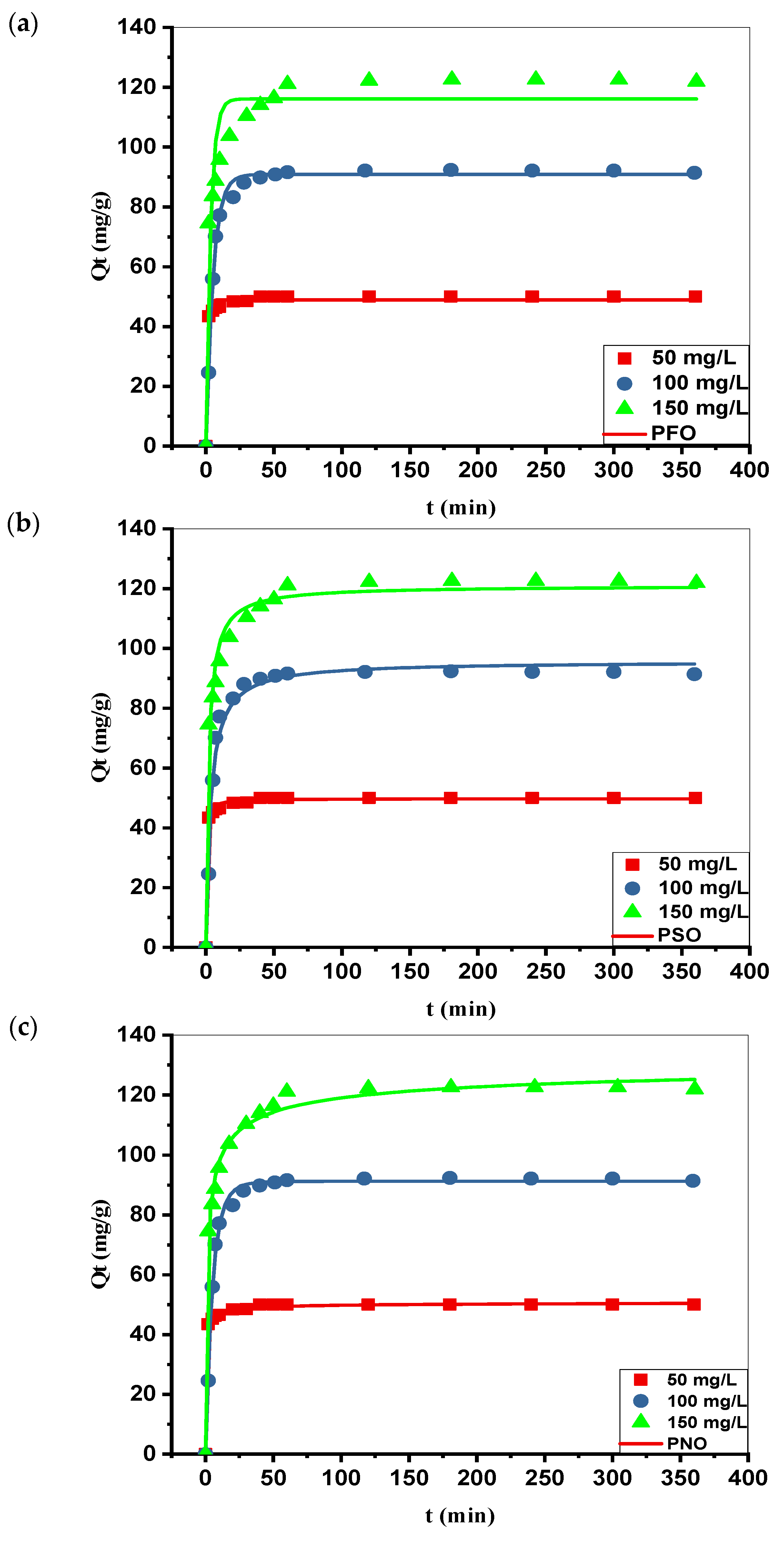
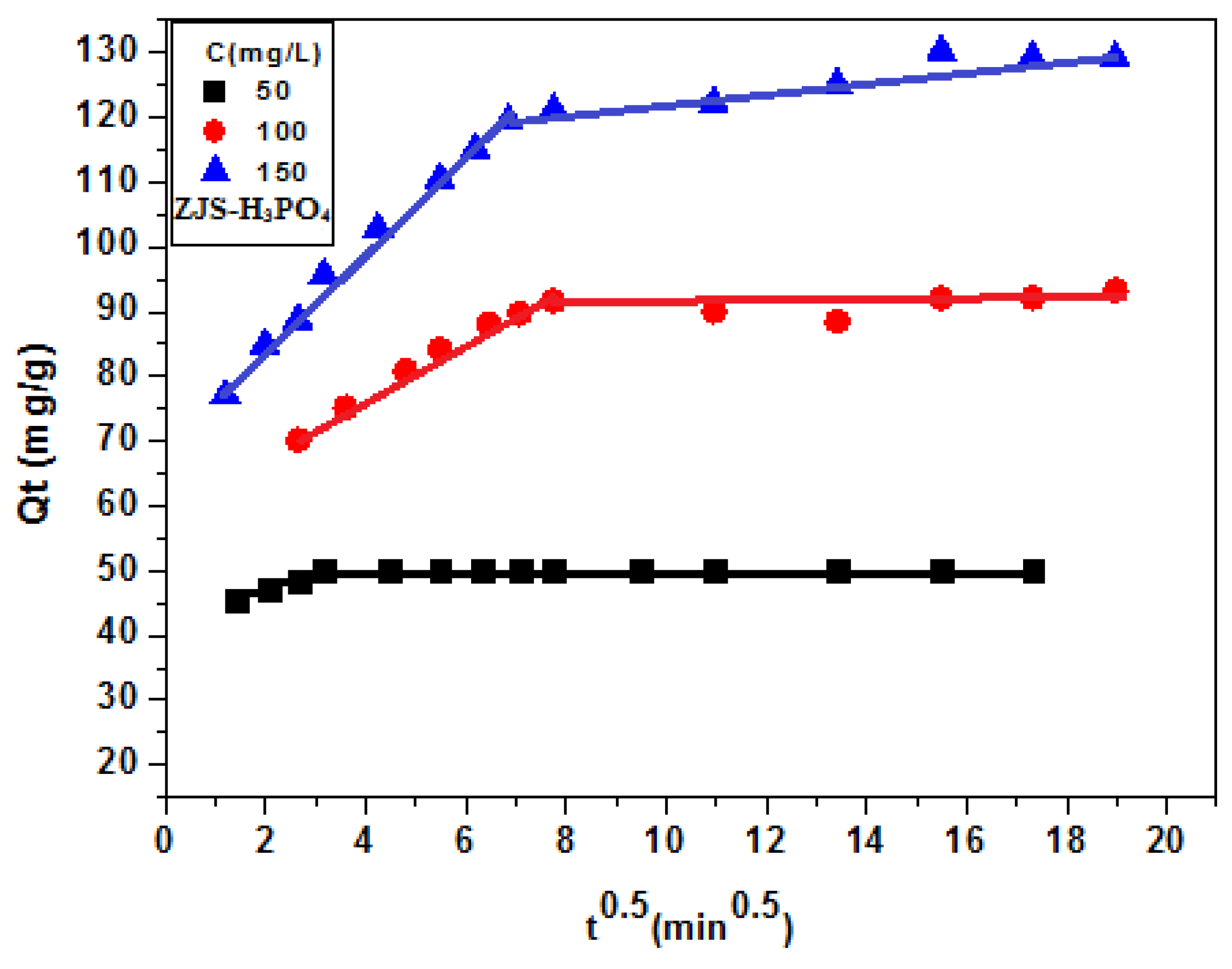
3.6. Kinetics Modeling
3.7. Effect of the Temperature
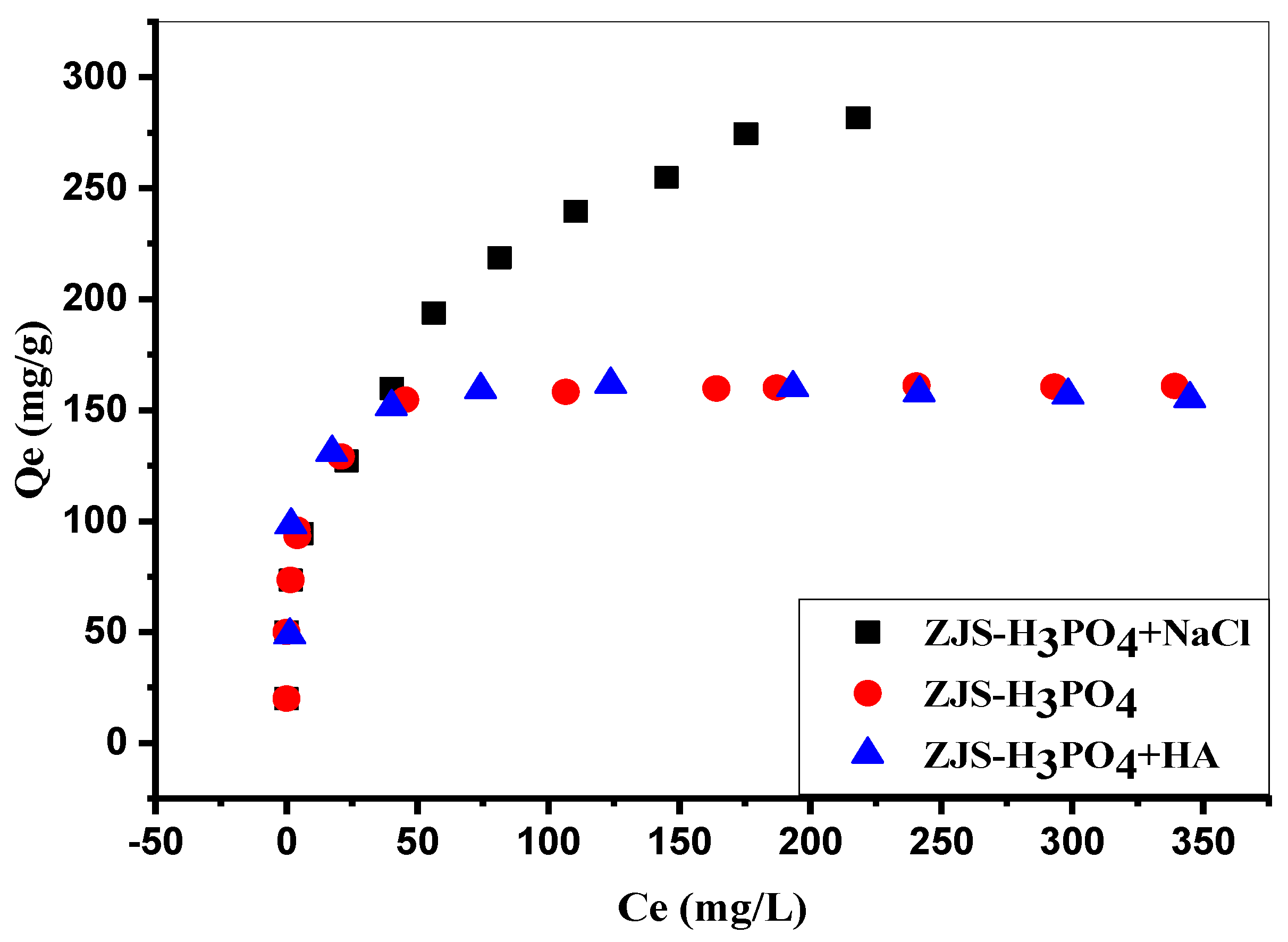
3.8. Effect of the Ionic Strength and the Humic Acid on Biosorption of MB onto ZJS-H3PO4
3.9. Statistical Physics Models
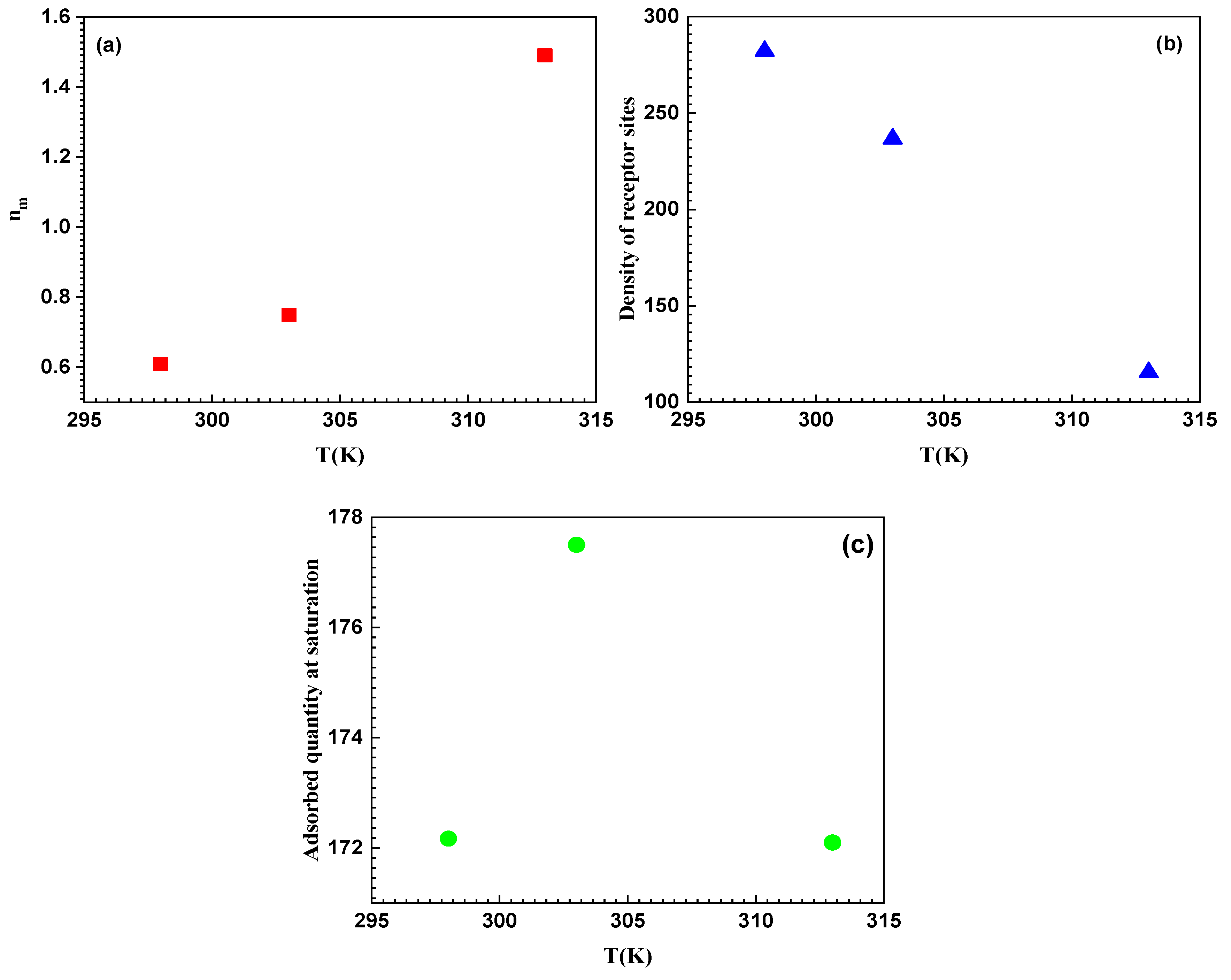
3.9.1. Steric Interpretation
- Parameter nm
- Parameter NM
- Parameter Q0
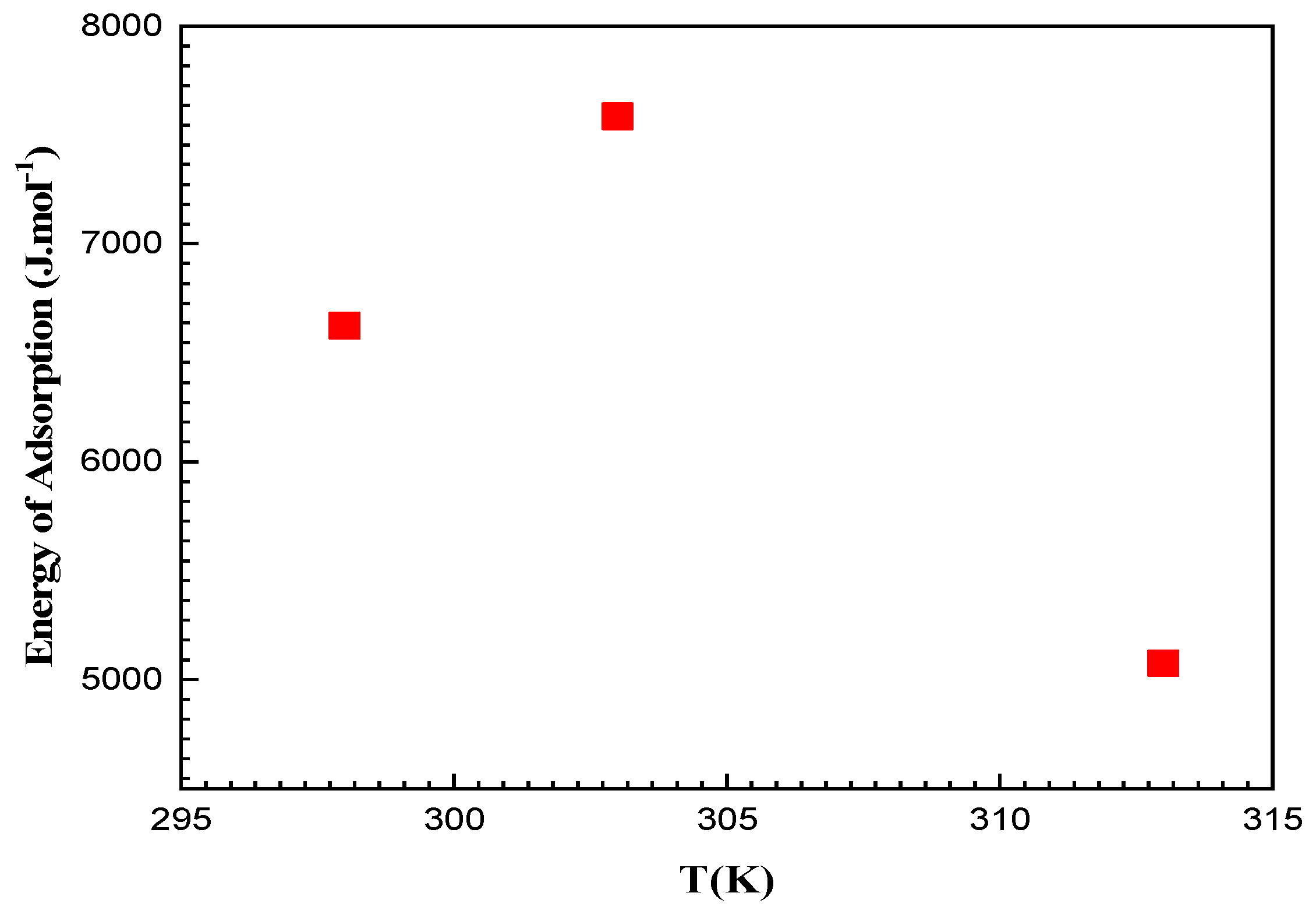
3.9.2. Energetic Interpretation
3.10. Gaussian Process Regression
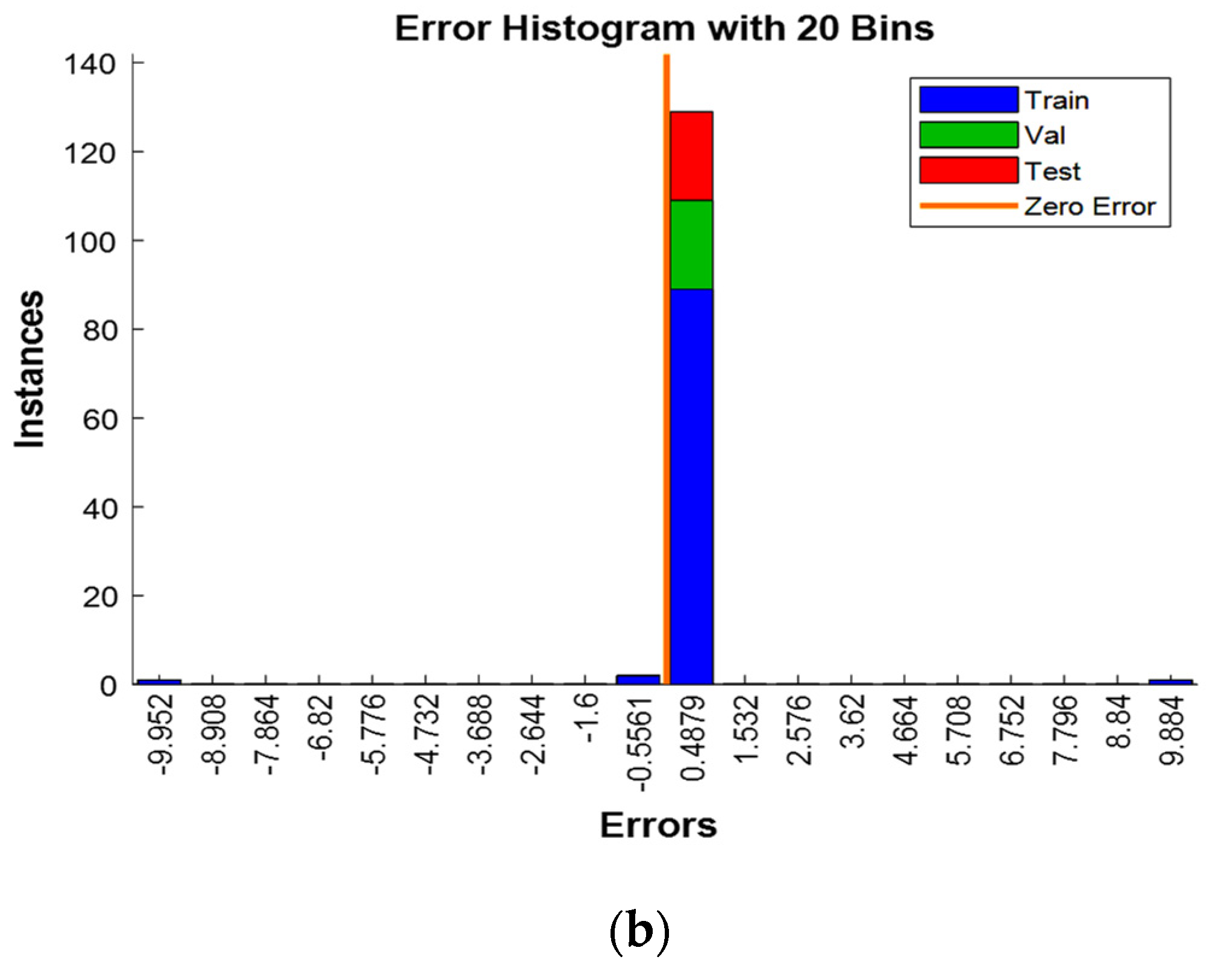
3.10.1. Residues Study
3.10.2. Interface for Optimization and Prediction
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deniz, F.; Kepekci, R.A. Dye Biosorption onto Pistachio By-Product: A Green Environmental Engineering Approach. J. Mol. Liq. 2016, 219, 194–200. [Google Scholar] [CrossRef]
- Temesgen, F.; Gabbiye, N.; Sahu, O. Biosorption of Reactive Red Dye (RRD) on Activated Surface of Banana and Orange Peels: Economical Alternative for Textile Effluent. Surf. Interfaces 2018, 12, 151–159. [Google Scholar] [CrossRef]
- Lessa, E.F.; Nunes, M.L.; Fajardo, A.R. Chitosan/Waste Coffee-Grounds Composite: An Efficient and Eco-Friendly Adsorbent for Removal of Pharmaceutical Contaminants from Water. Carbohydr. Polym. 2018, 189, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Moro, T.R.; Henrique, F.R.; Malucelli, L.C.; de Oliveira, C.M.R.; da Silva Carvalho Filho, M.A.; de Vasconcelos, E.C. Adsorption of Pharmaceuticals in Water through Lignocellulosic Fibers Synergism. Chemosphere 2017, 171, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Albadarin, A.B.; Solomon, S.; Kurniawan, T.A.; Mangwandi, C.; Walker, G. Single, Simultaneous and Consecutive Biosorption of Cr(VI) and Orange II onto Chemically Modified Masau Stones. J. Environ. Manag. 2017, 204, 365–374. [Google Scholar] [CrossRef] [PubMed]
- Torab-Mostaedi, M.; Asadollahzadeh, M.; Hemmati, A.; Khosravi, A. Equilibrium, Kinetic, and Thermodynamic Studies for Biosorption of Cadmium and Nickel on Grapefruit Peel. J. Taiwan Inst. Chem. Eng. 2013, 44, 295–302. [Google Scholar] [CrossRef]
- Lin, G.; Ma, R.; Zhou, Y.; Liu, Q.; Dong, X.; Wang, J. KOH Activation of Biomass-Derived Nitrogen-Doped Carbons for Supercapacitor and Electrocatalytic Oxygen Reduction. Electrochim. Acta 2018, 261, 49–57. [Google Scholar] [CrossRef]
- Rangabhashiyam, S.; Lata, S.; Balasubramanian, P. Biosorption Characteristics of Methylene Blue and Malachite Green from Simulated Wastewater onto Carica Papaya Wood Biosorbent. Surf. Interfaces 2018, 10, 197–215. [Google Scholar] [CrossRef]
- Riggert, J.; Humpe, A.; Legler, T.J.; Wolf, C.; Simson, G.; Köhler, M. Filtration of Methylene Blue-photooxidized Plasma: Influence on Coagulation and Cellular Contamination. Transfusion 2001, 41, 82–86. [Google Scholar] [CrossRef]
- Ihaddaden, S.; Aberkane, D.; Boukerroui, A.; Robert, D. Removal of Methylene Blue (Basic Dye) by Coagulation-Flocculation with Biomaterials (Bentonite and Opuntia Ficus Indica). J. Water Process Eng. 2022, 49, 102952. [Google Scholar] [CrossRef]
- Tahraoui, H.; Toumi, S.; Boudoukhani, M.; Touzout, N.; Sid, A.N.E.H.; Amrane, A.; Belhadj, A.-E.; Hadjadj, M.; Laichi, Y.; Aboumustapha, M. Evaluating the Effectiveness of Coagulation–Flocculation Treatment Using Aluminum Sulfate on a Polluted Surface Water Source: A Year-Long Study. Water 2024, 16, 400. [Google Scholar] [CrossRef]
- Ayekoe, C.Y.P.; Robert, D.; Lanciné, D.G. Combination of Coagulation-Flocculation and Heterogeneous Photocatalysis for Improving the Removal of Humic Substances in Real Treated Water from Agbô River (Ivory-Coast). Catal. Today 2017, 281, 2–13. [Google Scholar] [CrossRef]
- Kanjal, M.I.; Muneer, M.; Jamal, M.A.; Bokhari, T.H.; Wahid, A.; Ullah, S.; Amrane, A.; Hadadi, A.; Tahraoui, H.; Mouni, L. A Study of Treatment of Reactive Red 45 Dye by Advanced Oxidation Processes and Toxicity Evaluation Using Bioassays. Sustainability 2023, 15, 7256. [Google Scholar] [CrossRef]
- Ke, J.; Liu, J.; Sun, H.; Zhang, H.; Duan, X.; Liang, P.; Li, X.; Tade, M.O.; Liu, S.; Wang, S. Facile Assembly of Bi2O3/Bi2S3/MoS2 n-p Heterojunction with Layered n-Bi2O3 and p-MoS2 for Enhanced Photocatalytic Water Oxidation and Pollutant Degradation. Appl. Catal. B Environ. 2017, 200, 47–55. [Google Scholar] [CrossRef]
- Natarajan, T.S.; Thampi, K.R.; Tayade, R.J. Visible Light Driven Redox-Mediator-Free Dual Semiconductor Photocatalytic Systems for Pollutant Degradation and the Ambiguity in Applying Z-Scheme Concept. Appl. Catal. B Environ. 2018, 227, 296–311. [Google Scholar] [CrossRef]
- Shao, X.; Wang, J.; Liu, Z.; Hu, N.; Liu, M.; Duan, C.; Zhang, R.; Quan, C. Cellulose Based Cation-Exchange Fiber as Filtration Material for the Rapid Removal of Methylene Blue from Wastewater. Cellulose 2021, 28, 9355–9367. [Google Scholar] [CrossRef]
- Aghigh, A.; Alizadeh, V.; Wong, H.Y.; Islam, M.S.; Amin, N.; Zaman, M. Recent Advances in Utilization of Graphene for Filtration and Desalination of Water: A Review. Desalination 2015, 365, 389–397. [Google Scholar] [CrossRef]
- Dickhout, J.M.; Moreno, J.; Biesheuvel, P.M.; Boels, L.; Lammertink, R.G.H.; de Vos, W.M. Produced Water Treatment by Membranes: A Review from a Colloidal Perspective. J. Colloid Interface Sci. 2017, 487, 523–534. [Google Scholar] [CrossRef]
- Kenfoud, H.; Baaloudj, O.; Nasrallah, N.; Bagtache, R.; Assadi, A.A.; Trari, M. Structural and electrochemical characterizations of Bi12CoO20 sillenite crystals: Degradation and reduction of organic and inorganic pollutants. J. Mater. Sci. Mater. Electron. 2021, 32, 16411–16420. [Google Scholar] [CrossRef]
- Bekru, A.G.; Tufa, L.T.; Zelekew, O.A.; Goddati, M.; Lee, J.; Sabir, F.K. Green Synthesis of a CuO–ZnO Nanocomposite for Efficient Photodegradation of Methylene Blue and Reduction of 4-Nitrophenol. ACS Omega 2022, 7, 30908–30919. [Google Scholar] [CrossRef]
- Siong, V.L.E.; Lee, K.M.; Juan, J.C.; Lai, C.W.; Tai, X.H.; Khe, C.S. Removal of Methylene Blue Dye by Solvothermally Reduced Graphene Oxide: A Metal-Free Adsorption and Photodegradation Method. RSC Adv. 2019, 9, 37686–37695. [Google Scholar] [CrossRef]
- Baaloudj, O.; Assadi, A.A.; Azizi, M.; Kenfoud, H.; Trari, M.; Amrane, A.; Assadi, A.A.; Nasrallah, N. Synthesis and Characterization of ZnBi2O4 Nanoparticles: Photocatalytic Performance for Antibiotic Removal under Different Light Sources. Appl. Sci. 2021, 11, 3975. [Google Scholar] [CrossRef]
- Madi, K.; Chebli, D.; Ait Youcef, H.; Tahraoui, H.; Bouguettoucha, A.; Kebir, M.; Zhang, J.; Amrane, A. Green Fabrication of ZnO Nanoparticles and ZnO/rGO Nanocomposites from Algerian Date Syrup Extract: Synthesis, Characterization, and Augmented Photocatalytic Efficiency in Methylene Blue Degradation. Catalysts 2024, 14, 62. [Google Scholar] [CrossRef]
- Boillereau, C.; Peulon, S. An Efficient Eco-Friendly Water Depollution Process Based on Electrodeposited Birnessite Thin Films Coupled to Electrochemistry: Application to Methylene Blue Degradation as Phenothiazines Model Molecule. J. Water Process Eng. 2023, 54, 104024. [Google Scholar] [CrossRef]
- Shokoohi, R.; Nematollahi, D.; Samarghandi, M.R.; Azarian, G.; Latifi, Z. Optimization of Three-Dimensional Electrochemical Process for Degradation of Methylene Blue from Aqueous Environments Using Central Composite Design. Environ. Technol. Innov. 2020, 18, 100711. [Google Scholar] [CrossRef]
- Fadillah, G.; Saleh, T.A.; Wahyuningsih, S.; Putri, E.N.K.; Febrianastuti, S. Electrochemical Removal of Methylene Blue Using Alginate-Modified Graphene Adsorbents. Chem. Eng. J. 2019, 378, 122140. [Google Scholar] [CrossRef]
- Panizza, M.; Barbucci, A.; Ricotti, R.; Cerisola, G. Electrochemical Degradation of Methylene Blue. Sep. Purif. Technol. 2007, 54, 382–387. [Google Scholar] [CrossRef]
- Huang, Z.; Li, Y.; Chen, W.; Shi, J.; Zhang, N.; Wang, X.; Li, Z.; Gao, L.; Zhang, Y. Modified Bentonite Adsorption of Organic Pollutants of Dye Wastewater. Mater. Chem. Phys. 2017, 202, 266–276. [Google Scholar] [CrossRef]
- Konicki, W.; Aleksandrzak, M.; Mijowska, E. Equilibrium, Kinetic and Thermodynamic Studies on Adsorption of Cationic Dyes from Aqueous Solutions Using Graphene Oxide. Chem. Eng. Res. Des. 2017, 123, 35–49. [Google Scholar] [CrossRef]
- Ngabura, M.; Hussain, S.A.; Ghani, W.A.W.A.; Jami, M.S.; Tan, Y.P. Utilization of Renewable Durian Peels for Biosorption of Zinc from Wastewater. J. Environ. Chem. Eng. 2018, 6, 2528–2539. [Google Scholar] [CrossRef]
- Hamri, N.; Imessaoudene, A.; Hadadi, A.; Cheikh, S.; Boukerroui, A.; Bollinger, J.-C.; Amrane, A.; Tahraoui, H.; Tran, H.N.; Ezzat, A.O. Enhanced Adsorption Capacity of Methylene Blue Dye onto Kaolin through Acid Treatment: Batch Adsorption and Machine Learning Studies. Water 2024, 16, 243. [Google Scholar] [CrossRef]
- Somasekhara Reddy, M.C.; Sivaramakrishna, L.; Varada Reddy, A. The Use of an Agricultural Waste Material, Jujuba Seeds for the Removal of Anionic Dye (Congo Red) from Aqueous Medium. J. Hazard. Mater. 2012, 203–204, 118–127. [Google Scholar] [CrossRef]
- Marković, S.; Stanković, A.; Lopičić, Z.; Lazarević, S.; Stojanović, M.; Uskoković, D. Application of Raw Peach Shell Particles for Removal of Methylene Blue. J. Environ. Chem. Eng. 2015, 3, 716–724. [Google Scholar] [CrossRef]
- Goswami, M.; Phukan, P. Enhanced Adsorption of Cationic Dyes Using Sulfonic Acid Modified Activated Carbon. J. Environ. Chem. Eng. 2017, 5, 3508–3517. [Google Scholar] [CrossRef]
- Imessaoudene, A.; Cheikh, S.; Bollinger, J.-C.; Belkhiri, L.; Tiri, A.; Bouzaza, A.; El Jery, A.; Assadi, A.; Amrane, A.; Mouni, L. Zeolite Waste Characterization and Use as Low-Cost, Ecofriendly, and Sustainable Material for Malachite Green and Methylene Blue Dyes Removal: Box–Behnken Design, Kinetics, and Thermodynamics. Appl. Sci. 2022, 12, 7587. [Google Scholar] [CrossRef]
- Belhouchat, N.; Zaghouane-Boudiaf, H.; Viseras, C. Removal of Anionic and Cationic Dyes from Aqueous Solution with Activated Organo-Bentonite/Sodium Alginate Encapsulated Beads. Appl. Clay Sci. 2017, 135, 9–15. [Google Scholar] [CrossRef]
- Albadarin, A.B.; Collins, M.N.; Naushad, M.; Shirazian, S.; Walker, G.; Mangwandi, C. Activated Lignin-Chitosan Extruded Blends for Efficient Adsorption of Methylene Blue. Chem. Eng. J. 2017, 307, 264–272. [Google Scholar] [CrossRef]
- Guediri, A.; Bouguettoucha, A.; Chebli, D.; Chafai, N.; Amrane, A. Molecular Dynamic Simulation and DFT Computational Studies on the Adsorption Performances of Methylene Blue in Aqueous Solutions by Orange Peel-Modified Phosphoric Acid. J. Mol. Struct. 2019, 1202, 127290. [Google Scholar] [CrossRef]
- Amrhar, O.; El Gana, L.; Mobarak, M. Calculation of Adsorption Isotherms by Statistical Physics Models: A Review. Environ. Chem. Lett. 2021, 19, 4519–4547. [Google Scholar] [CrossRef]
- Dotto, G.L.; Pinto, L.A.A.; Hachicha, M.A.; Knani, S. New Physicochemical Interpretations for the Adsorption of Food Dyes on Chitosan Films Using Statistical Physics Treatment. Food Chem. 2015, 171, 1–7. [Google Scholar] [CrossRef]
- Knani, S.; Khalfaoui, M.; Hachicha, M.A.; Ben Lamine, A.; Mathlouthi, M. Modelling of Water Vapour Adsorption on Foods Products by a Statistical Physics Treatment Using the Grand Canonical Ensemble. Food Chem. 2012, 132, 1686–1692. [Google Scholar] [CrossRef]
- Gong, R.; Jin, Y.; Chen, J.; Hu, Y.; Sun, J. Removal of Basic Dyes from Aqueous Solution by Sorption on Phosphoric Acid Modified Rice Straw. Dyes Pigments 2007, 73, 332–337. [Google Scholar] [CrossRef]
- Kousha, M.; Daneshvar, E.; Sohrabi, M.S.; Jokar, M.; Bhatnagar, A. Adsorption of Acid Orange II Dye by Raw and Chemically Modified Brown Macroalga Stoechospermum Marginatum. Chem. Eng. J. 2012, 192, 67–76. [Google Scholar] [CrossRef]
- Yu, J.; Tong, M.; Sun, X.; Li, B. A Simple Method to Prepare Poly(Amic Acid)-Modified Biomass for Enhancement of Lead and Cadmium Adsorption. Biochem. Eng. J. 2007, 33, 126–133. [Google Scholar] [CrossRef]
- Bohli, T.; Ouederni, A.; Fiol, N.; Villaescusa, I. Evaluation of an Activated Carbon from Olive Stones Used as an Adsorbent for Heavy Metal Removal from Aqueous Phases. Comptes Rendus Chim. 2015, 18, 88–99. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, M.; Wang, H.; Li, Z. Enhancement of CO2 Adsorption on High Surface Area Activated Carbon Modified by N2, H2 and Ammonia. Chem. Eng. J. 2010, 160, 571–577. [Google Scholar] [CrossRef]
- Baaloudj, O.; Kenfoud, H.; Badawi, A.K.; Assadi, A.A.; El Jery, A.; Assadi, A.A.; Amrane, A. Bismuth Sillenite Crystals as Recent Photocatalysts for Water Treatment and Energy Generation: A Critical Review. Catalysts 2022, 12, 500. [Google Scholar] [CrossRef]
- Kebir, M.; Tahraoui, H.; Chabani, M.; Trari, M.; Noureddine, N.; Assadi, A.A.; Amrane, A.; Ben Hamadi, N.; Khezami, L. Water Cleaning by a Continuous Fixed-Bed Column for Cr (VI) Eco-Adsorption with Green Adsorbent-Based Biomass: An Experimental Modeling Study. Processes 2023, 11, 363. [Google Scholar] [CrossRef]
- Djama, C.; Bouguettoucha, A.; Chebli, D.; Amrane, A.; Tahraoui, H.; Zhang, J.; Mouni, L. Experimental and Theoretical Study of Methylene Blue Adsorption on a New Raw Material, Cynara Scolymus—A Statistical Physics Assessment. Sustainability 2023, 15, 10364. [Google Scholar] [CrossRef]
- Foo, K.Y.; Hameed, B.H. Insights into the Modeling of Adsorption Isotherm Systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Kumar, K.V.; Porkodi, K.; Rocha, F. Isotherms and Thermodynamics by Linear and Non-Linear Regression Analysis for the Sorption of Methylene Blue onto Activated Carbon: Comparison of Various Error Functions. J. Hazard. Mater. 2008, 151, 794–804. [Google Scholar] [CrossRef] [PubMed]
- Langmuir, I. The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Sivarajasekar, N.; Baskar, R. Adsorption of Basic Magenta II onto H2SO4 Activated Immature Gossypium hirsutum Seeds: Kinetics, Isotherms, Mass Transfer, Thermodynamics and Process Design. Arab. J. Chem. 2019, 12, 1322–1337. [Google Scholar] [CrossRef]
- Bounaas, M.; Bouguettoucha, A.; Chebli, D.; Reffas, A.; Harizi, I.; Rouabah, F.; Amrane, A. High Efficiency of Methylene Blue Removal Using a Novel Low-Cost Acid Treated Forest Wastes, Cupressus semperirens Cones: Experimental Results and Modeling. Part. Sci. Technol. 2019, 37, 504–513. [Google Scholar] [CrossRef]
- Redlich, O.; Peterson, D.L. A Useful Adsorption Isotherm. J. Phys. Chem. 1959, 63, 1024. [Google Scholar] [CrossRef]
- Baghdadi, M. UT (University of Tehran) Isotherm as a Novel and Useful Adsorption Isotherm for Investigation of Adsorptive Removal of Pollutants. J. Environ. Chem. Eng. 2017, 5, 1906–1919. [Google Scholar] [CrossRef]
- Lagergren, S. Zur Theorie Der Sogenannten Adsorption Geloster Stoffe. K. Sven. Vetenskapsakademiens Handl. 1898, 24, 1–39. [Google Scholar]
- Özer, A. Removal of Pb(II) Ions from Aqueous Solutions by Sulphuric Acid-Treated Wheat Bran. J. Hazard. Mater. 2007, 141, 753–761. [Google Scholar] [CrossRef] [PubMed]
- Bouguettoucha, A.; Chebli, D.; Mekhalef, T.; Noui, A.; Amrane, A. The Use of a Forest Waste Biomass, Cone of Pinus Brutia for the Removal of an Anionic Azo Dye Congo Red from Aqueous Medium. Desalination Water Treat. 2015, 55, 1956–1965. [Google Scholar] [CrossRef]
- Khalfaoui, M.; Knani, S.; Hachicha, M.A.; Lamine, A.B. New Theoretical Expressions for the Five Adsorption Type Isotherms Classified by BET Based on Statistical Physics Treatment. J. Colloid Interface Sci. 2003, 263, 350–356. [Google Scholar] [CrossRef]
- Sellaoui, L.; Guedidi, H.; Knani, S.; Reinert, L.; Duclaux, L.; Ben Lamine, A. Application of Statistical Physics Formalism to the Modeling of Adsorption Isotherms of Ibuprofen on Activated Carbon. Fluid Phase Equilibria 2015, 387, 103–110. [Google Scholar] [CrossRef]
- Mobarak, M.; Mohamed, E.A.; Selim, A.Q.; Eissa, M.F.; Seliem, M.K. Experimental Results and Theoretical Statistical Modeling of Malachite Green Adsorption onto MCM–41 Silica/Rice Husk Composite Modified by Beta Radiation. J. Mol. Liq. 2019, 273, 68–82. [Google Scholar] [CrossRef]
- Aouaini, F.; Knani, S.; Yahia, M.B.; Bahloul, N.; Kechaou, N.; Lamine, A.B. Application of Statistical Physics on the Modeling of Water Vapor Desorption Isotherms. Dry. Technol. 2014, 32, 1905–1922. [Google Scholar] [CrossRef]
- Tahraoui, H.; Belhadj, A.-E.; Amrane, A.; Houssein, E.H. Predicting the Concentration of Sulfate Using Machine Learning Methods. Earth Sci. Inform. 2022, 15, 1023–1044. [Google Scholar] [CrossRef]
- Tahraoui, H.; Belhadj, A.-E.; Triki, Z.; Boudellal, N.R.; Seder, S.; Amrane, A.; Zhang, J.; Moula, N.; Tifoura, A.; Ferhat, R. Mixed Coagulant-Flocculant Optimization for Pharmaceutical Effluent Pretreatment Using Response Surface Methodology and Gaussian Process Regression. Process Saf. Environ. Prot. 2023, 169, 909–927. [Google Scholar] [CrossRef]
- Yahoum, M.M.; Toumi, S.; Hentabli, S.; Tahraoui, H.; Lefnaoui, S.; Hadjsadok, A.; Amrane, A.; Kebir, M.; Moula, N.; Assadi, A.A.; et al. Experimental Analysis and Neural Network Modeling of the Rheological Behavior of Xanthan Gum and Its Derivatives. Materials 2023, 16, 2565. [Google Scholar] [CrossRef] [PubMed]
- Nedjhioui, M.; Nasrallah, N.; Kebir, M.; Tahraoui, H.; Bouallouche, R.; Assadi, A.A.; Amrane, A.; Jaouadi, B.; Zhang, J.; Mouni, L. Designing an Efficient Surfactant–Polymer–Oil–Electrolyte System: A Multi-Objective Optimization Study. Processes 2023, 11, 1314. [Google Scholar] [CrossRef]
- Tahraoui, H.; Toumi, S.; Hassein-Bey, A.H.; Bousselma, A.; Sid, A.N.E.H.; Belhadj, A.-E.; Triki, Z.; Kebir, M.; Amrane, A.; Zhang, J. Advancing Water Quality Research: K-Nearest Neighbor Coupled with the Improved Grey Wolf Optimizer Algorithm Model Unveils New Possibilities for Dry Residue Prediction. Water 2023, 15, 2631. [Google Scholar] [CrossRef]
- Liao, P.; Malik Ismael, Z.; Zhang, W.; Yuan, S.; Tong, M.; Wang, K.; Bao, J. Adsorption of Dyes from Aqueous Solutions by Microwave Modified Bamboo Charcoal. Chem. Eng. J. 2012, 195–196, 339–346. [Google Scholar] [CrossRef]
- Tran, H.N.; Wang, Y.-F.; You, S.-J.; Chao, H.-P. Insights into the Mechanism of Cationic Dye Adsorption on Activated Charcoal: The Importance of π–π Interactions. Process Saf. Environ. Prot. 2017, 107, 168–180. [Google Scholar] [CrossRef]
- Kumar, A.; Jena, H.M. Preparation and Characterization of High Surface Area Activated Carbon from Fox Nut (Euryale Ferox) Shell by Chemical Activation with H3PO4. Results Phys. 2016, 6, 651–658. [Google Scholar] [CrossRef]
- Nahil, M.A.; Williams, P.T. Pore Characteristics of Activated Carbons from the Phosphoric Acid Chemical Activation of Cotton Stalks. Biomass Bioenergy 2012, 37, 142–149. [Google Scholar] [CrossRef]
- Basu, S.; Ghosh, G.; Saha, S. Adsorption Characteristics of Phosphoric Acid Induced Activation of Bio-Carbon: Equilibrium, Kinetics, Thermodynamics and Batch Adsorber Design. Process Saf. Environ. Prot. 2018, 117, 125–142. [Google Scholar] [CrossRef]
- Guo, J.; Lua, A.C. Textural and Chemical Properties of Adsorbent Prepared from Palm Shell by Phosphoric Acid Activation. Mater. Chem. Phys. 2003, 80, 114–119. [Google Scholar] [CrossRef]
- Paduraru, C.; Tofan, L.; Teodosiu, C.; Bunia, I.; Tudorachi, N.; Toma, O. Biosorption of Zinc(II) on Rapeseed Waste: Equilibrium Studies and Thermogravimetric Investigations. Process Saf. Environ. Prot. 2015, 94, 18–28. [Google Scholar] [CrossRef]
- Hameed, B.H.; Ahmad, A.A. Batch Adsorption of Methylene Blue from Aqueous Solution by Garlic Peel, an Agricultural Waste Biomass. J. Hazard. Mater. 2009, 164, 870–875. [Google Scholar] [CrossRef]
- Donohue, M.D.; Aranovich, G.L. Classification of Gibbs Adsorption Isotherms. Adv. Colloid Interface Sci. 1998, 76–77, 137–152. [Google Scholar] [CrossRef]
- Kumar, K.V.; Kumaran, A. Removal of Methylene Blue by Mango Seed Kernel Powder. Biochem. Eng. J. 2005, 27, 83–93. [Google Scholar] [CrossRef]
- Chebli, D.; Bouguettoucha, A.; Mekhalef, T.; Nacef, S.; Amrane, A. Valorization of an Agricultural Waste, Stipa Tenassicima Fibers, by Biosorption of an Anionic Azo Dye, Congo Red. Desalination Water Treat. 2015, 54, 245–254. [Google Scholar] [CrossRef]
- Vieira, S.S.; Magriotis, Z.M.; Santos, N.A.V.; das Gracas Cardoso, M.; Saczk, A.A. Macauba Palm (Acrocomia aculeata) Cake from Biodiesel Processing: An Efficient and Low Cost Substrate for the Adsorption of Dyes. Chem. Eng. J. 2012, 183, 152–161. [Google Scholar] [CrossRef]
- Manna, S.; Roy, D.; Saha, P.; Gopakumar, D.; Thomas, S. Rapid Methylene Blue Adsorption Using Modified Lignocellulosic Materials. Process Saf. Environ. Prot. 2017, 107, 346–356. [Google Scholar] [CrossRef]
- Messaoudi, N.E.; Dbik, A.; Khomri, M.E.; Sabour, A.; Bentahar, S.; Lacherai, A. Date Stones of Phoenix dactylifera and Jujube Shells of Ziziphus lotus as Potential Biosorbents for Anionic Dye Removal. Int. J. Phytoremediation 2017, 19, 1047–1052. [Google Scholar] [CrossRef]
- Yahia, M.B.; Knani, S.; Hsan, L.B.H.; Yahia, M.B.; Nasri, H.; Ben Lamine, A. Statistical Studies of Adsorption Isotherms of Iron Nitrate and Iron Chloride on a Thin Layer of Porphyrin. J. Mol. Liq. 2017, 248, 235–245. [Google Scholar] [CrossRef]
- Knani, S.; Aouaini, F.; Bahloul, N.; Khalfaoui, M.; Hachicha, M.A.; Ben Lamine, A.; Kechaou, N. Modeling of Adsorption Isotherms of Water Vapor on Tunisian Olive Leaves Using Statistical Mechanical Formulation. Phys. Stat. Mech. Its Appl. 2014, 400, 57–70. [Google Scholar] [CrossRef]
- Li, Z.; Sellaoui, L.; Dotto, G.L.; Lamine, A.B.; Bonilla-Petriciolet, A.; Hanafy, H.; Belmabrouk, H.; Netto, M.S.; Erto, A. Interpretation of the Adsorption Mechanism of Reactive Black 5 and Ponceau 4R Dyes on Chitosan/Polyamide Nanofibers via Advanced Statistical Physics Model. J. Mol. Liq. 2019, 285, 165–170. [Google Scholar] [CrossRef]
- Sellaoui, L.; Knani, S.; Erto, A.; Hachicha, M.A.; Ben Lamine, A. Equilibrium Isotherm Simulation of Tetrachlorethylene on Activated Carbon Using the Double Layer Model with Two Energies: Steric and Energetic Interpretations. Fluid Phase Equilibria 2016, 408, 259–264. [Google Scholar] [CrossRef]
- Mechati, S.; Zamouche, M.; Tahraoui, H.; Filali, O.; Mazouz, S.; Bouledjemer, I.N.E.; Toumi, S.; Triki, Z.; Amrane, A.; Kebir, M. Modeling and Optimization of Hybrid Fenton and Ultrasound Process for Crystal Violet Degradation Using AI Techniques. Water 2023, 15, 4274. [Google Scholar] [CrossRef]


| Porosity (%) | Apparent Density (g mL−1) | Moisture Content (%) | Ash Content (%) | Acidity (m eq g g−1) | Basicity (m eq g g−1) | pHPCZ | pH in Water Solution | |
|---|---|---|---|---|---|---|---|---|
| ZJS | 80.21 ± 2 | 0.031 ± 0.005 | 0.15 ± 0.003 | 33.12 ± 2 | 0.31 ± 0.01 | 0.32 ± 0.01 | 7.4 ± 0.1 | 6.5 ± 0.1 |
| ZJS-H3PO4 | 87.29 ± 2 | 0.034 ± 0.005 | 0.12 ± 0.003 | 31.42 ± 2 | 0.35 ± 0.01 | 0.30 ± 0.01 | 6.8 ± 0.1 | 6.1 ± 0.1 |
| Elemental Composition by XRF | ||||||||
| Element | C (%) | O (%) | Mg (%) | Al (%) | Si (%) | P (%) | Others | |
| ZJS | 48.700 | 50.400 | 0.131 | 0.048 | 0.044 | 0.030 | 0.647 | |
| ZJS-H3PO4 | 47.500 | 51.700 | 0.022 | 0.106 | 0.150 | 0.110 | 0.412 | |
| Biosorbant | Qe (mg g−1) | Reference |
|---|---|---|
| Ziziphus jujuba stones (ZJS-H3PO4) | 179.83 | This work |
| Peach shells | 183.6 | [33] |
| Mango seed kernel | 142.9 | [78] |
| S. tenassicima fiber | 5.35 | [79] |
| Treated Macauba palm cake | 33.06 | [80] |
| Treated lignocellulosic | 769 | [81] |
| Models | Parameters | 25 °C | 30 °C | 40 °C | ||||
|---|---|---|---|---|---|---|---|---|
| Langmuir | Qexp (mg/g) | 160.85 | 173.45 | 179.83 | ||||
| Qm (mg/g) | 160.57 | 172.71 | 176.99 | |||||
| KL (L/mg) | 0.391 | 0.467 | 0.189 | |||||
| R2 | 0.977 | 0.968 | 0.981 | |||||
| APE (%) | 0.524 | 1.214 | 0.421 | |||||
| RL | 50 mg/L | 500 mg/L | 50 mg/L | 500 mg/L | 50 mg/L | 500 mg/L | ||
| 0.056 | 0.006 | 0.093 | 0.010 | 0.519 | 0.098 | |||
| Freundlich | 1/n | 0.125 | 0.116 | 0.123 | ||||
| KF(mg/g) (L/mg) 1/n | 82.710 | 90.734 | 91.973 | |||||
| R2 | 0.853 | 0.517 | 0.542 | |||||
| APE (%) | 4.265 | 10.351 | 11.125 | |||||
| Sips | Qm (mg/g) | 170.50 | 177.16 | 176.37 | ||||
| KS (L/mg) | 0.369 | 0.017 | 0.180 | |||||
| m | 0.645 | 0.223 | 1.18778 | |||||
| R2 | 0.976 | 0.958 | 0.949 | |||||
| APE (%) | 0.854 | 1.958 | 3.874 | |||||
| kRP (L/g) | 87.166 | 95.14 | 30.40 | |||||
| Redlich–Peterson | αR (L/mg) | 0.680 | 0.609 | 0.146 | ||||
| βR | 0.956 | 0.980 | 1.03 | |||||
| R2 | 0.972 | 0.958 | 0.928 | |||||
| APE (%) | 1.231 | 2.847 | 3.145 | |||||
| Model | Parameters | C0 (mg/L) | ||
|---|---|---|---|---|
| 50 | 100 | 150 | ||
| PFO | Qexp, (mg g−1) | 50.00 | 93.27 | 129.14 |
| Qecal, (mg g−1) | 48.89 | 90.86 | 116.10 | |
| K1, (min−1) | 1.06 | 0.188 | 0.289 | |
| R2 | 0.984 | 0.993 | 0.903 | |
| APE (%) | 3.128 | 2.452 | 5.763 | |
| PSO | Qecal, (mg g−1) | 49.75 | 95.69 | 121.01 |
| K2 × 104, (gmg−1 min−1) | 0.055 | 0.004 | 0.003 | |
| R2 | 0.996 | 0.978 | 0.975 | |
| APE (%) | 0.961 | 1.623 | 3.842 | |
| PNO | Qecal, (mg g−1) | 51.19 | 91.21 | 135.54 |
| kn, (min−1) (mg g−1) 1−n | 0.0022 | 0.115 | 1.64 × 10−6 | |
| n | 3.20 | 1.12 | 3.74 | |
| R2 | 0.998 | 0.993 | 0.991 | |
| APE (%) | 0.232 | 0.292 | 0.312 | |
| T (°C) | 25 °C | 30 °C | 40 °C | |||
|---|---|---|---|---|---|---|
| Model | R2 | AIC | R2 | AIC | R2 | AIC |
| Monolayer | 0.99126 | 6.01 | 0.99417 | 6.00 | 0.99721 | 6.00 |
| Double-layer model with two energies | 0.99109 | 8.01 | 0.99353 | 8.00 | 0.99811 | 8.00 |
| Double-layer model with one energy | 0.99109 | 6.01 | 0.99353 | 6.00 | 0.99811 | 6.00 |
| Limited multilayer | 0.999317 | 10.02 | 0.99447 | 10.00 | 0.99879 | 10.00 |
| Q0 | C1/2 | nm | R2 | |
|---|---|---|---|---|
| T = 25 °C | 172.17 | 2.76 | 0.61 | 099126 |
| T = 30 °C | 177.50 | 1.97 | 0.75 | 0.99417 |
| T = 40 °C | 172.14 | 5.69 | 1.49 | 0.99721 |
| Kernel Function | Basis Function | Kernel Scale | Sigma | R | RMSE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SigmaM | SigmaF | Train | Test | Val | ALL | Train | Test | Val | ALL | |||
| ARD-Exponential | Constant | 1.7642 83.2462 0.0347 0.2946 9.4089 | 8.6461 | 0.7340 | 0.9997 | 0.9997 | 0.9998 | 0.9998 | 0.312 | 0.161 | 0.346 | 0.2805 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guediri, A.; Bouguettoucha, A.; Tahraoui, H.; Chebli, D.; Zhang, J.; Amrane, A.; Khezami, L.; Assadi, A.A. The Enhanced Adsorption Capacity of Ziziphus jujuba Stones Modified with Ortho-Phosphoric Acid for Organic Dye Removal: A Gaussian Process Regression Approach. Water 2024, 16, 1208. https://doi.org/10.3390/w16091208
Guediri A, Bouguettoucha A, Tahraoui H, Chebli D, Zhang J, Amrane A, Khezami L, Assadi AA. The Enhanced Adsorption Capacity of Ziziphus jujuba Stones Modified with Ortho-Phosphoric Acid for Organic Dye Removal: A Gaussian Process Regression Approach. Water. 2024; 16(9):1208. https://doi.org/10.3390/w16091208
Chicago/Turabian StyleGuediri, Abderraouf, Abdallah Bouguettoucha, Hichem Tahraoui, Derradji Chebli, Jie Zhang, Abdeltif Amrane, Lotfi Khezami, and Amin Aymen Assadi. 2024. "The Enhanced Adsorption Capacity of Ziziphus jujuba Stones Modified with Ortho-Phosphoric Acid for Organic Dye Removal: A Gaussian Process Regression Approach" Water 16, no. 9: 1208. https://doi.org/10.3390/w16091208
APA StyleGuediri, A., Bouguettoucha, A., Tahraoui, H., Chebli, D., Zhang, J., Amrane, A., Khezami, L., & Assadi, A. A. (2024). The Enhanced Adsorption Capacity of Ziziphus jujuba Stones Modified with Ortho-Phosphoric Acid for Organic Dye Removal: A Gaussian Process Regression Approach. Water, 16(9), 1208. https://doi.org/10.3390/w16091208










