Abstract
With global warming and intensified human activities, extreme convective precipitation has become one of the most frequent natural disasters. An accurate and reliable assessment of severe convective precipitation events can support social stability and economic development. In order to investigate the accuracy enhancement methods and data fusion strategies for the assessment of severe convective precipitation events, this study is driven by the horizontal reflectance factor (ZH) and differential reflectance (ZDR) of the dual-polarization radar. This research work utilizes microphysical information of convective storms provided by radar variables to construct the precipitation event assessment model. Considering the problems of high dimensionality of variable data and low computational efficiency, this study proposes a dual-polarization radar echo-data-layering strategy. Combined with the results of mutual information (MI), this study constructs Bayes–Kalman filter (KF) models (RF, SVR, GRU, LSTM) for the assessment of severe convective precipitation events. Finally, this study comparatively analyzes the evaluation effectiveness and computational efficiency of different models. The results show that the data-layering strategy is able to reduce the data dimensions of 256 × 256 × 34,978 to 5 × 2213, which greatly improves the computational efficiency. In addition, the correlation coefficient of interval III–V calibration period is increased to 0.9, and the overall assessment accuracy of the model is good. Among them, the Bayes–KF-LSTM model has the best assessment effect, and the Bayes–KF-RF has the highest computational efficiency. Further, five typical precipitation events are selected for validation in this study. The stratified precipitation dataset agrees well with the near-surface precipitation, and the model’s assessment values are close to the observed values. This study completely utilizes the microphysical information offered by dual-polarized radar ZH and ZDR in precipitation event assessment, which provides a wide range of application possibilities for the assessment of severe convective precipitation events.
1. Introduction
In recent years, with global warming and intensified human activities, extreme precipitation weather often occurs in many regions of the world [1,2,3,4]. This type of weather causes serious urban disasters annually, leads to large-scale power outages, and seriously threatens both lives and social stability [5,6]. Heavy precipitation is highly heterogeneous in time and space, making accurate and reliable prediction challenging. Therefore, developing high-precision and high-resolution assessments of the timing and intensity of precipitation has become an urgent problem for meteorological departments [7,8,9].
Precipitation forecasting is an important issue in the field of meteorology, and the two mainstream methods are numerical model forecasting and radar echo extrapolation [10]. Numerical models forecast future atmospheric conditions by solving equations for atmospheric dynamics and thermodynamics, predicting further into the future than radar methods [11]. Compared with the radar echo extrapolation method, the numerical model can obtain the forecast results for a longer period of time in the future, but it also has some drawbacks. First, there are numerous uncertainties in the process of numerical simulation, such as inaccurate initial conditions and parameterization of physical processes [12]. The effect of the above factors can lead to a decrease in the reliability of the numerical model results [13]. Second, measurement errors in the input data make the solution process error magnified. Based on real-time radar images acquired, the radar echo extrapolation method realizes the prediction and assessment of precipitation events by analyzing the moving trend, shape and intensity changes of strong storms [14,15]. Capecchi et al. [16] investigated the impact of assimilated radar and automated weather station data on precipitation forecasts to improve the accuracy of early forecasting systems. The study by Ansh Srivastava et al. [17] demonstrated the important role played by radar echo data in extreme rainfall forecasting. Further, numerous scholars have conducted in-depth studies on the assessment of extreme rainfall forecasting based on radar echoes. However, these methods use only a small number of historical radar echo images to predict the next radar echo image. This results in low model data utilization, while the effective forecast time usually cannot exceed one hour [18].
In recent years, with the accumulation of big data and the development of computer arithmetic power, artificial intelligence and deep learning techniques have developed rapidly [19]. Deep learning methods are data-driven with strong nonlinear mapping capabilities and theoretically improve as the volume of training data increases. These methods are particularly well-suited for short-range forecasting, where extensive radar observation data are available [20]. Based on the scale-invariant feature transform (SIFT) and UNet convolutional neural network methods, Yao et al. [21,22] performed 0–2 h proximity forecasting of strong convective weather. Yu et al. [23] used a recurrent convolutional neural network in the UNet framework for 0–2 h proximity forecasting and achieved good results in some weather conditions. While the integration of deep learning has enhanced severe convective weather now-casting, challenges persist in managing massive radar raster datasets; these include overfitting, slow training speeds, and limited applicability [24].
The technology of combining dual linearly polarized weather radars and phased array antenna scanning modes has become increasingly mature over the past few years [25]. At the same time, Doppler radars with dual-polarization capability have been progressively upgraded in recent years [26,27]. Compared with the single-polarization weather radar, the bilinear polarization radar can simultaneously transmit polarized electromagnetic waves in the horizontal and vertical directions. It can obtain more accurate hydrometeorological estimation, which plays an important role in the prediction and monitoring of extreme precipitation events [28,29]. In addition, polarized radar variables such as differential reflectivity (ZDR) and specific differential phase (KDP) can provide richer convective storm microphysical information than radar reflectivity [30]. Meanwhile, ZDR and KDP contain the unique properties of raindrop size and distribution. These attributes may change greatly in different stages of storm evolution, thus helping to provide information on storm evolution [31]. Therefore, dual-polarization radar variables have great potential to improve the nowcasting of convective precipitation [32].
This study advances beyond traditional numerical simulations based on radar echoes by introducing a stratification strategy for radar echo data and developing a precipitation event evaluation model utilizing intelligent learning techniques. Compared with the current mainstream convolutional neural network method, this study greatly reduces the data dimension, improves the model’s computing efficiency, and enhances the model’s generalization performance. The findings demonstrate that the radar echo data stratification strategy and the intelligent learning-based precipitation evaluation method offer high computational reliability and efficiency, showcasing substantial practical value.
The rest of this paper is organized as follows. Section 2 introduces the data sources and quality control methods in detail. Meanwhile, the precipitation event assessment system based on radar echo data is presented in Section 3. Then, the result analysis and application cases are given in Section 4. Finally, and analysis and discussion are presented in Section 5. The general framework of this study is shown in Figure 1.
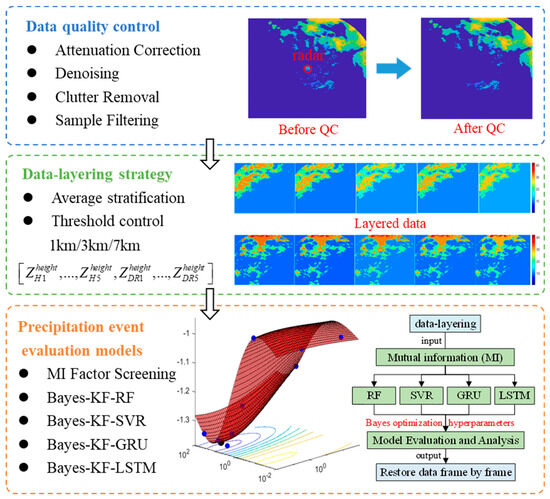
Figure 1.
The overall framework of severe convective precipitation evaluation method.
2. Dataset and Experimental Design
2.1. NJU-CPOL Dataset
Dual-polarization radar (DPR) is a radar system that uses two different polarizations, usually horizontal (H) and vertical (V) polarization. It transmits horizontal or vertical polarized microwave pulse signals through the antenna system, and obtains the following three microphysical variables for precipitation assessment. The horizontal reflectivity factor (ZH) is the echo intensity in the horizontal direction, which mainly reflects the strength of precipitation. Differential reflectivity (ZDR) is the difference in echo intensity between the horizontal and vertical directions, which mainly reflects the size of the precipitation particles in the observation area. The specific differential phase shift (KDP) is the phase difference between the horizontal and vertical echoes caused by precipitation particles per unit distance, which mainly reflects the liquid water content. Wen et al. [33,34] deeply studied the performance of KDP in simulating near-surface precipitation and proved its excellent performance. In addition, the radar system can also obtain reflected signals at different altitudes by adjusting the elevation angle of the antenna to cover the vertical height range of interest.
This study uses data from the NJU C-band dual-polarization weather radar, partially derived from Pan et al. [32]. The dataset (called NJU-CPOL) covers a total of 268 precipitation events from 2014 to 2019, including 35,133 data files. However, Pan et al. [32] only provided a dataset of dual-polarization radar at 3 km. This study collected and supplemented 1 km, 7 km ZH and ZDR datasets and near-surface precipitation (Rt) datasets. Referring to the work of Huang et al. [34,35], the near-surface precipitation calculation method used in this study is . At the same time, the radar data have been subjected to quality control and interpolated to Cartesian coordinates. All the data in this study have a spatial resolution of 1 km in the horizontal direction, and contain CAPPI (Constant altitude Plan Projection Indicator) data at altitudes of 1 km, 3 km, and 7 km in a 256 × 256 km area around the radar center, and the overall dataset has a temporal resolution of 6–7 min.
2.2. Experimental Design
In this study, the ZH and ZDR datasets under 1 km, 3 km and 7 km are used as the assessment factor sets for the rainfall event Rt. Firstly, we screen the evaluation factors at different time steps. These factors will be used as input data for the rainfall event assessment model. Equation (1) is the formula for evaluating rainfall events using ZH, ZDR factors under different time steps.
where is the near-surface precipitation event at moment t; M is the assessment model; Optional is the factor selection mechanism; is the ZH value at moment t at a height of 1 km, and and are similar; is the ZDR value at moment t at a height of 1 km, and and are similar; and K is the time step. We set the time step to be 5 when we performed the factor selection.
2.3. Evaluating Indicator
In this study, three evaluation metrics, namely correlation coefficient (r), root mean square error (RMSE) and mean absolute error (MAE), were used to assess the performance of the evaluation model. The calculation formula is as follows:
where cov(X, Y) is the covariance; var(X) is the variance; Ri is the observed value of the precipitation event; is the assessed value of the precipitation event; and n is the data length.
3. Methodology
3.1. Data-Layering Strategy
Considering that the weak precipitation scenario has limited reference significance for this study, this study set the minimum threshold of precipitation data coverage in the data-processing stage. Specifically, when the proportion of rainfall data exceeded 10% of the study area (256 × 256 km), we retained the data of the precipitation event. Meanwhile, the ZH and ZDR data under 1 km, 3 km and 7 km corresponding to the precipitation events that did not satisfy the threshold were excluded. We also removed redundant data (radar stations, building reflections) and anomalies, and replaced those exceeding the range of values with the mean of the surrounding values. Through this screening method, a total of 2213 valid precipitation event data files were collected and organized to provide data support for this study.
Eventually, the processed ZH values were restricted to the interval [0, 65] while the ZDR values were restricted to the interval [−1, 5]. Since there is an exponential relationship between radar reflectivity and precipitation intensity, the larger the reflectivity, the stronger the rainfall intensity. Therefore, in this study, the ZH of 1 km, 3 km and 7 km were all divided into five layers according to the target interval (0, 65]. At the same time, the raster positions after stratification according to ZH were mapped into ZDR and R, which, in turn, yielded the five-layer stratified data of ZDR and R under the heights of 1 km, 3 km and 7 km. In stratification, the non-zero values of each layer are summed up and averaged as the value of the layer, and different layers correspond to different intensities of precipitation, and the intensity of precipitation increases in the order of Ⅰ–Ⅴ layers.
The stratified frame-by-frame ZH and ZDR value factor sets are used as the factor set to be selected for the precipitation data Rt.
where height is the dual-polarization radar scanning height, which is 1 km, 3 km and 7 km, respectively.
3.2. Factor Screening Method
In this study, mutual information (MI) was used to assess the degree of correlation between ZH, ZDR and the rainfall event Rt at different heights and time steps. MI is a useful information metric in information theory that can be considered as the amount of information a random variable contains about another random variable. It is used to represent the degree of interdependence between variables [36,37]. Unlike the correlation coefficient, mutual information is not restricted to real-valued random variables; it is more general and determines the degree of similarity between the product of the joint and marginal distributions p(X), p(Y).
In general, the mutual information of two discrete random variables X and Y can be defined as follows:
where p(x, y) is the joint density function of X and Y, and p(x) and p(y) are the edge density functions of X and Y, respectively.
3.3. Data Noise Reduction Method
To reduce the effect of systematic errors in dual- polarization radar observation data, this work uses the Kalman filtering (KF) approach for smoothing and noise reduction in hierarchically processed radar data [38]. KF is renowned for its ability to estimate the state of dynamic systems accurately, making it particularly suited for sensor data plagued by noise. This technique not only forecasts system state variables effectively and optimizes future state predictions but also adeptly handles measurement errors and uncertainties inherent in system dynamics [39]. KF has been widely used as an extremely effective estimation tool in a variety of fields such as aerospace, navigation, robotics, finance, and signal processing. Its core idea is to characterize the system state in terms of a probability distribution and to continuously update this distribution to integrate new dynamic and measurement information in order to improve the accuracy of estimating the state of a dynamic system.
3.4. Rainfall Assessment Model
3.4.1. Random Forest
Random Forest (RF) is an integrated learning algorithm especially for classification and regression tasks. RF employs Bootstrap resampling to create multiple subsets from the original training set, each of which is used to build a decision tree [40,41]. It improves the accuracy and robustness of the model by constructing multiple decision trees and merging their results to obtain the final prediction. The Random Forest algorithm excels at coping with multidimensional inputs, determining the relevance of variables, and maintaining high classification accuracy. The effectiveness of the RF model hinges on various hyperparameters, including the number of trees, the branching complexity of these trees, and the data volume in their leaf nodes. To identify optimal hyperparameter settings, this paper employs Bayesian optimization, a method that effectively adapts to diverse data characteristics and enhances the model’s generalization capability.
3.4.2. Support Vector Regression
Support Vector Regression (SVR) is a regression method based on Support Vector Machine (SVM). The core idea of SVR lies in determining a hyperplane that approximates all training datasets as closely as possible [42,43]. Different from the goal of SVM to find the maximum interval between classifications, the goal of SVR is to make the hyperplane contain as many data points as possible while ensuring that the error is within an acceptable range. In many practical applications, SVR has become a widely used regression method because of its robustness and high efficiency. In this study, the Bayesian method is used to optimize the key hyperparameters in SVR to improve the performance of the model, such as kernel function type, kernel function parameters, error penalty coefficient and so on.
3.4.3. Gate Recurrent Unit
Gated Recurrent Unit (GRU) is an upgraded form of Recurrent Neural Networks (RNN) that addresses the issues of gradient vanishing and explosion in long-sequence situations. GRU introduces a gating mechanism that is better able to capture long-term dependencies in sequences while reducing the number of parameters [44]. GRU mainly includes two key gating units: Update Gate and Reset Gate. These gating mechanisms allow the GRU network to selectively update the state when processing sequential data while controlling the transmission of information. This method can help the model to identify the key features in the sequence more accurately. In order to improve the evaluation effect of GRU, this paper uses the Bayesian method to optimize some hyperparameters. These hyperparameters include the number of hidden layer nodes, initial learning rate, learning rate decay period, and factor.
3.4.4. Long Short-Term Memory
Since the introduction of the Artificial Neural Network (ANN) in the 1980s, its excellent nonlinear mapping ability has made it the focus of research in many fields. Long Short-Term Memory (LSTM) solves the problem of disappearing or exploding RNN gradients and insufficient long-term memory capacity. It greatly improves the performance of RNN in temporal prediction [45,46]. LSTM is mainly composed of an input gate, output gate and forgetting gate. It has the recursive attribute of RNN and can effectively use long-sequence data information, as shown in Figure 2. The unique memory structure and gating mechanism of LSTM make it well-adapted and reliable in feature learning. Therefore, it is widely used in time series model training. To improve the prediction performance of LSTM, this paper strategically adjusts hyperparameters, including the number of nodes in the hidden layer, the initial learning rate, and the rate of learning decay. Concurrently, it employs optimized L2 regularization to mitigate the risk of overfitting, ensuring a more reliable model performance.
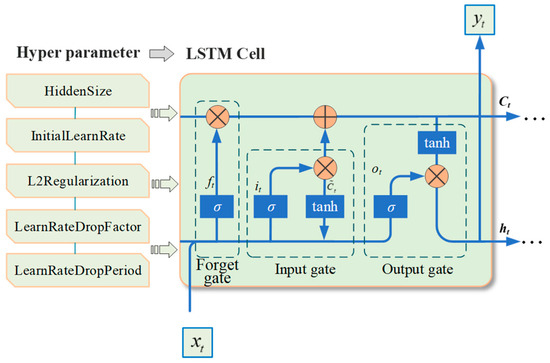
Figure 2.
LSTM hyperparameters and computing cell.
3.4.5. Bayesian Hyperparameter Optimization
In order to improve the evaluation performance of the model, the optimization of model-sensitive hyperparameters is crucial. The traditional exhaustive method is prone to a “dimensional disaster”. In order to avoid this problem, this study uses the Bayesian method to optimize the model’s hyperparameters [47,48]. Compared with other optimization methods, the Bayesian method uses the information of the probability model to find the optimal hyperparameter value faster. The Bayesian optimization method takes the surrogate model as the core. Based on the acquisition function (AF), the Bayesian optimization method selects a hyperparameter that is most promising to improve the performance of the model and updates the surrogate model. It will repeat this process until the optimal hyperparameter value is found.
In conclusion, Bayesian optimization is a powerful global optimization method that is particularly suitable for black-box objective functions that are computationally expensive and have high uncertainty. Therefore, this study uses Bayesian optimization to optimize the hyperparameters of RF, SVR, GRU and LSTM models, as shown in Table 1. In this study, the evaluation model and the Bayesian optimization algorithm are implemented using functions or tools in Matlab.

Table 1.
The optimized hyperparameters of different models.
4. Results Analysis
4.1. Data Stratification Results
This study explores the correlation between dual-polarization radar data and rainfall data from two dimensions of time and space. In the time dimension, this paper takes the sequence of frames in 258 rainfall processes as the timing standard. In the spatial dimension, this paper takes the 256 × 256 km plane area corresponding to each frame of data as the regional standard. According to the range of radar data after processing and the stratification strategy, the ZH value (256 × 256 km) is stratified in this paper. Finally, a total of 2215 hierarchical processing data values were obtained. The distribution of radar echo ZH after stratification is shown in Figure 3.
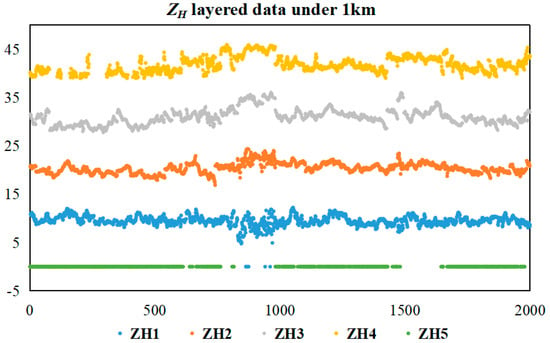
Figure 3.
Distribution of ZH observations after stratification.
The ZH contour plot is divided into five gradients of (0, 13), [13, 26), [26, 39), [39, 52), [52, 65] with 13 dBZ as the gradient. This study was carried out with an example of a precipitation event in the dataset, as shown in Figure 4.
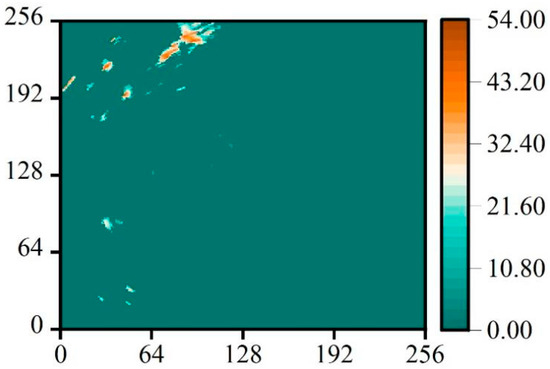
Figure 4.
ZH contour map of a precipitation event.
In this study, a precipitation event is used as an example to plot ZH contour maps under each stratum separately. Figure 5 shows that the ZH values of this precipitation event are concentrated in the Ⅱ and Ⅲ intervals. Since the relationship between radar reflectivity and precipitation intensity is empirically exponential, this indicates that the rainfall is moderate-intensity rainfall.
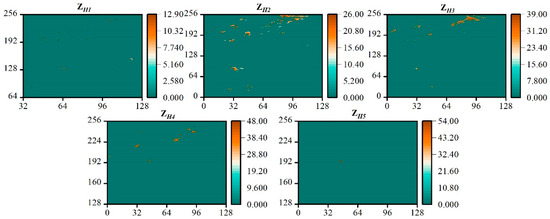
Figure 5.
The heat map of radar echo data after ZH stratification.
4.2. Analysis of MI Results
Combining the hierarchically processed data and the MI analysis method, this study performs correlation analysis on the radar echo data of 1 km, 3 km, and 7 km. The time step of ZH, ZDR, and KDP data is set to 5, and there are a total of 36 prediction factors in each interval. Too low or too high input data dimension will lead to underfitting and overfitting problems in the model. This study comprehensively considers all model features, and finally sets the model’s input dimension to 15.
Table 2 lists the top 15 input features of each interval MI value, and Figure 6 shows the MI vertical diagrams corresponding to 15 input features. Table 2 shows that precipitation events of different intensities are most strongly associated with ZH and ZDR at 1 km, followed by ZH and ZDR at 3 km. This indicates that the higher radar echo data have a limited contribution to the assessment of near-surface precipitation. Meanwhile, the radar echo data’s correlation with precipitation gradually decreases with the increase in time step. Combined with Figure 6, it can be seen that interval IV has the highest MI value and interval I has the lowest MI value. This indicates that there is a complex correlation between the MI value and the intensity of precipitation events.

Table 2.
The model’s input factors of different intervals.
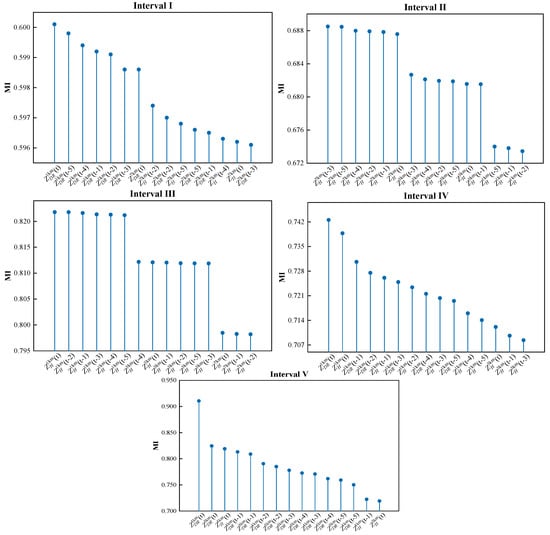
Figure 6.
MI vertical diagrams of different intervals.
4.3. Interval Evaluation Effect
In this study, the Bayesian optimization method described in Section 3.4.5 was used to optimize the hyperparameters of the RF, SVR, GRU and LSTM models. As an example, Figure 7 shows the optimization process of the SVR model for precipitation events Ⅰ-Ⅴ under the Bayesian optimization framework. In this process, the objective function was adjusted according to the research needs, and the BoxConstraint and KernelScale kept changing until the best combination was found. As can be seen in Figure 7, the potential optimal values in the pre-Bayes optimization period are obtained by random search. In this study, the 25 Bayesian iterations process is set, and the model gradually locks in the best combination of parameters. From the final result, the optimization process is very reasonable, and the objective function achieves the minimum requirement.
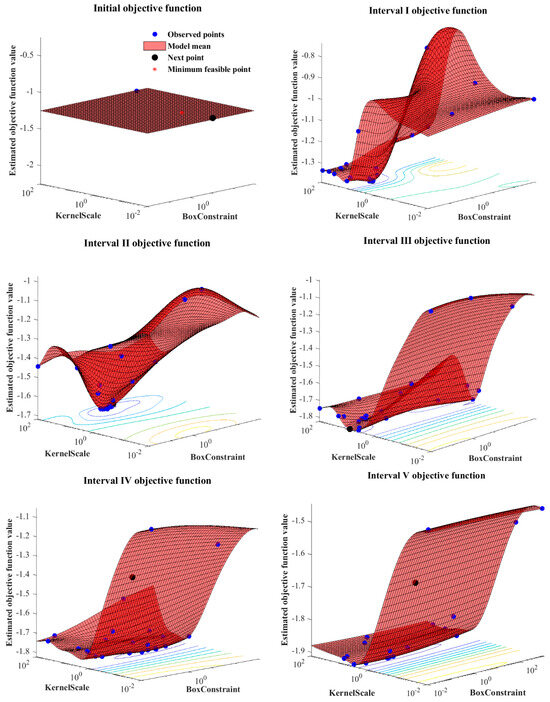
Figure 7.
Bayesian optimization SVR hyperparameter optimization process.
Based on the Bayesian optimization results of the model, this study establishes an assessment method for precipitation events. Table 3 demonstrates the precipitation assessment effect for each interval. The thickened data shows that the corresponding model performs better in this interval. The data in Table 3 show that the performance of precipitation event assessment for each interval is better overall, and the assessment effect of the calibration period is generally better than that of the validation period. This phenomenon may be due to the greater noise in the validation period data. Except for interval 4, the Bayes–KF-LSTM model has the most prominent assessment effect in other intervals, and thus it is recommended as the main precipitation assessment method. It should be noted that interval Ⅰ is relatively poorly assessed, which may be due to the under-representation of the data in the calibration period.

Table 3.
Interval Ⅰ–Ⅴ model precipitation assessment results.
4.4. Representative Cases
In order to evaluate the effectiveness of specific precipitation events, we utilize heat maps to visualize the model’s assessment accuracy before and after applying optimized parameters, combined with typical precipitation events. In Figure 8, we select a total of five typical precipitation event processes, and each typical precipitation time includes the observed value of the precipitation event, the interval stratification value, and the precipitation assessment value. Figure 9 shows that the assessment model’s precipitation events, which accurately predict the likely intensity of upcoming precipitation events, are in good agreement with the observed values, particularly in the region of strong convective precipitation. This makes the practical application of the model better. As the interval increases, that is, as the precipitation intensity continues to increase, the better the forecast effect. This is mainly because the larger the interval level, the fewer the corresponding heavy precipitation events. There are many 0 values in the data, which affect the final evaluation index.
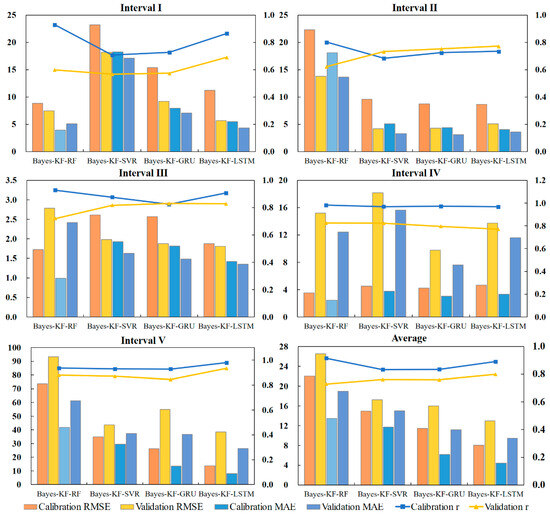
Figure 8.
Each interval index histogram.
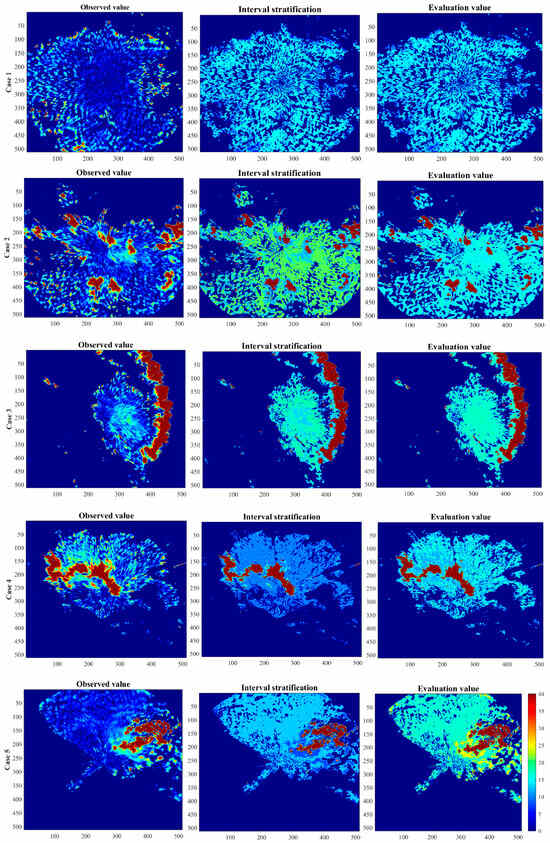
Figure 9.
Heat maps before and after assessment of five typical severe convective precipitation events.
In order to evaluate the computational efficiency of different models and intervals, this study sets the number of Bayes optimizations for each model to 25, and the average of its time is taken for each run 10 times. Table 4 shows the average computational time of different models under each interval, and Figure 10 shows the box plots of the running time of different models and intervals. Overall, RF has the shortest running time and the highest computational efficiency; GRU has the longest running time and the lowest computational efficiency, which may be related to the model’s structure and parameter settings. Combined with Figure 10, it can be seen that, except for the anomalies, the model’s running time is essentially within a reasonable range. At the same time, with the increase in rainfall intensity (Ⅰ–V), the running time of the whole model shows a weak downward trend. This may be due to the fact that there are more 0 values in layers Ⅳ–V after the stratification of heavy rainfall events.

Table 4.
Average running time for each model and interval.
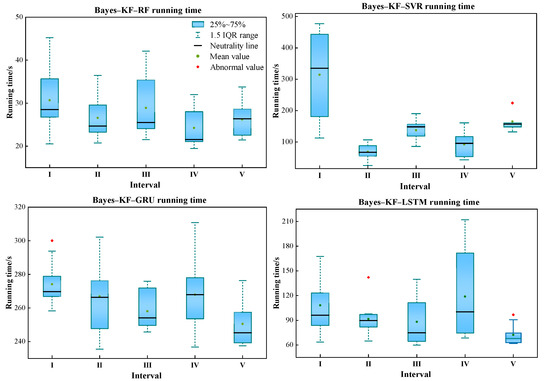
Figure 10.
Box plots of running times for each model and interval.
5. Summary and Discussion
This research work is driven by ZH and ZDR data from dual-polarization radar, and a data-layering strategy is proposed to reduce the data dimensionality. Further, this paper constructs the Bayes–KF-Models for evaluating strong convective precipitation events. The example verification shows that the data stratification strategy proposed in this paper can significantly reduce the data dimension and greatly improve the operation efficiency of the model. Kalman filtering can reduce the interference of radar echo data noise on the model to a certain extent. The radar data after stratification contains microphysical information such as rainfall intensity, which can provide a data basis for model construction. The results of the precipitation assessment model in this paper are very close to the near-surface precipitation data. The correlation coefficient r of the calibration period of the calibration intervals Ⅲ-Ⅴ can reach about 0.9. Among them, the Bayes–KF-LSTM model has the best evaluation effect, followed by the Bayes–KF-RF model. However, the Bayes–KF-RF model has the highest computational efficiency, which has the strong practicability. Considering that the model needs to have better applicability in precipitation events of different intensities, Bayes–KF-RF or Bayes–KF-LSTM are recommended as the main methods for the assessment of intense convective precipitation events.
The evaluation model of strong convective precipitation events constructed in this paper has good applicability and promotion value. However, this research work still requires further discussion, which can be further studied and improved in the future. For example, this study focuses only on the post-processing and assessment of severe convective precipitation events, and is understudied with respect to forecasting issues; the evaluation results of different models are quite different; and the uncertainty characteristics of severe convective precipitation events are difficult to quantify. In the future, research work can consider increasing the fusion results of multi-model evaluation effects to reduce the impact of data noise and system errors. Meanwhile, we need to pay more attention to the precipitation event forecasting method itself. The generalization performance and stability of the model can be improved through the above research. In summary, this study fully exploits the potential of dual-polarimetric radar ZH and ZDR data in precipitation event assessment. This research work can provide new ideas for the assessment of strong convective precipitation events, which has broad application prospects.
Author Contributions
Conceptualization, Z.T.; methodology, X.C.; software, X.C.; validation, Z.T. and W.X.; investigation, W.X.; resources, X.N.; data curation, H.L.; writing—original draft preparation, X.N.; writing—review and editing, X.C., Z.T. and X.N.; visualization, J.G., Z.T. and X.N.; supervision, J.G. and Z.T.; project administration, J.G. and Z.T.; funding acquisition, H.L. and W.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (No. 2021YFC3200301), the National Natural Science Foundation of China (No. 52109004, No. 51979113), and the Open Research Fund of Hubei Technology Innovation Center for Smart Hydropower (No. 1523020038). Special thanks are given to the editors and anonymous reviewers for their constructive comments.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to data copyright issues.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ma, Y.; Hu, Z.; Li, C.; Feng, T.; Meng, X.; Dong, W. Anthropogenic Climate Change Enhances the July 2021 Super-Heavy Rainfall Event in Central China. Bull. Am. Meteorol. Soc. 2023, 104, E736–E741. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, Z.; Meng, X.; Liu, F.; Dong, W. Was the record-breaking mei-yu of 2020 enhanced by regional climate change. Bull. Amer. Meteor. Soc. 2022, 103, S76–S82. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S. Future precipitation changes in Egypt under the 1.5 and 2.0 C global warming goals using CMIP6 multimodel ensemble. Atmos. Res. 2022, 265, 105908. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Wang, M.; Li, Y.; Gong, X.; Chen, Y.; Chen, Y.; Cao, W. Changes in daily extreme temperature and precipitation events in mainland China from 1960 to 2016 under global warming. Int. J. Climatol. 2021, 41, 1465–1483. [Google Scholar] [CrossRef]
- Guo, J.; Feng, T.; Cai, Z.; Lian, X.; Tang, W. Vulnerability Assessment for power transmission lines under typhoon weather based on a cascading failure state transition diagram. Energies 2020, 13, 3681. [Google Scholar] [CrossRef]
- Wang, L.; Dong, Y.; Zhang, C.; Heng, Z. Extreme and severe convective weather disasters: A dual-polarization radar nowcasting method based on physical constraints and a deep neural network model. Atmos. Res. 2023, 289, 106750. [Google Scholar] [CrossRef]
- Cao, X.; Qi, Y.; Ni, G. X-band polarimetric radar QPE for urban hydrology: The increased contribution of high-resolution rainfall capturing. J. Hydrol. 2023, 617, 128905. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Yang, Z.; Wang, J.; Lin, P.; Liang, J.; Li, Z.; Gu, Z. Improving flood simulation capability of the WRF-Hydro-RAPID model using a multi-source precipitation merging method. J. Hydrol. 2021, 592, 125814. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, K.; Chao, L.; Li, D.; Tian, X.; Bao, H.; Chen, G.; Xia, Y. Exploring the utility of radar and satellite-sensed precipitation and their dynamic bias correction for integrated prediction of flood and landslide hazards. J. Hydrol. 2021, 603, 126964. [Google Scholar] [CrossRef]
- Senocak, A.U.G.; Yilmaz, M.T.; Kalkan, S.; Yucel, I.; Amjad, M. An explainable two-stage machine learning approach for precipitation forecast. J. Hydrol. 2023, 627, 130375. [Google Scholar] [CrossRef]
- Nikhil Teja, K.; Manikanta, V.; Das, J.; Umamahesh, N.V. Enhancing the predictability of flood forecasts by combining Numerical Weather Prediction ensembles with multiple hydrological models. J. Hydrol. 2023, 625, 130176. [Google Scholar] [CrossRef]
- Saminathan, S.; Medina, H.; Mitra, S.; Tian, D. Improving short to medium range GEFS precipitation forecast in India. J. Hydrol. 2021, 598, 126431. [Google Scholar] [CrossRef]
- Stevens, B.; Bony, S. What are climate models missing? Science 2013, 340, 1053–1054. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Gao, J.; Zhang, G.; Zhang, F.; Yang, J.; Wang, S.; Xue, B.; Wang, K. A Rolling Real-Time Correction Method for Minute Precipitation Forecast Based on Weather Radars. Water 2023, 15, 1872. [Google Scholar] [CrossRef]
- Tian, W.; Wang, C.L.; Shen, K.L.; Zhang, L.X.; Sian, K. MSLKNet: A Multi-Scale Large Kernel Convolutional Network for Radar Extrapolation. Atmosphere 2024, 15, 52. [Google Scholar] [CrossRef]
- Capecchi, V.; Antonini, A.; Benedetti, R.; Fibbi, L.; Melani, S.; Rovai, L.; Ricchi, A.; Cerrai, D. Assimilating X-and S-band Radar Data for a Heavy Precipitation Event in Italy. Water 2021, 13, 1727. [Google Scholar] [CrossRef]
- Ansh Srivastava, N.; Mascaro, G. Improving the utility of weather radar for the spatial frequency analysis of extreme precipitation. J. Hydrol. 2023, 624, 129902. [Google Scholar] [CrossRef]
- Shi, E.; Li, Q.; Gu, D.; Zhao, Z. A Method of Weather Radar Echo Extrapolation Based on Convolutional Neural Networks. In Proceedings of the 24th International Conference, MMM 2018, Bangkok, Thailand, 5–7 February 2018. [Google Scholar] [CrossRef]
- Song, C.M. Data construction methodology for convolution neural network based daily runoff prediction and assessment of its applicability. J. Hydrol. 2022, 605, 127324. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Y.; Zou, Q.; Ye, L.; Zhu, S.; Zhang, H. Study on optimization and combination strategy of multiple daily runoff prediction models coupled with physical mechanism and LSTM. J. Hydrol. 2023, 624, 129969. [Google Scholar] [CrossRef]
- Trebing, K.; Staǹczyk, T.; Mehrkanoon, S. SmaAt-UNet: Precipitation nowcasting using a small attention-UNet architecture. Pattern Recognit. Lett. 2021, 145, 178–186. [Google Scholar] [CrossRef]
- Yao, Y.; Li, Z. 2017CIKM AnalytiCup 2017: Short-term precipitation forecasting based on radar reflectivity images. In Proceedings of the Conference on Information and Knowledge Management, Short-Term Quantitative Precipitation Forecasting Challenge, Singapore, 6–10 November 2017. [Google Scholar]
- Yu, Z.; Ming, W.; Nan, L.I.; Ilyas, A.M. Improved radar heavy precipitation estimation based on RNN. China Sci. 2020, 15, 585–592. [Google Scholar]
- Guo, J.; Zhou, J.; Qin, H.; Zou, Q.; Li, Q. Monthly streamflow forecasting based on improved support vector machine model. Expert Syst. Appl. 2011, 38, 13073–13081. [Google Scholar] [CrossRef]
- Otsubo, A.; Adachi, A. Short-Term Predictability of Extreme Rainfall Using Dual-Polarization Radar Measurements. J. Meteorol. Soc. Jpn. 2024, 102, 151–165. [Google Scholar] [CrossRef]
- Xiao, M.Y.; Wang, L.; Dong, Y.C.; Zhang, C.H.; Wang, S.J.; Yang, K.Q.; Zhang, K. An early warning approach for the rapid identification of extreme weather disasters based on phased array dual polarization radar cooperative network data. PLoS ONE 2024, 19, e0296044. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Mahale, V.N.; Putnam, B.J.; Qi, Y.; Cao, Q.; Byrd, A.D.; Bukovcic, P.; Zrnic, D.S.; Gao, J.; Xue, M. Current status and future challenges of weather radar polarimetry: Bridging the gap between radar meteorology/hydrology/engineering and numerical weather prediction. Adv. Atmos. Sci. 2019, 36, 571–588. [Google Scholar] [CrossRef]
- Crisologo, I.; Vulpiani, G.; Abon, C.C.; David, C.; Bronstert, A.; Heistermann, M. Polarimetric rainfall retrieval from a C-Band weather radar in a tropical environment (The Philippines). Asia Pac. J. Atmos. Sci. 2014, 50, 595–607. [Google Scholar] [CrossRef]
- Pallardy, Q.; Fox, N.I. Accounting for rainfall evaporation using dual-polarization radar and mesoscale model data. J. Hydrol. 2018, 557, 573–588. [Google Scholar] [CrossRef]
- Zhao, K.; Huang, H.; Wang, M.; Lee, W.; Chen, G.; Wen, L.; Wen, J.; Zhang, G.; Xue, M.; Yang, Z. Recent progress in dual-polarization radar research and applications in China. Adv. Atmos. Sci. 2019, 36, 961–974. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, K.; Xue, M.; Zhang, G.; Liu, S.; Wen, L.; Chen, G. Precipitation microphysics characteristics of a Typhoon Matmo (2014) rainband after landfall over eastern China based on polarimetric radar observations. J. Geophys. Res. Atmos. 2016, 121, 412–415,433. [Google Scholar] [CrossRef]
- Pan, X.; Lu, Y.; Zhao, K.; Huang, H.; Wang, M.; Chen, H. Improving Nowcasting of convective development by incorporating polarimetric radar variables into a deep-learning model. Geophys. Res. Lett. 2021, 48, e2021GL095302. [Google Scholar] [CrossRef]
- Wen, G.; Fox, N.I.; Market, P.S. The Quality Control and Rain Rate Estimation for the X-Band Dual-Polarization Radar: A Study of Propagation of Uncertainty. Remote Sens. 2020, 12, 1072. [Google Scholar] [CrossRef]
- Zhao, G.; Huang, H.; Yu, Y.; Zhao, K.; Yang, Z.W.; Chen, G.; Zhang, Y. Study on the Quantitative Precipitation Estimation of X-Band Dual-Polarization Phased Array Radar from Specific Differential Phase. Remote Sens. 2023, 15, 359. [Google Scholar] [CrossRef]
- Huang, H.; Zhao, K.; Zhang, G.; Lin, Q.; Wen, L.; Chen, G.; Yang, Z.; Wang, M.; Hu, D. Quantitative Precipitation Estimation with Operational Polarimetric Radar Measurements in Southern China: A Differential Phase–Based Variational Approach. J. Atmos. Ocean. Technol. 2018, 35, 1253–1271. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, D.; Zheng, X.; Shan, H.; Zhang, J. Mutual Information Boosted Precipitation Nowcasting from Radar Images. Remote Sens. 2023, 15, 1639. [Google Scholar] [CrossRef]
- Ning, Y.; Liang, G.; Ding, W.; Shi, X.; Fan, Y.; Chang, J.; Wang, Y.; He, B.; Zhou, H. A Mutual Information Theory-Based Approach for Assessing Uncertainties in Deterministic Multi-Category Precipitation Forecasts. Water Resour. Res. 2022, 58, e2022WR032631. [Google Scholar] [CrossRef]
- Na, W.; Yoo, C. Real-time bias correction of Beaslesan dual-pol radar rain rate using the dual Kalman filter. J. Korea Water Resour. Assoc. 2020, 53, 201–214. [Google Scholar]
- Grewal, M.S.; Andrews, A.P.; Bartone, C.G. Kalman Filtering; Wiley Telecom: Hoboken, NJ, USA, 2020. [Google Scholar]
- Chen, C.; Hu, B.; Li, Y. Easy-to-use spatial random-forest-based downscaling-calibration method for producing precipitation data with high resolution and high accuracy. Hydrol. Earth Syst. Sci. 2021, 25, 5667–5682. [Google Scholar] [CrossRef]
- Sekulić, A.; Kilibarda, M.; Heuvelink, G.B.; Nikolić, M.; Bajat, B. Random forest spatial interpolation. Remote Sens. 2020, 12, 1687. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, H.; Zeng, J.; Ma, L.; Guan, L. Short-term dynamic radar quantitative precipitation estimation based on wavelet transform and support vector machine. J. Meteorol. Res. 2020, 34, 413–426. [Google Scholar] [CrossRef]
- Zhang, F.; O’Donnell, L.J. Support vector regression. In Machine Learning; Elsevier: Amsterdam, The Netherlands, 2020; pp. 123–140. [Google Scholar]
- Cho, M.; Kim, C.; Jung, K.; Jung, H. Water level prediction model applying a long short-term memory (lstm)–gated recurrent unit (gru) method for flood prediction. Water 2022, 14, 2221. [Google Scholar] [CrossRef]
- Landi, F.; Baraldi, L.; Cornia, M.; Cucchiara, R. Working memory connections for LSTM. Neural Netw. 2021, 144, 334–341. [Google Scholar] [CrossRef] [PubMed]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Cho, H.; Kim, Y.; Lee, E.; Choi, D.; Lee, Y.; Rhee, W. Basic enhancement strategies when using Bayesian optimization for hyperparameter tuning of deep neural networks. IEEE Access 2020, 8, 52588–52608. [Google Scholar] [CrossRef]
- Lee, S.; Bae, J.H.; Hong, J.; Yang, D.; Panagos, P.; Borrelli, P.; Yang, J.E.; Kim, J.; Lim, K.J. Estimation of rainfall erosivity factor in Italy and Switzerland using Bayesian optimization based machine learning models. Catena 2022, 211, 105957. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).