Post-Analysis of Daniel Extreme Flood Event in Thessaly, Central Greece: Practical Lessons and the Value of State-of-the-Art Water-Monitoring Networks
Abstract
1. Introduction
2. Materials and Methods
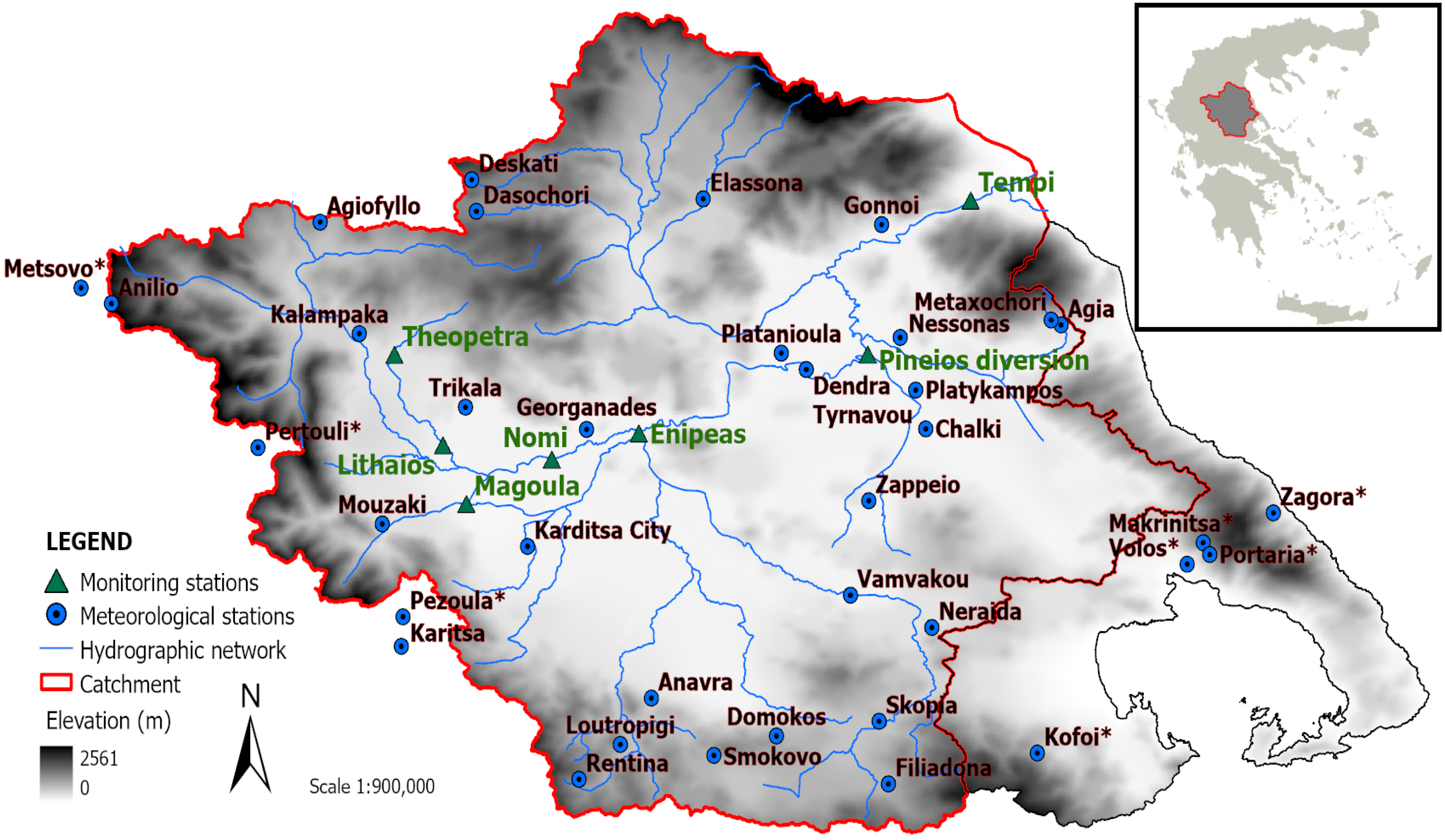
2.1. Study Area
2.1.1. Geomorphology and Climate
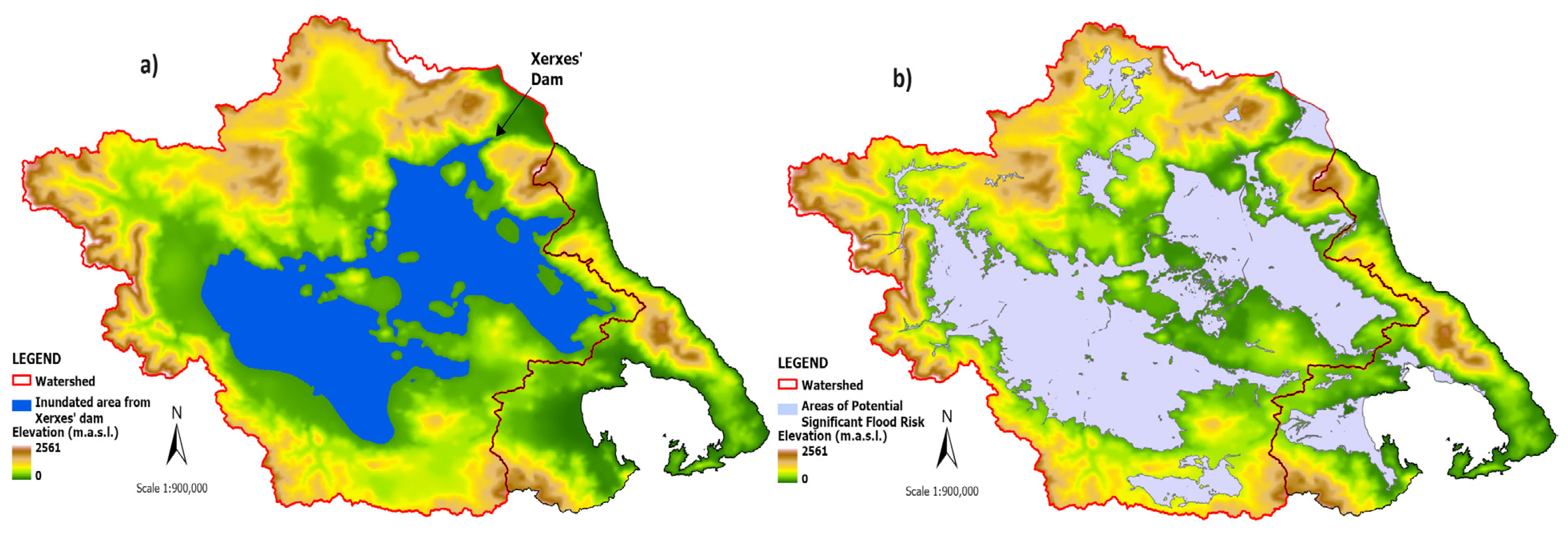
2.1.2. Flood Regime
“Xerxes asked his guides if there were any other outlet for the Peneus into the sea, and they, with their full knowledge of the matter, answered him: “The river, O king, has no other way into the sea, but this alone. This is so because there is a ring of mountains around the whole of Thessaly”. Upon hearing this Xerxes said: “These Thessalians are wise men; this, then, was the primary reason for their precaution long before when they changed to a better mind, for they perceived that their country would be easily and speedily conquerable. It would only have been necessary to let the river out over their land by barring the channel with a dam and to turn it from its present bed so that the whole of Thessaly, with the exception of the mountains, might be under water”.
2.1.3. Hydrometric Network
2.1.4. Rainfall Analysis
2.1.5. Flood-Event Analysis
3. Results
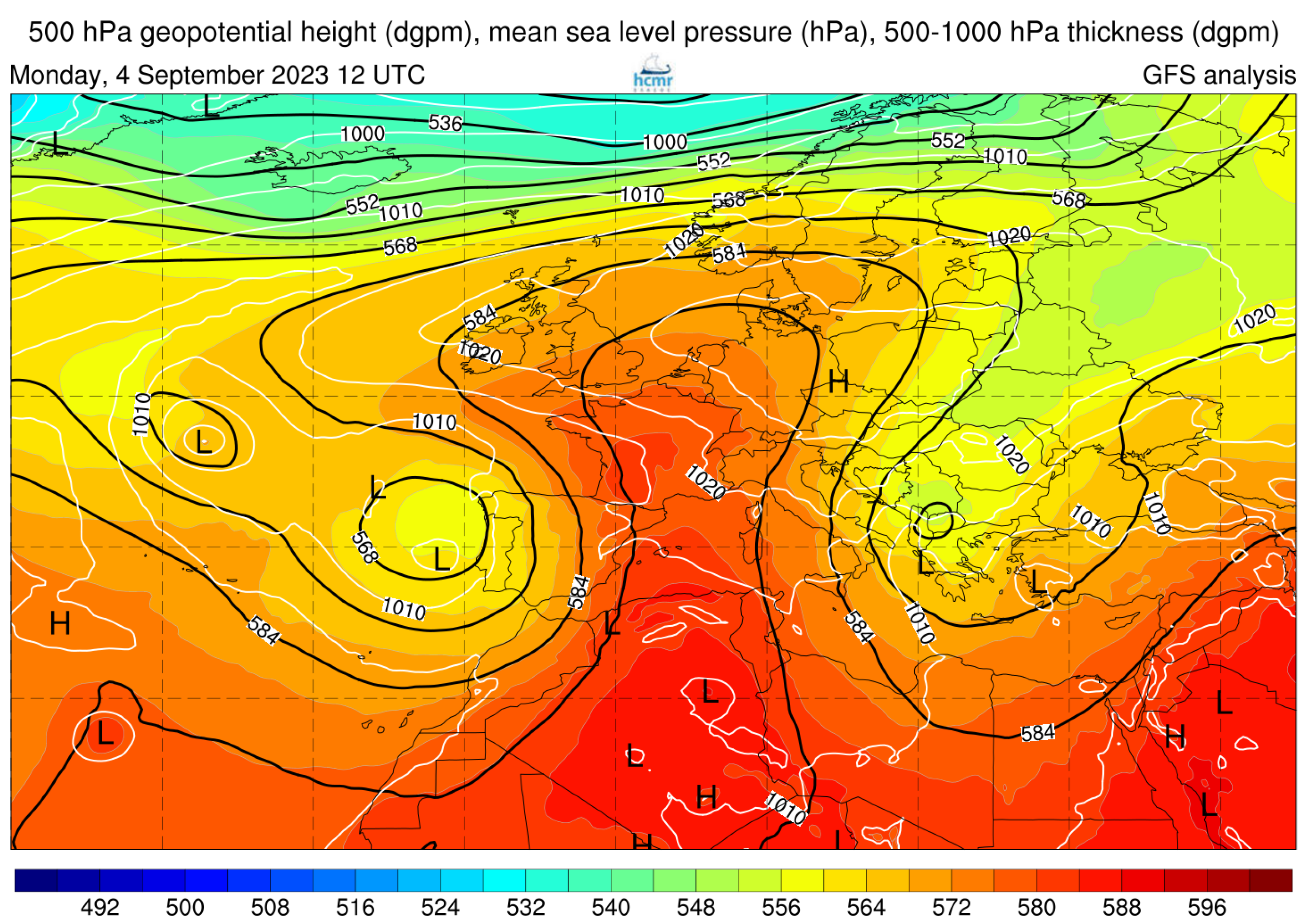
3.1. On the Extremeness of Storm Daniel
3.1.1. Overview and Physical Interpretation
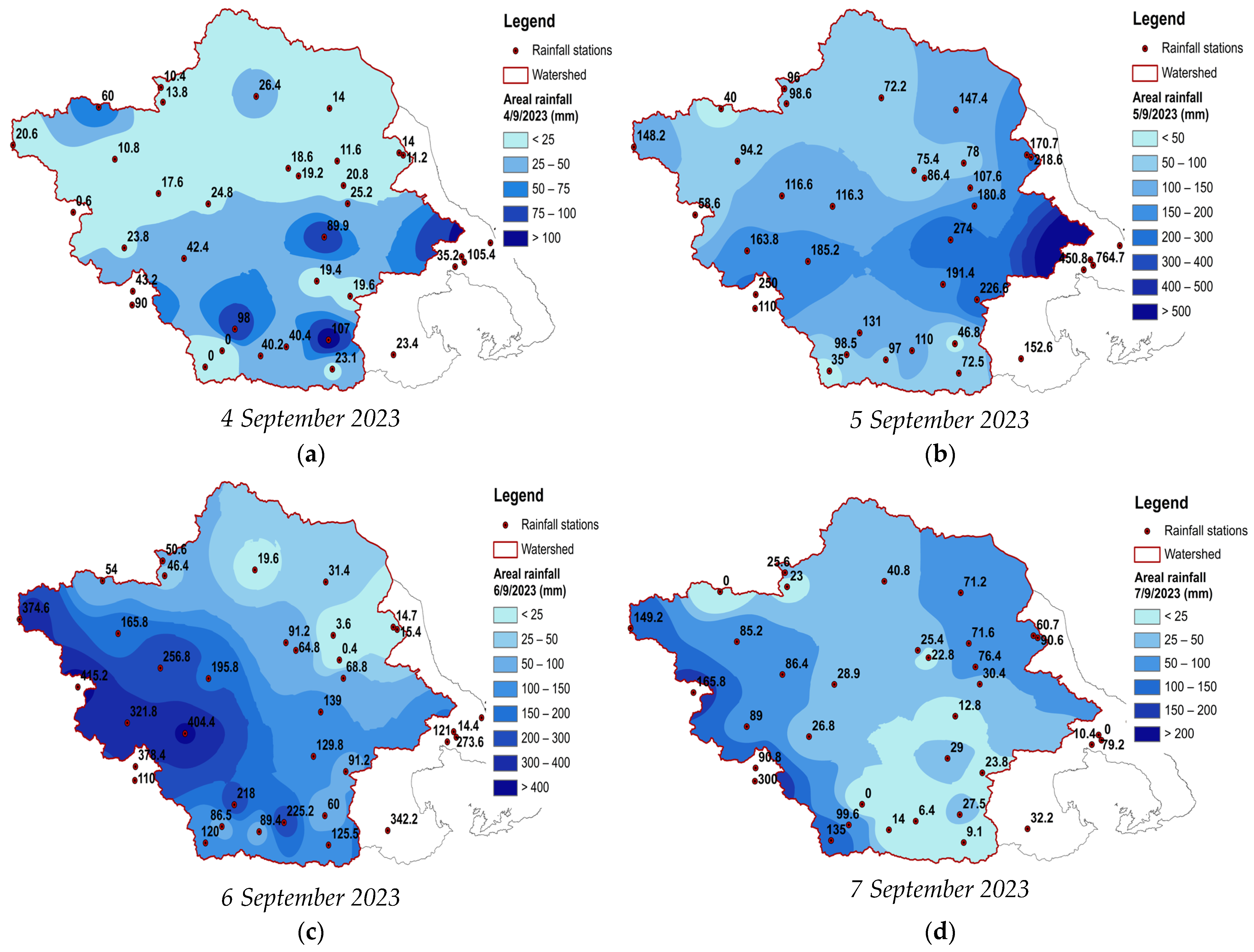
3.1.2. Rainfall Data
3.1.3. Spatiotemporal Analysis
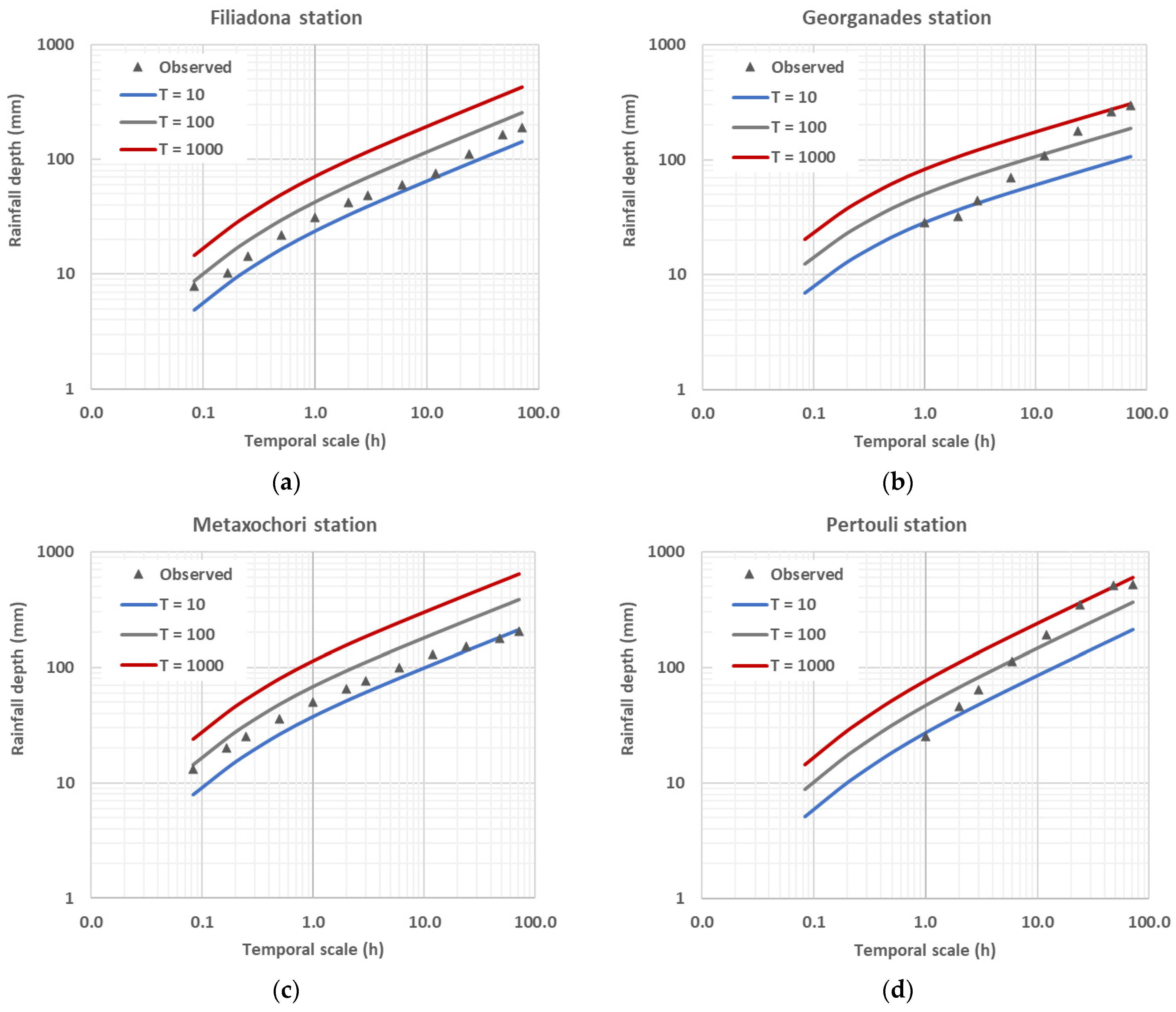
3.1.4. Estimation of Rainfall Return Periods across Stations
3.1.5. Insight into the Temporal Variability of Return Periods
3.2. Disentangling the Flood Phenomenon
3.2.1. Stage Data
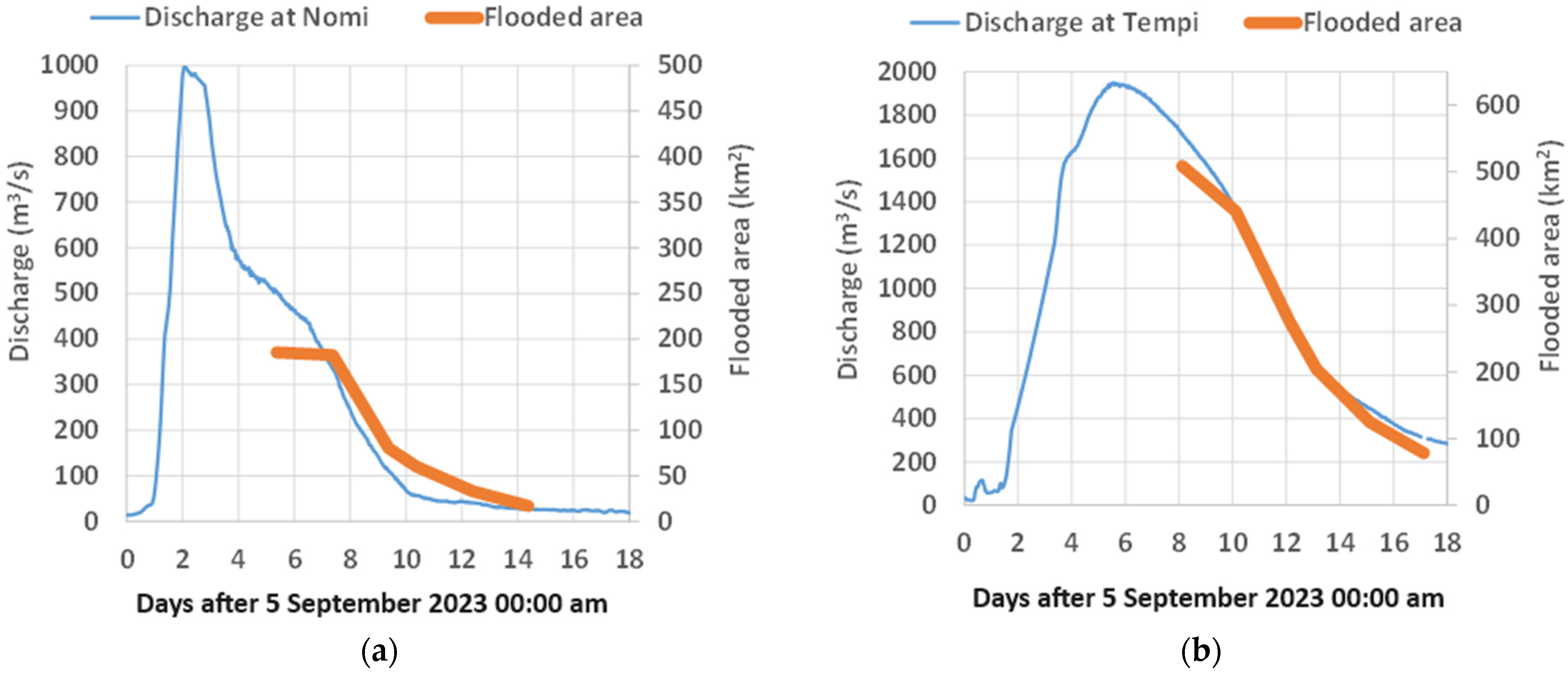
3.2.2. Discharge Analysis and Flood-Inundation Data
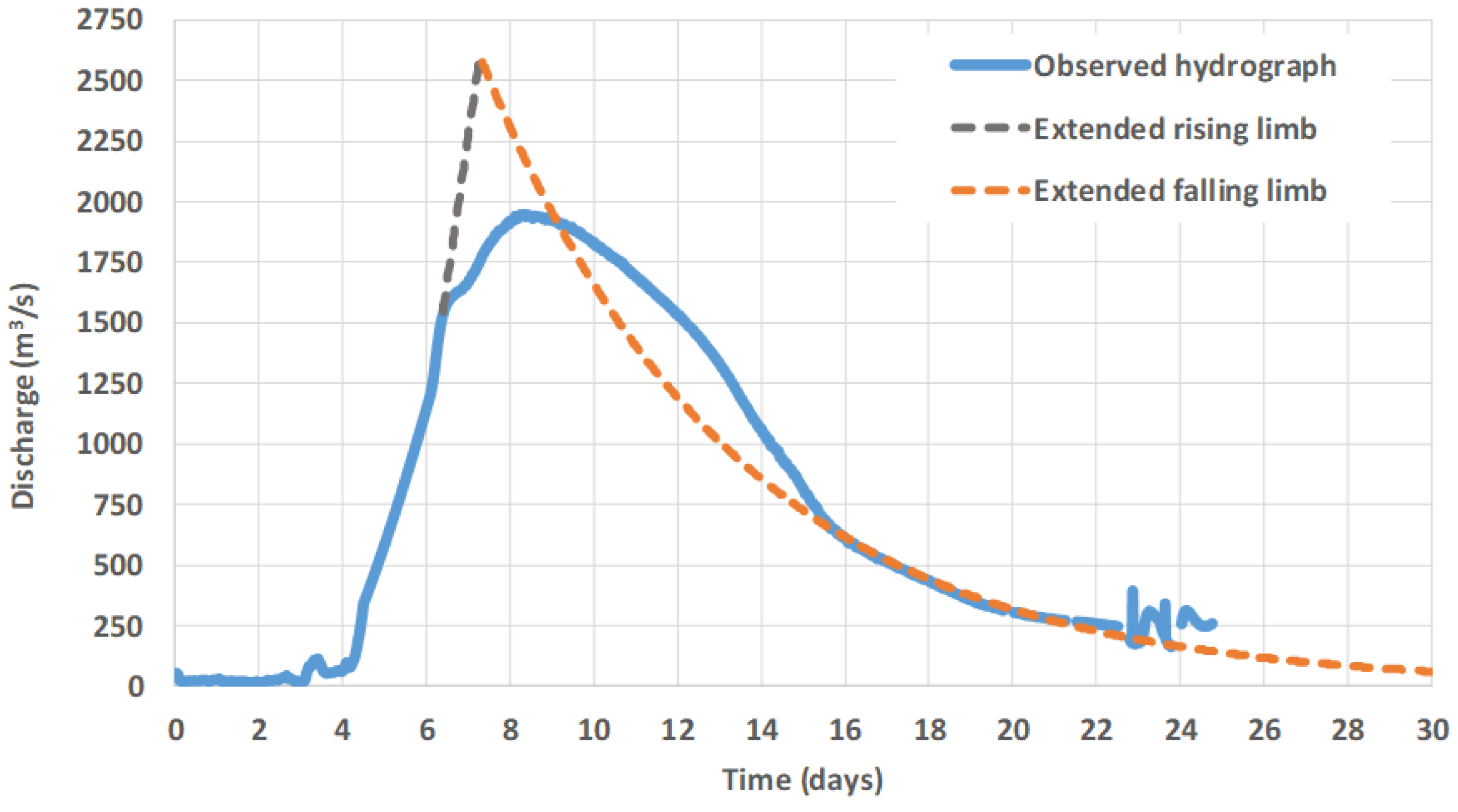
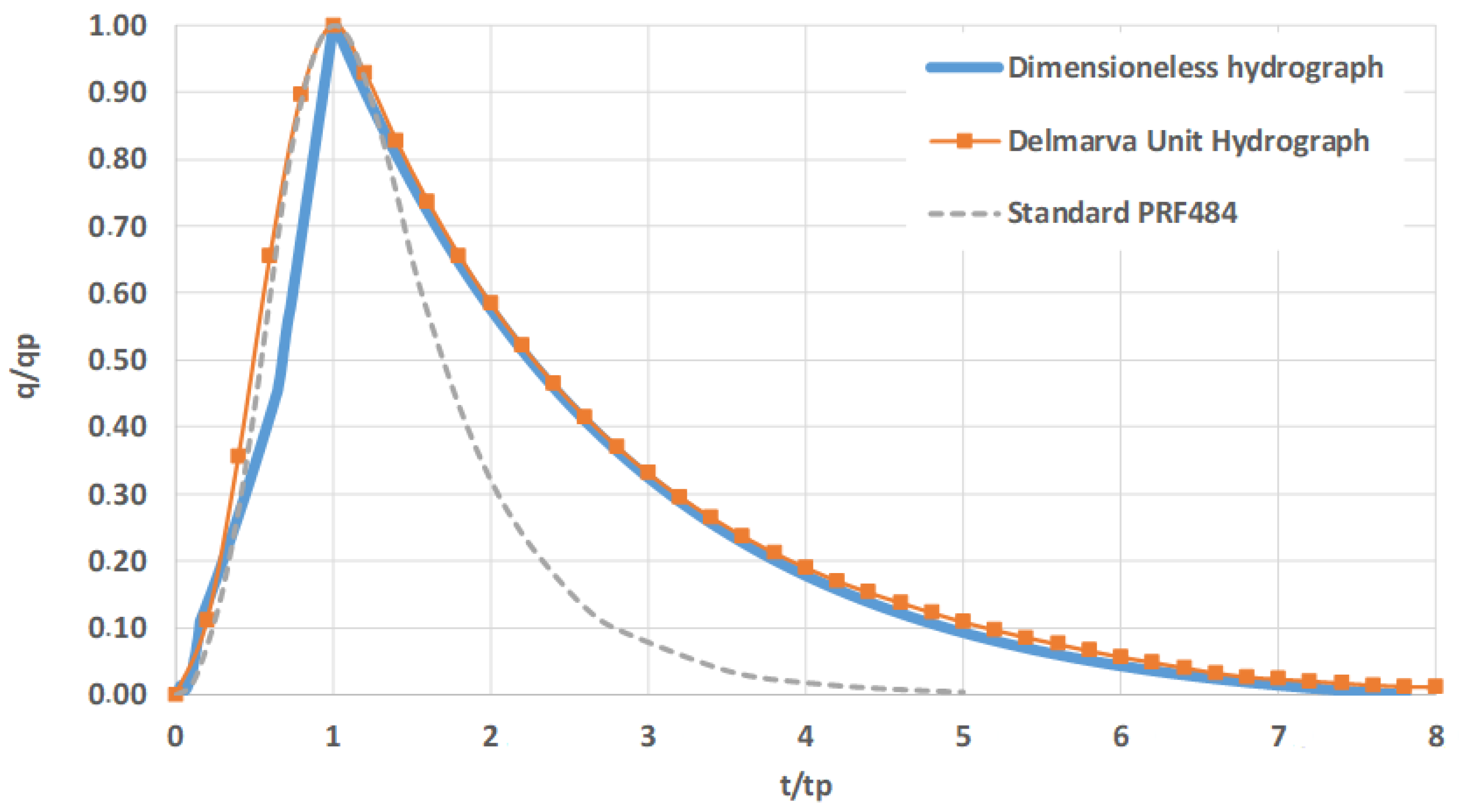
3.2.3. Insight into the Outflow Hydrograph (Tempi Station)
3.2.4. Rainfall–Runoff Analysis and Comparison with Past Events
4. Discussion
4.1. Early Warning Potential through Automatic Monitoring Networks
4.2. Daniel Flood Event
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jonkman, S.N. Global perspectives on loss of human life caused by floods. Nat. Hazards 2005, 34, 151–175. [Google Scholar] [CrossRef]
- Petrucci, O. Factors leading to the occurrence of flood fatalities: A systematic review of research papers published between 2010 and 2020. Nat. Hazards Earth Syst. Sci. 2022, 22, 71–83. [Google Scholar] [CrossRef]
- Ghimire, E.; Sharma, S.; Lamichhane, N. Evaluation of one-dimensional and two-dimensional HEC-RAS models to predict flood travel time and inundation area for flood warning system. ISH J. Hydraul. Eng. 2022, 28, 110–126. [Google Scholar] [CrossRef]
- Merz, B.; Blöschl, G.; Vorogushyn, S.; Dottori, F.; Aerts, J.C.; Bates, P.; Bertola, M.; Kemter, M.; Kreibich, H.; Lall, U.; et al. Causes, impacts and patterns of disastrous river floods. Nat. Rev. Earth Environ. 2021, 2, 592–609. [Google Scholar] [CrossRef]
- Papagiannaki, K.; Petrucci, O.; Diakakis, M.; Kotroni, V.; Aceto, L.; Bianchi, C.; Brázdil, R.; Gelabert, M.G.; Inbar, M.; Kahraman, A.; et al. Developing a large-scale dataset of flood fatalities for territories in the Euro-Mediterranean region, FFEM-DB. Sci. Data 2022, 9, 166. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Huang, W.; McKenzie, J.E.; Xu, R.; Yu, P.; Ye, T.; Wen, B.; Gasparrini, A.; Armstrong, B.; Tong, S.; et al. Mortality risks associated with floods in 761 communities worldwide: Time series study. BMJ 2023, 383, e075081. [Google Scholar] [CrossRef]
- Diakakis, M.; Deligiannakis, G.; Antoniadis, Z.; Melaki, M.; Katsetsiadou, N.K.; Andreadakis, E.; Spyrou, N.I.; Gogou, M. Proposal of a flash flood impact severity scale for the classification and mapping of flash flood impacts. J. Hydrol. 2020, 590, 125452. [Google Scholar] [CrossRef]
- Gaume, E.; Bain, V.; Bernardara, P.; Newinger, O.; Barbuc, M.; Bateman, A.; Blaškovičová, L.; Blöschl, G.; Borga, M.; Dumitrescu, A.; et al. A compilation of data on European flash floods. J. Hydrol. 2009, 367, 70–78. [Google Scholar] [CrossRef]
- Tegos, A.; Ziogas, A.; Bellos, V.; Tzimas, A. Forensic Hydrology: A Complete Reconstruction of an Extreme Flood Event in Data-Scarce Area. Hydrology 2022, 9, 93. [Google Scholar] [CrossRef]
- Avila-Aceves, E.; Plata-Rocha, W.; Monjardin-Armenta, S.A.; Rangel-Peraza, J.G. Geospatial modelling of floods: A literature review. Stoch. Environ. Res. Risk Assess. 2023, 37, 4109–4128. [Google Scholar] [CrossRef]
- Mård, J.; Di Baldassarre, G.; Mazzoleni, M. Nighttime light data reveal how flood protection shapes human proximity to rivers. Sci. Adv. 2018, 4, eaar5779. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Sun, D.; Goldberg, M.D.; Sjoberg, B.; Santek, D.; Hoffman, J.P.; DeWeese, M.; Restrepo, P.; Lindsey, S.; Holloway, E. Automatic near real-time flood detection using Suomi-NPP/VIIRS data. Remote Sens. Environ. 2018, 204, 672–689. [Google Scholar] [CrossRef]
- Pabi, O.; Egyir, S.; Attua, E.M. Flood hazard response to scenarios of rainfall dynamics and land use and land cover change in an urbanized river basin in Accra, Ghana. City Environ. Interact. 2021, 12, 100075. [Google Scholar] [CrossRef]
- Zelentsov, V.; Pimanov, I.; Potryasaev, S.; Sokolov, B.; Cherkas, S.; Alabyan, A.; Belikov, V.; Krylenko, I. River flood forecasting system: An interdisciplinary approach. In Flood Monitoring through Remote Sensing; Springer: Cham, Switzerland, 2018; pp. 81–100. [Google Scholar] [CrossRef]
- Barredo, J.I. Normalised flood losses in Europe: 1970–2006. Nat. Hazards Earth Syst. Sci. 2009, 9, 97–104. [Google Scholar] [CrossRef]
- Arriagada, L.; Rojas, O.; Arumí, J.L.; Munizaga, J.; Rojas, C.; Farias, L.; Vega, C. A new method to evaluate the vulnerability of watersheds facing several stressors: A case study in mediterranean Chile. Sci. Total Environ. 2019, 651, 1517–1533. [Google Scholar] [CrossRef] [PubMed]
- Stefanidis, S.; Alexandridis, V.; Theodoridou, T. Flood Exposure of Residential Areas and Infrastructure in Greece. Hydrology 2022, 9, 145. [Google Scholar] [CrossRef]
- Abdi-Dehkordi, M.; Bozorg-Haddad, O.; Salavitabar, A.; Mohammad-Azari, S.; Goharian, E. Development of flood mitigation strategies toward sustainable development. Nat. Hazards 2021, 108, 2543–2567. [Google Scholar] [CrossRef]
- Jacob, X.K.; Bisht, D.S.; Chatterjee, C.; Raghuwanshi, N.S. Hydrodynamic Modeling for Flood Hazard Assessment in a Data Scarce Region: A Case Study of Bharathapuzha River Basin. Environ. Model. Assess. 2020, 25, 97–114. [Google Scholar] [CrossRef]
- Mourato, S.; Fernandez, P.; Marques, F.; Rocha, A.; Pereira, L. An interactive Web-GIS fluvial flood forecast and alert system in operation in Portugal. Int. J. Disaster Risk Reduct. 2021, 58, 102201. [Google Scholar] [CrossRef]
- Nam, D.H.; Mai, D.T.; Udo, K.; Mano, A. Short-term flood inundation prediction using hydrologic-hydraulic models forced with downscaled rainfall from global NWP. Hydrol. Process. 2014, 28, 5844–5859. [Google Scholar] [CrossRef]
- Bruen, M.; Yang, J. Combined hydraulic and black-box models for flood forecasting in urban drainage systems. J. Hydrol. Eng. 2006, 11, 589–596. [Google Scholar] [CrossRef]
- Merkuryeva, G.; Merkuryev, Y.; Sokolov, B.V.; Potryasaev, S.; Zelentsov, V.A.; Lektauers, A. Advanced river flood monitoring, modelling and forecasting. J. Comput. Sci. 2015, 10, 77–85. [Google Scholar] [CrossRef]
- Smith, L.; Liang, Q.; James, P.; Lin, W. Assessing the utility of social media as a data source for flood risk management using a real-time modelling framework. J. Flood Risk Manag. 2017, 10, 370–380. [Google Scholar] [CrossRef]
- Bellos, V.; Kourtis, I.M.; Moreno-Rodenas, A.; Tsihrintzis, V.A. Quantifying Roughness Coefficient Uncertainty in Urban Flooding Simulations through a Simplified Methodology. Water 2017, 9, 944. [Google Scholar] [CrossRef]
- Bermúdez, M.; Cea, L.; Puertas, J. A rapid flood inundation model for hazard mapping based on least squares support vector machine regression. J. Flood Risk Manag. 2019, 12, e12522. [Google Scholar] [CrossRef]
- Jabbari, A.; Bae, D.H. Application of artificial neural networks for accuracy enhancements of real-time flood forecasting in the Imjin basin. Water 2018, 10, 1626. [Google Scholar] [CrossRef]
- Zahura, F.T.; Goodall, J.L.; Sadler, J.M.; Shen, Y.; Morsy, M.M.; Behl, M. Training machine learning surrogate models from a high-fidelity physics-based model: Application for real-time street-scale flood prediction in an urban coastal community. Water Resour. Res. 2020, 56, e2019WR027038. [Google Scholar] [CrossRef]
- Zanchetta, A.D.L.; Coulibaly, P. Recent Advances in Real-Time Pluvial Flash Flood Forecasting. Water 2020, 12, 570. [Google Scholar] [CrossRef]
- Budamala, V.; Baburao Mahindrakar, A. Integration of Adaptive Emulators and Sensitivity Analysis for Enhancement of Complex Hydrological Models. Environ. Process. 2020, 7, 1235–1253. [Google Scholar] [CrossRef]
- Wang, C.; Duan, Q.; Gong, W.; Ye, A.; Di, Z.; Miao, C. An evaluation of adaptive surrogate modeling based optimization with two benchmark problems. Environ. Model. Softw. 2014, 60, 167–179. [Google Scholar] [CrossRef]
- Zhang, J.; Chowdhury, S.; Messac, A. An adaptive hybrid surrogate model. Struct. Multidisc. Optim. 2012, 46, 223–238. [Google Scholar] [CrossRef]
- Budamala, V.; Baburao Mahindrakar, A. Approximation of metro water district basin using Parallel Computing of Emulator Based Spatial Optimization (PCESO). Water Resour. Manag. 2020, 34, 121–137. [Google Scholar] [CrossRef]
- Gong, W.; Duan, Q. An adaptive surrogate modeling-based sampling strategy for parameter optimization and distribution estimation (ASMO-PODE). Environ. Model. Softw. 2017, 95, 61–75. [Google Scholar] [CrossRef]
- Tang, X.; Knight, D.W.; Samuels, P.G. Wave speed–discharge relationship from cross-section survey. Proc. Inst. Civ. Eng.-Water Marit. Eng. 2001, 148, 81–96. [Google Scholar] [CrossRef]
- Reszler, C.; Bloeschl, G.; Komma, J. Identifying runoff routing parameters for operational flood forecasting in small to medium sized catchments. Hydrol. Sci. J. 2008, 53, 112–129. [Google Scholar] [CrossRef]
- Lamichhane, N.; Sharma, S. Development of Flood Warning System and Flood Inundation Mapping Using Field Survey and LiDAR Data for the Grand River near the City of Painesville, Ohio. Hydrology 2017, 4, 24. [Google Scholar] [CrossRef]
- Zhang, G.; Cui, P.; Yin, Y.; Liu, D.; Jin, W.; Wang, H.; Yan, Y.; Ahmed, B.N.; Wang, J. Real-time monitoring and estimation of the discharge of flash floods in a steep mountain catchment. Hydrol. Process. 2019, 33, 3195–3212. [Google Scholar] [CrossRef]
- Seibert, S.P.; Skublics, D.; Ehret, U. The potential of coordinated reservoir operation for flood mitigation in large basins—A case study on the Bavarian Danube using coupled hydrological–hydrodynamic models. J. Hydrol. 2014, 517, 1128–1144. [Google Scholar] [CrossRef]
- Skublics, D.; Blöschl, G.; Rutschmann, P. Effect of river training on flood retention of the Bavarian Danube. J. Hydrol. Hydromech. 2016, 64, 349. [Google Scholar] [CrossRef]
- Meyer, A.; Fleischmann, A.S.; Collischonn, W.; Paiva, R.; Jardim, P. Empirical assessment of flood wave celerity–discharge relationships at local and reach scales. Hydrol. Sci. J. 2018, 63, 2035–2047. [Google Scholar] [CrossRef]
- Sriwongsitanon, N.; Ball, J.E.; Cordery, I.A.N. An investigation of the relationship between the flood wave speed and parameters in runoff-routing models. Hydrol. Sci. J. 1998, 43, 197–213. [Google Scholar] [CrossRef]
- Turner-Gillespie, D.F.; Smith, J.A.; Bates, P.D. Attenuating reaches and the regional flood response of an urbanizing drainage basin. Adv. Water Resour. 2003, 26, 673–684. [Google Scholar] [CrossRef]
- Allen, G.H.; David, C.H.; Andreadis, K.M.; Hossain, F.; Famiglietti, J.S. Global estimates of river flow wave travel times and implications for low-latency satellite data. Geophys. Res. Lett. 2018, 45, 7551–7560. [Google Scholar] [CrossRef]
- Zoka, M.; Psomiadis, E.; Dercas, N. The Complementary Use of Optical and SAR Data in Monitoring Flood Events and Their Effects. Proceedings 2018, 2, 644. [Google Scholar] [CrossRef]
- Pisinaras, V.; Herrmann, F.; Panagopoulos, A.; Tziritis, E.; McNamara, I.; Wendland, F. Fully Distributed Water Balance Modelling in Large Agricultural Areas—The Pinios River Basin (Greece) Case Study. Sustainability 2023, 15, 4343. [Google Scholar] [CrossRef]
- Psomas, A.; Dagalaki, V.; Panagopoulos, Y.; Konsta, D.; Mimikou, M. Sustainable agricultural water management in Pinios river basin using remote sensing and hydrologic modeling. Procedia Eng. 2016, 162, 277–283. [Google Scholar] [CrossRef]
- Bathrellos, G.D.; Skilodimou, H.D.; Soukis, K.; Koskeridou, E. Temporal and spatial analysis of flood occurrences in the drainage basin of pinios river (thessaly, central greece). Land 2018, 7, 106. [Google Scholar] [CrossRef]
- 2007/60/EC; 1st Update of the Preliminary Flood Risk Assessment Based on the Flood Directive. Ministry of the Environment and Energy of Greece: Athens, Greece, 2020.
- Godley, A.D. Herodotus; Godley, A.D., Ed.; Nabu Press: Charleston, SC, USA, 2011; p. 450. [Google Scholar]
- Koutsoyiannis, D.; Mamassis, N.; Efstratiadis, A.; Zarkadoulas, N.; Markonis, Y. Floods in Greece. In Changes of Flood Risk in Europe, 1st ed.; Kundzewicz, Z.W., Ed.; IAHS Press, Wallingford—International Association of Hydrological Sciences: Wallingford, UK, 2012; pp. 238–256. [Google Scholar]
- Mamassis, N.; Mazi, K.; Dimitriou, E.; Kalogeras, D.; Malamos, N.; Lykoudis, S.; Koukouvinos, A.; Tsirogiannis, I.L.; Papageorgaki, I.; Papadopoulos, A.; et al. OpenHi.net: A synergistically built, national-scale infrastructure for monitoring the surface waters of Greece. Water 2021, 13, 2779. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Iliopoulou, T.; Koukouvinos, A.; Malamos, N.; Mamassis, N.; Dimitriadis, P.; Tepetidis, N.; Markantonis, D. Production of Maps with Updated Parameters of the Ombrian Curves at Country Level (Implementation of the EU Directive 2007/60/EC in Greece), Technical Report; Department of Water Resources and Environmental Engineering—National Technical University of Athens: Athens, Greece, 2023; Available online: https://www.itia.ntua.gr/2273/ (accessed on 29 November 2023).
- Iliopoulou, T.; Malamos, N.; Koutsoyiannis, D. Regional ombrian curves: Design rainfall estimation for a spatially diverse rainfall regime. Hydrology 2022, 9, 67. [Google Scholar] [CrossRef]
- Malamos, N.; Koutsoyiannis, D. Bilinear surface smoothing for spatial interpolation with optional incorporation of an explanatory variable. Part 1: Theory. Hydrol. Sci. J. 2016, 61, 519–526. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Stochastics of Hydroclimatic Extremes—A Cool Look at Risk, 3rd, ed.; Kallipos Open Academic Editions: Athens, Greece, 2023; 391p, ISBN 978-618-85370-0-2. [Google Scholar]
- Tallaksen, L. A review of baseflow recession analysis. J. Hydrol. 1995, 165, 349–370. [Google Scholar] [CrossRef]
- USDA National Resources Conservation Service. National Engineering Handbook: Part 630—Hydrology; U.S. Department of Agriculture (USDA): Washington, DC, USA, 2004. [Google Scholar]
- He, K.; Yang, Q.; Shen, X.; Dimitriou, E.; Mentzafou, A.; Papadaki, C.; Stoumboudi, M.; Anagnostou, E.N. Brief communication: Storm Daniel Flood Impact in Greece 2023: Mapping Crop and Livestock Exposure from SAR. Nat. Hazards Earth Syst. Sci. Discuss 2023, preprint. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Dimas, P.; Pouliasis, G.; Tsoukalas, I.; Kossieris, P.; Bellos, V.; Sakki, G.K.; Makropoulos, C.; Michas, S. Revisiting flood hazard assessment practices under a hybrid stochastic simulation framework. Water 2022, 14, 457. [Google Scholar] [CrossRef]
- Aksoy, H.; Wittenberg, H. Nonlinear baseflow recession analysis in watersheds with intermittent streamflow. Hydrol. Sci. J. 2011, 56, 226–237. [Google Scholar] [CrossRef]
- Szilagyi, J.; Parlange, M.B. Baseflow separation based on analytical solutions of the Boussinesq equation. J. Hydrol. 1998, 204, 251–260. [Google Scholar] [CrossRef]
- Linsley, R.K.; Kohler, M.A.; Paulhus, J.L.H. Hydrology for Engineers; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1975; p. 482. [Google Scholar]
- White, K.E.; Sloto, R.A. Base-Flow Frequency Characteristics of Selected Pennsylvania Streams; US Department of the Interior, U.S. Geological Survey: Harrisburg, PA, USA, 1990. [Google Scholar]
- Shirmohammadi, A.; Knisel, W.G.; Sheridan, J.M. An approximate method for partitioning daily streamflow data. J. Hydrol. 1984, 74, 335–354. [Google Scholar] [CrossRef]
- Bosch, D.D.; Arnold, J.G.; Allen, P.G.; Lim, K.J.; Park, Y.S. Temporal variations in baseflow for the Little River experimental watershed in South Georgia, USA. J. Hydrol. Reg. Stud. 2017, 10, 110–121. [Google Scholar] [CrossRef]
- Sakki, G.-K.; Tsoukalas, I.; Efstratiadis, A. A reverse engineering approach across small hydropower plants: A hidden treasure of hydrological data? Hydrol. Sci. J. 2022, 67, 94–106. [Google Scholar] [CrossRef]
- Dimas, P.; Sakki, G.-K.; Kossieris, P.; Tsoukalas, I.; Efstratiadis, A.; Makropoulos, C.; Mamassis, N.; Pipili, K. Outlining a master plan framework for the design and assessment of flood mitigation infrastructures across large-scale watersheds. In Proceedings of the 12th World Congress on Water Resources and Environment (EWRA 2023) “Managing Water-Energy-Land-Food under Climatic, Environmental and Social Instability”, Thessaloniki, Greece, 27 June–1 July 2023. [Google Scholar]
- Natural Resources Conservation Service. Hydrographs. In National Engineering Handbook: Part 630—Hydrology; U.S. Department of Agriculture (USDA): Washington, DC, USA, 2007. [Google Scholar]
- McCuen, R.H.; Bondelid, T.R. Estimating unit hydrograph peak rate factors. J. Irrig. Drain. Eng. 1983, 109, 238–250. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Koussis, A.D.; Koutsoyiannis, D.; Mamassis, N. Flood design recipes vs. reality: Can predictions for ungauged basins be trusted? Nat. Hazards Earth Syst. Sci. 2014, 14, 1417–1428. [Google Scholar] [CrossRef]
- Shi, W.; Wang, N. An Improved SCS-CN Method Incorporating Slope, Soil Moisture, and Storm Duration Factors for Runoff Prediction. Water 2020, 12, 1335. [Google Scholar] [CrossRef]
- Koussis, A.D. Assessment and review of the hydraulics of storage flood routing 70 years after the presentation of the Muskingum method. Hydrol. Sci. J. 2009, 54, 43–61. [Google Scholar] [CrossRef]
- Rogers, D.P.; Tsirkunov, V. Weather and Climate Resilience: Effective Preparedness through National Meteorological and Hydrological Services. Directions in Development--Environment and Sustainable Development; World Bank: Washington, DC, USA, 2013; Available online: http://hdl.handle.net/10986/15932 (accessed on 12 February 2024).
- Perera, D.; Seidou, O.; Agnihotri, J.; Rasmy, M.; Smakhtin, V.; Coulibaly, P.; Mehmood, H. Flood Early Warning Systems: A Review of Benefits, Challenges and Prospects; United Nations University-Institute for Water, Environment and Health: Hamilton, ON, Canada, 2019; UNU-INWEH Report Series; Issue 08, ISBN: 978-92-808-6096-2; Available online: http://inweh.unu.edu/publications/ (accessed on 10 February 2024).
- Schröter, K.; Sempere Torres, D.; Nachtnebel, H.P.; Beyene, M.; Rubín, C.; Gocht, M. Effectiveness and Efficiency of Early Warning Systems for Flash Floods (EWASE). CRUE ERA-NET Research Report No I-5. 2008. Available online: https://www.crue-eranet.net/publications.asp (accessed on 10 February 2024).
- Cools, J.; Innocenti, D.; O’Brien, S. Lessons from flood early warning systems. Environ. Sci. Policy 2016, 58, 117–122. [Google Scholar] [CrossRef]
- Georgakakos, K.P. Overview of the Global Flash Flood Guidance system and its application worldwide. WMO Bull. 2018, 67, 37–42. [Google Scholar]
- Georgakakos, K.P.; Modrick, T.M.; Shamir, E.; Campbell, R.; Cheng, Z.; Jubach, R.; Sperfslage, J.A.; Spencer, C.R.; Banks, R. The Flash Flood Guidance System Implementation Worldwide: A Successful Multidecadal Research-to-Operations Effort. Bull. Am. Meteorol. Soc. 2022, 103, E665–E679. [Google Scholar] [CrossRef]
- Liu, C.; Guo, L.; Ye, L.; Zhang, S.; Zhao, Y.; Song, T. A review of advances in China’s flash flood early-warning system. Nat. Hazards 2018, 92, 619–634. [Google Scholar] [CrossRef]
- Mentzafou, A.; Panagopoulos, Y.; Dimitriou, E. Designing the national network for automatic monitoring of water quality parameters in Greece. Water 2019, 11, 1310. [Google Scholar] [CrossRef]
- Mazi, K.; Koussis, A.D.; Lykoudis, S.; Psiloglou, B.E.; Vitantzakis, G.; Kappos, N.; Katsanos, D.; Rozos, E.; Koletsis, I.; Kopania, T. Establishing and operating (pilot phase) a telemetric streamflow monitoring network in Greece. Hydrology 2023, 10, 19. [Google Scholar] [CrossRef]
- Lasco, J.D.D.; Olivera, F.; Sharif, H.O. Unit Hydrograph Peak Rate Factor Estimation for Texas Watersheds. J. Hydrol. Eng. 2022, 27, 4022026. [Google Scholar] [CrossRef]
- Huynh-Ba, G.; Williams, C.; McGee, C.; Orlins, J. Measurement and Modeling of Hydrologic Response in a Southern New Jersey Watershed. In Managing Watersheds for Human and Natural Impacts; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 1–11. [Google Scholar] [CrossRef]
- Huang, T.; Merwade, V. Developing Customized NRCS Unit Hydrographs (Finley UHs) for Ungauged Watersheds in Indiana; (Joint Transportation Research Program Publication No. FHWA/IN/JTRP-2023/10); Purdue University: West Lafayette, IN, USA, 2023. [Google Scholar] [CrossRef]
- Michel, C.; Andréassian, V.; Perrin, C. Soil Conservation Service Curve Number method: How to mend a wrong soil moisture accounting procedure? Water Resour. Res. 2005, 41, 6. [Google Scholar] [CrossRef]
- Koussis, A.D.; Lagouvardos, K.; Mazi, K.; Kotroni, V.; Sitzmann, D.; Lang, J.; Zaiss, H.; Buzzi, A.; Malguzzi, P. Flood forecasts for an urban basin with integrated hydro-meteorological model. J. Hydrol. Eng. 2003, 8, 1–11. [Google Scholar] [CrossRef]




| Monitoring Station | Lat. (°) | Lon. (°) | Elev. (m) | Upstream Area (km2) | Discharge Estimation | Time Step |
|---|---|---|---|---|---|---|
| Tempi | 39.8968 | 22.6152 | 3.5 | 10,591 | Velocity | 30 min |
| Peneus diversion | 39.6525 | 22.4078 | 61.9 | 6544 | - | 30 min |
| Nomi | 39.5266 | 21.9383 | 91.2 | 2243 | Velocity | 30 min |
| Magoula | 39.4634 | 21.7995 | 106.0 | 222 | Stage–discharge curve | 1 h |
| Enipeas | 39.5635 | 22.0802 | 86.1 | 2640 | Stage–discharge curve | 30 min |
| Theopetra | 39.6748 | 21.6788 | 173.0 | 118 | Stage–discharge curve | 1 h |
| Station | (m) | (m) | (m) | Owner | Daily Rainfall Values (mm) | Total (mm) | |||
|---|---|---|---|---|---|---|---|---|---|
| 4/9 | 5/9 | 6/9 | 7/9 | ||||||
| Agia | 393,482 | 4,396,908 | 200.0 | NOA | 11.2 | 218.6 | 15.4 | 90.6 | 335.8 |
| Agiofyllo | 291,669 | 4,415,392 | 584.1 | MinEnv | 60.0 | 40.0 | 54.0 | - | 154.5 |
| Anavra | 335,689 | 4,338,439 | 196.3 | MinEnv | 98.0 | 131.0 | 218.0 | 0.0 | 447.0 |
| Anilio | 262,521 | 4,403,261 | 1660.0 | NOA | 20.6 | 148.2 | 374.6 | 149.2 | 692.6 |
| Chalki | 374,539 | 4,380,625 | 75.0 | NOA | 25.2 | 180.8 | 68.8 | 30.4 | 305.2 |
| Dasochori | 313,228 | 4,416,564 | 737.0 | NOA | 13.8 | 98.6 | 46.4 | 23.0 | 181.8 |
| Dendra Tyrnavou | 358,191 | 4,390,372 | 75.0 | NOA | 19.2 | 86.4 | 64.8 | 22.8 | 193.2 |
| Deskati | 312,700 | 4,421,617 | 769.0 | NOA | 10.4 | 96.0 | 50.6 | 25.6 | 182.6 |
| Domokos | 352,968 | 4,332,057 | 570.0 | NOA | 40.4 | 110.0 | 225.2 | 6.4 | 382.0 |
| Elassona | 344,494 | 4,417,838 | 282.0 | NOA | 26.4 | 72.2 | 19.6 | 40.8 | 159.0 |
| Filiadona | 368,423 | 4,324,135 | 487.0 | WU | 23.1 | 72.5 | 125.5 | 9.1 | 230.2 |
| Georganades | 327,623 | 4,381,444 | 92.0 | HCMR | 24.8 | 116.3 | 195.8 | 28.9 | 365.8 |
| Gonnoi | 368,984 | 4,413,284 | 111.0 | NOA | 14.0 | 147.4 | 31.4 | 71.2 | 264.0 |
| Kalampaka | 296,582 | 4,397,471 | 238.0 | NOA | 10.8 | 94.2 | 165.8 | 85.2 | 356.0 |
| Karditsa City | 319,027 | 4,362,984 | 121.0 | NOA | 42.4 | 185.2 | 404.4 | 26.8 | 658.8 |
| Karitsa | 301,118 | 4,347,487 | 1074.3 | MinEnv | 90.0 | 110.0 | 110.0 | 300.0 | 610.0 |
| Kofoi * | 389,232 | 4,328,735 | 500.0 | NOA | 23.4 | 152.6 | 342.2 | 32.2 | 550.4 |
| Loutropigi | 331,211 | 4,331,131 | 722.1 | MinEnv | 0.0 | 98.5 | 86.5 | 99.6 | 284.6 |
| Makrinitsa * | 412,701 | 4,361,962 | 850.0 | NOA | 125.2 | 757.4 | 273.6 | 79.2 | 1235.4 |
| Makrinitsa * | 412,260 | 4,361,258 | 685.4 | MinEnv | 75.0 | 82.0 | - | 38.4 | - |
| Metaxochori | 392,122 | 4,397,704 | 340.0 | WU | 14.0 | 170.7 | 14.7 | 60.7 | 260.1 |
| Metsovo * | 258,410 | 4,405,870 | 1240.0 | NOA | 20.2 | 91.8 | 204.0 | 75.8 | 391.8 |
| Mouzaki | 298,972 | 4,367,063 | 175.0 | NOA | 23.8 | 163.8 | 321.8 | 89.0 | 598.4 |
| Neraida | 374,872 | 4,348,963 | 243.0 | NOA | 19.6 | 226.6 | 91.2 | 23.8 | 361.2 |
| Nessonas | 371,249 | 4,395,250 | 92.0 | NOA | 11.6 | 78.0 | 3.6 | 71.6 | 164.8 |
| Pertouli * | 282,096 | 4,379,705 | 1170.0 | WU | 0.6 | 58.6 | 415.2 | 165.8 | 640.2 |
| Pezoula * | 301,465 | 4,352,189 | 891.0 | NOA | 43.2 | 250.0 | 378.4 | 90.8 | 762.4 |
| Platanioula | 354,786 | 4,393,054 | 83.0 | NOA | 18.6 | 75.4 | 91.2 | 25.4 | 210.6 |
| Platykampos | 373,254 | 4,386,828 | 72.0 | NOA | 20.8 | 107.6 | 0.4 | 76.4 | 205.2 |
| Portaria * | 413,586 | 4,360,067 | 600.0 | NOA | 105.4 | 764.7 | 14.4 | 0.0 | 884.5 |
| Rentina | 325,324 | 4,325,708 | 884.9 | MinEnv | 0.0 | 35.0 | 120.0 | 135.0 | 290.0 |
| Skopia | 367,299 | 4,334,140 | 444.7 | MinEnv | 107.0 | 46.8 | 60.0 | 27.5 | 241.3 |
| Smokovo | 344,199 | 4,329,129 | 444.0 | NOA | 40.2 | 97.0 | 89.4 | 14.0 | 240.6 |
| Trikala | 310,958 | 4,385,388 | 163.0 | NOA | 17.6 | 116.6 | 256.8 | 86.4 | 477.4 |
| Vamvakou | 363,669 | 4,354,301 | 148.0 | NOA | 19.4 | 191.4 | 129.8 | 29.0 | 369.6 |
| Volos * | 410,437 | 4,358,560 | 52.0 | NOA | 35.2 | 450.8 | 121.0 | 10.4 | 617.4 |
| Zagora * | 422,470 | 4,366,615 | 505.0 | NOA | 134.6 | 759.6 | 3.8 | 197.6 | 1095.6 |
| Zappeio | 366,461 | 4,369,310 | 172.3 | MinEnv | 89.9 | 274.0 | 139.0 | 12.8 | 515.7 |
| Weighted sum | - | - | 329.5 | - | 31.6 | 139.3 | 143.6 | 49.4 | 363.9 |
| Station | Spatially Varying Ombrian Curve Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| (mm/h) | (years) | 24 h | 48 h | 72 h | 24 h | 48 h | 72 h | ||
| Agia | 0.619 | 69.22 | 0.037 | 218.6 | 231.9 | 266.5 | 55 | 24 | 23 |
| Agiofyllo | 0.643 | 34.94 | 0.014 | 60.0 | 97.3 | 116.3 | 3 | 8 | 9 |
| Anavra | 0.618 | 42.75 | 0.017 | 218.0 | 289.0 | 341.7 | 200 | 214 | 225 |
| Anilio | 0.560 | 25.92 | 0.011 | 374.6 | 523.3 | 597.7 | 5043 | 5790 | 3944 |
| Chalki | 0.716 | 57.57 | 0.032 | 180.8 | 227.8 | 253.6 | 361 | 417 | 401 |
| Dasochori | 0.619 | 37.58 | 0.019 | 98.6 | 128.7 | 146.6 | 13 | 13 | 12 |
| Dendra Tyrnavou | 0.730 | 63.36 | 0.033 | 86.4 | 128.4 | 150.0 | 16 | 35 | 42 |
| Deskati | 0.596 | 33.86 | 0.017 | 96.0 | 126.5 | 145.2 | 11 | 11 | 10 |
| Domokos | 0.615 | 40.66 | 0.021 | 225.2 | 283.4 | 316.3 | 340 | 284 | 230 |
| Elassona | 0.658 | 60.12 | 0.060 | 72.2 | 95.2 | 116.5 | 6 | 6 | 8 |
| Filiadona | 0.603 | 37.46 | 0.023 | 125.5 | 166.3 | 187.6 | 32 | 33 | 28 |
| Georganades | 0.721 | 54.33 | 0.021 | 195.8 | 268.4 | 300.9 | 503 | 880 | 880 |
| Gonnoi | 0.706 | 84.74 | 0.032 | 147.4 | 170.1 | 201.4 | 25 | 20 | 24 |
| Kalampaka | 0.641 | 39.82 | 0.014 | 165.8 | 255.5 | 289.0 | 113 | 256 | 230 |
| Karditsa City | 0.691 | 58.03 | 0.023 | 404.4 | 510.4 | 559.9 | 6354 | 6878 | 5816 |
| Karitsa | 0.489 | 24.94 | 0.015 | 300.0 | 355.0 | 413.3 | 497 | 209 | 162 |
| Loutropigi | 0.600 | 38.21 | 0.017 | 99.6 | 185.6 | 218.6 | 9 | 33 | 33 |
| Makrinitsa | 0.510 | 50.90 | 0.041 | 757.4 | 956.8 | 1049.7 | 6290 | 3724 | 2232 |
| Metaxochori | 0.619 | 69.22 | 0.037 | 170.7 | 185.0 | 210.0 | 21 | 11 | 10 |
| Mouzaki | 0.639 | 63.53 | 0.017 | 321.8 | 448.2 | 498.3 | 307 | 442 | 365 |
| Neraida | 0.620 | 41.36 | 0.027 | 226.6 | 282.0 | 308.4 | 463 | 374 | 278 |
| Nessonas | 0.734 | 69.18 | 0.034 | 78.0 | 85.6 | 112.0 | 9 | 6 | 11 |
| Pertouli | 0.539 | 32.18 | 0.013 | 415.2 | 527.4 | 565.0 | 1904 | 1276 | 720 |
| Pezoula | 0.489 | 24.19 | 0.015 | 378.4 | 548.8 | 620.0 | 1794 | 1939 | 1279 |
| Platanioula | 0.721 | 65.21 | 0.037 | 91.2 | 141.6 | 164.6 | 16 | 42 | 48 |
| Platykampos | 0.735 | 74.03 | 0.034 | 107.6 | 118.2 | 147.2 | 23 | 16 | 24 |
| Rentina | 0.586 | 34.69 | 0.017 | 135.0 | 205.0 | 233.3 | 31 | 52 | 44 |
| Skopia | 0.619 | 51.27 | 0.030 | 107.0 | 130.4 | 167.3 | 9 | 7 | 10 |
| Smokovo | 0.619 | 35.62 | 0.018 | 97.0 | 161.8 | 188.1 | 15 | 41 | 40 |
| Trikala | 0.696 | 48.45 | 0.016 | 256.8 | 358.3 | 398.0 | 1365 | 2448 | 2231 |
| Vamvakou | 0.661 | 47.16 | 0.025 | 191.4 | 266.0 | 300.5 | 270 | 410 | 380 |
| Volos | 0.729 | 106.64 | 0.029 | 450.8 | 528.9 | 558.4 | 1737 | 1497 | 1143 |
| Zappeio | 0.661 | 43.61 | 0.026 | 274.0 | 388.5 | 430.9 | 2167 | 3731 | 3151 |
| Areal | 0.648 | 49.99 | 0.024 | 143.6 | 283.0 | 280.0 | 44 | 133 | 144 |
| Monitoring Station | Max. Stage (m) | Date/Time at Peak | Time to Peak (h) | Max. Discharge (m3/s) |
|---|---|---|---|---|
| Tempi | 7.83 | 10 September 14:30 | 126 | 1947.1 |
| Peneus diversion | 8.47 | 8 September 20:30 | 130 | - |
| Nomi | 6.42 | 7 September 2:00 | 38 | 998.6 |
| Magoula | 5.03 | 6 September 8:00 | 23 | 206.9 |
| Enipeas | 5.33 | 7 September 5:00 | 39 | 1190.0 |
| Theopetra | 2.49 | 7 September 4:00 | 12 | 140.9 |
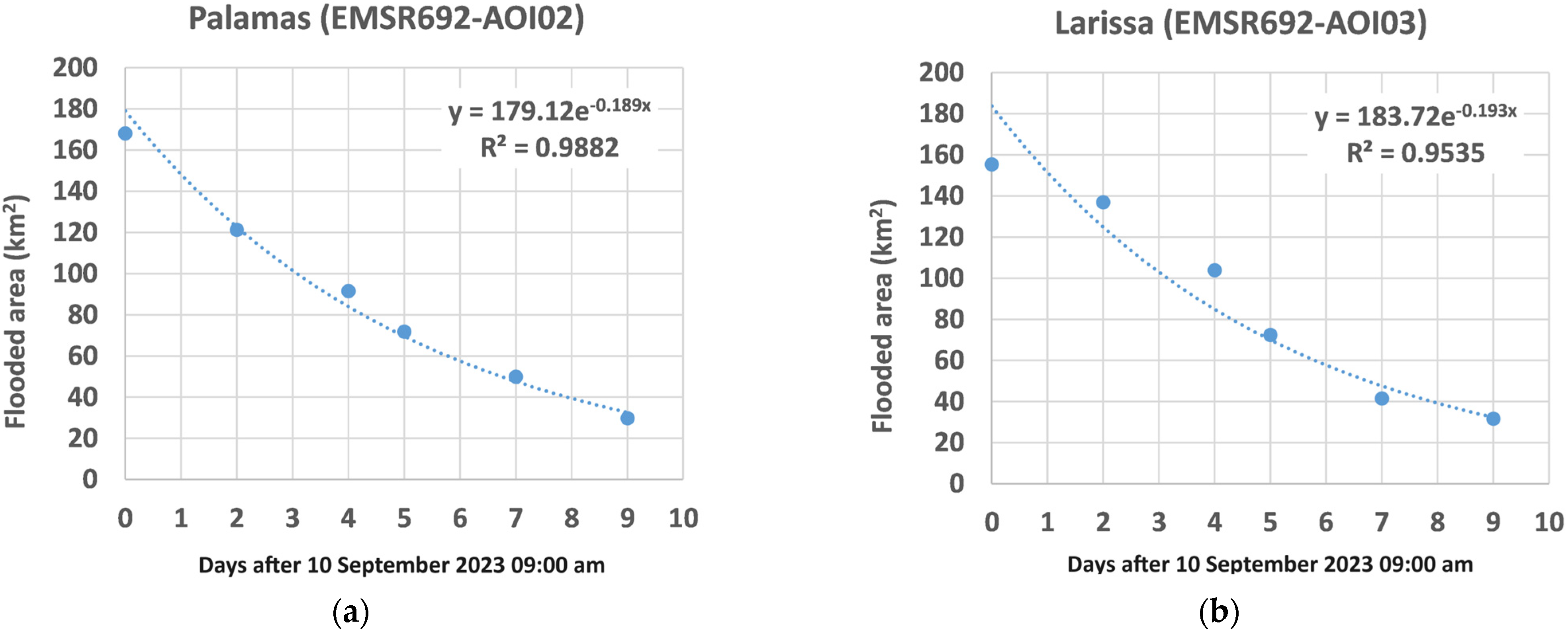
| Date | Karditsa (EMSR692-AOI0) | Palamas (EMSR692-AOI02) | Larissa (EMSR692-AOI03) | Total |
|---|---|---|---|---|
| 10 September 2023 9:00 | 18,519 | 16,808 | 15,532 | 50,859 |
| 12 September 2023 9:00 | 18,251 | 12,129 | 13,691 | 44,072 |
| 14 September 2023 9:00 | 8018 | 9157 | 10,383 | 27,558 |
| 15 September 2023 9:00 | 6000 | 7183 | 7244 | 20,427 |
| 17 September 2023 9:00 | 3315 | 4988 | 4156 | 12,459 |
| 19 September 2023 9:00 | 1700 | 2982 | 3163 | 7845 |
| Examined Event | Monitoring Station | Max Flow (m3/s) | Max Depth (m) | Time at Max | Peak Flow Travel Time (h) | Direct Runoff Volume (hm3) |
|---|---|---|---|---|---|---|
| September 2023 (Daniel) | Nomi | 999 | 6.42 | 7 September 2023 2:00 | 84.5 | |
| Tempi | 1947 | 7.83 | 10 September 2023 14:30 | 1670 | ||
| September 2020 (Ianos) | Nomi | 523 | 4.39 | 19 September 2020 20:30 | 64.5 | |
| Tempi | 787 | 3.92 | 22 September 2020 13:00 | 317 | ||
| April 2020 | Nomi | 525 | 4.40 | 5 April 2020 23:30 | 58.5 | |
| Tempi | 913 | 4.39 | 8 April 2020 10:00 | |||
| January 2021, 1st peak | Nomi | 543 | 4.49 | 4 January 2021 21:30 | 53.5 | |
| Tempi | 584 | 3.12 | 7 January 2021 3:00 | |||
| January 2021, 2nd peak | Nomi | 648 | 4.99 | 12 January 2021 15:00 | 45.0 | |
| Tempi | 704 | 3.60 | 14 January 2021 12:00 | |||
| November–December 2021 | Nomi | 557 | 4.56 | 30 November 2021 16:30 | 40.0 | |
| Tempi | 430 | 2.47 | 2 December 2021 8:30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitriou, E.; Efstratiadis, A.; Zotou, I.; Papadopoulos, A.; Iliopoulou, T.; Sakki, G.-K.; Mazi, K.; Rozos, E.; Koukouvinos, A.; Koussis, A.D.; et al. Post-Analysis of Daniel Extreme Flood Event in Thessaly, Central Greece: Practical Lessons and the Value of State-of-the-Art Water-Monitoring Networks. Water 2024, 16, 980. https://doi.org/10.3390/w16070980
Dimitriou E, Efstratiadis A, Zotou I, Papadopoulos A, Iliopoulou T, Sakki G-K, Mazi K, Rozos E, Koukouvinos A, Koussis AD, et al. Post-Analysis of Daniel Extreme Flood Event in Thessaly, Central Greece: Practical Lessons and the Value of State-of-the-Art Water-Monitoring Networks. Water. 2024; 16(7):980. https://doi.org/10.3390/w16070980
Chicago/Turabian StyleDimitriou, Elias, Andreas Efstratiadis, Ioanna Zotou, Anastasios Papadopoulos, Theano Iliopoulou, Georgia-Konstantina Sakki, Katerina Mazi, Evangelos Rozos, Antonios Koukouvinos, Antonis D. Koussis, and et al. 2024. "Post-Analysis of Daniel Extreme Flood Event in Thessaly, Central Greece: Practical Lessons and the Value of State-of-the-Art Water-Monitoring Networks" Water 16, no. 7: 980. https://doi.org/10.3390/w16070980
APA StyleDimitriou, E., Efstratiadis, A., Zotou, I., Papadopoulos, A., Iliopoulou, T., Sakki, G.-K., Mazi, K., Rozos, E., Koukouvinos, A., Koussis, A. D., Mamassis, N., & Koutsoyiannis, D. (2024). Post-Analysis of Daniel Extreme Flood Event in Thessaly, Central Greece: Practical Lessons and the Value of State-of-the-Art Water-Monitoring Networks. Water, 16(7), 980. https://doi.org/10.3390/w16070980













