Hydrodynamic Characterization of Carbonate Aquifers Using Atypical Pumping Tests without the Interruption of the Drinking Water Supply
Abstract
1. Introduction
2. Materials and Methods
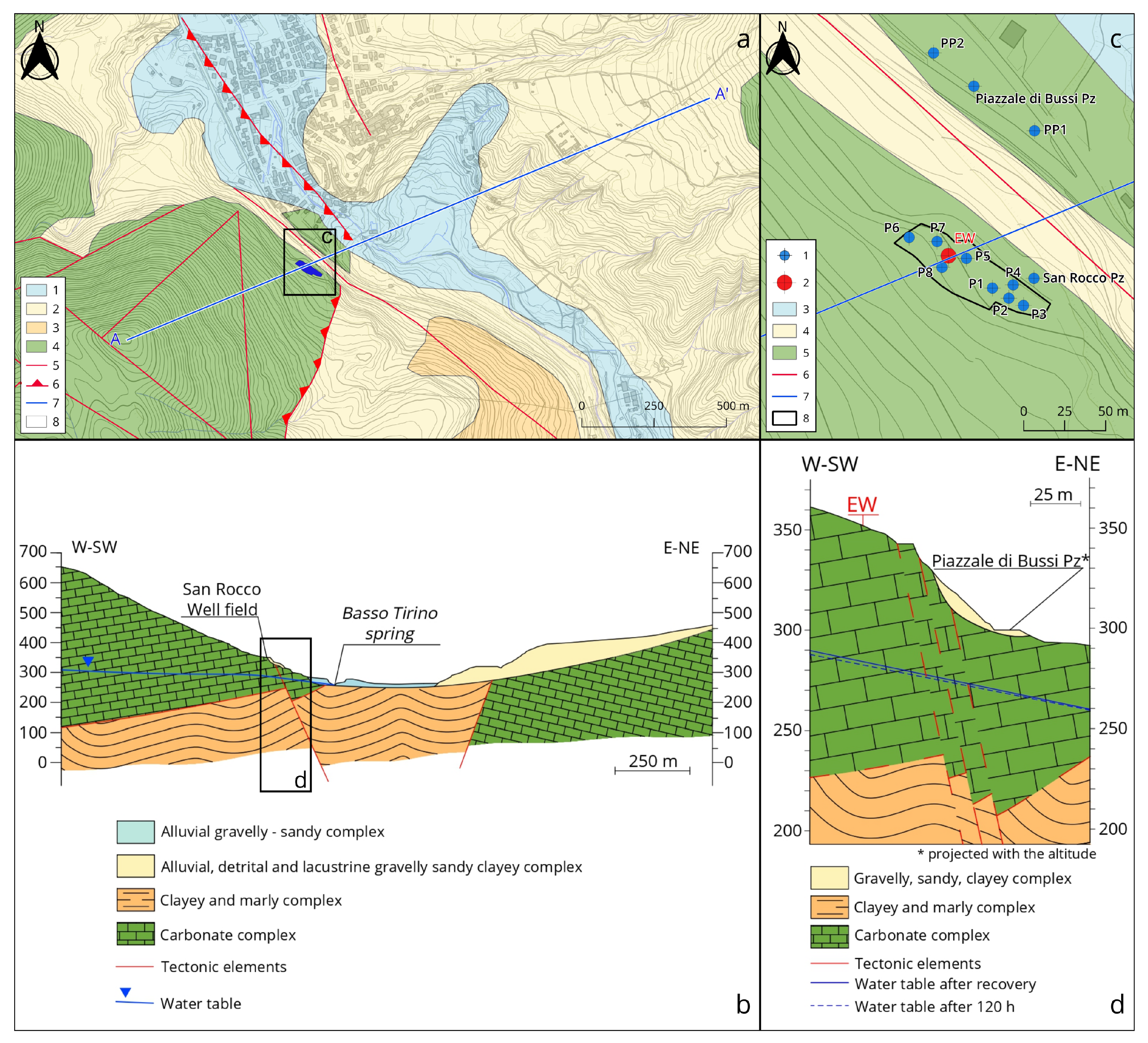
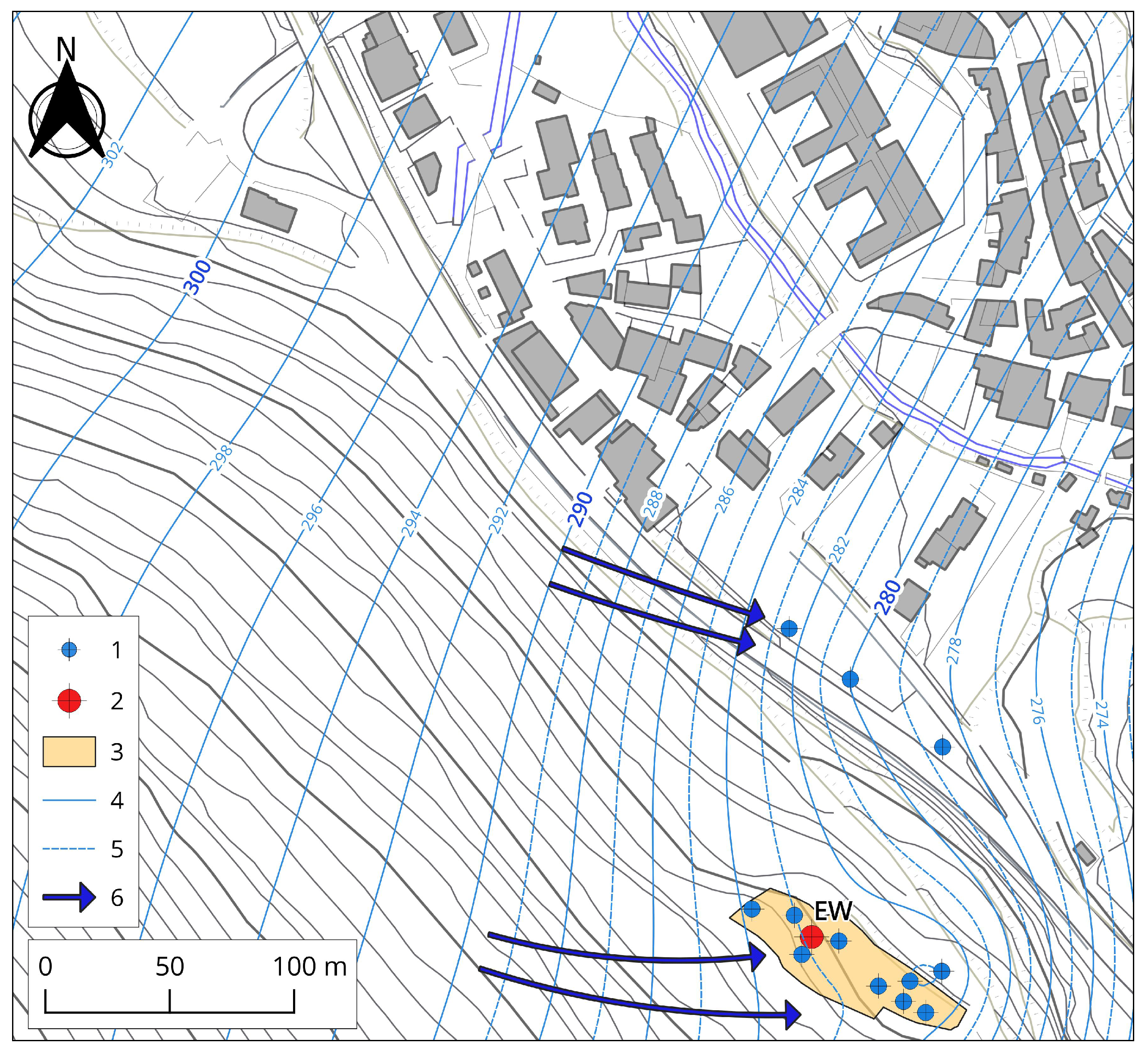
2.1. Site Description
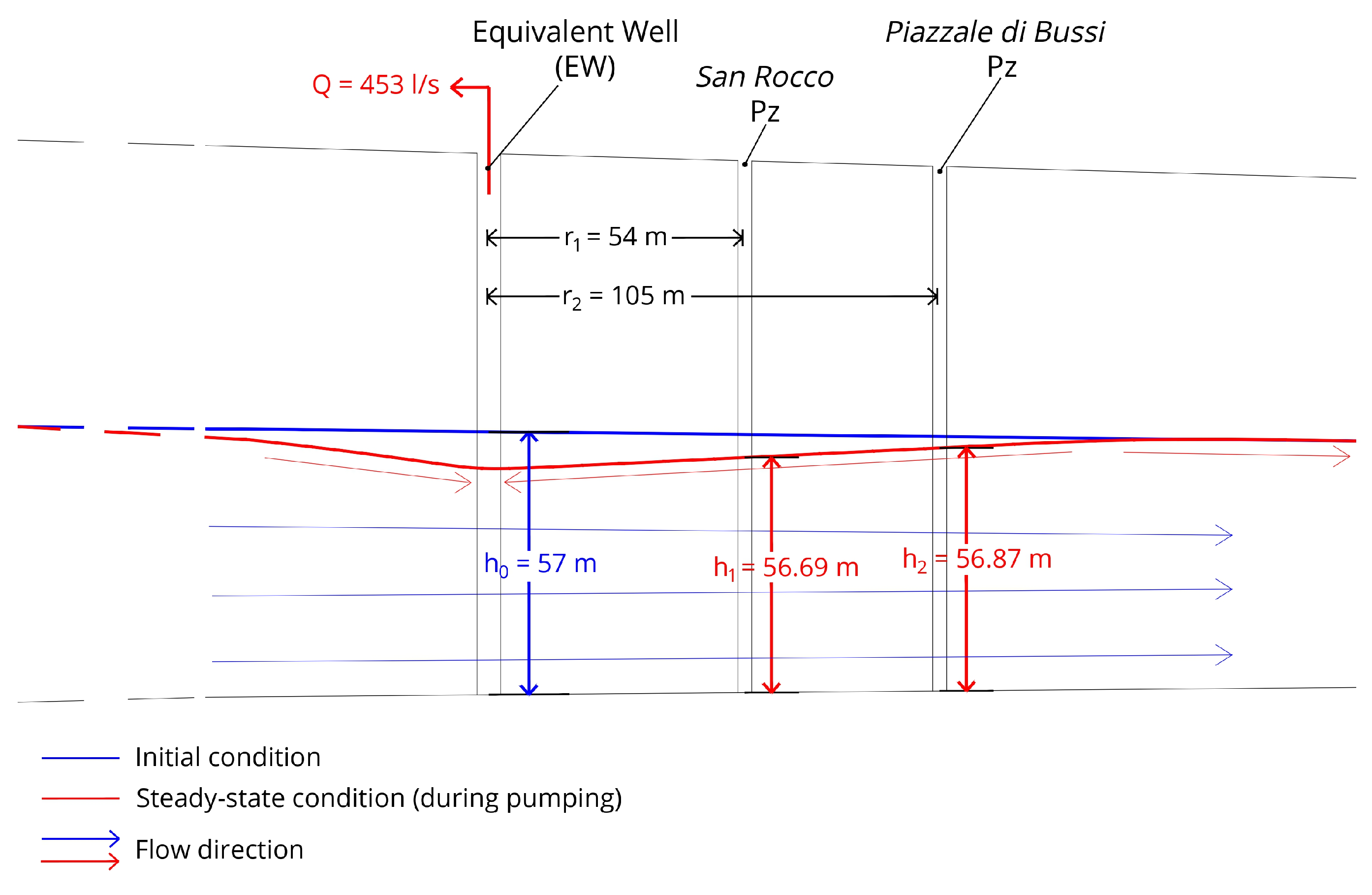
2.2. Well Field Set-Up
2.3. Step-Drawdown Test
2.4. Data Elaboration
2.5. Hydrochemical Parameters
2.6. Consideration about the Atypicality of the Test
- This test has been defined as atypical because of the use of some approximations:
- The well field was pumping water during the test;
- The pumping rate was increased using a higher number of pumping wells instead of raising a single one;
- The pumping rate for each step was decided by the managing organization based on the features of the available pumps;
- This method was applied to a carbonate aquifer that was considered like a porous one;
- The conceptual model (Figure 3) was simplified compared to the reality;
- The data elaborations were executed using an equivalent well, instead of a single one.
3. Results
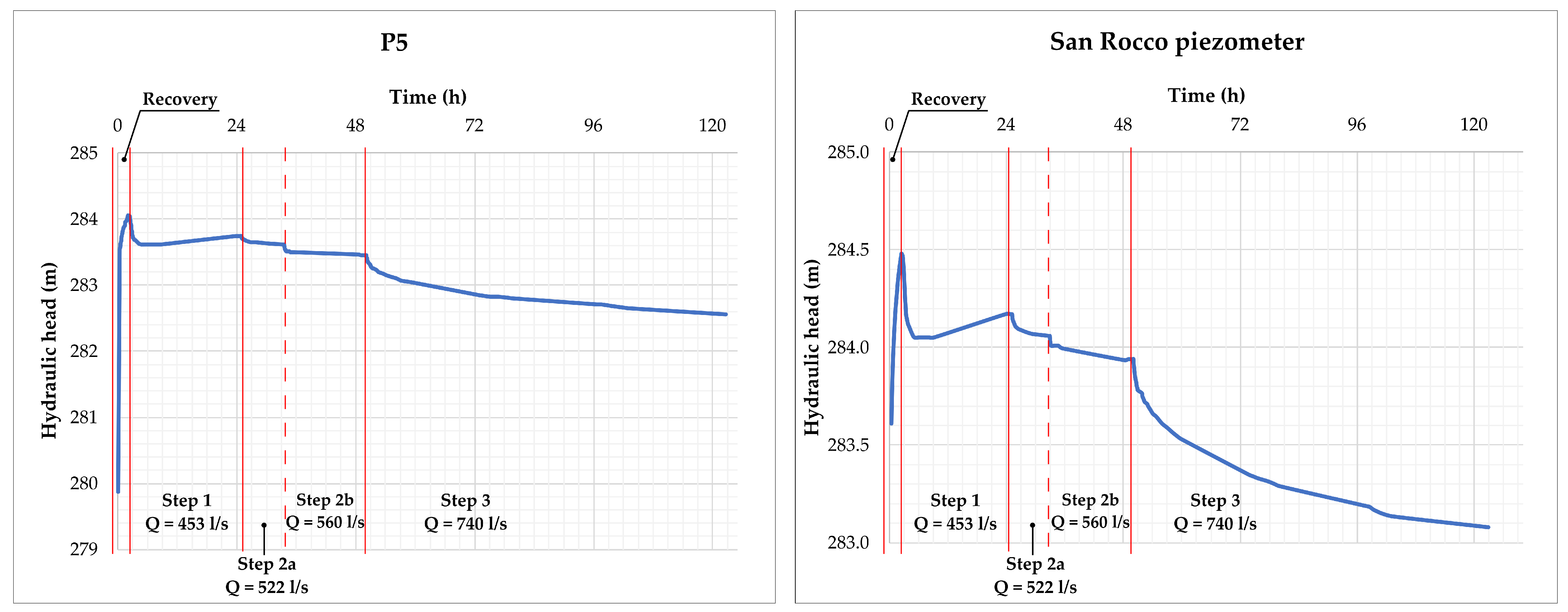
3.1. Step-Drawdown Test, Steady-State Condition
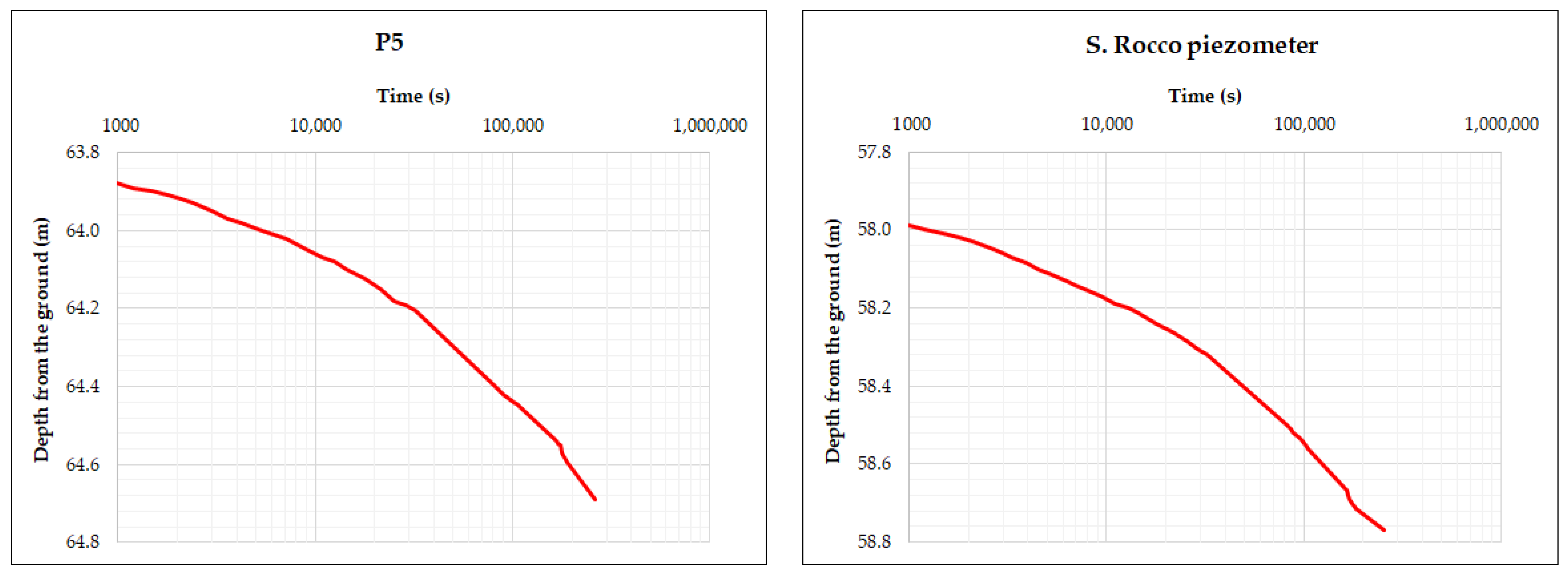
3.2. Step-Drawdown Test, Unsteady-State Condition
3.3. Long-Term Observations
3.4. Hydrochemical Parameters
4. Discussion
4.1. Step-Drawdown Test, Steady-State Condition
4.2. Step-Drawdown Test, Unsteady-State Condition
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lemieux, J.M.; Therrien, R.; Kirkwood, D. Small scale study of groundwater flow in a fractured carbonate-rock aquifer at the St-Eustache quarry, Québec, Canada. Hydrogeol. J. 2006, 14, 603–612. [Google Scholar] [CrossRef]
- Boni, C.; Bono, P.; Capelli, G. Schema Idrogeologico dell’Italia Centrale. Mem. Soc. Geol. Ital. 1986, 35, 991–1012. [Google Scholar]
- Cassa per il Mezzogiorno; Celico, P. Idrogeologia dei massicci carbonatici, delle piane quaternarie e delle aree vulcaniche dell’Italia centro-meridionale. In Quaderni della Cassa per il Mezzogiorno; Cassa per il Mezzogiorno: Rome, Italy, 1983; Volume 4. [Google Scholar]
- Celico, P. Considerazioni sull’idrogeologia di alcune zone dell’Italia centro-meridionale alla luce dei risultati di recenti indagini geognostiche. Mem. Note Ist. Geol. Appl. 1979, 15, 1–43. [Google Scholar]
- Petitta, M.; Tallini, M. Idrodinamica sotterranea del massiccio del Gran Sasso (Abruzzo); nuove indagini idrologiche, idrogeologiche e idrochimiche (1994–2001). Boll. Soc. Geol. Ital. 2002, 121, 343–363. [Google Scholar]
- Dragoni, W.; Sukhija, B.S. Climate Change and Groundwater: A Short Review. Geol. Society Spec. Pubbl. 2008, 288, 1–12. [Google Scholar] [CrossRef]
- Green, T.R.; Taniguchi, M.; Kooi, H.; Gurdak, J.J.; Allen, D.M.; Hiscock, K.M.; Treidel, H.; Aureli, A. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 2011, 405, 532–560. [Google Scholar] [CrossRef]
- Ndehedehe, C.E.; Adeyeri, O.E.; Onojeghuo, A.O.; Ferreira, V.G.; Kalu, I.; Okwuashi, O. Understanding global groundwater-climate interactions. Sci. Total Environ. 2023, 904, 166571. [Google Scholar] [CrossRef] [PubMed]
- Lorenzi, V.; Sbarbati, C.; Banzato, F.; Lacchini, A.; Petitta, M. Recharge assessment of the Gran Sasso aquifer (Central Italy): Time-variable infiltration and influence of snow cover extension. J. Hydrol. Reg. Stud. 2022, 41, 101090. [Google Scholar] [CrossRef]
- Petitta, M.; Banzato, F.; Lorenzi, V.; Matani, E.; Sbarbati, C. Determining recharge distribution in fractured carbonate aquifers in central Italy using environmental isotopes: Snowpack cover as an indicator for future availability of groundwater resources. Hydrogeol. J. 2022, 30, 1619–1636. [Google Scholar] [CrossRef]
- Theis, C.V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using groundwater storage. Am. Geophys. Union Trans. 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Cooper, H.H., Jr.; Jacob, C.E. A generalized graphical method for evaluating formation constants and summarizing well field history. Am. Geophys. Union Trans. 1946, 27, 526–534. [Google Scholar] [CrossRef]
- Chow, V.T. On the determination of transmissibility and storage coefficients from pumping test data. Trans. Am. Geophys. Union 1952, 33, 397–404. [Google Scholar] [CrossRef]
- Jacob, C.E. Radial flow in a leaky artesian aquifer. Trans. Am. Geophys. Union 1946, 27, 198–208. [Google Scholar]
- Hantush, M.S. Analysis of data from pumping tests in leaky aquifers. Trans. Am. Geophys. Union 1956, 37, 702–714. [Google Scholar] [CrossRef]
- Boulton, N.S. Unsteady radial flow to a pumped well allowing for delayed yield from storage. Int. Assoc. Sci. Hydrol. Publ. 1954, 2, 472–477. [Google Scholar]
- Boulton, N.S. Analysis of data from non-equilibrium pumping tests allowing for delayed yield from storage. Proc. Inst. Civ. Eng. 1963, 26, 469–482. [Google Scholar] [CrossRef]
- Prickett, T.A. Type-curve solution to aquifer tests under water table conditions. Groundwater 1965, 3, 5–14. [Google Scholar] [CrossRef]
- Neuman, S.P. Theory of flow in unconfined aquifers considering delayed response of the water table. Water Resour. Res. 1972, 8, 1031–1045. [Google Scholar] [CrossRef]
- Neuman, S.P. Effect of partial penetration on flow in unconfined aquifers considering delayed gravity response. Water Resour. Res. 1974, 10, 303–312. [Google Scholar] [CrossRef]
- Moench, A.F. Combining the Neuman and Boulton models for flow to a well in an unconfined aquifer. Groundwater 1995, 33, 378–384. [Google Scholar] [CrossRef]
- Samani, S.; Vadiati, M.; Azizi, F.; Zamani, E.; Kisi, O. Groundwater level simulation using soft computing methods with emphasis on major meteorological components. Water Resour. Manag. 2022, 36, 3627–3647. [Google Scholar] [CrossRef]
- Samani, S.; Vadiati, M.; Nejatijahromi, Z.; Etebari, B.; Kisi, O. Groundwater level response identification by hybrid wavelet–machine learning conjunction models using meteorological data. Environ. Sci. Pollut. Res. 2023, 30, 22863–22884. [Google Scholar] [CrossRef] [PubMed]
- Lin, G.F.; Chen, G.R. An improved neural network approach to the determination of aquifer parameters. J. Hydrol. 2006, 316, 281–289. [Google Scholar] [CrossRef]
- Vadiati, M.; Rajabi Yami, Z.; Eskandari, E.; Nakhaei, M.; Kisi, O. Application of artificial intelligence models for prediction of groundwater level fluctuations: Case study (Tehran-Karaj alluvial aquifer). Environ. Monit. Assess. 2022, 194, 619. [Google Scholar] [CrossRef] [PubMed]
- Ayvaz, M.T. Simultaneous determination of aquifer parameters and zone structures with fuzzy c-means clustering and meta-heuristic harmony search algorithm. Adv. Water Resour. 2007, 30, 2326–2338. [Google Scholar] [CrossRef]
- Tayfur, G.; Nadiri, A.A.; Moghaddam, A.A. Supervised intelligent committee machine method for hydraulic conductivity estimation. Water Resour. Manag. 2014, 28, 1173–1184. [Google Scholar] [CrossRef]
- Prasad, K.L.; Rastogi, A.K. Estimating net aquifer recharge and zonal hydraulic conductivity values for Mahi Right Bank Canal project area, India by genetic algorithm. J. Hydrol. 2001, 243, 149–161. [Google Scholar] [CrossRef]
- Samuel, M.P.; Jha, M.K. Estimation of aquifer parameters from pumping test data by genetic algorithm optimization technique. J. Irrig. Drain Eng. 2003, 129, 348–359. [Google Scholar] [CrossRef]
- Ha, D.; Zheng, G.; Zhou, H.; Zeng, C.; Zhang, H. Estimation of hydraulic parameters from pumping tests in a multiaquifer system. Undergr. Space 2020, 5, 210–222. [Google Scholar] [CrossRef]
- Tadj, W.; Chettih, M.; Mouattah, K. A new hybrid algorithm for estimating confined and leaky aquifers parameters from transient time-drawdown data. Soft Comput. 2021, 25, 15463–15476. [Google Scholar] [CrossRef]
- Dashti, Z.; Nakhaei, M.; Vadiati, M.; Karami, G.H.; Kisi, O. A literature review on pumping test analysis (2000–2022). Environ. Sci. Pollut. Res. 2023, 30, 9184–9206. [Google Scholar] [CrossRef] [PubMed]
- Tsoflias, G.P.; Halihan, T.; Sharp, J.M., Jr. Monitoring pumping test response in a fractured aquifer using ground-penetrating radar. Water Resour. Res. 2001, 37, 1221–1229. [Google Scholar] [CrossRef]
- Conese, M.; Nanni, T.; Peila, C.; Rusi, S.; Salvati, R. Idrogeologia della Montagna del Morrone (Appennino abruzzese): Dati Preliminari. Mem. Soc. Geol. It. 2001, 56, 181–196. [Google Scholar]
- Boni, C.; Pianelli, A.; Pierdominici, S.; Ruisi, M. Le grandi sorgenti del fiume Tirino (Abruzzo). Boll. Soc. Geol. Ital. 2002, 121, 411–431. [Google Scholar]
- Regione Abruzzo, Servizio Acque e Demanio Idrico, Piano di Tutela delle Acque (PTA). Available online: https://www.regione.abruzzo.it/pianoTutelaacque/ (accessed on 21 February 2024).
- Biava, F.; Consonni, M.; Francani, V.; Gattinoni, P.; Scesi, L. Delineation of Protection Zones for the Main Discharge Area of the Gran Sasso Aquifer (Central Italy) through an Integrated Geomorphological and Chronological Approach. J. Water Resour. Prot. 2014, 6, 1816–1832. [Google Scholar] [CrossRef]
- Bigi, S.; Calamita, F.; Centamore, E. Carta Geologico-Strutturale dell’Area Compresa tra il Gran Sasso e il F. Pescara—Scala 1:50,000; Studio Faro: Rome, Italy, 1995. [Google Scholar]
- APAT (Agenzia per la Protezione dell’Ambiente e per i Servizi Tecnici). Carta Geologica d’Italia in Scala 1:50,000, Foglio 360 “Torre de’ Passeri”; SEL.CA.: Florence, Italy, 2005. [Google Scholar]
- APAT (Agenzia per la Protezione dell’Ambiente e per i Servizi Tecnici). Carta Geologica d’Italia in Scala 1:50,000, Foglio 369 “Sulmona”; SEL.CA.: Florence, Italy, 2005. [Google Scholar]
- Jacob, C.E. Drawdown test to determine effective radius of artesian well. Trans. Am. Soc. Civ. Eng. 1947, 112, 1047–1070. [Google Scholar] [CrossRef]
- Clark, L. The analysis and planning of step drawdown tests. Q. J. Eng. Geol. Hydrogeol. 1977, 10, 125–143. [Google Scholar] [CrossRef]
- Dupuit, J. Mouvement de l’eau a travers le terrains permeables. C. R. Hebd. Seances Acad. Sci. 1857, 45, 92–96. [Google Scholar]
- Darcy, H. Les Fontaines Publiques de la ville de Dijon; Dalmont: Paris, France, 1856. [Google Scholar]
- Thiem, G. Hydrologische Methoden; J.M. Gebhardt: Leipzig, Germany, 1906. [Google Scholar]
- Sichardt, W. Das Fassungsvermögen von Rohrbrunnen und Seine Bedeutung für die Grundwasserabsenkung, Insbesondere für Größere Absenkungstiefen; Springer: Berlin/Heidelberg, Germany, 1928. [Google Scholar]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall, Inc.: Englewood Cliff, NJ, USA, 1979. [Google Scholar]



| Step | Period | Pumping Rate (L/s) | Working Wells | Monitoring Wells |
|---|---|---|---|---|
| T0 | 635 | |||
| Recovery | 2.00 | 0 | – | P5—P6—Pz San Rocco–Pz Piazzale–Pz Cartignano |
| 1 | 22.45 | 453 | P1—P2—P3—P7—P8 | P5—P6—Pz San Rocco–Pz Piazzale–Pz Cartignano |
| 2a | 7.55 | 522 | P1—P2—P3—P4—P7—P8 | P5—P6—Pz San Rocco–Pz Piazzale–Pz Cartignano |
| 2b | 16.20 | 560 | P1—P3—P4—P5—P7—P8 | P5—P6—Pz San Rocco–Pz Piazzale–Pz Cartignano |
| 3 | 72.55 | 740 | P1—P2—P3—P4—P5—P6—P7—P8 | P5—P6—Pz San Rocco–Pz Piazzale–Pz Cartignano |
| Well/Piez. | Step | Pumping Rate (L/s) | Distance from EW (m) | h1 (m) | h2 (m) | Δh (m) | ΔhTOT (m) |
|---|---|---|---|---|---|---|---|
| P5 | Recovery | 0 | 11 | 57.51 | 57.00 | −0.51 | - |
| 1 | 453 | 11 | 57.00 | 56.68 | 0.32 | 0.32 | |
| 2a | 522 | 11 | 56.68 | 56.57 | 0.19 | 0.51 | |
| 2b | 560 | 11 | 56.57 | 56.39 | 0.10 | 0.61 | |
| 3 | 740 | 11 | 56.39 | 55.50 | 0.89 | 1.50 | |
| P6 | Recovery | 0 | 27 | 57.72 | 57.00 | −0.72 | - |
| 1 | 453 | 27 | 57.00 | 56.88 | 0.12 | 0.12 | |
| 2a | 522 | 27 | 56.88 | 56.82 | 0.06 | 0.18 | |
| 2b | 560 | 27 | 56.82 | 56.71 | 0.11 | 0.29 | |
| 3 | 740 | 27 | 56.71 | 49.17 | 7.54 | 7.83 | |
| San Rocco Pz | Recovery | 0 | 54 | 57.87 | 57.00 | −0.87 | - |
| 1 | 453 | 54 | 57.00 | 56.69 | 0.31 | 0.31 | |
| 2a | 522 | 54 | 56.69 | 56.58 | 0.11 | 0.42 | |
| 2b | 560 | 54 | 56.58 | 56.46 | 0.12 | 0.54 | |
| 3 | 740 | 54 | 56.46 | 55.60 | 0.86 | 1.40 | |
| Piazzale di Bussi Pz | Recovery | 0 | 105 | 57.55 | 57.00 | −0.55 | - |
| 1 | 453 | 105 | 57.00 | 56.86 | 0.14 | 0.14 | |
| 2a | 522 | 105 | 56.86 | 56.80 | 0.06 | 0.20 | |
| 2b | 560 | 105 | 56.80 | 56.68 | 0.12 | 0.32 | |
| 3 | 740 | 105 | 56.68 | 55.99 | 0.69 | 1.01 | |
| Cartignano Pz | Recovery | 0 | 1158 | 57.01 | 57.00 | −0.01 | - |
| 1 | 453 | 1158 | 57.00 | 57.00 | 0.00 | - | |
| 2a | 522 | 1158 | 57.00 | 57.00 | 0.00 | - | |
| 2b | 560 | 1158 | 57.00 | 57.00 | 0.00 | - | |
| 3 | 740 | 1158 | 57.00 | 57.00 | 0.00 | - |
| Monitoring Well Pairs | ||||
|---|---|---|---|---|
| P5 –Piazzale Pz | San Rocco Pz– Piazzale Pz | |||
| Step | Pumping Rate (L/s) | K (m/s) | K (m/s) | T (m2/s) |
| 1 | 453 | 0.0050 | 0.0050 | 0.285 |
| 2a | 522 | 0.0044 | 0.0044 | 0.250 |
| 2b | 560 | - | 0.0048 | 0.274 |
| 3 | 740 | - | 0.0036 | 0.205 |
| Equation | Step | Pumping Rate (L/s) | h2 (Piazzale Pz) (m) | h1 (San Rocco Pz) (m) | r0 (m) |
|---|---|---|---|---|---|
| Dupuit | 1 | 453 | 56.86 | 56.69 | 180 |
| 2 | 560 | 56.68 | 56.46 | 280 | |
| 3 | 740 | 55.99 | 55.6 | 590 | |
| Equation | Step | Pumping Rate (L/s) | h0 (m) | hw (m) | r0 (m) |
| Sichard | 1 | 453 | 57 | 56.70 | 64 |
| 2 | 560 | 56.40 | 123 | ||
| 3 | 740 | 55.50 | 302 |
| Well/Piez. | Step | Q (L/s) | C | t0 (s) | T (m2/s) | K (m/s) | S |
|---|---|---|---|---|---|---|---|
| P5 | 1 | 453 | 0.42 | 0.20 | 0.003 | ||
| 3 I log cycle | 740 | 0.18 | 0.75 | 0.013 | |||
| 3 II log cycle. | 740 | 0.38 | 0.36 | 0.006 | |||
| Pz San Rocco | 1 | 453 | 0.39 | 0.21 | 0.004 | ||
| 3 I log cycle | 740 | 0.175 | 250 | 0.77 | 0.014 | 0.15 | |
| 3 II log cycle | 740 | 0.36 | 1600 | 0.38 | 0.007 | 0.46 | |
| Pz Piazzale di Bussi | 1 | 453 | 0.21 | 0.39 | 0.007 | ||
| 3 I log cycle | 740 | 0.14 | 280 | 0.97 | 0.017 | 0.06 | |
| 3 II log cycle | 740 | 0.32 | 2200 | 0.42 | 0.007 | 0.19 |
| Well/Piezometer | Distance from EW | Head (Steady-State Cond.) | Drawdown * (After 5 Days) | Drawdown * (After 114 Days) |
|---|---|---|---|---|
| P5 | 11 m | 284.06 | −2.0 m | −1.3 m |
| P6 | 26.5 m | 284.81 | −7.8 m | −8.7 m |
| Pz San Rocco | 54 m | 284.48 | −1.4 m | −1.3 m |
| Pz Piazzale di Bussi | 105 m | 280.93 | −1.0 m | −1.2 m |
| Time from Test Beginning (hour·min) | T (°C) | χ (µS/cm) | pH | Eh (mV) |
|---|---|---|---|---|
| 7.00 | 12.2 | 583 | 8.3 | 126 |
| 24.15 | 11.7 | 580 | 8.2 | 155 |
| 25.50 | 11.8 | 573 | 8.0 | 173 |
| 27.00 | 11.8 | 573 | 8.2 | 144 |
| 29.05 | 11.8 | 573 | 8.1 | 194 |
| 34.50 | 11.6 | 579 | 8.1 | 155 |
| 47.40 | 11.7 | 578 | 8.2 | 147 |
| 50.30 | 11.8 | 574 | 8.1 | 213 |
| 52.40 | 11.9 | 574 | 8.2 | 223 |
| 56.45 | 11.7 | 572 | 8.2 | 160 |
| 72.05 | 11.8 | 576 | 8.2 | 178 |
| 76.00 | 11.9 | 577 | 8.2 | 216 |
| 78.35 | 12.0 | 577 | 8.1 | 189 |
| 95.45 | 11.7 | 535 | 8.0 | 164 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rusi, S.; Di Curzio, D.; Di Giovanni, A. Hydrodynamic Characterization of Carbonate Aquifers Using Atypical Pumping Tests without the Interruption of the Drinking Water Supply. Water 2024, 16, 1047. https://doi.org/10.3390/w16071047
Rusi S, Di Curzio D, Di Giovanni A. Hydrodynamic Characterization of Carbonate Aquifers Using Atypical Pumping Tests without the Interruption of the Drinking Water Supply. Water. 2024; 16(7):1047. https://doi.org/10.3390/w16071047
Chicago/Turabian StyleRusi, Sergio, Diego Di Curzio, and Alessia Di Giovanni. 2024. "Hydrodynamic Characterization of Carbonate Aquifers Using Atypical Pumping Tests without the Interruption of the Drinking Water Supply" Water 16, no. 7: 1047. https://doi.org/10.3390/w16071047
APA StyleRusi, S., Di Curzio, D., & Di Giovanni, A. (2024). Hydrodynamic Characterization of Carbonate Aquifers Using Atypical Pumping Tests without the Interruption of the Drinking Water Supply. Water, 16(7), 1047. https://doi.org/10.3390/w16071047








