The Mechanism of Dust Transportation Based on Wind Tunnel Experiments and Numerical Simulations

Abstract

The process of dust transportation is widespread, leading to the formation of regions such as the Loess Plateau. In order to understand the mechanisms of dust particle transportation, this study conducted wind tunnel experiments to simulate natural wind-driven dust transport processes. Theoretical derivations were carried out to establish the relationship between particle size and transportation distance, which was then validated through numerical simulations. The following conclusions were drawn: (1) wind tunnel experiments, theoretical derivations, and numerical simulations yielded consistent results, indicating the effectiveness of the wind tunnel experiments; (2) Under the influence of wind forces, the ideal transportation distance of particles is inversely proportional to the square of their size; (3) turbulent wind fields have a minor impact on dust transport, while particle roundness has a significant effect on transport; (4) clay particles and dust particles in loess regions share the same source areas and transport pathways.

1. Introduction

During the Quaternary period, the surface weathering debris from the Qilian Mountains, Gobi-Altai, and Hangayn mountains is transported southeastward under the influence of the northwest winter monsoon [1,2], forming a distribution of deserts, gobis, and the Loess Plateau from the northwest to the southeast [3]. The Loess Plateau has a total area of approximately 640,000 square kilometers, and its unique particle size distribution due to eolian loess makes it prone to geological hazards while being suitable for human habitation and agriculture [4,5]. Consequently, numerous scholars have been attracted to conduct extensive and in-depth research on the formation process of loess.

The process of ground release, airborne transport, and gradual settling can be effectively simulated through wind tunnel experiments. Zheng tested a movable environmental wind tunnel and found its various performance indicators to be satisfactory, suitable for subsequent research [6]. Goossens’ study revealed that the deposition patterns of dust in wind tunnel experiments closely matched those found in natural loess deposition, demonstrating the effectiveness of wind tunnel experiments in simulating loess deposition [7]. Cai investigated the interaction mechanisms between wind flow on the leeward side of sand dunes and sand transport through wind tunnel experiments [8]. Liang used a portable wind tunnel apparatus to study the initiation mechanism of sand grains in the Gobi region, suggesting that the Gobi region is an underestimated source of dust [9]. Yassin studied the diffusion of pollutants in different regions through wind tunnel experiments, with results matching field data well [10]. Merrison obtained data on Martian aerosols at low wind speeds through wind tunnel experiments [11]. These studies highlight the effectiveness of wind tunnel experiments in simulating the transportation and deposition processes of dust materials.

Physical models can help in understanding the dust transport process. Huang used a physical modeling and numerical simulation to establish a physics-based near-surface wind field statistical model [12]. Yarmohamadi predicted the trajectory of dust storm transport based on convolutional neural networks and geographical environment [13]. Rodakoviski found that current climate models underestimate the time of particle transportation in the air and further investigated it using turbulent motion [14]. Jung studied the impact of convection on dust transport using a new model [15]. Qin conducted a dynamic analysis to obtain the transport flux and distance of dust particles with different sizes and analyzed the deposition environment information of loess in the field [16]. Numerical simulation software gradually computes results based on physical models, providing reliability and visualization. Zhang researched the settling patterns inside dust removal pipelines and their effects on subsequent operations using Fluent 2022R1 software [17]. Chang studied the deformation and failure process of loess slopes under seismic action using PFC 5.0 [18]. Both physical modeling and numerical simulations play a crucial role in the research conducted by geoscientists.

This study differs from previous research on dust transport processes by employing a combination of wind tunnel experiments, theoretical derivation, and Particle Flow Code (PFC) numerical simulations to investigate the particle size distribution patterns after dust particle deposition. The findings of this study are relevant for research related to loess and modern dust control.

2. Methodology

This study utilizes wind tunnel experiments to simulate the transportation process of dust particles in nature. Based on the wind tunnel experiment results, theoretical derivations of the particle transport process were conducted and PFC numerical simulations were set up for validation and further investigation.

2.1. Wind Tunnel Experiment

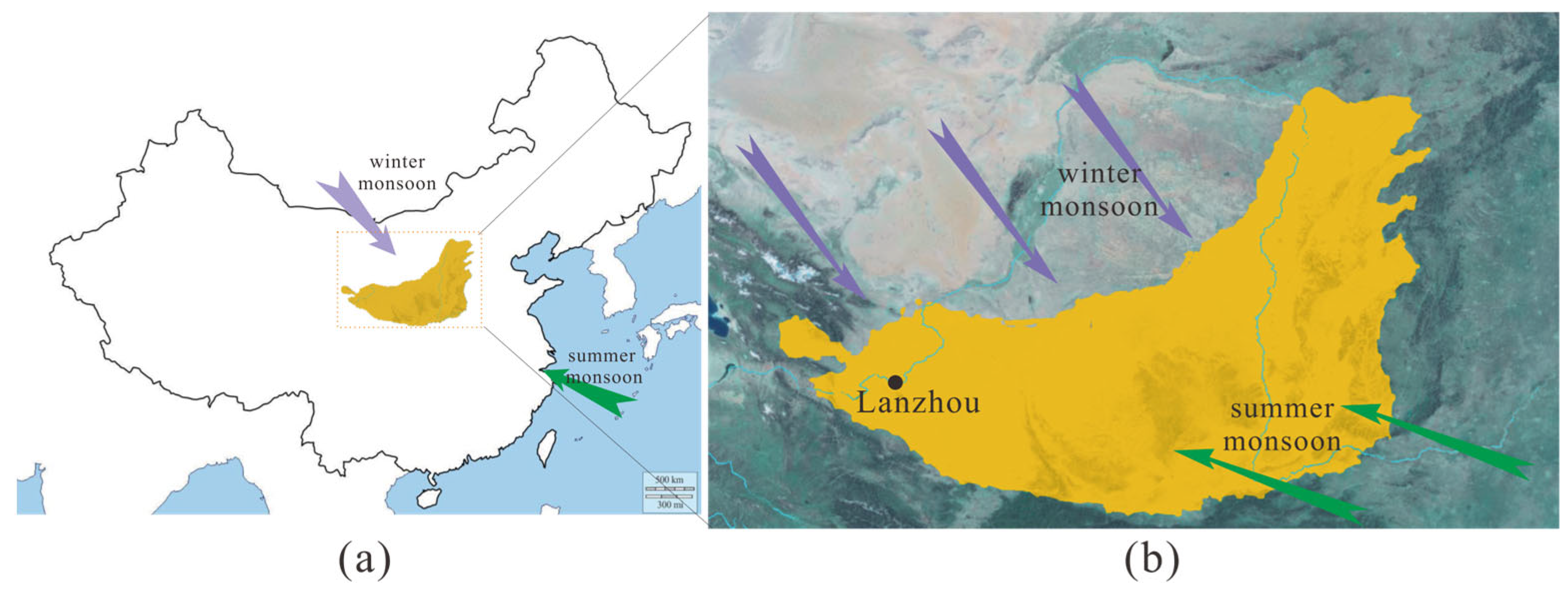
2.1.1. Sampling Location and Sample Pretreatment

The Loess Plateau region is influenced by the winter northwest monsoon and summer southwest monsoon [19]. There are abundant sources of sand and dust in the northwest, with particle size decreasing gradually from northwest to southeast. Therefore, scholars believe that the loess in this region is primarily transported and formed under the influence of the winter northwest monsoon [20]. The sampling site for this study is located in Lanzhou City, Shaanxi Province, China, which is a typical loess region. The geographical distribution of the sampling site and the monsoon distribution in the area are shown in Figure 1. Approximately 20 kg of loose loess samples were collected and their particle density was measured to be 1.35 g/cm³ according to the National Geotechnical Test Standard [21]. The loess sample was then lightly compacted using a rubber roller on a rubber sheet until the particles were uniform without any significant clumping.

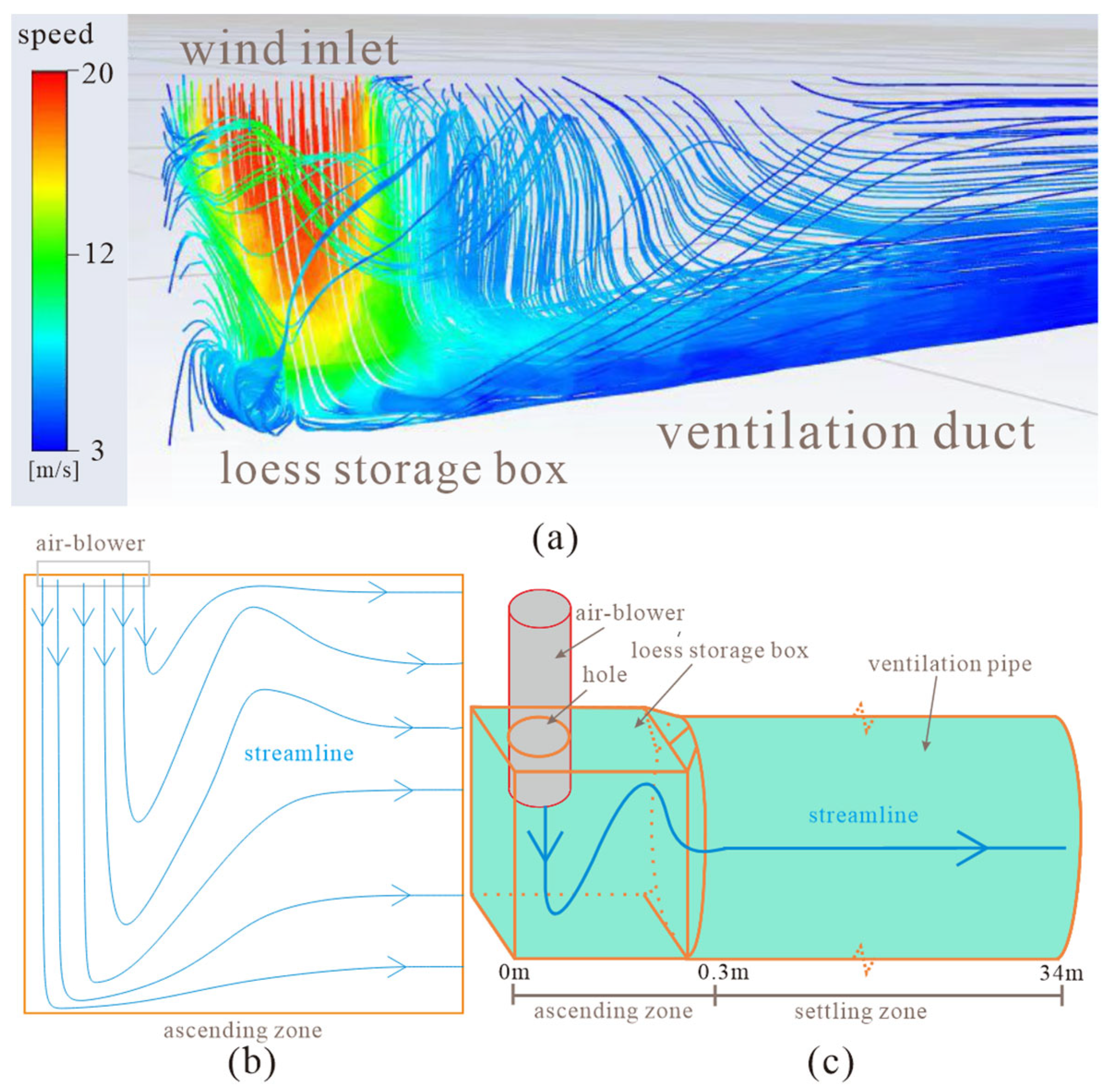
2.1.2. Wind Tunnel Experimental Device and Experimental Procedure

This study utilized a self-designed wind tunnel experimental device for the experiments. The device consists of three main components: an air-blower, a loess storage box, and a ventilation duct. The loess storage box has dimensions of 20 cm × 20 cm × 30 cm and is assembled from wooden boards, with the top opening serving as the inlet for the air-blower. A CRISTIN blower was used with an outlet wind speed of 20 m/s. The ventilation duct is a hollow circular tube made of polyethylene material, with a diameter of 13 cm and a length of 34 m. It is semi-transparent to observe the internal movement of dust particles. The soft boundary material is capable of changing shape according to variations in the wind field. The bottom has an opening for collecting deposited loess particles and measuring wind speed. Apart from the air-blower inlet and the wind outlet at the end of the duct, the experimental device is completely sealed. A SMART SENSOR AS816 was used for wind speed measurement, capable of measuring wind speeds from 0.5 to 30 m/s with an error margin of less than 5%. The experimental device is illustrated in Figure 2a,b.

Before starting the experiment, the air-blower is started to input wind power and the wind speed inside the measurement device is measured every meter as shown in Figure 2c. Approximately 150 g of loess dust is added to the loess storage box; then, the air-blower is started to introduce wind force. The wind force input is stopped after the dust has completely settled. Subsequently, another 150 g of loess is added to the loess storage box and this process is repeated multiple times until a sufficient amount of loess dust has accumulated at the bottom of the duct at the end position (33–34 m), at which point the experiment is concluded. Temperature differences in the experimental environment are less than 1 °C and relative humidity differences are less than 1%. After the experiment is stopped, the deposited dust is collected every meter to measure the particle size distribution as shown in Figure 2d. The Bettersize 2000 laser particle size analyzer is used to analyze the particle size of the particles collected at every meter during the wind tunnel test. Particle size analysis, also known as particle sizing, is an important tool for studying particle sizes and their percentage content [24].

2.2. Derivation of the Particle Motion Equations

Using Fluent 2022R1 to analyze the airflow inside the wind tunnel test setup, the variation in wind direction was obtained as shown in Figure 3a. A simplified description of the wind streamline diagram is provided in Figure 3b. The dust transport process was segmented into ascending and descending stages, as illustrated in Figure 3c.

Analyzing the motion of particles in both horizontal and vertical directions, with the vertical movement divided into the lifting and settling stages.

2.2.1. Horizontal Direction

In the horizontal direction, particles undergo accelerated motion due to the horizontal wind force. According to Newton’s second law:

$$F_f=ma$$

(1)

F_f represents the viscous drag force exerted on the dust particles by the wind. m denotes the particle mass with m = ρ × V where ρ is the particle density. V is the particle volume given by V = π × d³/6, where d is the particle diameter. a represents the particle acceleration given by a = d(v_h)/dt, where v_h is the particle’s horizontal velocity and the initial velocity is zero, and t is time. According to previous studies on viscous drag force [25], the aforementioned F_f is calculated as:

$$F_f=6\pi \eta r\left(v_{fh}-v_h\right)$$

(2)

where η is the dynamic viscosity of the fluid (air), r is the particle radius, and v_fh is the horizontal wind speed during the lifting stage, assumed to be constant. By combining Equations (1) and (2) and letting k = 6πηr, according to the solution proposed by Timothy [26], the differential equation is solved to obtain the function v_h(t) in terms of time t.

$$v_h=v_{fh}-v_{fh}\times e^{-\frac{k\ast t}{m}}$$

(3)

According to Equation (3), the equilibrium velocity of particles in the horizontal direction can be determined.

$$v_h\left(\max \right)=v_{fh}$$

(4)

2.2.2. Vertical Direction Ascending Segment

In the vertical direction, particles move under the influence of gravity and wind force:

$$F_f-mg=ma$$

(5)

F_f represents the viscous drag force, and its magnitude at this stage is:

$$F_f=6\pi \eta r\left(v_{fv}-v_y\right)$$

(6)

v_fv represents the vertical wind speed during the lifting stage. v_y is the vertical velocity of the dust particles, with an initial velocity of zero, where a = d(v_y)/dt. By combining Equations (5) and (6), the function v_y(t) is solved with respect to time t.

$$v_y\times \left(t\right)=\left(k\times v_{fv}-mg\right)\times \left(1-e^{-\frac{k\times t}{m}}\right)/k$$

(7)

2.2.3. Vertical Direction Settling Segment

In the settling stage, particles descend in the vertical direction under the influence of gravity and viscous drag force.

$$F_f-mg=ma$$

(8)

The magnitude of the viscous drag force F_f is:

$$F_f=6\pi \eta r{v}_c$$

(9)

where v_c is the settling velocity of the particle, with an initial velocity of zero, and a = d(v_c)/dt. By combining Equations (8) and (9), the differential equation is solved for v_c (t).

$$v_c=\left(mg-mg\times e^{-\frac{k\times t}{m}}\right)/k$$

(10)

When time t tends to infinity, the particle reaches its maximum settling velocity, which is the equilibrium velocity:

$$v_c\left(\max \right)=\frac{2\rho g}{9\eta }\times r^2$$

(11)

The final settling velocity is directly proportional to the square of the particle diameter.

For the particle transport process, different particle settling heights are considered as h₀ (height of ventilation duct), with the settling speed being the equilibrium settling velocity v_c(max) (Formula (11)) and the horizontal wind speed in the settling stage as v_f. The transport distance s can be obtained as:

$$s=\frac{9v_f{h}_0\eta }{2\rho g}\times \frac{1}{r^2}$$

(12)

2.3. Numerical Simulation

Using Particle Flow Code (PFC) for numerical simulation, 10 size intervals were defined for particles ranging from 10 to 110 μm, divided into 10 equal parts, with an equal number of particles in each interval distributed uniformly along the height as depicted in Figure 4. The model dimensions were 50 cm × 50 cm × 25 m. The numerical simulation process only includes the settling segment as per the theoretical derivation and does not involve the rising segment.

2.4. Software Introduction

In this study, two software programs, FLUENT and PFC, were used. Computational Fluid Dynamics (CFD) simulation methods enable the analysis and visualization of fluid flow processes. FLUENT is one of the comprehensive and versatile CFD software systems widely used in China [27].

Particle Flow Code (PFC) examines the mechanical properties and behavior of media from a microscopic structural perspective, with particles as the fundamental components. Using PFC numerical simulations allows for observing the transport process of dust particles from a microscopic angle.

3. Results and Analysis

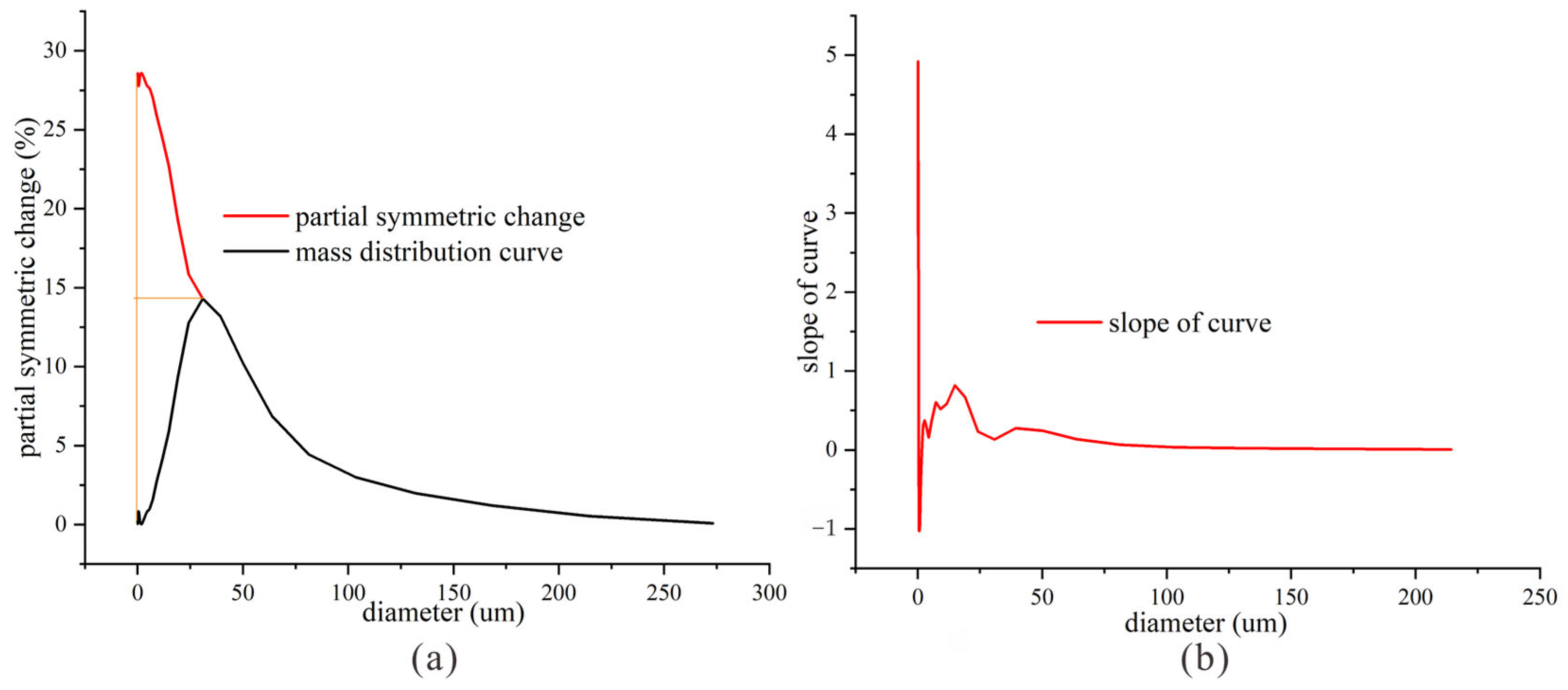
3.1. Particle Size Analysis in the Experimental Results

The particle content at different distances in the wind tunnel test results is shown in Figure 5a. As the particle content varies with distance, particle sizes exhibiting peak values are selected and the relationship between particle size and transporting distance is plotted in Figure 5b.

In Figure 5a, significant differences are observed between the curves at different distances, indicating a pronounced wind sorting effect. The distance corresponding to the peak values of the curves in Figure 5b is regarded as the ideal transporting distance for particles, representing the distance that the particles of that size would ideally reach under the experimental conditions.

3.2. Particle Motion Process

According to the theoretical derivation in Section 2.2, an analysis of the particle motion process is conducted using the parameters specified in

Table 1. Parameters used in model derivation.

	g (N/kg)	ρ1 (g/cm3)	ρ2 (kg/m3)	η (N × s/m2)	h0 (m)	vf (m/s)
Value	9.8	2.65	1.29	1.79 × 10−5	0.25	3.0

. The parameters used are as follows: g: gravitational acceleration, ρ₁: particle density, ρ₂: air density, η: aerodynamic viscosity of air, h₀: height of the ventilation duct, and v_f: horizontal wind speed in the settling stage.

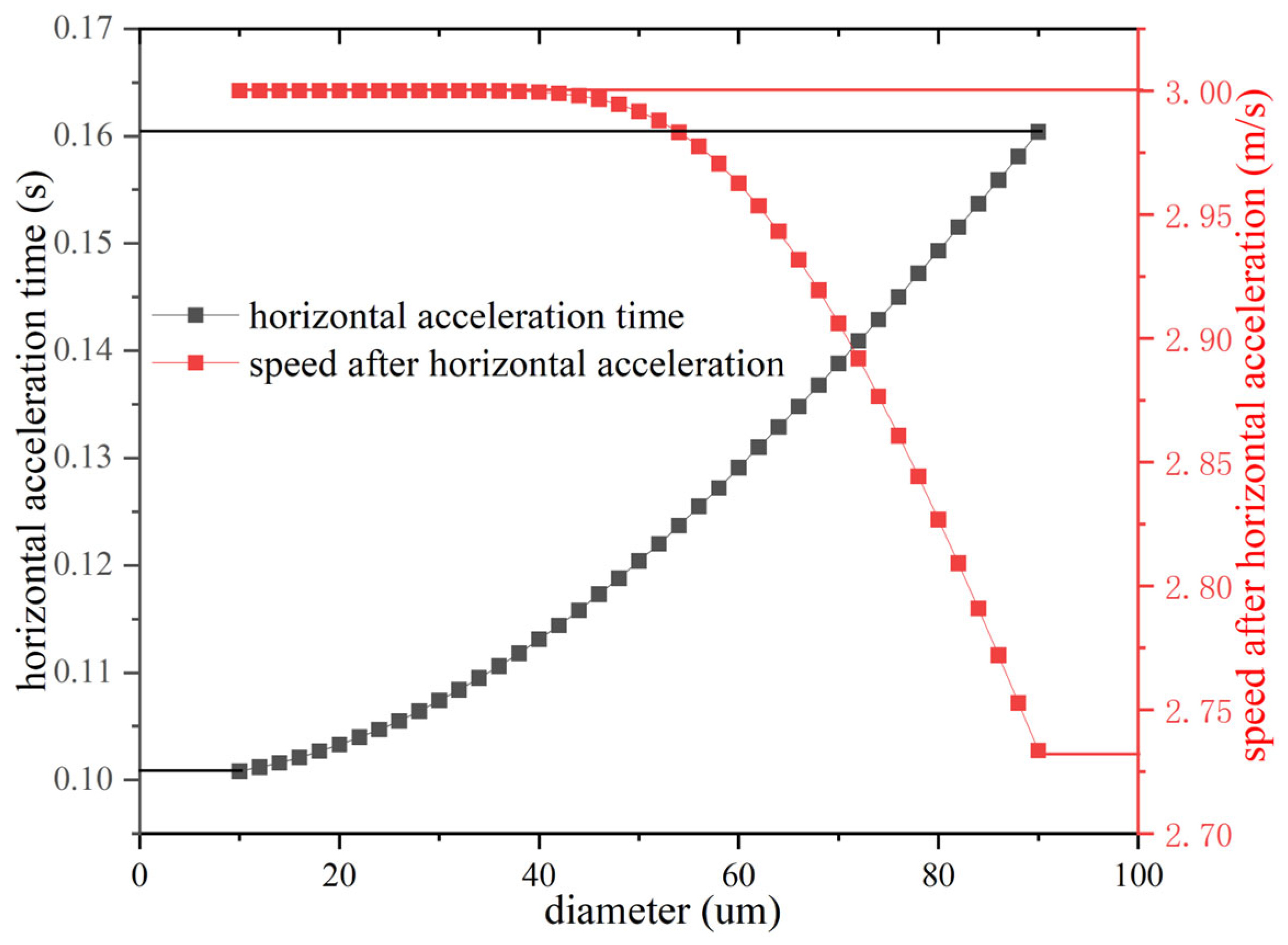
3.2.1. Influence of the Ascending Wind Speed Values

The horizontal wind speed v_f in the settling stage can be obtained through a wind speed measuring instrument. However, it is difficult to measure the horizontal and vertical wind speeds within the lifting stage. An analysis of their potential values and impact is conducted.

(1)

Horizontal wind speed

During the experimental process, at a distance of 0.3 m from the wind inlet, the surface of the ventilation duct remains stable and dust is completely diffused longitudinally. Therefore, the horizontal distance of the rising section is defined as 0.3 m. When v_fh = v_f, according to Formula (3), the speed reached and the time required to pass through the rising section can be obtained as shown in Figure 6. It can be seen that, after passing through the rising section, the speed reached basically matches the wind speed (with a deviation of less than 10%). Furthermore, the horizontal wind speed at the end of the rising section is v_f; hence, v_fh is set to equal v_f.

(2)

Vertical wind speed

Different vertical wind speeds in the rising section (0.4–1.2 times v_f) were set and, based on Formulas (3), (7), and (10), the upward height of particles in the rising section (Figure 7a) and the horizontal transport distance in the settling section (Figure 7b) were obtained. According to Formula (12), the particle transport distance is inversely proportional to the square of the particle radius. In Figure 7b, different curves are fitted to Formula (12) and R2 (a parameter evaluating the degree of fit between the fitted curve and the original curve, with a value closer to 1 indicating a higher degree of match) is obtained. Additionally, the distribution of dust particles uniformly along the height according to different particle sizes and its fitting results are included (representing the particle distribution pattern used in numerical simulations).

According to Figure 8a,b, when v_fv is not greater than 0.8 v_f, the higher the wind speed, the greater the upward height of particles within the rising section and the longer the transport distance in the settling section. When v_fv exceeds 0.8 v_f, there are no longer significant differences. The fitting R2 values for different curves are all 0.999, indicating strong fit of the transport distance–particle size relationship with the derived Formula (12). The varying values of vertical wind speed in the rising section do not affect the accuracy of the results. Therefore, v_fv is set equal to v_fh. Additionally, particles with different sizes distributed uniformly along the height exhibit slight deviations from the ideal curve but show good fitting results (R2 = 0.999), suggesting that the setting of particle distribution in numerical simulations does not affect the accuracy of the results.

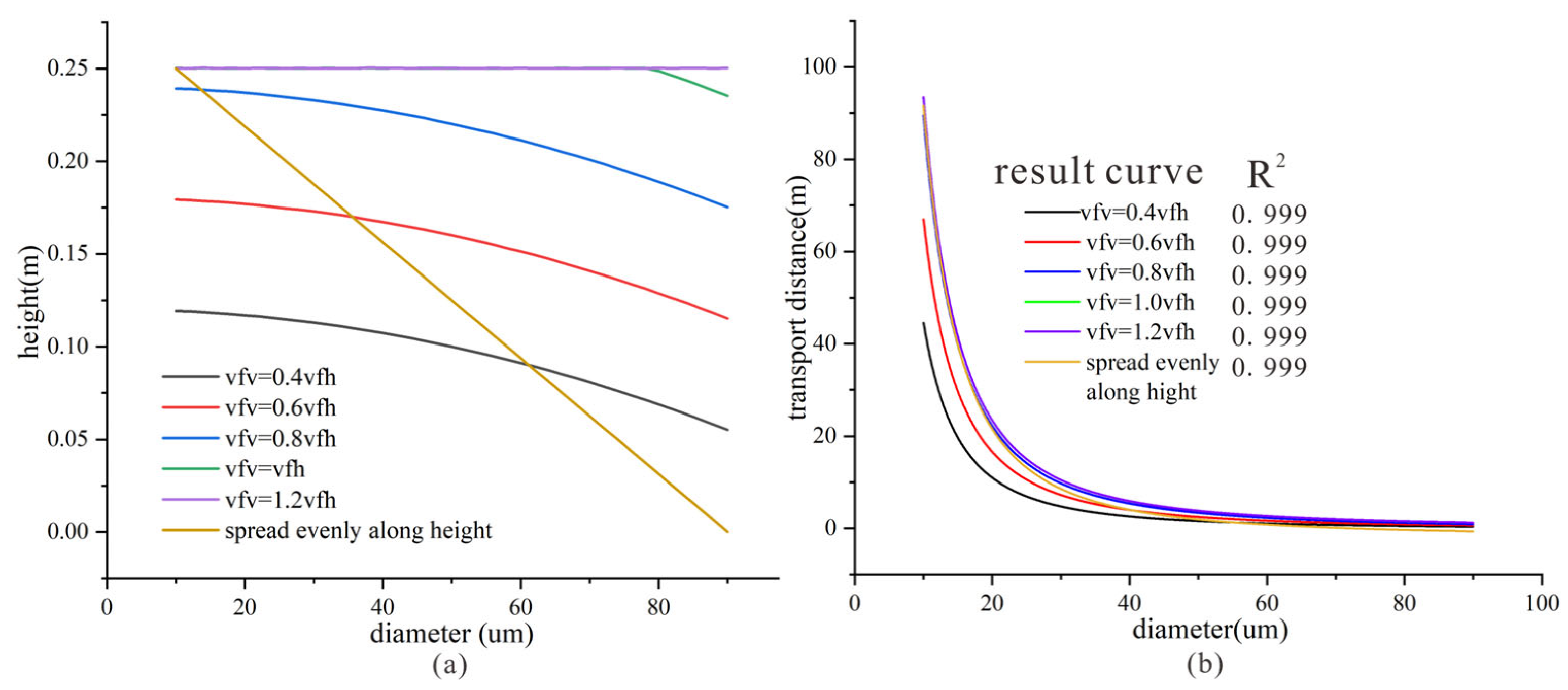
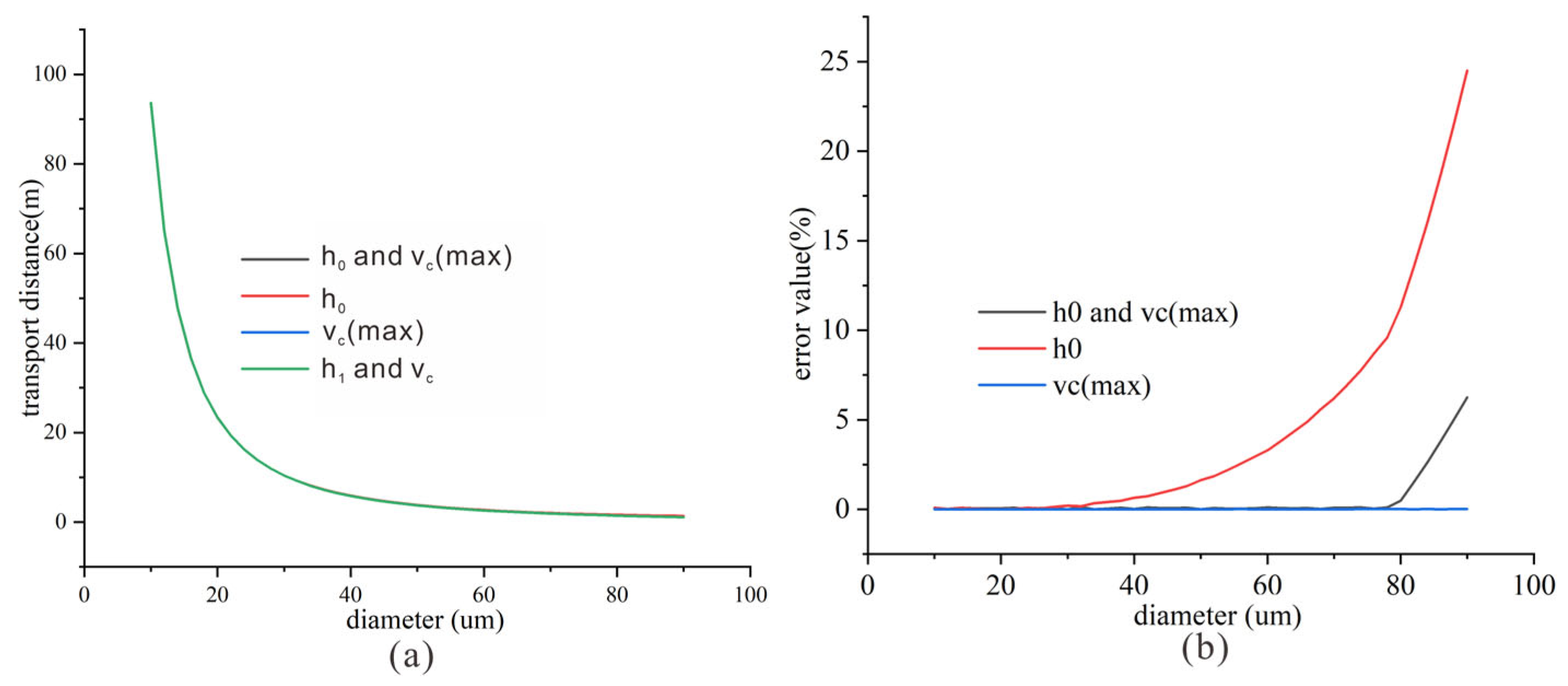
3.2.2. Analysis of the Influence of Approximate Values for Settling Velocity and Height in the Descending Segment

Using Formulas (3) and (7), the total upward height h1 of particles in the rising section is obtained. Based on h1 and Formulas (3), (10), and (11), the horizontal transport distance of particles is determined. In the derivation of Formula (12), h1 is approximated as h0, and the settling velocity vc is taken as the settling equilibrium velocity vc(max). According to whether h1 and vc are approximated, there are a total of four combinations, resulting in particle transport distances as shown in Figure 8a. The errors for three cases with approximated values compared to the non-approximated case are depicted in Figure 8b.

From Figure 8b, it can be observed that, when using h₀ alone as an approximation for h₁, there is a significant curve error. However, when approximating both h₀ and v_c(max) simultaneously, only particles of size 80–90 μm exhibit a deviation of less than 5%. Therefore, the use of approximations does not affect the accuracy and reliability of Formula (12).

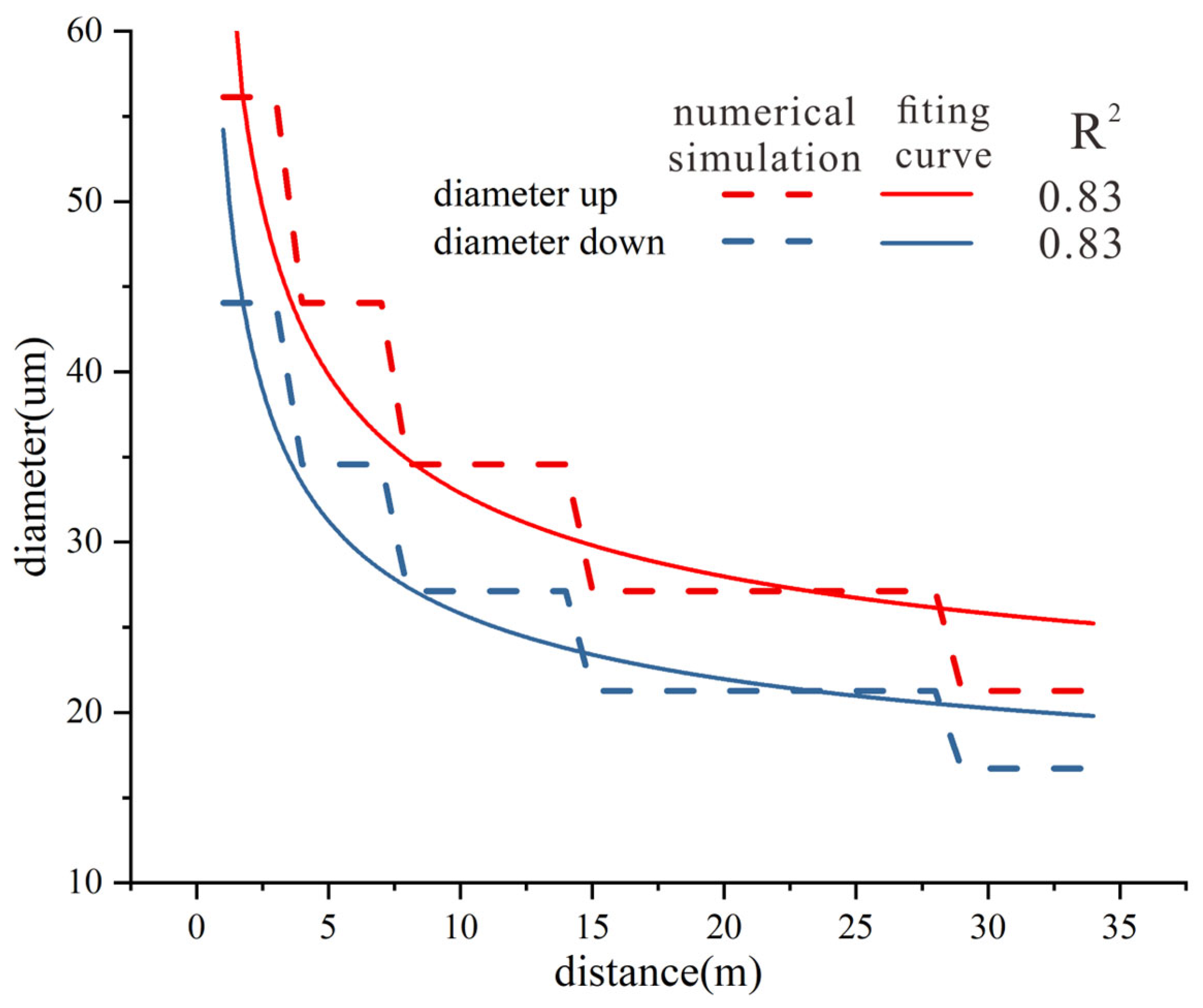
3.2.3. Fitting of Theoretical Formulas with Experimental Results

The particles with the highest content at different distances in Figure 4b along with their corresponding particle sizes are plotted in Figure 9 and fitted with Formula (12).

Due to fluctuations in the experimental data, the fitting R2 is relatively small. However, the overall trend of the fitting curve aligns with the data curve, indicating that the experimental results are consistent with our theoretical derivation. Therefore, it can be concluded that the theoretical predictions fit well with the experimental results.

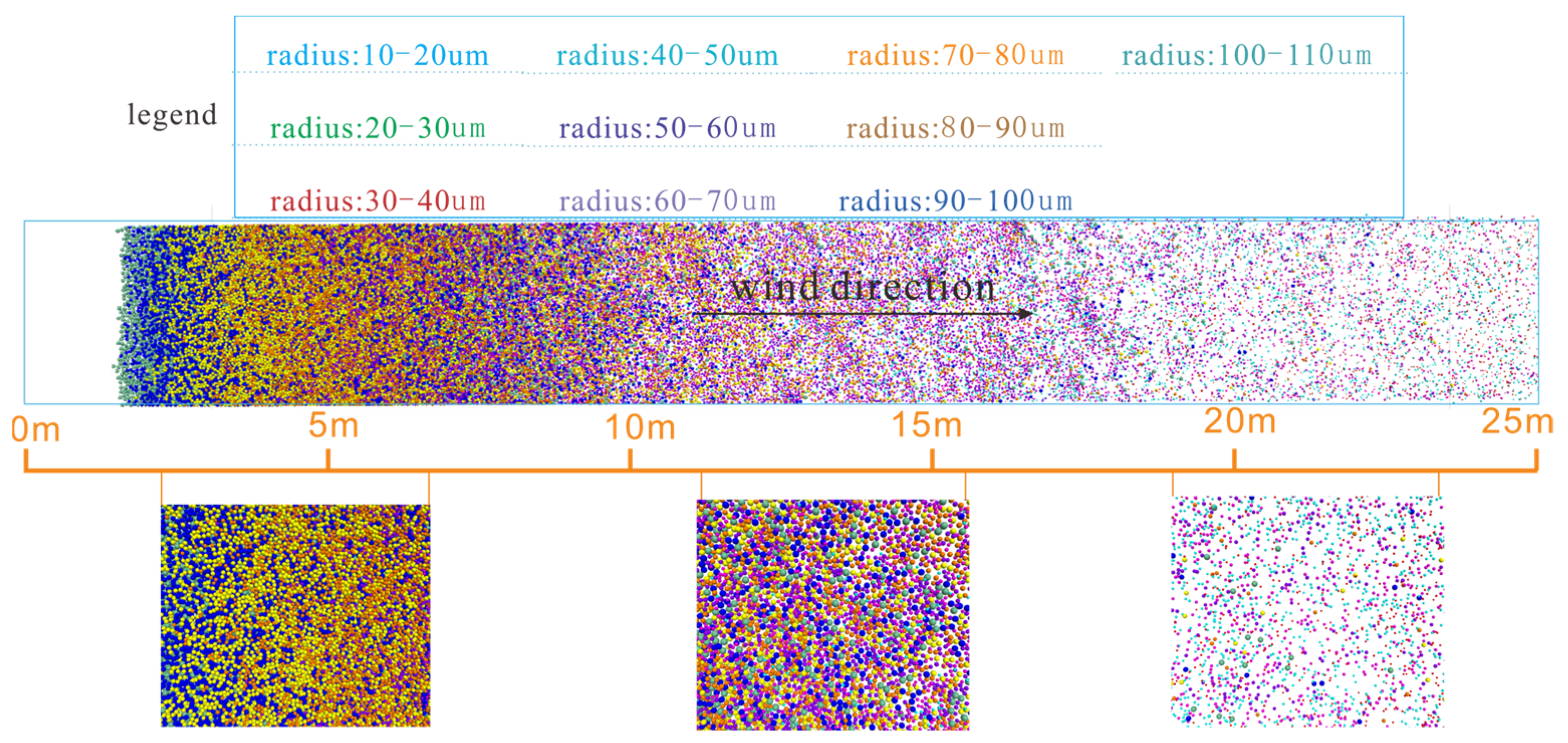
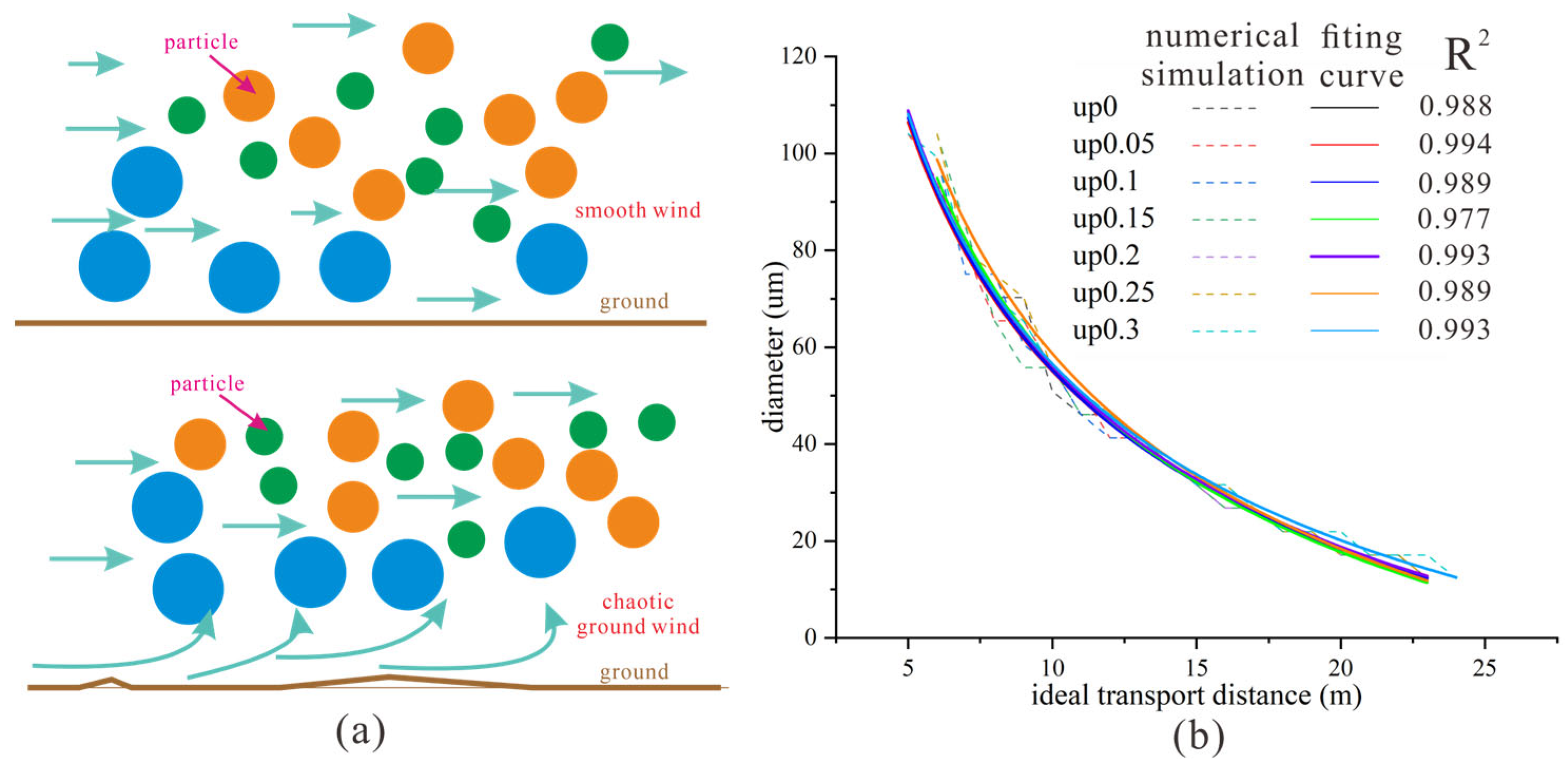
3.3. Numerical Simulation Results

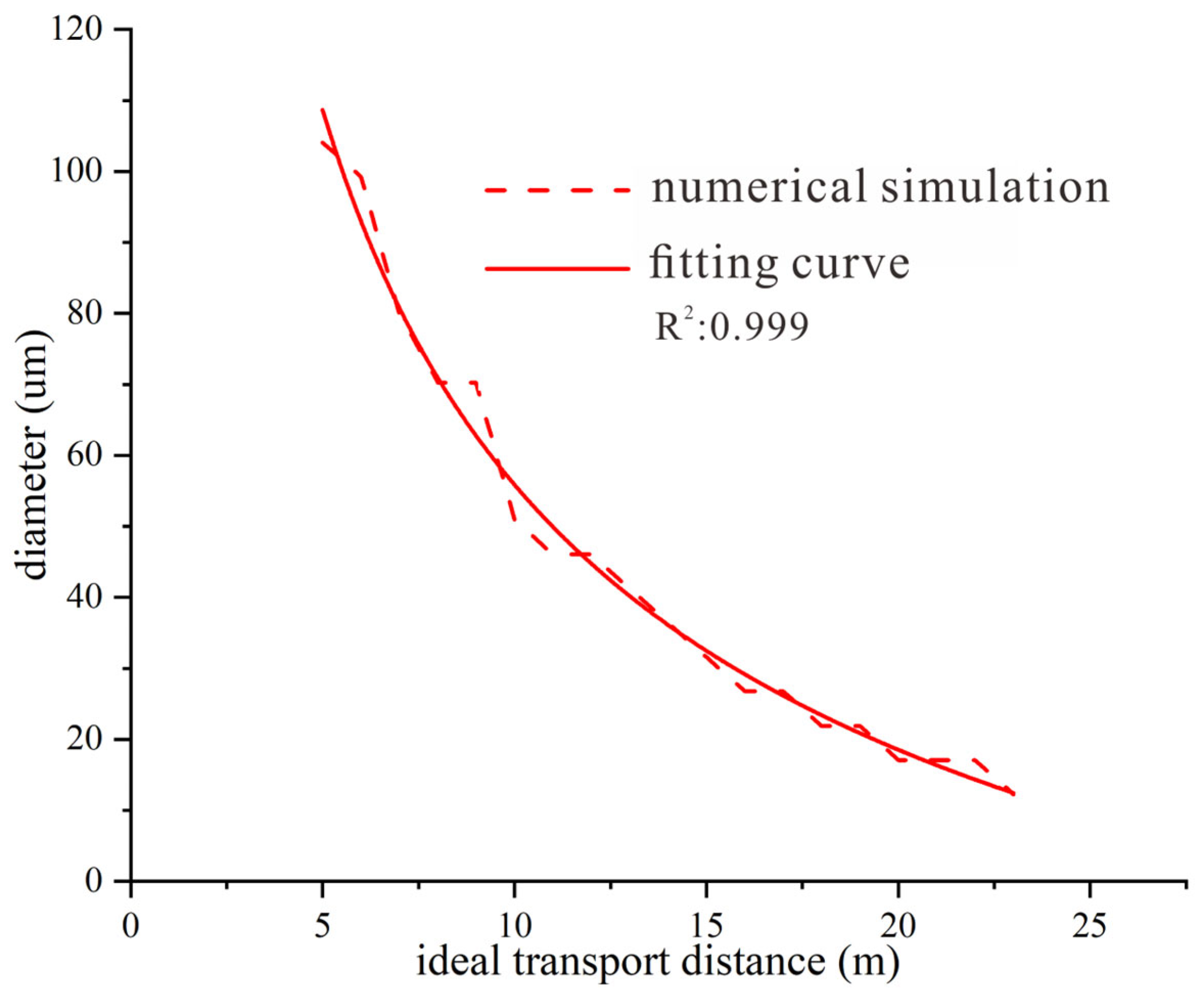
3.3.1. Alignment of Numerical Simulation Results with Theoretical Formulas

In the numerical simulation, the dust transporting process ends as shown in Figure 10. It can be observed that, at the same distance, the deposited particles are mainly of a certain size range, with a small amount of particles from other size ranges present. In the downwind direction, the particle size decreases gradually and the number of particles reduces progressively.

The particle size information is measured in the numerical simulation and the relationship plotted between the particle size with the highest content and the transport distance, as shown in Figure 11. At distances of 3–5 m, the particle sizes are the same, all being the maximum size. Specifically, at 5 m, it represents the ideal deposition distance for particles with the largest size generated in this simulation. Since there are no particles larger than this size, the maximum content particle size remains the same within the range of 3–5 m and is excluded from further fitting. From 5 to 25 m, the data are fitted with Formula (12), yielding a fitting R2 of 0.999, indicating a close agreement between the data and the formula. This suggests that the transport distance is inversely proportional to the square of the particle size, consistent with the results obtained from wind tunnel experiments and theoretical derivations.

3.3.2. Analysis of Other Conditions in Nature Based on Numerical Simulations

In the existing simulation, ideal combinations of particle sizes, initial particle position distributions, and wind conditions were used to obtain particle deposition patterns consistent with experimental and physical model results. Considering the various influencing factors in nature, the next steps involve examining the effects of wind conditions (turbulent updrafts and turbulent ground winds) and particle roundness (different friction coefficients and damping coefficients) on the transport outcomes.

(1)

The impact of turbulent updrafts

When the updraft wind field is stable, as mentioned earlier, dust particles of different sizes exhibit a distinct distribution pattern along the height. However, when the updraft wind field in nature becomes highly turbulent, this distribution pattern may no longer be evident. Particles of different sizes are randomly distributed in space, as shown in Figure 12a. Numerical simulations were used to observe the transport and deposition patterns of dust particles under two different initial conditions, as illustrated in Figure 12b.

It is evident that, when the initial particles are randomly distributed in space, larger particles are significantly affected, leading to longer transport distances, while smaller particles are minimally influenced, resulting in a poorer overall curve fitting. This indicates that the distribution of the initial updraft wind field has a relatively weak impact on the particle transport and deposition patterns.

(2)

The impact of turbulent surface winds

In nature, the interaction between wind and the ground often leads to a more turbulent near-surface wind field. The continuous near-surface wind is not a laminar flow parallel to the ground but, rather, generates turbulence that deflects in the direction of movement, thereby disturbing the particles. When particles are affected by upward turbulent wind, smaller particles are more likely to remain suspended and are thus transported over longer distances, as shown in Figure 13a. The relationship between wind speed and its turbulent fluctuation velocity in the wind field is complex, with higher near-surface wind speeds generally leading to increased turbulence and greater deflection wind speeds. In the simulation, vertical upward winds ranging from 0 to 0.3 times the horizontal wind speed (increment of 0.05) were set throughout the process at half the height of the pipe to represent near-surface wind conditions. The deposition results under different conditions are observed as shown in Figure 13b.

It can be seen that, under different wind strengths, there is no significant change in the relationship between particle size and transport distance, as well as in the fitting results. Therefore, the weak disturbances from the near-surface wind field in a stable wind field do not affect the expression of particle transport and deposition patterns.

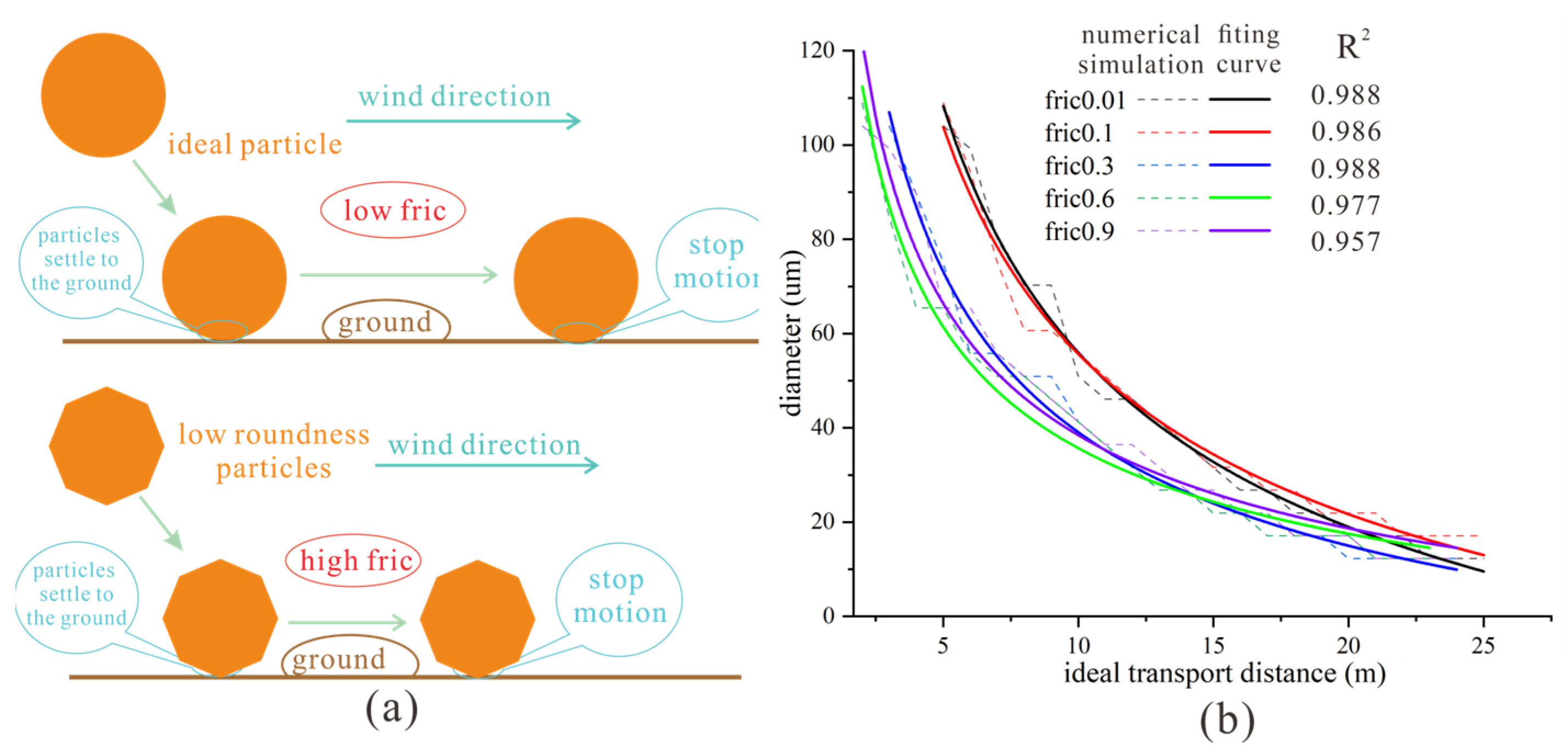
(3)

The impact of different friction coefficients

During the dust transport process, there is a certain amount of friction between the particles and the ground, causing the dust particles deposited on the ground to gradually come to a stop and reach the ideal transport distance. The roundness of the particles and the smoothness of the ground significantly influence this parameter, as shown in Figure 14a. By adjusting the friction coefficient between the particles and the ground, the impact of different friction forces on the transport and deposition patterns of dust particles is observed, as illustrated in Figure 14b.

When the friction coefficient ‘fric’ between the particles and the ground is 0.01, it corresponds to the working conditions simulating wind tunnel experiments. When ‘fric’ is set to 0.1, particles with a diameter larger than 80 um are transported closer, while particles with a diameter smaller than 80 um are transported farther. The friction force reduces the transport distance of larger particles, allowing smaller particles to be transported farther due to less obstruction by larger particles at greater distances. For ‘fric’ values ranging from 0.3 to 0.9, there is a significant decrease in the transport distance for particles of different sizes, indicating that higher friction forces have a notable impact on the particle transport distance.

(4)

The impact of different damping coefficients

When dust particles collide with other particles or the ground, they experience a certain amount of energy loss, resulting in a decrease in velocity, which needs to be reaccelerated under the influence of wind forces. When a large number of dust particles are transported together, this effect becomes more significant. To gain a deeper understanding of this process, we varied the ‘damp’ parameter (referring to energy loss during particle collision processes; higher ‘damp’ values indicate greater energy loss as shown in Figure 15a) in the simulation to observe the impact of energy loss after particle collisions on particle motion. The relationship between particle diameter and transport distance in the deposition results is illustrated in Figure 15b.

When ‘damp’ is set to 0.1, it corresponds to the working conditions simulating wind tunnel experiments. We can observe that, as ‘damp’ increases, the particle transport distance significantly decreases and, at the same time, there is a noticeable change in the shape of the curve, with the R² value of the fitting curve continuously decreasing.

(5)

Comprehensive analysis of combined influences

The influencing factors and their impact have been summarized in

Table 2. Influence of different factors.

	Disturbed Upwind	Disturbed Surface Wind (0–0.3)	Fric (0.1–0.9)	Damp (0.1–0.9)
influence	low	none	middle	high

above.

It is evident that wind forces have a relatively small impact on the transport results, while particle roundness has a significant impact, with lower roundness leading to shorter transport distances. As particles are transported over long distances, the roundness increases continuously. Therefore, in natural dust transport processes, the transport distances between particles vary significantly in different regions.

4. Discussion

Compared to studies by other scholars, this paper focuses more on the particle size distribution of deposited dust particles. Furthermore, there are shortcomings in the design of the wind tunnel experiments in this study that need further improvement.

4.1. Comparison with Studies Conducted by Other Scholars

Qin’s research focuses on the dust transport flux of particles of different sizes during the transport process [16]. Such studies are primarily applicable to modern desertification control. The aim of this study is to understand the mechanism of particle size distribution in loess areas and lay the groundwork for further investigations into the relationship between disasters and particle sizes. Therefore, no explanation was provided regarding dust transport flux in this study. Additionally, Qin obtained the particle settling equilibrium velocity:

$$v=\frac{g{d}^2}{18\mu }\left(\frac{{\rho }_d}{\rho }-1\right)$$

(13)

The units on both sides of Equation (13) are not consistent. Upon investigation, it was found that the reference formula was improperly used [28], thus leading to inaccuracies in the study of viscous resistance on dust settling. This paper chose to rederive and obtained Formula (11), hoping to provide a reference for studies on dust transport.

Based on multiple sediment grain size data samples, some scholars classify them into different end-members according to particle size, with each end-member corresponding to different source areas and transport pathways [29,30]. In the wind tunnel experiments of this study, a partial symmetric transformation was applied to the relationship curve between particle content and particle size at a transport distance of 10 m, and the graph was plotted as shown in Figure 16a. The slopes of the curve after the symmetric transformation were calculated, as depicted in Figure 16b.

From Figure 16a, it can be observed that the curve becomes smoother after the symmetric transformation. Figure 16b indicates that, as the particle size increases, the slope of the curve shows slight fluctuations before gradually stabilizing. During the transport process, collisions occur among numerous particles, causing smaller particles to be more susceptible to settling due to obstruction by larger particles. Consequently, the trend of particle settling is influenced, with smaller particle sizes exhibiting more pronounced fluctuations in slope. Based on the experimental results of this study, it can be concluded that particles of different sizes in loess areas share the same sources and transport pathways, contradicting the conclusions of some scholars [30]. This necessitates further research analysis and remains one of the future research directions of this study.

4.2. Reasons for Selecting the Sampling Location

The frequent occurrence of disasters in loess regions underscores the importance of a thorough understanding of the processes involved for scholars to study disaster mechanisms. Loess regions can generally be divided into the sandy loess belt, typical loess belt, and clay loess belt [31], with the typical loess belt being characterized by the most complex types of disasters [32,33,34]. Therefore, focusing on the soil in the typical loess belt for research purposes can provide valuable insights for related studies. The conclusions of this study indicate that the transport distance of particles is inversely proportional to the square of their particle size. During the actual process of particle transport, factors such as collisions can lead to deviations between the actual and ideal transport distances of particles. The larger the deviation distance, the less likely such deviations will occur. Hence, in loess, the particle size distribution curve exhibits a normal distribution curve. In typical loess areas dominated by silt at the inflection point of the relationship curve between particle transport distance and particle size (Figure 8), further analysis can be conducted to distinguish the relationship between them.

4.3. Insufficient Research and Future Research Directions

The limited scale of the wind tunnel test setup in this study has made it challenging to clarify some issues in the model experiments, such as boundary problems. The ambiguity in the distribution of wind fields in certain regions has also made it more difficult to interpret the regularities of the results for explaining corresponding processes in the natural world. Additionally, there are significant differences between the model boundaries and ground parameters, while the differences in parameters among dust particles at different transport distances are relatively small. Based on the numerical simulation of the experimental process, we have been able to surpass the limitations of the experimental setup and obtain more effective information, such as the varied effects caused by different wind fields in different regions and different parameters of particles. However, the lack of integration with actual processes in nature somewhat weakens the persuasiveness of the results.

Based on the conclusions and findings of this study, in the future, we plan to conduct wind tunnel experiments in different regions (desert areas, sandy loess belts, and clay loess belts [31]) using more advanced experimental setups. Additionally, integrating field data will be a key focus area for us [35]. The transport of dust is related to weathering processes and the level of aridity [36]. As global warming and future increases in aridity levels continue, research on dust cycling processes will become increasingly important [37].

5. Conclusions

This study conducted wind tunnel experiments to observe the particle size distribution pattern of loess dust particles after transportation and deposition under the influence of wind forces, and derived the equations governing the motion of these particles. Numerical simulations were then used to obtain results consistent with the experimental process, serving as the basis for simulating and observing the wind-driven dust transport processes under various natural conditions. The main conclusions of this study are as follows:

(1)

In the wind tunnel experiment results, significant differences were observed in the mass distribution curves of particles at different transport distances, indicating effective particle sorting under wind forces for particles of different sizes.

(2)

For a specific particle size, the distance corresponding to the peak percentage content represents the ideal deposition distance for that particle size, with the ideal transport distance of particles being inversely proportional to the square of their size.

(3)

Turbulent wind fields have a minimal impact on dust transport, while particle roundness significantly influences the transport outcomes.

(4)

Both clay and silt particles in loess regions share the same sources and transport pathways, with clay particles depositing extensively in Chinese regions due to the shielding effect of silt particles, thereby affecting local engineering geological properties.

This study is significant for modern dust control, microscopic structure research of loess, and dust cycle investigation.