Experimental Study on the Slip–Stick Vibration of Plane Gate
Abstract
1. Introduction
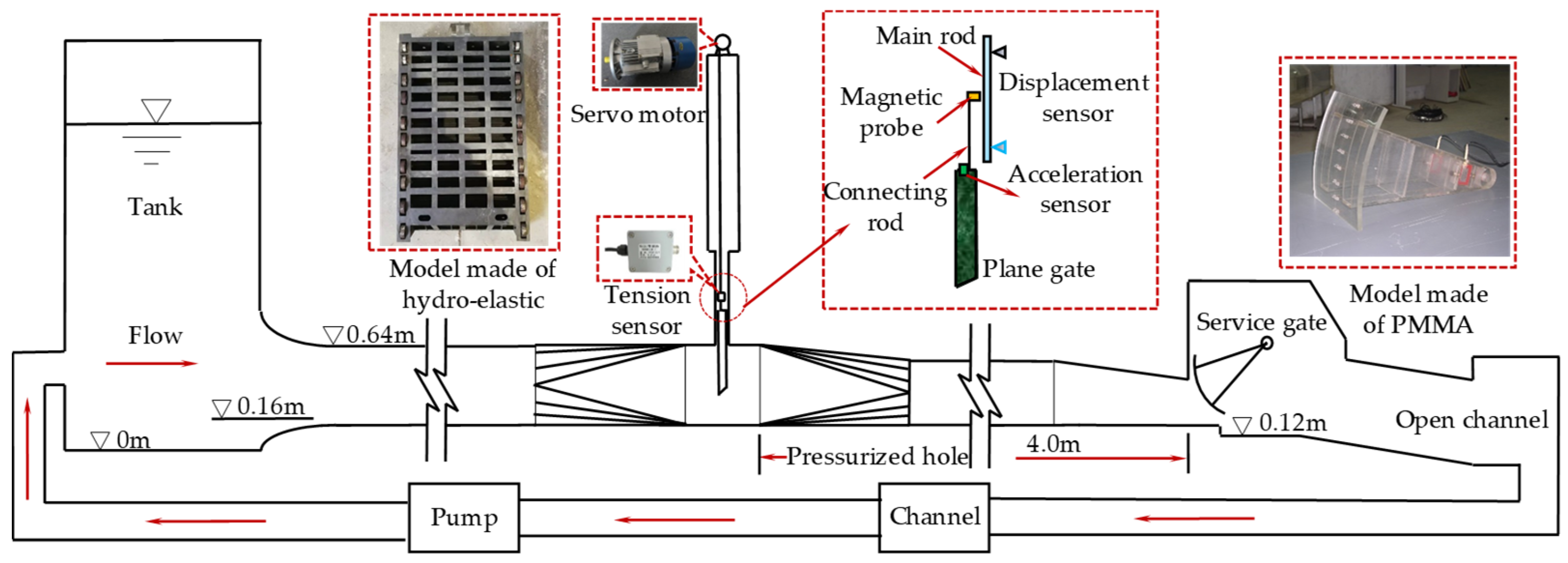
2. Physical Experiment
2.1. Model Setup
2.2. Methods
2.3. Test Conditions
3. Results
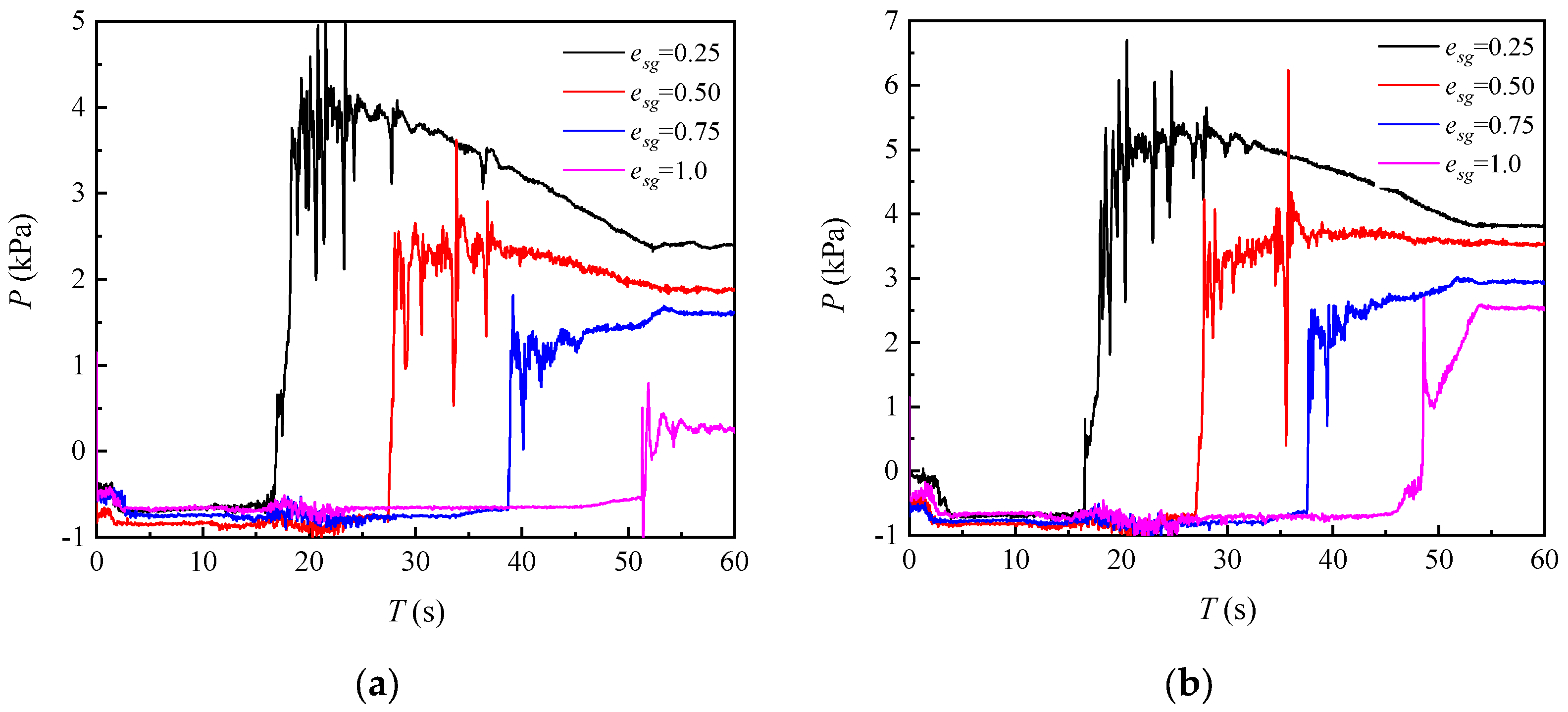
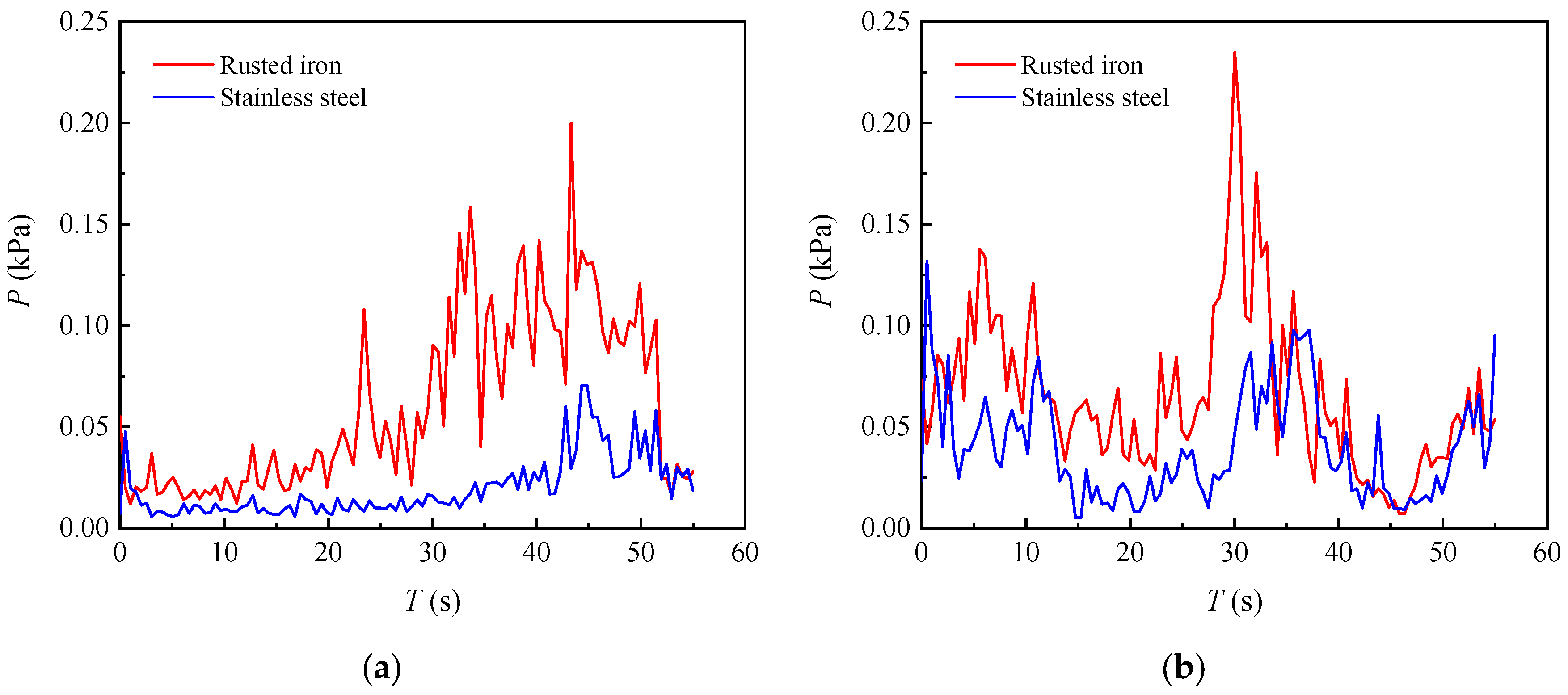
3.1. Water Pressure
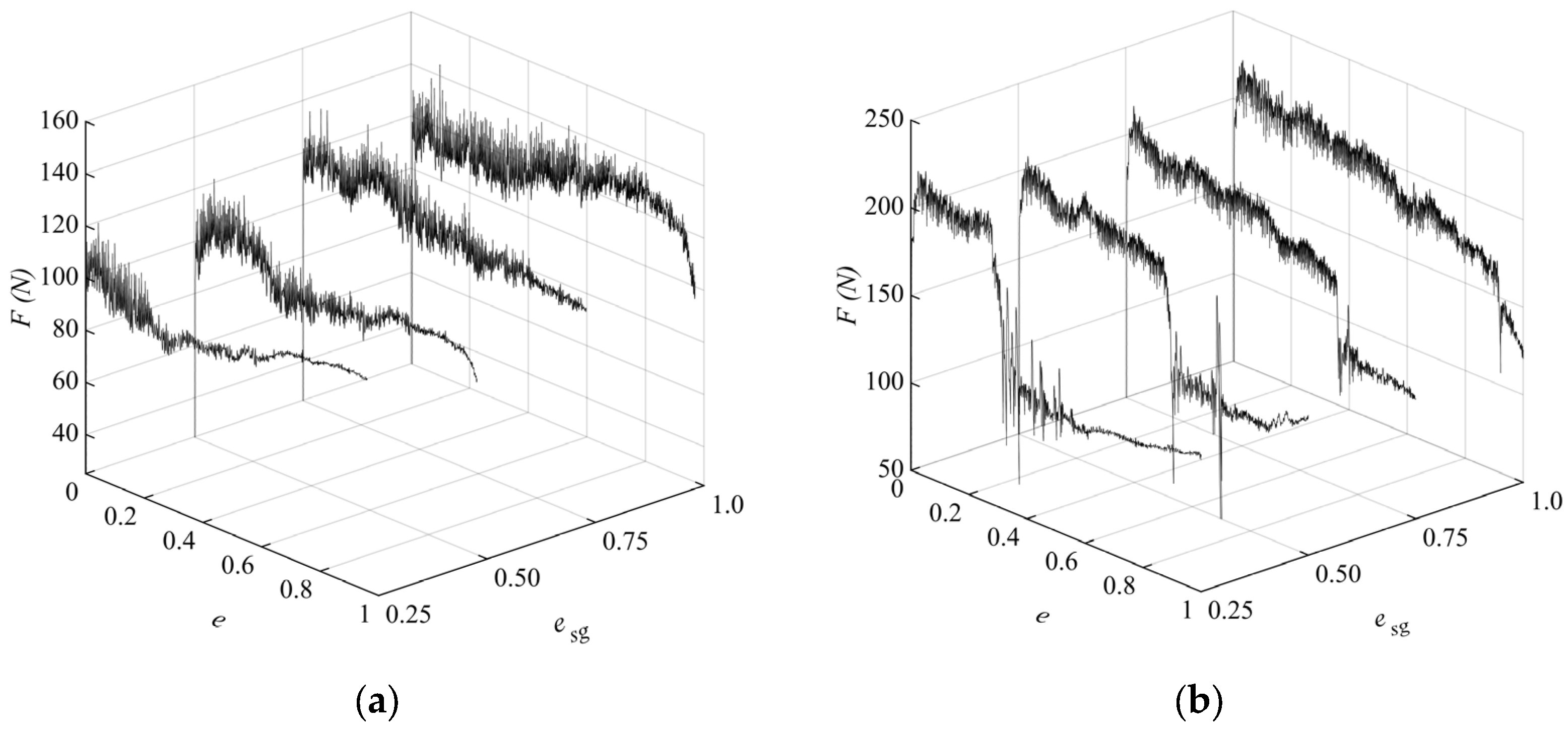
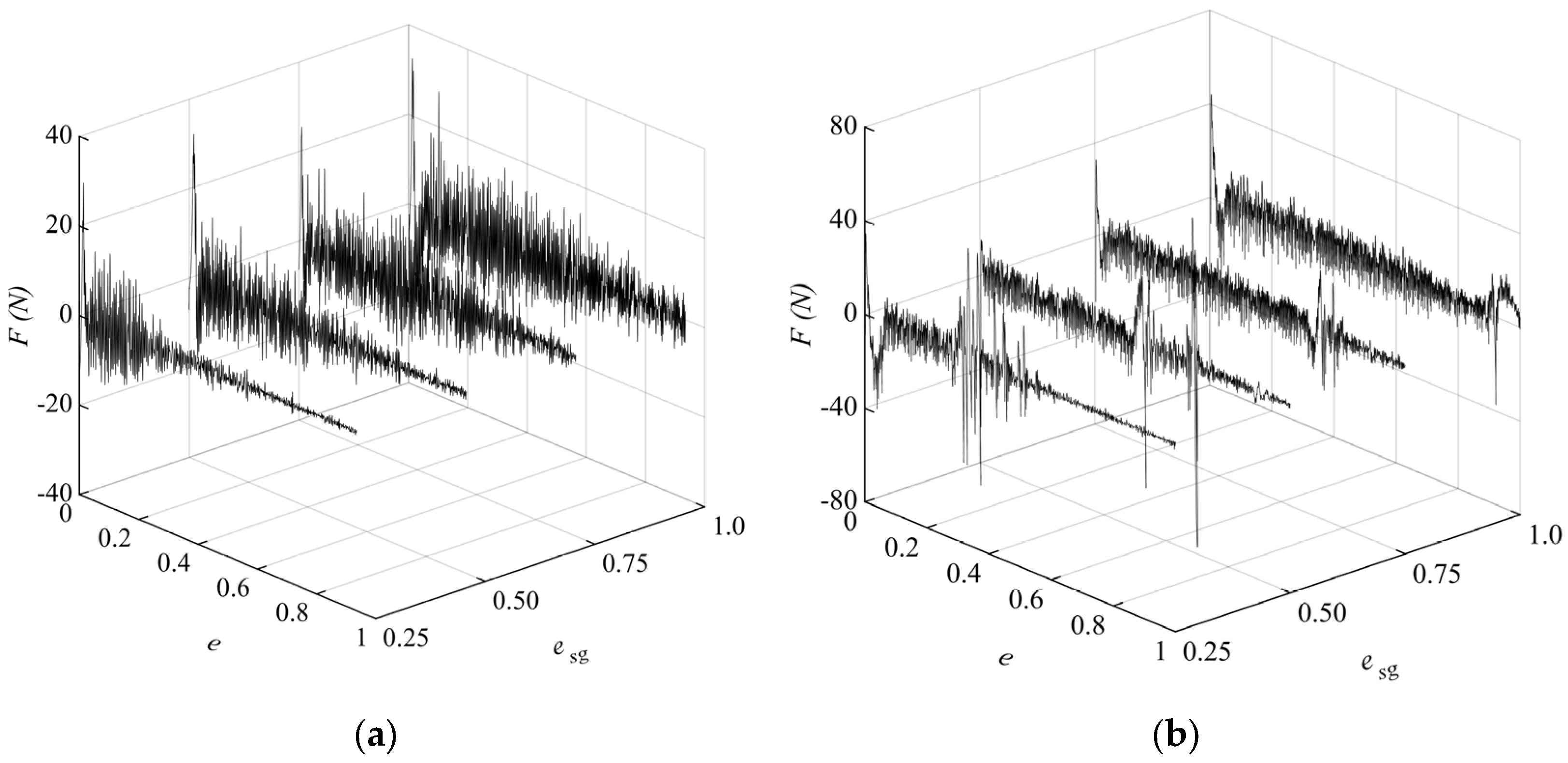
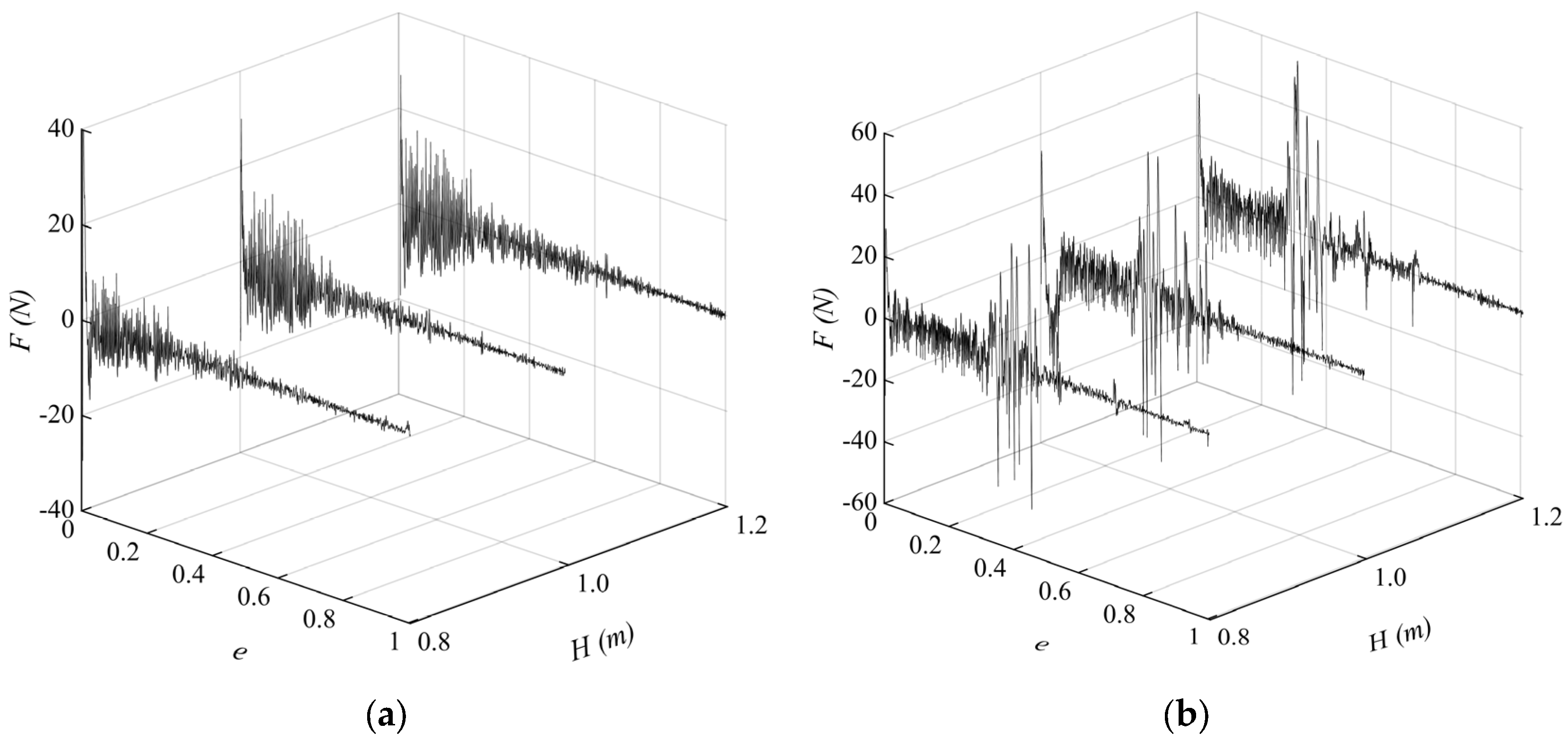
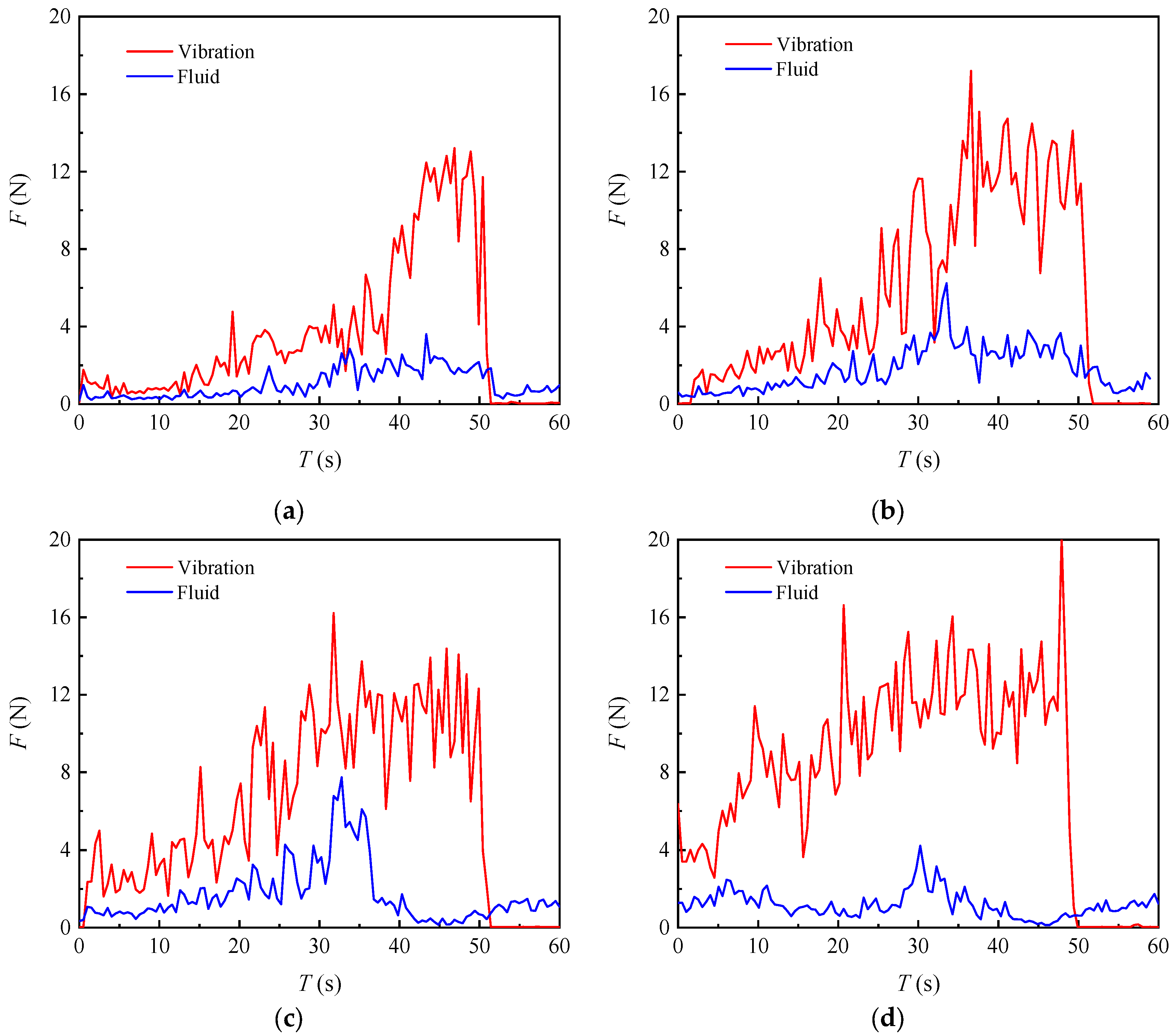
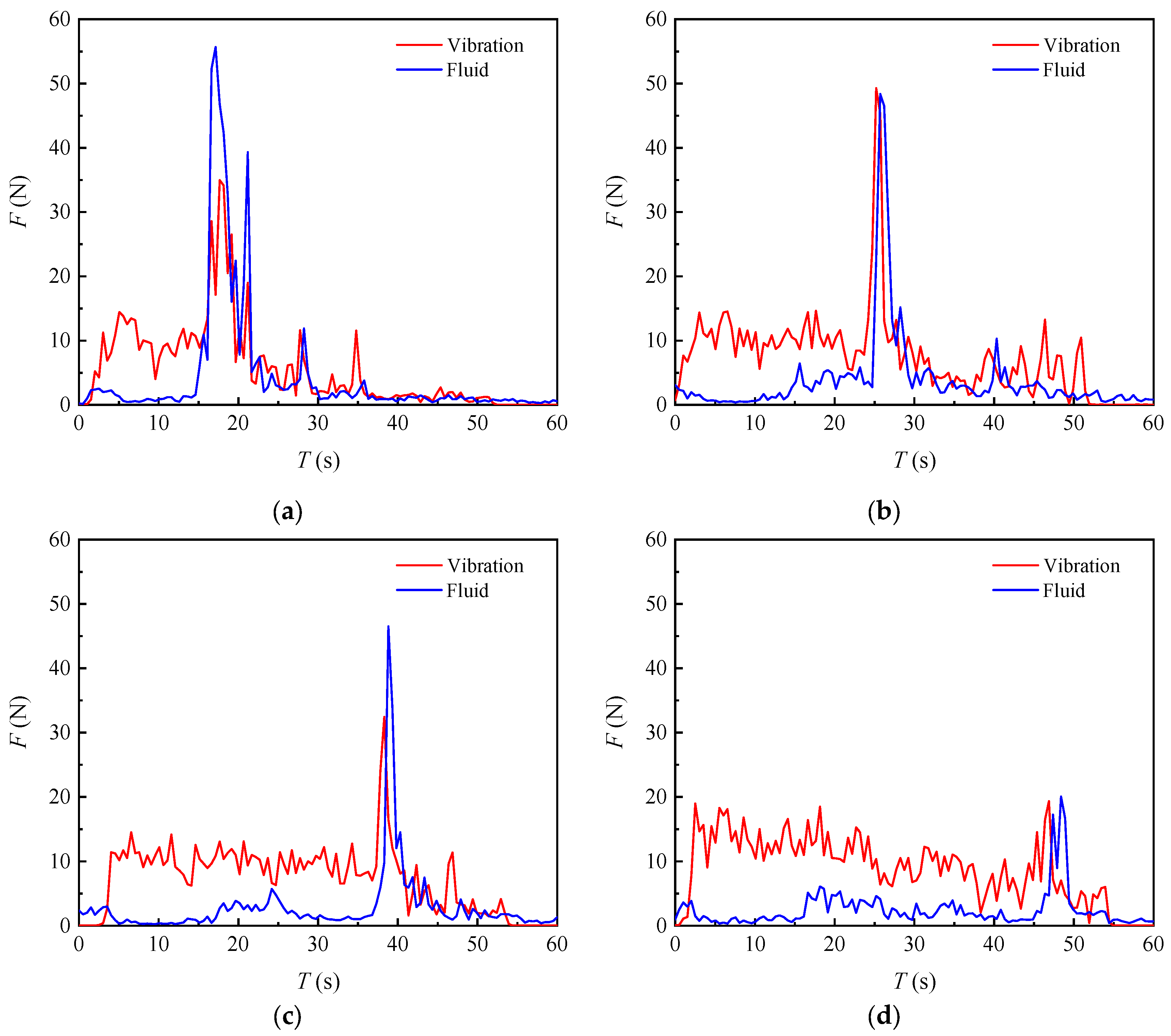
3.2. Hoist Force
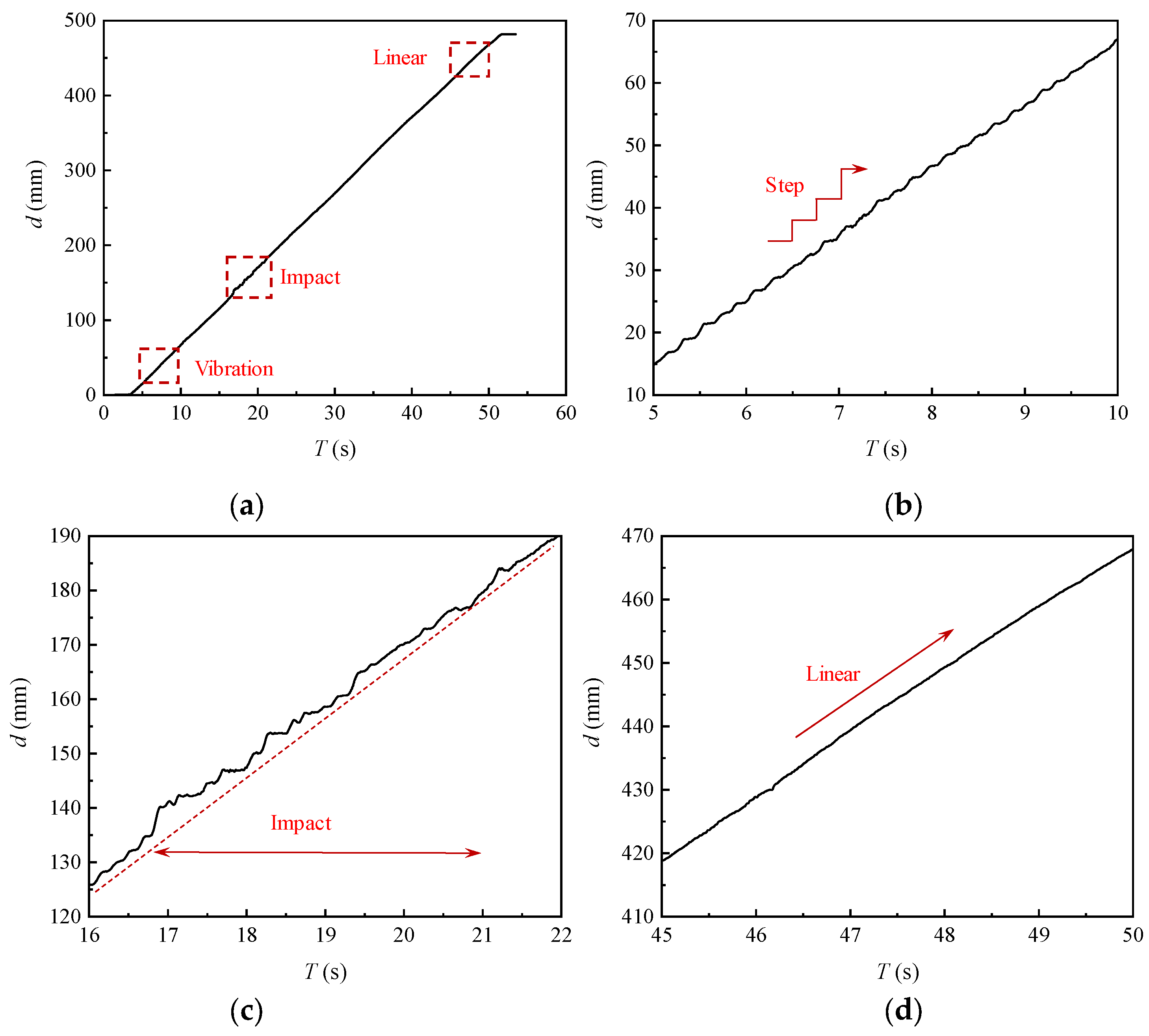
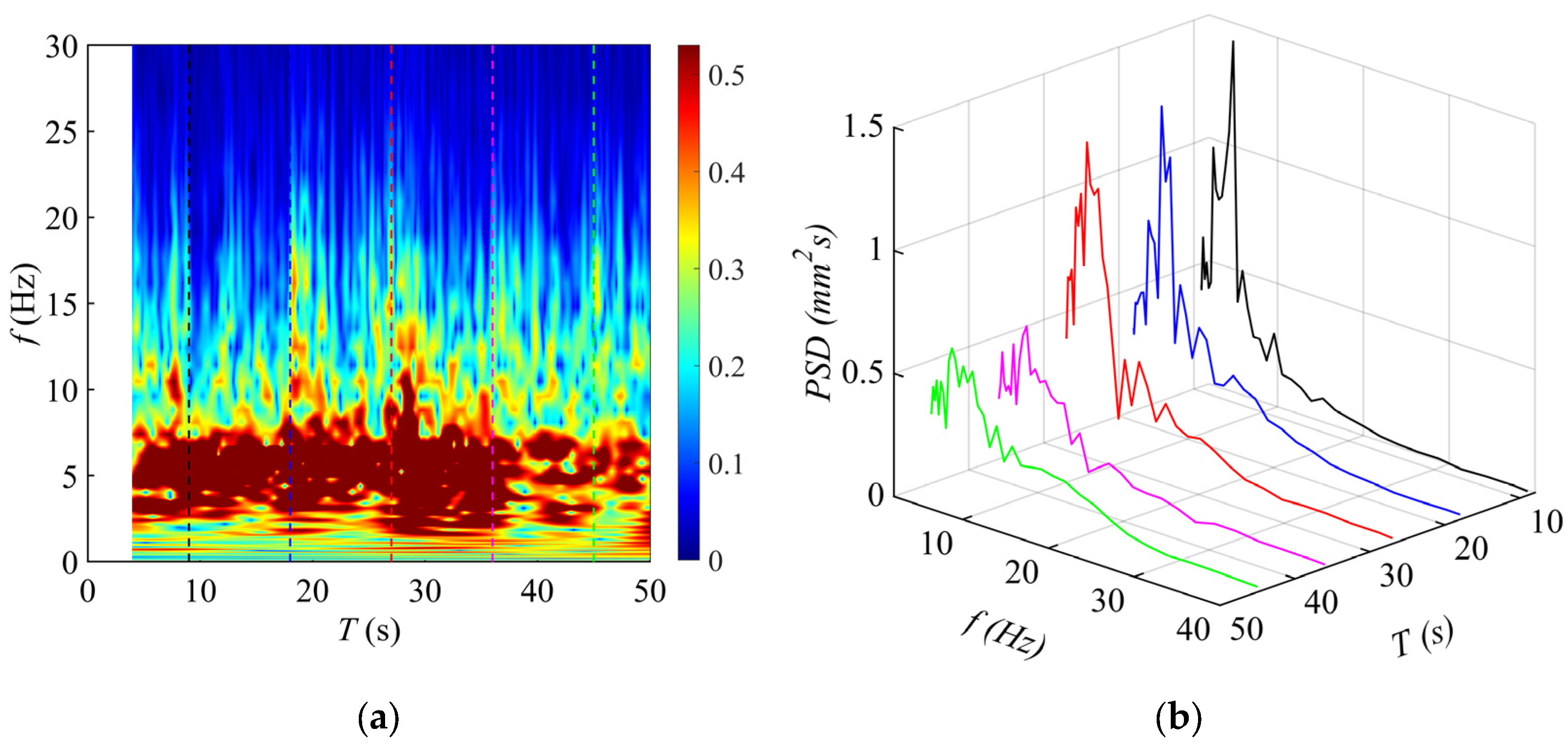
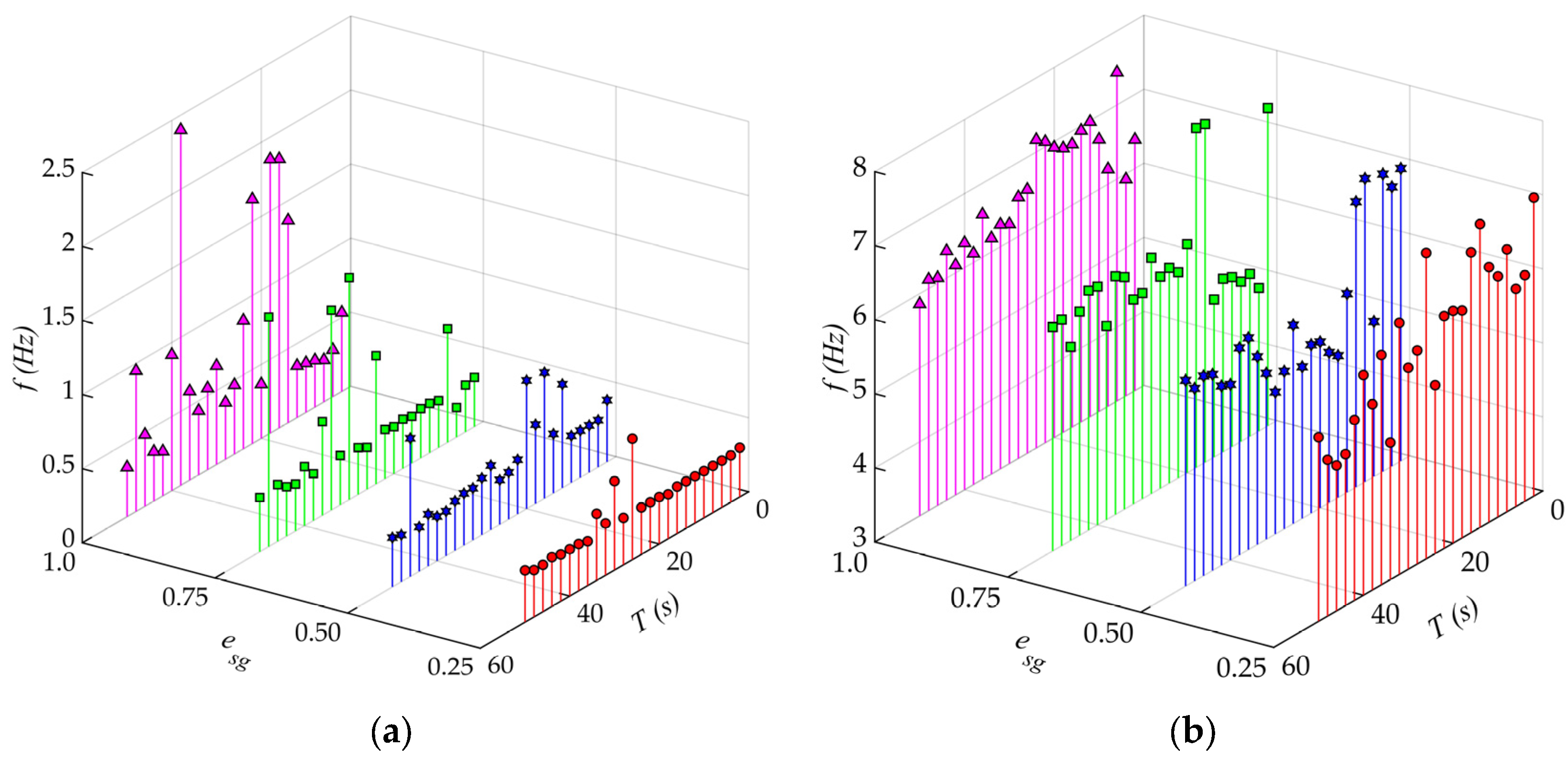
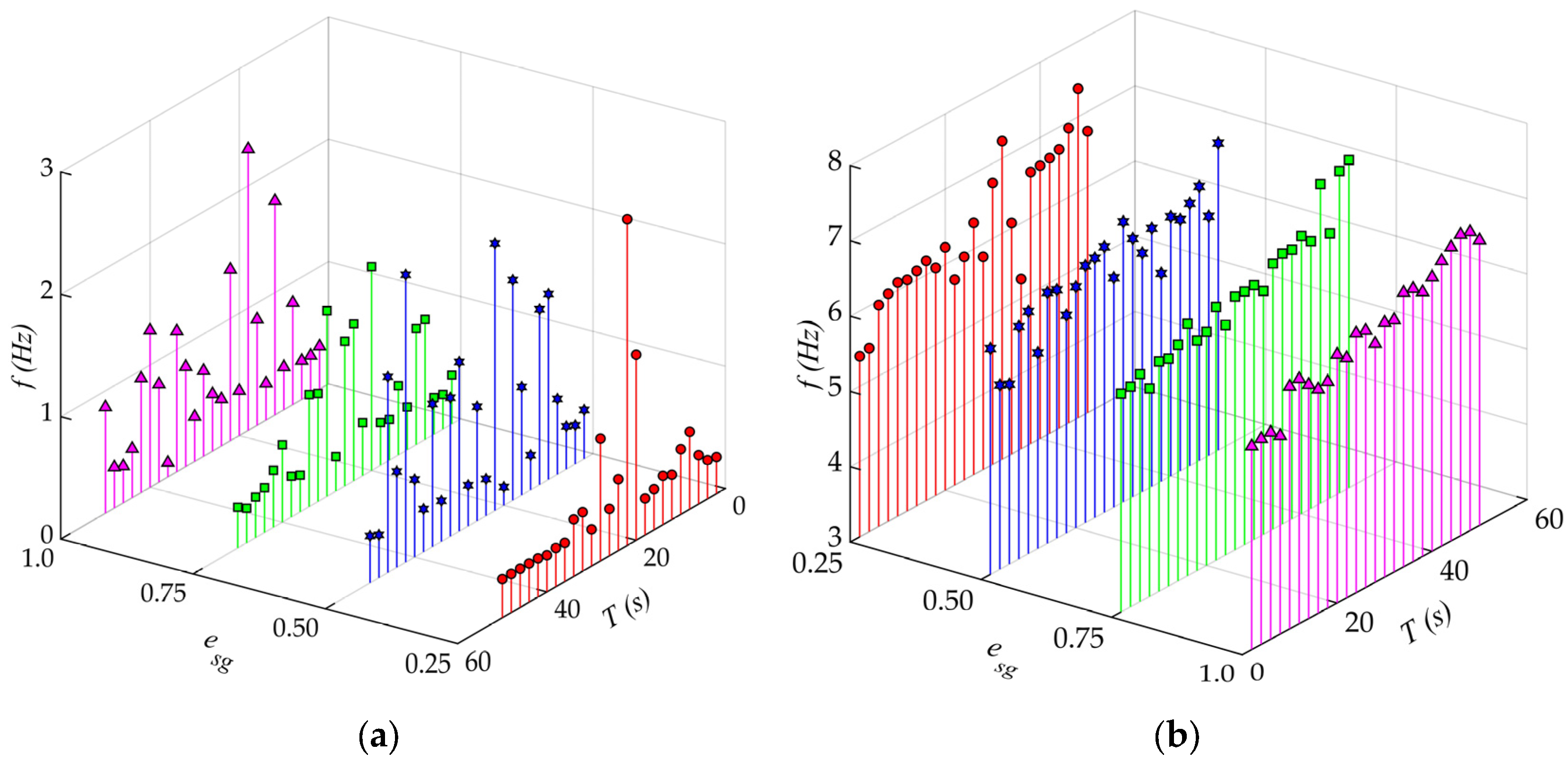
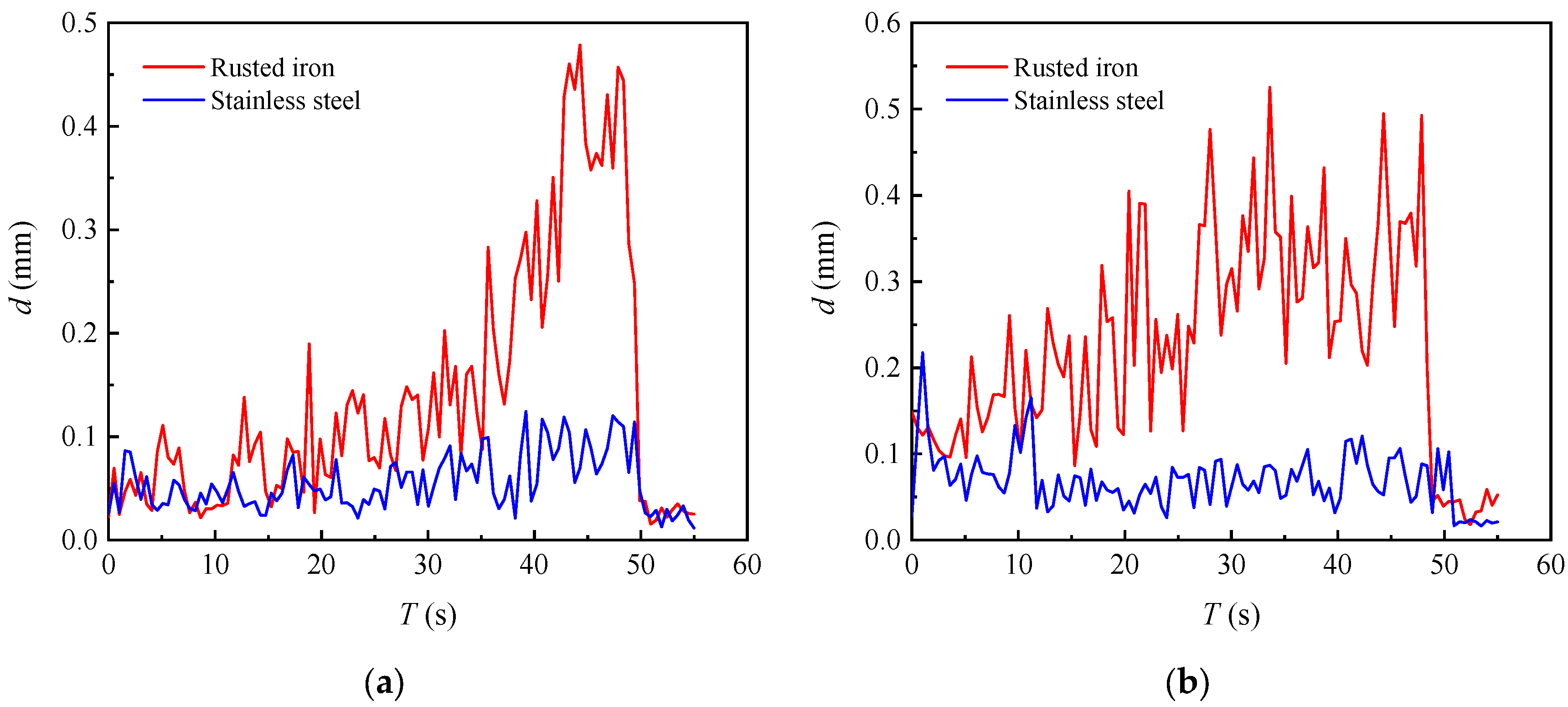
3.3. Acceleration and Displacement of the Slip–Stick Vibration
4. Discussion
4.1. Influence of the Fluid Excitation on Slip–Stick Vibration
4.2. Influence of Friction Factors on Slip–Stick Vibration
4.3. Friction-Induced Vibration and Flow-Induced Vibration
5. Conclusions
- (i)
- The intensity and period of the slip–stick vibration of the plane gate both increase with the opening degree of the plane gate decreasing. The frequency of the slip–stick vibration of the plane gate is consistent with the simplified natural frequency, indicating that the slip–stick vibration is a nonlinear self-excited vibration.
- (ii)
- The variation intensity and dominant frequency between the slip–stick vibration and fluid excitation of the plane gate have a significant difference. Fluid excitation acting on the plane gate is not the main cause of gate slip–stick vibration. The slip–stick vibration intensity can be influenced by special fluid excitation, but the vibration mechanism would not change.
- (iii)
- The friction factor between gate support and track is the main cause of the slip–stick vibration of the plane gate. The slip–stick vibration is the friction-induced vibration caused by the gate’s active motion.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lian, J.J.; Chen, L.; Liang, C.; Liu, F. Presentation and verification of an optimal operating scheme aiming at reducing the ground vibration induced by high dam flood discharge. Int. J. Environ. Res. Public Health 2020, 17, 377. [Google Scholar] [CrossRef] [PubMed]
- Lian, J.J.; Chen, L.; Ma, B.; Liang, C. Analysis of the cause and mechanism of hydraulic gate vibration during flood discharging from the perspective of structural dynamics. Appl. Sci. 2020, 2, 629. [Google Scholar] [CrossRef]
- Ma, C.; Sheng, C.M.; Lian, J.J.; Ma, B.; Liu, F. Failure analysis of a leaf gate jammed in closing process. Eng. Fail. Anal. 2020, 110, 104391. [Google Scholar] [CrossRef]
- Liu, X.P.; Zhao, L.H.; Cao, H.Y.; Sun, X.-P. Lifting force acting on a gate with high head. J. Hydrodyn. 2011, 23, 379–383. [Google Scholar] [CrossRef]
- Hardwick, J.D. Flow-induced vibration of vertical-lift gate. ASCE J. Hydraul. Div. 1974, 100, 631–644. [Google Scholar] [CrossRef]
- Kolkman, P.A. A simple scheme for calculating the added mass of hydraulic gates. J. Fluids Struct. 1988, 2, 339–353. [Google Scholar] [CrossRef]
- Naudascher, E.; Rockwell, D. Oscillator-model approach to the identification and assessment of flow-induced vibrations in a system. J. Hydraul. Res. 1980, 18, 59–82. [Google Scholar] [CrossRef]
- Thang, N.D. Gate vibrations due to unstable flow separation. J. Hydraul. Eng. 1990, 116, 342–361. [Google Scholar] [CrossRef]
- Jongeling, T.H.G. Flow-induced self-excited in-flow vibrations of gate plates. J. Fluids Struct. 1988, 2, 541–566. [Google Scholar] [CrossRef]
- Thang, N.D.; Naudascher, E. Vortex-excited vibrations of underflow gates. J. Hydraul. Res. 1986, 24, 133–151. [Google Scholar] [CrossRef]
- Thang, N.D.; Naudascher, E. Self-excited vibrations of vertical-lift gates. J. Hydraul. Res. 1986, 24, 391–404. [Google Scholar] [CrossRef]
- Yang, M.; Lian, J.J.; Lin, J.Y. Analysis and calculation of flow-induced vertical vibration of plate gate. J. Basic Sci. Eng. 1995, 3, 61–66. (In Chinese) [Google Scholar]
- Yang, M.; Lian, J.J.; Lin, J.Y. Excitation mechanism of flow induced plane gate vibration. J. Hydrodyn. 1997, 4, 437–449. (In Chinese) [Google Scholar]
- Naudascher, E. Flow-induced vibrations at hydraulic structures. J. Fluids Struct. 1987, 1, 265–298. [Google Scholar] [CrossRef]
- Erdbrink, C.D.; Krzhizhanovskaya, V.V.; Sloot, P. Reducing cross-flow vibrations of underflow gates: Experiments and numerical studies. J. Fluids Struct. 2014, 50, 25–48. [Google Scholar] [CrossRef]
- Jafari, A.; Kabiri-Samani, A.; Behnamfar, F. Flow-induced horizontal and vertical vibration of sluice gates. Proc. Inst. Civ. Eng.-Water Manag. 2018, 171, 152–162. [Google Scholar] [CrossRef]
- Kostecki, S.W. Numerical analysis of hydrodynamic forces due to flow instability at lift gate. Arch. Civ. Mech. Eng. 2011, 11, 943–961. [Google Scholar] [CrossRef]
- Novak, G.; Mlačnik, J.; Bombač, M.; Vošnjak, S. Hydrodynamic forces during the operation of a model radial gate. J. Appl. Water Eng. Res. 2017, 51, 70–77. [Google Scholar] [CrossRef]
- Ji, S.K.; Zhou, L.J.; Han, G.; Duanmu, L.M.; Lin, J.Y. Vibration analysis of sluice gate closure process for diversion of Yellow River. Water Resour. Hydropower Eng. 2001, 12, 64–66. (In Chinese) [Google Scholar]
- Liang, C.; Zhang, J.J.; Lian, J.J.; Liu, F. Research on slip-stick vibration of emergency gate induced by high dam flood discharge. J. Hydraul. Eng. 2018, 49, 1503–1511. (In Chinese) [Google Scholar]
- Duan, Y.; Xu, G.B.; Wang, Y.Z.; Yang, D. The middle Huaihe River stability analysis and optimization of hydrological chaos forecasting model. Geomat. Nat. Hazards Risk 2020, 11, 1805–1826. [Google Scholar] [CrossRef]
- Billeter, P.; Staubli, T. Flow-induced multiple-mode vibrations of gates with submerged discharge. J. Fluids Struct. 2000, 14, 323–338. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Xu, G.B.; Li, W.S.; Liu, F.; Duan, Y. Characteristics of plane gate vibration and holding force in closing process by experiments. Appl. Sci. 2020, 10, 6111. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Xu, G.B.; Liu, F. Holding force and vertical vibration of emergency gate in the closing process: Physical and numerical modelling. Appl. Sci. 2021, 11, 8440. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Xu, G.B.; Liu, F. Numerical inversion and influencing factors of creeping vibration of emergency gate. J. Hydroelectr. Eng. 2022, 41, 55–62. (In Chinese) [Google Scholar]
- Ishii, N. Flow-induces vibration of long-span gates part I: Model development. J. Fluids Struct. 1992, 6, 539–562. [Google Scholar] [CrossRef]
- Ishii, N.; Knisely, C. Flow-induced vibration of long-span gates due to shed vortices. JSME Int. J. 1992, 35, 1–8. [Google Scholar]
- Yang, T.T.; He, S.H.; Shen, C.Y.; Yang, Q. Fluid-induced vibrations test of hydraulic plane gate for different conditions. In Proceedings of the International Conference on Sensors, Nanjing, China, 11–13 November 2016; pp. 1083–1089. [Google Scholar]
- Dai, H.L.; Wang, L.; Qian, Q.; Ni, Q. Vortex-induced vibrations of pipes conveying fluid in the subcritical and supercritical regimes. J. Fluids Struct. 2013, 39, 322–334. [Google Scholar] [CrossRef]
- Zhu, H.J.; Gao, Y. Effect of gap on the vortex-induced vibration suppression of a circular cylinder using two rotating rods. Ships Offshore Struct. 2018, 13, 119–131. [Google Scholar] [CrossRef]


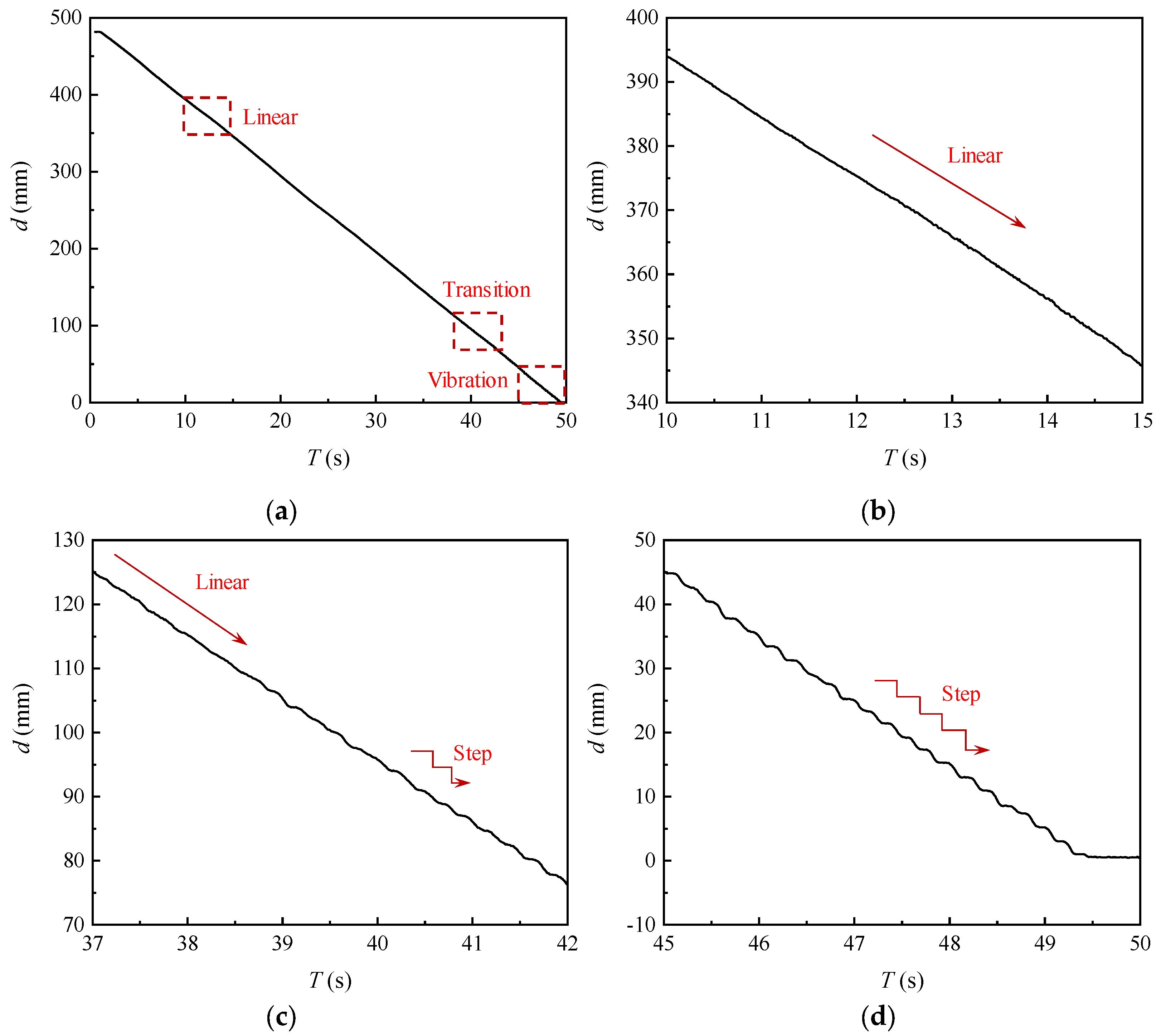

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xu, G.; Liu, Z.; Yang, D. Experimental Study on the Slip–Stick Vibration of Plane Gate. Water 2024, 16, 912. https://doi.org/10.3390/w16060912
Wang Y, Xu G, Liu Z, Yang D. Experimental Study on the Slip–Stick Vibration of Plane Gate. Water. 2024; 16(6):912. https://doi.org/10.3390/w16060912
Chicago/Turabian StyleWang, Yanzhao, Guobin Xu, Zhicheng Liu, and Deming Yang. 2024. "Experimental Study on the Slip–Stick Vibration of Plane Gate" Water 16, no. 6: 912. https://doi.org/10.3390/w16060912
APA StyleWang, Y., Xu, G., Liu, Z., & Yang, D. (2024). Experimental Study on the Slip–Stick Vibration of Plane Gate. Water, 16(6), 912. https://doi.org/10.3390/w16060912




