Monitoring and Early Warning Method of Debris Flow Expansion Behavior Based on Improved Genetic Algorithm and Bayesian Network
Abstract
1. Introduction
2. Debris Flow Expansion Behavior Monitoring and Early Warning
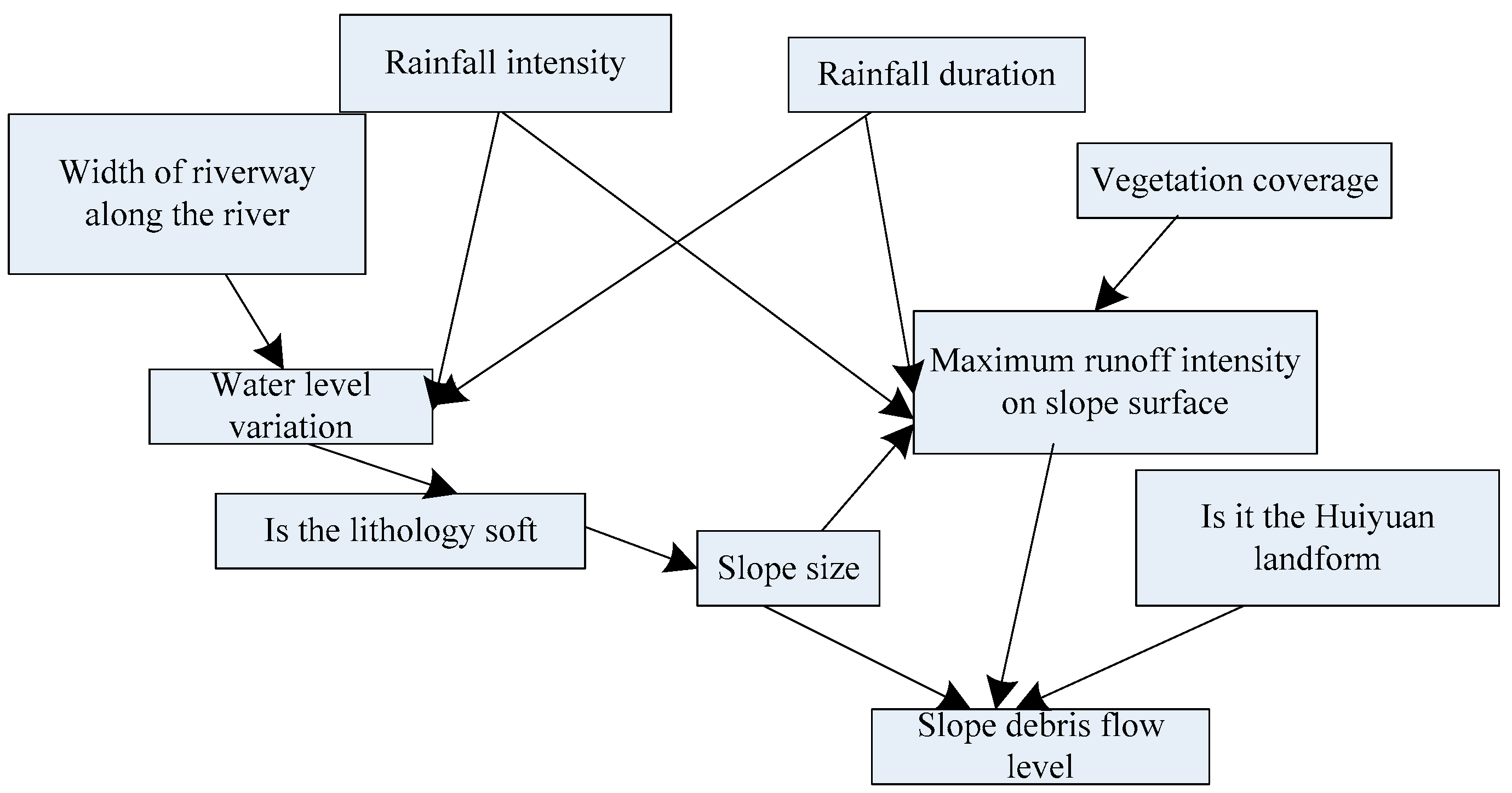
2.1. Debris Flow Disaster Monitoring Network Node Variable Analysis
2.2. Improved Early Warning Method of Genetic Algorithm Based on Niche Technology
2.2.1. Optimization of Variable Factors of Debris Flow Expansion Behavior
2.2.2. Bayesian Network Learning under Global Optimization
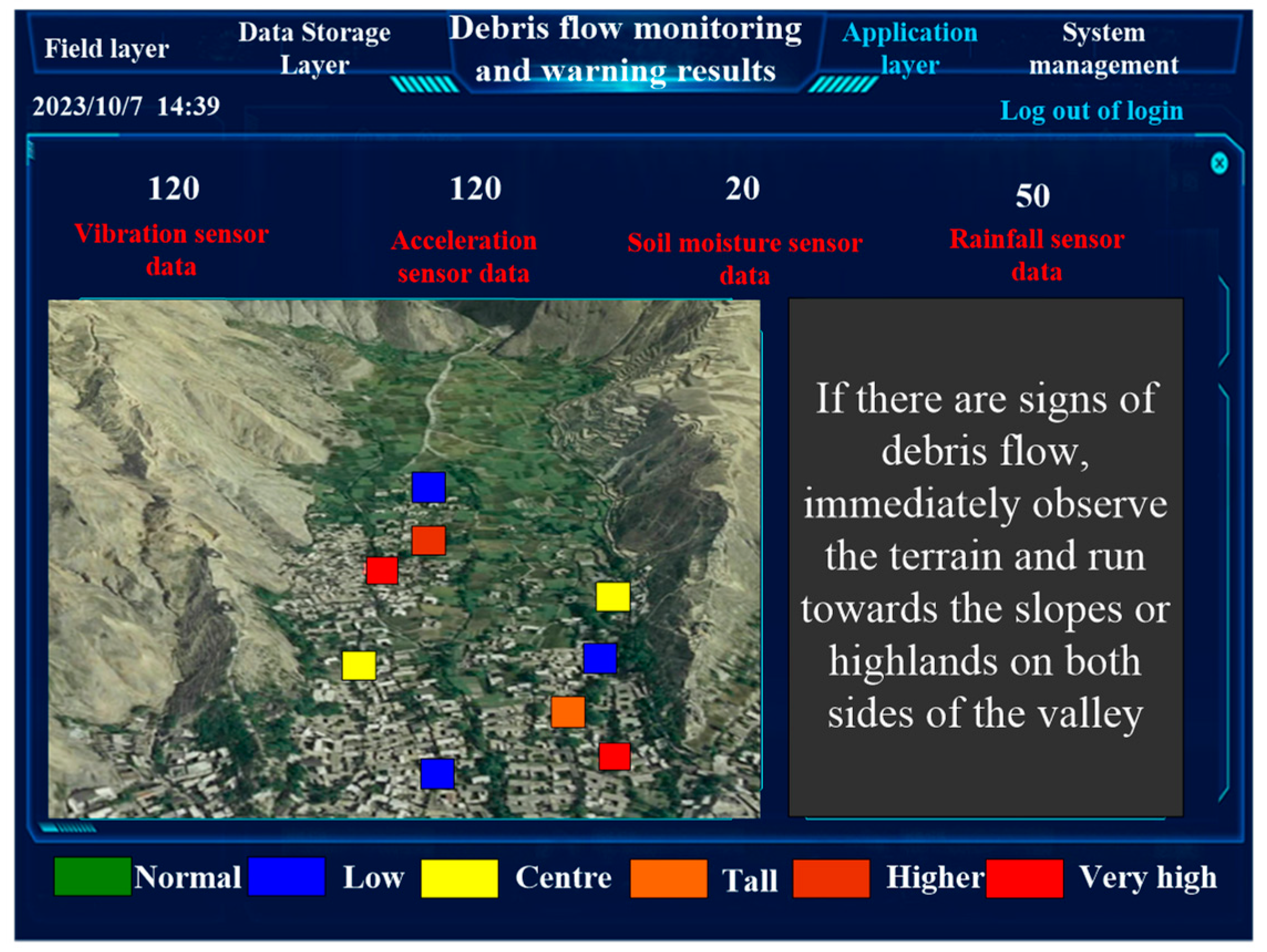
2.2.3. Hierarchical Early Warning Method Based on Bayesian Network Learning Results
3. Experiment and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kersten, J.; Klan, F. What happens where during disasters? A workflow for the multifaceted characterization of crisis events based on twitter data. J. Contingencies Crisis Manag. 2020, 28, 1468–1473. [Google Scholar] [CrossRef]
- Inoguchi, M.; Tamura, K.; Uo, K.; Kobayashi, M.; Morishima, A. Time-cost estimation for early disaster damage assessment methods, depending on affected area. J. Disaster Res. 2021, 16, 733–746. [Google Scholar] [CrossRef]
- Wang, M.W.; Wang, Y.; Shen, F.Q.; Jin, J.L. Projection Pursuit Method Based on Connection Cloud Model for Assessment of Debris Flow Disasters. J. Environ. Inform. 2023, 41, 118–129. [Google Scholar] [CrossRef]
- Bernard, M.; Gregoretti, C. The use of rain gauge measurements and radar data for the model-based prediction of runoff-generated debris-flow occurrence in early warning systems. Water Resour. Res. 2021, 57, e2020WR027893. [Google Scholar] [CrossRef]
- Savi, R.; Valletta, A.; Carri, A.; Cavalca, E.; Segalini, A. Development and preliminary tests of a low-power automatic monitoring system for flexible debris flow barriers. Transp. Res. Procedia 2021, 55, 1783–1790. [Google Scholar] [CrossRef]
- Yang, Z.; Xiong, J.; Zhao, X.; Meng, X.; Wang, S.; Li, R.; Wang, Y.; Chen, M.; He, N.; Yang, Y.; et al. Column-Hemispherical Penetration Grouting Mechanism for Newtonian Fluid Considering the Tortuosity of Porous Media. Processes 2023, 11, 1737. [Google Scholar] [CrossRef]
- Coviello, V.; Theule, J.I.; Crema, S.; Arattano, M.; Marchi, L. Combining instrumental monitoring and high-resolution topography for estimating sediment yield in a debris-flow catchment. Environ. Eng. Geosci. 2021, 27, 95–111. [Google Scholar] [CrossRef]
- Rui, B.I.; Gan, S.; Raobo, L.I.; Lin, H.U. Application research of unmanned aerial vehicle remote sensing detection for 3d terrain modeling and feature analysis of debris flow gullies in complex mountainous area of Dongchuan. Chin. J. Geol. Hazard Control 2021, 32, 91–100. [Google Scholar]
- Jin, Y.Q.; Xu, F. Monitoring and Early Warning the Debris Flow and Landslides Using VHF Radar Pulse Echoes from Layering Land Media. IEEE Geosci. Remote Sens. Lett. 2011, 8, 575–579. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Chaobiao, Z. Early warning of debris flow using optimized self-organizing feature mapping network. Water Sci. Technol. Water Supply 2020, 20, 2455–2470. [Google Scholar] [CrossRef]
- Niu, Y.; Ma, J. Bayesian Network Structure Learning Method Based on Differential Evolution Strategy. Comput. Simul. 2021, 38, 242–246. [Google Scholar]
- Asghari, K.; Masdari, M.; Gharehchopogh, F.S.; Saneifard, R. A fixed structure learning automata-based optimization algorithm for structure learning of Bayesian networks. Expert Syst. 2021, 38, e12734. [Google Scholar] [CrossRef]
- Meyrat, G.; Mcardell, B.; Ivanova, K.; Müller, C.; Bartelt, P. A dilatant, two-layer debris flow model validated by flow density measurements at the Swiss illgraben test site. Landslides 2022, 19, 265–276. [Google Scholar] [CrossRef]
- Sujatha, E.R. A spatial model for the assessment of debris flow susceptibility along the Kodaikkanal-Palani traffic corridor. Front. Earth Sci. 2020, 14, 326–343. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Zhao, X.G.; Chen, M.; Zhang, J.; Yang, Y.; Chen, W.T.; Bai, X.F.; Wang, M.M.; Wu, Q. Characteristics, dynamic analyses and hazard assessment of debris flows in Niumiangou Valley of Wenchuan County. Appl. Sci. 2023, 13, 1161. [Google Scholar] [CrossRef]
- Yang, Z.-Q.; Wei, L.; Liu, Y.-Q.; He, N.; Zhang, J.; Xu, H.-H. Discussion on the Relationship between Debris Flow Provenance Particle Characteristics, Gully Slope, and Debris Flow Types along the Karakoram Highway. Sustainability 2023, 15, 5998. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Yang, Z.Q.; Chen, M.; Xu, H.H.; Yang, Y.; Zhang, J.; Wu, Q.; Wang, M.M.; Song, Z.; Ding, F.S. Research Hotspots and Frontiers of Mountain Flood Disaster: Bibliometric and Visual Analysis. Water 2023, 15, 673. [Google Scholar] [CrossRef]
- Mandal, A.; Nandi, A.; Shakoor, A. Application of a hydrological model for estimating infiltration for debris flow initiation: A case study from the great smoky mountains national park, Tennessee. Environ. Eng. Geosci. 2022, 28, 93–111. [Google Scholar]
- Sun, Y.; Xu, J.; Lin, G.; Ji, W.; Wang, L. RBF neural network-based supervisor control for maglev vehicles on an elastic track with network time delay. IEEE Trans. Ind. Inform. 2022, 18, 509–519. [Google Scholar] [CrossRef]
- Zegers, G.; Mendoza, P.A.; Garces, A.; Montserrat, S. Sensitivity and identifiability of rheological parameters in debris flow modeling. Nat. Hazards Earth Syst. Sci. 2020, 20, 1919–1930. [Google Scholar] [CrossRef]
- Yang, L.; Chen, R.; He, N.; Luo, N. Analysis of the cause of the “6·26” large debris flow in Yihai Town, Mianning County, Liangshan Prefecture, Sichuan Province. Chin. J. Geol. Hazard Control 2023, 34, 94–101. [Google Scholar]
- Yang, Z.; Chen, M.; Zhang, J.; Ding, P.; He, N.; Yang, Y. Effect of initial water content on soil failure mechanism of loess mudflow disasters. Front. Ecol. Evol. 2023, 11, 1141155. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, Z.; Meng, X.; Wang, S.; Li, R.; Xu, H.; Wang, X.; Ye, C.; Xiang, T.; Xu, W.; et al. Study on Mechanism and Verification of Columnar Penetration Grouting of Time-Varying Newtonian Fluids. Processes 2023, 11, 1151. [Google Scholar] [CrossRef]



| Variable Type | Variable |
|---|---|
| Input variables | Rainfall intensity |
| Rainfall duration | |
| State variable | Lithological structure |
| Geological structure | |
| Loose soil | |
| Topographic features | |
| Original water system | |
| Output variables | Debris flow |
| Number of Data Groups | GS Method | HC Method | Proposed Method | |
|---|---|---|---|---|
| 500 | Network Structure Rating | −919.325 | −916.537 | −912.716 |
| Missing Edges | 0.2 | 0 | 0 | |
| Redundant Edge | 0 | 0.1 | 0 | |
| Reverse Edge | 1.6 | 1.1 | 0.7 | |
| 1000 | Network Structure Rating | −187.254 | −187.254 | −187.254 |
| Missing Edges | 0 | 1 | 0 | |
| Redundant Edge | 0 | 0 | 0 | |
| Reverse Edge | 0.9 | 1.1 | 0.4 | |
| Index | Network Structure Rating | Average Number of Iterations |
|---|---|---|
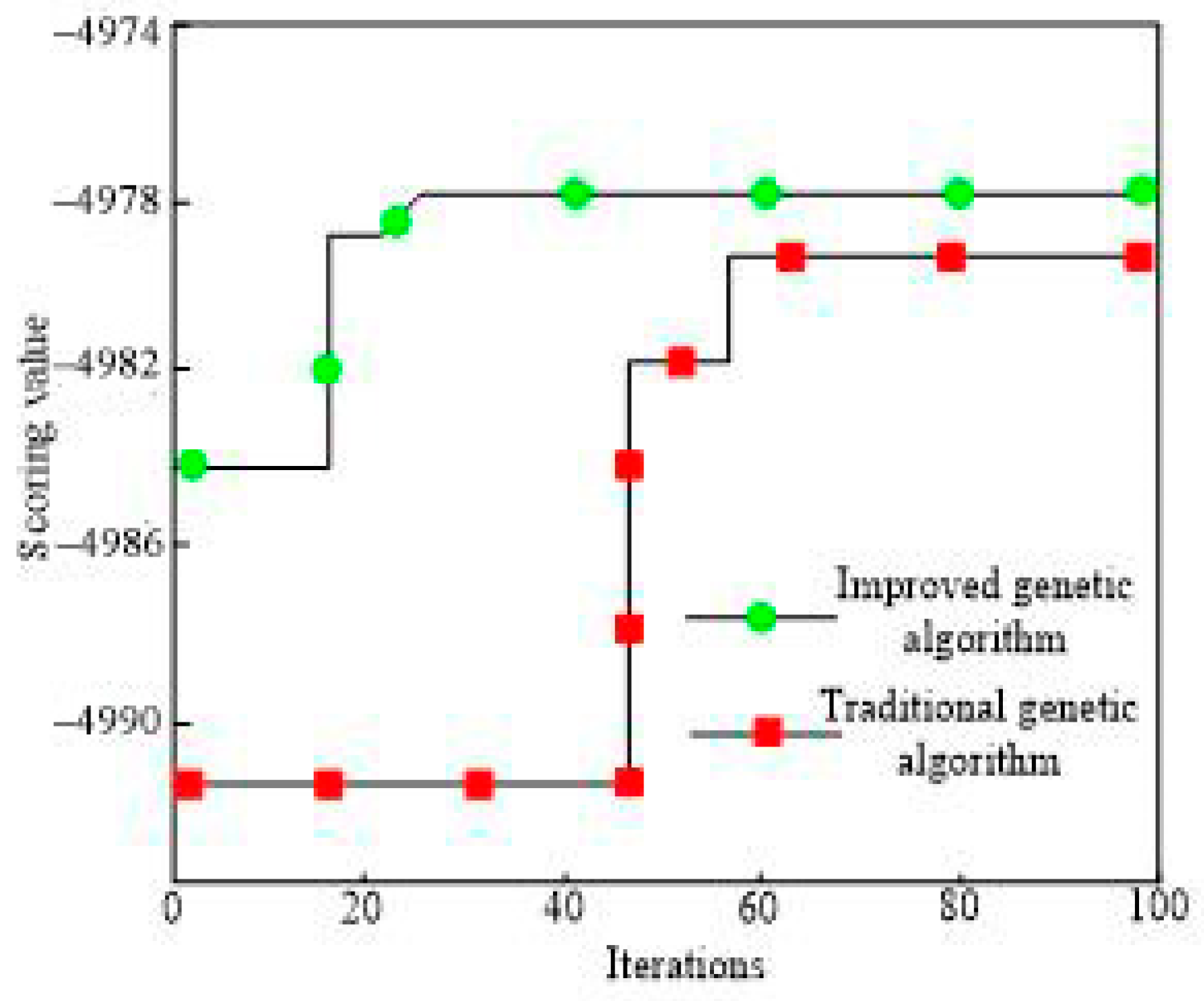
| Improved Genetic Algorithm | −4966.1 | 30 |
| Standard Genetic Algorithm | −4988.7 | 81 |
| Learning Method | Learning Time | Wrong Number of Edges | Network Structure Scoring |
|---|---|---|---|
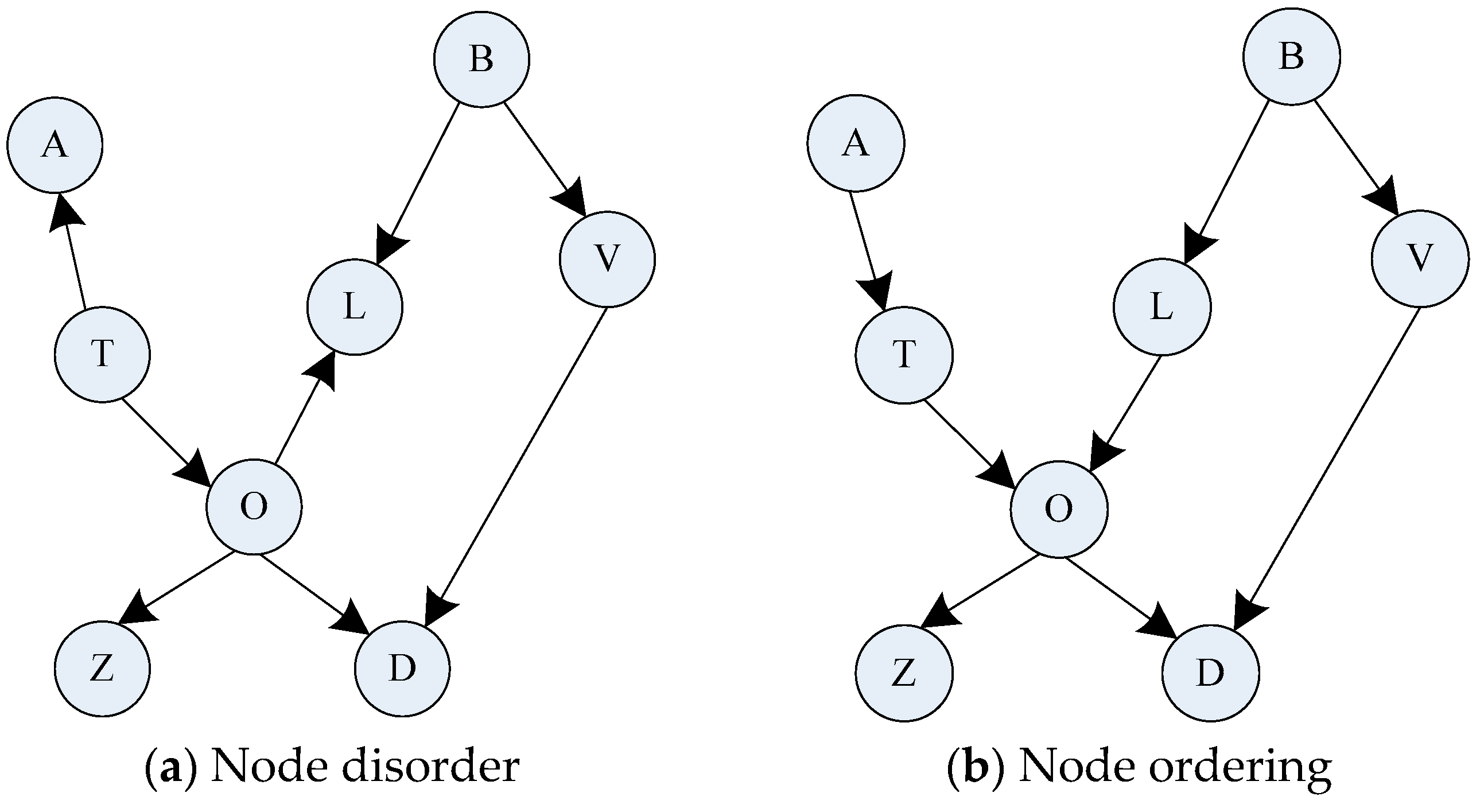
| The method proposed in this paper when nodes are out of order | 0.66 s | 2 | −44,816 |
| The method proposed in this paper when nodes are ordered | 0.41 s | 0 | −44,816 |
| GA method | 107.28 s | 7 | −44,842 |
| MWST method | 0.94 s | 4 | −45,879 |
| State and City | County and District | Joint Probability | Risk Level |
|---|---|---|---|
| State A | County 1 | 93.18 | Very high |
| State A | County 2 | 92.02 | Very high |
| City B | County 3 | 86.68 | Higher |
| State C | County 4 | 83.73 | Higher |
| State D | County 5 | 81.89 | Higher |
| State C | County 6 | 81.66 | Higher |
| State D | County 7 | 81.39 | Higher |
| State C | County 8 | 76.83 | Tall |
| State A | County 9 | 68.82 | Tall |
| State A | County 10 | 60.29 | Tall |
| State C | County 11 | 44.82 | Center |
| State D | County 12 | 43.71 | Center |
| State A | County 13 | 23.79 | Low |
| State A | County 14 | 22.89 | Low |
| State A | County 15 | 22.22 | Low |
| City B | County 16 | 20.74 | Low |
| City B | County 17 | 20.16 | Low |
| State A | County 18 | 16.75 | Normal |
| City B | County 19 | 12.62 | Normal |
| State A | County 20 | 5.39 | Normal |
| State A | County 21 | 2.24 | Normal |
| State A | County 22 | 2.02 | Normal |
| State A | County 23 | 1.39 | Normal |
| City B | County 24 | 0.38 | Normal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Tanoli, J.I.; Zhou, M.; Gurkalo, F. Monitoring and Early Warning Method of Debris Flow Expansion Behavior Based on Improved Genetic Algorithm and Bayesian Network. Water 2024, 16, 908. https://doi.org/10.3390/w16060908
Li J, Tanoli JI, Zhou M, Gurkalo F. Monitoring and Early Warning Method of Debris Flow Expansion Behavior Based on Improved Genetic Algorithm and Bayesian Network. Water. 2024; 16(6):908. https://doi.org/10.3390/w16060908
Chicago/Turabian StyleLi, Jun, Javed Iqbal Tanoli, Miao Zhou, and Filip Gurkalo. 2024. "Monitoring and Early Warning Method of Debris Flow Expansion Behavior Based on Improved Genetic Algorithm and Bayesian Network" Water 16, no. 6: 908. https://doi.org/10.3390/w16060908
APA StyleLi, J., Tanoli, J. I., Zhou, M., & Gurkalo, F. (2024). Monitoring and Early Warning Method of Debris Flow Expansion Behavior Based on Improved Genetic Algorithm and Bayesian Network. Water, 16(6), 908. https://doi.org/10.3390/w16060908






