Experimental Study of the Injectability of Infiltration Grouting in Surface Moraine of Pulang Copper Mine
Abstract
1. Introduction
2. Injection Experimental Scheme
2.1. Grouting Slurry
2.2. Experimental Device
2.3. Sample Preparation
2.4. Experimental Ratio
2.5. Criteria for Notability
- (1)
- Based on the experimental conditions, slurry with a grouting depth exceeding 18 cm was considered fully injectable.
- (2)
- If the slurry’s grouting depth was less than 2 cm, it could not be injected.
- (3)
- Grouting depths ranging from 2 to 18 cm were insufficient for injection purposes.
- (4)
- The portion of non-uniform penetration was decreased proportionally to the area ratio, as indicated in Figure 3.
3. Experimental Results and Analysis
3.1. Influence of Porosity on the Injectivity of Moraine
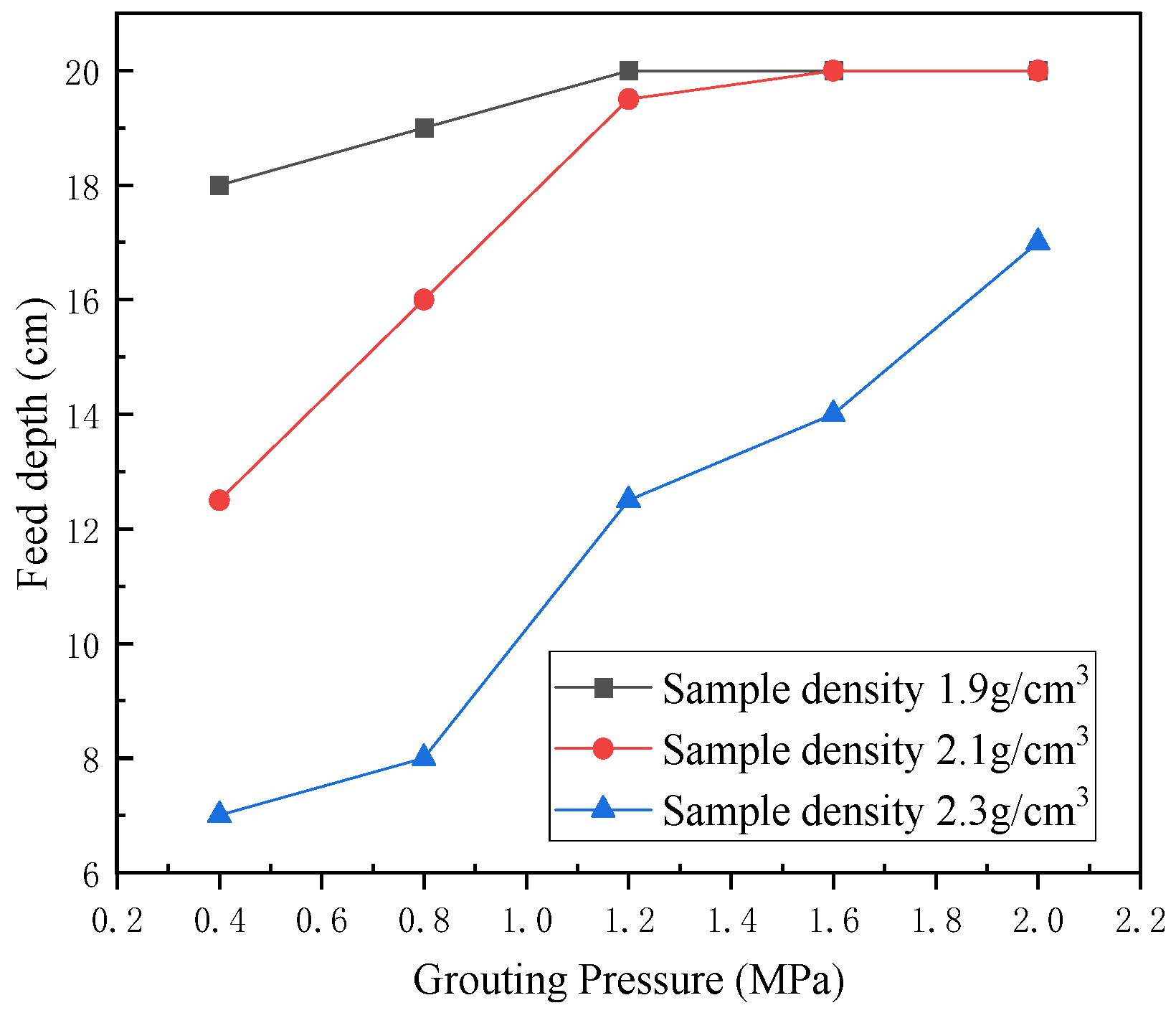
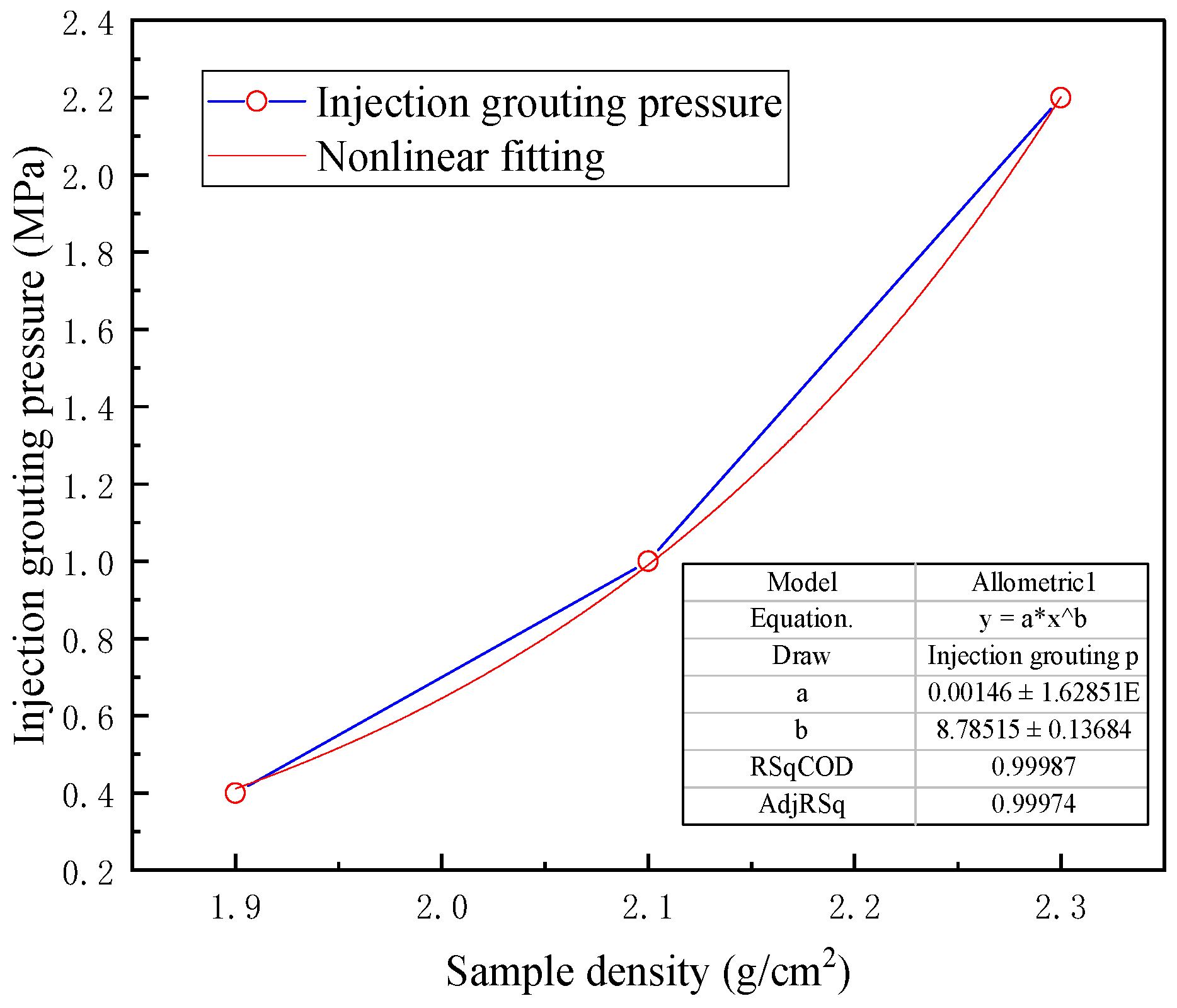
3.2. Influence of Grouting Pressure on the Injectivity of Moraine
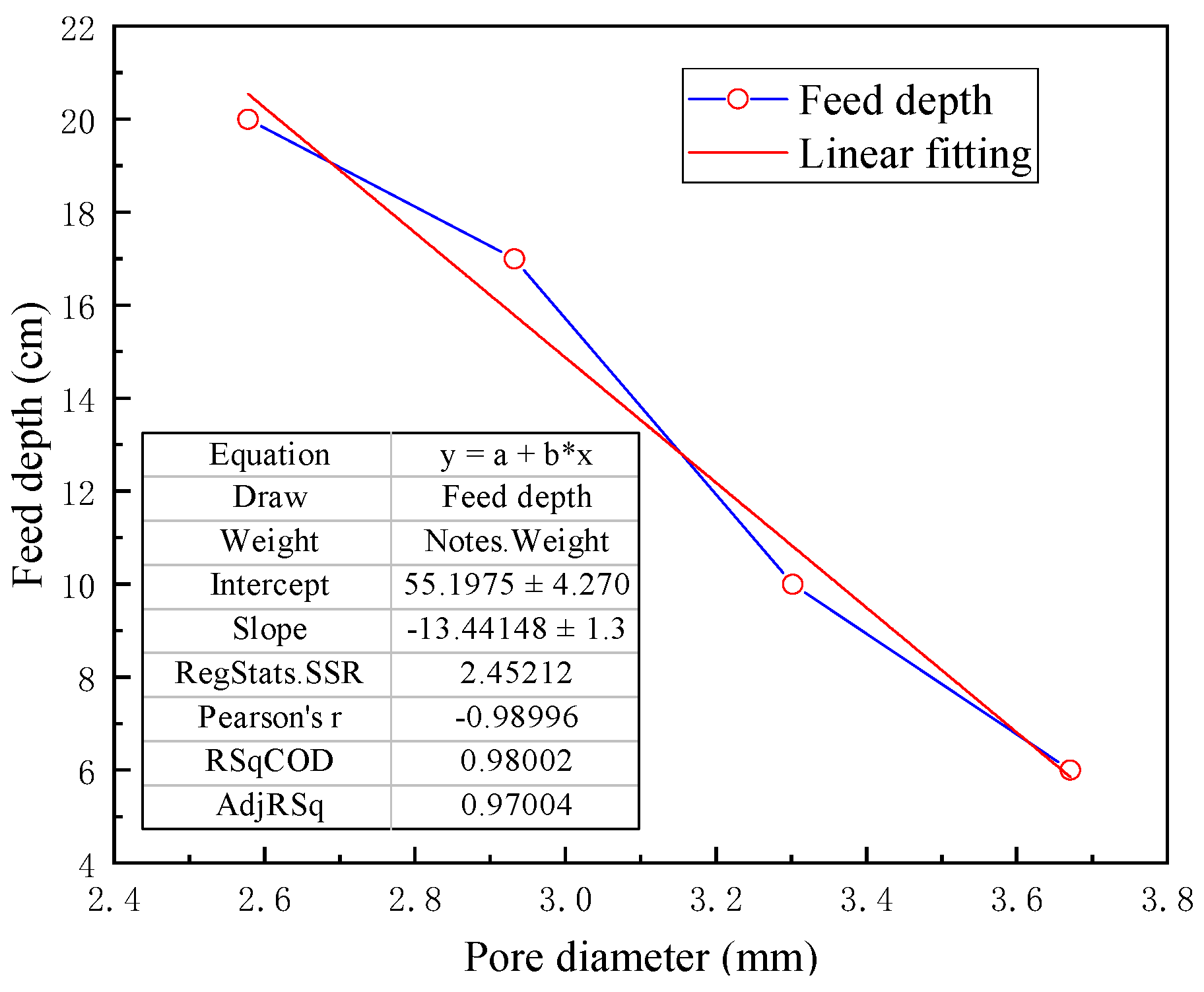
3.3. Influence of Pore Diameter on the Injectivity of Moraine
4. Grouting Mechanism Analysis
5. Conclusions
- (1)
- The density of the moraine samples decreased, resulting in an increase in sample porosity and the entering depth of chemical slurry.
- (2)
- When keeping the density of samples constant, increasing the grouting pressure increases the grouting depth of the chemical slurry, and this increase is approximately linear. The relationship between sample density, grouting pressure, and grouting depth can be expressed as H = 66.87597 + 6.35877P − 27.0974ρ when grouting a fine-drift (−8 mm) sample.
- (3)
- At equal sample densities, an increase in coarse particle content leads to an overall increase in the effective particle diameter and pore diameter. As a result, the longitudinal grouting depth of the sample increases, while the transverse diffusion distance decreases, ultimately leading to a decrease in the final penetration distance of the sample. The outcome is the formation of a grouting mode in which split grouting plays the main role, with penetration grouting serving as an auxiliary.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| n | porosity. |
| ρD | dry density of sample. |
| ρT | true density of sample. |
| D0 | the effective diameter of sand particles in the sand-layer medium. |
| D1 | medium diameter of sand particle gradation. |
| q1 | the percentage corresponding to the sieve diameter is the dimensionalized quantity. |
| D0 | medium pore diameter. |
| D1 | effective particle diameter of sand medium. |
| n | the porosity of sand medium. |
| r | pore diameter. |
| h | feed depth. |
References
- Yang, D.; Wang, J.; Yang, D. Evaluation method of slope structure and stability of moraine in Palong Zangbu Basin. Yangtze River 2019, 50, 108–112+129. [Google Scholar]
- Wang, T.; Song, D.; Dun, Z. Dynamic compaction treatment and test detection of plateau airport moraine soil foundation. Geotech. Eng. Tech. 2012, 26, 152–154. [Google Scholar]
- Feng, X.; Li, Z.; Jiang, M.; Wang, S.; Chen, C.; Sun, W. Experimental study of soil erosion on moraine-consolidated slopes under heavy rainfall. Heliyon 2024, 10, e26721. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Zeng, B.; Tao, K.; Zhang, C.; Zhao, H.; Li, D.; Zhang, J. A constitutive model to reveal the anchorage mechanism of fully bonded bolts. Rock Mech. Rock Eng. 2023, 56, 1739–1757. [Google Scholar] [CrossRef]
- Xia, X. Research on Optimization Ratio of Grouting Materials and Grouting Test. Master’s Thesis, Anhui University of Science and Technology, Huainan, China, 2012. [Google Scholar]
- Yang, Y.; Xua, H.; Li, K.; Geng, H.; Ma, L. Experimental study on the injectivity of calcareous sand by permeation grouting. Prot. Eng. 2020, 42, 10–17. [Google Scholar]
- Zou, H. Study on Mechanism and Effect Evaluation of Grouting Diffusion Reinforcement of Soil-Rock Mixed Backfill. Master’s Thesis, Chongqing University, Chongqing, China, 2022. [Google Scholar]
- Ren, J.; Zhao, H.; Zhang, L.; Zhao, Z.; Xu, Y.; Cheng, Y.; Wang, M.; Chen, J.; Wang, J. Design optimization of cement grouting material based on adaptive boosting algorithm and simplicial homology global optimization. J. Build. Eng. 2022, 49, 104049. [Google Scholar] [CrossRef]
- Qian, Z.; Jiang, Z.; Cao, L.; Sun, Q. Model test of porous media grouting with weak cementation. Rock Soil Mech. 2013, 34, 139–142+147. [Google Scholar]
- Zhang, L.; Zhang, Q.; Liu, R.; Li, S.; Wang, H.; Li, W.; Zhang, S.; Zhu, G. Study on diffusion mechanism of quick-setting grout infiltration grouting considering temporal and spatial changes of grout viscosity. Rock Soil Mech. 2017, 38, 443–452. [Google Scholar]
- Chen, X.; Rong, Y.; Jiao, H.; Yang, L.; Zhang, H.; Zhang, W. Strength Laws and Crack Evolution Mechanism of Slurry Grouting under High-Permeability and High-Stress Curing Conditions. Buildings 2022, 12, 1236. [Google Scholar] [CrossRef]
- Maghous, S.; Saada, Z.; Dormieux, L.; Canou, J.; Dupla, J.C. A model for in situ grouting with account for particle filtration. Comput. Geotech. 2007, 34, 164–174. [Google Scholar] [CrossRef]
- Bouchelaghem, F. Multi-scale modelling of the permeability evolution of fine sands during cement suspension grouting with filtration. Comput. Geotech. 2009, 36, 1058–1071. [Google Scholar] [CrossRef]
- Zeng, Q.; Gao, P.; Li, K.; Dong, G.; Jin, G.; Sun, X.; Zhao, J.; Chen, L. Experimental Research on the Properties and Formulation of Fly Ash Based Geopolymer Grouting Material. Buildings 2022, 12, 503. [Google Scholar] [CrossRef]
- Güllü, H.; Yetim, M.E.; Güllü, E.B. Effect of using nano-silica on the rheological, fresh and strength characteristics of cement-based grout for grouting columns. J. Build. Eng. 2023, 76, 107100. [Google Scholar] [CrossRef]
- Wang, A.; Li, Z.; Liu, P.; Liu, K.; Yu, G.; Zheng, Q.; Han, Y.; Xu, H.; Sun, D. Preparation and Properties of Double Liquid Grouting Materials (DLGMs) Used for the Regenerated Roof of a Coal Mine. Buildings 2023, 13, 584. [Google Scholar] [CrossRef]
- Zhong, Z.; Bie, C.; Fan, Y. Experimental study on grouting diffusion mechanism and influencing factors of soil-rock mixture. Rock Soil Mech. 2019, 40, 4194–4202. [Google Scholar]
- Jiang, X.; Zhu, H.; Yan, Z.; Yan, Z.; Zhang, F.; Ye, F.; Li, P.; Zhang, X.; Dai, Z.; Bai, Y.; et al. A state-of-art review on development and progress of backfill grouting materials for shield tunneling. Dev. Built Environ. 2023, 16, 100250. [Google Scholar] [CrossRef]
- King, J.C.; Bush, D. Symposium on grouting of granular materials. J. Soil Mech. Found. Div. ASCE 1961, 87, 1–31. [Google Scholar] [CrossRef]
- Mitchell, J.K. In-place treatment of foundation soils. J. Soil Mech. Found. Div. ASCE 1970, 96, 73–109. [Google Scholar] [CrossRef]
- Incecik, M.; Ceren, I. Cement grouting model tests. Bull. Tech. Univ. Istanb. 1995, 48, 305–317. [Google Scholar]
- Akbulut, S.; Saglamer, A. Estimating the groutability of granular soils: A new approach. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2002, 17, 371–380. [Google Scholar] [CrossRef]
- Kim, J.S.; Lee, I.M.; Jang, J.H.; Choi, H. Groutability of cement-based grout with consideration of viscosity and filtration phenomenon. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 1771–1797. [Google Scholar] [CrossRef]
- Zhang, L. Mechanism and Engineering Application of Grouting Diffusion and Reinforcement in Subway Crossing Sand Layer. Ph.D. Thesis, Shandong University, Jinan, China, 2017. [Google Scholar]
- Xiong, L. Seepage Grouting Mechanism and Experimental Study of Water-Rich Sand Layer Considering Percolation Effect. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar]
- Liu, H. Study on the Flocculation Effect of Cement Slurry Particles and the Injectivity of Porous Media. Master’s Thesis, Shandong University, Jinan, China, 2019. [Google Scholar]
- Liu, L.; Wang, H.; Zheng, S.; Dong, L.; Yu, Y.; Yang, C. Damage Model and Experimental Study of a Sand Grouting-Reinforced Body under Seepage. Processes 2022, 10, 256. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Indraratna, B. The energy transformation of internal erosion based on fluid-particle coupling. Comput. Geotech. 2020, 121, 103475. [Google Scholar] [CrossRef]
- Tang, Y. Study on the Permeability of Saturated Sand Tunnel Surrounding Rock under Dynamic Water Conditions Based on CFD-DEM. Master’s Thesis, Guangdong University of Technology, Guangzhou, China, 2023. [Google Scholar]
- Zhu, G.; Zhang, Q.; Liu, R.; Zhang, L.; Guo, Y. Sand streamability prediction model based on PSO-LSSVM and its sensitivity analysis. J. Harbin Inst. Technol. 2020, 52, 175–182. [Google Scholar]
- Fraccica, A.; Spagnoli, G.; Romero, E.; Arroyo, M.; Gómez, R. Permeation grouting of silt-sand mixtures. Transp. Geotech. 2022, 35, 100800. [Google Scholar] [CrossRef]
- Yu, X. Preparation and structure analysis of aluminum oxide/water glass/polyurethane composite grouting material for mining. J. Build. Eng. 2023, 76, 107170. [Google Scholar] [CrossRef]
- Geotechnical Grouting Theory and Engineering Practice Group. Geotechnical Injection Theory and Engineering Example; Science Press: Beijing, China, 2011. [Google Scholar]






| ID | Grouting Quantity /g | Grouting Pressure /MPa | Maximum Particle Size /mm | Density /g/cm3 | Porosity /% |
|---|---|---|---|---|---|
| HX1 | 400 g | 0.4 MPa | 8 mm | 1.9 g/cm3 | 28.84% |
| HX2 | 400 g | 0.8 MPa | 8 mm | 1.9 g/cm3 | 28.84% |
| HX3 | 400 g | 1.2 MPa | 8 mm | 1.9 g/cm3 | 28.84% |
| HX4 | 400 g | 1.6 MPa | 8 mm | 1.9 g/cm3 | 28.84% |
| HX5 | 400 g | 2.0 MPa | 8 mm | 1.9 g/cm3 | 28.84% |
| HX6 | 400 g | 0.4 MPa | 8 mm | 2.1 g/cm3 | 17.23% |
| HX7 | 400 g | 0.8 MPa | 8 mm | 2.1 g/cm3 | 17.23% |
| HX8 | 400 g | 1.2 MPa | 8 mm | 2.1 g/cm3 | 17.23% |
| HX9 | 400 g | 1.6 MPa | 8 mm | 2.1 g/cm3 | 17.23% |
| HX10 | 400 g | 2.0 MPa | 8 mm | 2.1 g/cm3 | 17.23% |
| HX11 | 400 g | 0.4 MPa | 8 mm | 2.3 g/cm3 | 13.86% |
| HX12 | 400 g | 0.8 MPa | 8 mm | 2.3 g/cm3 | 13.86% |
| HX13 | 400 g | 1.2 MPa | 8 mm | 2.3 g/cm3 | 13.86% |
| HX14 | 400 g | 1.6 MPa | 8 mm | 2.3 g/cm3 | 13.86% |
| HX15 | 400 g | 2.0 MPa | 8 mm | 2.3 g/cm3 | 13.86% |
| ID | Type of Slurry | Density /g/cm3 | Grouting Quantity /g | 8–20 mm Content | Grouting Pressure /MPa | Effective Particle Diameter /mm | Pore Diameter /mm |
|---|---|---|---|---|---|---|---|
| KX1 | Chemical slurry | 2.1 g/cm3 | 400 g | 50% | 2.0 MPa | 8.191 | 2.578 |
| KX2 | Chemical slurry | 2.1 g/cm3 | 400 g | 60% | 2.0 MPa | 9.310 | 2.932 |
| KX3 | Chemical slurry | 2.1 g/cm3 | 400 g | 70% | 2.0 MPa | 10.483 | 3.302 |
| KX4 | Chemical slurry | 2.1 g/cm3 | 400 g | 80% | 2.0 MPa | 11.655 | 3.671 |
| ID | Grouting Pressure /MPa | Density /g/cm3 | Porosity /% | Feed Depth /cm | Notability Determination |
|---|---|---|---|---|---|
| HX1 | 0.4 MPa | 1.9 g/cm3 | 28.84% | 18 cm | Fully injectable |
| HX2 | 0.8 MPa | 1.9 g/cm3 | 28.84% | 19 cm | Fully injectable |
| HX3 | 1.2 MPa | 1.9 g/cm3 | 28.84% | 20 cm | Fully injectable |
| HX4 | 1.6 MPa | 1.9 g/cm3 | 28.84% | 20 cm | Fully injectable |
| HX5 | 2.0 MPa | 1.9 g/cm3 | 28.84% | 20 cm | Fully injectable |
| HX6 | 0.4 MPa | 2.1 g/cm3 | 17.23% | 12.5 cm | Insufficient injection |
| HX7 | 0.8 MPa | 2.1 g/cm3 | 17.23% | 16 cm | Insufficient injection |
| HX8 | 1.2 MPa | 2.1 g/cm3 | 17.23% | 19.5 cm | Fully injectable |
| HX9 | 1.6 MPa | 2.1 g/cm3 | 17.23% | 20 cm | Fully injectable |
| HX10 | 2.0 MPa | 2.1 g/cm3 | 17.23% | 20 cm | Fully injectable |
| HX11 | 0.4 MPa | 2.3 g/cm3 | 13.86% | 7 cm | Insufficient injection |
| HX12 | 0.8 MPa | 2.3 g/cm3 | 13.86% | 9 cm | Insufficient injection |
| HX13 | 1.2 MPa | 2.3 g/cm3 | 13.86% | 12.5 cm | Insufficient injection |
| HX14 | 1.6 MPa | 2.3 g/cm3 | 13.86% | 14 cm | Insufficient injection |
| HX15 | 2.0 MPa | 2.3 g/cm3 | 13.86% | 17 cm | Insufficient injection |
| ID | Type of Slurry | 8–20 mm Content /% | Pore Diameter /mm | Feed Depth /cm | Grouting Quantity /g |
|---|---|---|---|---|---|
| KX1 | Chemical slurry | 50% | 2.578 | 20 | 124 |
| KX2 | Chemical slurry | 60% | 2.932 | 17 | 79 |
| KX3 | Chemical slurry | 70% | 3.302 | 10 | 79 |
| KX4 | Chemical slurry | 80% | 3.671 | 6 | 44 |
| Sample Density ρ g/cm2 | Porosity % | Fitting Formula | Injection Grouting Pressure |
|---|---|---|---|
| 1.9 | 28.84% | H = 2.5P + 17 | 0.4 |
| 2.1 | 17.23% | H = 8.75P + 9 | 1.0 |
| 2.3 | 13.86% | H = 6.25P + 4.4 | 2.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Sun, W.; Feng, X.; Wang, S.; Chen, C.; Song, H.; Jiang, M.; Fan, K. Experimental Study of the Injectability of Infiltration Grouting in Surface Moraine of Pulang Copper Mine. Water 2024, 16, 728. https://doi.org/10.3390/w16050728
Liu Z, Sun W, Feng X, Wang S, Chen C, Song H, Jiang M, Fan K. Experimental Study of the Injectability of Infiltration Grouting in Surface Moraine of Pulang Copper Mine. Water. 2024; 16(5):728. https://doi.org/10.3390/w16050728
Chicago/Turabian StyleLiu, Zeng, Wei Sun, Xinglong Feng, Shaoyong Wang, Chong Chen, Hao Song, Minggui Jiang, and Kai Fan. 2024. "Experimental Study of the Injectability of Infiltration Grouting in Surface Moraine of Pulang Copper Mine" Water 16, no. 5: 728. https://doi.org/10.3390/w16050728
APA StyleLiu, Z., Sun, W., Feng, X., Wang, S., Chen, C., Song, H., Jiang, M., & Fan, K. (2024). Experimental Study of the Injectability of Infiltration Grouting in Surface Moraine of Pulang Copper Mine. Water, 16(5), 728. https://doi.org/10.3390/w16050728







