Stresses and Permeability in Sand–Attapulgite Cut-Off Walls

Abstract

The long-term performance of sand–attapulgite cut-off walls in landfills is highly dependent on the permeability of the wall material. Laboratory tests show that the hydraulic conductivity of wall material decreases significantly with the increase in consolidation pressure. Therefore, to accurately estimate the hydraulic conductivity of the cut-off wall in the field, the effective stress must be calculated correctly. In this paper, the ‘modified lateral squeezing model’ is used to calculate the stress distribution of the sand–attapulgite cut-off wall, and the distribution of the hydraulic conductivity of the cut-off wall in the field is calculated based on the stress distribution of the wall and laboratory test results. The results show that the effective stress of the sand–attapulgite cut-off wall in the field increases with the increase in the depth of the wall, and the change in the hydraulic conductivity is the opposite. The effective stress of the cut-off wall is less than 100 kPa. When the wall depth is below 0.5 m, the hydraulic conductivity of the cut-off wall is less than 1.0 × 10⁻⁹ m/s. The properties of the in situ foundation soil and the width of the cut-off wall will affect the stress and hydraulic conductivity of the cut-off wall, but the influence on the hydraulic conductivity is very limited, not exceeding one time. Therefore, in the actual construction, special attention should be paid to the anti-seepage measures in the shallow part of the cut-off wall. Our findings are expected to provide a valuable reference for the application of sand–attapulgite cut-off walls in landfills.

1. Introduction

It is increasingly common to build barriers around landfills to prevent soil and groundwater contamination [1,2,3]. The application of attapulgite cut-off walls in landfills has attracted more and more attention because of its good adsorption capacity and insensitivity to chemical environments [4,5,6,7,8,9,10,11,12,13]. The final stress of the cut-off wall in the field is usually unknown. But this final stress is important because it not only affects the permeability of the wall, but higher in situ stress also increases the wall’s resistance to hydraulic fracturing and chemical erosion [14]. In addition, the cut-off wall’s final stress state will affect the wall’s deformation and the surrounding soil and buildings. Therefore, it is necessary to further understand the stress state of sand–attapulgite cut-off walls in the field [14,15,16].

The stress state of a cut-off wall in the field is much lower than the effective stress of the cut-off wall considering only the static load of the overlying soil [17,18,19,20,21]. If the pressure under the static load of the overlying soil is used as the effective consolidation pressure or confining pressure to test the hydraulic conductivity of the cut-off wall, the obtained hydraulic conductivity will be much lower than that in the field, which will cause the overestimation of the anti-seepage performance of the cut-off wall.

At present, there are mainly two simplified theories used to calculate the stress distribution of clay-based cut-off walls in the field: the ‘arching theory’ and the ‘lateral squeezing theory’ [17,19]. Evans et al. [17] applied the ‘arching theory’ to the stress calculation of a soil–bentonite cut-off wall. This theory assumes that the side wall of the trench is rigid and fixed and does not have lateral displacement. The soil–bentonite backfill filled into the trench is compressible, and the backfill will have vertical displacement in the process of gravity consolidation. In the process of displacement, the friction between the wall material and the side wall of the trench causes the vertical stress of the wall to be less than the gravity of the overlying soil. The assumption that the side wall of the trench is fixed and does not have lateral displacement will cause the theory to underestimate the influence of horizontal stress on the wall so that the stress of the wall calculated by the ‘arching theory’ is lower than the actual one.

Filz [19] applied the ‘lateral squeezing theory’ to the stress calculation of soil–bentonite cut-off walls, which assumed that the friction between the wall and the sidewall of the trench was sufficient to offset the weight of the overlying soil on the wall, so that the wall does not bear the vertical stress but only bears the horizontal stress when the trench is displaced in the direction of the center line of the wall. Ruffing et al. [21] then proposed a ‘modified lateral squeezing theory’ to calculate the in situ stress state of the cut-off wall by further considering the stress dependence of the compressibility of the wall. However, this theory has certain limitations because it assumes that the friction between the wall and the sidewall of the trench can offset the weight of the overlying soil on the wall, so it is not suitable for the analysis of wide and shallow walls [22]. Li et al. [22] combined the ‘arching theory’ and the ‘lateral squeezing theory’ and, based on Winkler’s idealization, simplified the foundation soil around the cut-off wall into independent elastic springs and proposed a new calculation model for the stress distribution of a clay-based cut-off wall.

Filz and Mitchell [23] found that the stress of a cut-off wall is affected by the ‘lateral squeezing theory’ by analyzing the stress of a soil–bentonite cut-off wall at 23 m in the field, and only when the trench or wall width exceeds 3.3 m is the stress of the cut-off wall affected by the ‘arching theory’. However, in practical engineering, there will be almost no such wide trench and cut-off walls. Compared with the ‘arching theory’, the ‘lateral squeezing theory’ can more realistically reflect the stress state of a cut-off wall in the field [19,24].

Zhang et al. [11] found that the effective consolidation pressure has an important influence on the hydraulic conductivity of sand–attapulgite cut-off walls. Therefore, the accurate calculation of the effective stress distribution of the sand–attapulgite cut-off wall in the field is very important for obtaining a more accurate hydraulic conductivity of the cut-off wall. However, most of the previous studies focus on the effective stress distribution of soil–bentonite cut-off walls in the field, and there are few studies on the effective stress distribution and hydraulic conductivity distribution of sand–attapulgite cut-off walls in the field.

In this paper, the ‘modified lateral squeezing model’ proposed by Ruffing et al. [21] is used to calculate the stress distribution of the sand–attapulgite cut-off wall, and the relationship between the effective consolidation stress and the void ratio obtained by the previous research of the research group and the relationship between the void ratio and hydraulic conductivity are combined to calculate the hydraulic conductivity distribution of a sand–attapulgite cut-off wall in the field. In addition, the influence of different parameters on the stress distribution and hydraulic conductivity distribution of a sand–attapulgite cut-off wall was analyzed based on the ‘modified lateral squeezing model’. Our findings are expected to provide a valuable reference for the application of sand–attapulgite cut-off walls in landfills.

2. Model Description

Filz [19] believes that the lateral displacement of the cut-off wall trench can be divided into three stages: (1) during trench excavation and mud filling, the trench sidewall will move inward; (2) the trench sidewall may rebound during the backfilling stage of the cut-off wall material; (3) the trench sidewall will move inward again during the consolidation stage of the cut-off wall material. Filz [19] assumed that the friction between the cut-off wall and the sidewall of the trench is sufficient to offset the weight of the overlying soil on the wall material, and the wall only bears the horizontal stress when the trench is displaced toward the centerline of the wall. The stress of the wall is hypothesized to be lateral one-dimensional compression, and a ‘lateral squeezing model’ is proposed for calculating the stress distribution of the cut-off wall:

$${\sigma }_{\mathrm{h}}^{\prime }=K_{\mathrm{am}}{\sigma }_{\mathrm{vo}}^{\prime }=D_{\mathrm{b}}\frac{2\Delta }{B}$$

(1)

$${\sigma }_{\mathrm{vo}}^{\prime }={\gamma }_{\mathrm{w}}^{\prime }z$$

(2)

where ${\sigma }_{\mathrm{h}}^{\prime }$ is the horizontal effective stress of the wall; ${\sigma }_{\mathrm{vo}}^{\prime }$ is the vertical effective stress of in situ foundation soil outside the trench; ${\gamma }_{\mathrm{w}}^{\prime }$ is the buoyant unit weight of the wall material; z is the depth of the cut-off wall; $\Delta$ is the unilateral deflection of the trench side wall; $K_{\mathrm{am}}$ is the mobilized active earth pressure coefficient of the in situ foundation soil, which is a function of $\Delta$; $D_{\mathrm{b}}$ is the constrained modulus of the wall material; and B is the width of the wall.

D_b is not a constant; it varies with consolidation stress, or with the depth of the wall. This will make the calculation process of the ‘lateral squeezing model’ more complicated. To solve this problem, Ruffing et al. [21] proposed a ‘modified lateral squeezing model’ for calculating the stress distribution of the cut-off wall:

$${\sigma }_{\mathrm{h}}^{\prime }={ K}_{\mathrm{am}}{\sigma }_{\mathrm{vo}}^{\prime }={10}^{\left(\frac{2\Delta -B{C}_1}{B{C}_{c\epsilon }}\right)}$$

(3)

where C₁ is the strain value under unit stress; C_cε is the modified compression index; and C₁ and C_cε are constants that can be obtained by a one-dimensional consolidation test in the laboratory.

3. Stress Distribution and Hydraulic Conductivity Distribution Calculation

3.1. Stress Distribution Calculation

Based on the previous work of our study, when the attapulgite content in the cut-off wall was ≥30%, the hydraulic conductivity of the sand–attapulgite cut-off wall was lower than 1.0 × 10⁻⁹ m/s [11]. The sand–attapulgite cut-off walls with 30% (A30S70), 40% (A40S60), and 60% (A60S40) attapulgite content presented in the work of Zhang et al. [11] were selected for this study. The values of ${\gamma }_w^{\prime }$, C₁, and C_cε of the sand–attapulgite cut-off wall were calculated according to the research group’s preliminary test results [11] and 1D consolidation tests [25]. In addition, the geometric parameters of the cut-off wall and the related parameters of the in situ foundation soil were summarized from Ruffing et al. [21] and Li et al. [22]. The geometric and material parameters used to calculate the stress distribution of the cut-off wall are listed in

Table 1. Geometric and material parameters used to calculate stress distribution of cut-off walls [21,22,26,27].

Parameter	Parameter Values
	Soil–Bentonite Cut-Off Wall	Sand–Attapulgite Cut-Off Wall
		A30S70	A40S60	A60S40
B (m)	0.8	0.8	0.8	0.8
H (m)	30	30	30	30
${\gamma }_w^{\prime }$ (kN/m3)	9.3	8.4	7.4	6.6
Ccε	0.10	0.10	0.12	0.13
C1	−0.09	−0.08	−0.11	−0.12
${\phi }_0^{\prime }$ (°)	35.0	35.0	35.0	35.0

. The stress distribution of the cut-off walls is calculated by using Equation (3) when the wall width B is 0.8 m and the in situ foundation soil is medium dense sand (the effective internal friction angle of the foundation soil is ${\phi }_0^{\prime }$ = 35.0°; $K_{\mathrm{am}}$ = 25,200(Δ/H)² − 127(Δ/H) + 0.426, H is the depth of the cut-off wall), considering the groundwater level at the surface of the wall.

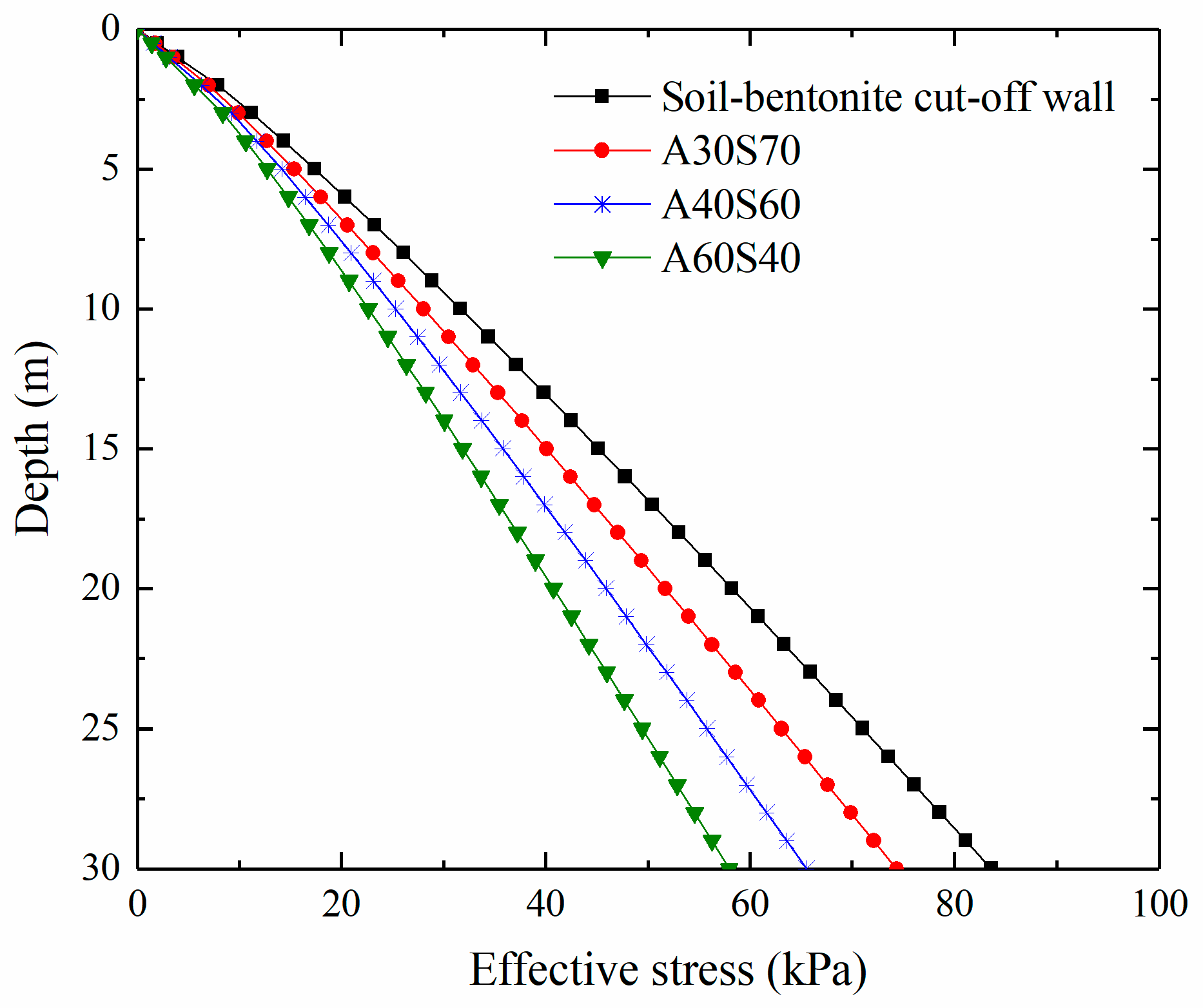
At the same time, the parameters presented in the work of Ruffing et al. [21] were selected to calculate the stress distribution of the soil–bentonite cut-off wall, which was used to compare the stress distribution of the sand–attapulgite cut-off wall and the soil–bentonite cut-off wall. The calculation results are shown in Figure 1.

According to Figure 1, (1) the effective stress of the cut-off wall increases with the increase in depth; (2) the effective stress of the sand–attapulgite cut-off wall is less than 100 kPa; (3) at the same depth, the effective stress of the sand–attapulgite cut-off wall decreases with the increase in the content of attapulgite in the wall; (4) the effective stress of a sand–attapulgite cut-off wall is smaller than that of a soil–bentonite cut-off wall at the same depth, which is because the buoyant unit weight of the sand–attapulgite cut-off wall is smaller than that of the soil–bentonite cut-off wall.

3.2. Hydraulic Conductivity Distribution Calculation

The ‘modified lateral squeezing model’ assumes that the stress process of the wall is similar to the lateral one-dimensional compression of the wall. Therefore, the horizontal stress ${\sigma }_h^{\prime }$ calculated by the model can be equivalent to the effective consolidation pressure σ′ of the one-dimensional consolidation test in the laboratory. When the stress distribution of the wall is known, the relation between the void ratio and consolidation pressure can be obtained by the consolidation test. The hydraulic conductivity of the wall can be calculated by the void ratio [22].

According to the one-dimensional consolidation test, the relationship between the void ratio (e) and the effective consolidation pressure (σ′) and the relationship between the hydraulic conductivity (k) and the void ratio (e) of the sand–attapulgite cut-off wall can be obtained. For the sand–attapulgite cut-off wall A30S70, e = −0.1644log(σ′) + 0.9933 (R² = 0.999), k = 1 × 10⁻¹⁰ × e^2.4002e (R² = 0.999); for A40S60, e = −0.2329log(σ′) + 1.2771 (R² = 0.999), k = 2 × 10⁻¹⁰ × e^1.229e (R² = 0.996); for A60S40, e = −0.2964log(σ′) + 1.6133 (R² = 0.998), k = 5 × 10⁻¹¹ × e^1.9014e (R² = 0.949). Combining these equations, the relationship between the effective consolidation pressure (σ′) and the hydraulic conductivity (k) of the sand–attapulgite cut-off wall can be obtained. For the sand–attapulgite cut-off wall A30S70, k = 1 × 10⁻¹⁰ × e^{2.4002(−0.1644log(σ′) + 0.9933)}; for A40S60, k = 2 × 10⁻¹⁰ × e^{1.229(−0.2329log(σ′) + 1.2771)}; for A60S40, k = 5 × 10⁻¹¹ × e^{1.9014(−0.2964log(σ′) + 1.6133)}.

In this section, the expressions for the relationship between the effective consolidation pressure (σ′) and the hydraulic conductivity (k) of the sand–attapulgite cut-off wall are used to calculate the hydraulic conductivity distribution of the sand–attapulgite cut-off wall in the field, combined with the effective stress distribution of the sand–attapulgite cut-off wall with different attapulgite contents in Section 3.1.

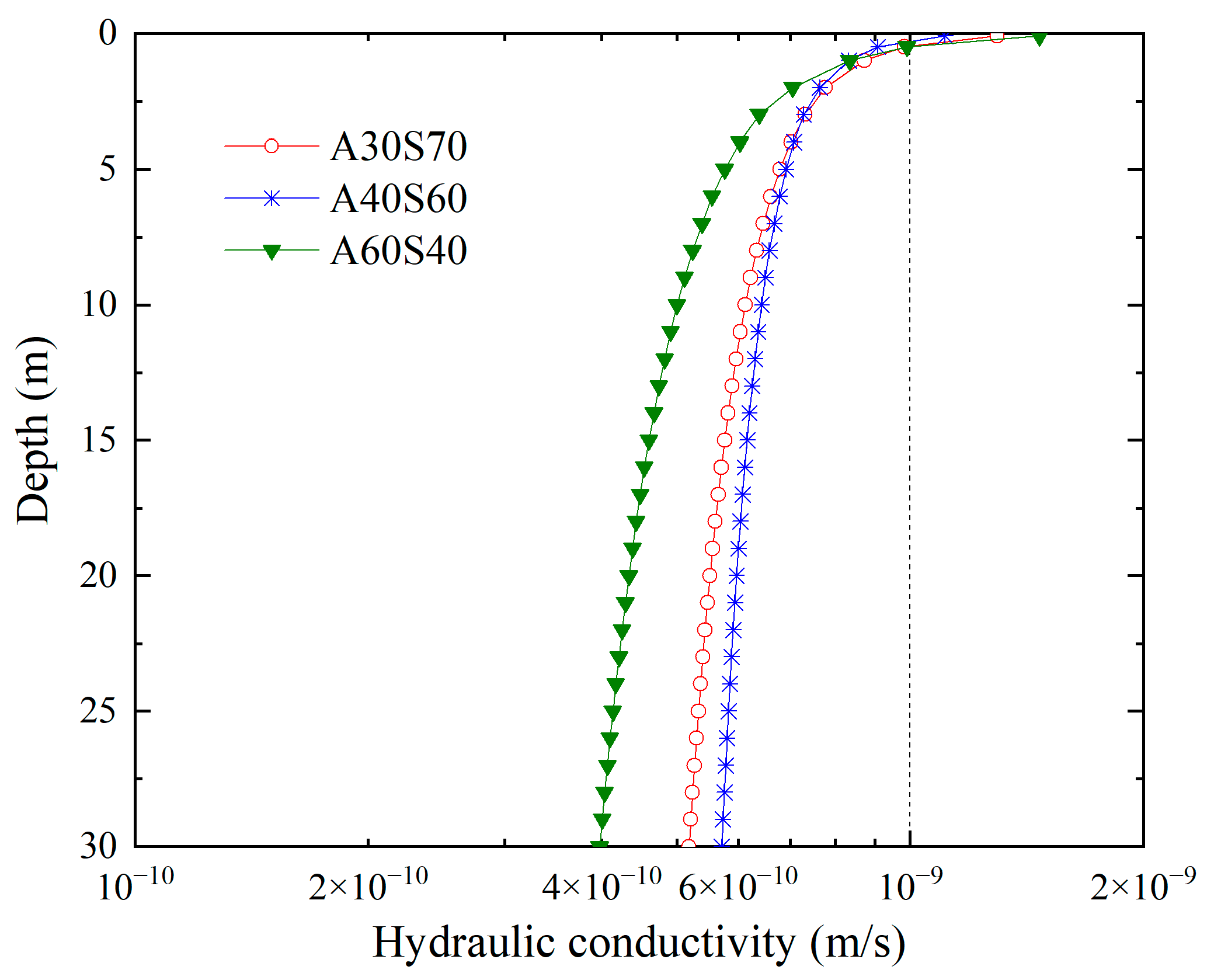
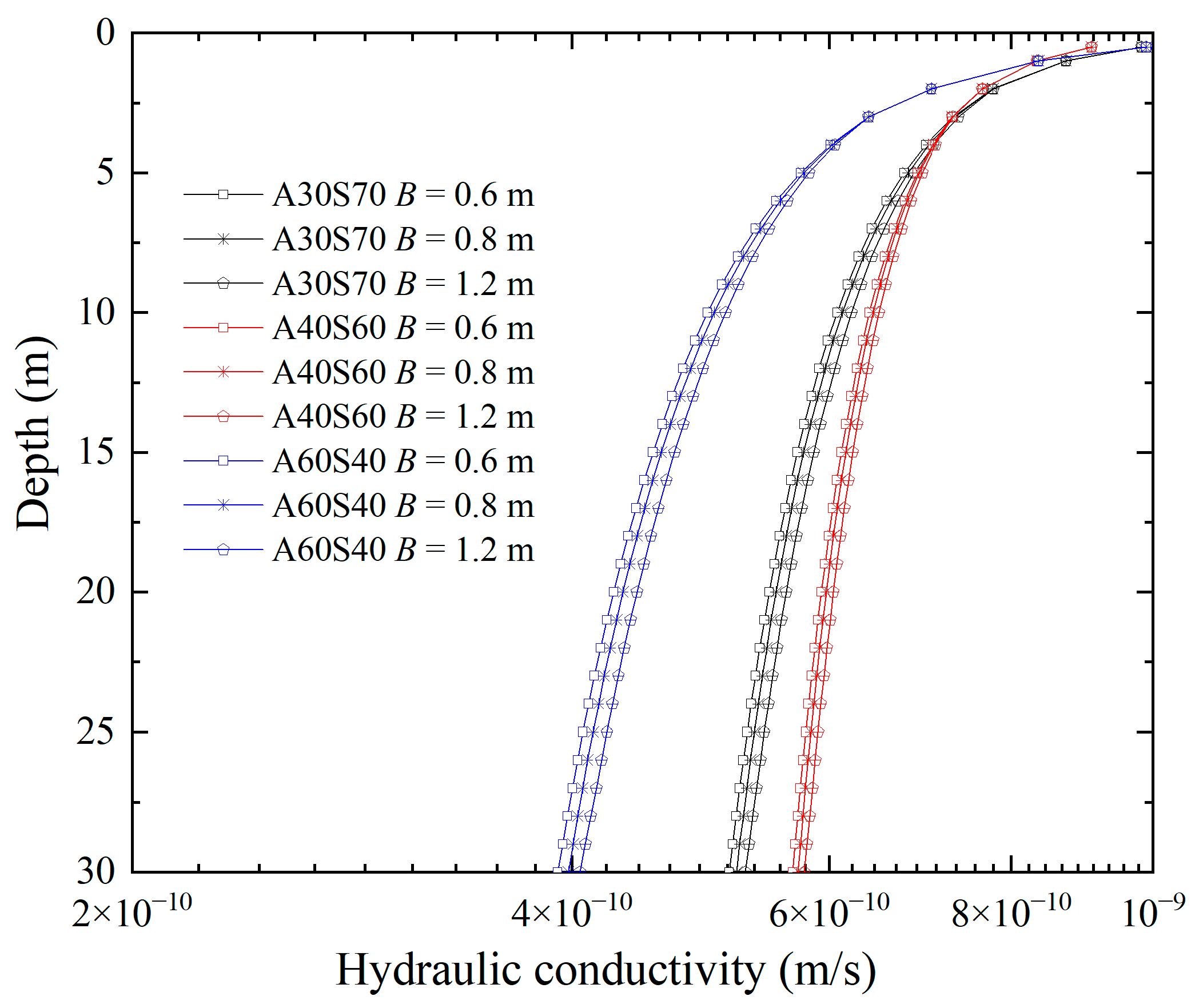
It can be seen from Figure 2 that the hydraulic conductivity of the sand–attapulgite cut-off wall decreases with the increase in depth. This is caused by the fact that the effective stress of the wall increases with increasing depth (Figure 1). However, when the depth of the wall exceeds 5 m, the decrease in the hydraulic conductivity becomes small (Figure 2). Below 0.5 m, the hydraulic conductivity of the wall is less than 1.0 × 10⁻⁹ m/s (Figure 2). Pan [28] calculated the hydraulic conductivity distribution of a soil–bentonite cut-off wall in the field and concluded that the hydraulic conductivity of the wall is relatively large in the shallow area less than 2.5 m. Therefore, during the actual construction, special attention should be paid to the anti-seepage measures at the shallow part of the cut-off wall.

4. Parametric Sensitivity Analysis

It can be seen from Equation (3) that the properties of in situ foundation soil near the cut-off wall and the geometric size of the wall will affect the stress distribution of the wall. The change in stress will lead to a change in hydraulic conductivity. In this section, the influence of these parameters on the stress distribution and hydraulic conductivity distribution of the wall will be discussed.

4.1. Influence of Foundation Soil Parameter

4.1.1. Influence of Foundation Soil Parameter on Stress Distribution

The relevant parameters used to study the influence of foundation soil on the stress distribution of a sand–attapulgite cut-off wall are listed in

Table 2. Geometric and material parameters used in the study of the influence of the related parameters of the foundation soil on the stress distribution of cut-off walls [21,22,26,27].

Parameters	Parameter Values
	Sand–Attapulgite Cut-Off Wall
	A30S70	A40S60	A60S40
B (m)	0.8	0.8	0.8
H (m)	30	30	30
${\gamma }_w^{\prime }$ (kN/m3)	8.4	7.4	6.6
Ccε	0.10	0.12	0.13
C1	−0.08	−0.11	−0.12
${\phi }_0^{\prime }$ (°)	35.0 (30.0, 40.0) 1	35.0 (30.0, 40.0)	35.0 (30.0, 40.0)

Notes: ¹ The values in front of the brackets in the table are the reference values, and the values in the brackets are the parameter change values to be studied.

. According to Table 2 and Equation (3), the stress distribution of the wall is calculated. The values of effective internal friction angle ${\phi }_0^{\prime }$ of foundation soil are 30.0°, 35.0°, and 40.0°, which represent the situations of the in situ foundation soil being saturated loose sand, medium dense sand, and dense sand, respectively [21]. Accordingly, the relationship between K_am and $\Delta$ is K_am = 8260(Δ/H)² − 74.5(Δ/H) + 0.500, K_am = 25,200(Δ/H)² − 127(Δ/H) + 0.426, and K_am = 115,000(Δ/H)² − 255(Δ/H) + 0.357 [21].

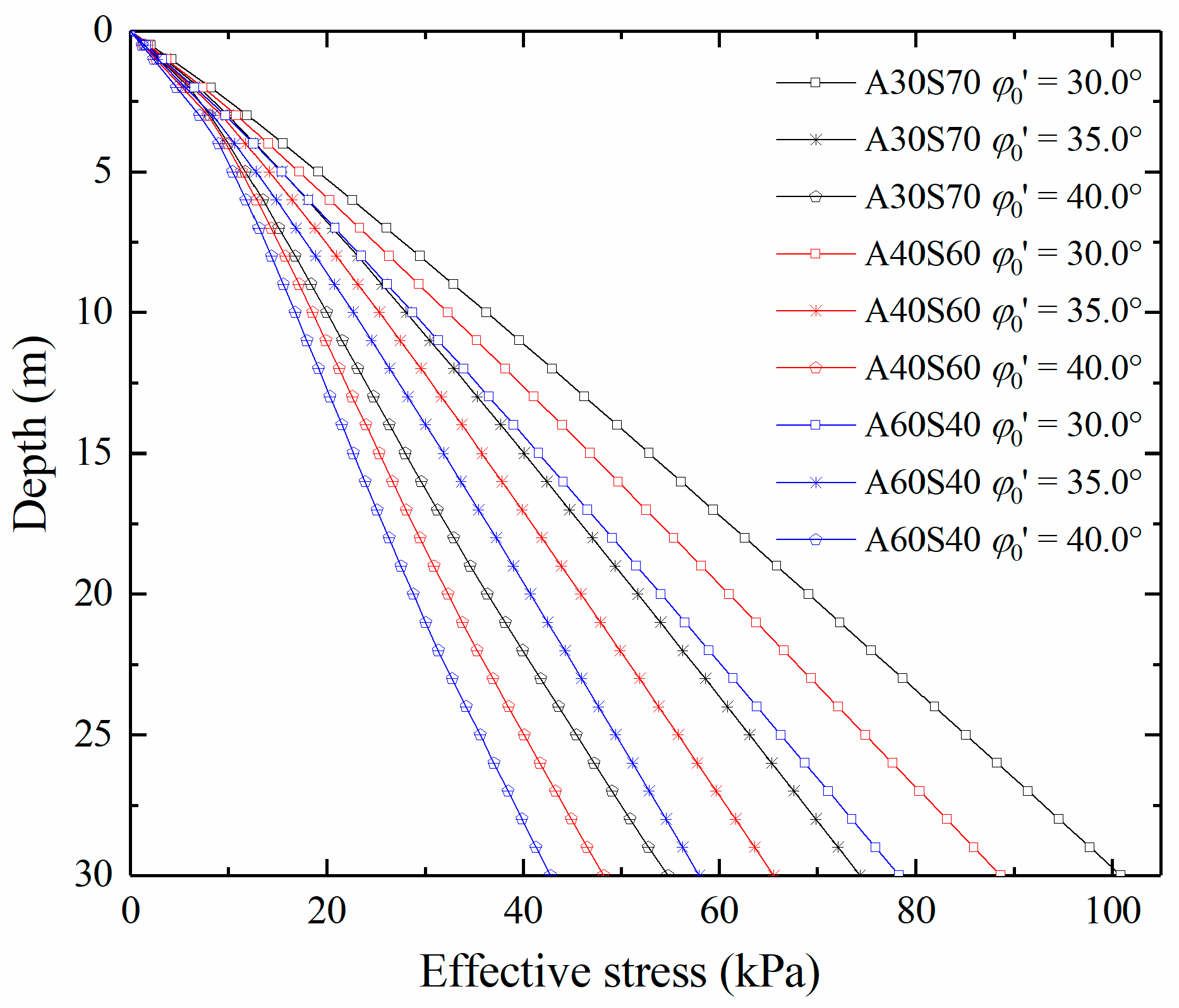
It can be seen from Figure 3 that the effective internal friction angle ${\phi }_0^{\prime }$ of foundation soil has a significant influence on the stress distribution of the sand–attapulgite cut-off wall. At the same depth, with the increase in ${\phi }_0^{\prime }$, the effective stress of the wall decreases (Figure 3). As the foundation soil changes from saturated loose sand to dense sand, the lateral displacement of the foundation soil decreases, and the lateral extrusion effect of the trench side wall on the cut-off wall decreases, so the effective stress of the cut-off wall decreases. For example, at the depth of 20 m, when the in situ foundation soil changes from loose sand to dense sand, the effective stresses of sand–attapulgite cut-off walls A30S70, A40S60, and A60S40 decrease from 69 kPa, 61 kPa, and 54 kPa to 36 kPa, 32 kPa, and 29 kPa, respectively.

4.1.2. Influence of Foundation Soil Parameter on Hydraulic Conductivity Distribution

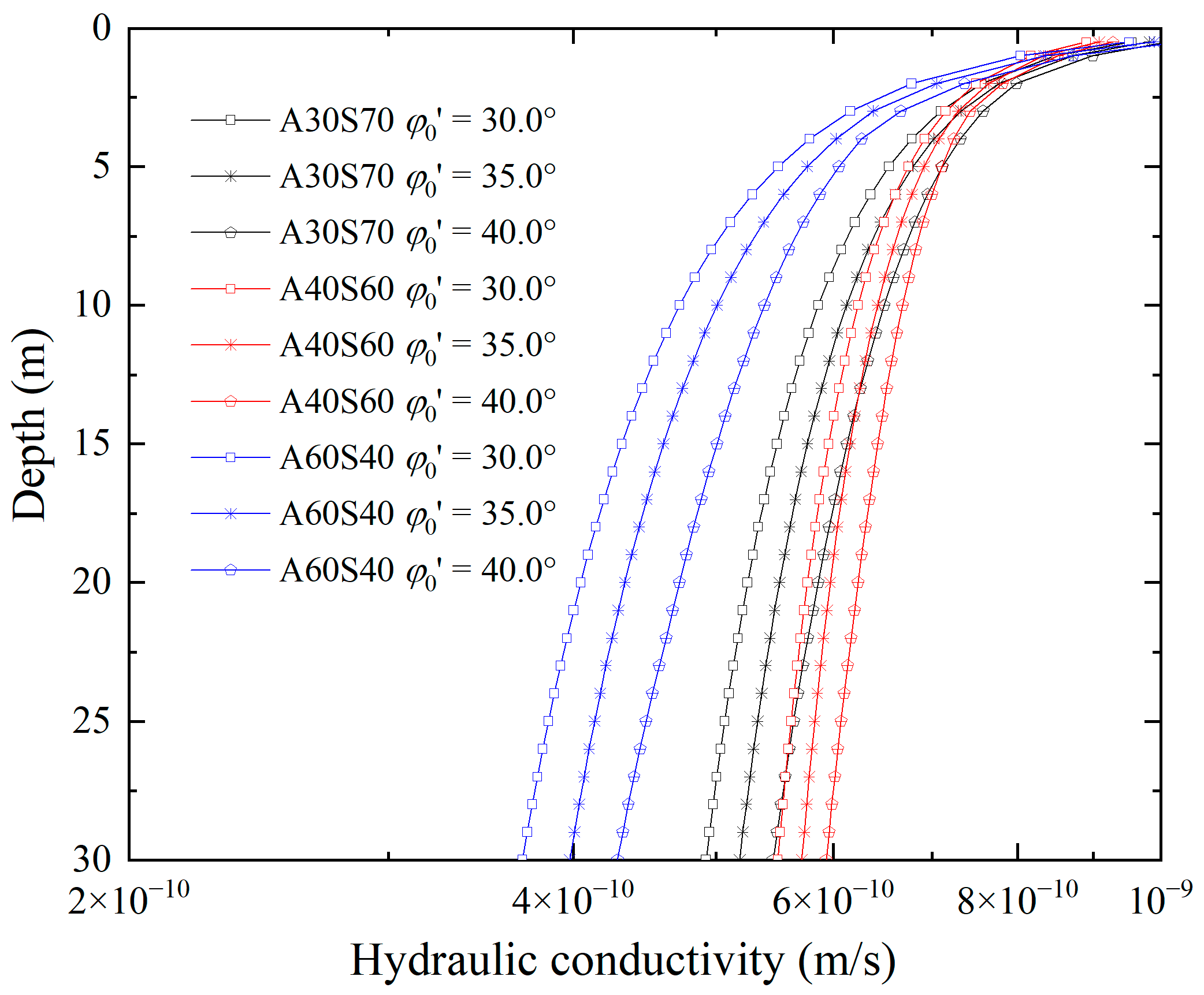
At the same depth, the hydraulic conductivity of the sand–attapulgite cut-off wall increases with the increase in the effective internal friction angle ${\phi }_0^{\prime }$ of the foundation soil (Figure 4). This is caused by the fact that the effective stress of the sand–attapulgite cut-off wall decreases with the increase in ${\phi }_0^{\prime }$. In addition, with the increase in depth, the hydraulic conductivity of the wall increases more and more with the increase in ${\phi }_0^{\prime }$, and the increase remains unchanged when the wall depth exceeds 10 m. As shown in Figure 4, at the deepest 30 m, when ${\phi }_0^{\prime }$ increases from 30° to 35° and 40°, the hydraulic conductivity of the sand–attapulgite cut-off wall A30S40 increases from 4.9 × 10⁻¹⁰ m/s to 5.2 × 10⁻¹⁰ m/s and 5.5 × 10⁻¹⁰ m/s, increasing by 6.1% and 12.2%, respectively. For A40S60, the hydraulic conductivity of the wall increases from 5.5 × 10⁻¹⁰ m/s to 5.7 × 10⁻¹⁰ m/s and 5.9 × 10⁻¹⁰ m/s, increasing by 3.6% and 7.3%, respectively. For A60S40, the hydraulic conductivity of the wall increases from 3.7 × 10⁻¹⁰ m/s to 4.0 × 10⁻¹⁰ m/s and 4.3 × 10⁻¹⁰ m/s, increasing by 8.1% and 16.2%, respectively.

It can be concluded that the hydraulic conductivity of the sand–attapulgite cut-off wall increases with the increase in the effective internal friction angle ${\phi }_0^{\prime }$ of the foundation soil, and the increase is limited, no more than one time, and the content of attapulgite in the cut-off wall does not affect this increasing trend.

4.2. Influence of the Geometric Size of the Wall

4.2.1. Influence of Geometric Size on Stress Distribution

The relevant parameters used to study the influence of wall geometry size on the stress distribution of sand–attapulgite cut-off walls are listed in

Table 3. Relevant parameters used in the study of the influence of wall geometric size on the stress distribution of cut-off walls [21,22,26,27].

Parameters	Parameter Values
	Sand–Attapulgite Cut-Off Wall
	A30S70	A40S60	A60S40
B (m)	0.8 (0.6, 1.2) 1	0.8 (0.6, 1.2)	0.8 (0.6, 1.2)
H (m)	30	30	30
${\gamma }_w^{\prime }$ (kN/m3)	8.4	7.4	6.6
Ccε	0.10	0.12	0.13
C1	−0.08	−0.11	−0.12
${\phi }_0^{\prime }$ (°)	35.0	35.0	35.0

Notes: ¹ The values in front of the brackets in the table are the reference values, and the values in the brackets are the parameter change values to be studied.

. According to Table 3 and Equation (3), the stress distribution of the sand–attapulgite barrier wall is calculated.

According to Figure 5, at the same depth, the effective stress of the sand–attapulgite cut-off wall decreases with the increase in wall width B. For example, at 20 m depth, when the wall width B increases from 0.6 m to 1.2 m, the effective stress of sand–attapulgite cut-off walls A30S70, A40S60, and A60S40 decreases from 55 kPa, 49 kPa, and 43 kPa to 47 kPa, 42 kPa, and 37 kPa, respectively. The main reason is that with the increase in wall width, the lateral extrusion effect of the trench side wall on the cut-off wall is weakened, so the effective stress of the cut-off wall is reduced.

It can be seen from Figure 3 and Figure 5 that, compared with the wall width, the properties of the in situ foundation soil have a greater impact on the effective stress of the sand–attapulgite cut-off wall.

4.2.2. Influence of Geometric Size on Hydraulic Conductivity Distribution

At the same depth, the hydraulic conductivity of the sand–attapulgite cut-off wall increases with the increase in the wall width B (Figure 6). This is caused by the fact that the effective stress of the sand–attapulgite cut-off wall decreases with the increase in wall width B. However, the hydraulic conductivity of the wall increased only slightly with the increase in the wall width B. At the deepest 30 m, when the wall width B increases from 0.6 m to 0.8 m and 1.2 m, the hydraulic conductivity of A30S40 increases from 5.1 × 10⁻¹⁰ m/s to 5.2 × 10⁻¹⁰ m/s and 5.3 × 10⁻¹⁰ m/s, increasing by 2.0% and 3.9%, respectively. For A40S60, the hydraulic conductivity increases from 5.6 × 10⁻¹⁰ m/s to 5.7 × 10⁻¹⁰ m/s and 5.8 × 10⁻¹⁰ m/s, with an increase of 1.8% and 3.6%, respectively. For A60S40, the hydraulic conductivity increases from 3.9 × 10⁻¹⁰ m/s to 4.0 × 10⁻¹⁰ m/s and 4.1 × 10⁻¹⁰ m/s, increasing by 2.6% and 5.1%, respectively. Therefore, the hydraulic conductivity of the sand–attapulgite cut-off wall increases by a very limited number with the increase in wall width B, which is no more than 0.2 times, and the content of attapulgite in the wall does not affect this increasing trend.

5. Conclusions

In this paper, the stress distribution of a sand–attapulgite cut-off wall in the field is calculated by the ‘modified lateral squeezing model’. At the same time, the hydraulic conductivity of the sand–attapulgite cut-off wall in the field is calculated by combining the relationship between the effective consolidation pressure and the void ratio and the relationship between the void ratio and the hydraulic conductivity obtained from a one-dimensional consolidation test. Finally, the influence of different parameters on the stress and hydraulic conductivity distribution of a sand–attapulgite cut-off wall is analyzed. The main conclusions are as follows:

(1) The effective stress of a sand–attapulgite cut-off wall increases with the increase in wall depth, and the effective stress is less than 100 kPa. At the same depth, the effective stress decreases with the increase in the content of attapulgite in the wall. The hydraulic conductivity of the sand–attapulgite cut-off wall decreases with the increase in wall depth. When the depth is less than 0.5 m, the hydraulic conductivity is less than 1.0 × 10⁻⁹ m/s. Therefore, during the actual construction, special attention should be paid to the seepage prevention measures for the shallow part of the cut-off wall.

(2) The properties of the in situ foundation soil (the effective internal friction angle ${\phi }_0^{\prime }$) have a significant influence on the stress distribution of the sand–attapulgite cut-off wall. The effective stress decreases with the increase in the effective internal friction angle ${\phi }_0^{\prime }$. The hydraulic conductivity distribution of the sand–attapulgite cut-off wall is also affected by the effective internal friction angle ${\phi }_0^{\prime }$; it increases with the increase in ${\phi }_0^{\prime }$, but the increase is very limited, no more than one time.

(3) The wall width B also affects the stress distribution of the sand–attapulgite cut-off wall, and the effective stress decreases with the increase in wall width B. The hydraulic conductivity of the sand–attapulgite cut-off wall is also affected by wall width B, which increases with the increase in wall width B, but the increase is not more than 0.2 times.