Ex-Ante Flooding Damages’ Monetary Valuation Model for Productive and Environmental Resources
Abstract
1. Introduction
2. Principles of Flood Damage Valuation
2.1. Types of Flood Damages
2.2. Flood Damages to Productive Assets
- For residential properties, including those designated for tourist–recreational purposes, the measure of damage can be determined in terms of a reduction in value or income, linked to the transition from the pre-event situation to the post-event situation.
- For properties used for productive purposes generating business income, the damage is generally quantifiable through the decrease in net income resulting from the interruption of work phases, or the loss of goods and final services due to flooding. This general rule does not apply to industrial or commercial enterprises in the start-up or decline phase, as they may, in such cases, produce negative income or, in any case, limited positive income [38].
2.3. Damages to Environmental Resources and Contingent Valuation Method (CVM)
2.4. Indirect Damages
3. Methods for Ex-Ante Flooding Damages’ Monetary Valuation
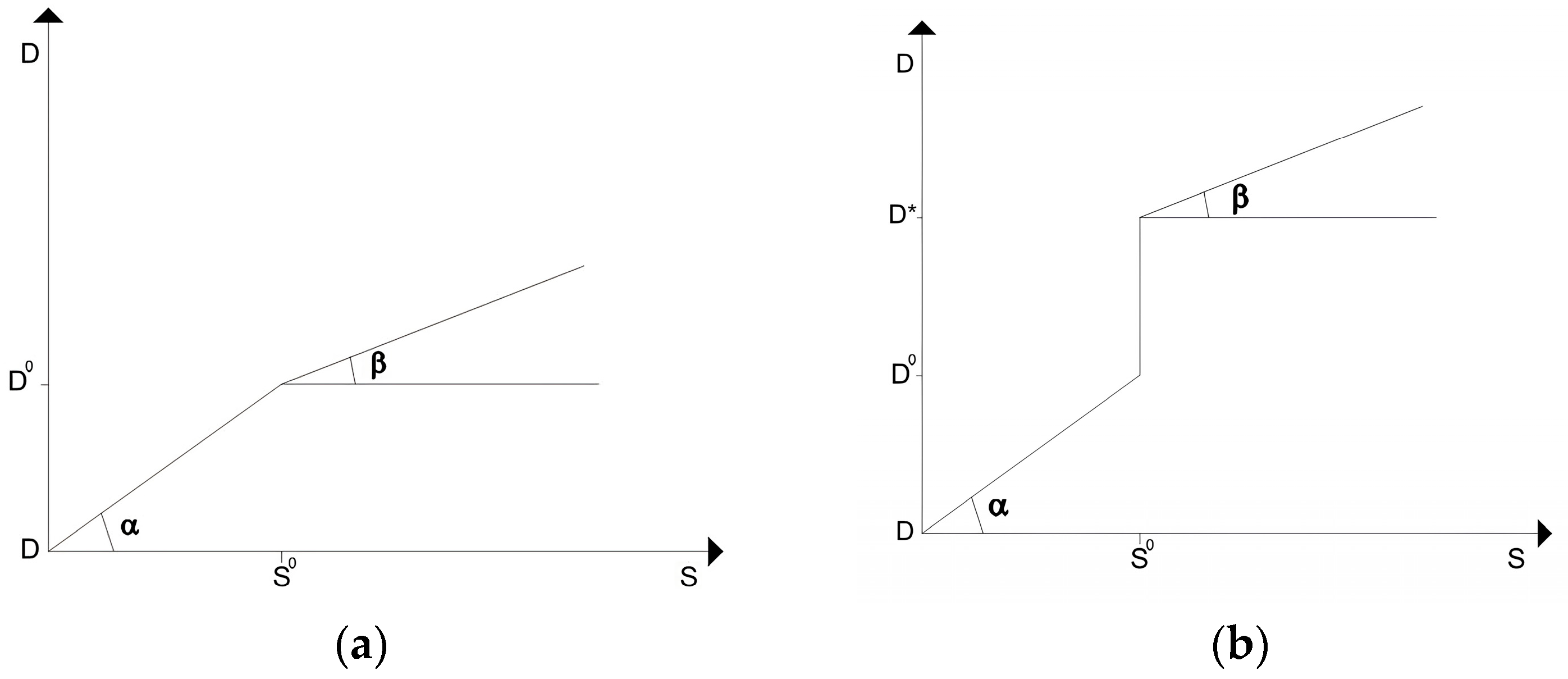
3.1. Productive Resources
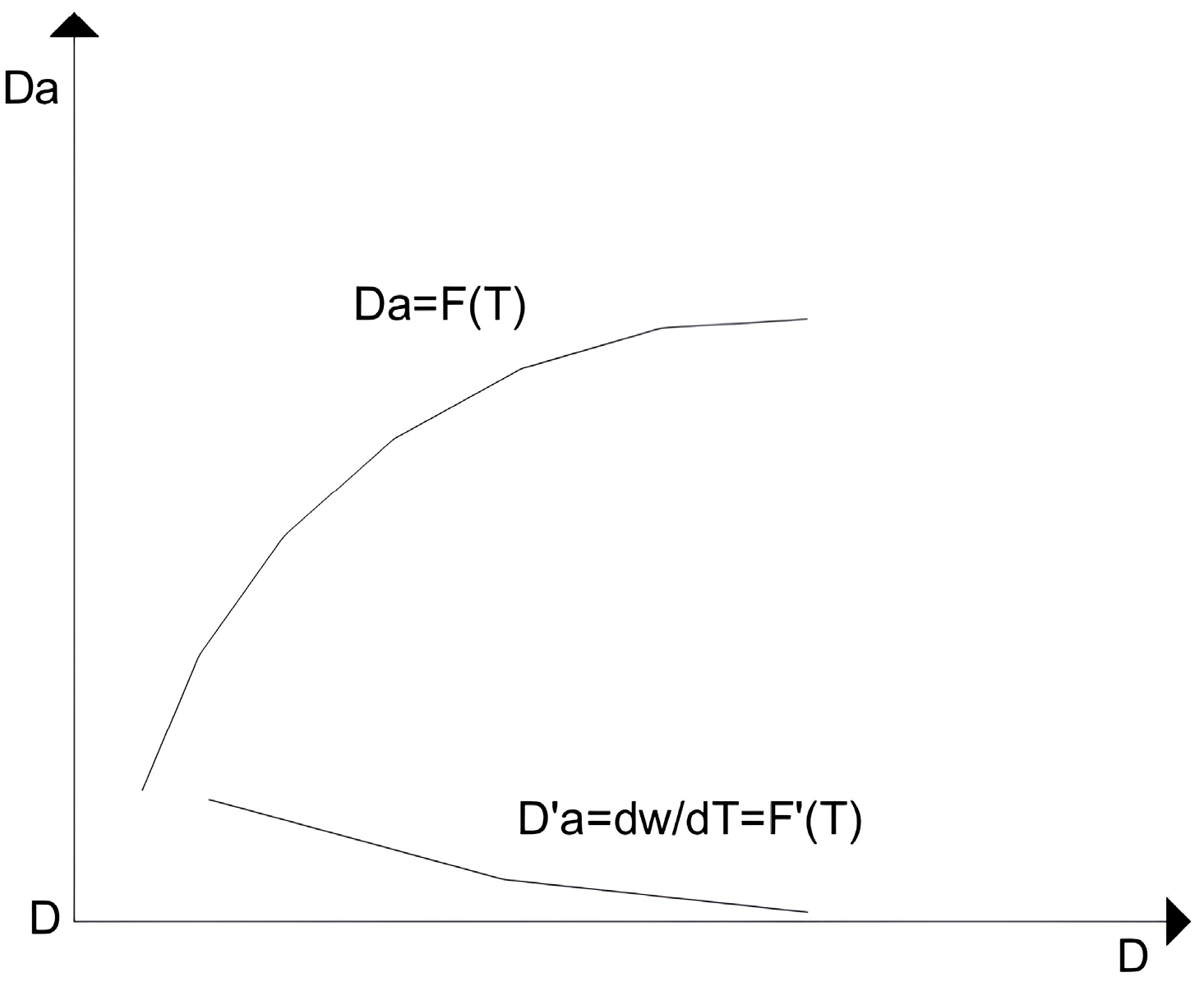
3.2. Environmental Resources
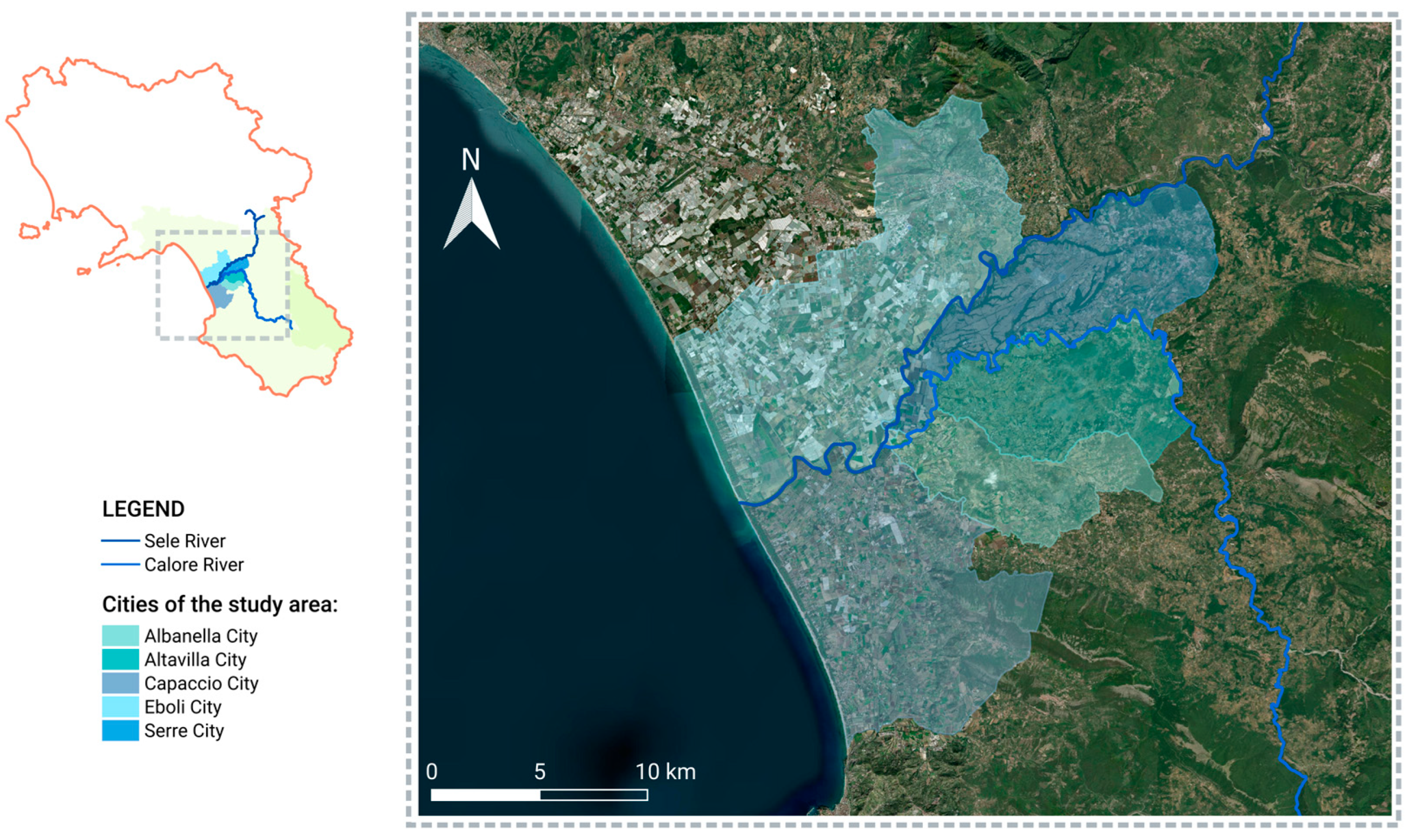
4. Case Study
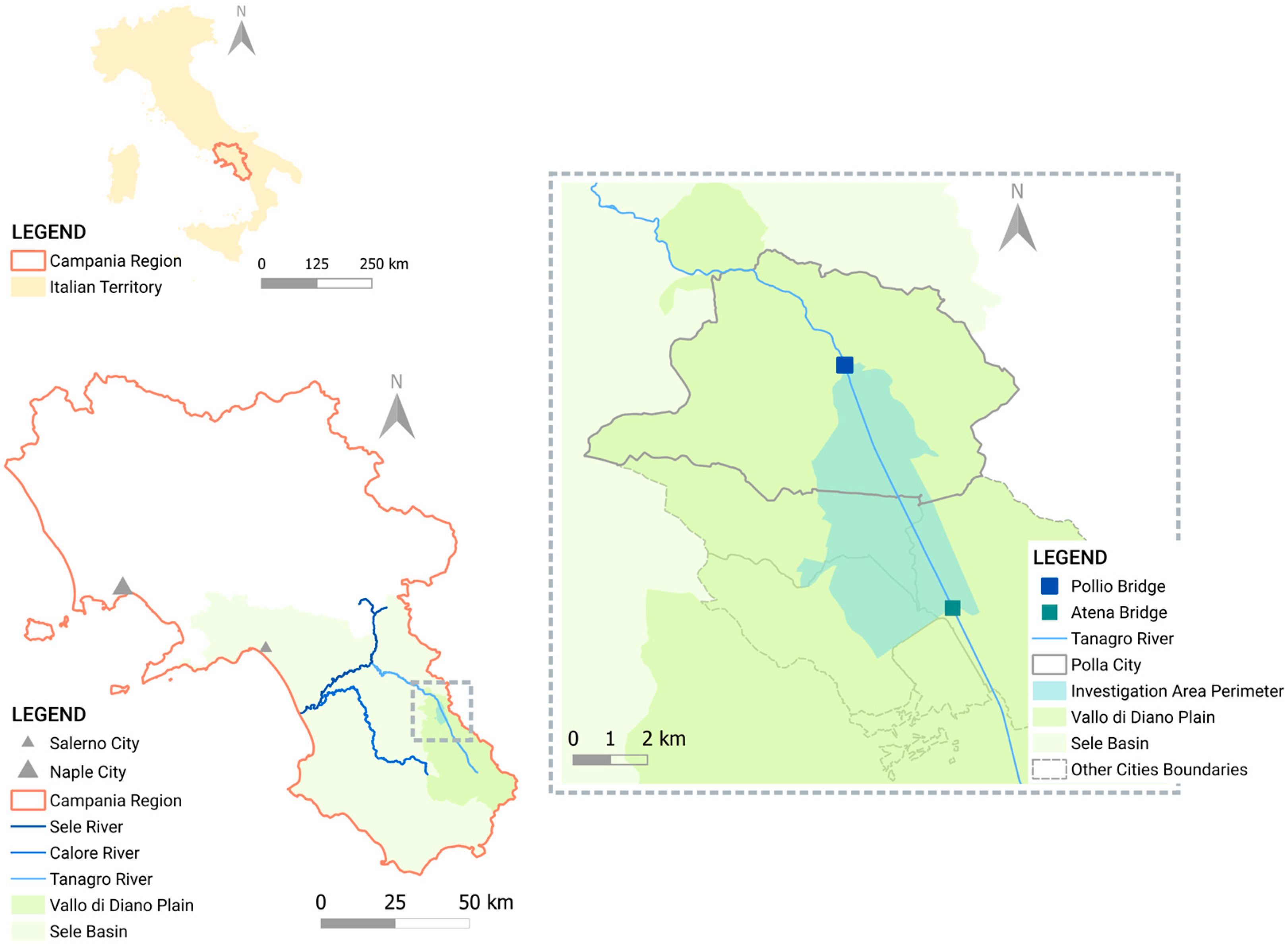
4.1. Investigation Areas
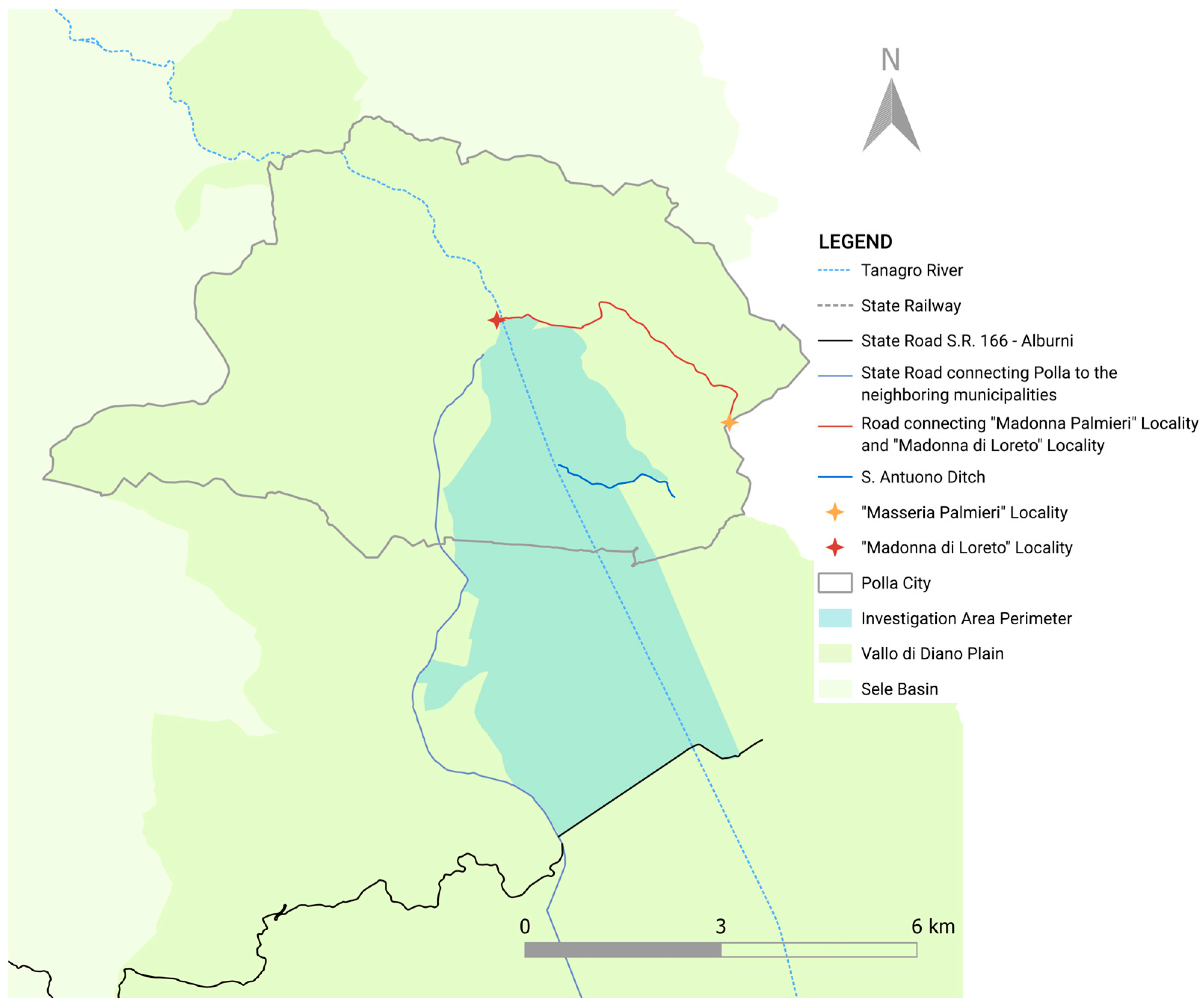
4.1.1. Vallo di Diano
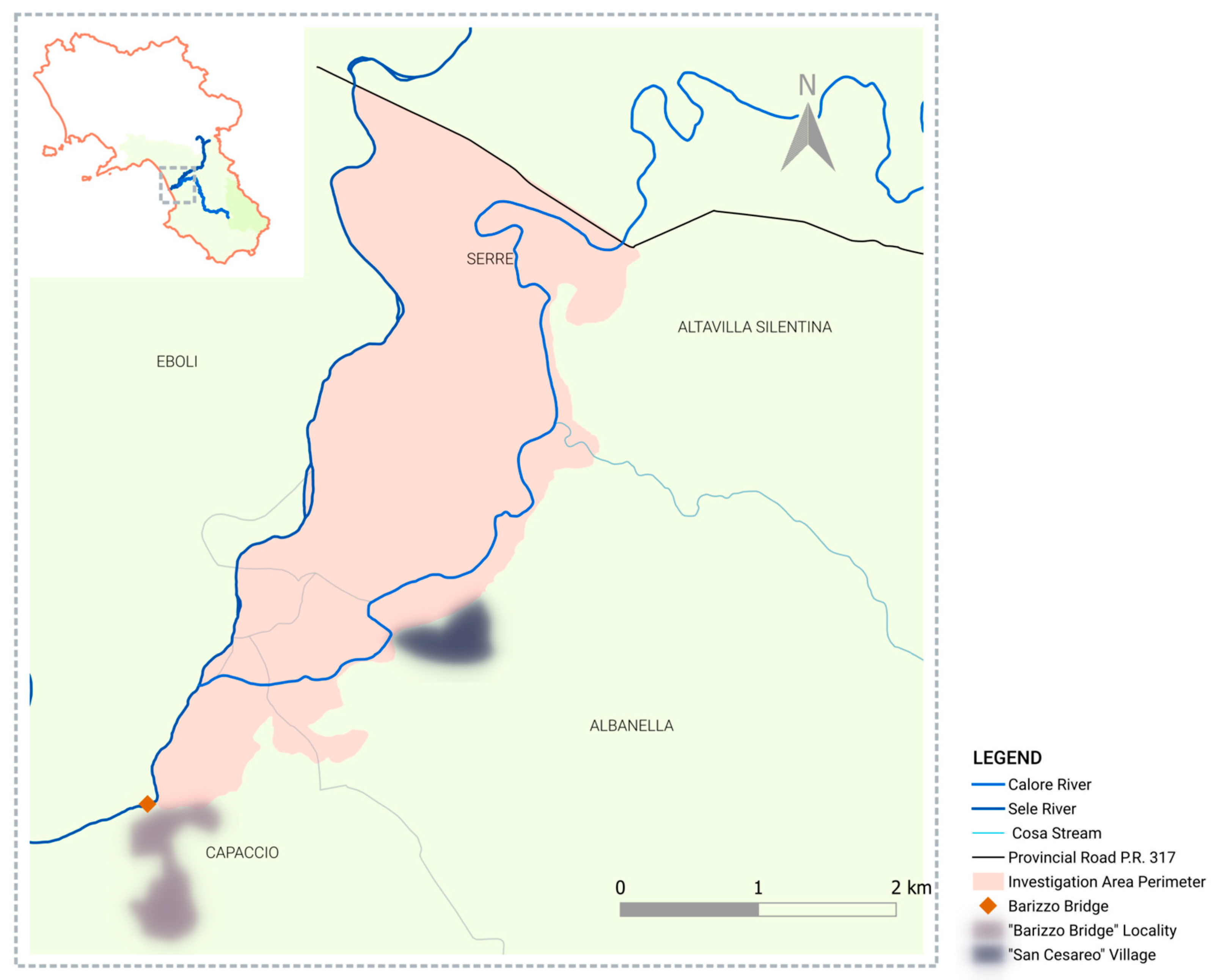
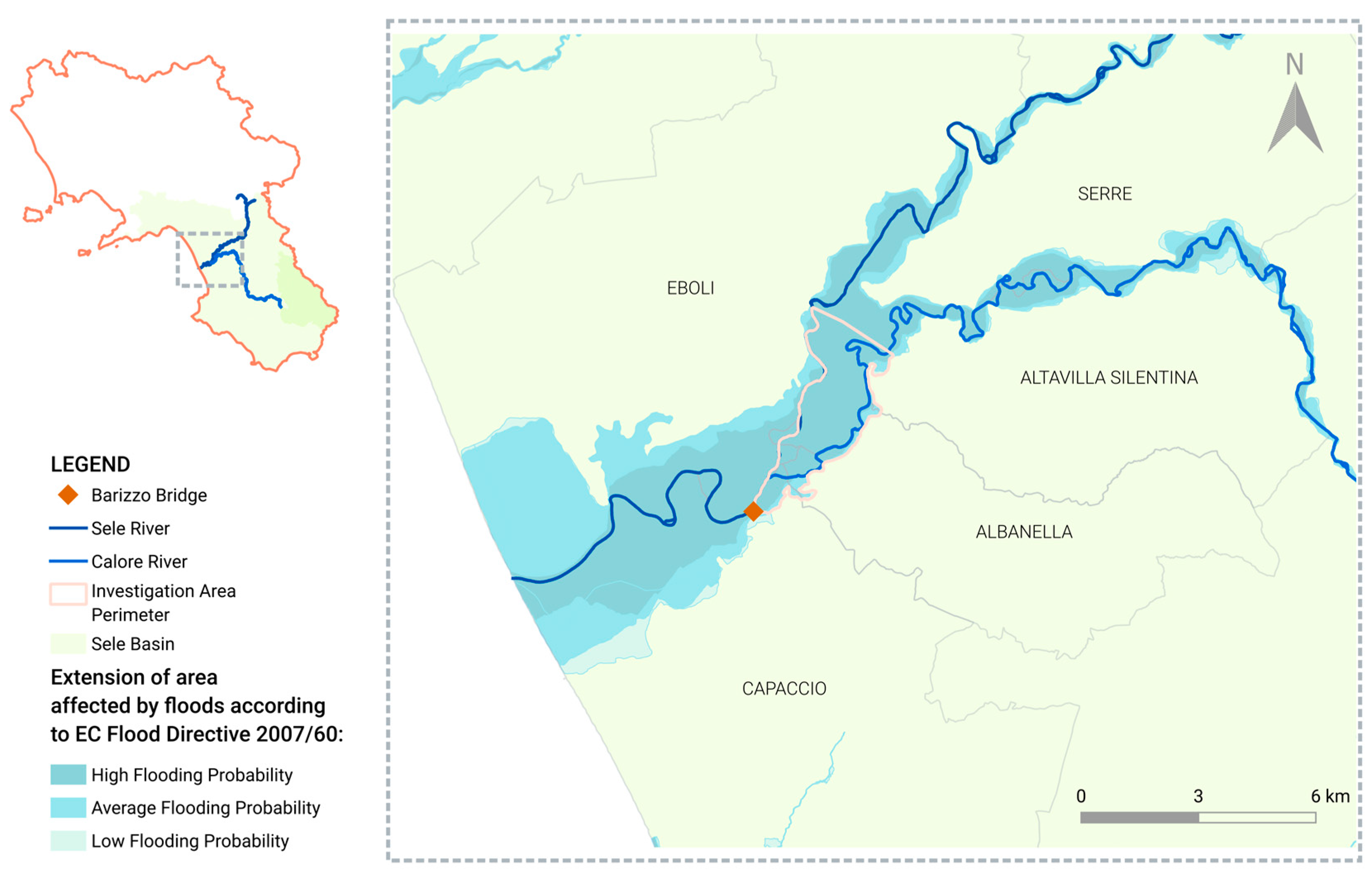
4.1.2. Sele–Calore Rivers’ Confluence
4.2. Damages to Productive Resources
4.2.1. Damages to Agriculture
4.2.2. Damages to Urban Areas
- For buildings, damages were measured by the cost of restoring the external finishes of premises affected by flooding. Assuming an average value per premise of 413.16 EUR/m2, the unit damage was conservatively set at about 30% of that value, or about 123.94 EUR/m2. The unit damage to basement premises of structures was estimated at 25% of that amount, or about 30.99 EUR/m2.
- For appurtenance areas of buildings, damages were estimated at an amount equal to the reconstruction costs of the wear layer, averaging 15.49 EUR/m2.
- For gardens and green areas, a unit damage of 0.52 EUR/m2 and 0.026 EUR/m2, respectively, was assumed.
4.2.3. Damages to Network Infrastructures
4.2.4. Total Damages
4.3. Implementation of the Damage Estimation Model
- Determination of the variation law of the flooded area based on the flood event’s return period,
- Calculation of the damage per unit of flooded area and application of the relationship between the flooded area and the damage amount.
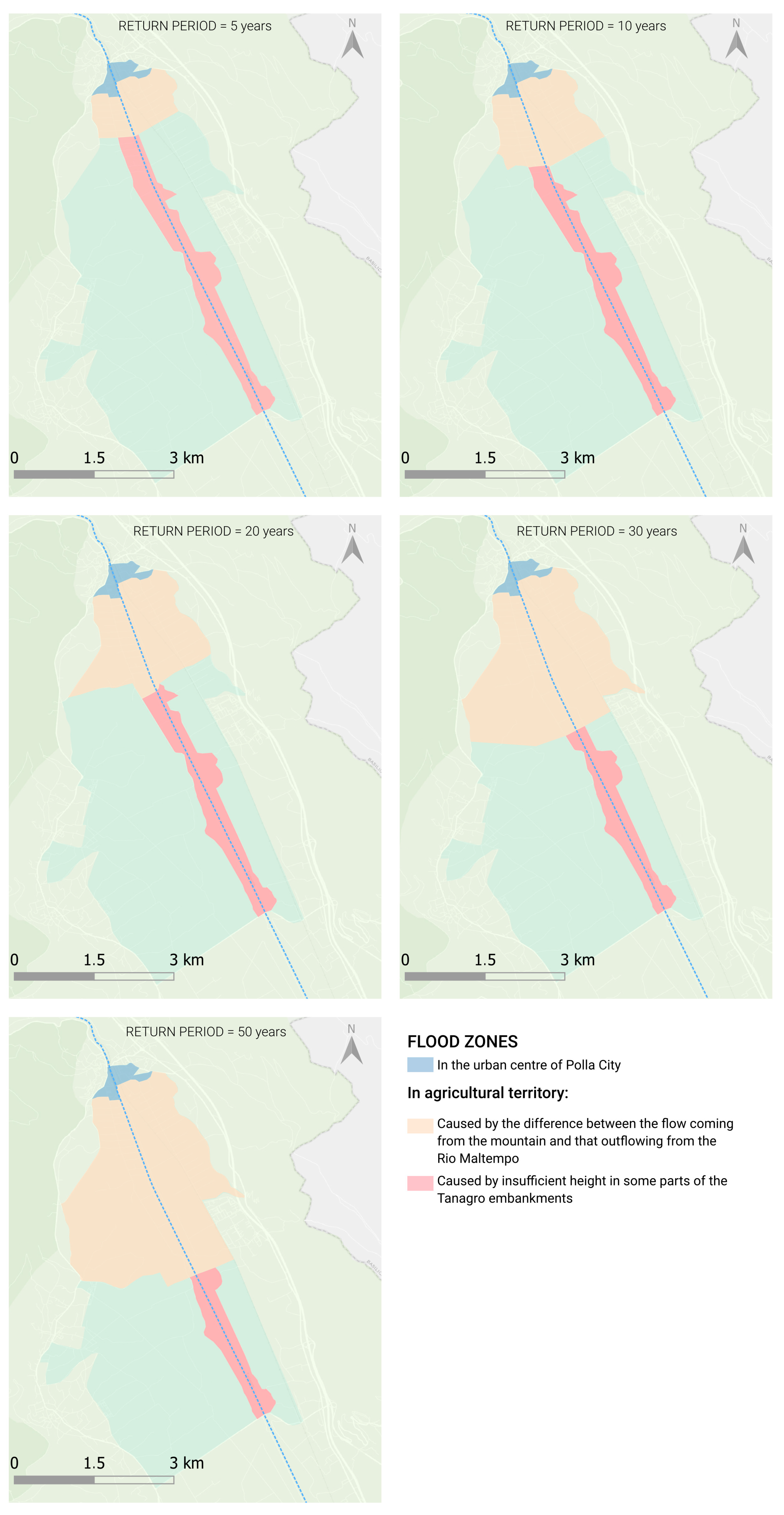
4.3.1. Vallo di Diano
4.3.2. Sele–Calore Rivers’ Confluence
4.4. Damages to Environmental Resources Using CVM
- Cartographic delimitation within the investigation area of zones subject to the reference flooding event,
- Defining a statistically representative sample of the population of “users” of environmental resources present in the zone subject to the considered flooding event,
- Estimating the “average individual WTP” calculated on the sample, based on the amount that the user is willing to pay to avoid damages to the resources affected by the event; additionally, determining the “total WTP” calculated for the entire population of resource users corresponding to the “accounting price” of the environmental damage produced by the considered event.
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cevasco, A.; Diodato, N.; Revellino, P.; Fiorillo, F.; Grelle, G.; Guadagno, F.M. Storminess and geo-hydrological events affecting small coastal basins in a terraced Mediterranean environment. Sci. Total Environ. 2015, 532, 208–219. [Google Scholar] [CrossRef]
- Diodato, N. Climatic fluctuations in southern Italy since the 17th century: Reconstruction with precipitation records at Benevento. Clim. Chang. 2007, 80, 411–431. [Google Scholar] [CrossRef]
- Knox, J.C. Large increase in flood magnitude in response to modest changes in climate. Nature 1993, 361, 430–432. [Google Scholar] [CrossRef]
- Vennari, C.; Parise, M.; Santangelo, N.; Santo, A. A database on flash flood events in Campania, southern Italy, with an evaluation of their spatial and temporal distribution. Nat. Hazards Earth Syst. Sci. 2016, 16, 2485–2500. [Google Scholar] [CrossRef]
- Pereira, P.; Barceló, D.; Panagos, P. Soil and water threats in a changing environment. Environ. Res. 2020, 186, 109501. [Google Scholar] [CrossRef] [PubMed]
- Keating, A.; Campbell, K.; Mechler, R.; Michel-Kerjan, E.; Mochizuki, J.; Kunreuther, H.; Bayer, J.; Hanger, S.; McCallum, I.; See, L.; et al. Operationalizing Resilience against Natural Disaster Risk: Opportunities, Barriers, and a Way Forward. Zurich Flood Resilience Alliance; IIASA: Zurich, Switzerland, 2014. [Google Scholar]
- Dutta, D.; Herath, S.; Musiake, K. A mathematical model for flood loss estimation. J. Hydrol. 2003, 277, 24–49. [Google Scholar] [CrossRef]
- Velasco, M.; Cabello, À.; Russo, B. Flood damage assessment in urban areas. Application to the Raval district of Barcelona using synthetic depth damage curves. Urban Water J. 2016, 13, 426–440. [Google Scholar] [CrossRef]
- Lekuthai, A.; Vongvisessomjai, S. Intangible flood damage quantification. Water Resour. Manag. 2001, 15, 343–362. [Google Scholar] [CrossRef]
- Parker, D.J.; Green, C.H.; Thompson, P.M. Urban Flood Protection Benefits: A Project Appraisal Guide; Gower Technical Press: Aldershot, UK, 1987. [Google Scholar]
- Smith, K.; Ward, R. Floods: Physical Processes and Human Impacts; John Wiley & Sons: Chichester, UK, 1998. [Google Scholar]
- Appelbaum, S.J. Determination of urban flood damages. J. Water Resour. Plan. Manag. 1985, 111, 269–283. [Google Scholar] [CrossRef]
- Sindhu, K.; Durga Rao, K.H.V. Hydrological and hydrodynamic modeling for flood damage mitigation in Brahmani–Baitarani River Basin, India. Geocarto Int. 2017, 32, 1004–1016. [Google Scholar]
- Eleuterio, J. Flood Risk Analysis: Impact of Uncertainty in Hazard Modelling and Vulnerability Assessments. Ph.D. thesis, University of Strasbourg, Strasbourg, France, 2012. [Google Scholar]
- Merz, B.; Kreibich, H.; Schwarze, R.; Thieken, A. Assessment of Economic Flood Damage. Nat. Hazards Earth Syst. Sci. 2010, 10, 1697–1724. [Google Scholar] [CrossRef]
- Smith, D.I. Flood damage estimation—A review of urban stagedamage curves and loss functions. Water Sa 1994, 20, 231–238. [Google Scholar]
- Gissing, A.; Blong, R. Accounting for Variability in Commercial Flood Damage Estimation. Aust. Geogr. 2004, 35, 209–222. [Google Scholar] [CrossRef]
- Aribisala, O.D.; Yum, S.G.; Adhikari, M.D.; Song, M.S. Flood Damage Assessment: A Review of Microscale Methodologies for Residential Buildings. Sustainability 2022, 14, 13817. [Google Scholar] [CrossRef]
- Pistrika, A.; Tsakiris, G.; Nalbantis, I. Flood DepthDamage Functions for Built Environment. Environ. Process. 2014, 1, 553–572. [Google Scholar] [CrossRef]
- Meyer, V.; Messner, F. National Flood Damage Evaluation Methods: A Review of Applied Methods in England, The Netherlands, the Czech Republic and Germany; UFZ-Umweltforschungszentrum Leipzig-Halle: Leipzig, Germany, 2005. [Google Scholar]
- Messner, F.; Penning-rowsell, E.; Green, C.; Meyer, V.; Tunstall, S.; Van Der Veen, A. Evaluating Flood Damages: Guidance and Recommendations on Principles and Methods; FLOODsite Project Deliverable D9.1; Helmholz Unweltforschungszentrum (UFZ): Wallingford, UK, 2007. [Google Scholar]
- Sulong, S.; Romali, N.S. Flood damage assessment: A review of multivariate flood damage models. Int. J. GEOMATE 2022, 22, 106–113. [Google Scholar] [CrossRef]
- Romali, N.S.; Yusop, Z.; Sulaiman, M.; Ismail, Z. Flood risk assessment: A review of flood damage estimation model for Malaysia. J. Teknol. 2018, 80, 145–153. [Google Scholar] [CrossRef]
- Meyer, V.; Becker, N.; Markantonis, V.; Schwarze, R.; van den Bergh, J.C.J.M.; Bouwer, L.M.; Bubeck, P.; Ciavola, P.; Genovese, E.; Green, C.; et al. Assessing the costs of natural hazards—State of the art and knowledge gaps. Nat. Hazards Earth Syst. Sci. 2013, 13, 1351–1373. [Google Scholar] [CrossRef]
- Przyluski, V.; Hallegatte, S. Indirect Costs of Natural Hazards—CONHAZ Report. 2011. Available online: https://climate-adapt.eea.europa.eu/en/metadata/guidances/indirect-costs-of-natural-hazards (accessed on 1 February 2024).
- Cochrane, H.C. Chapter 3. Indirect Losses from Natural Disasters: Measurement and Myth. In Modeling the Spatial and Economic Effects of Disasters; Okuyama, Y., Chang, S.E., Eds.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Rose, A.; Liao, S.Y. Modeling Regional Economic Resilience to Disasters: A Computable General Equilibrium Analysis of Water Service Disruptions. J. Reg. Sci. 2005, 45, 75–112. [Google Scholar] [CrossRef]
- Rose, A. Economic Principles, Issues and Research Priorities in Hazard Loss Estimation. In Modeling the Spatial and Economic Effects of Disasters; Okuyama, Y., Chang, S.E., Eds.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Pearce, D.W.; Smale, R. Appraising flood control investments in the UK. In Cost-Benefit-Analysis and Water Resource Management; Brouwer, R., Pearce, D.W., Eds.; Edward Elgar: Cheltenham, UK, 2005; pp. 71–92. [Google Scholar]
- Serpieri, A. Il Metodo di Stima dei Beni Fondiari; Tipografia Di Mariano Picci: Firenze, Italy, 1917. [Google Scholar]
- Brizi, A. Lezioni di Metodo dell’Estimo Agrario; Della Torre: Portici, Italy, 1936. [Google Scholar]
- Morano, N. Valutazione dei Danni da Piena; Consorzio Piano Bacino Sele: Napoli, Italy, 1991. [Google Scholar]
- Hoes, O.; Schuurmans, W. Flood Standards or Risk Analyses for Polder Management in the Netherlands. Irrig. Drain. 2006, 55, S113–S119. [Google Scholar]
- Citeau, J.M. A New Control Concept in the Oise Catchment Area: Definition and Assessment of Flood Compatible Agricultural Activities; FIG Working Week: Paris, France, 2003. [Google Scholar]
- Forster, S.; Kuhlmann, B.; Lindenschmidt, K.E.; Bronstert, A. Assessing flood risk for a rural detention area. Nat. Hazards Earth Syst. Sci. 2008, 8, 311–322. [Google Scholar] [CrossRef]
- Penning-Rowsell, E.C.; Chatterton, J.B. The Benefits of Flood Alleviation: A Manual of Assessment Techniques; Gower Technical Press: Aldershot, UK, 1977. [Google Scholar]
- Forte, F. Le Imposte Sulle Vendite e Sul Valore Aggiunto; Einaudi: Turin, Italy, 1973. [Google Scholar]
- Orefice, M. Estimo; UTET: Torino, Italy, 1984. [Google Scholar]
- Verlynde, N.; Voltaire, L.; Chagnon, P. Exploring the link between flood risk perception and public support for funding on flood mitigation policies. J. Environ. Plan. Manag. 2019, 62, 2330–2351. [Google Scholar] [CrossRef]
- Davis, R.K. The value of big game hunting in a private forest. In Proceedings of the Transactions of the Twenty-Ninth North American Wildlife and Natural Resources Conference, Las Vegas, NV, USA, 9–11 March 1964; Volume 29, pp. 393–403. [Google Scholar]
- Ridker, R.G. Economic Costs of Air Pollution; Praeger: New York, NY, USA, 1967. [Google Scholar]
- Boyle, K.J.; Bishop, R.C. Welfare measurements using contingent valuation: A comparison of techniques. Am. J. Agric. Econ. 1988, 70, 20–28. [Google Scholar] [CrossRef]
- Loomis, J.B. Balancing public trust resources of Mono Lake and Los Angeles’ water right: An economic approach. Water Resour. Res. 1987, 23, 1449–1456. [Google Scholar] [CrossRef]
- Shultz, S.D.; Lindsay, B.E. The willingness to pay for groundwater protection. Water Resour. Res. 1990, 26, 1869–1875. [Google Scholar] [CrossRef]
- Markantonis, V.; Meyer, V.; Lienhoop, N. Evaluation of the environmental impacts of extreme floods in the Evros River basin using Contingent Valuation Method. Nat. Hazards 2013, 69, 1535–1549. [Google Scholar] [CrossRef]
- Arrow, K.; Solow, R.; Portney, P.; Leamer, E.; Radner, R.; Schuman, H. Report of the NOAA Panel on Contingent Valuation; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1993. [Google Scholar]
- Daun, C.M.; Clark, D. Flood Risk and Contingent Valuation Willingness to Pay Studies: A Methodological Review and Applied Analysis; Institute for Urban Environmental Risk Management, Marquette University: Milwaukee, WI, USA, 2000. [Google Scholar]
- Birol, E.; Karousakis, K.; Koundouri, P. Using economic valuation techniques to inform water resources management: A survey and critical appraisal of available techniques and an application. Sci. Total Environ. 2006, 365, 105–122. [Google Scholar] [CrossRef] [PubMed]
- Hoevenagel, R. The Contingent Valuation Method: Scope and Validity; Vrije University: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Shavell, S. Contingent valuation of the nonuse value of natural resources: Implications for public policy and the liability system. Contrib. Econ. Anal. 1993, 220, 371–388. [Google Scholar]
- Diamond, P.A.; Hausman, J.A. Contingent valuation: Is some number better than no number? J. Econ. Perspect. 1994, 8, 45–64. [Google Scholar] [CrossRef]
- Kahneman, D.; Knetsch, J.L. Valuing public goods: The purchase of moral satisfaction. J. Environ. Econ. Manag. 1992, 22, 57–70. [Google Scholar] [CrossRef]
- Loomis, J.; Lockwood, M.; DeLacy, T. Some empirical evidence on embedding effects in contingent valuation of forest protection. J. Environ. Econ. Manag. 1993, 25, 45–55. [Google Scholar] [CrossRef]
- Whitehead, J.C. A practitioner’s primer on contingent valuation. In Handbook on Contingent Valuation; Alberini, A., Kahn, J.R., Eds.; Edward Elgar Publishing: Cheltenham, UK, 2006; Chapter 3; pp. 92–115. [Google Scholar]
- Kroll, C.A.; Landis, J.D.; Shen, Q.; Stryker, S. Economic Impacts of the Loma Prieta Earthquake: A Focus on Small Businesses; 1991. Available online: https://escholarship.org/uc/item/6s67g8mh (accessed on 1 February 2024).
- Molinari, D.; Menoni, S.; Aronica, G.T.; Ballio, F.; Berni, N.; Pandolfo, C.; Stelluti, M.; Minucci, G. Ex post damage assessment: An Italian experience. Nat. Hazards Earth Syst. Sci. 2014, 14, 901–916. [Google Scholar] [CrossRef]
- Pfurtscheller, C. Regional Economic Impacts of Natural Hazards—The Case of the 2005 Alpine flood event in Tyrol (Austria). Nat. Hazards Earth Syst. Sci. 2014, 14, 359–378. [Google Scholar] [CrossRef]
- Albala-Bertrand, J.M. Natural disaster situations and growth: A macroeconomic model for sudden disaster impacts. World Dev. 1993, 21, 1417–1434. [Google Scholar] [CrossRef]
- Cavallo, E.; Galiani, S.; Noy, I.; Pantano, J. Catastrophic Natural Disasters and Economic Growth. Rev. Econ. Stat. 2013, 95, 1549–1561. [Google Scholar] [CrossRef]
- Noy, I.; Nualsri, A. What do Exogenous Shocks Tell Us about Growth Theories? Working Paper, No. 07-16; University of California, Santa Cruz Institute for International Economics (SCIIE): Santa Cruz, CA, USA, 2007. [Google Scholar]
- Strobl, E. The Economic Growth Impact of Hurricanes: Evidence from U.S. Coastal Counties. Rev. Econ. Stat. 2010, 93, 575–589. [Google Scholar] [CrossRef]
- Hallegatte, S. An adaptive regional input-output model, and its application to the assessment of the economic cost of Katrina. Risk Anal. 2008, 28, 779–799. [Google Scholar] [CrossRef]
- Hallegatte, S.; Ranger, N.; Mestre, O.; Corfee-Morlot, P.D.J.; Herweijer, C.; Muir, R. Assessing climate change impacts, sea level rise and storm surge risk in port cities: A case study on Copenhagen. Clim. Chang. 2011, 104, 113–137. [Google Scholar] [CrossRef]
- Henriet, F.; Hallegatte, S.; Tabourier, L. Firm-network characteristics and economic robustness to natural disasters. J. Econ. Dyn. Control 2012, 36, 150–167. [Google Scholar] [CrossRef]
- Okuyama, Y. Disaster, and economic structural change: Case study on the 1995 Kobe earthquake. Econ. Syst. Res. 2014, 26, 37–41. [Google Scholar] [CrossRef]
- Okuyama, Y.; Hewings, G.D.; Sonis, M. Measuring Economic Impacts of Disasters: Interregional Input-Output Analysis Using Sequential Interindustry Model. In Modeling Spatial and Economic Impacts of Disasters; Okuyama, Y., Chang, S., Eds.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2004; pp. 77–101. [Google Scholar]
- Ranger, N.; Hallegatte, S.; Bhattacharya, S.; Bachu, M.; Priya, S.; Dhore, K.; Corfee-Morlot, J. An assessment of the potential impact of climate change on flood risk in Mumbai. Clim. Chang. 2011, 104, 139–167. [Google Scholar] [CrossRef]
- Berrittella, M.; Hoekstra, A.Y.; Rehdanz, K.; Roson, R.; Tol, R.S.J. The economic impact of restricted water supply: A computable general equilibrium analysis. Water Res. 2007, 41, 1799–1813. [Google Scholar] [CrossRef] [PubMed]
- Haddad, E.A.; Teixeira, E. Economic impacts of natural disasters in megacities: The case of floods in São Paulo, Brazil. Habitat Int. 2015, 45, 106–113. [Google Scholar] [CrossRef]
- Jonkhoff, W. Flood risk assessment and policy in the Netherlands. Green Cities 2009, 220. [Google Scholar]
- Pauw, K.J.T.; Bachu, M.; Van Seventer, D.E. The economic costs of extreme weather events: A hydrometeorological CGE analysis for Malawi. Environ. Dev. Econ. 2011, 16, 177–198. [Google Scholar] [CrossRef]
- Rose, A.; Benavides, J.; Chang, S.E.; Szczesniak, P.; Lim, D. The Regional Economic Impact of an Earthquake: Direct and Indirect Effects of Electricity Lifeline Disruptions. J. Reg. Sci. 1997, 37, 437–458. [Google Scholar] [CrossRef]
- Tsuchiya, S.; Tatano, H.; Okada, N. Economic loss assessment due to railroad and highway disruptions. Econ. Syst. Res. 2007, 19, 147–162. [Google Scholar] [CrossRef]
- Okuyama, Y. Economic modeling for disaster impact analysis: Past, present, and future. Econ. Syst. Res. 2007, 19, 115–124. [Google Scholar] [CrossRef]
- Carrera, L.; Standardi, G.; Bosello, F.; Mysiak, J. Assessing direct and indirect economic impacts of a flood event through the integration of spatial and computable general equilibrium modelling. Environ. Model. Softw. 2015, 63, 109–122. [Google Scholar] [CrossRef]
- Mishan, E.J. The use of compensating and equivalent variations in cost-benefit analysis. Economica 1976, 43, 185–197. [Google Scholar] [CrossRef]
- Bishop, R.C.; Heberlein, T.A. Measuring values of extramarket goods: Are indirect measures biased? Am. J. Agric. Econ. 1979, 61, 926–930. [Google Scholar] [CrossRef]
- Signorello, G. La stima dei benefici di tutela di un’area naturale: Un’applicazione della Contingent Valuation. Genio Rural. 1990, 9, 21–35. [Google Scholar]
- Ietto, F.; Salvo, F.; Cantasano, N. The quality-of-life conditioning with reference to the local environmental management: A pattern in Bivona country (Calabria, Southern Italy). Ocean. Coast. Manag. 2014, 102, 340–349. [Google Scholar] [CrossRef]
- Cellerino, R. L’Italia delle alluvioni. In Un’analisi Economica; Franco Angeli: Milan, Italy, 2004. [Google Scholar]
- Molinari, D.; Aronica, G.T.; Ballio, F.; Berni, N.; Pandolfo, C. Le curve di danno quale strumento a supporto della direttiva alluvioni: Criticità dei dati italiani. In Proceedings of the XXXIII Convegno Nazionale di Idraulica e Costruzioni Idrauliche, Brescia, Italy, 10–15 September 2012. [Google Scholar]
- Schwarz, J.; Maiwald, H. Damage and loss prediction model based on the vulnerability of building types. In Proceedings of the 4th International Symposium on Flood Defence, Toronto, ON, Canada, 6–8 May 2008. [Google Scholar]
- Manganelli, B.; Vona, M.; De Paola, P. Evaluating the cost and benefits of earthquake protection of buildings. J. Eur. Real Estate Res. 2018, 11, 263–278. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P. Undivided real estate shares: Appraisal and interactions with capital markets. Appl. Mech. Mater. 2014, 584–586, 2522–2527. [Google Scholar] [CrossRef]
- Forte, F.; Antoniucci, V.; De Paola, P. Immigration and the Housing Market: The Case of Castel Volturno, in Campania Region, Italy. Sustainability 2018, 10, 343. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P.; Forte, F. The appraisal of office towers in bilateral monopoly’s market: Evidence from application of Newton’s physical laws to the directional centre of Naples. Int. J. Appl. Eng. Res. 2016, 11, 9455–9459. [Google Scholar]
- Del Giudice, V.; De Paola, P. The effects of noise pollution produced by road traffic of Naples Beltway on residential real estate values. Appl. Mech. Mater. 2014, 587–589, 2176–2182. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P. Geoadditive models for property market. Appl. Mech. Mater. 2014, 584–586, 2505–2509. [Google Scholar] [CrossRef]

| Damages Category | Tangible | Intangible |
|---|---|---|
| Direct | Damage to building structures and their contents, infrastructures, agriculture (e.g., soil erosion/harvest destruction), business goods, livestock, and land and environment recoveries. | Loss of life, injuries, psychological distress, cultural heritage damages, and negative effects on ecosystems. |
| Indirect | Business interruption, public services/utility interruption (e.g., communication systems), induced production losses to companies outside the flooded area (e.g., suppliers of flooded companies), traffic disruption costs, and tax revenue losses due to migration of companies in the aftermath of a flood. | Traumatic experiences, loss of trust in authorities, deteriorating health, and emotional damages. |
| T (Years) | Qc (m3/s) | S (Ha) | Dw (m3/s∙106) | l (km) |
|---|---|---|---|---|
| 5 | 300 | 120 1 | - | 0.4 2 |
| 10 | 400 | 240 1 | - | 0.8 2 |
| 20 | 500 | 360 | 1.4 | 1.2 |
| 30 | 600 | 660 | 4.6 | 2.2 |
| 50 | 700 | 900 | 9.2 | 3.0 |
| Items | Return Period of Events (Years) | ||||
|---|---|---|---|---|---|
| 5 | 10 | 20 | 30 | 50 | |
| Area of flood zones (Ha) | |||||
| 62 | 62 | 62 | 62 | 62 |
| - | - | - | - | - |
| 120 | 240 | 360 | 660 | 900 |
| 245 | 219 | 201 | 147 | 117 |
| Total: | 427 | 521 | 623 | 869 | 1.079 |
| Urban areas, network infrastructure areas, watercourses, and drainage canals (Ha) | 120 | 127 | 131 | 141 | 151 |
| Farm area (Ha) | 307 | 394 | 492 | 728 | 928 |
| Areas occupied by rural buildings, farm and farm roads, ditches, and drains and installations serving agricultural activity (Ha) | 18 | 24 | 28 | 44 | 55 |
| Usable agricultural area (Ha) | 289 | 370 | 464 | 684 | 873 |
| T (Years) | Qc (m3/s) | S (Ha) |
|---|---|---|
| 5 | 1300 | 333 1 |
| 10 | 1700 | 466 1 |
| 20 | 2000 | 466 |
| 30 | 2300 | 542 |
| 50 | 2700 | 612 |
| Items | Return Period of Events (Years) | ||||
|---|---|---|---|---|---|
| 5 | 10 | 20 | 30 | 50 | |
| Area of flood zones (Ha) | 333 | 466 | 542 | 612 | - |
| Urban areas, network infrastructure areas, watercourses, and drainage canals (Ha) | 33 | 46 | 46 | 52 | 62 |
| Farm area (Ha) | 300 | 420 | 420 | 490 | 550 |
| Areas occupied by rural buildings, farm and farm roads, ditches, and drains and installations serving agricultural activity (Ha) | 20 | 30 | 30 | 35 | 40 |
| Usable agricultural area (Ha) | 280 | 390 | 390 | 455 | 510 |
| Degrees of Event | Damages to Agricultural Productions (EUR·103) | Damages to Agricultural Structures (EUR·103) | Total (EUR·103) |
|---|---|---|---|
| Five years | 251.16 | 204.00 | 455.16 |
| Ten years | 340.61 | 224.66 | 565.27 |
| Twenty years | 400.52 | 246.35 | 646.87 |
| Thirty years | 578.14 | 250.48 | 828.62 |
| Fifty years | 750.69 | 254.61 | 1005.30 |
| Degrees of Event | Damages to Agricultural Productions (EUR·103) | Damages to Agricultural Structures (EUR·103) | Total (EUR·103) |
|---|---|---|---|
| Five years | 817.04 | 4338 | 821.37 |
| Ten years | 1025.17 | 6042 | 1031.21 |
| Twenty years | 1025.17 | 6042 | 1031.21 |
| Thirty years | 1092.31 | 6972 | 1099.28 |
| Fifty years | 1265.84 | 7902 | 1273.74 |
| Items | Size (m2) | Unit Cost (EUR/m2) | Value (EUR·103) |
|---|---|---|---|
| Dwellings | 94,400 | 361.52 | 34,127.49 |
| Commercial premises | 32,000 | 516.46 | 16,526.72 |
| Basement rooms | 31,600 | 118.78 | 3753.45 |
| Appurtenances | 29,600 | 103.29 | 3057.38 |
| Gardens 1 | 20,000 | 2.06 | 41.20 |
| Green areas 2 | 112,000 | 0.26 | 29.12 |
| Total: | 57,506.34 |
| Items | Exposed Area (sqm) | Unit Damage (EUR/sqm) | Total Damage (EUR·103) |
|---|---|---|---|
| Dwellings | 94,400 | 123.95 | 11,700.88 |
| Commercial premises | 32,000 | 123.95 | 3966.40 |
| Basement rooms | 31,600 | 30.99 | 979.28 |
| Appurtenances | 29,600 | 15.49 | 458.50 |
| Gardens | 20,000 | 0.52 | 10.40 |
| Green areas | 112,000 | 0.026 | 2.92 |
| Total: | 17,118.38 |
| Items | Amounts of Damages for Flood Event Degree (EUR·103) | ||||
|---|---|---|---|---|---|
| 5 | 10 | 20 | 30 | 50 | |
| Roads | 77.48 | 141.51 | 294.38 | 362.04 | 528.85 |
| Aqueducts | 5.16 | 8.78 | 17.04 | 21.17 | 29.95 |
| Sewer mains | 5.68 | 8.26 | 15.49 | 20.14 | 28.40 |
| Sewers | - | - | 1.03 | 1.55 | 2.06 |
| Buried power lines | 1.03 | 2.58 | 5.16 | 7.75 | 10.84 |
| Buried telephone lines | 1.03 | 2.06 | 3.61 | 5.68 | 8.26 |
| Reclamation canals | 61.97 | 107.42 | 149.77 | 193.15 | 264.42 |
| Total: | 152.35 | 260.71 | 486.48 | 611.48 | 872.78 |
| Items | Amounts of Damages for Flood Event Degree (EUR·103) | ||||
|---|---|---|---|---|---|
| 5 | 10 | 20 | 30 | 50 | |
| Roads | 82.12 | 113.10 | 113.10 | 128.60 | 150.81 |
| Aqueducts | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 |
| Reclamation canals | 44.42 | 63.52 | 63.52 | 71.79 | 82.12 |
| Irrigation network | 37.70 | 52.16 | 52.16 | 60.94 | 69.21 |
| Total: | 165.27 | 229.82 | 229.82 | 262.36 | 303.16 |
| Sector | Amounts of Damages for Flood Event Degree (EUR·103) | ||||
|---|---|---|---|---|---|
| 5 | 10 | 20 | 30 | 50 | |
| Agriculture | 455.00 | 565.00 | 646.60 | 828.40 | 1005.02 |
| Urban areas | 17,118.48 | 17,118.48 | 17,118.48 | 17,118.48 | 17,118.48 |
| Network infrastructures | 152.35 | 270.62 | 486.50 | 611.48 | 872.81 |
| Total: | 17,725.83 | 17,954.10 | 18,251.58 | 18,558.36 | 19,002.31 |
| Sector | Amounts of Damages for Flood Event Degree (EUR·103) | ||||
|---|---|---|---|---|---|
| 5 | 10 | 20 | 30 | 50 | |
| Agriculture | 821.16 | 1031.21 | 1031.21 | 1099.28 | 1273.74 |
| Network infrastructures | 165.27 | 229.82 | 229.82 | 262.36 | 303.16 |
| Total: | 986.38 | 1261.19 | 1261.19 | 1361.38 | 1577.26 |
| Return Period of Flood Events (Years) | Flooded Area (Ha) |
|---|---|
| 5 | 120 (*) |
| 10 | 240 (*) |
| 20 | 360 |
| 30 | 660 |
| 50 | 900 |
| 100 | 1140 |
| 200 | 1350 |
| Return Period of Flood Events (Years) | Total Damage (EUR·103) |
|---|---|
| 10 | 17,946.88 |
| 20 | 18,363.66 |
| 30 | 18,607.94 |
| 50 | 18,915.23 |
| Return Period of Flood Events (Years) | Flooded Area (Ha) |
|---|---|
| 5 | 333 |
| 10 | 466 |
| 20 | 466 |
| 30 | 542 |
| 50 | 612 |
| 100 | 759 (*) |
| Return Period of Flood Events (years) | Total Damage (EUR·103) |
|---|---|
| 10 | 1,046,858 |
| 30 | 1,335,557 |
| 50 | 1,499,791 |
| Characteristic | Category | Albanella | Altavilla Silentina | Capaccio | Eboli | Serre |
|---|---|---|---|---|---|---|
| Number of Interviewees | ||||||
| Age | 0–19 | 4 | 1 | 5 | 3 | 3 |
| 20–34 | 5 | 15 | 11 | 13 | 10 | |
| 35–49 | 15 | 7 | 9 | 10 | 15 | |
| 50–64 | 6 | 11 | 12 | 9 | 11 | |
| >65 | 12 | 8 | 5 | 7 | 3 | |
| Gender | Male | 15 | 18 | 21 | 21 | 19 |
| Female | 27 | 24 | 21 | 21 | 23 | |
| Education Level | Bachelor’s degree | 4 | 2 | 3 | 8 | 4 |
| High school degree | 10 | 17 | 18 | 21 | 18 | |
| Middle school degree | 15 | 14 | 13 | 8 | 18 | |
| Elementary degree | 13 | 9 | 8 | 5 | 2 | |
| Literate | 0 | 0 | 0 | 0 | 0 | |
| Illiterate | 0 | 0 | 0 | 0 | 0 | |
| Occupation | Craft, manual, or agricultural professions | 15 | 13 | 14 | 9 | 13 |
| Professions with a low level of competence | 17 | 20 | 15 | 19 | 22 | |
| Professions with a high–medium level of specialization | 7 | 9 | 10 | 12 | 7 | |
| Unemployed | 3 | 0 | 3 | 2 | 0 | |
| Income Level | <10,000 | 0 | 0 | 1 | 1 | 2 |
| 10,000–15,000 | 19 | 15 | 22 | 17 | 19 | |
| 15,000–26,000 | 8 | 12 | 10 | 5 | 9 | |
| 26,000–55,000 | 8 | 10 | 7 | 11 | 8 | |
| 55,000–75,000 | 7 | 4 | 2 | 6 | 4 | |
| 75,000–120,000 | 0 | 1 | 0 | 1 | 0 | |
| >120,000 | 0 | 0 | 0 | 1 | 0 | |
| Donation Amount (EUR) | Size of the Sub-Sample | Number of Responses | |
|---|---|---|---|
| YES | NO | ||
| 2.58 | 12 | 11 | 1 |
| 5.16 | 15 | 13 | 2 |
| 10.33 | 14 | 12 | 2 |
| 12.91 | 12 | 9 | 3 |
| 15.49 | 14 | 10 | 4 |
| 18.07 | 9 | 6 | 3 |
| 20.66 | 20 | 12 | 5 |
| 25.82 | 11 | 6 | 5 |
| 30.99 | 9 | 4 | 5 |
| 36.15 | 16 | 6 | 10 |
| 41.32 | 8 | 2 | 6 |
| 46.48 | 10 | 2 | 8 |
| 51.64 | 10 | 2 | 8 |
| 64.55 | 24 | 4 | 20 |
| 77.47 | 16 | 2 | 14 |
| 103.29 | 10 | 1 | 9 |
| Variable | Model I | Model II | Model III |
|---|---|---|---|
| Constant | 1.585248 | 1.578688 | 15.033495 |
| Donation | −0.00025 | ||
| ln (1-donation/income) | 321.959046 | ||
| ln (donation) | −1.405207 |
| Probability of Truncation of the Distribution | ||||
|---|---|---|---|---|
| Prob. (Xmax) a | Prob. (0.100) | Prob. (0.050) | Prob. (0.010) | |
| Model I | 43.94 | 41.384 | 42.823 | 43.850 |
| 0.00043 * | 0.00043 * | 0.00043 * | 0.00043 * | |
| 35.930 ** | 34.422 ** | 35.539 ** | 36.391 ** | |
| 103.291 *** | 78.139 *** | 93.575 *** | 127.675 *** | |
| Model II | 44.069 | 42.297 | 43.662 | 44.700 |
| 0.00043 * | 0.00043 * | 0.00043 * | 0.00043 * | |
| 36.534 ** | 35.064 ** | 36.196 ** | 37.056 ** | |
| 103.291 *** | 79.578 *** | 95.215 *** | 129.632 *** | |
| Model III | 35.109 | 35.721 | 41.102 | 50.005 |
| 103.291 *** | 109.238 *** | 185.913 *** | 601.811 *** | |
| (Years) | (Ha) | (EUR·103) | (N) | (EUR·103) |
|---|---|---|---|---|
| 5 | 333 | 540.730 | 10 | 5407.304 |
| 10 | 466 | 757.126 | 5 | 3785.629 |
| 20 | 466 | 757.126 | 2 | 1514.252 |
| 30 | 542 | 880.559 | 1 | 880.559 |
| 50 | 763 | 1239.496 | 1 | 1239.496 |
| D = 12,827.240 |
| Return Period of Flood Events (years) | Amount of Damage (EUR·103) | Divergence (%) | |
|---|---|---|---|
| T-Dp Model | Direct Appraisal | ||
| 10 | 17,946.88 | 17,954.10 | 0.04 |
| 20 | 18,363.66 | 18,251.58 | 0.61 |
| 30 | 18,607.94 | 18,558.36 | 0.27 |
| 50 | 18,915.23 | 19,002.31 | 0.46 |
| Return Period of Flood Events (Years) | Amount of Damage (EUR·103) | Divergence (%) | |
|---|---|---|---|
| T-Dp Model | Direct Appraisal | ||
| 10 | 1,046,858 | 1261.19 | 20.47 |
| 30 | 1,335,557 | 1361.38 | 1.93 |
| 50 | 1,499,791 | 1577.26 | 5.17 |
| Return Period of Flood Events (Years) | Amount of Damage (EUR·103) |
|---|---|
| 15 | 18,190.640 |
| 25 | 18,497.950 |
| 35 | 18,700.390 |
| 40 | 18,780.950 |
| 45 | 18,851.190 |
| 100 | 19,332.010 |
| 200 | 19,748.790 |
| Return Period of Flood Events (Years) | Amount of Damage (EUR·103) |
|---|---|
| 25 | 1281.846 |
| 35 | 1383.071 |
| 40 | 1425.421 |
| 45 | 1464.155 |
| 100 | 1760.805 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Giudice, V.; Salvo, F.; De Paola, P.; Del Giudice, F.P.; Tavano, D. Ex-Ante Flooding Damages’ Monetary Valuation Model for Productive and Environmental Resources. Water 2024, 16, 665. https://doi.org/10.3390/w16050665
Del Giudice V, Salvo F, De Paola P, Del Giudice FP, Tavano D. Ex-Ante Flooding Damages’ Monetary Valuation Model for Productive and Environmental Resources. Water. 2024; 16(5):665. https://doi.org/10.3390/w16050665
Chicago/Turabian StyleDel Giudice, Vincenzo, Francesca Salvo, Pierfrancesco De Paola, Francesco Paolo Del Giudice, and Daniela Tavano. 2024. "Ex-Ante Flooding Damages’ Monetary Valuation Model for Productive and Environmental Resources" Water 16, no. 5: 665. https://doi.org/10.3390/w16050665
APA StyleDel Giudice, V., Salvo, F., De Paola, P., Del Giudice, F. P., & Tavano, D. (2024). Ex-Ante Flooding Damages’ Monetary Valuation Model for Productive and Environmental Resources. Water, 16(5), 665. https://doi.org/10.3390/w16050665











