Extreme Flood Flow Routing for Panchet and Maithan Reservoirs of India Using Modified Puls Technique
Abstract
1. Introduction
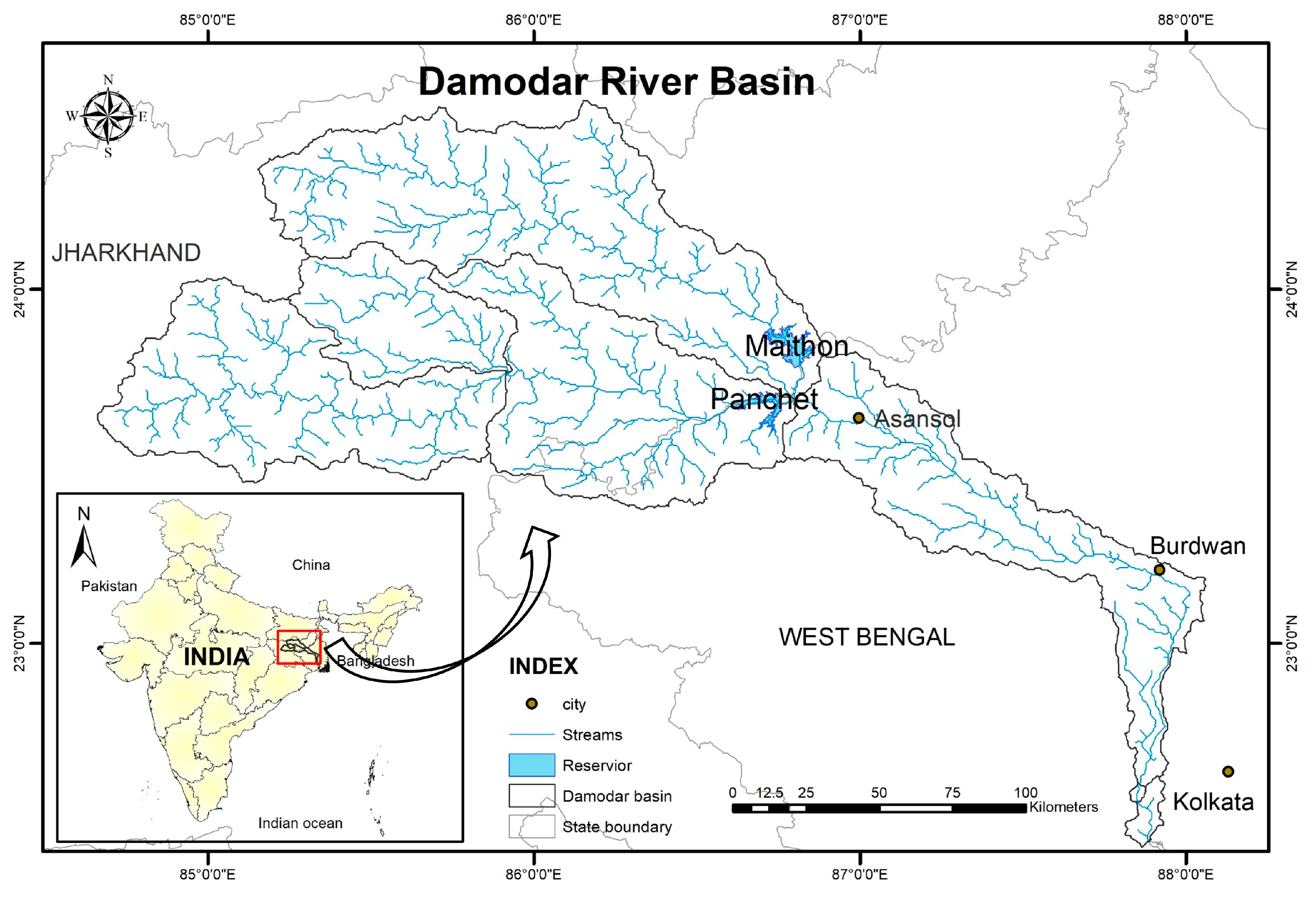
2. Study Area
3. Database and Methodology
- ○
- From the storage-elevation and discharge-elevation data, (S + Q∆t/2) versus elevation and discharge versus elevation curves are prepared.
- ○
- The storage, elevation, and discharge at the start of routing are known, and (S − Q∆t/2) is determined.
- ○
- Starting from this value of (S − Q∆t/2) and from Equation (6), the term (S + Q∆t/2) is determined at the end of the first time step ∆t.
- ○
- From the discharge versus elevation and (S + Q∆t/2) versus elevation curves, water-surface elevation corresponding to (S + Q∆t/2) and outflow discharges are determined.
- ○
- Deducting Q∆t from (S + Q∆t/2) of the previous step gives (S − Q∆t/2) for the beginning of the next time step.
- ○
- The procedure is repeated until the entire outflow hydrograph is routed.
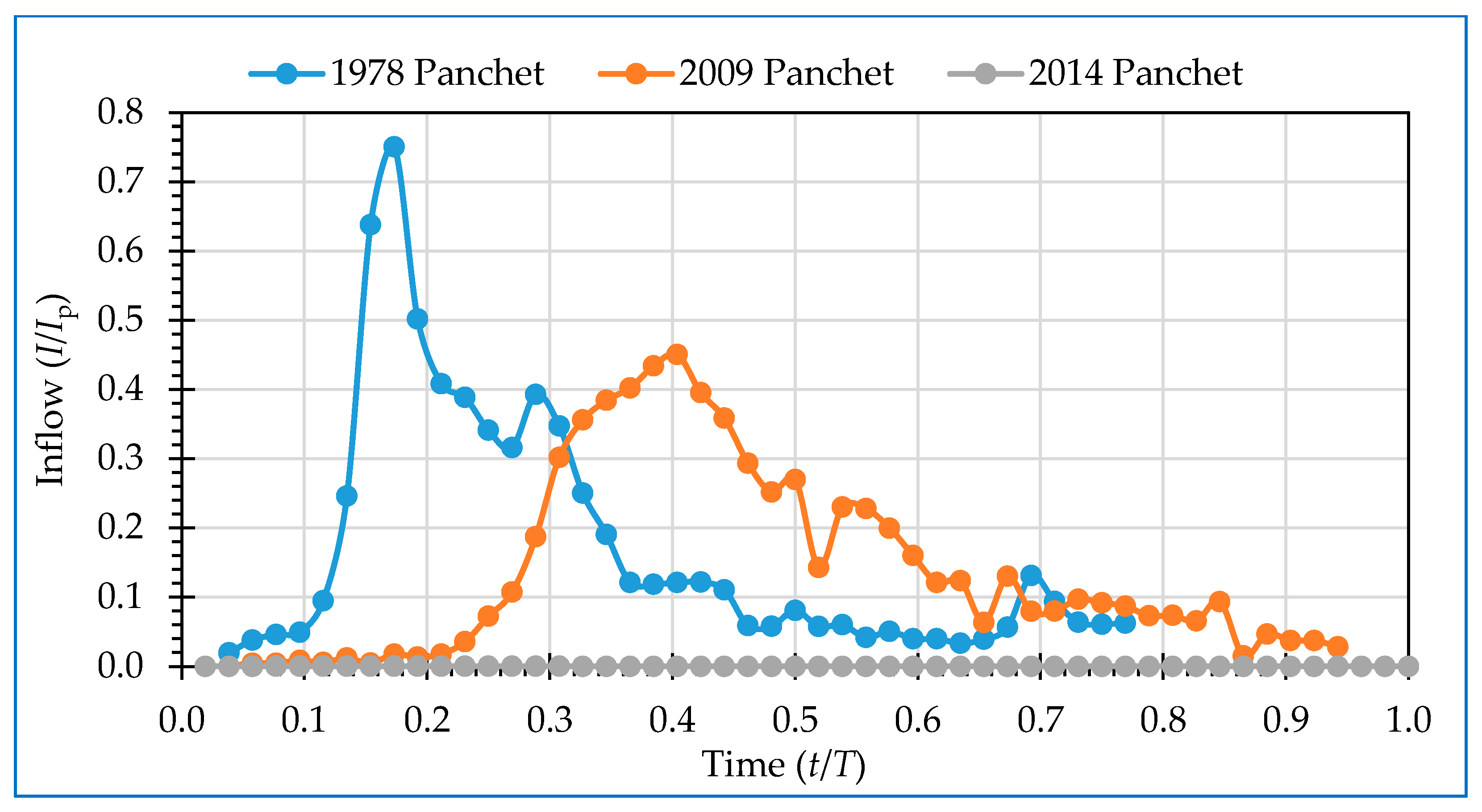
4. Results and Discussion
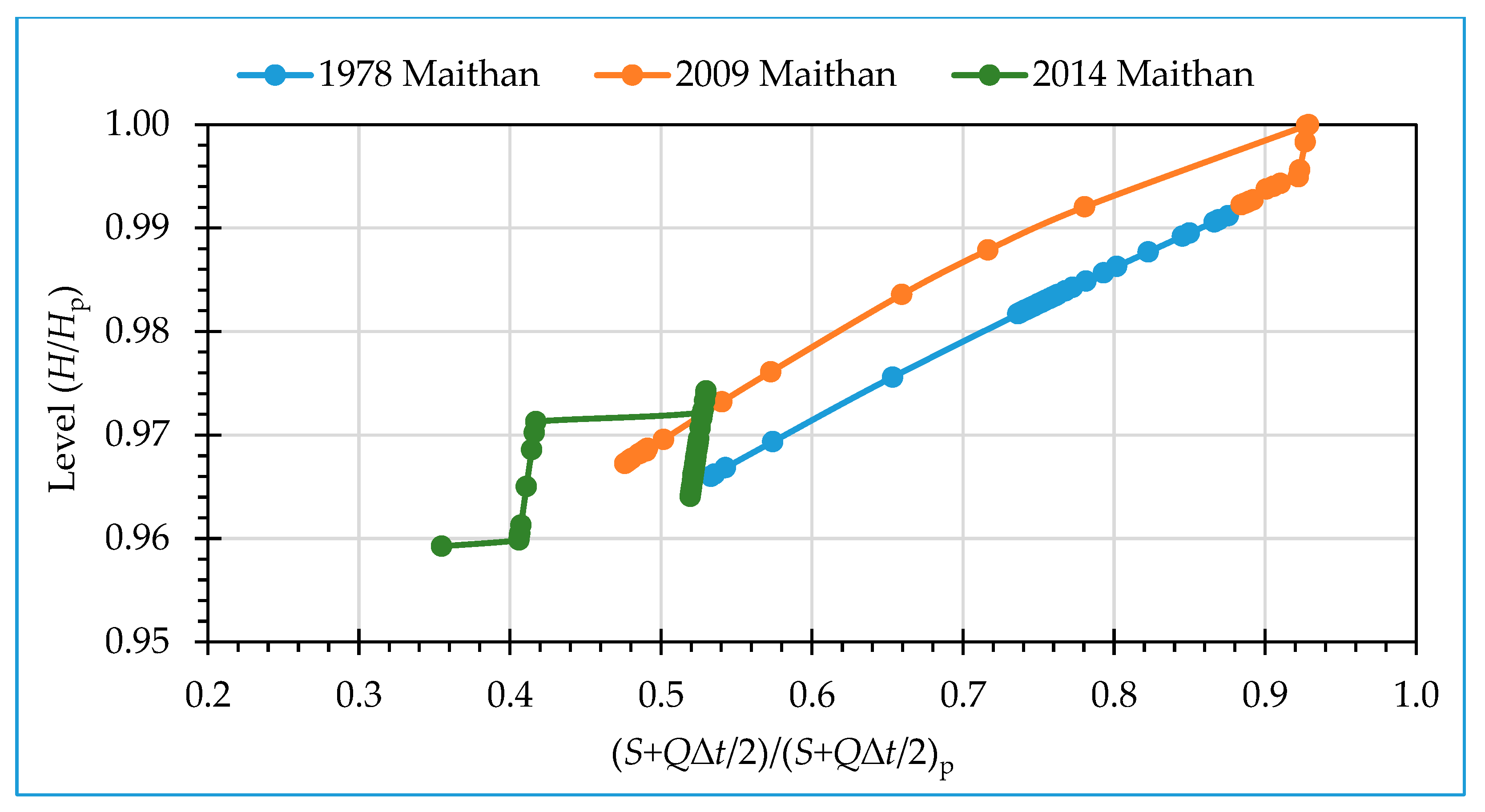
4.1. Storage Calculation
4.2. Determine Discharge Equations Based on Reservoir Characteristics
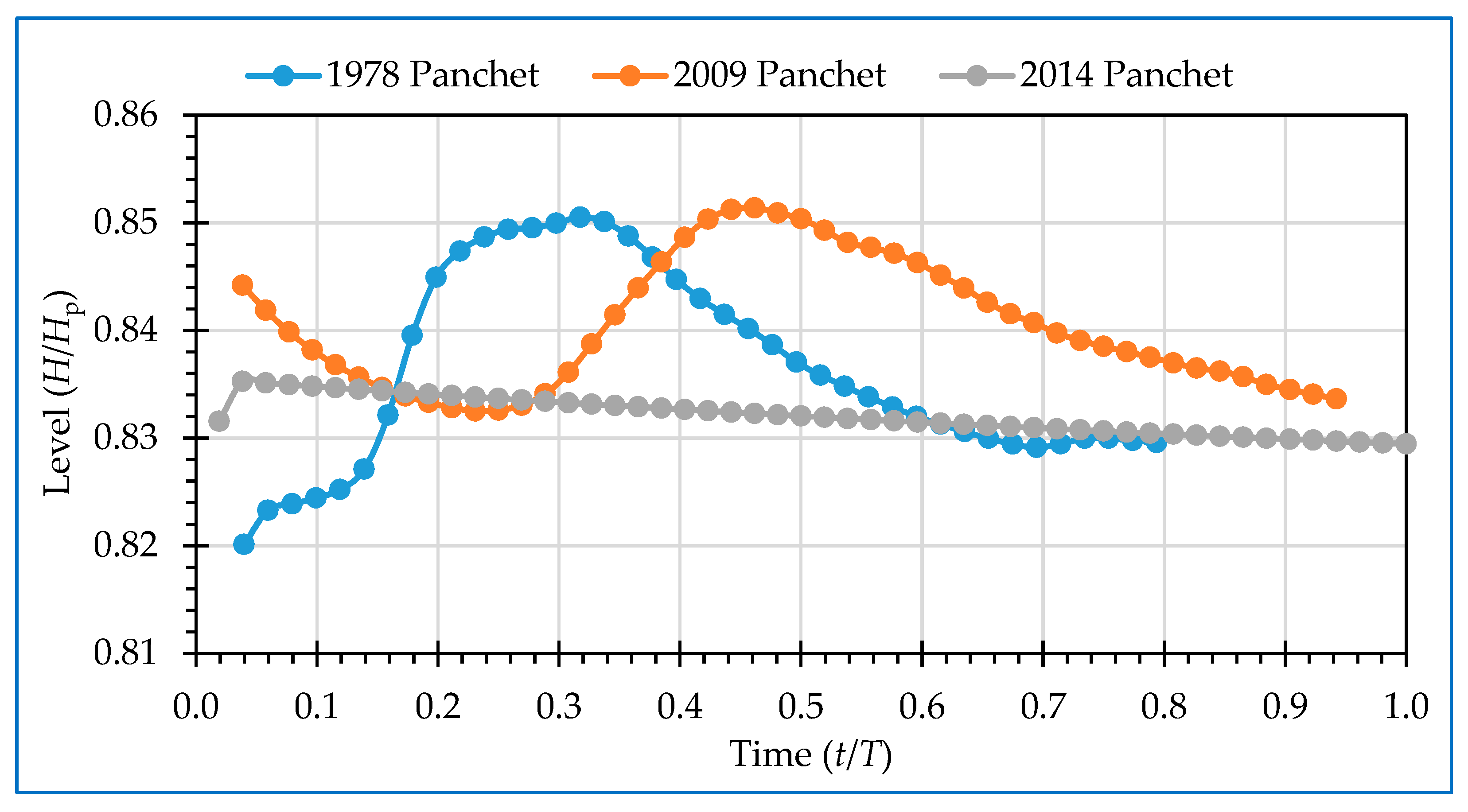
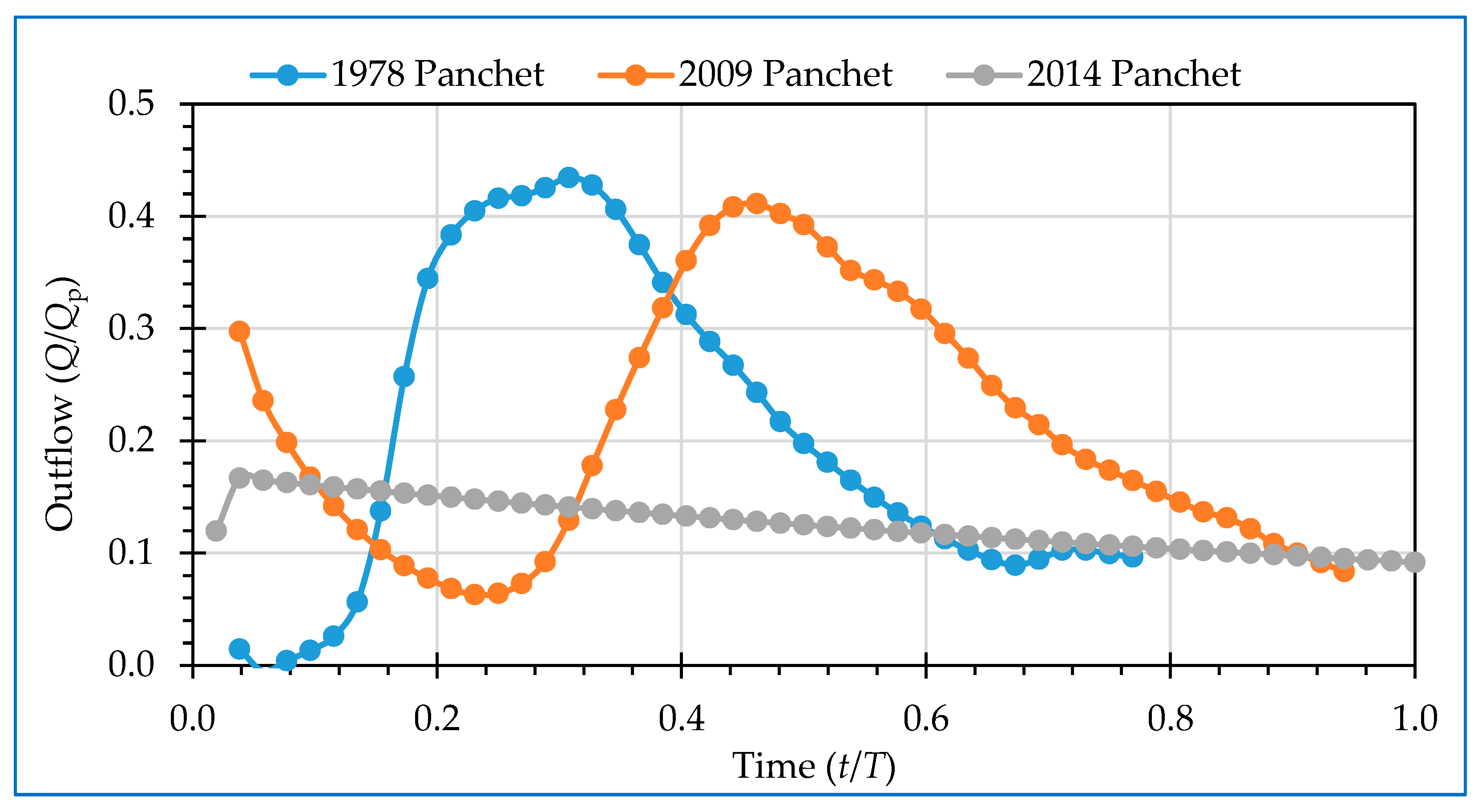
4.3. Reservoir Routing by Modified Puls Technique
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Clark, C.O. Storage and The Unit Hydrograph. Am. Soc. Civ. Eng. Trans. 1943, 110, 1419–1446. [Google Scholar] [CrossRef]
- Chow, V.T. A Practical Procedure of Flood Routing. In Civil Engineering Studies. Hydraulic Engineering Series No. 1, Civil Engineering and Public Works Review; CORE: London, UK, 1951; Volume 46. [Google Scholar]
- Nash, J.E. A note on the Muskingum flood-routing method. J. Geophys. Res. 1959, 64, 1053–1056. [Google Scholar] [CrossRef]
- Carter, R.W.; Godfrey, R.G. Storage and Flood Routing. In Manual of Hydrology: Part 3. Flood-Flow Techniques; Geological Survey Water-Supply: Washington, DC, USA, 1960; p. 1543-B. [Google Scholar] [CrossRef]
- Overton, D.E. Muskingum flood routing of upland streamflow. J. Hydrol. 1966, 4, 185–200. [Google Scholar] [CrossRef]
- Gill, M.A. Flood routing by the Muskingum method. J. Hydrol. 1978, 36, 353–363. [Google Scholar] [CrossRef]
- Weinmann, P.E.; Laurenson, E.M. Approximate Flood Routing Methods: A Review. J. Hydraul. Div. 1979, 105, 1521–1536. [Google Scholar] [CrossRef]
- Tung, Y.K. River Flood Routing by Nonlinear Muskingum Method. J. Hydraul. Eng. 1985, 111, 1460–1477. [Google Scholar] [CrossRef]
- Becker, A.; Kundzewicz, Z.W. Nonlinear flood routing with multilinear models. Water Resour. Res. 1987, 23, 1043–1048. [Google Scholar] [CrossRef]
- Ponce, V.M. Chapter of Reservoir Routing. In Engineering Hydrology; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; pp. 252–260. [Google Scholar]
- Fenton, J.D. Reservoir routing. Hydrol. Sci. J. 1992, 37, 233–246. [Google Scholar] [CrossRef]
- Bacchi, B.; Brath, A.; Nath, K.T. Analysis of the relationships between flood peaks and flood volumes based on crossing properties of river flow processes. Water Resour. Res. 1992, 28, 2773–2782. [Google Scholar] [CrossRef]
- Khan, H.M. Muskingum flood routing model for multiple tributaries. Water Resour. Res. 1993, 29, 1057–1062. [Google Scholar] [CrossRef]
- Calver, A.; Lamb, R. Flood frequency estimation using continuous rainfall-runoff modelling. Phys. Chem. Earth 1995, 20, 479–483. [Google Scholar] [CrossRef]
- Hicks, F.E. Hydraulic flood routing with minimal channel data: Peace River, Canada. Can. J. Civil Eng. 1996, 23, 524–535. [Google Scholar] [CrossRef]
- Guo, Y.; Adams, B.J. An analytical probabilistic approach to sizing flood control detention facilities. Water Resour. Res. 1999, 35, 2457–2468. [Google Scholar] [CrossRef]
- Choudhury, P.; Shrivastava, R.K.; Narulkar, S.M. Flood Routing in River Networks Using Equivalent Muskingum Inflow. J. Hydrol. Eng. 2002, 7, 413–419. [Google Scholar] [CrossRef]
- Gou, J.C.Y. Hydrology-Based Approach to Storm Water Detention Basin Design Using New Routing Schemes. J. Hydrol. Eng. 2004, 9, 333–336. [Google Scholar] [CrossRef]
- Blazkov, S.D.; Beven, K. Flood frequency estimation by continuous simulation of subcatchment rainfalls and discharges with the aim of improving dam safety in a large basin in the Czech Republic. J. Hydrol. 2004, 292, 153–172. [Google Scholar] [CrossRef]
- Tewolde, M.H.; Smithers, J.C. Flood routing in ungauged catchments using Muskingum methods. Water SA 2006, 32, 379–388. [Google Scholar] [CrossRef]
- Samani, J.M.V.; Heydari, M. Reservoir Routing through Successive Rockfill Detention Dams. J. Agric. Sci. Technol. 2007, 9, 317–326. [Google Scholar]
- Sivapragasam, C.; Maheswaran, R.; Venkatesh, V. Genetic programming approach for flood routing in natural channels. Hydrol. Process. 2007, 22, 623–628. [Google Scholar] [CrossRef]
- Singh, K.P.; Durgunoglu, A. A new method for estimating future reservoir storage capacity. J. Am. Water Resour. Assoc. 2007, 25, 263–274. [Google Scholar] [CrossRef]
- Requena, A.I.; Mediero, L.; Garrot, L. A bivariate return period based on copulas for hydrologic dam design: Accounting for reservoir routing in risk estimation. Hydrol. Earth Syst. Sci. 2013, 17, 3023–3038. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Barbetta, S.; Brocca, L.; Moramarco, T. River Discharge Estimation by Using Altimetry Data and Simplified Flood Routing Modeling. Remote Sens. 2013, 5, 4145–4162. [Google Scholar] [CrossRef]
- Kim, D.H.; Georgakakoset, A.P. Hydrologic routing using nonlinear cascaded reservoirs. Water Resour. Res. 2014, 50, 7000–7019. [Google Scholar] [CrossRef]
- Hossain, M.M. Analysis of Flood Routing. Dhaka Univ. J. Sci. 2015, 62, 69–73. [Google Scholar] [CrossRef]
- Bharali, B. Estimation of Reservoir Storage Capacity by using Residual Mass Curve. J. Civil Eng. Environ. Technol. 2015, 2, 15–18. [Google Scholar]
- Gioia, A. Reservoir Routing on Double-Peak Design Flood. Water 2016, 8, 553. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, X. Evaluating the Effects of Low Impact Development Practices on Urban Flooding under Different Rainfall Intensities. Water 2017, 9, 548. [Google Scholar] [CrossRef]
- Balistrocchi, M.; Roberto, R.; Stefano, O.; Baldassare, B. Flood Routing Efficiency Assessment: An Approach Using Bivariate Copulas. In Proceedings of the 13th International Conference on Hydroinformatics (HIC 2018), Palermo, Italy, 1–6 July 2018; Volume 3, pp. 1–8. [Google Scholar] [CrossRef][Green Version]
- Husain, A. Flood Routing in Reservoir using Modified Puls Method. Int. J. Sci. Res. 2018, 7, 1187–1194. [Google Scholar]
- Pandey, R.; Kumar, V.; Pandey, R.D. Analysis of Flood Routing in Channels. Int. J. Eng. Dev. Res. 2018, 6, 11–18. [Google Scholar]
- Sane, M.L.; Sombou, S.; Leye, I.; Ndione, D.M.; Kane, S.; Tamba, S.; Diatta, M. A New Approach of the Estimation of the Parameters of the Linear Muskingum Model for River Flow Simulation. Moussé Land. Sane J. Eng. Res. Appl. 2018, 8, 20–27. [Google Scholar]
- Gutenson, J.L.; Tavakoly, A.A.; Wahl, M.D.; Follum, M.L. Comparison of Generalized Non-Data-Driven Reservoir Routing Models for Global-Scale Hydrologic Modeling. Hydrol. Earth Syst. Sci. 2019, 24, 2711–2729. [Google Scholar] [CrossRef]
- Badanapuri, V.R. Design Principles that are involved in the Design of Flow over an Ogee Crest Spillway. Int. J. Sci. Res. 2019, 8, 245–254. [Google Scholar]
- Roy, D.; Mukherjee, S.; Bose, B. Regulation of a multipurpose reservoir system: Damodar Valley, India. In Man’s Influence on Freshwater Ecosystems and Water Use; Proceedings of a Boulder Symposium; International Association of Hydrological Sciences: Montpellier, France, 1995. [Google Scholar]
- Jana, S.; Das, M.; Roy, D.; Das, S.; Mazumdar, A. Simulation of climate change impact in a river basin in Eastern India. Int. J. Hydrol. Sci. Technol. 2015, 5, 314–332. [Google Scholar] [CrossRef]
- Jana, S.; Dutta, S.; Das, S.; Roy, D. Uncertainty in Hydrologic Response of a River Basin in India to Changed Climate Scenario. Water Energy Int. 2018, 61, 68–75. [Google Scholar]
- Chaudhuri, D. Damodar River Valley: An Indian Parallel to The Tennessee River Valley. J. Hydraul. Eng. 2000, 126, 395–397. [Google Scholar] [CrossRef]
- Chaudhuri, D. Life of Maithon Reservoir on Ground of Sedimentation: Case Study in India. J. Hydraul. Eng. 2006, 132, 875–880. [Google Scholar] [CrossRef]
- Mani, P.; Chakravorty, B. Dam break flood simulation for Maithon and Panchet dams using NWS DAMBRK model and inundation mapping. J. Inst. Eng. 2008, 89, 16–19. [Google Scholar]
- Bhattacharyya, K. The Lower Damodar River India Understanding the Human Role in Changing Fluvial Environment; Springer: Dordrecht, The Netherlands; Berlin/Heidelberg, Germany; New York, NY, USA, 2012. [Google Scholar]
- Chaudhuri, D. Evaluation of Maithon Reservoir Performance. Master’s, Dissertation, Department of Hydrology, Indian Institute of Technology, Roorkee, India, 2012. [Google Scholar]
- Chaudhuri, D.; Banerjee, S. Reservoir Sedimentation and its Remedies. In Proceedings of the Conference India Water Week 2013, New Delhi, India, 8–12 April 2013; pp. 1–19. [Google Scholar]
- Sanyal, J.; Carbonneau, P.; Densmore, A.L. Hydraulic routing of extreme floods in a large ungauged river and the estimation of associated uncertainties: A case study of the Damodar River, India. Nat. Hazard. 2013, 66, 1153–1177. [Google Scholar] [CrossRef]
- Ghosh, S.; Mistri, B. Performance of D.V.C. in Flood Moderation of Lower Damodar River, India and Emergent Risk of Flood. East. Geogr. 2013, XIX, 55–66. [Google Scholar]
- Mukherjee, B.; Das, S.; Mazumdar, A. Mathematical analysis for the loss of future storage capacity at Maithon reservoir, India. ARPN J. Eng. Appl. Sci. 2013, 8, 841–845. [Google Scholar]
- Chatterjee, M.; Roy, D.; Das, S.; Mazumder, A. Assessment of Water Resources Under Climate Change: Damodar River Basin, India. ARPN J. Eng. Appl. Sci. 2014, 9, 2183–2191. [Google Scholar]
- Biswas, S.S. Multipurpose Projects Serve as a Flood Controller- Is this the Reality? A Study of DVC Projects of the Damodar River of West Bengal, India. J. Environ. Earth Sci. 2015, 5, 70–79. [Google Scholar]
- IMD. 2017. Available online: https://idup.gov.in/site/writereaddata/siteContent/IDUP-14-09-17/Maithon-Dam-Design-Flood-Estimation.pdf (accessed on 11 February 2023).
- Islam, A.; Sarkar, B. Analysing flood history and simulating the nature of future floods using Gumbel method and Log-Pearson Type III: The case of the Mayurakshi River Basin, India. Bull. Geogr. Phys. Geogr. Ser. 2020, 19, 43–69. [Google Scholar] [CrossRef]
- IS 6934-1998; Hydraulic Design of High Ogee Overflow Spillways—Recommendations. First Revision, Reaffirmed 2003. Bureau of Indian Standards: New Delhi, India, 1998.
- Subramanya, K. Engineering Hydrology, 4th ed.; McGraw Hill Education (India) Private Limited: New Delhi, India, 2013. [Google Scholar]
- Mukherjee, B.; Das, S.; Mazumdar, A. Environmental Study and Analysis of Silts Deposition at Maithon Reservoir. Indian J. Environ. Prot. 2015, 35, 177–187. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dasgupta, M.; Das, S. Extreme Flood Flow Routing for Panchet and Maithan Reservoirs of India Using Modified Puls Technique. Water 2024, 16, 663. https://doi.org/10.3390/w16050663
Dasgupta M, Das S. Extreme Flood Flow Routing for Panchet and Maithan Reservoirs of India Using Modified Puls Technique. Water. 2024; 16(5):663. https://doi.org/10.3390/w16050663
Chicago/Turabian StyleDasgupta, Mayuree, and Subhasish Das. 2024. "Extreme Flood Flow Routing for Panchet and Maithan Reservoirs of India Using Modified Puls Technique" Water 16, no. 5: 663. https://doi.org/10.3390/w16050663
APA StyleDasgupta, M., & Das, S. (2024). Extreme Flood Flow Routing for Panchet and Maithan Reservoirs of India Using Modified Puls Technique. Water, 16(5), 663. https://doi.org/10.3390/w16050663






