1. Introduction
The dam had functions such as flood control, irrigation, and power generation. However, as a relatively large man-made structure, the dam needed regular maintenance [
1,
2,
3]. On the one hand, this extended its service life. On the other hand, it reduced the impact of other disasters on the safety of the dam. The safety assessment of the dam was an ongoing process that required the establishment of a system for regular monitoring and evaluation to technologically assess any potential abnormal conditions [
4,
5,
6]. These assessments helped identify issues in the operation and maintenance of the dam and addressed them specifically based on the assessment results to enable the dam to quickly return to normal operational status. The scope, depth, and subsequent measures of dam safety assessment depended on factors affecting dam safety, including but not limited to categories of dam disaster risks related to casualties and economic losses; the size, type, height, and water storage capacity of the dam; and the operational status and performance of the dam over the past several years, as well as engineering evaluations of its integrity [
7].
Since dam failure posed a serious danger to people and property located downstream, the safety assessment of dams gained more and more attention. Wang et al. [
8] proposed an improved variable weight AHP method to overcome the effect of the subjectivity and blindness of the equilibrium coefficient in the traditional method on the final result. Taking the Mamiao Reservoir as an example, the secondary index variable weight, the scores of primary indicators, and the comprehensive score of the overall objective were compared based on the traditional variable weight AHP and the proposed method. The results indicated that the scores of dams based on the constant weight, traditional variable weight, and modified variable weight methods were 79.70, 79.05, and 77.95, respectively. The proposed method in this study avoided the imbalance problem in the traditional variable weight AHP method. It also reduced the blindness caused by the equal balance coefficient of the secondary indicators and improved the accuracy of the evaluation results. Wang et al. [
9] presented a multi-source information evaluation model based on the D-S evidence theory for dam safety assessment. The multiple sources of evidence indicators included monitoring data, numerical simulation, field surveys, and mechanical tests. The Euclidean weighted method was used to determine the quality allocation function for relevant levels; then, the weights of evidence indicators were calculated based on the comparative method and entropy method. Taking the earth-fill dam as an example, the implementation process of the proposed method was illustrated. The results showed that the geological structure and overlying rock lithology were the most significant qualitative indicators. The weights for water level and dam settlement were 0.44161 and 0.2213, respectively. Furthermore, the observation information that obtained the weight of 0.4981 was the most important factor to reflect the operational status of the dam. The comprehensive judgment indicated that the dam was in a relatively unsafe state, which was consistent with the safety assessment conclusion. Thus, the effectiveness of the proposed method was validated. Samaras et al. [
10] used the AHP and the Elimination Et Shoix Traduisant La Realite (ELECTRE) I methods to assess the risk of earth-fill dams. The advantages and disadvantages of the two methods were compared by assessing the risks of three dams. The results indicated that the overall performances of the three dams were 0.35, 0.31, and 0.34, respectively. The risk level of the first dam in Aghia Paraskevi, Chasia, was the highest, followed by the third dam; the risk level of the second dam was the lowest based on the AHP method. However, according to the ELECTRE I method, the risk level of the third dam was the lowest. Landslides, floods, and internal erosion were the greatest risk sources for the first, second, and third dams, respectively. Both methods indicated that internal erosion was a very important risk source when taking three dams as an aggregate. Although there was considerable research on dam safety assessment, many scholars tended to use a single method (i.e., SWM or OWM) to assign weights to various indicators of dams and then obtain the final safety level. These approaches easily led to inaccurate evaluation results. Additionally, the current standard for dam safety assessment in China only provided the qualitative analysis methodology, which resulted in unreliable assessment [
11].
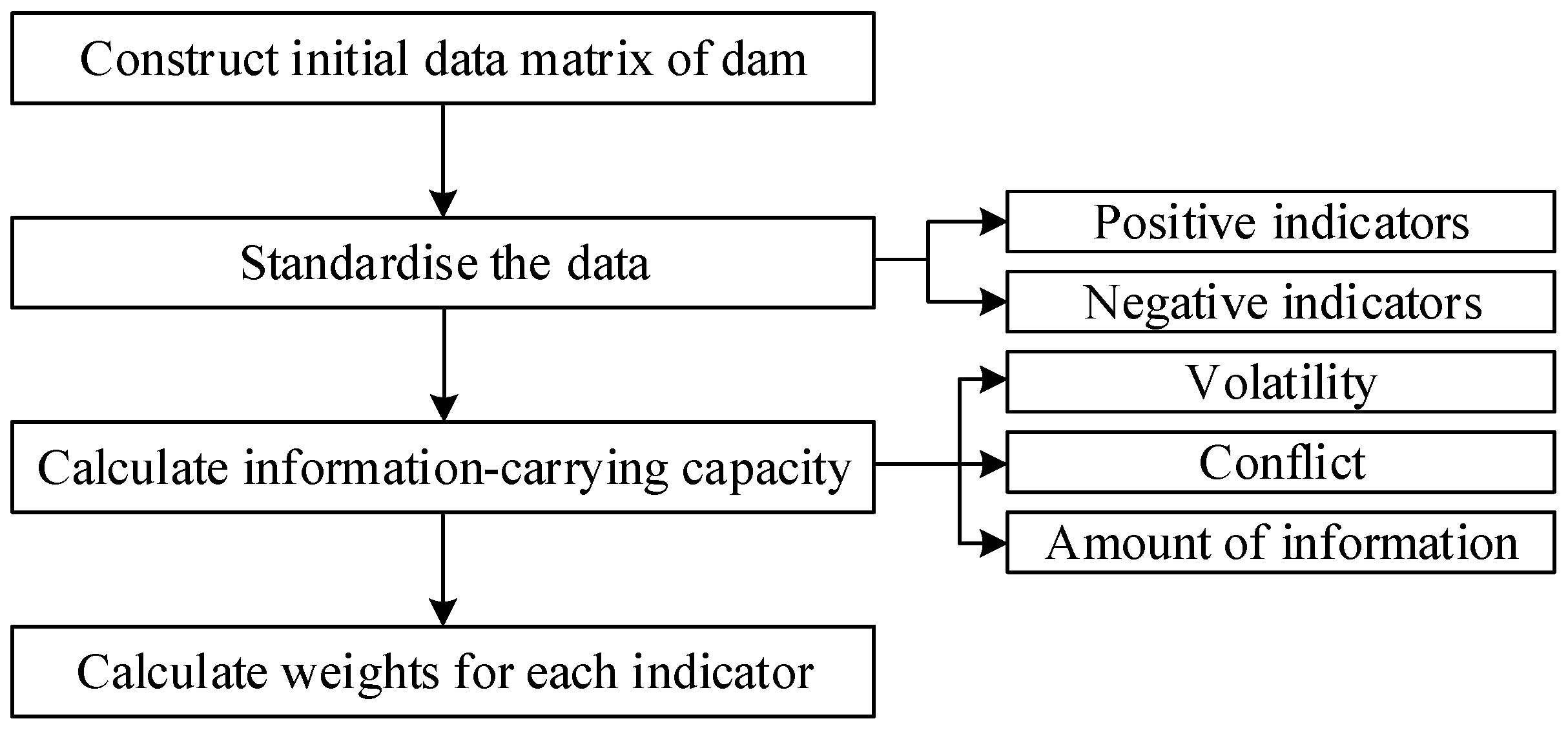
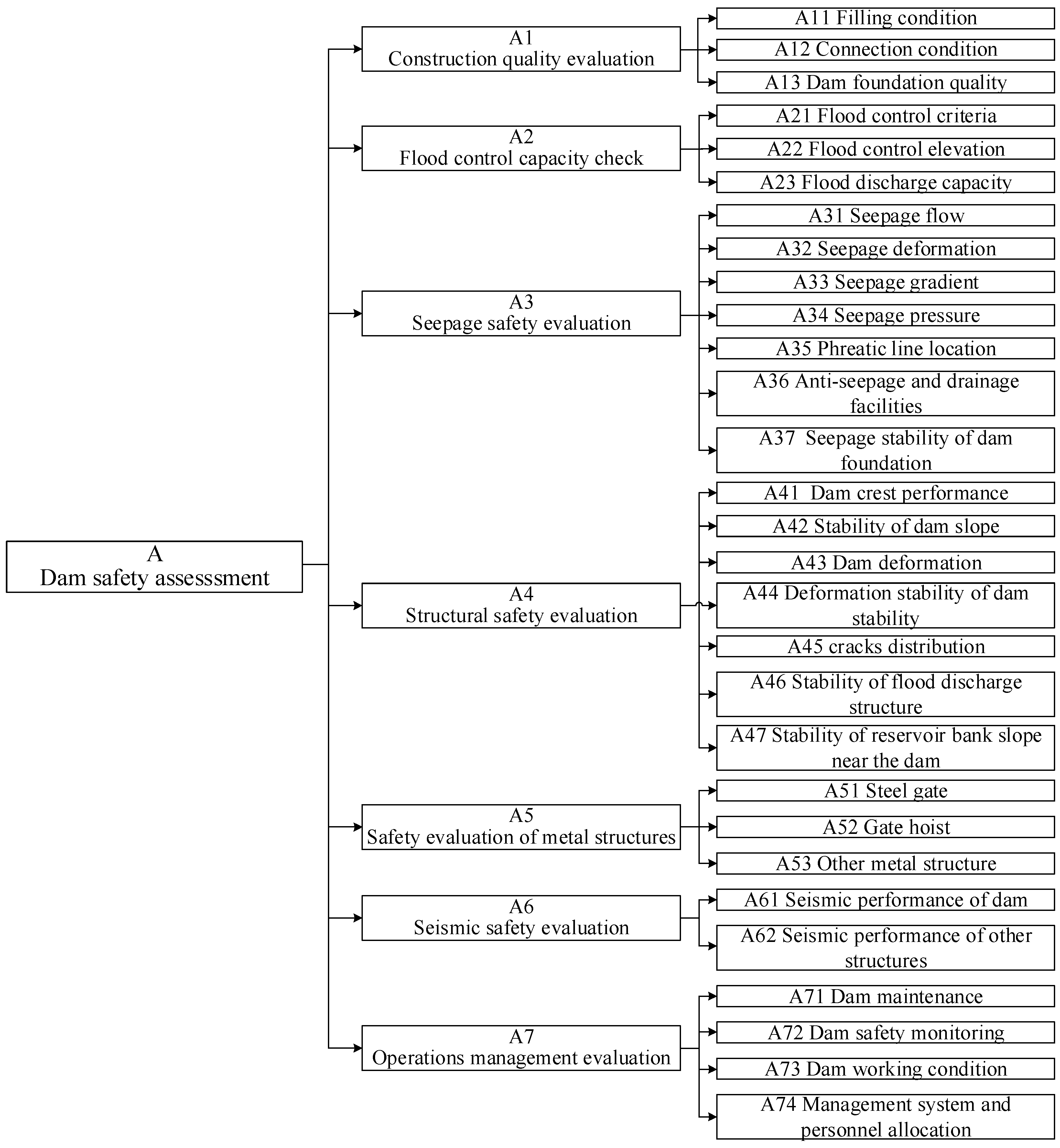
This study proposed the GT-based DSPM method for quantitatively evaluating the safety of dams, which comprehensively considered the advantages of different weighting methods. The dam safety involved various indicators, such as structural safety [
12,
13], seepage safety [
14], and seismic safety [
15]. Although the scores of the indicators could be obtained through actual measurement, field survey, and expert evaluation, the weights of these indicators needed to be determined to assess the final score of the whole dam. This study selected two methods, namely, the SWM and the OWM. For the SWM, the AHP method that was commonly used in dam safety evaluation was chosen [
16,
17,
18]. Meanwhile, for the OWM, the CRITIC method was adopted [
19,
20]. The two selected different weighting methods that were commonly used in the dam safety assessment had different principles, resulting in different weights for each indicator in the evaluation of dam safety and, consequently, leading to different final evaluation results. The AHP method was limited by the expertise of the decision maker while the CRITIC method might lead to situations that did not correspond to reality. Therefore, to overcome the problems existing in a single method, this study further improved the two methods based on GT. The weights of indicators were treated as the variables and the weights of these indicators were assessed according to the programming and numeric computing platform MATLAB [
21]. The proposed GT method re-weighted the initial weights obtained from different methods (i.e., SWM and OWM) and, then, evaluated the safety of reservoir dams based on the weights obtained from GT. In addition, this study proposed the DSPM and dam safety classification method to assess dam safety levels, making the results closer to the actual situation. Using five reservoirs as examples, the implementation process of the entire method was illustrated. The proposed GT-based DSPM method provided references for the safety evaluation of dams.
4. Conclusions
This study proposed the GT-based DSPM method to assess dam safety, considering the safety conditions of their assessment indicators and associated weights. Different weighting methods were used to evaluate the weights of the various indicators and the DSPMs were calculated to assess the safety level of dams. The safety levels obtained from AHP-based, CRITIC-based, and GT-based DSPM methods were compared and discussed. The effectiveness of the proposed GT-based DSPM method was also verified by comparing it with the code-based method (i.e., SL 258-2017). The main conclusions were as follows:
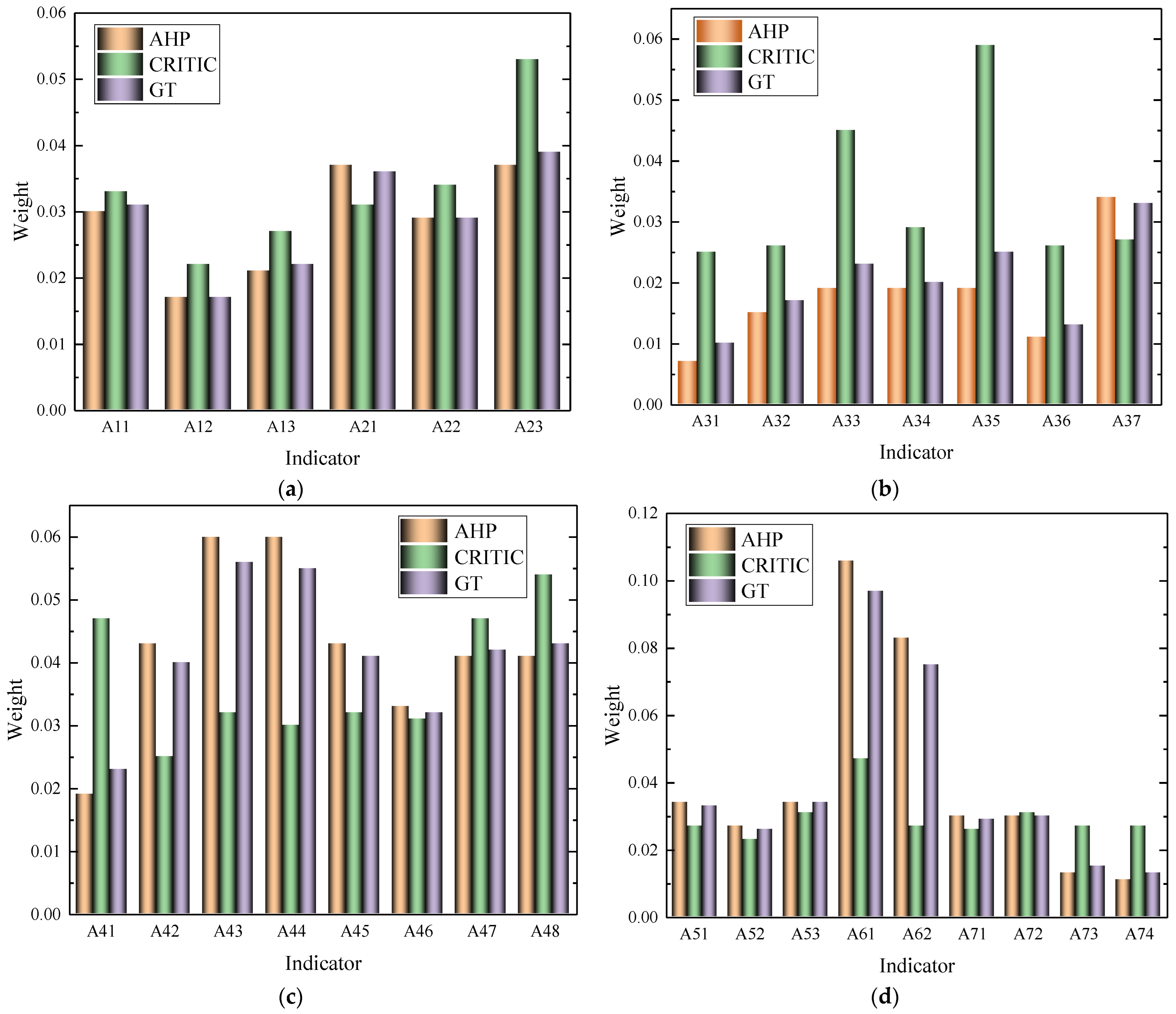
(1) The weights of indicators based on the AHP and CRITIC methods were different, and the maximum percentage difference was the seepage flow indicator. The weights obtained from only one method were unreliable. The weight based on the GT method proposed in this study was located between these two traditional methods. To capture the advantages of the SWM and OWM, the proposed GT method was suggested to assess the weights;
(2) Although the safety levels of the studied dams obtained from the AHP-based DSPM method, CRITIC-based DSPM method, and GT-based DSPM method were basically consistent, except for the Gaojia Reservoir Dam, it was recommended to use the GT-based DSPM method to accurately assess the dam safety due to severe impacts, such as large economic losses and casualties caused by dam failure;
(3) The SIRs of the GT-based DSPM method and the code-based method were consistent, which verified the effectiveness of the GT-based DSPM method proposed in this study. The dam classification in the code-based method was too rough to capture the dam performance accurately, which provided unreliable information for the stakeholders. The proposed method gave a more detailed classification concerning dam safety, which provided important information on wise investments for the stakeholders when enhancing the performance of deficient dams.
Note that the traditional weighting methods selected in the present study were AHP and CRITIC; the GT-based DSPM method could be modified to incorporate the other weighting methods that significantly influenced the dam safety assessment.