Abstract
Remote sensing technology is an essential tool for tracking human-induced alterations on the water cycle, among which irrigation prevails. The possibility of obtaining detailed and accurate information on the actual irrigation extent through remote-sensing-based approaches is of paramount importance for water resources management. In this study, an update of the TSIMAP (Temporal-Stability-derived Irrigation MAPping) method, originally developed with satellite soil moisture as an input, is proposed. To demonstrate that the flexibility of the approach does not affect its main strength point (i.e., good accuracy in the face of high simplicity for users), a dual analysis relying on 1 km NDVI (Normalised Difference Vegetation Index) instead of soil moisture is carried out over the Ebro basin (Spain); data delivered by the Copernicus Global Land Service (CGLS) are used. First, results of this work are compared with outcomes from the method’s original implementation obtained over a focus area (denominated “Ebro_CATAR”) through satellite soil moisture. In the proposed configuration relying on NDVI, an overall accuracy (OA) up to 93% is found. Results highlight an increase in OA ranging from +2% to +6% depending on the validation strategy with respect to the TSIMAP implementation relying on soil moisture. Then, a basin-scale application is performed, providing performances still satisfactory (OA = 75%) notwithstanding a higher degree of heterogeneity.
1. Introduction
Irrigation is the prevalent source of anthropogenic water consumption. Its effects have repercussions on multiple dynamics affecting human beings and Earth’s surface [1], such as food production [2,3,4], spread of diseases [5,6], freshwater availability [7,8,9] and climate [10,11,12]. Notwithstanding this, irrigation is still often not considered a hydrological variable in its own right, and data on irrigation dynamics are often missing [13,14,15] or not scientifically organised [16].
The detailed knowledge of actual irrigation extents is crucial for many hydrological and water resource management applications [17,18,19]. Starting from the early 2000s, several irrigation mapping techniques relying on satellite information have been developed. As pointed out by the comprehensive review by Massari et al. [20], various types of satellite retrievals from optical [21,22,23,24], to cite a few, and microwave, see, e.g., [25,26,27,28], sensors can be successfully exploited for mapping irrigated areas at different spatial scales. Methods relying on multi-source input data also exist [29,30,31,32,33,34]. Most of the approaches available in the scientific literature rely on supervised machine learning models requiring training; hence, ancillary ground-truth information is required for their implementation. By contrast, Dari et al. [27] proposed a novel approach for speedy irrigation mapping relying on a combination of statistical features derived from the temporal stability theory [35] and the unsupervised k-means clustering algorithm [36], henceforth defined as TSIMAP (Temporal-Stability-derived Irrigation MAPping) approach. The method does not require any training procedure and, as recently pointed out in a comparative analysis by Bazzi et al. [37], ensures satisfactory performances in face of its simplicity. So far, the method has been developed and implemented with satellite soil moisture at different spatial resolutions as input [27,28]. Nevertheless, it is supposed to work with any kind of input information that is a proxy for irrigation occurrence.
The aim of this work is to actually demonstrate the flexibility of the TSIMAP method, whose applicability is not limited by a single type of input data. In order to achieve this, a twofold analysis carried out over the Ebro basin (Spain) by exploiting 1 km NDVI (Normalised Difference Vegetation Index) from the Copernicus Global Land Service (CGLS) is proposed. First, a comparative analysis with outcomes from the method’s implementation relying on satellite soil moisture by Dari et al. [27] is carried out. The comparison is focused over the same period (2016–2017) and the same portion of the Ebro basin considered in a previous study by the authors. As a second step, a basin-scale application considering the irrigation seasons in the time span of 2015–2020is performed.
2. Materials and Methods
2.1. Study Area
The study is focused over the Ebro basin (Spain), a site that has attracted, in recent years, the interest of many researchers working on the topic of irrigation monitoring through satellite data [26,34,38,39,40,41]. This is because the Ebro catchment is an area rich in irrigation data, a rather rare feature worldwide.
With a total drainage area of about 86,000 km2, the Ebro basin is the largest Mediterranean catchment of Spain; it is prevalently characterised by a cold semi-arid climate with an oceanic climate area in its Northern portion [42], where several reservoirs store water from the Pyrenees to be delivered to the crops located downstream in the central valley through a complex network of irrigation canals [39]. The analysis presented in this study is carried out on the basin’s flat agricultural portions only, which are shown in Figure 1. Such a domain includes both irrigated and non-irrigated areas; it is outlined through the 100 m resolution Corine Land Cover data set referring to the year 2018 (CLC 2018), distributed by the Copernicus Land Monitoring Service (https://doi.org/10.2909/960998c1-1870-4e82-8051-6485205ebbac (accessed on 13 November 2019). The land cover types that are considered are listed in the figure’s legend. It is important to specify that the information from the CLC 2018 is only used to delineate the spatial domain of agricultural areas (rainfed and irrigated) to be considered; as a benchmark for the actual extent of irrigated areas, we use more site-specific and accurate data sets as described in Section 2.3. Moreover, a double-scale analysis is carried out. First, the area enclosed by the red box of Figure 1 is considered in order to compare results with outcomes of Dari et al. [27]; such portion, whose extension is 10,000 km2, encloses a wide irrigated area shared between the Catalonia and Aragon regions and is henceforth denominated “Ebro_CATAR”. Then, a basin-scale application is performed (see Section 2.3 for further details).
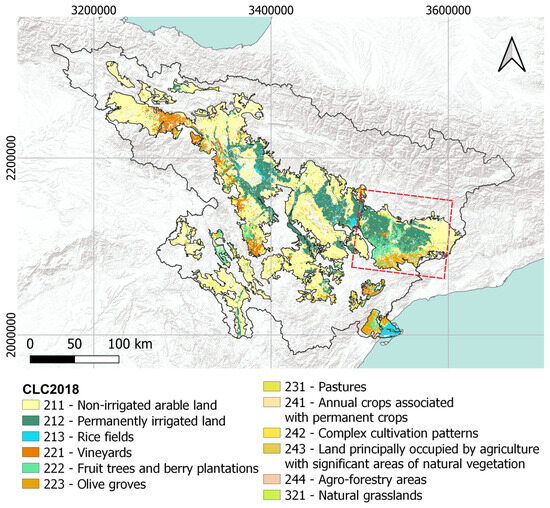
Figure 1.
Land cover classes according to the Corine Land Cover 2018 (CLC 2018) data set that are enclosed in the portion of the Ebro basin considered in this study. The comparison with results from Dari et al. [27] is carried out over the portion delimited by the red box, the Ebro_CATAR area. Coordinates refer to the projection ETRS89-extended/LAEA Europe, EPSG:3035.
2.2. The TSIMAP Method: Theory and Input Data
The TSIMAP method was first proposed by Dari et al. [27]. It relies on the temporal stability concept originally formulated by Vachaud et al. [35] for optimising soil moisture measurement networks [43,44,45,46]. Morbidelli et al. [47] also explored the possibility of adapting the concept to raingauge network design. The theory relies on statistical features able to describe the spatiotemporal dynamics of the input data set. Hence, if applied to an irrigation proxy variable, it is possible to use the temporal stability theory to detect where irrigation actually occurs. With this intuition, the approach was originally proposed by exploiting satellite soil moisture as an input [27]. In this study, the method is implemented using NDVI data from the CGLS (https://land.copernicus.eu/global/products/ndvi (accessed on 29 November 2023)), retrieved through the VEGETATION sensor aboard the SPOT (Satellite Pour l’Observation de la Terre) platform, subsequently substituted, from 2013 onwards, by PROBA-V (PRoject for On-Board Autonomy-VEGETATION) [48]. Specifically, product version 2.2 characterised by a spatial resolution of 1 km and sampled at a temporal frequency of 10 days is used [49]. Data from 2015 to 2020 are considered.
Considering the NDVI value observed at the pixel and time step , , and the time-varying spatial average, , the relative differences, , are defined as
While the relative differences reveal features of spatial patterns of the input data set, the temporal anomalies, , provide information on temporal dynamics. values indicate, for each pixel, the magnitude of the discrepancy with its temporal mean, ; they can be calculated as
If averaged in time during the highest intensity irrigation season, which for the study area coincides with the period spanning from May to September [27], the relative differences and the temporal anomalies can be used as diagnostic indices for detecting where irrigation occurs. In fact, during the irrigation seasons, irrigated crops are expected to show well-developed vegetation conditions, which can be translated into higher values of relative differences and of temporal anomalies with respect to rainfed areas. On the basis of such an assumption, the temporal-stability-derived indices can be used as input features for the k-means clustering method [36]. It allows to group data points into clusters on the basis of their similarity, expressed by the minimum Euclidian distance with each cluster’s centroid. The k-means is an unsupervised clustering algorithm; hence, it does not require any training, but the user is asked to interpret the clusters’ meaning. Further details can be found in Dari et al. [27,28]. In this work, the mean relative differences (RD) and the mean temporal anomalies (TA) during the highest intensity irrigation seasons are used as input data points for k-means clustering. The final output consists in binary maps of rainfed and irrigated areas at 1 km spatial resolution.
2.3. Work Logic and Ground Truth Data Sets
A twofold analysis is carried out. First, a comparison between results obtained by forcing the TSIMAP approach with NDVI data and outcomes of the method’s first implementation relying on soil moisture [27] is performed. The analysis iscarried out over the same basin’s portion considered in Dari et al. [27], the Ebro_CATAR domain (10,000 km2), enclosing the largest irrigated portion of the entire basin. In this first analysis, the same validation strategy proposed in the previous work by the authors is implemented to ensure that the comparison is as fair as possible. The crop maps produced over the domain of the Geographic Information System for Agricultural Parcels (SIGPAC) and distributed by the Department d’Agricultura, Ramaderia, Pesca i Alimentació are used. This data set, henceforth referred to as SIGPAC data, is available at the plot scale and for each year at http://agricultura.gencat.cat/ca/serveis/cartografia-sig/aplicatius-tematics-geoinformacio/sigpac/mapa-cultius/ (accessed on 9 October 2019). It is noteworthy that the data set is available for the Catalonia region only. The pre-processing chain to aggregate SIGPAC data from the original resolution to 1 km is fully described in Dari et al. [27]; the only difference adopted in this work is that natural or forested areas are not considered, so, this kind of pixels are masked out. Two types of information contained in the SIGPAC data set are exploited, resulting in an equal number of validation assessments. First, the irrigated/non-irrigated attribute is exploited (first validation). Even though the irrigated areas of the Ebro basin are quite static in time, as thoroughly explained in Dari et al. [27], the irrigation attribute in the SIGPAC data set means that the irrigation network can reach a specific field, but it does not necessarily imply that irrigation actually occurs there. Hence, the information referring to summer crops only, which are very likely irrigated during the irrigation season, is considered in the second validation, in which all the other crops are considered as rainfed. Similarly to what was performed in Dari et al. [27], this first analysis covers the 2-year period of 2016–2017. It is important to mention that in the previous work by the authors, experiments considering three clusters (rainfed, natural/forested and irrigated areas) were carried out. To ensure a consistent comparison with the authors’ previous study, the best performing classification in reproducing irrigated areas resulting in that work is re-implemented here by considering only two clusters, i.e., rainfed and irrigated areas. In this way, results obtained in Dari et al. [27] and in this work are fully comparable.
As a second step, a basin-scale application is proposed. Hence, the method is applied over the whole domain of agricultural areas (see Figure 1). In this case, as a ground truth information, the map of the basin’s irrigated areas according to the Hydrological Plan of the Ebro basin is used. The map, produced by the Ebro Hydrological Confederation (CHEBRO, https://www.chebro.es/ (accessed on 15 April 2020)), is dated 2004; hence, it could miss some irrigation portions recently developed. Nevertheless, the main irrigation districts were already developed at that time. Such information, henceforth defined as the CHEBRO map, is used to validate a static map obtained by applying the TSIMAP method to all the irrigation seasons of the considered period, i.e., from 2015 to 2020. This choice is led by the reasonable assumption of irrigation extents quite static in time at the basin scale and also by the nature of the available ground truth information. For validating the basin-scale irrigation map, all the pixels of the CHEBRO map are considered as irrigated (since the map only provides the edges of irrigated areas), while the other pixels of the agricultural areas within the Ebro basin are considered as rainfed. Figure 2 provides a scheme summarising the main features of the analyses carried out.
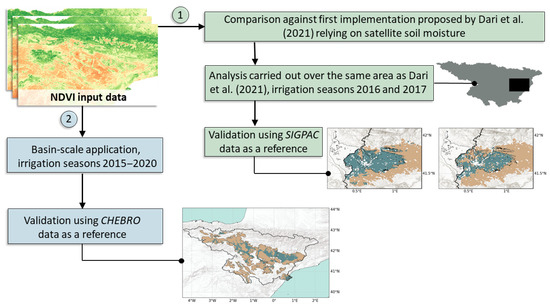
Figure 2.
Overview of the analyses carried out: (1) comparison of results obtained in this study through NDVI against outcomes of method’s first implementation through remotely sensed soil moisture [27] and (2) basin-scale application.
3. Results
3.1. Comparison with Original Implementation Relying on Soil Moisture
In this section, results obtained over the smaller domain considered in Dari et al. [27] and validated with detailed ground truth information from the SIGPAC data set are presented. Outcomes referring to the irrigation seasons of 2016 and 2017 are shown in Figure 3 and Figure 4, respectively. Both figures are organised in six panels: Figure 3a and Figure 4a show the location of the Ebro_CATAR area with respect to the basin extension, Figure 3b, Figure 4b and Figure 3c, Figure 4c show the mean RD and the mean TA, respectively, during the highest-intensity irrigation season (May–September), Figure 3d, Figure 4d and Figure 3e, Figure 4e provide the SIGPAC ground truth maps according to the two validation strategies, and Figure 3f and Figure 4f show the rainfed/irrigated map resulting from the TSIMAP method, respectively. In Figures from Figure 3d and Figure 4d to Figure 3f and Figure 4f, light brown and blue green are used to indicate rainfed and irrigated areas, respectively. We note that for Figures from Figure 3b and Figure 4b to Figure 3f and Figure 4f, data are shown over the portion falling into the Catalonia region only, as this is the domain where benchmark information from the SIGPAC data set is available, respectively. Even with different magnitudes, for both irrigation seasons of 2016 and 2017, the mean RD and TA of NDVI prove themselves to be promising diagnostic indices for detecting irrigated areas. In fact, the maps of Figure 3b, Figure 3c and Figure 4b and Figure 4c show consistent spatial patterns with higher (mostly positive) values over areas where irrigation is expected to occur and lower (mostly negative) values over the surrounding dryland area extending to the east, respectively.
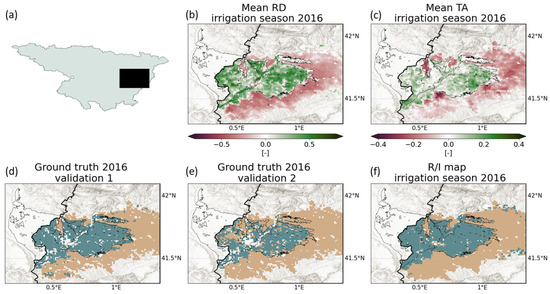
Figure 3.
Results obtained in this study over the Ebro_CATAR domain and referring to the irrigation season of 2016: panel (a) provides the location of the Ebro_CATAR area, panels (b,c) show the mean relative differences (RD) and the mean temporal anomalies (TA), respectively, during the highest-intensity irrigation season (May–September), panels (d,e) show the SIGPAC ground truth maps according to Validations 1 and 2, and panel (f) shows the resulting rainfed/irrigated (R/I) map. We note that in panels (d–f), light brown and blue green are used to indicate rainfed and irrigated areas, respectively.
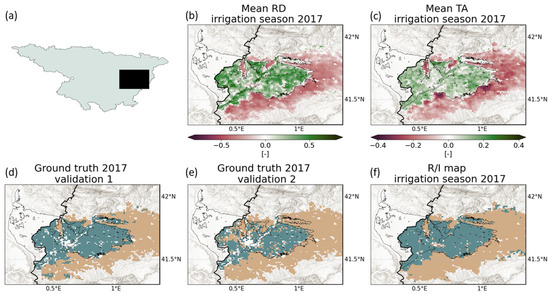
Figure 4.
Same as Figure 3 but referring to the irrigation season of 2017.
For both irrigation seasons of 2016 and 2017, the mean RD and TA are used as input data points to perform the k-means classification and produce the 1 km maps of rainfed and irrigated areas shown in Figure 3f and Figure 4f, respectively. Figure 5a provides the confusion matrices synthesising the accuracy of the resulting maps according to the two validation approaches, i.e., comparing maps in Figure 3f, Figure 4f with those shown in Figure 3d, Figure 4d and Figure 3e, Figure 4e. Overall, a satisfying accuracy in properly reproducing rainfed and irrigated portions is obtained in both irrigation seasons of 2016 and 2017. According to Validation 1, 88% and 87% of irrigated areas are properly reproduced by the TSIMAP method in 2016 and 2017, respectively. Almost all the rainfed areas are properly classified, since in both irrigation seasons of 2016 and 2017 an accuracy of 97% is reached. According to Validation 2, the same results are obtained for both irrigation seasons considered. The accuracy in properly classifying irrigated areas rises to 98%, but this happens at the expense of the accuracy in reproducing rainfed areas, which drops to 84%.
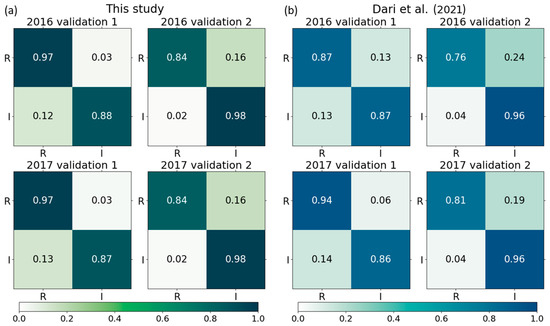
Figure 5.
Panel (a): Confusion matrices synthesising the accuracy of the classifications into rainfed (R) and irrigated (I) areas according to the two validation approaches implemented. Panel (b): same but referring to the classifications proposed in Dari et al. [27] modified considering rainfed (R) and irrigated (I) areas only. For both panels, the first row refers to 2016, while the second one refers to 2017; ground truth classes are represented on the y-axis, while the classes obtained through the TSIMAP method are shown on the x-axis.
Dari et al. [27] explored different combinations of input parameters derived from satellite soil moisture to map irrigation. The authors found that the standard deviation of RD and mean TA calculated for the 1 km DISPATCH (Disaggregation based on Physical and Theoretical scale Change) downscaled SMAP (Soil Moisture Active Passive) product [50] were the best diagnostic indices for reproducing irrigated areas, reporting a maximum accuracy of 78% reached according to Validation 2 considering the irrigation season of 2017. However, as explained in Section 2.3, such a result refers to the capability in reproducing three different clusters, and not in discerning between rainfed and irrigated areas only as in this case. For this reason, the experiment offering the best accuracy according to Dari et al. [27] is repeated here by considering two clusters only and results are summarised by the confusion matrices of Figure 5b. The differences with the implementation relying on NDVI proposed here thin out, especially in the capability of the method in reproducing actual irrigated areas; accuracies differ by 1–2%, still in favour of the new implementation. Higher differences are found with respect to the capability of recognising rainfed areas. The classification based on satellite soil moisture provides accuracies lower than those relying on NDVI by 10% and 8% (and by 3%) for both the validation experiments in 2016 (2017).
3.2. Basin-Scale Application
The TSIMAP method is then applied at the basin scale to produce a static map of rainfed and irrigated agricultural areas across the years of 2015–2020. The k-means classification is carried out by using as input data points the mean RD and TA during the irrigation seasons (May–September) of the period of 2015–2020. The resulting maps are shown in Figure 6; consistent spatial patterns of higher average RD and TA values are found over areas known to be irrigated, such as agricultural lands within the Ebro_CATAR domain, the narrow area in the basin central valley running along the main reach of the Ebro and the river delta [39].
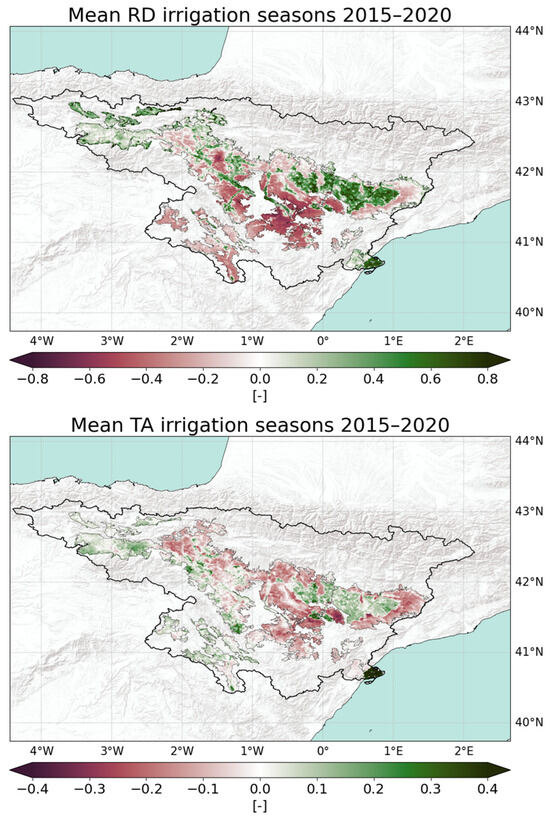
Figure 6.
Mean relative differences (RD) and temporal anomalies (TA) during the highest-intensity irrigation seasons (May–September) of the period of 2015–2020.
The accuracy of the map of rainfed/irrigated areas derived from the input indices shown in Figure 6 is assessed through comparison with the CHEBRO map. Results are summarised in Figure 7. Figure 7a shows the map produced by the TSIMAP method, Figure 7b provides the ground truth map and Figure 7c contains the confusion matrix. As can be depicted by visual inspection of maps in Figure 7a and Figure 7b and by accuracies reported in Figure 7c, irrigated areas are satisfactorily reproduced at the basin scale also, which is characterised by higher heterogeneity. The percentage of irrigated areas properly classified is equal to 81% of the total. Higher uncertainty exists in properly classifying rainfed areas, for which the accuracy drops to 72%.
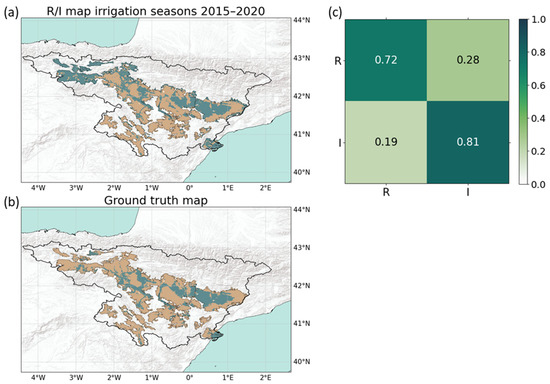
Figure 7.
Assessment of results of the basin-scale application: panel (a) shows the map of rainfed (R, indicated in light brown) irrigated (I, indicated in green blue) areas produced through the TSIMAP method and panel (b) provides the CHEBRO ground truth map. Panel (c) shows the corresponding confusion matrix, with ground truth classes on the Y-axis and predicted ones on the X-axis.
4. Discussion
The aim of this work is to showcase the flexibility of the TSIMAP method originally proposed in a previous work by the authors with satellite soil moisture data as an input. However, the method is expected to provide satisfactory results with any input observation that can be an irrigation proxy and for which the temporal stability concept applies, without losing its characteristic of ease of use that distinguishes it from other methods available in the literature [37].
For this reason, the approach is implemented with 1 km NDVI data from the CGLS, as several studies linking irrigation dynamics with NDVI are available in the literature [23,51,52,53]. The comparison against outcomes from the method’s first implementation reveal a slight increase in the capability of properly classifying irrigated areas and more substantial improvements in detecting rainfed areas when forcing the approach with NDVI observations. In terms of overall accuracy (OA), a value of 93% and 92% is reached according to Validation 1 for the irrigation seasons of 2016 and 2017, respectively. For Validation 2, the OA is 88% for both years. Over the same area, Elwan et al. [34] reported an accuracy on the order of 87% through a supporting vector machine classification fed with statistical features from Sentinel-1 and Sentinel-2 as an input. Gao et al. [26] reached an accuracy of 81% using Sentinel-1-derived features over the same domain, but three classes (irrigated crops, irrigated trees, and non-irrigated fields) were considered in that work. In both works by Gao et al. [26] and Elwan et al. [34], methods requiring training were adopted, while the TSIMAP approach did not require this step. It is important to point out that results from Gao et al. [26] and Elwan et al. [34] refer to a finer spatial scale (at the field level) with respect to the 1 km scale adopted in this work.
In the basin-scale application, an OA equal to 75% is reached. Even though a decreasing accuracy can be encountered when enlarging the considered domain and thus facing higher heterogeneity, it is important to point out that results of the two analyses carried out are not directly comparable since different ground truth data sets are used. A closer look at NDVI dynamics can help in assessing results. Figure 8 shows the rainfed and irrigated areas properly classified (true rainfed and true irrigated, respectively), the irrigated areas erroneously classified as rainfed (false rainfed) and the rainfed areas wrongly classified as irrigated (false irrigated). The 14-day aggregated time series of NDVI averaged over each one of the domains above are also shown in Figure 8b, where the main watering seasons (May–September) are highlighted in light grey. False rainfed areas are scattered and often located adjacent to the edges of irrigated areas; hence, it is possible that the 1 km sampling adopted here is not fine enough to properly detect complex patterns. However, the NDVI signal over those areas is similar to the one detected over true rainfed portions (see light brown and pink lines in Figure 8b). The green blue line referring to true irrigated areas clearly shows a second NDVI peak during the period May–September attributable to irrigation occurrence. False irrigated areas (mostly located in the northwestern side) represent the highest source of uncertainties. For those areas, the NDVI time series (black line in Figure 8b) do not show a clear peak during the irrigation season, but values are comparable to those detected over true irrigated areas. This can be an index of areas where NDVI is systematically higher than the basin average (see also Figure 6), thus leading to wrong classification. Nevertheless, uncertainties could come from the ground truth data set as well. As explained in Section 2.3, the CHEBRO map dates back to 2004; hence, it is possible that recently developed irrigated areas are detected by satellite NDVI but are still classified as rainfed in the benchmark data set.
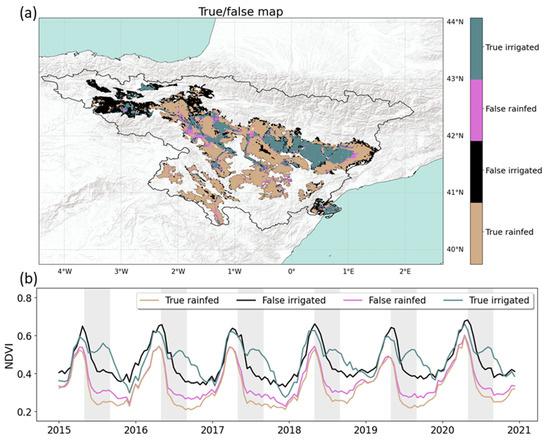
Figure 8.
Panel (a) shows the map of true irrigated, false rainfed, false irrigated, and true rainfed areas. Panel (b) provides the 14-day aggregated NDVI time series averaged over each domain.
5. Conclusions
The analyses carried out in this work demonstrate the flexibility of the TSIMAP method, able to provide optimal performances in face of its simplicity for end-users [37]. The approach’s applicability is not limited to the use of satellite soil moisture as an input, as the method can be fed with any irrigation-proxy data (e.g., vegetation indices, evapotranspiration estimates, land surface temperature records). To showcase this, an implementation relying on 1 km NDVI is proposed. Results outperform the method’s first implementation by Dari et al. [27], with increases of OA equal to +6% in the irrigation season of 2016 according to both validation procedures implemented and to +2% and +3% according to Validations 1 and 2, respectively, considering 2017. A basin-scale application is performed as well, producing a static map across irrigation seasons within the period of 2015–2020 providing satisfactory results despite a higher heterogeneity. The method’s flexibility allows potential operational applications at different spatial resolutions [28]. For instance, the TSIMAP approach represents a useful tool to refine irrigation water use estimates from satellite data, as hinted by Kragh et al. [54] and Dari et al. [39]. Further assessments of the performances of the proposed approach with different types of input (e.g., merging soil moisture and vegetation indices) data with respect to varying climatic contexts are the foreseen next steps of this research.
Author Contributions
Conceptualisation, J.D.; methodology, J.D., R.M., P.Q.-S. and L.B.; software, J.D.; validation, J.D.; formal analysis, J.D.; investigation, J.D.; data curation, J.D.; writing—original draft preparation, J.D.; writing—review and editing, J.D., R.M., P.Q.-S. and L.B.; visualisation, J.D.; supervision, R.M., P.Q.-S. and L.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The NDVI data from the CGLS are available at: https://land.copernicus.eu/global/products/ndvi (accessed on 29 November 2023). The SIGPAC ground truth data set is available at: http://agricultura.gencat.cat/ca/serveis/cartografia-sig/aplicatius-tematics-geoinformacio/sigpac/mapa-cultius/ (accessed on 9 October 2019), while the CHEBRO map is available from the authors upon reasonable request.
Acknowledgments
The authors acknowledge the support from ESA under the CCI-AWU (Climate Change Initiative-Anthropogenic Water Use) precursor project (contract n. 4000142449/23/I-NB). The authors wish to thank the SIGPAC and CHEBRO teams for providing the ground truth data sets used in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sacks, W.J.; Cook, B.I.; Buenning, N.; Levis, S.; Helkowski, J.H. Effects of Global Irrigation on the Near-Surface Climate. Clim. Dyn. 2009, 33, 159–175. [Google Scholar] [CrossRef]
- Schultz, B.; Thatte, C.D.; Labhsetwar, V.K. Irrigation and Drainage. Main Contributors to Global Food Production. Irrig. Drain. 2005, 54, 263–278. [Google Scholar] [CrossRef]
- Liu, J.; Hertel, T.W.; Lammers, R.B.; Prusevich, A.; Baldos, U.L.C.; Grogan, D.S.; Frolking, S. Achieving Sustainable Irrigation Water Withdrawals: Global Impacts on Food Security and Land Use. Environ. Res. Lett. 2017, 12, 104009. [Google Scholar] [CrossRef]
- D’Odorico, P.; Davis, K.F.; Rosa, L.; Carr, J.A.; Chiarelli, D.; Dell’Angelo, J.; Gephart, J.; MacDonald, G.K.; Seekel, D.A.; Suweis, S.; et al. The Global Food-Energy-Water Nexus. Rev. Geophys. 2018, 56, 456–531. [Google Scholar] [CrossRef]
- Partyka, M.L.; Bond, R.F. Wastewater Reuse for Irrigation of Produce: A Review of Research, Regulations, and Risks. Sci. Total Environ. 2022, 828, 154385. [Google Scholar] [CrossRef] [PubMed]
- Jiang, A.; Lee, M.; Selvaraj, P.; Degefa, T.; Getachew, H.; Merga, H.; Yewhalaw, D.; Yan, G.; Hsu, K. Investigating the Impact of Irrigation on Malaria Vector Larval Habitats and Transmission Using a Hydrology-Based Model. GeoHealth 2023, 7, e2023GH000868. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.-H. Emerging Trends in Global Freshwater Availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef]
- Peña-Arancibia, J.L.; Mainuddin, M.; Ahmad, M.D.; Hodgson, G.; Ibn Murad, K.F.; Ticehurst, C.; Maniruzzaman, M.; Golam Mahboob, M.; Kirby, J.M. Groundwater Use and Rapid Irrigation Expansion in a Changing Climate: Hydrological Drivers in One of the World’s Food Bowls. J. Hydrol. 2020, 581, 124300. [Google Scholar] [CrossRef]
- Dari, J.; Flammini, A.; Morbidelli, R.; Rahi, A.; Salatalippi, C. Evolution of freshwater availability in a climate-changing Mediterranean context: The case of Umbria region, central Italy. Hydrol. Process. 2023, 37, e15050. [Google Scholar] [CrossRef]
- Mueller, N.D.; Rhines, A.; Butler, E.E.; Ray, D.K.; Siebert, S.; Holbrook, N.M.; Huybers, P. Global Relationships between Cropland Intensification and Summer Temperature Extremes over the Last 50 Years. J. Clim. 2017, 30, 7505–7528. [Google Scholar] [CrossRef]
- Rosa, L.; Chiarelli, D.D.; Sangiorgio, M.; Beltran-Peña, A.A.; Rulli, M.C.; D’Odorico, P.; Fung, I. Potential for Sustainable Irrigation Expansion in a 3 °C Warmer Climate. Proc. Natl. Acad. Sci. USA 2020, 117, 29526–29534. [Google Scholar] [CrossRef]
- Thiery, W.; Visser, A.J.; Fischer, E.M.; Hauser, M.; Hirsch, A.L.; Lawrence, D.M.; Lejeune, Q.; Davin, E.L.; Seneviratne, S.I. Warming of Hot Extremes Alleviated by Expanding Irrigation. Nat. Commun. 2020, 11, 290. [Google Scholar] [CrossRef]
- Neumann, K.; Stehfest, E.; Verburg, P.H.; Siebert, S.; Müller, C.; Veldkamp, T. Exploring Global Irrigation Patterns: A Multilevel Modelling Approach. Agric. Syst. 2011, 104, 703–713. [Google Scholar] [CrossRef]
- Foster, T.; Mieno, T.; Brozović, N. Satellite-Based Monitoring of Irrigation Water Use: Assessing Measurement Errors and Their Implications for Agricultural Water Management Policy. Water Resour. Res. 2020, 56, e2020WR028378. [Google Scholar] [CrossRef]
- Brombacher, J.; Silva, I.R.D.O.; Degen, J.; Pelgrum, H. A Novel Evapotranspiration Based Irrigation Quantification Method Using the Hydrological Similar Pixels Algorithm. Agric. Water Manag. 2022, 267, 107602. [Google Scholar] [CrossRef]
- Zappa, L.; Schlaffer, S.; Bauer-Marschallinger, B.; Nendel, C.; Zimmerman, B.; Dorigo, W. Detection and Quantification of Irrigation Water Amounts at 500 m Using Sentinel-1 Surface Soil Moisture. Remote Sens. 2021, 13, 1727. [Google Scholar] [CrossRef]
- Ozdogan, M.; Yang, Y.; Allez, G.; Cervantes, C. Remote Sensing of Irrigated Agriculture: Opportunities and Challenges. Remote Sens. 2010, 2, 2274–2304. [Google Scholar] [CrossRef]
- Deines, J.M.; Kendall, A.D.; Butler, J.J.; Hyndman, D.W. Quantifying Irrigation Adaptation Strategies in Response to Stakeholder-Driven Groundwater Management in the US High Plains Aquifer. Environ. Res. Lett. 2019, 14, 044014. [Google Scholar] [CrossRef]
- Puy, A.; Borgonovo, E.; Lo Piano, S.; Levin, S.A.; Saltelli, A. Irrigated Areas Drive Irrigation Water Withdrawals. Nat. Commun. 2021, 12, 4525. [Google Scholar] [CrossRef] [PubMed]
- Massari, C.; Modanesi, S.; Dari, J.; Gruber, A.; De Lannoy, G.J.M.; Girotto, M.; Quintana-Seguí, P.; Le Page, M.; Jarlan, L.; Zribi, M.; et al. A Review of Irrigation Information Retrievals from Space and Their Utility for Users. Remote Sens. 2021, 13, 4112. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Biradar, C.M.; Turral, H.; Noojipady, P.; Li, Y.J.; Vithanage, J.; Dheeravath, V.; Velpuri, M.; Schull, M.; Cai, X.L.; et al. An Irrigated Area Map of the World (1999), Derived from Remote Sensing; International Water Management Institute: Colombo, Sri Lanka, 2006; pp. 1–78. ISBN 978-92-9090-646-9. [Google Scholar]
- Salmon, J.M.; Friedl, M.A.; Frolking, S.; Wisser, D.; Douglas, E.M. Global Rain-Fed, Irrigated, and Paddy Croplands: A New High Resolution Map Derived from Remote Sensing, Crop Inventories and Climate Data. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 321–334. [Google Scholar] [CrossRef]
- Ambika, A.K.; Wardlow, B.; Mishra, V. Remotely Sensed High Resolution Irrigated Area Mapping in India for 2000 to 2015. Sci. Data 2016, 3, 160118. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, D.; Luo, L.; Pokhrel, Y.; Deb, K.; Huang, J.; Ran, Y. Detecting Irrigation Extent, Frequency, and Timing in a Heterogeneous Arid Agricultural Region Using MODIS Time Series, Landsat Imagery, and Ancillary Data. Remote Sens. Environ. 2018, 204, 197–211. [Google Scholar] [CrossRef]
- Lawston, P.M.; Santanello, J.A.; Kumar, S.V. Irrigation Signals Detected From SMAP Soil Moisture Retrievals. Geophys. Res. Lett. 2017, 44, 11860–11867. [Google Scholar] [CrossRef]
- Gao, Q.; Zribi, M.; Escorihuela, M.; Baghdadi, N.; Quintana-Seguí, P. Irrigation Mapping Using Sentinel-1 Time Series at Field Scale. Remote Sens. 2018, 10, 1495. [Google Scholar] [CrossRef]
- Dari, J.; Quintana-Seguí, P.; Escorihuela, M.J.; Stefan, V.; Brocca, L.; Morbidelli, R. Detecting and Mapping Irrigated Areas in a Mediterranean Environment by Using Remote Sensing Soil Moisture and a Land Surface Model. J. Hydrol. 2021, 596, 126129. [Google Scholar] [CrossRef]
- Dari, J.; Brocca, L.; Quintana-Seguí, P.; Casadei, S.; Escorihuela, M.J.; Stefan, V.; Morbidelli, R. Double-Scale Analysis on the Detectability of Irrigation Signals from Remote Sensing Soil Moisture over an Area with Complex Topography in Central Italy. Adv. Water Resour. 2022, 161, 104130. [Google Scholar] [CrossRef]
- Singh, D.; Gupta, P.K.; Pradhan, R.; Dubey, A.K.; Singh, R.P. Discerning Shifting Irrigation Practices from Passive Microwave Radiometry over Punjab and Haryana. J. Water Clim. Chang. 2017, 8, 303–319. [Google Scholar] [CrossRef]
- Bousbih, S.; Zribi, M.; El Hajj, M.; Baghdadi, N.; Lili-Chabaane, Z.; Gao, Q.; Fanise, P. Soil Moisture and Irrigation Mapping in A Semi-Arid Region, Based on the Synergetic Use of Sentinel-1 and Sentinel-2 Data. Remote Sens. 2018, 10, 1953. [Google Scholar] [CrossRef]
- Demarez, V.; Helen, F.; Marais-Sicre, C.; Baup, F. In-Season Mapping of Irrigated Crops Using Landsat 8 and Sentinel-1 Time Series. Remote Sens. 2019, 11, 118. [Google Scholar] [CrossRef]
- Bazzi, H.; Baghdadi, N.; Amin, G.; Fayad, I.; Zribi, M.; Demarez, V.; Belhouchette, H. An Operational Framework for Mapping Irrigated Areas at Plot Scale Using Sentinel-1 and Sentinel-2 Data. Remote Sens. 2021, 13, 2584. [Google Scholar] [CrossRef]
- Le Page, M.; Jarlan, L.; El Hajj, M.M.; Zribi, M.; Baghdadi, N.; Boone, A. Potential for the Detection of Irrigation Events on Maize Plots Using Sentinel-1 Soil Moisture Products. Remote Sens. 2020, 12, 1621. [Google Scholar] [CrossRef]
- Elwan, E.; Le Page, M.; Jarlan, L.; Baghdadi, N.; Brocca, L.; Modanesi, S.; Dari, J.; Quintana Seguí, P.; Zribi, M. Irrigation Mapping on Two Contrasted Climatic Contexts Using Sentinel-1 and Sentinel-2 Data. Water 2022, 14, 804. [Google Scholar] [CrossRef]
- Vachaud, G.; Passerat de Silans, A.; Balabanis, P.; Vauclin, M. Temporal stability of spatial measured soil water probability density function. Soil Sci. Soc. Am. J. 1985, 49, 822–828. [Google Scholar] [CrossRef]
- Macqueen, J.B. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
- Bazzi, H.; Baghdadi, N.; Zribi, M. Comparative Analysis between Two Operational Irrigation Mapping Models over Study Sites in Mediterranean and Semi-Oceanic Regions. Water 2022, 14, 1341. [Google Scholar] [CrossRef]
- Fontanet, M.; Fernández-Garcia, D.; Ferrer, F. The Value of Satellite Remote Sensing Soil Moisture Data and the DISPATCH Algorithm in Irrigation Fields. Hydrol. Earth Syst. Sci. 2018, 22, 5889–5900. [Google Scholar] [CrossRef]
- Dari, J.; Brocca, L.; Modanesi, S.; Massari, C.; Tarpanelli, A.; Barbetta, S.; Quast, R.; Vreugdenhil, M.; Freeman, V.; Barella-Ortiz, A.; et al. Regional Data Sets of High-Resolution (1 and 6 Km) Irrigation Estimates from Space. Earth Syst. Sci. Data 2023, 15, 1555–1575. [Google Scholar] [CrossRef]
- Paolini, G.; Escorihuela, M.J.; Merlin, O.; Laluet, P.; Bellvert, J.; Pellarin, T. Estimating Multi-Scale Irrigation Amounts Using Multi-Resolution Soil Moisture Data: A Data-Driven Approach Using PrISM. Agric. Water Manag. 2023, 290, 108594. [Google Scholar] [CrossRef]
- Laluet, P.; Olivera-Guerra, L.E.; Altés, V.; Paolini, G.; Ouaadi, N.; Rivalland, V.; Jarlan, L.; Villar, J.M.; Merlin, O. Retrieving the Irrigation Actually Applied at District Scale: Assimilating High-Resolution Sentinel-1-Derived Soil Moisture Data into a FAO-56-Based Model. Agric. Water Manag. 2024, 293, 108704. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- Cosh, M.H.; Jackson, T.J.; Starks, P.; Heathman, G. Temporal Stability of Surface Soil Moisture in the Little Washita River Watershed and Its Applications in Satellite Soil Moisture Product Validation. J. Hydrol. 2006, 323, 168–177. [Google Scholar] [CrossRef]
- Mittelbach, H.; Seneviratne, S.I. A New Perspective on the Spatio-Temporal Variability of Soil Moisture: Temporal Dynamics versus Time-Invariant Contributions. Hydrol. Earth Syst. Sci. 2012, 16, 2169–2179. [Google Scholar] [CrossRef]
- Yetbarek, E.; Ojha, R. Spatio-Temporal Variability of Soil Moisture in a Cropped Agricultural Plot within the Ganga Basin, India. Agric. Water Manag. 2020, 234, 106108. [Google Scholar] [CrossRef]
- Zhao, W.; Cui, Z.; Zhou, C. Spatiotemporal Variability of Soil–Water Content at Different Depths in Fields Mulched with Gravel for Different Planting Years. J. Hydrol. 2020, 590, 125253. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Cifrodelli, M.; Dari, J.; Corradini, C.; García-Marín, A.P.; Moramarco, T. On the Applicability of Temporal Stability Analysis to Raingauge Network Design. Hydrol. Sci. J. 2019, 64, 1424–1438. [Google Scholar] [CrossRef]
- Dierckx, W.; Sterckx, S.; Benhadj, S.; Livens, S.; Duhoux, G.; Van Achteren, M.; Francois, M.; Mellab, K.; Saint, G. PROBA-V mission for global vegetation monitoring: Standard products and image quality. Int. J. Remote Sens. 2014, 35, 2589–2614. [Google Scholar] [CrossRef]
- Sterckx, S.; Benhadj, I.; Duhoux, G.; Livens, S.; Dierckx, W.; Goor, E.; Adriaensen, S.; Heyns, W.; Van Hoof, K.; Strackx, G.; et al. The PROBA-V mission: Image processing and calibration. Int. J. Remote Sens. 2014, 35, 2565–2588. [Google Scholar] [CrossRef]
- Merlin, O.; Escorihuela, M.J.; Mayoral, M.A.; Hagolle, O.; Al Bitar, A.; Kerr, Y. Self-Calibrated Evaporation-Based Disaggregation of SMOS Soil Moisture: An Evaluation Study at 3 Km and 100 m Resolution in Catalunya, Spain. Remote Sens. Environ. 2013, 130, 25–38. [Google Scholar] [CrossRef]
- Maselli, F.; Papale, D.; Chiesi, M.; Matteucci, G.; Angeli, L.; Raschi, A.; Seufert, G. Operational Monitoring of Daily Evapotranspiration by the Combination of MODIS NDVI and Ground Meteorological Data: Application and Evaluation in Central Italy. Remote Sens. Environ. 2014, 152, 279–290. [Google Scholar] [CrossRef]
- Shahriar Pervez, M.D.; Budde, M.; Rowland, J. Mapping Irrigated Areas in Afghanistan over the Past Decade Using MODIS NDVI. Remote Sens. Environ. 2014, 149, 155–165. [Google Scholar] [CrossRef]
- Chiesi, M.; Angeli, L.; Battista, P.; Fibbi, L.; Rapi, B.; Gozzini, B.; Maselli, F. Monitoring and Analysis of Crop Irrigation Dynamics in Central Italy through the Use of MODIS NDVI Data. Eur. J. Remote Sens. 2022, 55, 23–36. [Google Scholar] [CrossRef]
- Kragh, S.J.; Fensholt, R.; Stisen, S.; Koch, J. The Precision of Satellite-Based Net Irrigation Quantification in the Indus and Ganges Basins. Hydrol. Earth Syst. Sci. 2023, 27, 2463–2478. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).