Advantages of the Event Method for the Simulation of Water Quality in Pressurised Water Systems

Abstract

In this paper, several methods for the calculation of water quality evolution in drinking water distribution networks are analysed. The Lagrangian Time-Driven method has been implemented in the Epanet simulation software since version 2.0. In version 2.2, some improvements were implemented to deal with mass imbalances (Lagrangian Time-Driven improved method). However, it sometimes presents inaccuracies in calculations, especially when there are short-length pipes. To solve this problem, the implementation of the Lagrangian Event-Driven method is proposed, which provides more accurate quality results. In order to detail the differences and similarities of the results of the different methods and to determine under what conditions the results provided by Epanet are sufficiently adjusted, two practical examples have been carried out, one of them on a hydraulic model of a real network.

1. Introduction

The daily challenges faced by water supply network operators are increasingly complex and evolving due to population growth, water scarcity, infrastructure ageing, and climate change, among others [1,2,3]. Nowadays, alongside the traditional goals of guaranteeing sufficient flow and pressure, there is the requirement of guaranteeing the quality of the water supplied, which depends not only on the water quality at the network sources but also on the changes that water undergoes as it flows through the network.

In this way, drinking water network models are of great interest, as they provide deep knowledge of the system status and behaviour, allowing us to identify system needs and lacks in terms of water quality and to determine the most suitable actions to be taken in order to guarantee a safe and reliable supply.

For this reason, computational tools such as Epanet have been used for more than 20 years to develop hydraulic and water quality models of drinking water distribution networks [4,5,6]. While the development and use of hydraulic models are now broadly extended, as they have been consolidated as key tools to support network management, the use of quality models has not been widespread in the same way (although it was initially conceived for the simulation of water quality). However, today, quality models are becoming more necessary since, as mentioned before, drinking water network management is increasingly challenging, and water quality preservation is a major concern for operators [7,8].

The limited use of water quality models is mainly due to the complexity that their construction presents. First, the basis of quality simulation is hydraulic simulation since the different flows through pipes and their mixings have a direct impact on quality results. In this way, for a water quality model to be reliable, it is essential to first have a hydraulic model that is as calibrated as possible, which already is a challenge [9,10,11,12]. Also, the water’s quality experiences a significant deterioration in the last part of the distribution network (tertiary network) and in tanks, which precisely coincides with the part modelled with the least precision, as it is the most complex [13,14]. Therefore, in order to adequately model the quality that reaches the users, it is necessary to develop detailed models with all the elements. In third place, even the practical implementation of transport equations is not a simple problem (e.g., the mass imbalances and travel time inaccuracies of the Lagrangian model), nor is the diffusion or mixing at T junctions [15]; all of these issues have still not been definitely solved. In addition, water quality sensor data contain considerable uncertainties due to real water quality measurements usually being scarce, inexistent, or not consistent, so it is already a challenge to obtain a valid dataset to calibrate water quality models [16,17]. Moreover, determining bulk and wall coefficients is difficult [18,19,20] since they depend on multiple factors such as material, temperature, etc. Finally, the analysis and interpretation of quality simulation results is far from intuitive, as there are multiple mixing, growth, and decay processes occurring along various water paths through the network.

Because of all this, it is very difficult to guarantee and assess the reliability of the quality models, which is why they either do not exist or are very imperfect.

The most commonly used transport methods to carry out both hydraulic and water quality simulations are the Eulerian Discrete Volume (EDV), the Lagrangian Time-Driven (LTD), and the Lagrangian Event-Driven (LED) methods. This technical paper is focused on the analyses of those implemented in Epanet 2.0 and 2.2, the LTD and LTD improved (LTDI) methods, which are compared with the proposed LED method.

The transport methods used in the Epanet software have evolved over the years. The EDV method [21,22], initially implemented in Epanet since version 1.1, consists of observing the evolution of a substance as it travels down a given pipe segment. In this way, each pipe is divided into several segments with a length that is fixed but different for each pipe, depending on its flow, trying to equal the travel time of each segment with the water quality time step. In each segment, an incoming, outgoing, and reacting substance balance is made, which allows us to determine the evolution of the substance’s concentration in each segment through time. In the junctions (and tanks), a mixing process is also carried out at every time step in order to determine the quality of the first segments of the outgoing pipes based on the mixing that occurs in the last segments of the inlet pipes (and the concentration of the volume already stored in tanks). When updating flows at every hydraulic time step, all pipe segments are redefined so as not to have mass imbalances in the process.

In 1996, all methods were analysed in terms of their accuracy, computational time, and memory usage. The LTD method turned out to be more efficient and versatile than EDV [22]. Therefore, subsequent Epanet versions, up to the latest one, have incorporated this method.

The LTD method [23] also consists of splitting pipes into segments, but in this case, each segment’s behaviour is followed as it travels down the pipe. The segments move along the pipe and do not change in size as they move, but their size begins to decrease as soon as the segment reaches the downstream junction of the pipe (or tank/reservoir) until it is completely consumed. Moreover, segments grow in size upstream of the pipes, leaving the junction (or tank/reservoir) as the outflow from the junction enters them. The concentration upstream of the pipes leaving the junction is determined following a mixing process, considering the concentration of the downstream segments of the incoming pipes, the possible injection into the junction, and the concentration of the water that is already stored in the case of tanks/reservoirs. When, at a given instant, the water quality leaving the junction changes above a certain threshold (quality tolerance), the outgoing segment leaving the junction stops growing, and a new segment is created. While these segments travel through the pipe, their water quality does not change except due to the reacting processes within each segment, as their size remains constant while travelling. When the flow conditions change, there is no need to redefine new segments, but the existing ones will travel, grow, or consume at a different rate, depending on the new flows.

The LED method [24,25] is another method for determining water quality in pipes. It is based on the principle that the water quality remains constant while flowing through a pipe unless a reaction process occurs. Consider that a flow enters the network from a supply source and is distributed through several pipes; each particle will arrive at the end of the pipes at a different time, depending on the flow velocity and the length of each pipe. The first particle to reach the downstream junction determines an event, and as a consequence of this event, a mixing process takes place at the downstream junction, where the water quality of all flows entering the junction at that moment is considered for the mixing process. The arrival of a particle (event) at a junction triggers a new list of potential events corresponding to the arrival times of the particles resulting from mixing at the junction towards each of its outgoing pipes. The method manages a list of potential events, which are the arrival times of particles of different quality at their downstream junctions, and the next event to occur is the first on the list, kept in order of increasing arrival time. If a substance reaction occurs, it is evaluated when an event takes place, based on the time elapsed since the previous event that affected the downstream junction of the pipe. All junctions are continuously considered in the list of potential events, allowing for multiple events to be triggered at the same junction but at different times. If the time gap between two consecutive events for the same junction is less than the quality tolerance, the new event is not executed in order to reduce the size of potential events. The scheduling of this method is more complex, mainly due to the process of reorganising events when flows change, but according to the author, it is more efficient.

From Epanet version 2.0, the LTD method was implemented and was widely accepted and used for many years. However, in recent years, several authors have highlighted problems with mass imbalances and deviations in travel times. To address these issues, some improvements to the LTD method have been introduced in Epanet version 2.2, resulting in the implementation of the LTDI method. Despite this, the new method still shows deviations in terms of mass imbalances and travel times [26,27,28], as will be deeply discussed in the following lines.

In general, these errors occur when the volume transported through a pipe in a simulation time step (∆t) is greater than the pipe volume, a very frequent situation when there are short pipes. Thus, to minimise these errors, a generalised solution is to use smaller simulation time steps, although this does not completely eliminate errors and increases the calculation time.

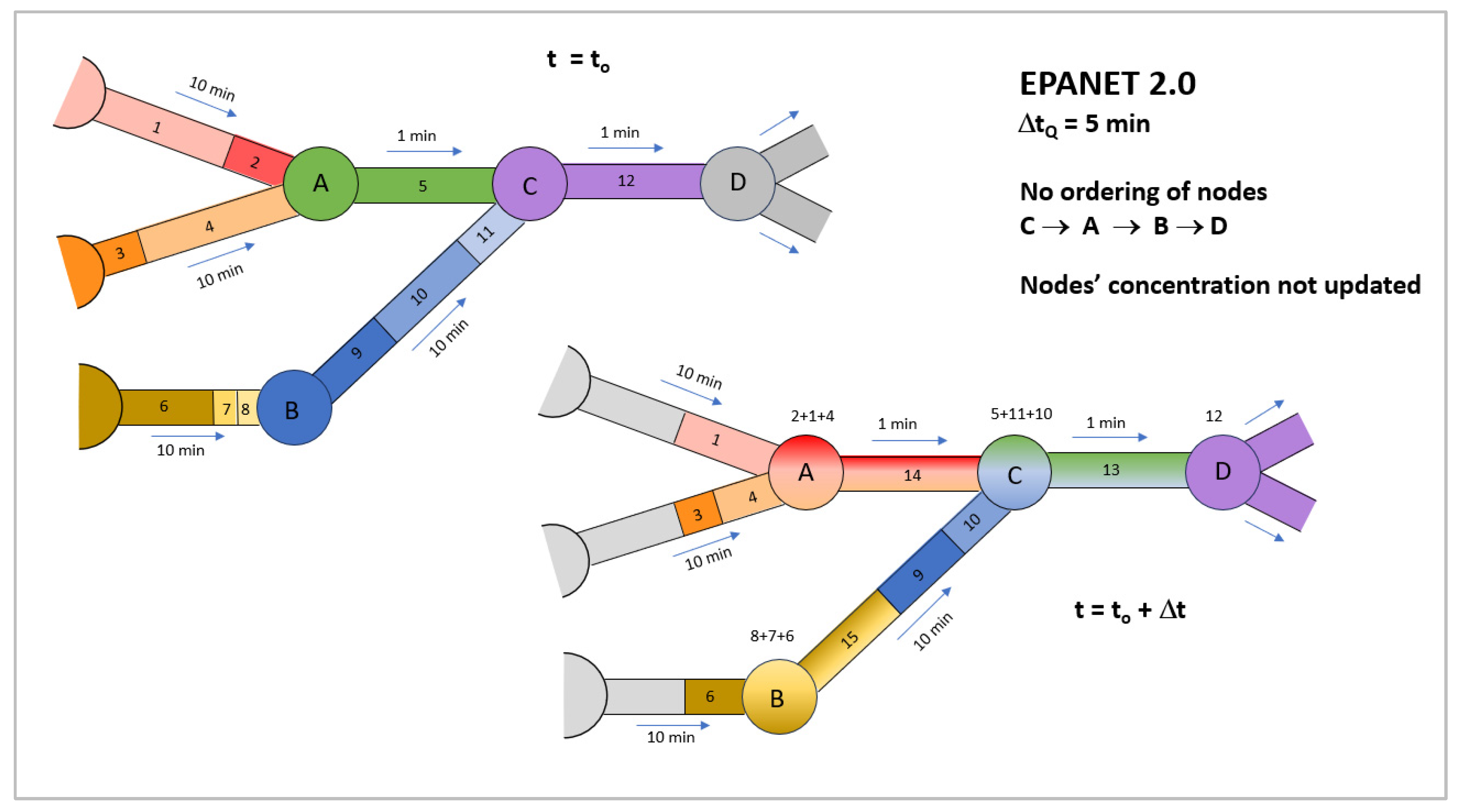
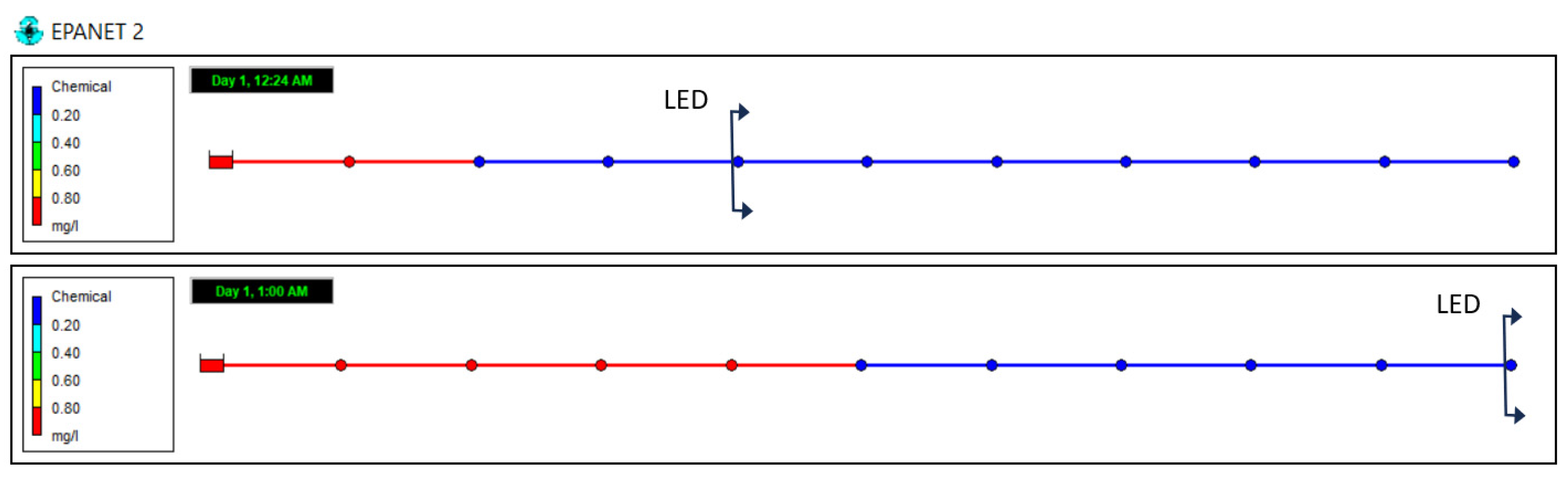
Figure 1 illustrates the process carried out by the LTD method implemented in Epanet version 2.0 to simulate the transport and mixing processes at junctions.

Figure 1 contains several pipes divided into segments with a different concentration at time t₀. Each segment is numbered from 1 to 12 and is distinguished by a different colour. Moreover, the junctions have been identified alphabetically and share the same concentration or colour as the first segment of the pipes that originate from them. Finally, the time taken for a particle of water to travel along each pipe for the current velocities, determined by the flow rate and the pipe section, is indicated. Note the presence of two short pipes, 5 and 12, with a travel time of the short pipes is 1 min, exactly 1/5 of the simulation time step, ∆t = 5 min.

In Epanet 2.0, the order in which the junction concentrations are updated for each time step ∆t is indifferent. The order follows the sequence in which they are declared in the .inp file. Assuming the order is as shown in Figure 1 (C → A → B → D), the mixing is initially performed at junction C, which is reached during the time interval ∆t by the whole segment 11, half of segment 10, and the whole segment 5. With regard to this last segment, it should be noted that at time step ∆t, up to 5 times the volume of segment 5 enters junction C, i.e., a volume greater than the volume of water contained in the pipe. However, the method implemented in Epanet 2.0 does not allow for the consideration of the concentration of segments located upstream of the upstream junction of the pipe, thus preventing the advancement of the water contained in the following upstream segments 2, part of 1 and 4. Hence the colour assigned to junction C is a blend of three colours (segments 5, 11, and 10) instead of six (segments 5, 11, 10, 4, 2, and 1). This inaccuracy affects the calculation of the concentration of junction C, resulting in a ‘mass imbalance’ carried over to the following time steps. Also, an inaccuracy in the calculation of the progress of the contaminant through the network is seen due to the delay of the front upstream of the upstream junction.

Following the discretisation process of the transport equation, after mixing at all junctions, the concentration of the junctions is transferred to their downstream pipes, creating new segments if the new concentration is different from the existing one, while the existing segments are moved downstream to fill the gap left by the segment(s) consumed by updating the concentration of the junctions; for instance, new segment 15 and the relocation of segment 9 and the left portion of segment 10 (note that segment 11 and a part of segment 10 vanish as they have entered junction C to calculate its new concentration). However, if the same process is performed with segment 13 leaving junction C, the length of the new segment exceeds the downstream pipe travel time by a factor of 5. Epanet 2.0 does not consider going beyond the downstream junction, resulting in the loss of four parts of the outflow volume and further contributing to the ‘mass deficit’ issue. Figure 1 shows the new concentrations in the considered pipe segments after the mixing process at all junctions and the transfer of their concentrations to the downstream pipes.

Mass imbalances and inaccuracies in travel time are well-known issues when a substance flows through short pipes. These issues have led to an improvement in the quality model implemented in version 2.0, which was released in version 2.2 and is a variation of the previous model to extend mass transport beyond contiguous junctions for short pipes.

The new Epanet version 2.2 considers the concentration of the upstream junction when mixing at each junction, if necessary, i.e., if the upstream segment has a travel time higher than ∆t because the pipe is a short section. The latest segment is prolonged as necessary once the water in that pipe has been consumed, assuming the concentration of the upstream junction. Furthermore, the order in which the concentrations of the junctions are updated is no longer arbitrary. Instead, it is done in a sorted manner with the direction of flows from upstream to downstream so that when the latest segment is extended in the short sections, the concentration of the upstream junction is assumed to be the one just calculated in the current time step, not the one from the previous time step. These three improvements, sorting, prolongation, and updating, largely mitigate mass imbalances. However, the method shows significant deviations when there is a continuous sequence of short sections.

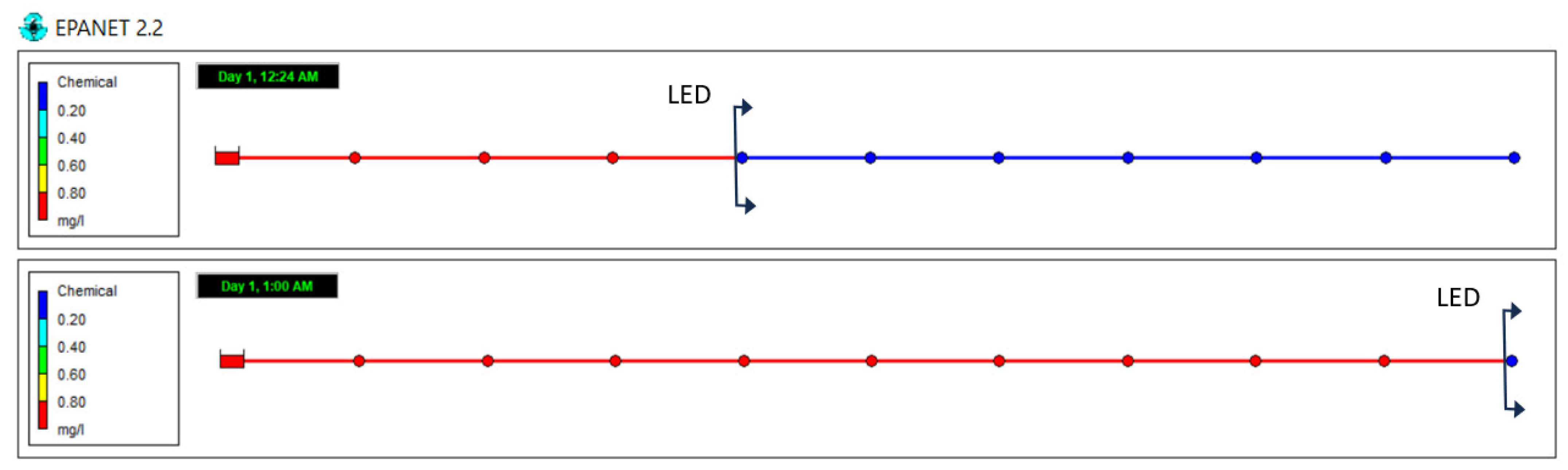
To gain a better understanding of the differences from the previous method, we will now refer to Figure 2. This figure solves the same example but with the mentioned improvements. First, note that the order in which concentrations at the junctions are updated is now as follows: A → B → C → D, according to the flow direction. Furthermore, the concentration of a junction is updated when the concentrations of all upstream junctions have been updated for each time step.

Figure 2 shows that during the initial mixing process at junction A, for a time step of ∆t = 5 min, segment 2 is fully consumed along with a portion of segments 1 and 4. Next, the mixing is carried out at junction B in the same way, consuming segments 8 and 7 and part of segment 6. Mixing is then carried out at junction C, consuming segments 5 and 11 and part of segment 10. As previously stated, the volume of the pipe containing segment 5 is lower than the displaced volume in ∆t. Therefore, a new last segment, four times the size of the one already consumed, is added. The concentration of this new segment is taken from the upstream junction A, and its concentration has already been updated in the previous step. Then, the concentrations of segments 5, 2, 1, 4, 11, and 10 contribute to determining the new concentration of junction C. Finally, at junction D, mixing is carried out following the same process described above. A short section contributes to the mixing, and its concentration will be determined by the concentration of segment 5 and all the other segments that contributed to updating the mixing at junction C, located upstream. The concentration of junctions is represented by the colour codes used in Figure 2.

After mixing at all junctions, the next step is to create new segments in the outlet pipes of the junctions with their calculated concentrations. Then, we move all other segments downstream by advancing ∆t. If the downstream pipe is short, part of the transported mass will inevitably be lost, as the method does not extend downstream.

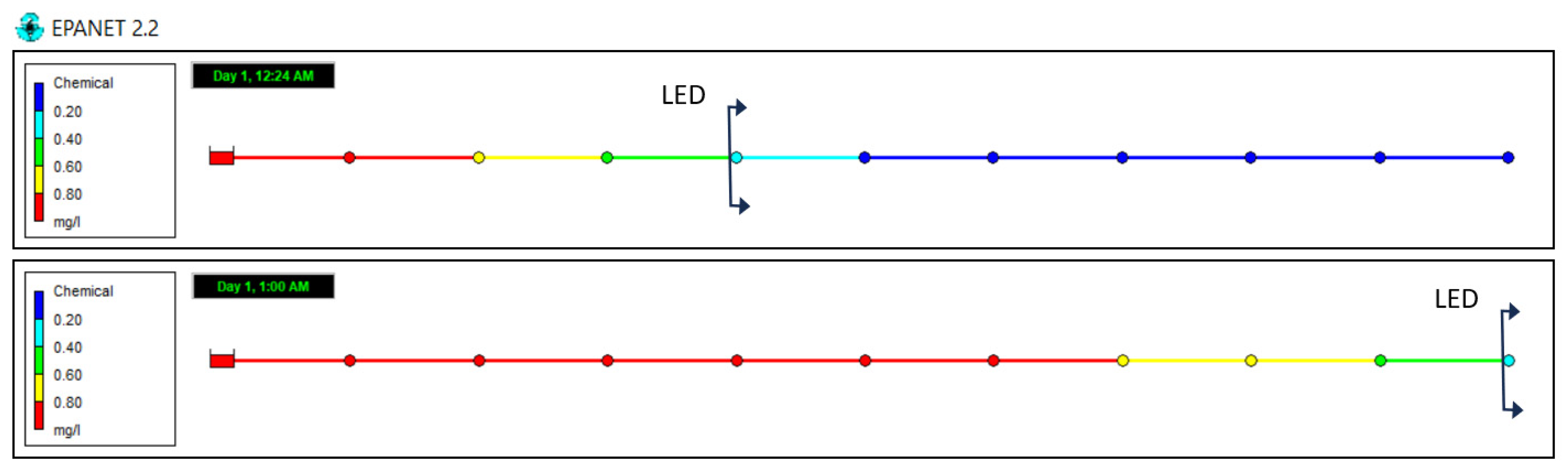
When comparing Figure 1 and Figure 2a significant difference can be seen in the calculation of the concentration of the different segments after one ∆t. In the first method, the concentration of segment 2 will not reach junction D until after three intervals ∆t, whereas in the second method, it already reaches junction D in the first interval ∆t. This is closer to reality since the travel time between junctions A and D is only 2 min. However, the new method still makes certain assumptions, such as considering the quality of the upstream junction for the complementary segment of the upstream section when it is created due to short pipe sections. It should be noted that this may not always be the case. In the case of short pipes, mass is lost in the downstream transport. However, it must be said that the fact of following order in the direction of the flows attenuates these errors, which, in practice, are known as numerical diffusion errors, i.e., associated with the discretisation process itself.

In order to reduce the errors due to mass imbalances and travel times, a generalised solution is to reduce the quality calculation time step. Regardless of how much these are reduced, the errors introduced by the LTD method are not eliminated, as they would have to be reduced to the point where no pipe would transport more volume in a quality time step than is contained in the pipe itself, and this is very difficult to achieve when there are pipes of small length.

This is particularly important today when it is possible to develop very detailed models that include all elements so that pipes are divided into several segments to take into consideration the house connections, manual valves, etc. Nowadays, the tools available for the development of models and the information contained in Geographic Information Systems (GIS) make it possible to build very accurate, detailed models in which all network elements are reflected [29,30]. This is essential, as the hydraulic behaviour of each component directly affects the mixing and transport processes, which have a great impact on the simulation of water quality in the distribution network, where it deteriorates the most. Moreover, these detailed models, by including all the elements of the system, often contain short pipes, making the deviations in the quality calculations more pronounced and significantly penalising the results of the current LTD and LTDI methods.

Therefore, the LED method represents a significant advance in adapting quality models to new challenges and in maintaining the precision of the calculations intended by incorporating all the elements of the network into the model. The main novelty of the LED method is that it accurately calculates the mass balances at junctions each time a new quality segment reaches a junction, regardless of the length of the pipe and the time at which it occurs. In contrast, in previous methods, the calculation interval is fixed, and during this time, a quality segment may reach several junctions, especially if the pipes are short, leading to mass imbalances.

In this way, the LED is the only method that makes it possible to calculate travel times with precision and to reduce mass imbalances to zero.

The following paper aims to describe the LED method and the considerations that need to be taken into account in its practical implementation. For now, we have considered the case of looped networks with pipes of any length in which a single non-reactive contaminant is transported. It remains for further research to consider the presence of tanks where the water quality varies according to different mixing processes, the presence of pumps and regulating valves, the transport of reactive substances, and even the transport of several substances reacting simultaneously, all of which increase the complexity of the problem, but are nonetheless extensible to these cases.

2. Materials and Methods

The LED event-simulation method consists of directly tracking the advance of the boundaries, also called event fronts, that separate the different quality segments. If we consider the contaminant to be non-reactive, the water quality of a segment does not change over time, nor does the quality of the junction downstream of the pipe through which it flows. When an event front reaches a junction, it causes a change in the concentration of the junction, resulting from the mixing of all the pipes that converge at the junction.

The arrival of a front at a junction is known as an event. In this way, to follow the evolution of water quality through the network over time, all that is required is to monitor all active event fronts at each moment, determine the arrival times at the downstream junctions, and proceed in an orderly manner according to the arrival times.

When a new segment with a different concentration reaches a junction, i.e., when an event takes place, the LED method calculates the concentration of the new junction as follows:

$$C_{i,t}=\frac{Q_j{ C}_j+{\sum }_{k\in {\{I}_i-j\}}{Q}_k{ C}_k}{{\sum }_{k\in I_i}{Q}_k}$$

(1)

where i = the junction reached by an event front; j = the upstream pipe carrying the event front; $C_{i,t}$ = the concentration of junction i at time t; $Q_j$ = the flow of pipe j; $C_j$ = the concentration of the first segment of pipe j; $Q_k$ = the incoming flows of the remaining pipes that reach junction i; and $C_k$ = the concentration of the corresponding last segments of pipe k. Finally, I_i is the set of pipes incoming to node i. Furthermore, if some external mass flows were injected into node i, it would be added to the numerator.

As the calculation times are given by the times at which an event takes place, only the last segment (or part of it) of the inlet pipe of each node reaches it. Thus, the mixing process is more accurate, and errors are reduced as the following conditions are met:

$$Q_j∆t_Q=V_j$$

(2)

where $V_j$ is the volume of the segment of the event that takes place. And also:

$$Q_k∆t_Q\le V_k$$

(3)

This means that the rest of the inlet pipes contribute to the mixing with their last segment, or part of it, but never exceed the size of that last segment.

To go into more detail, consider a network that is supplied from one source with a certain concentration of a non-reactive substance (contaminant). If the network is initially clear of such substance, when the contaminant enters the network, the first events are created, one for each outlet pipe of the junction where the substance is injected. The event involves an abrupt change in concentration and the creation of a front that separates the uncontaminated water from the contaminated water. In fact, any change in concentration at the outlet of a junction will cause a new event to advance downstream. Each front will arrive at the end of the pipe through which it flows at a different time, depending on the flow velocity and the pipe length. The one that arrives first at the corresponding downstream junction will determine a new event, which is caused by a change in concentration resulting from the mixing process at that junction, where the concentration of at least one of the inlet pipes has changed. This will result in a new list of events corresponding to the new fronts created by each of the pipes leaving the junction, which will begin to move towards the downstream junctions at the speed of water circulation in them. The method always keeps a list of active events updated, and the next event to be treated is the first to arrive at its corresponding downstream junction, which requires keeping the list always in ascending order by the arrival time of each event at its downstream junction.

Several events can be considered simultaneous if the time gap between arrival times is lower than a threshold. On the other hand, if a junction is reached by several consecutive events and the time gap between them is lower than the threshold, it can be considered as a single event, thus reducing the number of active events. Also, if the new concentration resulting from the junction mixing differs from the concentration in the upper segment of the outlet pipe by less than a certain tolerance, a new front is not created in this outlet pipe, helping to reduce the number of active events. Finally, the events die out definitively (without creating new events) when they reach a sink-type junction from which there is no flow except for an external flow or discharge to a reservoir/tank.

If the substance is reactive, its concentration would be evaluated at the moment of arrival of an event at the downstream junction and would be applied to all water volumes entering the junction at that moment, taking as reference the last moment in which the quality of each of the segments reaching that junction was evaluated.

In summary, in the LED method, the time interval used to update the concentrations is variable, depending on the arrival time of the event fronts at their downstream junctions, which are updated each time an event reaches a junction or when the velocities in the pipes change by achieving the end of a hydraulic interval. In addition, the concentrations of the junctions are only updated when an event takes place and only for the corresponding junction, being maintained for the rest of the junctions as long as the concentrations of the inflows do not change. In this way, for each event, only the concentration of the affected junction is updated and not that of all the junctions in the network, thus significantly reducing the calculation time. Only when the results are to be observed are the concentrations of all junctions in the network updated simultaneously.

Figure 3 shows the sequence of steps that constitute the execution of the LED method, following the considerations discussed in the previous paragraph.

Initially, the concentration is assumed to be 0 in all nodes except tanks and reservoirs if they have stated initial concentrations. An empty event front list is then created and populated with the first event fronts. Once the first hydraulic simulation is performed, the event fronts are updated with their corresponding arrival times and distances to their downstream junctions (t_end, d_end). At the same time, the time to the next hydraulic interval is determined (∆t_H). When the next event takes place, the concentration at the arrival junction is updated, considering contaminant injection into the mixing node, if existing. New event fronts are then created in the pipes downstream of the junction if the quality tolerance is exceeded. After reordering the list of event fronts by arrival time (t_end) and updating the gap to the next hydraulic time step (∆t_H), a comparison is done: if the next hydraulic time step occurs before the next event time, then the hydraulic is updated, the existing event fronts are updated, and new event fronts are created in each junction due to flow changes; otherwise, the process repeats from step 3.

Figure 4 illustrates the process carried out by the implemented LED method, which is an improvement on the methods currently implemented in EPANET to simulate the processes of transport and mixing of substances in junctions.

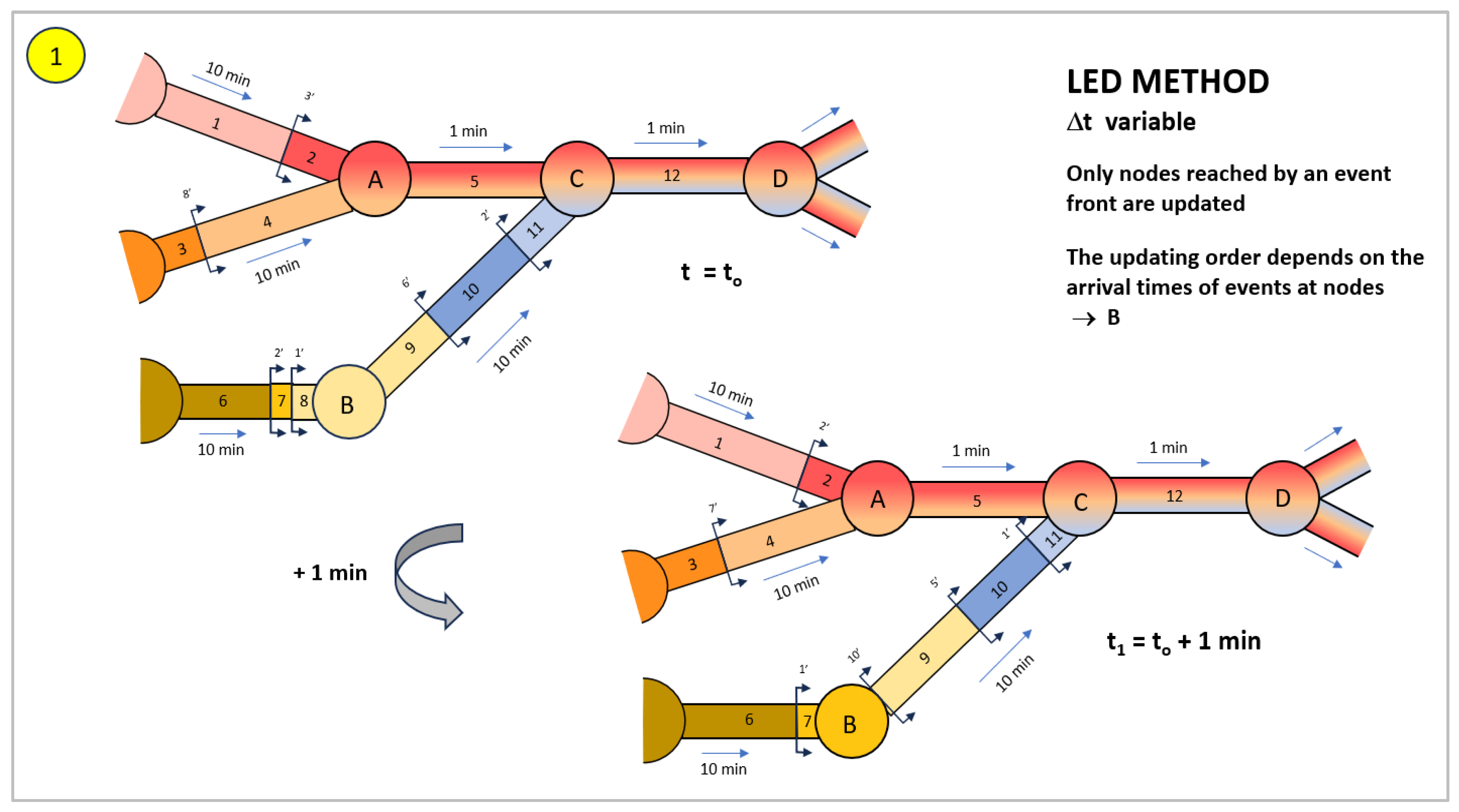
In Figure 4, the events have been represented by arrows indicating the position and direction of the different fronts at a generic instant t₀. Above them, the travel times of the pipes for the current velocities are noted (for simplicity, only two travel times have been considered, 10 min or 1 min). In addition, the arrival time of the front at the downstream junction, in minutes (’), is noted for each front. It is assumed that the concentration of the segment behind each front is constant until another upstream front or the upstream junction of the pipe. The concentration of the different pipe segments has been differentiated by colours, with each segment being assigned a different number, from 1 to 12, as in Figure 2. The fundamental difference between the two figures is that the initial concentration of the junctions is now related to the concentrations of the incoming flows (by colour grading) since the mixing at the junctions is continuous and always related to the incoming concentrations.

Figure 4 shows that the first junction reached by an event front is junction B (there is now no predefined order of visit), with ∆t₀ = t_end = 1 min. When the new front arrives at junction B, the current event is discarded, and the concentration of the junction is updated by mixing the concentrations of the segments arriving there. In this case, the concentration at B becomes that of segment 7 in ochre. Then, the concentration of junction B is compared with the concentration of the first segment of its corresponding outgoing pipes, and if the difference between both exceeds the quality tolerance, a new event is created for each of the outgoing pipes of junction B; in this case, a single pipe with t_end = 10 min; the new front confines segment 9 and will create a new segment starting from B for the following instances. The rest of the junctions maintain their concentrations, while their arrival times are updated to account for the advance of the segments in the time interval considered; in this case, this means reducing the arrival times of the rest of the events by 1 min.

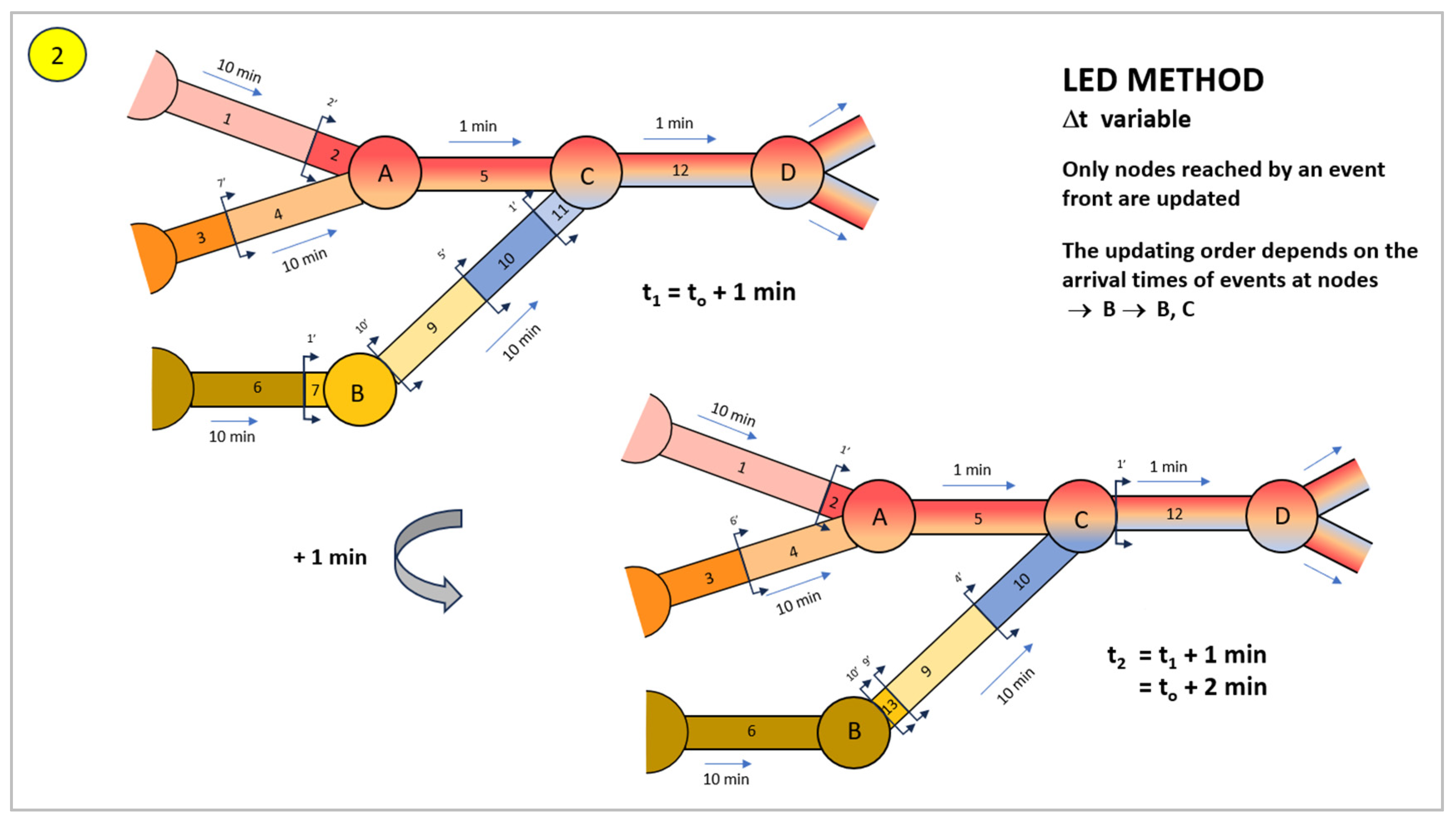
The next events to arrive at a downstream junction will be the front of segment 6, which will also reach junction B, and the front of segment 10, which will reach junction C, also in the new time interval ∆t₁ = t_end = 1 min, as shown in Figure 5. In this case, it will be necessary to simultaneously update the concentrations of junctions B and C and apply the same procedure, creating new fronts in the outgoing pipes of both junctions. Note that events 8 and 7 are considered different because they are separated by a time of 1 min, supposedly longer than the time threshold established.

If the steps followed are analysed in detail, it is concluded that the event method considers all the mass entering the junctions when performing the mass balance at the considered instant, thus avoiding the mass imbalances observed in the other methods described in the introduction.

An important aspect to consider in the practical implementation of either method is computational efficiency. In the case of the LED method, the number of mixtures performed at junctions is lower than for the LTD and LTDI methods since, in the LED method, only the concentration of the junction at which the event arrives is updated, whereas, in the other methods, the mixtures for all junctions in the network must be updated at each ∆t_Q. For example, for a network of 1000 junctions with ∆t_Q = 1 s, the LTD and LTDI methods would calculate 1000 × 3600 concentrations at the junctions every hour. On the other hand, in the LED method, perhaps the event arrival time at the junctions will be 1 s for some pipes but not for all. There will be times between events of 1 s, but many others will be longer, and since the LED method only updates the concentration of the junction where the event arrives, this compensates for the computational effort, as it is unlikely that 1000 events will arrive at their corresponding downstream junctions every second. Thus, the computational effort may be similar for all methods, but the computational accuracy is higher for the LED method.

3. Results

As previously explained, the LTD and LTDI methods present inaccuracies in the calculation of the quality evolution. To analyse these inaccuracies, two examples have been developed: a simpler one consisting of a linear pipe divided into 10 equal sections and a more complex one corresponding to an area of a real network.

Both examples show the results of the LTD method (Epanet 2.0), the LTDI method (Epanet 2.2), and the LED method. The aim is to detail the differences and similarities between the results of the three methods and to determine under which conditions the results provided by Epanet are sufficiently accurate.

3.1. Linear Pipe with 10 Sections

The first case study has a demonstrative purpose to show the inaccuracies of the LTD and LTDI methods implemented in Epanet 2.0 and 2.2. For this purpose, a simple network configured only by a series of short, aligned sections has been considered.

The following example consists of a 3600 m long pipe divided into 10 sections of 360 m each. All the pipe sections have a diameter of DN200 mm and carry a flow rate of 31.41 l/s, so the flow velocity is 1 m/s. A water particle thus takes 6 min to travel through each section, and 60 min to travel through the whole pipe.

Figure 6 shows the configuration of this first example.

In general, as mentioned above, both the LTD and the LTDI methods present good results as long as ∆t is lower than the time it takes for the total volume contained in each pipe to travel through it (renewal time).

The results obtained by simulating with the LTD (Epanet 2.0), the LTDI (Epanet 2.2), and the LED methods, the intrusion of a non-reactive contaminant into the source reservoir at a concentration of 1 ppm, are discussed below. The contaminant travels through the linear pipe, reaching each of its junctions at 6-min intervals and completes the entire length of the pipe in 60 min.

Figure 7 compares the results obtained when simulating in Epanet 2.0 (LTD) with a quality time step ∆t_Q = 6 min, together with the advancement of the event front that is obtained when simulating with the LED method. Since ∆t_Q does not exceed the renewal time, the simulation results are accurate and show no deviations, and the results obtained when simulating with both methods are the same.

Figure 8 shows the comparative results obtained with Epanet 2.0 when doubling ∆t_Q = 12 min and with the LED method. In this case, in each calculation interval, twice the volume contained in the pipes is transported through them, but this is not considered by the LTD method, resulting in a ‘mass defect’ and, thus, important errors in the quality calculation. Furthermore, for each calculation interval, the contaminant front does not advance beyond the upstream junction, thus leading to a front advance speed that is half of the real one, as the quality interval is set to twice the travel time of each section.

Being aware of this problem, in the LTDI method implemented in Epanet 2.2, modifications have been made to the quality calculation methodology that mitigates the inaccuracies in the quality calculation that occurred in version 2.0. Figure 9 shows the results obtained when simulating the same network in Epanet 2.2 with ∆t_Q = 6 min, together with the event front advance obtained when simulating with the LED method. As with the Epanet 2.0 simulation, the results are accurate and consistent with those obtained using the LED method since no more volume is transported through the pipes at ∆t_Q than is contained within the pipes.

However, when ∆t_Q is increased to 12 min (Figure 10), it is observed that the front is not lagging behind, as in Figure 8, but that part of the contaminant reaches the fourth junction at 24 min, although the concentration is lower than the expected (delayed diffusion), and there is also an advanced diffusion effect that leads the concentration to reach the fifth junction when it has not really had time to reach there. After 60 min, the LTDI method shows that the substance has reached the extreme junction but not at full concentration. In this way, the LTDI method attenuates the errors of the LTD method, but they are not totally eliminated, as a mass defect is still observed.

In this case, a contaminant concentration is observed at the location of the event front calculated by the LED method, although its concentration is lower than expected (delayed diffusion). In addition, it is interesting to note that a contaminant concentration is observed downstream of the event front prior to the arrival of the contaminant event front (forward diffusion).

This first example is a good illustration of the inaccuracies that occur when performing water quality calculations using the LTD and LTDI methods in terms of mass balances and substances transport through the network. When in a quality time step, a volume of water is transported through the pipes greater than the volume contained in them, the mixing in the junctions is carried out in the first stage with a volume of water in which the concentration of the substance is known, and the rest of the volume entering the junction for mixing presents an estimated concentration, which in the case of the LTD method is equal to the concentration of the upstream junction calculated in the previous time step. In the case of the LTDI method, this is equal to the concentration of the upstream junction updated for the current time step. However, even this last improvement is not definitive, as there may be several upstream pipe sections that determine the final quality of the junction under consideration.

The LED method solves all these problems and provides accurate concentrations at the junctions, regardless of the length of the sections, since the calculation time step to be considered at each moment is adapted to the length of the sections. Moreover, the calculations are not increased since only the concentration of the junction reached by an event front is updated at each time step.

3.2. Hydraulic Model of a Real Network

The hydraulic behaviour of the system directly affects the results of the quality simulation, as the mixing and transport processes have a strong influence on the results obtained. Therefore, the development of accurate quality models requires the use of detailed network models in which as many components as possible are considered. On the other hand, this will lead to the appearance of pipe sections of short length in the model, which, as has been shown before, are the precursors of the inaccuracies in the quality calculations carried out with the LTD and LTDI methods.

The aim of this second example is to determine the impact of the inaccuracies in the calculation of water quality using the LTD and LTDI methods implemented in Epanet on hydraulic models of real networks.

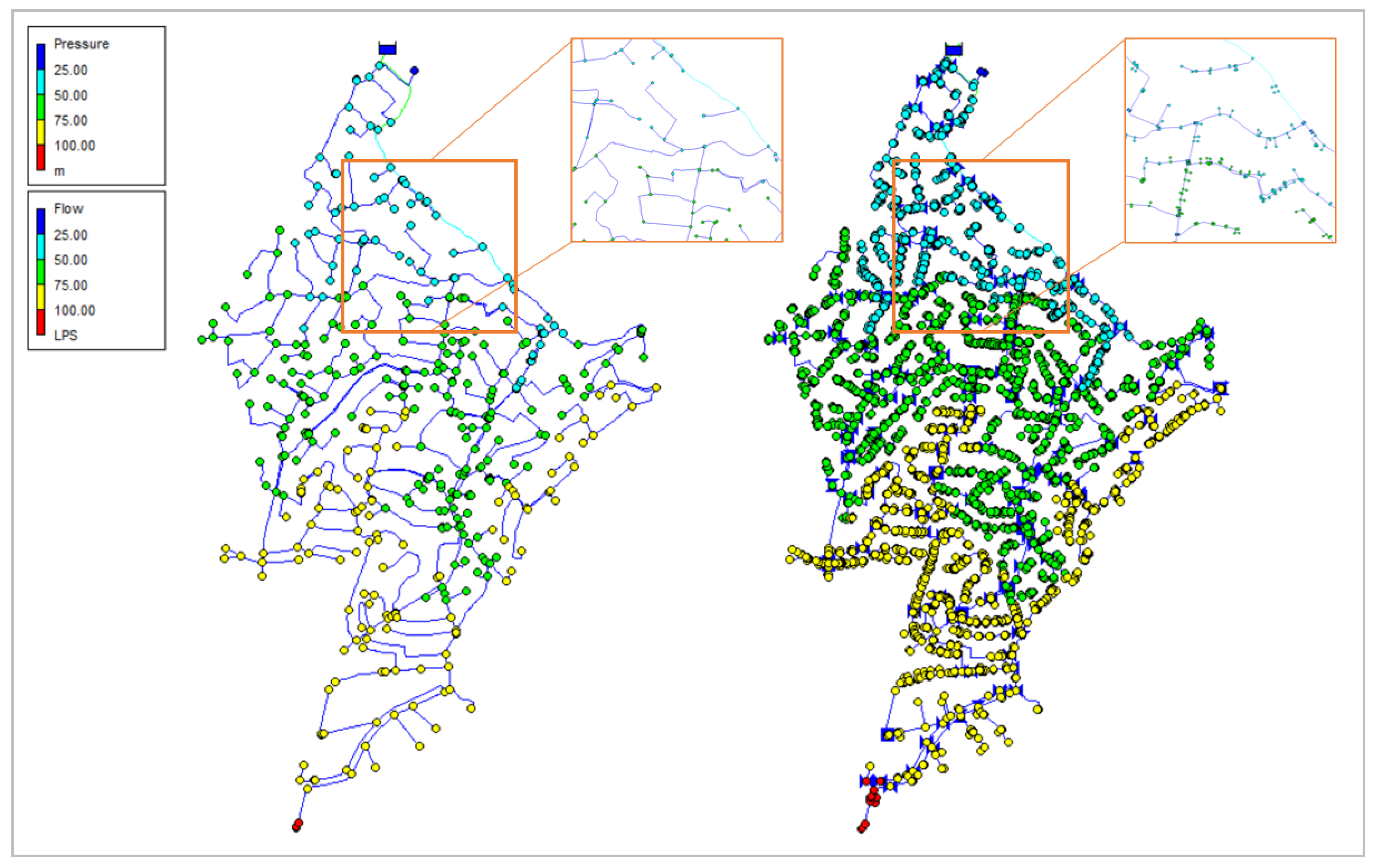
For this purpose, two models of the same network have been created, one of them simplified, where the service connections and isolation valves have not been included in the model. The second model is more detailed and includes the service connections of the users and the isolation valves that split the pipes. Figure 11 shows both models as follows: the simplified model on the left and the detailed model on the right.

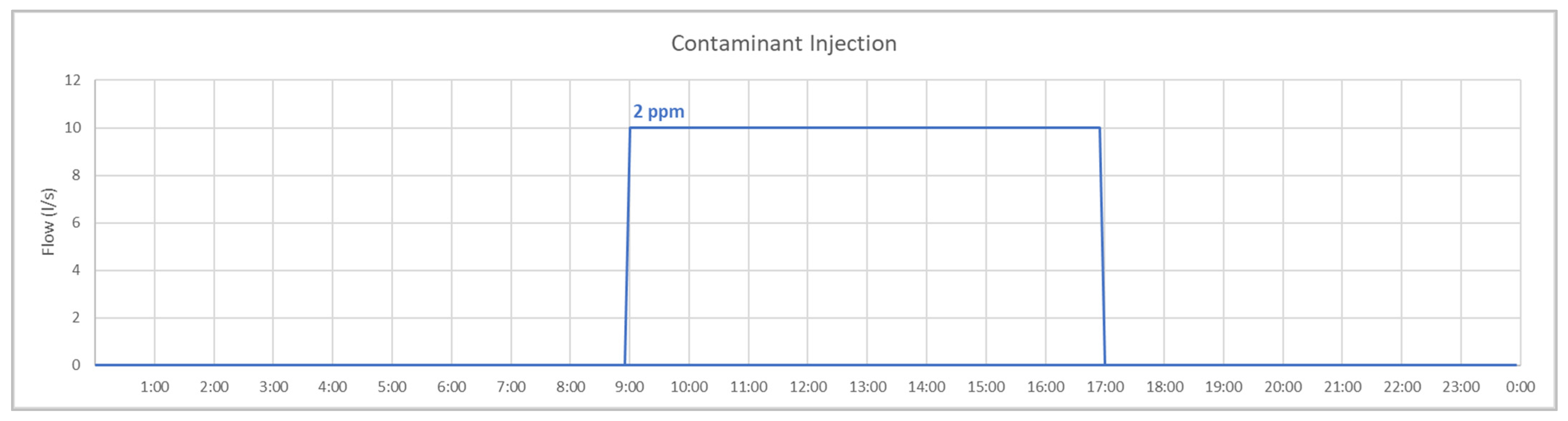
As shown in Figure 11, the network consists of a single supply point, which feeds the entire system by gravity, with no intermediate control elements. From 9 am to 5 pm, a flow of 10 l/s with a concentration of 2 ppm of a given non-reactive substance is injected into a junction of the network (Figure 12).

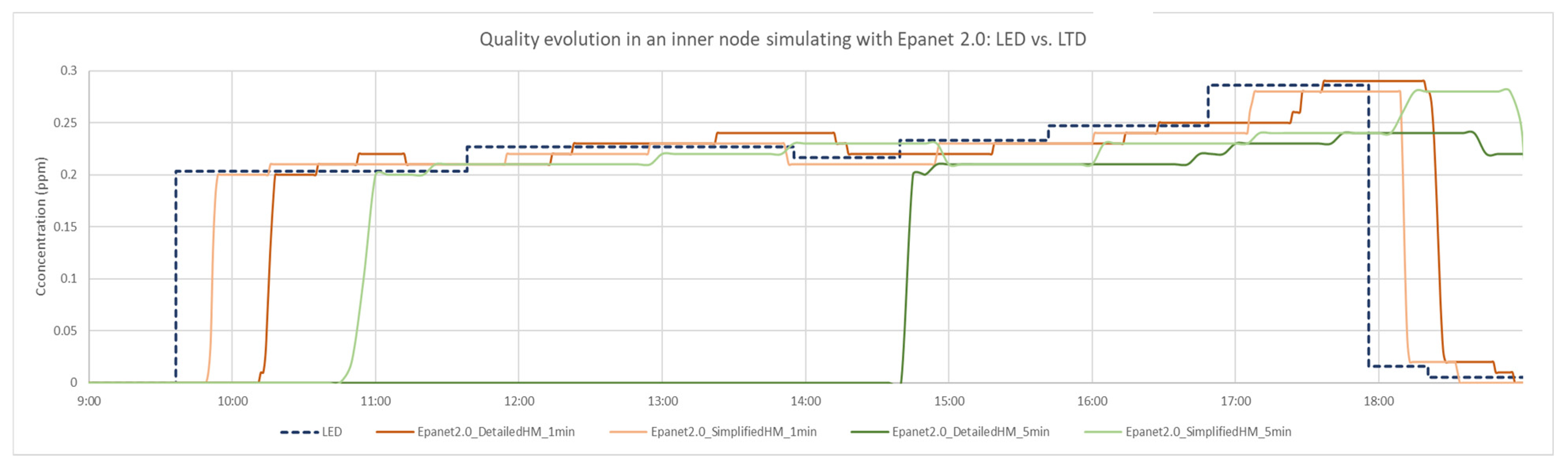
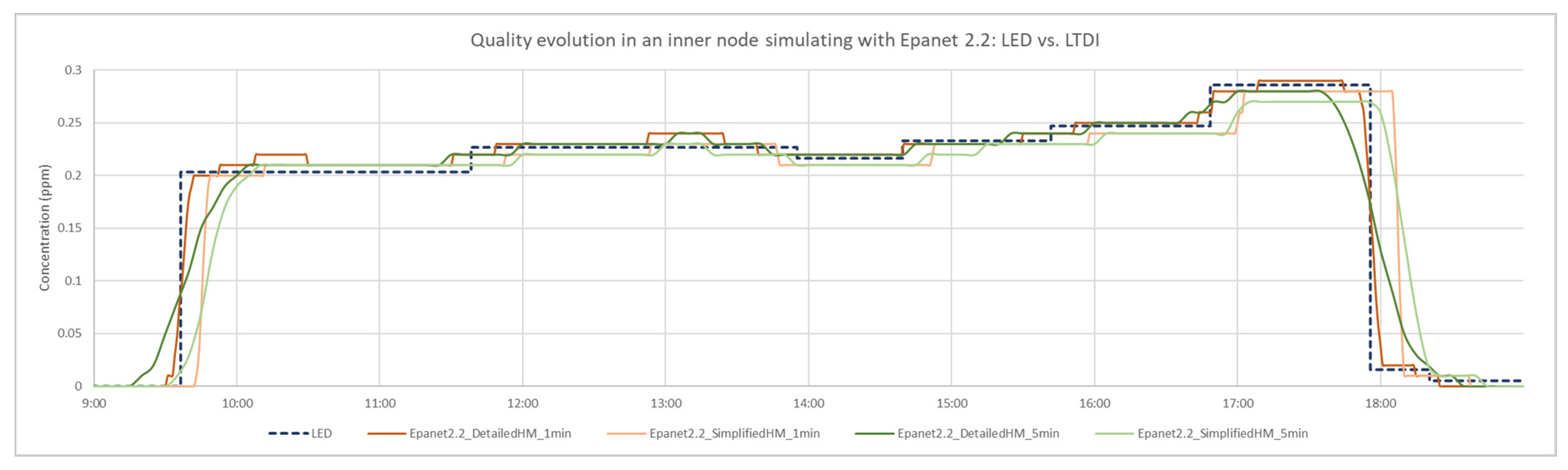
A comparison of the results of the simulation using the different methods was carried out at various points in the network, with similar conclusions in all cases. Figure 13 and Figure 14 show the quality results obtained at one of the intermediate junctions of the network, for two ∆t_Q considered: 1 min and 5 min.

In the case of the LTD method (Epanet 2.0), a considerable delay in the arrival of the contaminant is observed. This delay becomes more pronounced in the case of the detailed models due to the existence of short-length sections that penalise the quality calculation. Moreover, this delay increases significantly with increasing ∆t_Q, reaching several hours.

On the other hand, the LTDI method (Epanet 2.2) presents less pronounced deviations in the calculations; the differences observed being of a few minutes. In this case, it should be noted that for a small ∆t_Q, even if the detailed model contains short sections, the observed calculation inaccuracies are not so significant.

4. Discussion

The comparison of the three methods reviewed for the calculation of water quality in drinking water distribution networks shows that, although the LED method is the only one that provides accurate results for the hydraulic models of real networks in terms of the transport of substances, the LTDI method presents quite good results when simulating with very small intervals ∆t, even in the case of detailed models with multiple pipes of short length. This was not the case with the LTD method implemented in previous versions of Epanet, where the results obtained presented significant deviations.

The LTDI method still presents certain inaccuracies in the calculation, but in real cases, more examples will have to be tested to see to what extent these inaccuracies can be significant. This inaccuracy will always depend on the interval ∆t_Q considered, whereas the event method is insensitive to this parameter as ∆t_Q is adaptive. In particular, these inaccuracies can be more critical when backtracking methods are used to locate the origin of a contaminant, where the accuracy of the travel times and the exact calculation of the concentrations at each instant are an essential part of the problem.

5. Conclusions

There are several methods for calculating the evolution of water quality in drinking water distribution networks. In the present paper, two simulation methods, LTD and LTDI, implemented in Epanet, have been analysed and described in detail, and the inaccuracies they present in the calculations have been shown, especially in cases where there are pipes of short length and when the time intervals used for the quality calculation are not sufficiently small so that in some pipes, a volume greater than the volume of water contained in them is transported, leading to the inaccuracies described throughout this paper.

To try to solve this problem, the implementation of the LED method, based on the method initially proposed by Paul Boulos in 1994 [24], has been proposed. In this sense, the main considerations to be made when implementing this method have been detailed.

Finally, two examples have been developed, one illustrative and the other corresponding to a real network model, both simplified and detailed, in which the results obtained by the three methods have been compared. Since the LED method is the one that provides the most accurate results, it is remarkable that the LTDI method, implemented in the latest version of Epanet, does not present important deviations for the cases considered, although the differences that still exist may have repercussions on the reliability of other processes based on the quality models’ results, such as the location of the entry point of a contaminant from the sensor measurements.

As future work, the generalisation of the practical implementation of the LED method to take into account the transport of reactive substances, the presence of regulation elements such as pumps and valves, and storage elements such as tanks and reservoirs remain. In these cases, the solution proposed a priori is to treat all these cases following the same guidelines that are currently used in the quality models already implemented in Epanet.