Correlation between Turbidity and Inherent Optical Properties as an Initial Recognition for Backscattering Coefficient Estimation
Abstract
1. Introduction
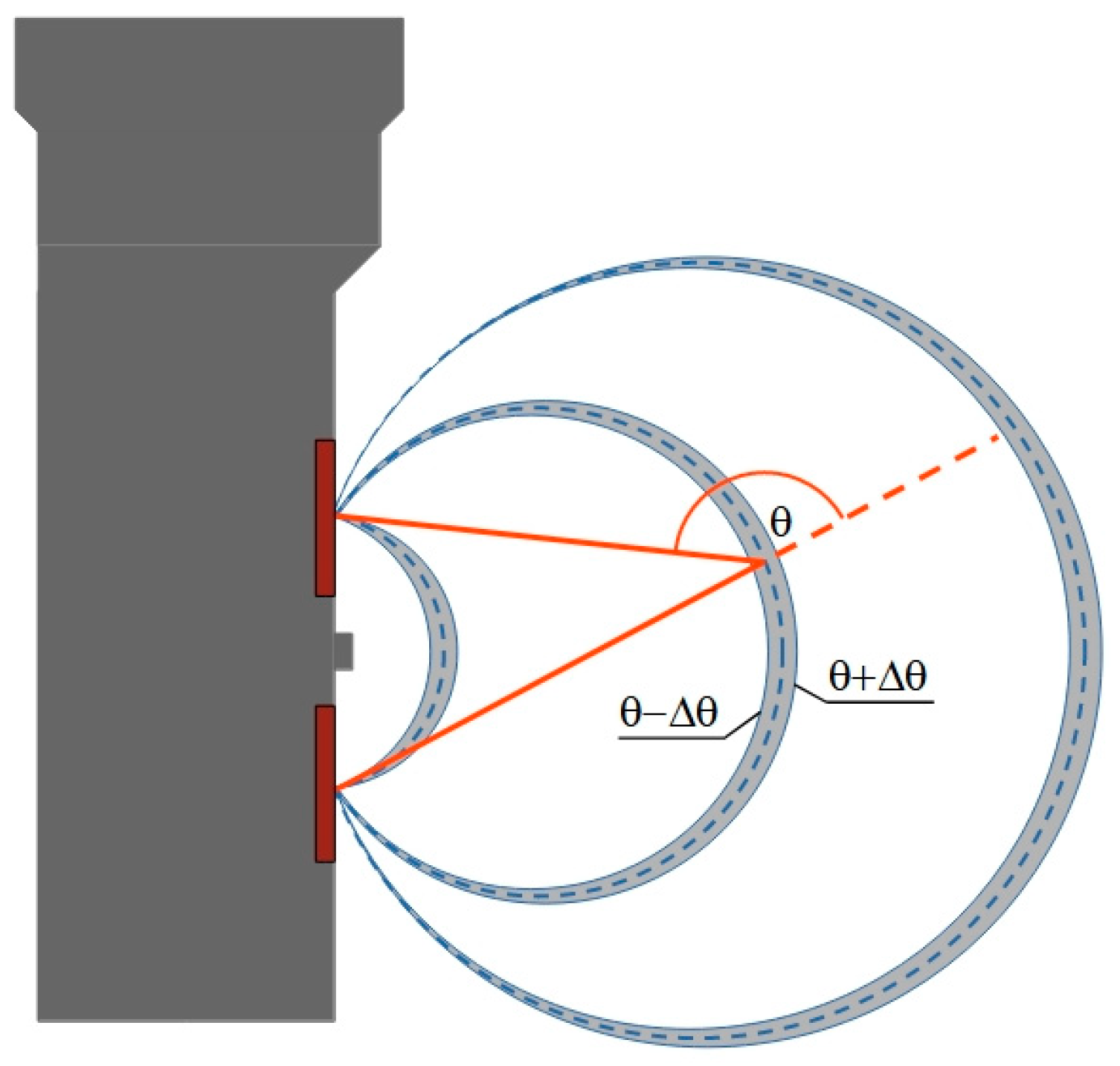
- Determining the angular weighting function that would define what part of the volume scattering function is recorded by the turbidity meter. This function will be defined as γ(θ) in the next chapter;
- Determining angular scattering properties, as well as the magnitude of the signal, measured by the turbidity meter for different fractions of the model suspension;
- Finding the correlation of the turbidimeter signal with elements of the scattering properties of the suspension.
2. Materials and Methods
2.1. Mathematical Description of Turbidity under Single Scattering Regime
2.2. Measurements of the Angular Weighting Function
2.3. Model of Inorganic Particle Suspension
3. Results
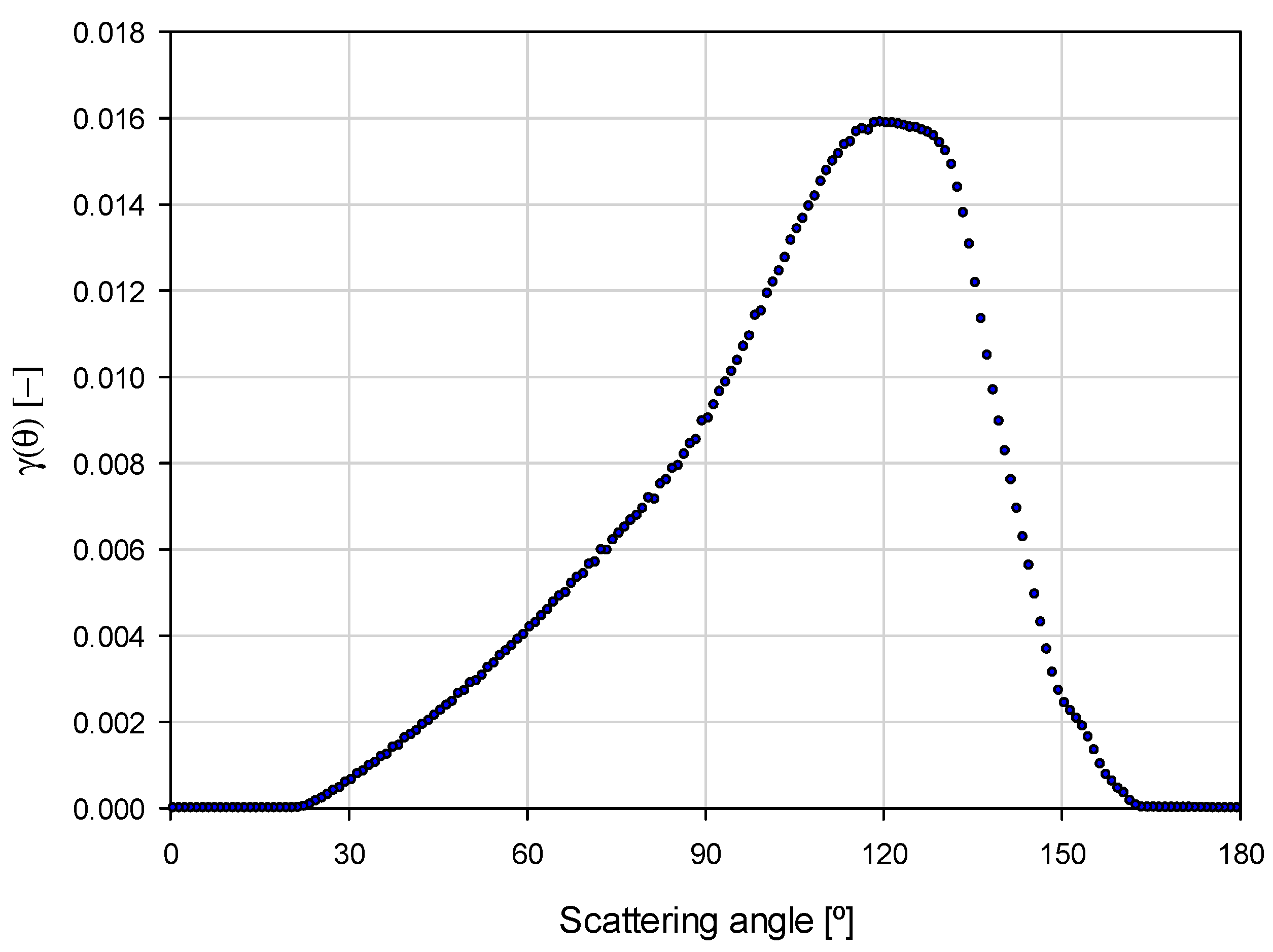
3.1. The Turbidimeter’s Angular Weighting Function
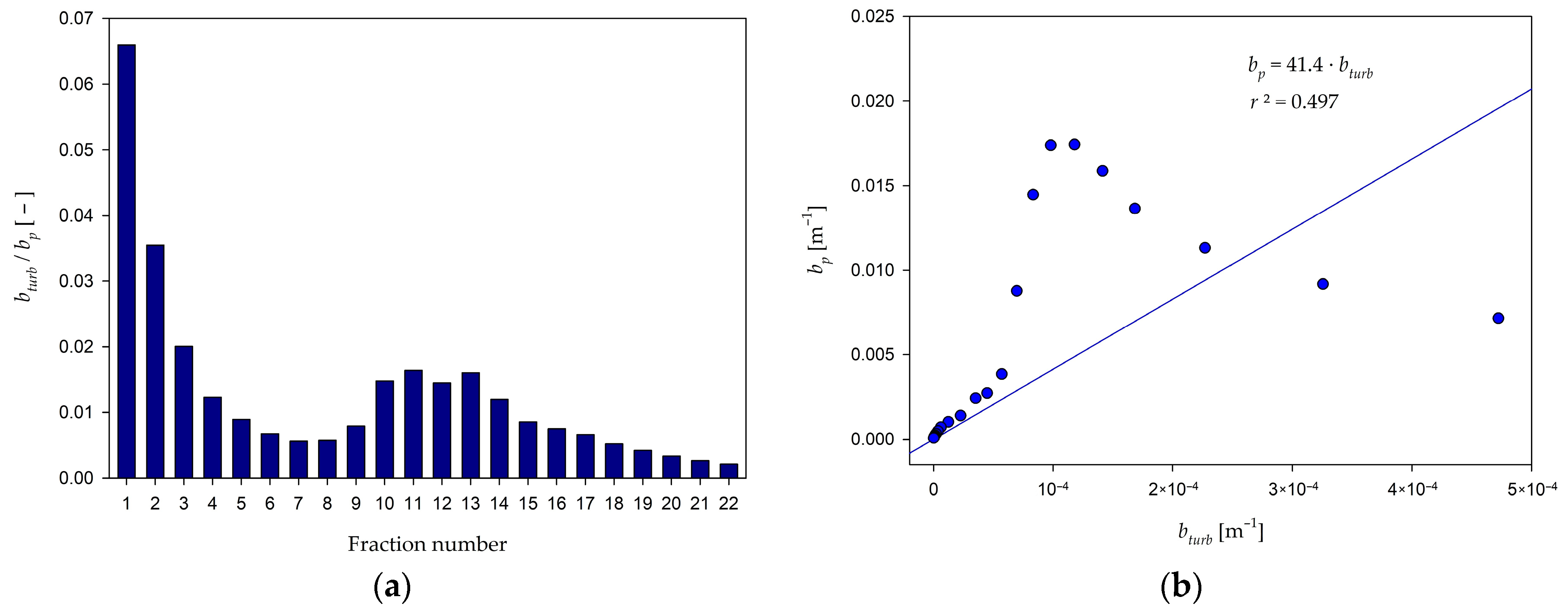
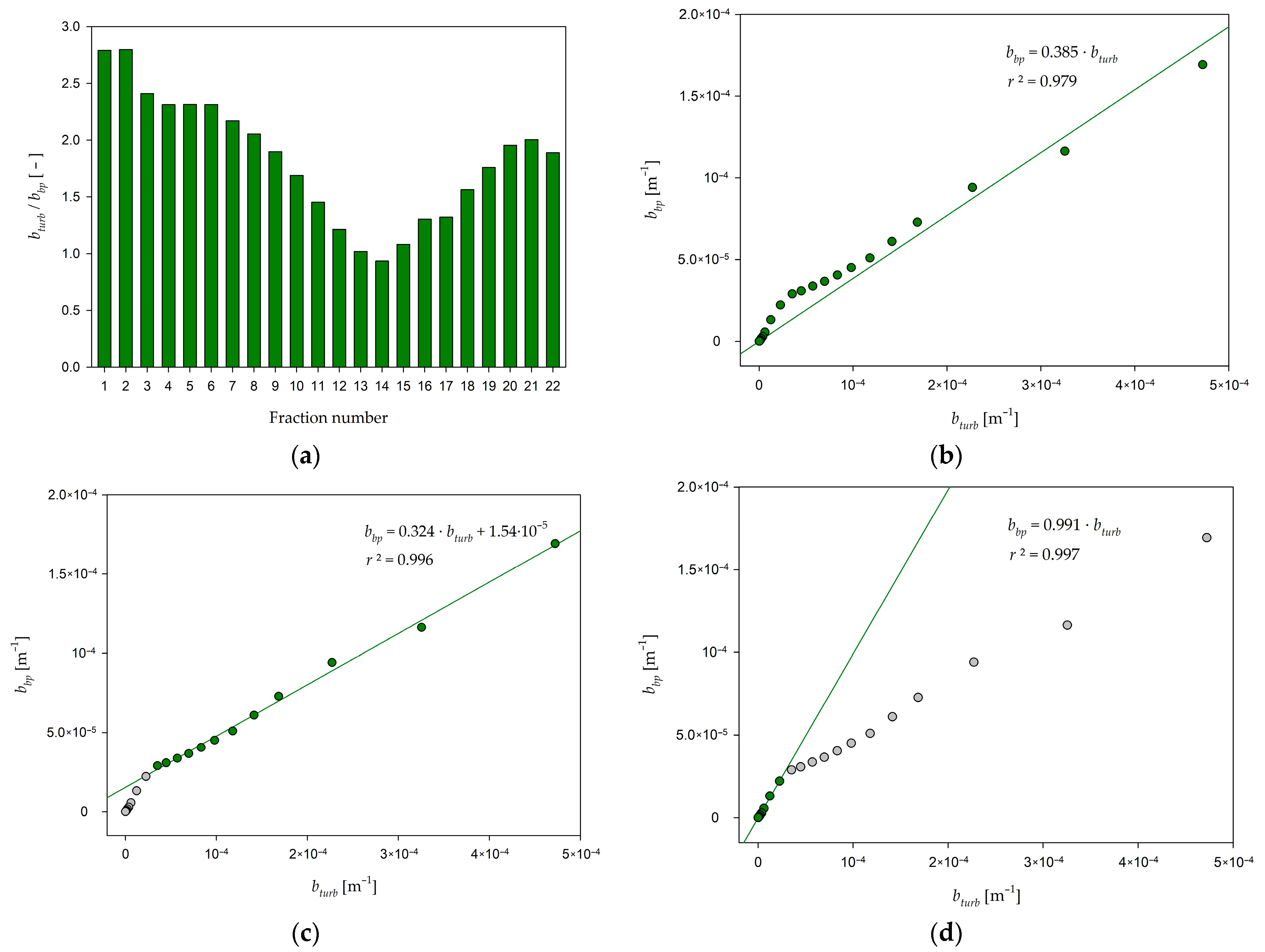
3.2. Scattering Coefficients and Volume Scattering Functions of Inorganic Suspensions
4. Discussion
5. Conclusions
- This function has a high FWHM of 55° and 90% of the function falls in a wide range of scattering angles from 62° to 146°.
- Based on the modeling results, the turbidimeter signal has a good linear correlation with bbp, but the best fit is obtained when we approximated bbp separately for particles below 13.8 µm and particles larger than 13.8 µm.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Directive 2000/60/EC of the European Parliament and of the Council of 23 October 2000 Establishing a Framework for Community Action in the Field of Water Policy. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A02000L0060-20141120#E0039 (accessed on 18 December 2023).
- Aas, E.; Høkedal, J.; Sørensen, K. Experiments with the Secchi disk. Ocean Sci. Discuss. 2013, 10, 1833–1893. [Google Scholar]
- Tyler, J.E. The Secchi disc. Limnol. Oceanogr. 1968, 13, 1–6. [Google Scholar] [CrossRef]
- Preisendorfer, R.W. American Society of Limnology and Oceanography Executive Secretary. Limnol. Oceanogr. 1989, 34, 1366. [Google Scholar]
- Renk, H.; Nakonieczny, J.; Ochocki, S.; Lorenz, Z.; Majchrowski, R.; Ficek, D. Secchi depth-chlorophyll relationship in the Baltic. Acta Ichthyol. Piscat. 1991, 21, 203–211. [Google Scholar] [CrossRef][Green Version]
- Bright, C.E.; Mager, S.M.; Horton, S.L. Predicting suspended sediment concentration from nephelometric turbidity in organic-rich waters. River Res. Applic. 2018, 34, 640–648. [Google Scholar] [CrossRef]
- Sadar, M. Making Sense of Turbidity Measurements—Advantages in Establishing Traceability between Measurements and Technology. In Proceedings of the 2004 National Monitoring Conference, Chattanooga, TN, USA, 17–20 May 2004. [Google Scholar]
- Lednicka, B.; Kubacka, M.; Freda, W.; Haule, K.; Dembska, G.; Galer-Tatarowicz, K.; Pazikowska-Sapota, G. Water Turbidity and Suspended Particulate Matter Concentration at Dredged Material Dumping Sites in the Southern Baltic. Sensors 2022, 22, 8049. [Google Scholar] [CrossRef]
- Dera, J. Marine Physics; PWN: Warsaw, Poland, 2003; pp. 1–514. [Google Scholar]
- Pawlik, M.M.; Ficek, D. Validation of measurements of pine pollen grain concentrations in Baltic Sea waters. Oceanologia 2022, 64, 233–243. [Google Scholar] [CrossRef]
- Pawlik, M.M.; Ficek, D. Spatial Distribution of Pine Pollen Grains Concentrations as a Source of Biologically Active Substances in Surface Waters of the Southern Baltic Sea. Water 2023, 15, 978. [Google Scholar] [CrossRef]
- Constantin, S.; Doxaran, D.; Constantinescu, S. Estimation of water turbidity and analysis of its spatio-temporal variability in the Danube River plume (Black Sea) using MODIS satellite data. Cont. Shelf Res. 2016, 112, 14–30. [Google Scholar] [CrossRef]
- Bin Omar, A.F.; Bin MatJafri, M.Z. Turbidimeter Design and Analysis: A Review on Optical Fiber Sensors for the Measurement of Water Turbidity. Sensors 2009, 9, 8311–8335. [Google Scholar] [CrossRef] [PubMed]
- Haule, K.; Toczek, H.; Borzycka, K.; Darecki, M. Influence of Dispersed Oil on the Remote Sensing Reflectance—Field Experiment in the Baltic Sea. Sensors 2021, 21, 5733. [Google Scholar] [CrossRef] [PubMed]
- Baszanowska, E.; Otremba, Z.; Piskozub, J. Modelling Remote Sensing Reflectance to Detect Dispersed Oil at Sea. Sensors 2020, 20, 863. [Google Scholar] [CrossRef]
- Sadar, M. Turbidimeter Instrument Comparison: Low-Level Sample Measurement; Technical Information Series No. 7063; Hach Company: Loveland, CO, USA, 1999. [Google Scholar]
- Anderson, C.W. Chapter A6. Section 6.7. Turbidity. In Techniques of Water-Resources Investigations 09-A6.7; Version 2.1; U.S. Geological Survey: Reston, VA, USA, 2005; pp. 1–55. [Google Scholar]
- Haule, K.; Freda, W. Remote Sensing of Dispersed Oil Pollution in the Ocean—The Role of Chlorophyll Concentration. Sensors 2021, 21, 3387. [Google Scholar] [CrossRef] [PubMed]
- Rymszewicz, A.; O’Sullivan, J.J.; Bruen, M.; Turner, J.N.; Lawler, D.M.; Conroy, E.; Kelly-Quinn, M. Measurement differences between turbidity instruments, and their implications for suspended sediment concentration and load calculations: A sensor inter-comparison study. J. Environ. Manag. 2017, 199, 99–108. [Google Scholar] [CrossRef] [PubMed]
- Gray, J.R.; Gartner, J.W. Technological advances in suspended-sediment surrogate monitoring. Water Resour. Res. 2009, 45, 1–20. [Google Scholar] [CrossRef]
- Gray, J.R.; Glysson, G.D. (Eds.) Proceedings of the Federal Interagency Workshop on Turbidity and Other Sediment Surrogates, Reno, Nevada, USA, 30 April 30–2 May 2002; Circular 1250; U.S. Geological Survey: Reston, VA, USA, 2003; pp. 1–56. [Google Scholar]
- Merten, G.H.; Capel, P.D.; Minella, J.P.G. Effects of suspended sediment concentration and grain size on three optical turbidity sensors. J. Soils Sediments 2014, 14, 1235–1241. [Google Scholar] [CrossRef]
- Trevathan, J.; Read, W.; Sattar, A. Implementation and Calibration of an IoT Light Attenuation Turbidity Sensor. Internet Things 2022, 19, 100576. [Google Scholar] [CrossRef]
- EPA/600/R–93/100; Methods for the Determination of Inorganic Substances in Environmental Samples. U.S. Environmental Protection Agency: Cincinatti, OH, USA, 1993; pp. 1–178.
- ISO 7027:1999(en); Water Quality—Determination of Turbidity. International Organization for Standardization: Geneva, Switzerland, 1999; pp. 1–10.
- Gohin, F.; Bryère, P.; Lefebvre, A.; Sauriau, P.-G.; Savoye, N.; Vantrepotte, V.; Bozec, Y.; Cariou, T.; Conan, P.; Coudray, S.; et al. Satellite and In Situ Monitoring of Chl-a, Turbidity, and Total Suspended Matter in Coastal Waters: Experience of the Year 2017 along the French Coasts. J. Mar. Sci. Eng. 2020, 8, 665. [Google Scholar] [CrossRef]
- Ouillon, S.; Douillet, P.; Andréfouët, S. Coupling satellite data with in situ measurements and numerical modeling to study fine suspended-sediment transport: A study for the lagoon of New Caledonia. Coral Reefs 2004, 23, 109–122. [Google Scholar]
- Jafar-Sidik, M.; Gohin, F.; Bowers, D.; Howarth, J.; Hull, T. The relationship between suspended particulate matter and turbidity at a mooring station in a coastal environment: Consequences for satellite-derived products. Oceanologia 2017, 59, 365–378. [Google Scholar] [CrossRef]
- Münzberg, M.; Hass, R.; Dinh Duc Khanh, N.; Reich, O. Limitations of turbidity process probes and formazine as their calibration standard. Anal. Bioanal. Chem. 2017, 409, 719–728. [Google Scholar] [CrossRef] [PubMed]
- Garaba, S.P.; Badewien, T.H.; Braun, A.; Schulz, A.-C.; Zielinski, O. Using ocean colour remote sensing products to estimate turbidity at the Wadden Sea time series station Spiekeroog. J. Eur. Opt. Soc.—Rapid Publ. 2014, 9, 14020. [Google Scholar] [CrossRef]
- Wang, Y.W.; Peng, Y.; Du, Z.; Lin, H.; Yu, Q. Calibrations of suspended sediment concentrations in high-turbidity waters using different in Situ optical instruments. Water 2020, 12, 3296. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Cambridge, MA, USA, 1994; pp. 1–592. [Google Scholar]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 1983; pp. 1–533. [Google Scholar]
- Jonasz, M.; Fournier, G.R. Light Scattering by Particles in Water; Academic Press: Cambridge, MA, USA, 2007; pp. 1–714. [Google Scholar]
- Available online: https://www.britannica.com/science/clay-mineral (accessed on 6 February 2024).
- Rodríguez-de Marcos, L.V.; Larruquert, J.I.; Méndez, J.A.; Aznárez, J.A. Self-consistent optical constants of SiO2 and Ta2O5 films. Opt. Mater. Express 2016, 6, 3622–3637. [Google Scholar] [CrossRef]
- Haule, K.; Freda, W. The effect of dispersed Petrobaltic oil droplet size on photosynthetically active radiation in marine environment. Environ. Sci. Pollut. Res. 2016, 23, 6506–6516. [Google Scholar] [CrossRef] [PubMed]
- Santalices, D.; de Castro, A.J.; Briz, S. New Method to Calculate the Angular Weighting Function for a Scattering Instrument: Application to a Dust Sensor on Mars. Sensors 2022, 22, 9216. [Google Scholar] [CrossRef]
- Heintzenberg, J.; Wiedensohler, A.; Tuch, T.; Covert, D.; Sheridan, P.; Ogren, J.; Gras, J.; Nessler, R.; Kleefeld, C.; Kalivitis, N.; et al. Intercomparisons and aerosol calibrations of 12 commercial integrating nephelometers of three manufacturers. J. Atmos. Ocean. Technol. 2006, 23, 902–914. [Google Scholar] [CrossRef]
- McKee, D.; Piskozub, J.; Röttgers, R.; Reynolds, R.A. Evaluation and Improvement of an Iterative Scattering Correction Scheme for in situ Absorption and Attenuation Measurements. J. Atmos. Ocean. Technol. 2013, 30, 1527–1541. [Google Scholar] [CrossRef][Green Version]
- Oishi, T. Significant relationship between the backward scattering coefficient of sea water and the scatterance at 120°. Appl. Opt. 1990, 29, 4658–4665. [Google Scholar] [CrossRef]
- Maffione, R.A.; Dana, D.R. Instruments and methods for measuring the backward-scattering coefficient of ocean waters. Appl. Opt. 1997, 36, 6057–6067. [Google Scholar] [CrossRef]
- Boss, E.; Pegau, W.S. Relationship of light scattering at an angle in the backward direction to the backscattering coefficient. Appl. Opt. 2001, 40, 5503–5507. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, J.M.; Twardowski, M.S. Angular shape of the oceanic particulate volume scattering function in the backward direction. Appl. Opt. 2009, 48, 6811–6819. [Google Scholar] [CrossRef] [PubMed]
- Freda, W. Spectral dependence of the correlation between the backscattering coefficient and the volume scattering function measured in the southern Baltic Sea. Oceanologia 2012, 54, 355–367. [Google Scholar] [CrossRef]
- Zhang, X.; Boss, E.; Gray, D.J. Significance of scattering by oceanic particles at angles around 120 degree. Opt. Express 2014, 22, 31329–31336. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Qiu, Z.; Zhou, Y.; Sun, D.; Wang, S.; Wu, W.; Perrie, W. Comparisons of algorithms to estimate water turbidity in the coastal areas of China. Int. J. Remote Sens. 2016, 37, 6165–6186. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, O.B.; Jacobs, M.M. Computed relationship between the inherent and apparent optical properties of a flat homogeneous ocean. Appl. Optics 1975, 14, 417–427. [Google Scholar] [CrossRef]
- Dogliotti, A.I.; Ruddick, K.G.; Nechad, B.; Doxaran, D.; Knaeps, E. A single algorithm to retrieve turbidity from remotely-sensed data in all coastal and estuarine waters. Remote Sens. Envrion. 2015, 156, 157–168. [Google Scholar] [CrossRef]





| Detector Geometry | Light Wavelength | |
|---|---|---|
| White or Broadband (with a Peak Spectral Output of 400–680 nm) | Monochrome (Spectral Output Typically Near-Infrared, 780–900 nm) | |
| Single Illumination Beam Light Source | ||
| At 90° to the incident beam | Nephelometric Turbidity Unit (NTU) 1 (P63675) | Formazin Nephelometric Unit (FNU) 2 (P63680) |
| At 90° and other angles. An instrument algorithm uses a combination of detector readings, which may differ for values of varying magnitude | Nephelometric Turbidity Ratio Unit (NTRU) (P63676) | Formazin Nephelometric Ratio Unit (FNRU) (P63681) |
| At 30° ± 15° to the incident beam (backscatter) | Backscatter Unit (BU) (P63677) | Formazin Backscatter Unit (FBU) (P63682) |
| At 180° to the incident beam (attenuation) | Attenuation Unit (AU) (P63678) | Formazin Attenuation Unit (FAU) (P63683) |
| Multiple illumination beam light source | ||
| At 90° and possibly other angles to each beam. An instrument algorithm uses a combination of detector readings, which may differ for values of varying magnitude | Nephelometric Turbidity Multibeam Unit (NTMU) (P63679) | Formazin Nephelometric Multibeam Unit (FNMU) (P63684) |
| Fraction Number | Diameter Range [μm] | Concentration [m−3] | Scattering Coefficient bp [m−1] | Backscattering Coefficient bbp [m−1] |
|---|---|---|---|---|
| 1 | 0.59–0.77 | 1.13 × 1011 | 7.16 × 10−3 | 1.69 × 10−4 |
| 2 | 0.77–1 | 4.85 × 1010 | 9.18 × 10−3 | 1.16 × 10−4 |
| 3 | 1–1.30 | 2.07 × 1010 | 1.13 × 10−2 | 9.42 × 10−5 |
| 4 | 1.30–1.69 | 8.80 × 109 | 1.37 × 10−2 | 7.28 × 10−5 |
| 5 | 1.69–2.20 | 3.75 × 109 | 1.59 × 10−2 | 6.11 × 10−5 |
| 6 | 2.20–2.86 | 1.60 × 109 | 1.74 × 10−2 | 5.10 × 10−5 |
| 7 | 2.86–3.71 | 6.82 × 108 | 1.74 × 10−2 | 4.51 × 10−5 |
| 8 | 3.71–4.83 | 2.91 × 108 | 1.45 × 10−2 | 4.06 × 10−5 |
| 9 | 4.83–6.28 | 1.24 × 108 | 8.78 × 10−3 | 3.67 × 10−5 |
| 10 | 6.28–8.16 | 5.28 × 107 | 3.85 × 10−3 | 3.38 × 10−5 |
| 11 | 8.16–10.6 | 2.25 × 107 | 2.73 × 10−3 | 3.09 × 10−5 |
| 12 | 10.6–13.8 | 9.60 × 106 | 2.43 × 10−3 | 2.90 × 10−5 |
| 13 | 13.8–17.9 | 4.09 × 106 | 1.41 × 10−3 | 2.22 × 10−5 |
| 14 | 17.9–23.3 | 1.74 × 106 | 1.03 × 10−3 | 1.32 × 10−5 |
| 15 | 23.3–30.3 | 7.43 × 105 | 7.14 × 10−4 | 5.67 × 10−6 |
| 16 | 30.3–39.4 | 3.17 × 105 | 4.94 × 10−4 | 2.85 × 10−6 |
| 17 | 39.4–51.2 | 1.35 × 105 | 3.31 × 10−4 | 1.66 × 10−6 |
| 18 | 51.2–66.5 | 5.76 × 104 | 2.33 × 10−4 | 7.77 × 10−7 |
| 19 | 66.5–86.5 | 2.45 × 104 | 1.63 × 10−4 | 3.94 × 10−7 |
| 20 | 86.5–112 | 1.05 × 104 | 1.20 × 10−4 | 2.06 × 10−7 |
| 21 | 112–146 | 4.46 × 103 | 9.27 × 10−5 | 1.23 × 10−7 |
| 22 | 146–190 | 1.90 × 103 | 7.24 × 10−5 | 8.12 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haule, K.; Kubacka, M.; Toczek, H.; Lednicka, B.; Pranszke, B.; Freda, W. Correlation between Turbidity and Inherent Optical Properties as an Initial Recognition for Backscattering Coefficient Estimation. Water 2024, 16, 594. https://doi.org/10.3390/w16040594
Haule K, Kubacka M, Toczek H, Lednicka B, Pranszke B, Freda W. Correlation between Turbidity and Inherent Optical Properties as an Initial Recognition for Backscattering Coefficient Estimation. Water. 2024; 16(4):594. https://doi.org/10.3390/w16040594
Chicago/Turabian StyleHaule, Kamila, Maria Kubacka, Henryk Toczek, Barbara Lednicka, Bogusław Pranszke, and Włodzimierz Freda. 2024. "Correlation between Turbidity and Inherent Optical Properties as an Initial Recognition for Backscattering Coefficient Estimation" Water 16, no. 4: 594. https://doi.org/10.3390/w16040594
APA StyleHaule, K., Kubacka, M., Toczek, H., Lednicka, B., Pranszke, B., & Freda, W. (2024). Correlation between Turbidity and Inherent Optical Properties as an Initial Recognition for Backscattering Coefficient Estimation. Water, 16(4), 594. https://doi.org/10.3390/w16040594








