Study on Numerical Simulation of Reactive-Transport of Groundwater Pollutants Caused by Acid Leaching of Uranium: A Case Study in Bayan-Uul Area, Northern China
Abstract
1. Introduction
2. Conceptual Model and Mathematical Model
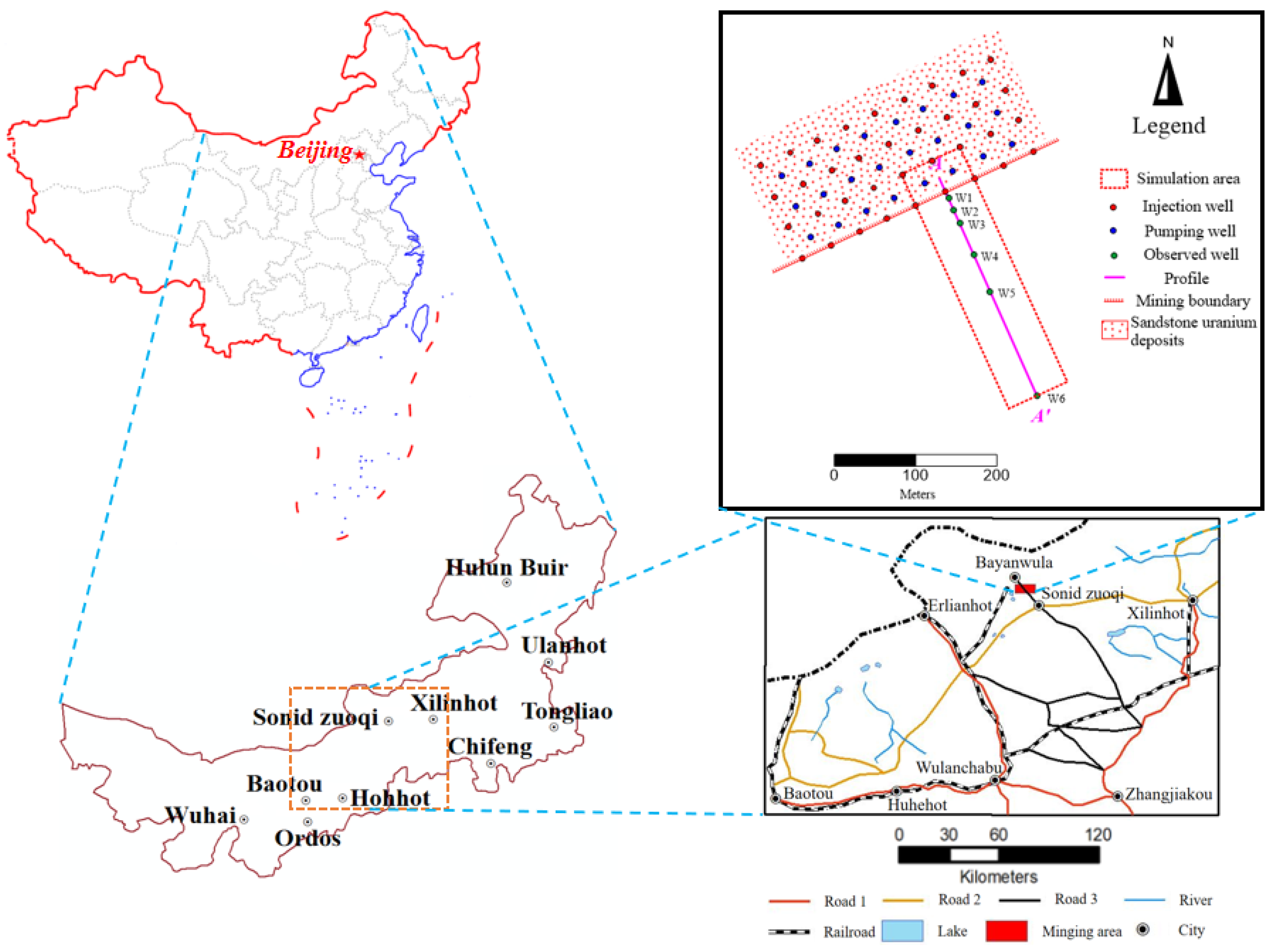
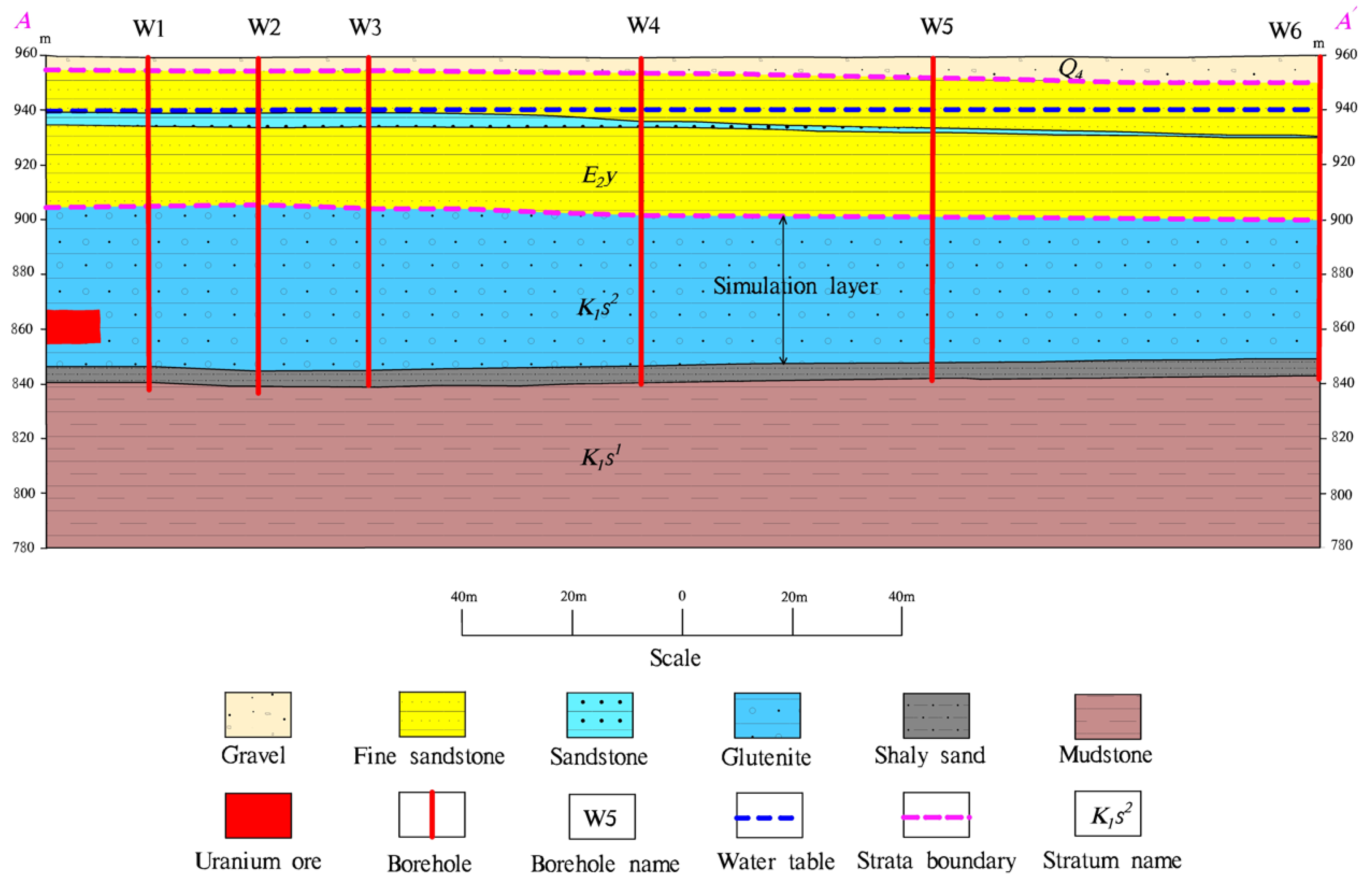
2.1. Geological Environment of the Study Area
- (1)
- Geology settings
- (2)
- Conceptual model
2.2. Governing Equations
- (1)
- Water flow equation
- (2)
- Chemical reaction mathematical models
- (3)
- Models of mineral dissolution or precipitation
- (4)
- Relative permeability and capillary pressure calculation model
2.3. Initial Conditions and Boundary Conditions
- (1)
- Initial conditions
- (2)
- Boundary conditions
2.4. Source and Sink
3. Numerical Model
3.1. Selection of Simulator
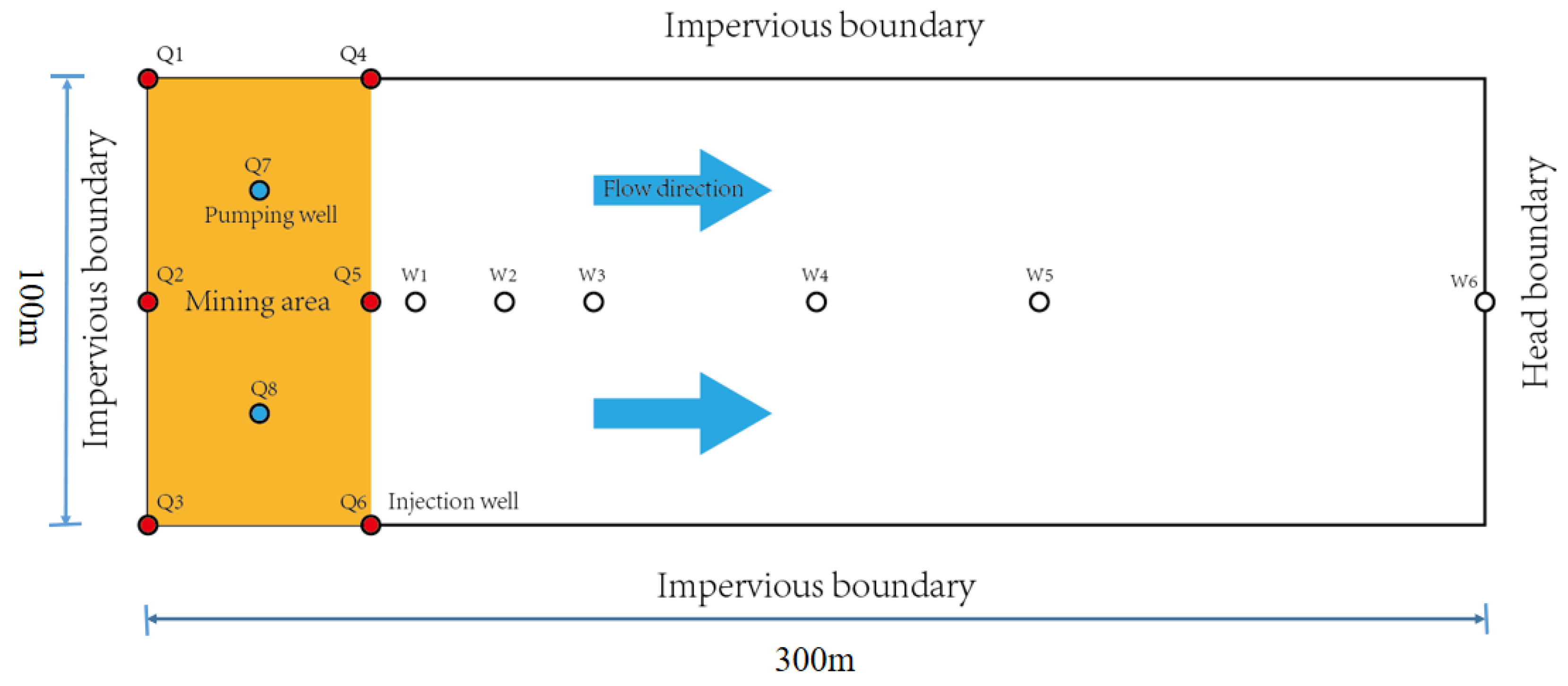
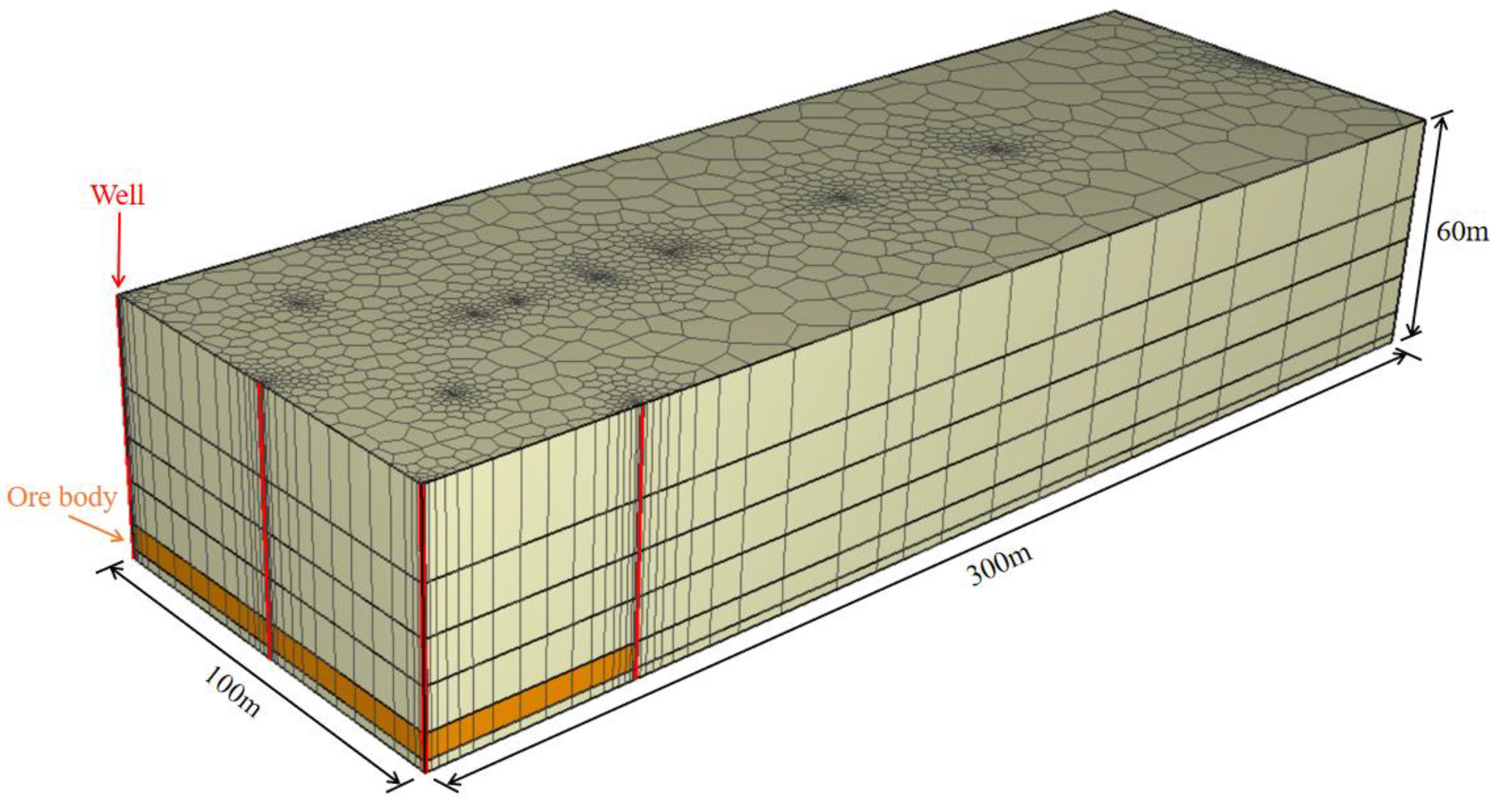
3.2. Mesh Generation
3.3. The Physical Parameters and the Chemical Reaction Parameters
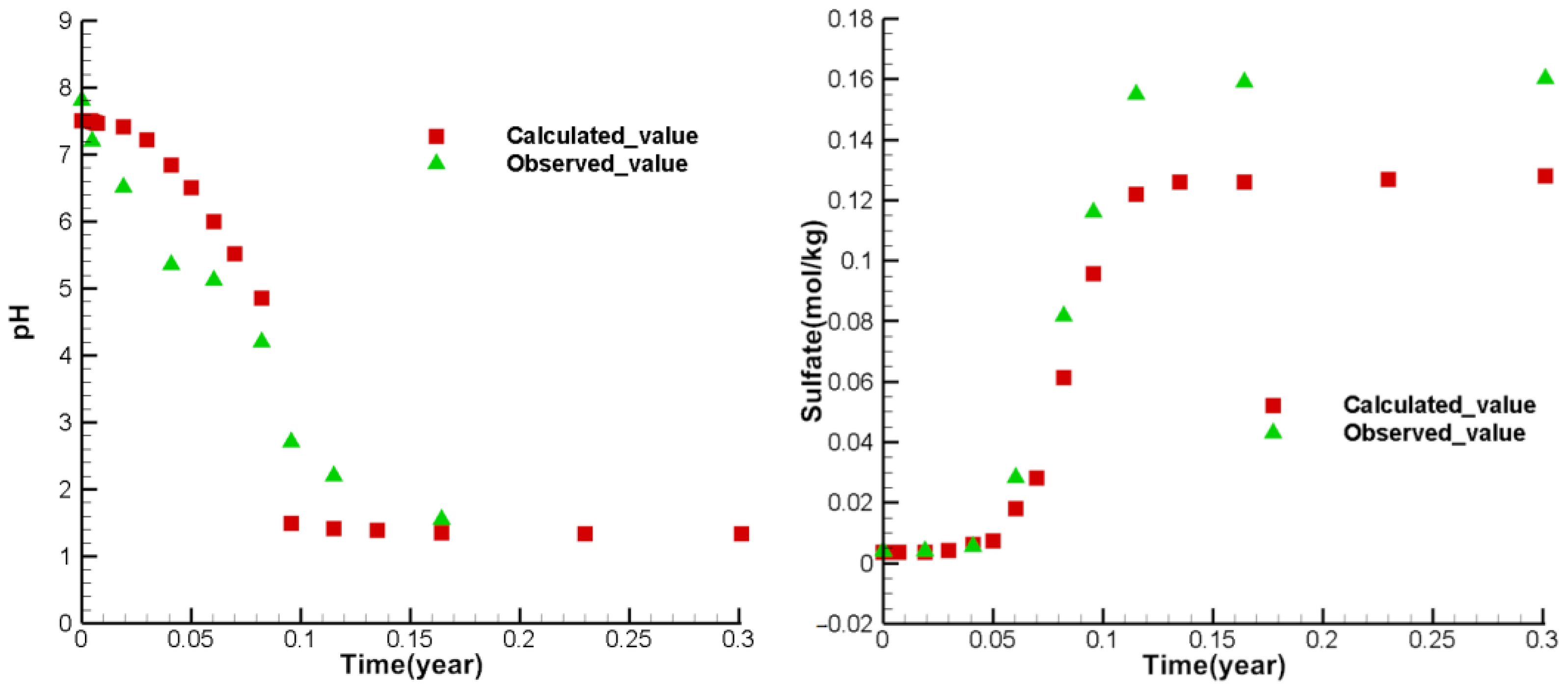
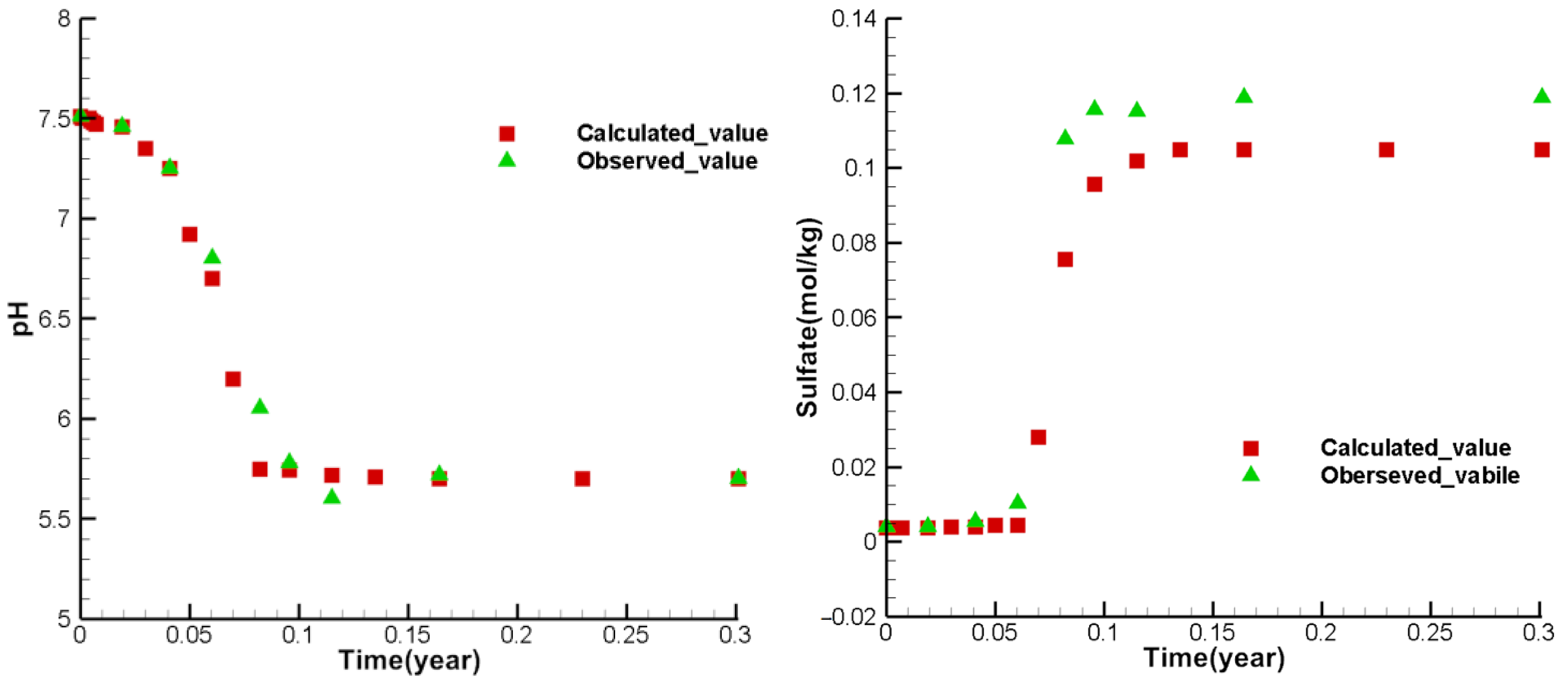
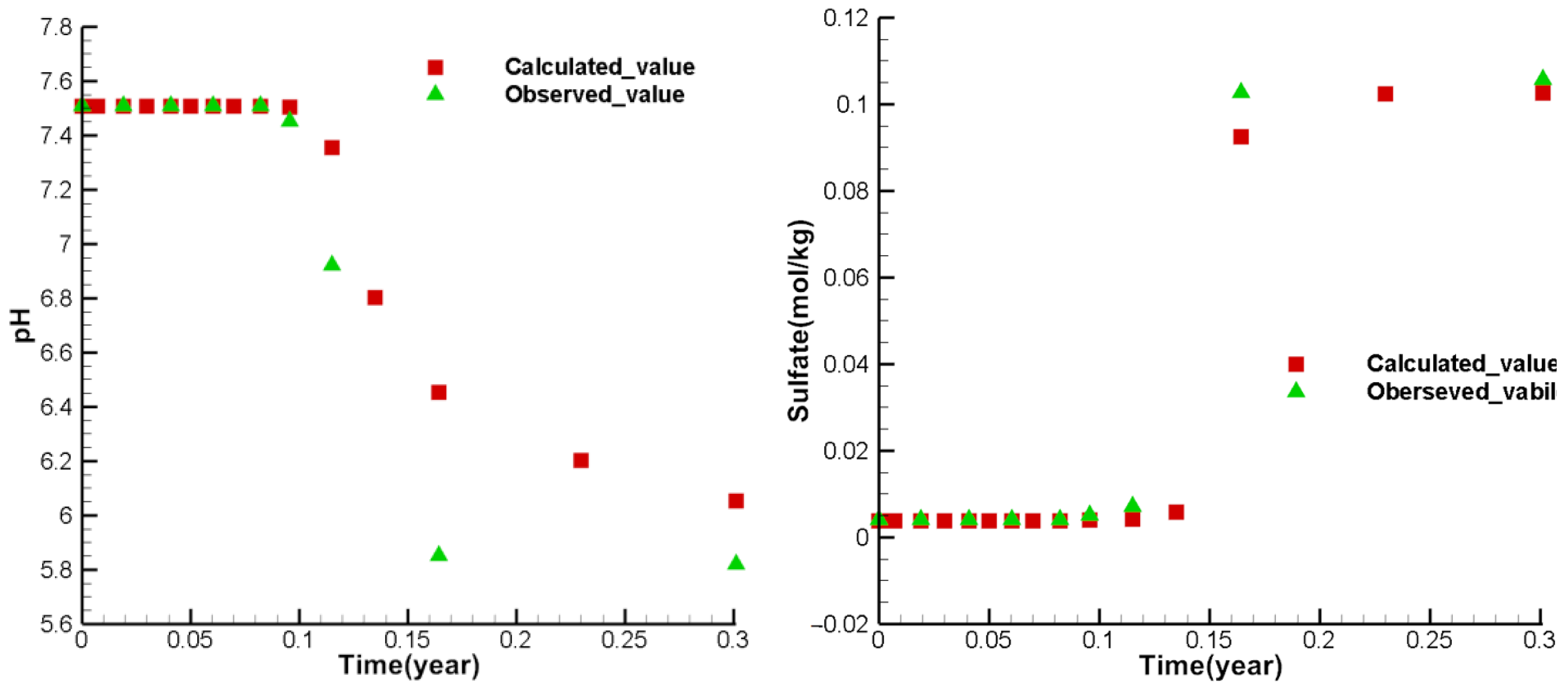
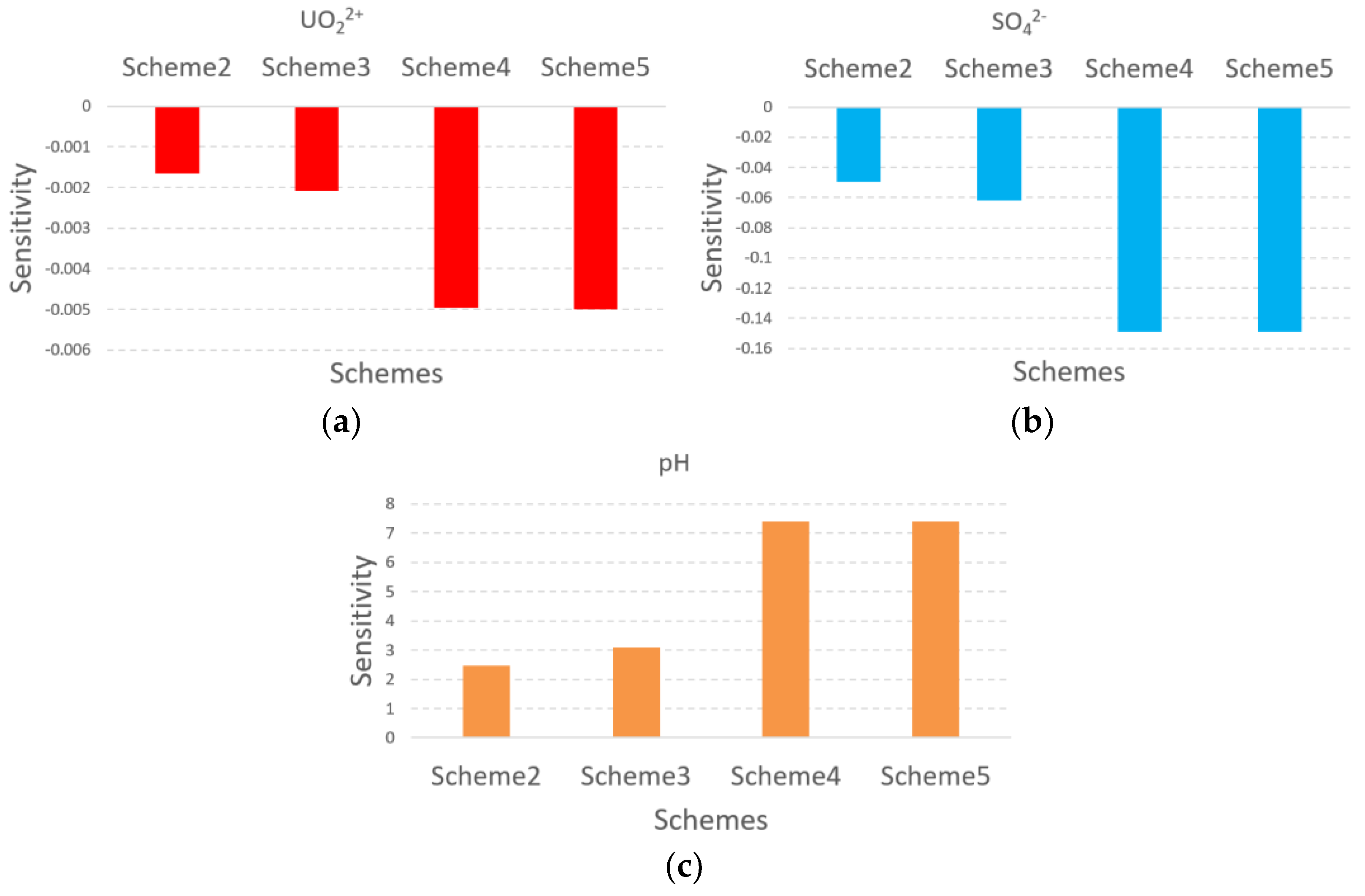
3.4. Model Calibration and Sensitivity Analysis
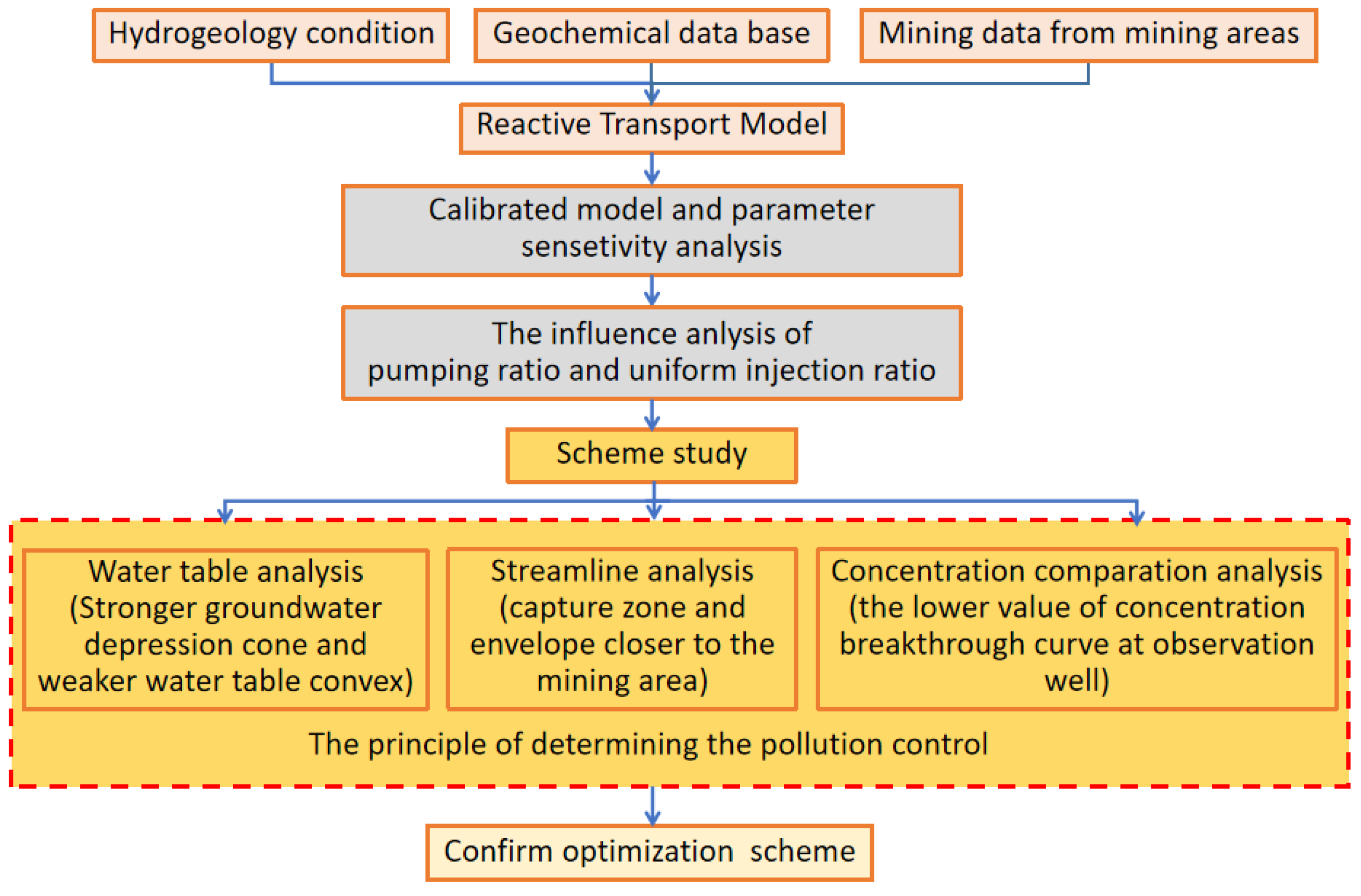
4. Influence of Pumping Ratio and Non-Uniform Injection Ratio of ISL on Groundwater Quality and the Scheme Study
4.1. Cases Setting
- (1)
- Pumping ratio
- (2)
- Non-uniform injection ratio
4.2. Simulation Schemes Design and the Principle of Pollution Control
- (1)
- Simulation schemes design
- (2)
- Influence analysis
- (3)
- The principle of determining the pollution control
- (a)
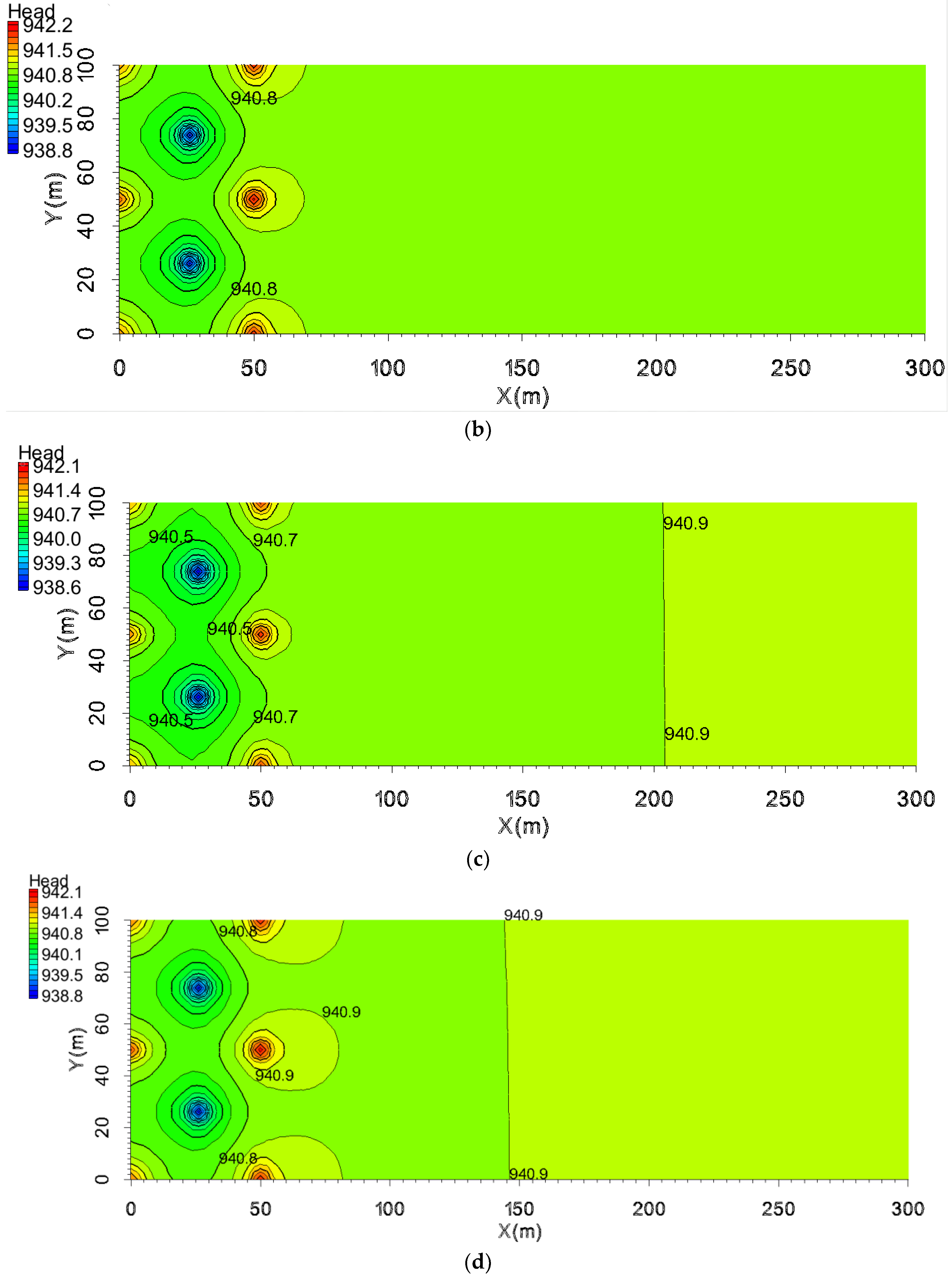
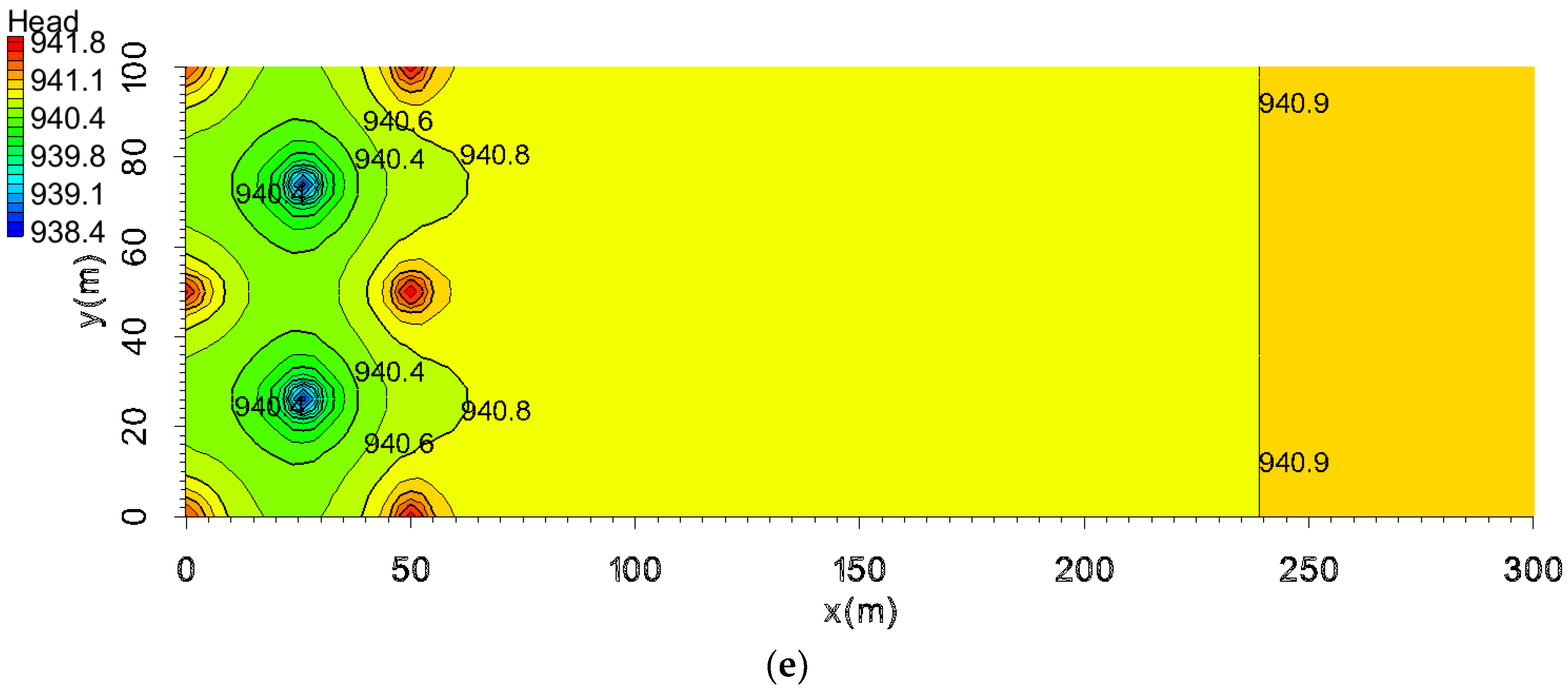
- Principle of pollution control based on water level
- (b)
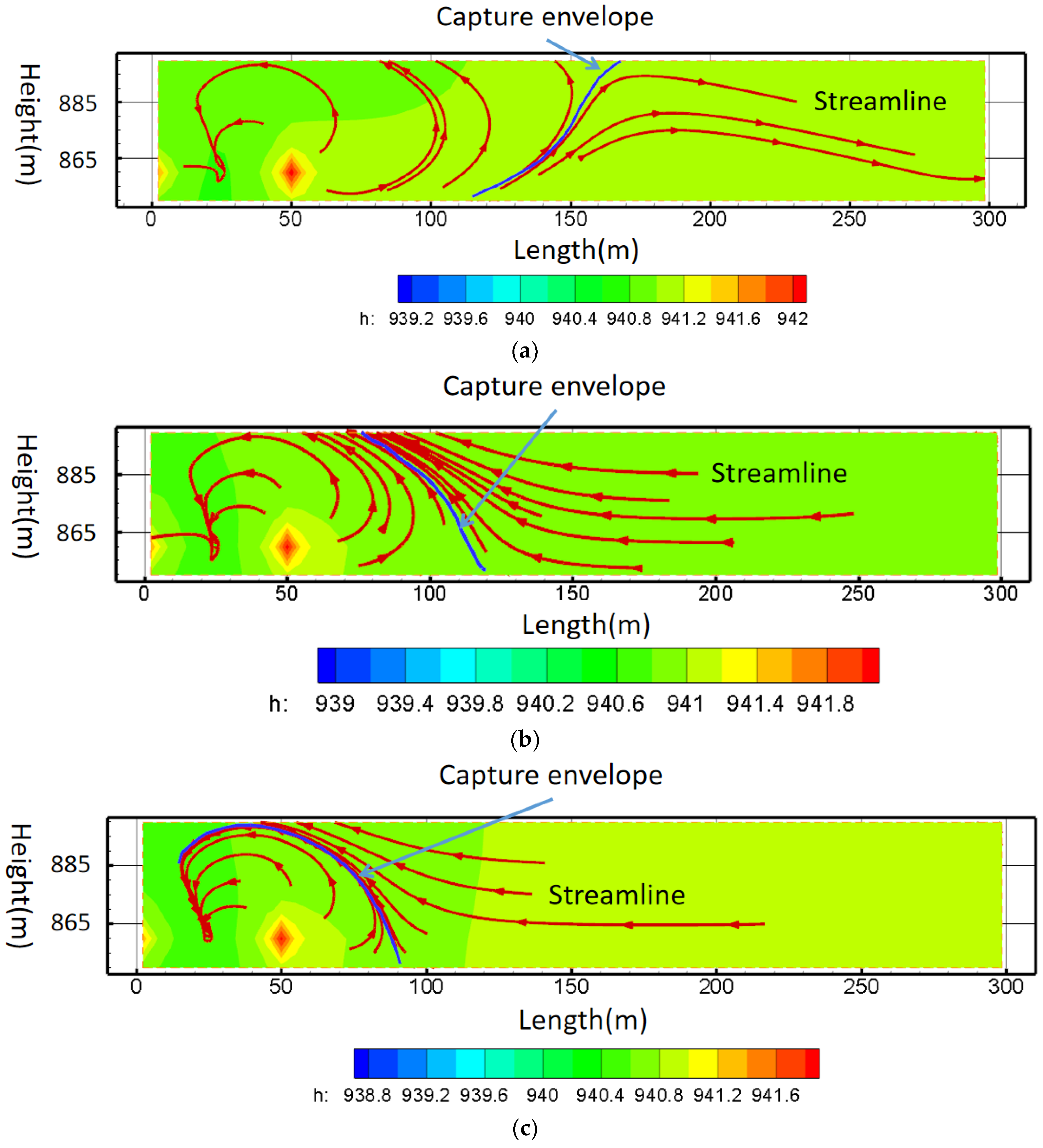
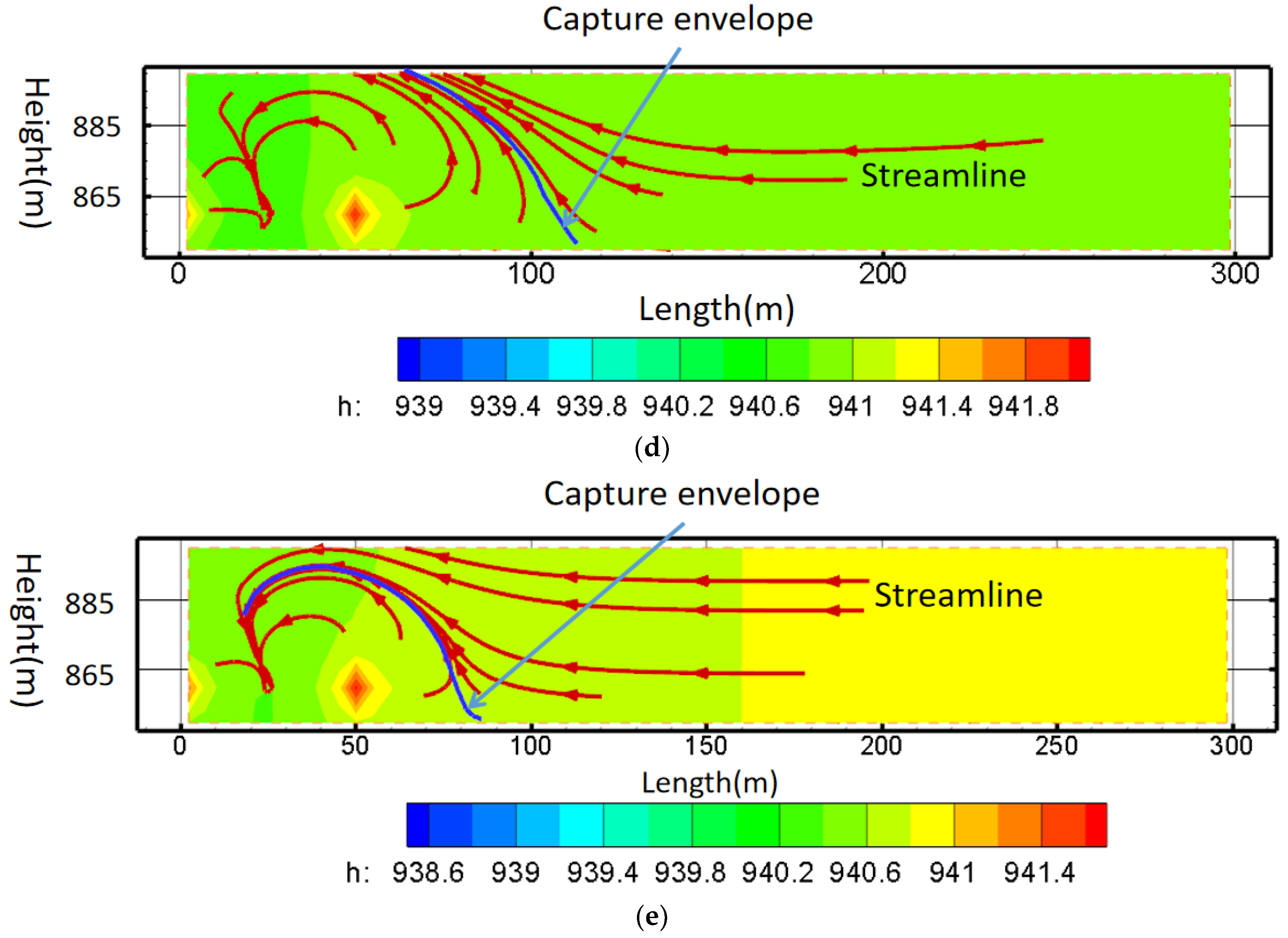
- Principle of pollution control based on streamline
- (c)
- Comparison of concentrations at the observation well W1
5. Results and Discussion
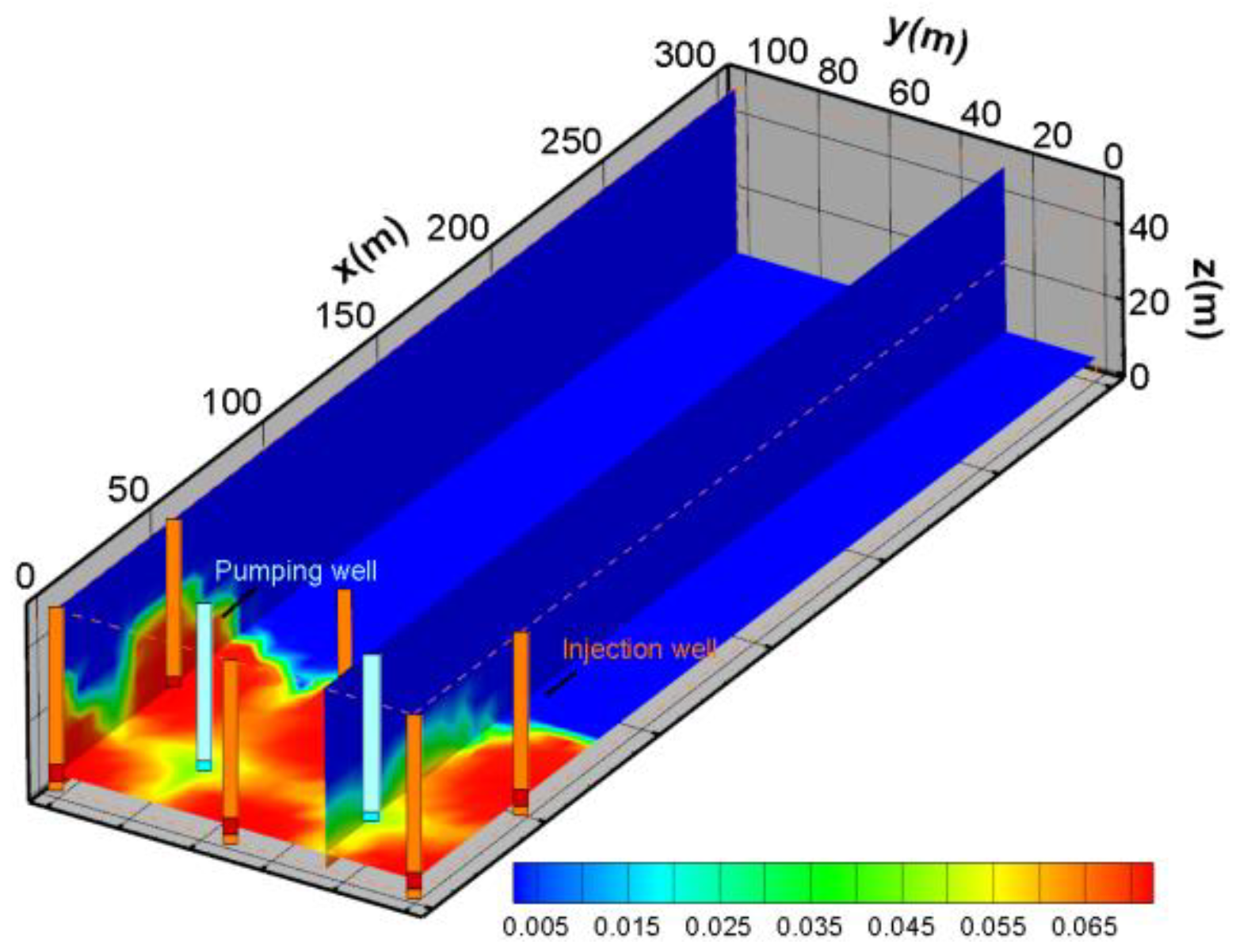
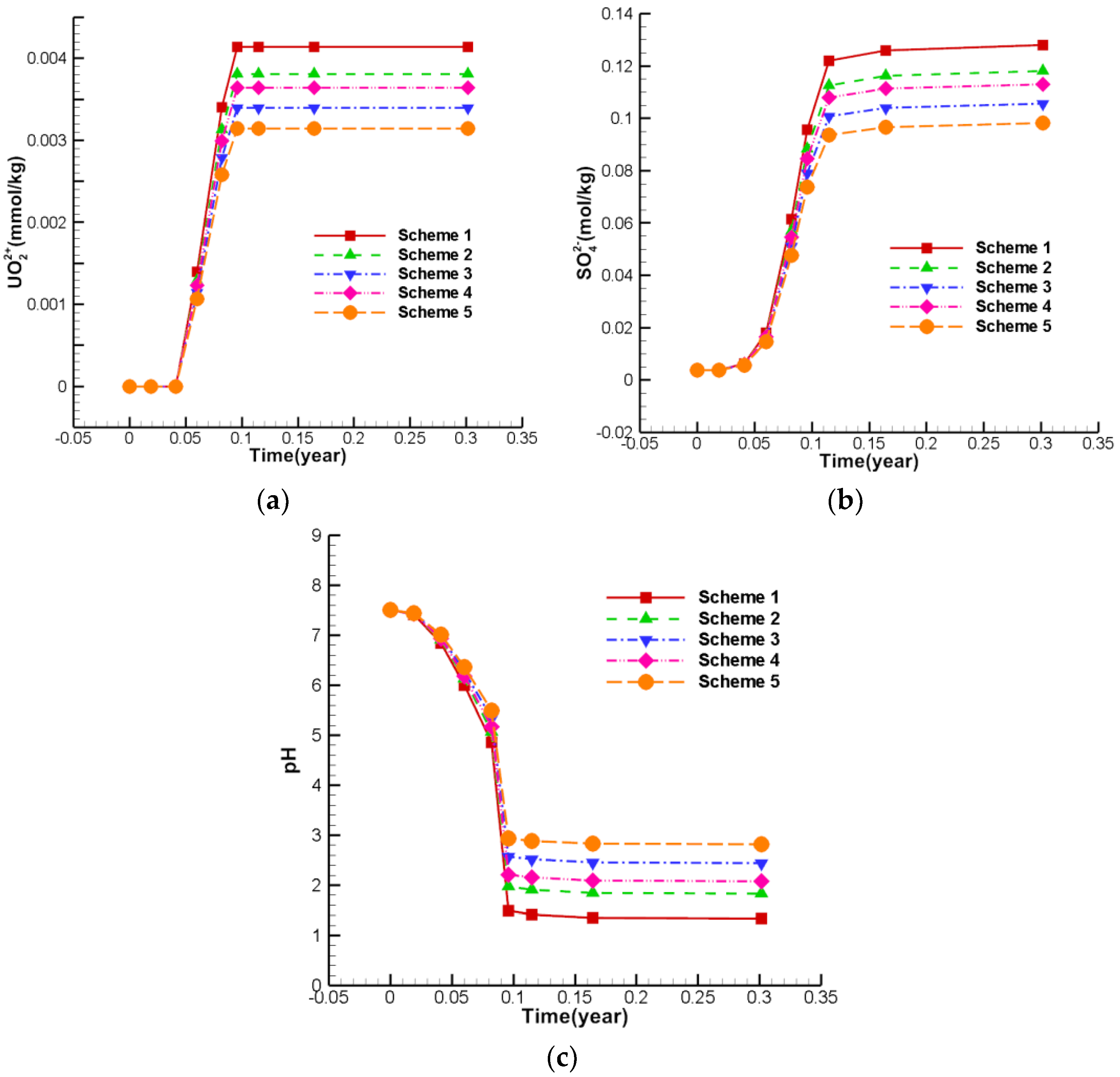
5.1. The Variation in Uranium Ore, UO22+, SO42−,H+ for Base Scheme (Scheme 1)
- (1)
- Variation in uranium ore content and migration of UO22+
- (2)
- SO42− Spatial distribution characteristics
- (3)
- H+ spatial distribution characteristics
5.2. The Influence of Pumping Ratio and Non-Uniform Injection Ratio for Concentration of UO22+, SO42−, and H+
5.3. The Pollution Control Results Based on the Water Table
5.4. The Hydrodynamic Pollution Control Results Based on Streamline and Capture Envelope
5.5. The Pollution Control Results of Concentration Characteristics at Well W1 by RTM
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saunders, J.A.; Pivetz, B.E.; Voorhies, N.; Wilkin, R.T. Potential aquifer vulnerability in regions down-gradient from uranium in situ recovery (ISR) sites. J. Environ. Manag. 2016, 183, 67–83. [Google Scholar] [CrossRef] [PubMed]
- Bhargava, S.K.; Ram, R.; Pownceby, M.; Grocott, S.; Ring, B.; Tardio, J.; Jones, L. A review of acid leaching of uraninite. Hydrometallurgy 2015, 151, 10–24. [Google Scholar] [CrossRef]
- Wellmer, F.W.; Becker-Platen, J.D. Sustainable development and the exploitation of mineral and energy resources: A review. Int. J. Earth Sci. 2002, 91, 723–745. [Google Scholar]
- Poole, T.; Bruneton, P.; Fairclough, M.; Schnell, H.; Valter, O. Uranium Resources as Co- and By-products of Polymetallic Base, Rare Earth and Precious Metal Ore Deposits; International Atomic Energy Agency: Vienna, Austria, 2018. [Google Scholar]
- Tulsidas, H.; Fairclough, M. World Distribution of Uranium Deposits (UDEPO); International Atomic Energy Agency: Vienna, Austria, 2018. [Google Scholar]
- Edwards, C.R.; Oliver, A.J. Uranium processing: A review of current methods and technology. JOM J. Miner. Met. Mater. Soc. 2000, 52, 12–20. [Google Scholar] [CrossRef]
- Mudd, G.M. Critical review of acid in situ leach uranium mining: 2. Soviet Block and Asia. Environ. Geol. 2001, 41, 404–416. [Google Scholar] [CrossRef]
- Zhang, C.; Tan, K.; Xie, T.; Tan, Y.; Fu, L.; Gan, N.; Kong, L. Flow Microbalance Simulation of Pumping and Injection Unit in In Situ Leaching Uranium Mining Area. Processes 2021, 9, 1288. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, T.T.; Tan, K.X.; Yao, Y.X.; Wang, Y.A.; Li, C.G.; Li, Y.M.; Zhang, Y.; Wang, H. Hydrodynamic Simulation of the Influence of Injection Flowrate Regulation on In-Situ Leaching Range. Minerals 2022, 12, 787. [Google Scholar] [CrossRef]
- Collet, A.; Regnault, O.; Ozhogin, A.; Imantayeva, A.; Garnier, L. Three-dimensional reactive transport simulation of Uranium in situ recovery: Large-scale well field applications in Shu Saryssu Bassin, Tortkuduk deposit (Kazakhstan). Hydrometallurgy 2022, 211, 105873. [Google Scholar] [CrossRef]
- Mibus, J.; Sachs, S.; Pfingsten, W.; Nebelung, C.; Bernhard, G. Migration of uranium(IV)/(VI) in the presence of humic acids in quartz sand: A laboratory column study. J. Contam. Hydrol. 2007, 89, 199–217. [Google Scholar] [CrossRef]
- Kurmanseiit, M.B.; Tungatarova, M.S.; Kaltayev, A.; Royer, J.J. Reactive Transport Modeling during Uranium In Situ Leaching (ISL): The Effects of Ore Composition on Mining Recovery. Minerals 2022, 12, 1340. [Google Scholar] [CrossRef]
- Yabusaki, S.B.; Fang, Y.; Waichler, S.R. Building conceptual models of field-scale uranium reactive transport in a dynamic vadose zone-aquifer-river system. Water Resour. Res. 2008, 44, W12403. [Google Scholar] [CrossRef]
- Kohler, M.; Curtis, G.P.; Kent, D.B.; Davis, J.A. Experimental Investigation and Modeling of Uranium (VI) Transport Under Variable Chemical Conditions. Water Resour. Res. 1996, 32, 3539–3551. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, C.; Wang, J.; Liu, Q.; Li, R.; Yang, P.; Zhang, M. Removal of uranium(VI) from aqueous solutions by magnetic Schiff base: Kinetic and thermodynamic investigation. Chem. Eng. J. 2012, 198–199, 412–419. [Google Scholar] [CrossRef]
- Bear, J.; Jacobs, M. On the movement of water bodies injected into aquifers. J. Hydrol. 1965, 3, 37–57. [Google Scholar] [CrossRef]
- Samani, N.; Zarei-Doudeji, S. Capture zone of a multi-well system in confined and unconfined wedge-shaped aquifers. Adv. Water Resour. 2012, 39, 71–84. [Google Scholar] [CrossRef]
- Muskat, M. The Flow of Homogeneous Fluids through Porous Media; McGraw-Hill Book Company: New York, NY, USA; London, UK, 1937; p. 306. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; Elsevier: New York, NY, USA, 1972; pp. 125–129. [Google Scholar]
- Zlotnik, V.A. Effects of anisotropy on the capture zone of a partially penetrating well. Groundwater 1997, 35, 842–847. [Google Scholar] [CrossRef]
- Shan, C. An analytical solution for the capture zone of two arbitrarily located wells. J. Hydrol. 1999, 222, 123–128. [Google Scholar] [CrossRef]
- Christ, J.A.; Goltz, M.N. Hydraulic containment: Analytical and semi-analytical models for capture zone curve delineation. J. Hydrol. 2002, 262, 224–244. [Google Scholar] [CrossRef]
- Zhan, H.B.; Zlotnik, V.A. Ground water flow to horizontal and slanted wells in unconfined aquifers. Water Resour. Res. 2002, 38, 1108. [Google Scholar] [CrossRef]
- Xu, S.; Zhu, X. Hydraulic capture technique for remedy of groundwater contaminated by petroleum and its numerical model. J. Hydraul. Eng. 1999, 1, 71–76. [Google Scholar] [CrossRef]
- Javandel, I.; Tsang, C.F. Capture-zone type curves-A tool for aquifer cleanup. Ground Water 1986, 24, 616–625. [Google Scholar] [CrossRef]
- Faybishenko, B.A.; Javandel, I.; Witherspoon, P.A. Hydrodynamics of the capture zone of a partially penetrating well in a confied aquifer. Water Resour. Res. 1995, 31, 859–866. [Google Scholar] [CrossRef]
- Bair, E.S.; Roadcap, G.S. Comparison of flow models used to delineate capture zones of wells.1.leaky-confined fractured-car bonate aquifer. Ground Water 1992, 30, 199–211. [Google Scholar] [CrossRef]
- Wang, J.C.; Booker, J.R.; Carter, J.P. Analysis of the remediation of a contaminated aquifer by a multi-well system. Comput. Geotech. 1999, 25, 171–189. [Google Scholar] [CrossRef]
- Fienen, M.N.; Luo, J.; Kitanidis, P.K. Semi-analytical homogeneous anisotropic capture zone delineation. J. Hydrol. 2005, 312, 39–50. [Google Scholar] [CrossRef]
- Ahlfeld, D.P.; Sawyer, C.S. Well location in capture zone design using simulation and optimization techniques. Groundwater 1990, 28, 507–512. [Google Scholar] [CrossRef]
- Hudak, P.F. Numerical modeling assessment of three-gate structures for capturing contaminated groundwater. Environ. Geol. 2008, 55, 1311–1317. [Google Scholar] [CrossRef]
- Kurmanseiit, M.B.; Tungatarova, M.S.; Royer, J.-J.; Aizhulov, D.Y.; Shayakhmetov, N.M.; Kaltayev, A. Streamline-based reactive transport modeling of uranium mining during in-situ leaching: Advantages and drawbacks. Hydrometallurgy 2023, 220, 106107. [Google Scholar] [CrossRef]
- Aizhulov, D.; Tungatarova, M.; Kaltayev, A. Streamlines Based Stochastic Methods and Reactive Transport Simulation Applied to Resource Estimation of Roll-Front Uranium Deposits Exploited by In-Situ Leaching. Minerals 2022, 12, 1209. [Google Scholar] [CrossRef]
- Zheng, H.Q.Y. Site Conditions Experiments for Field Test on In-Situ Leaching and Hydrodynamic Simulation of Uranium in Bayan-Uul; East China University of Technology: Nanchang, China, 2017. [Google Scholar]
- Chang, Y. Simulation Study on Groundwater Dynamics Control of Leaching Range of in-situ Uranium Well Field; University of South China: Hengyang, Hunan, 2020. [Google Scholar]
- Chen, Q.Q. Numerical Simulation of In-situ Leaching of Uranium by Acid Method Based on Reactive Solute Transport Theory; East China University of Technology: Nanchang, China, 2020. [Google Scholar]
- Wang, B.; Luo, Y.; Liu, J.H.; Li, X.; Zheng, Z.H.; Chen, Q.Q.; Li, L.Y.; Wu, H.; Fan, Q.R. Ion migration in in-situ leaching (ISL) of uranium: Field trial and reactive transport modelling. J. Hydrol. 2022, 615, 128634. [Google Scholar] [CrossRef]
- Wang, B.; Luo, Y.; Qian, J.Z.; Li, J.H.; Li, X.; Zhang, Y.H.; Chen, Q.Q.; Li, L.Y.; Liang, D.Y.; Huang, J. Machine learning-based optimal design of the in-situ leaching process parameter (ISLPP) for the acid in-situ leaching of uranium. J. Hydronal 2023, 626, 130234. [Google Scholar] [CrossRef]
- Xu, T.; Spycher, N.; Sonnenthal, E.; Zheng, L.; Pruess, K. TOUGHREACT User’s Guide: A Simulation Program for Non-isothermal Multiphase Reactive Transport in Variably Saturated Geologic Media, Version 2.0.; Earth Sciences Division, Lawrence Berkeley National Laboratory University of California: Berkeley, CA, USA, 2012. [Google Scholar]
- Xu, T.; Apps, J.A.; Pruess, K. Reactive geochemical transport simulation to study mineral trapping for CO2 disposal in deep arenaceous formations. J. Geophys. Res. Solid. Earth 2003, 108, 2071. [Google Scholar] [CrossRef]
- Pruess, K.; Oldenburg, C.M.; Moridis, G.J. TOUGH2 User’s Guide Version 2; Earth Sciences Division, Lawrence Berkeley National Laboratory University of California: Berkeley, CA, USA, 1999. [Google Scholar]
- Xu, T.; Spycher, N.; Sonnenthal, E.; Zhang, G.; Zheng, L.; Pruess, K. TOUGHREACT Version 2.0: A simulator for subsurface reactive transport under non-isothermal multiphase flow conditions. Comput. Geosci. 2011, 37, 763–774. [Google Scholar] [CrossRef]
- Dobson, P.F.; Salah, S.; Spycher, N.; Sonnenthal, E.L. Simulation of water-rock interaction in the yellowstone geothermal system using TOUGHREACT. Geothermics 2004, 33, 493–502. [Google Scholar] [CrossRef]
- Sonnenthal, E.; Ito, A.; Spycher, N.; Yui, M.; Apps, J.; Sugita, Y.; Conrad, M.; Kawakami, S. Approaches to modeling coupled thermal, hydrological, and chemical processes in the drift scale heater test at Yucca Mountain. Int. J. Rock. Mech. Min. Sci. 2005, 42, 698–719. [Google Scholar] [CrossRef]
- Spycher, N.F.; Sonnenthal, E.L.; Apps, J.A. Fluid flow and reactive transport around potential nuclear waste emplacement tunnels at Yucca Mountain, Nevada. J. Contam. Hydrol. 2003, 62–63, 653–673. [Google Scholar] [CrossRef]
- Aradottir, E.S.P.; Sonnenthal, E.L.; Bjornsson, G.; Jonsson, H. Multidimensional reactive transport modeling of CO2 mineral sequestration in basalts at the Hellisheidi geothermal field, Iceland. Int. J. Greenh. Gas. Control 2012, 9, 24–40. [Google Scholar] [CrossRef]
- Audigane, P.; Gaus, I.; Czernichowski-Lauriol, I.; Pruess, K.; Xu, T.F. Two-dimensional reactive transport modeling of CO2 injection in a saline Aquifer at the Sleipner site, North Sea. Am. J. Sci. 2007, 307, 974–1008. [Google Scholar] [CrossRef]
- Zheng, C.M.; Bennett, G.D. Applied Contaminant Transport Modeling, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2002. [Google Scholar]
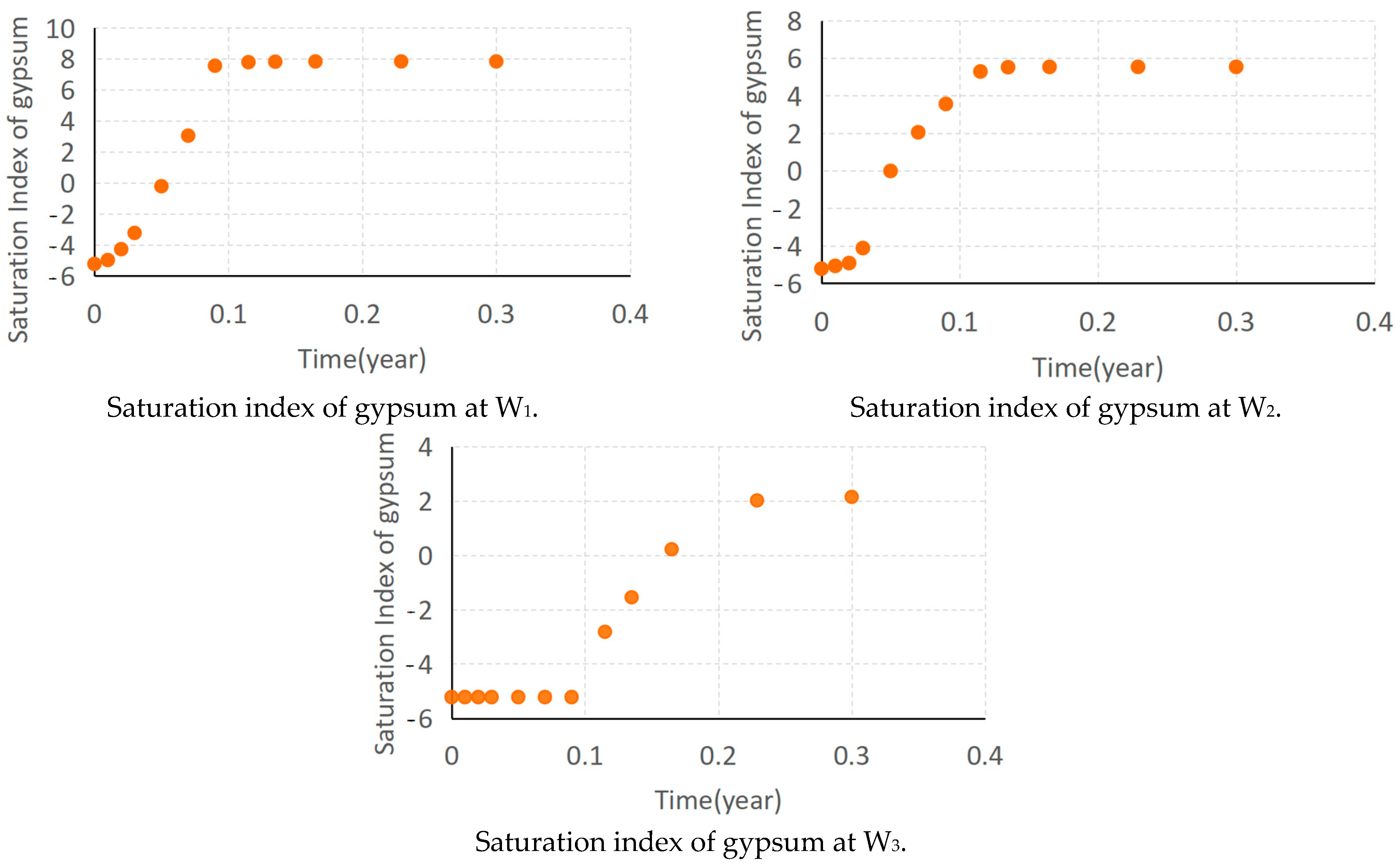
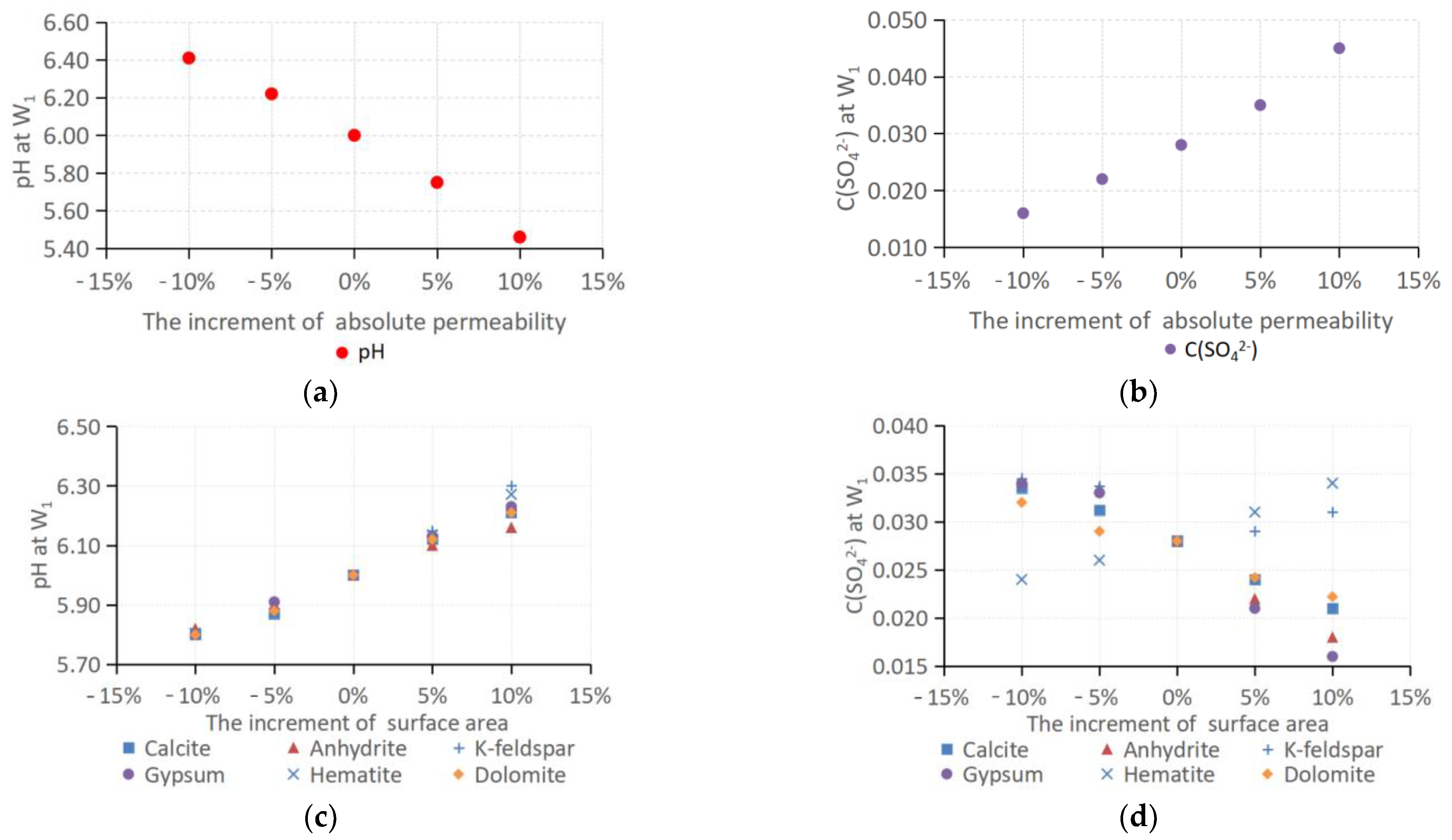
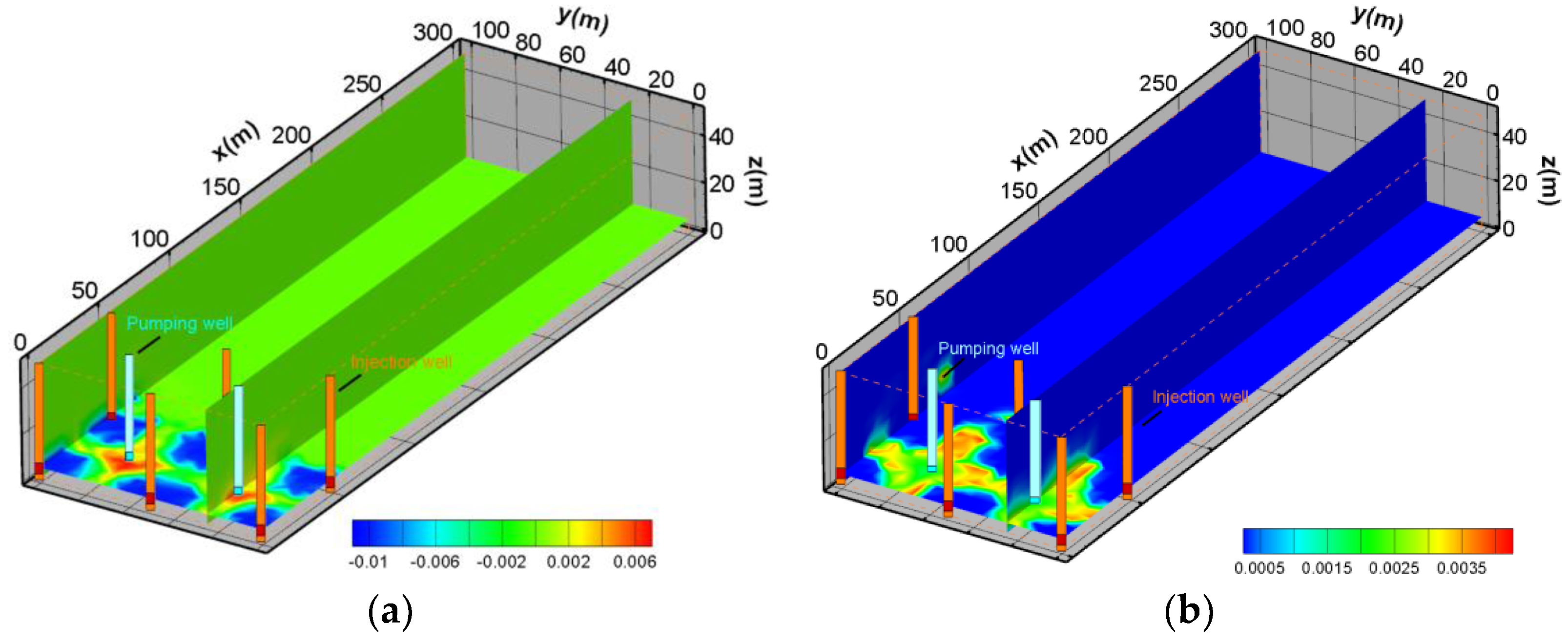
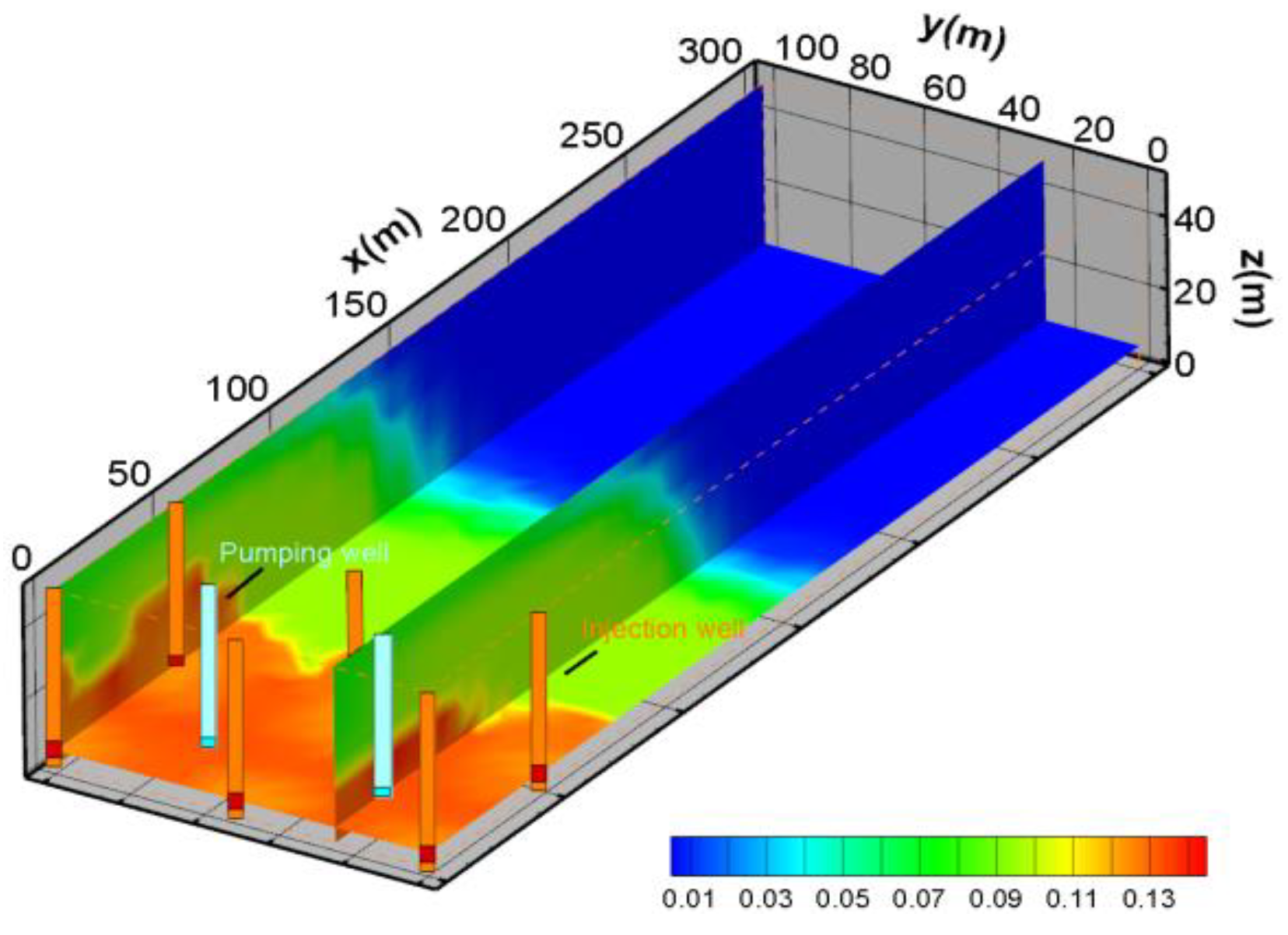


| Symbol | Meaning | Units | Symbol | Meaning | Units |
|---|---|---|---|---|---|
| kg | Saturation | dimensionless | |||
| Time | s | Porosity | dimensionless | ||
| m/s | Absolute permeability | m2 | |||
| kg/s | Relative permeability | dimensionless | |||
| Water phase | dimensionless | Viscosity | dimensionless | ||
| Concentration | mol/l | Liquid phase | dimensionless | ||
| Mass fraction | dimensionless | Gas phase | dimensionless | ||
| Density | kg/m3 | Dispersion | m2 | ||
| Velocity of flow | m/s | Reaction rate | mol·m−2s−1 | ||
| Stoichiometric number | dimensionless | dimensionless | |||
| Pressure | Pa | dimensionless |
| Index | Concentration |
|---|---|
| Temperature (°C) | 9 |
| pH | 7.226 |
| ORP (mV) | 196.1 |
| DO (mg/L) | 7.37 |
| Na (mg/L) | 495 |
| K (mg/L) | 8.46 |
| Ca (mg/L) | 76.6 |
| Mg (mg/L) | 55.2 |
| SO42− (mg/L) | 407 |
| CI− (mg/L) | 410 |
| HCO3− (mg/L) | 1110 |
| Fe (mg/L) | 0.747 |
| U (µg/L) | 30.1 |
| Name | Chemical Formula | Initial Mineral Volume Fraction of Ore Body | Initial Mineral Volume Fraction of Surrounding Rock |
|---|---|---|---|
| Quartz | SiO2 | 0.48686 | 0.48686 |
| K-feldspar | KAlSi3O8 | 0.21550 | 0.21550 |
| Oligoclase | CaNa4Al6Si14O40 | 0.01134 | 0.01134 |
| Na-smectite | Ca0.145Mg0.26Al1.77Si3.97O10(OH)2 | 0.08391 | 0.08391 |
| Ca-smectite | Na0.29Mg0.26Al1.77Si3.97O10(OH)2 | 0.02597 | 0.02597 |
| Illite | K0.6Mg0.25Al1.8(Al0.5Si3.5O10)(OH)2 | 0.02137 | 0.02137 |
| Kaolinite | Al2Si2O5(OH)2 | 0.01520 | 0.01520 |
| Uraninite | UO2 | 0.01143 | 0.00000 |
| Hematite | Fe2O3 | 0.01880 | 0.01880 |
| Calcite | CaCO3 | 0.03320 | 0.01140 |
| Index | Concentration |
|---|---|
| Temperature (°C) | 15.2 |
| pH | 0.443 |
| ORP (mV) | 227.6 |
| DO (mg/L) | 9.12 |
| Na (mg/L) | 1950 |
| K (mg/L) | 533 |
| Ca (mg/L) | 441 |
| Mg (mg/L) | 916 |
| SO42− (mg/L) | 27,300 |
| CI− (mg/L) | 464 |
| HCO3− (mg/L) | 35 |
| Fe (mg/L) | 1580 |
| Layer ID | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Top elevation (m) | 60 | 40 | 28.5 | 18.5 | 8.5 | 2.5 |
| Bottom elevation (m) | 40 | 28.5 | 18.5 | 8.5 | 2.5 | 0 |
| Thickness (m) | 20 | 11.5 | 10 | 10 | 6 | 2.5 |
| Parameters | Value |
|---|---|
| Aquifer thickness (m) | 60 |
| Rock grain density (kg/m3) | 2600 |
| Porosity | 0.085 |
| K: absolute permeability(m2) | 3 × 10−6 |
| Temperature (°C) | 9 |
| Rock grain specific heat (J/(Kg·°C)) | 920 |
| Formation heat conductivity (W/(m·°C)) | 2.51 |
| Pressure (MPa) | 0.1 |
| Minerals | Chemical Formula | Surface Area (cm2/g) | Parameters for Kinetic Rate Law | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Neutral Mechanism | Acid Mechanism | Base Mechanism | ||||||||
| k25(mol/ m2/s) | Ea (KJ/mol) | k25(mol /m2/s) | Ea (KJ/mol) | n (H+) | k25(mol/ m2/s) | Ea (KJ/mol) | n(OH−) | |||
| Calcite | CaCO3 | 9.8 | Equilibrium | |||||||
| Anhydrite | CaSO4 | 9.8 | Equilibrium | |||||||
| Quartz | SiO2 | 9.8 | 1.023 × 10−14 | 87.7 | ||||||
| Illite | K0.6Mg0.25Al1.8(Al0.5Si3.5O10)(OH)2 | 151.6 | 1.660 × 10−13 | 35.0 | 1.047 × 10−11 | 23.6 | 0.34 | 3.020 × 10−17 | 58.9 | −0.4 |
| K-feldspar | KAlSi3O8 | 9.8 | 3.890 × 10−13 | 38.0 | 8.710 × 10−11 | 51.7 | 0.5 | 6.310 × 10−22 | 94.1 | −0.823 |
| Chlorite | Mg2.5Fe2.5Al2Si3O10(OH)8 | 20.0 | 3.020 × 10−13 | 88.0 | 7.762 × 10−12 | 88.0 | 0.50 | |||
| Na-smectite | Na0.29Mg0.26Al1.77Si3.97O10(OH)2 | 151.6 | 1.660 × 10−13 | 35.0 | 1.047 × 10−11 | 23.6 | 0.34 | 3.020 × 10−17 | 58.9 | −0.4 |
| Kaolinite | Al2Si2O5(OH)4 | 23.0 | 6.918 × 10−14 | 22.2 | 4.898 × 10−12 | 65.9 | 0.777 | 8.913 × 10−18 | 17.9 | −0.472 |
| Ca-smectite | Ca0.145Mg0.26Al1.77Si3.97O10(OH)2 | 151.6 | 1.660 × 10−13 | 35.0 | 1.047 × 10−11 | 23.6 | 0.34 | 3.020 × 10−17 | 58.9 | −0.4 |
| Gypsum | CaSO4 | 9.8 | 1.6218 × 10−7 | |||||||
| Pyrite | FeS2 | 12.9 | 2.52 × 10−12 | 56.9 | −0.5 | 2.8184 × 10−5 | 56.9 | 0.5(n(O2(aq))) | ||
| Oligoclase | CaNa4Al1.77Si3.97O10(OH)2 | 10.0 | 1.4454 × 10−13 | 69.80 | ||||||
| Hematite | Fe2O3 | 12.9 | 2.512 × 10−15 | 66.2 | 4.0738 × 10−10 | 66.2 | 1 | |||
| Muscovite | KAl2(AlSi3O10)(OH)2 | 152.0 | 3.0200 × 10−13 | 88.0 | 7.7624 × 10−12 | 88.0 | 0.5 | 3.0200 × 10−13 | ||
| Siderite | FeCO3 | 10.0 | 1.26 × 10−9 | 62.76 | 6.46 × 10−4 | 36.1 | 0.5 | |||
| Dolomite | CaMg(CO3)2 | 12.9 | 2.52 × 10−12 | 62.76 | 2.34 × 10−7 | 43.54 | 1 | |||
| Ankerite | CaMg0.3Fe0.7(CO3)2 | 9.8 | 1.26 × 10−9 | 62.76 | 6.46 × 10−4 | 36.1 | 0.5 | |||
| Magnesite | MgCO3 | 10.0 | 4.5709 × 10−10 | 23.50 | 4.1687 × 10−7 | 14.4 | 1 | |||
| Schemes (Simulation Time = 1 Year) | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Pumping ratio | 0 | 0.01 | 0.02 | 0 | 0 |
| Non-uniform injection ratio | 0 | 0 | 0 | 0.05 | 0.1 |
| Inner injection rate (m3/d) (Q1,Q2,Q3) | 176.00 | 174.24 | 172.48 | 184.82 | 194.09 |
| Outer injection rate (m3/d) (Q4,Q5,Q6) | 176.00 | 174.24 | 172.48 | 167.18 | 158.89 |
| Pumping rate (m3/d) (Q7,Q8) | 264.00 | 265.76 | 267.52 | 264.00 | 264.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Tang, Z.; Xiang, D. Study on Numerical Simulation of Reactive-Transport of Groundwater Pollutants Caused by Acid Leaching of Uranium: A Case Study in Bayan-Uul Area, Northern China. Water 2024, 16, 500. https://doi.org/10.3390/w16030500
Li H, Tang Z, Xiang D. Study on Numerical Simulation of Reactive-Transport of Groundwater Pollutants Caused by Acid Leaching of Uranium: A Case Study in Bayan-Uul Area, Northern China. Water. 2024; 16(3):500. https://doi.org/10.3390/w16030500
Chicago/Turabian StyleLi, Haibo, Zhonghua Tang, and Dongjin Xiang. 2024. "Study on Numerical Simulation of Reactive-Transport of Groundwater Pollutants Caused by Acid Leaching of Uranium: A Case Study in Bayan-Uul Area, Northern China" Water 16, no. 3: 500. https://doi.org/10.3390/w16030500
APA StyleLi, H., Tang, Z., & Xiang, D. (2024). Study on Numerical Simulation of Reactive-Transport of Groundwater Pollutants Caused by Acid Leaching of Uranium: A Case Study in Bayan-Uul Area, Northern China. Water, 16(3), 500. https://doi.org/10.3390/w16030500





