Identifying the Most Discriminative Parameter for Water Quality Prediction Using Machine Learning Algorithms
Abstract
1. Introduction
2. Methodology
2.1. Experimental Dataset
2.2. Machine Learning Algorithms
- Xj: The jth predictor variable
- βj: The coefficient estimate for the jth predictor variable
2.3. Proposed Methodology
2.3.1. Pre-processing
2.3.2. Parameter Selection
2.3.3. Model Building
3. Results and Discussion
- (a)
- Performance evaluation of the ML models by using all 17 raw parameters
- (b)
- Performance evaluation of the ML models by using only statistically significant parameters
- (c)
- Performance evaluation of the ML models by using the most statistically significant parameter Cr.
3.1. Performance of Different Sets of Parameters
3.2. Performance Comparison of the Proposed Method with Existing Methods
4. Conclusions
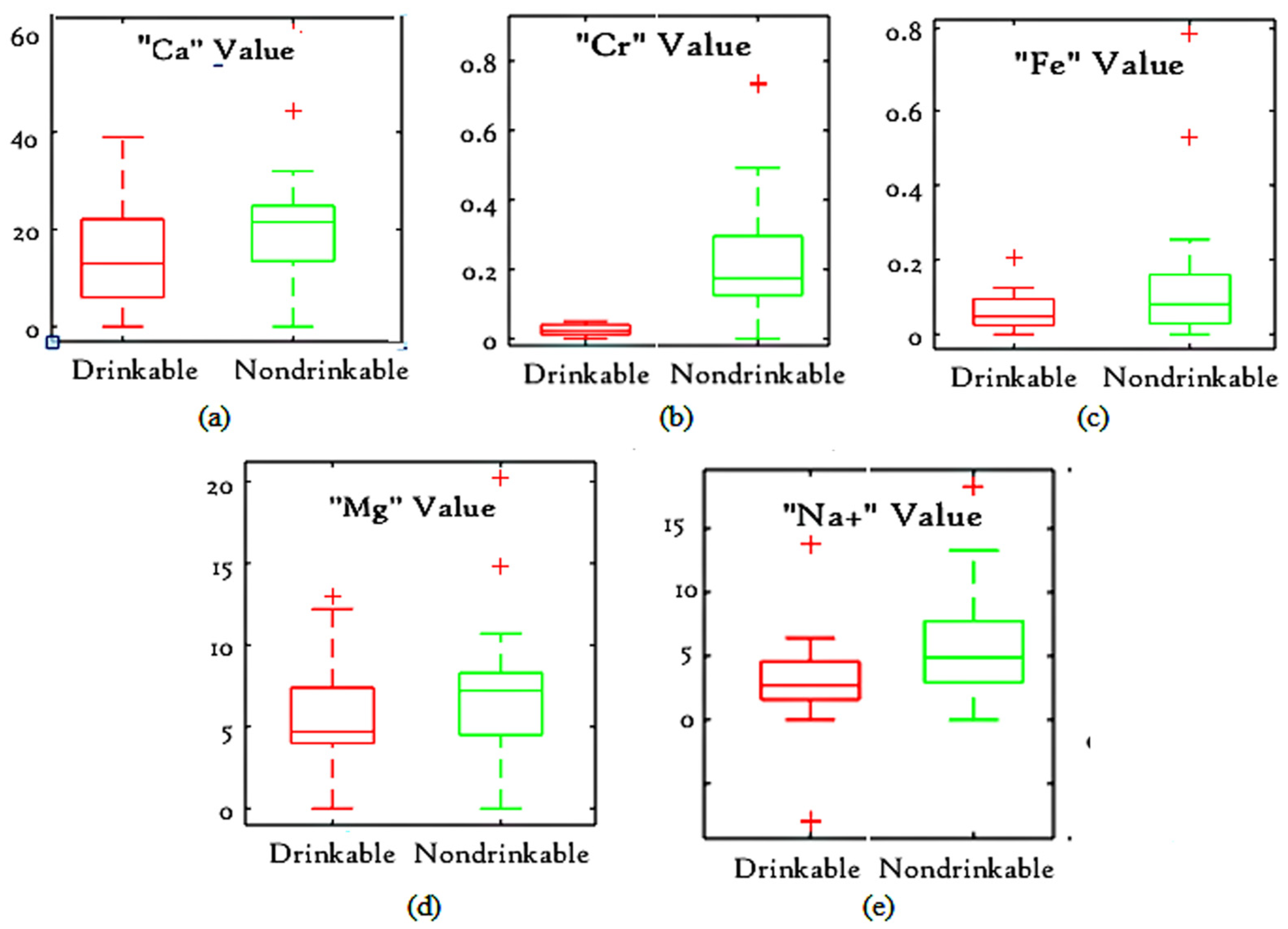
- (a)
- The MWW test reveals that out of all 19 parameters, five parameters including Fe, Cr, , Ca and Mg are statistically significant in water quality prediction.
- (b)
- Out of all these five statistically significant parameters, Cr is the most significant, as the range of Cr values for drinkable water differs from the range of Cr values for non-drinkable water.
- (c)
- The experimental results show that compared to LR and KNN, ANN is more efficient for water quality prediction. For different sets of parameters, the ANN always shows better results than both LR and KNN. Most of the time the difference is not less than 10%.
- (d)
- The system that utilizes only the statistically significant features like Fe, Cr, , Ca, and Mg achieves higher classification accuracy when compared to the system considering all parameters.
- (e)
- The system’s development with the single parameter ‘Cr’ has resulted in the most efficient system, achieving an impressive classification accuracy of 91.67% using ANN.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmed, U.; Mumtaz, R.; Anwar, H.; Shah, A.A.; Irfan, R.; García-Nieto, J. Efficient water quality prediction using supervised machine learning. Water 2019, 11, 2210. [Google Scholar] [CrossRef]
- Malik, A.; Yasar, A.; Tabinda, A.B.; Abubakar, M. Water-borne diseases, cost of illness and willingness to pay for diseases interventions in rural communities of developing countries. Iran. J. Public Health 2012, 41, 39. [Google Scholar] [PubMed]
- Tong, S.T.; Chen, W. Modeling the relationship between land use and surface water quality. J. Environ. Manag. 2002, 66, 377–393. [Google Scholar] [CrossRef] [PubMed]
- Babiker, I.S.; Mohamed, M.A.; Hiyama, T. Assessing groundwater quality using GIS. Water Resour. Manag. 2007, 21, 699–715. [Google Scholar] [CrossRef]
- Singha, S.; Pasupuleti, S.; Singha, S.S.; Singh, R.; Kumar, S. Prediction of groundwater quality using efficient machine learning technique. Chemosphere 2021, 276, 130265. [Google Scholar] [CrossRef] [PubMed]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Lenat, D.R. Water quality assessment of streams using a qualitative collection method for benthic macroinvertebrates. J. North Am. Benthol. Soc. 1988, 7, 222–233. [Google Scholar] [CrossRef]
- Bonney, R.; Ballard, H.; Jordan, R.; McCallie, E.; Phillips, T.; Shirk, J.; Wilderman, C.C. Public Participation in Scientific Research: Defining the Field and Assessing Its Potential for Informal Science Education. A CAISE Inquiry Group Report. Online Submission. 2009. Available online: https://eric.ed.gov/?id=ED519688 (accessed on 1 July 2009).
- Tim, U.S.; Jolly, R. Evaluating agricultural nonpoint-source pollution using integrated geographic information systems and hydrologic/water quality model. J. Environ. Qual. 1994, 23, 25–35. [Google Scholar] [CrossRef]
- Tyagi, S.; Sharma, B.; Singh, P.; Dobhal, R. Water quality assessment in terms of water quality index. Am. J. Water Resour. 2013, 1, 34–38. [Google Scholar] [CrossRef]
- Atulegwu, P.U.; Njoku, J.D. The impact of biocides on the water quality. Int. Res. J. Eng. Sci. Technol. 2004, 1, 47–52. [Google Scholar]
- Yisa, J.; Tijani, J.O. Analytical studies on water quality index of river Landzu. Am. J. Appl. Sci. 2010, 7. [Google Scholar] [CrossRef]
- Yan, T.; Shen, S.L.; Zhou, A. Indices and models of surface water quality assessment: Review and perspectives. Environ. Pollut. 2022, 308, 119611. [Google Scholar] [CrossRef]
- Sarker, B.; Keya, K.N.; Mahir, F.I.; Nahiun, K.M.; Shahida, S.; Khan, R.A. Surface and ground water pollution: Causes and effects of urbanization and industrialization in South Asia. Sci. Rev. 2021, 7, 32–41. [Google Scholar] [CrossRef]
- Camara, M.; Jamil, N.R.; Abdullah, A.F.B. Impact of land uses on water quality in Malaysia: A review. Ecol. Process. 2019, 8, 1–10. [Google Scholar] [CrossRef]
- Gangwar, S. Water quality monitoring in India: A review. Int. J. Inform. Comput. Technol. 2013, 3, 851–856. [Google Scholar]
- Kord, M.; Arshadi, B. Applying the water quality index with fuzzy logic as a way to analyze multiple long-term groundwater quality data: A case study of Dehgolān plain. Arab. J. Geosci. 2022, 15, 253. [Google Scholar] [CrossRef]
- Agbasi, J.C.; Egbueri, J.C. Assessment of PTEs in water resources by integrating HHRISK code, water quality indices, multivariate statistics, and ANNs. Geocarto Int. 2022, 37, 10407–10433. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Homaei, F.; Mohamadi, S. Reliability evaluation of groundwater quality index using data-driven models. Environ. Sci. Pollut. Res. 2022, 29, 8174–8190. [Google Scholar] [CrossRef]
- Nsabimana, A.; Wu, J.; Wu, J.; Xu, F. Forecasting groundwater quality using automatic exponential smoothing model (AESM) in Xianyang City, China. Hum. Ecol. Risk Assess. Int. J. 2022, 29, 347–368. [Google Scholar] [CrossRef]
- Agrawal, P.; Sinha, A.; Kumar, S.; Agarwal, A.; Banerjee, A.; Villuri, V.G.K.; Annavarapu, C.S.R.; Dwivedi, R.; Dera, V.V.R.; Sinha, J.; et al. Exploring artificial intelligence techniques for groundwater quality assessment. Water 2021, 13, 1172. [Google Scholar] [CrossRef]
- Gupta, R.; Singh, A.N.; Singhal, A. Application of ANN for water quality index. Int. J. Mach. Learn. Comput 2019, 9, 688–693. [Google Scholar] [CrossRef]
- Sakizadeh, M. Artificial intelligence for the prediction of water quality index in groundwater systems. Model. Earth Syst. Environ. 2016, 2, 8. [Google Scholar] [CrossRef]
- Mosavi, A.; Hosseini, F.S.; Choubin, B.; Abdolshahnejad, M.; Gharechaee, H.; Lahijanzadeh, A.; Dineva, A.A. Susceptibility prediction of groundwater hardness using ensemble machine learning models. Water 2020, 12, 2770. [Google Scholar] [CrossRef]
- Zaresefat, M.; Derakhshani, R.; Nikpeyman, V.; GhasemiNejad, A.; Raoof, A. Using artificial intelligence to identify suitable artificial groundwater recharge areas for the Iranshahr basin. Water 2023, 15, 1182. [Google Scholar] [CrossRef]
- Tiyasha, T.; Tung, T.M.; Bhagat, S.K.; Tan, M.L.; Jawad, A.H.; Mohtar, W.H.M.W.; Yaseen, Z.M. Functionalization of remote sensing and on-site data for simulating surface water dissolved oxygen: Development of hybrid tree-based artificial intelligence models. Mar. Pollut. Bull. 2021, 170, 112639. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, K.; Bali, V.; Nawaz, N.; Bali, S.; Mathur, S.; Mishra, R.K.; Rani, S. A machine-learning approach for prediction of water contamination using latitude, longitude, and elevation. Water 2022, 14, 728. [Google Scholar] [CrossRef]
- Gaagai, A.; Aouissi, H.A.; Bencedira, S.; Hinge, G.; Athamena, A.; Heddam, S.; Gad, M.; Elsherbiny, O.; Elsayed, S.; Eid, M.H.; et al. Application of water quality indices, machine learning approaches, and GIS to identify groundwater quality for irrigation purposes: A case study of Sahara Aquifer, Doucen Plain, Algeria. Water 2023, 15, 289. [Google Scholar] [CrossRef]
- Ongley, E.D. Water quality management: Design, financing and sustainability considerations. In Proceedings of the African Water Resources Policy Conference, Nairobi, Kenya, 26–28 May 1999. [Google Scholar]
- Asadollah, S.B.H.S.; Sharafati, A.; Motta, D.; Yaseen, Z.M. River water quality index prediction and uncertainty analysis: A comparative study of machine learning models. J. Environ. Chem. Eng. 2021, 9, 104599. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Olbert, A.I. A review of water quality index models and their use for assessing surface water quality. Ecol. Indic. 2021, 122, 107218. [Google Scholar] [CrossRef]
- Singha, S.; Pasupuleti, S.; Singha, S.S.; Kumar, S. Effectiveness of groundwater heavy metal pollution indices studies by deep-learning. J. Contam. Hydrol. 2020, 235, 103718. [Google Scholar] [CrossRef]
- Agrawal, P.; Sinha, A.; Pasupuleti, S.; Nune, R.; Saha, S. Geospatial analysis coupled with logarithmic method for water quality assessment in part of Pindrawan Tank Command Area in Raipur District of Chhattisgarh. In Climate Impacts on Water Resources in India: Environment and Health; Springer: Cham, Switzerland, 2021; pp. 57–78. [Google Scholar]
- Agrawal, P.; Sinha, A.; Pasupuleti, S.; Sinha, J.; Chatterjee, A.; Kumar, S. A mathematical approach to evaluate the extent of groundwater contamination using polynomial approximation. Water Supply 2022, 22, 6070–6082. [Google Scholar] [CrossRef]
- Bui, D.T.; Khosravi, K.; Tiefenbacher, J.; Nguyen, H.; Kazakis, N. Improving prediction of water quality indices using novel hybrid machine-learning algorithms. Sci. Total Environ. 2020, 721, 137612. [Google Scholar] [CrossRef] [PubMed]
- Khalil, A.; Almasri, M.N.; McKee, M.; Kaluarachchi, J.J. Applicability of statistical learning algorithms in groundwater quality modeling. Water Resour. Res. 2005, 41, W05010. [Google Scholar] [CrossRef]
- Lingjun, H.; Levine, R.A.; Fan, J.; Beemer, J.; Stronach, J. Random forest as a predictive analytics alternative to regression in institutional research. Pract. Assess. Res. Eval. 2019, 23, 1. [Google Scholar]
- Sperandei, S. Understanding logistic regression analysis. Biochem. Medica 2014, 24, 12–18. [Google Scholar] [CrossRef]
- Zhang, Z. Introduction to machine learning: K-nearest neighbors. Ann. Transl. Med. 2016, 4, 218. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Fundamentals of artificial neural networks and deep learning. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer International Publishing: Cham, Switzerland, 2022; pp. 379–425. [Google Scholar]
- Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics: Methodology and Distribution; Springer: New York, NY, USA, 1992; pp. 196–202. [Google Scholar]
- Shafi, U.; Mumtaz, R.; Anwar, H.; Qamar, A.M.; Khurshid, H. Surface water pollution detection using internet of things. In Proceedings of the 2018 15th International Conference on Smart Cities: Improving Quality of life Using ICT & IoT (HONET-ICT), Islamabad, Pakistan, 8–10 October 2018. [Google Scholar]

| Features | Drinkable (Mean ± SD) | Non-Drinkable (Mean ± SD) | p-Values |
|---|---|---|---|
| pH | 7.93 ± 0.358 | 7.81 ± 0.302 | 0.8247 |
| Cond | 601.733 ± 391.01 | 735.16 ± 433.29 | 0.1199 |
| TDS | 361.0667 ± 234.54 | 444.24 ± 268.43 | 0.1199 |
| Alk | 162 ± 66.23 | 183.86 ± 74.68 | 0.0938 |
| 102 ± 54.43 | 103.63 ± 70.03 | 0.3146 | |
| Hd | 215.67 ± 98.06 | 194.77 ± 103.85 | 0.5451 |
| Fe | 0.076 ± 0.047 | 0.156 ± 0.175 | 0.0237 |
| Cr | 0.0254 ± 0.0150 | 0.2478 ± 0.190 | 6.34 × 10−8 |
| Na | 3.88 ± 3.12 | 6.281 ± 4.216 | 0.0097 |
| K | 6.819 ± 8.452 | 7.516 ± 7.780 | 0.1571 |
| HCO3 | 4.167 ± 0.906 | 4.25 ± 1.175 | 0.2421 |
| Cl | 0.148 ± 0.089 | 0.164 ± 0.138 | 0.421 |
| Ca | 20.067 ± 9.961 | 24.675 ± 11.55 | 0.0186 |
| Mg | 6.93 ± 3.061 | 8.22 ± 3.85 | 0.0244 |
| HNO3 | 5.28 ± 1.520 | 5.595 ± 1.25 | 0.1033 |
| Fluoride | 0.58 ± 0.144 | 0.485 ± 0.163 | 0.866 |
| SO4 | 35.2 ± 6.220 | 36.59 ± 5.66 | 0.082 |
| ML | Performance Measure | (Setup—1) All Features | (Setup—2) Statistically Significant Features | (Setup—3) ‘Cr’ |
|---|---|---|---|---|
| ANN | ACC | 66.67% | 83.33% | 91.67% |
| LR | ACC | 50.00% | 66.70% | 75.50% |
| KNN | ACC | 37.50% | 81.50% | 87.50% |
| ANN | SN/RC | 83.33% | 100.00% | 83.33% |
| LR | SN/RC | 50.00% | 83.33% | 100.00% |
| KNN | SN/RC | 25.00% | 83.33% | 100.00% |
| ANN | SP | 50.00% | 66.67% | 100.00% |
| LR | SP | 37.50% | 50.00% | 57.14% |
| KNN | SP | 50.00% | 83.33% | 83.33% |
| ANN | PR | 57.00% | 69.00% | 89.00% |
| LR | PR | 49.00% | 52.00% | 57.15 |
| KNN | PR | 51.00% | 52.00% | 60.00% |
| Authors, Year | Size of the Dataset | Model Used | Number of Parameters Used | Performance | |||
|---|---|---|---|---|---|---|---|
| ACC | SN/RC | SP | PR | ||||
| U. Ahmed et al. [1], 2019 | 663 Samples | 10 ML algorithms, MLP gave the highest result | 4-Temperature, Turbidity, pH and total dissolved solids | 0.8507 | 0.5640 | __ | 0.5659 |
| U. Shafi [42], 2018 | 667 Samples | SVM, NN, KNN & Deep NN | 3-Turbidity, temperature and pH | 0.93 | 0.93 | --- | 0.94 |
| Our proposed method | 37 Samples | ANN | 1- Cr | 0.9167 | 0.83 | 1 | 0.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatterjee, T.; Gogoi, U.R.; Samanta, A.; Chatterjee, A.; Singh, M.K.; Pasupuleti, S. Identifying the Most Discriminative Parameter for Water Quality Prediction Using Machine Learning Algorithms. Water 2024, 16, 481. https://doi.org/10.3390/w16030481
Chatterjee T, Gogoi UR, Samanta A, Chatterjee A, Singh MK, Pasupuleti S. Identifying the Most Discriminative Parameter for Water Quality Prediction Using Machine Learning Algorithms. Water. 2024; 16(3):481. https://doi.org/10.3390/w16030481
Chicago/Turabian StyleChatterjee, Tapan, Usha Rani Gogoi, Animesh Samanta, Ayan Chatterjee, Mritunjay Kumar Singh, and Srinivas Pasupuleti. 2024. "Identifying the Most Discriminative Parameter for Water Quality Prediction Using Machine Learning Algorithms" Water 16, no. 3: 481. https://doi.org/10.3390/w16030481
APA StyleChatterjee, T., Gogoi, U. R., Samanta, A., Chatterjee, A., Singh, M. K., & Pasupuleti, S. (2024). Identifying the Most Discriminative Parameter for Water Quality Prediction Using Machine Learning Algorithms. Water, 16(3), 481. https://doi.org/10.3390/w16030481








