1. Introduction
To unlock the promising blue energy market potential in the Mediterranean Sea and develop technologies that can be globally exported, it seems crucial to guarantee solutions effectively optimized for this closed basin. Among stand-alone systems or blue energy farms, a new solution is emerging to boost offshore energy harvesting in the Mediterranean area: the floating energy archipelago. It represents a multi-use energy hub for exploiting marine renewable energy with the possibility of combined and/or co-located solutions to reduce the variability of the power output, among other benefits [
1].
The solution, proposed by the National Research Council of Italy, facilitates the implementation of various technologies for the generation of clean energy such as solar islands [
2] and offshore wind farms [
3]. The entirety of the produced energy can be stored and used to support the development of new productive activities, such as aquaculture, seawater desalination, and
production. All these installations are spatially closed and protected by an array of floating breakwater modules. Implementing the twofold use of these modules, as an offshore breakwater and wave energy converter (WEC), is an interesting challenge. To achieve this, variable submergence (draft) is required. In more frequent mild sea states, the floating breakwater assumes the function of a wave energy converter, contributing to the energy production of the archipelago. In this configuration, the maximum energy is harvested when the floating module motions are in resonance with the waves (low draft). Otherwise, in extreme and severe sea states, it should strictly work as a passive breakwater, absorbing the incoming waves and protecting the devices installed in the archipelago. For the latter case, the module is filled with seawater to obtain a larger draft, increasing its stability.
Floating breakwaters (FBs) represent a category of maritime defenses usually known as “unconventional”. Since 1811, when the first concept of a wooden floating breakwater was proposed to protect Plymouth Sound [
4], engineers and researchers have shown a growing interest in the topic due to the significant benefits obtainable through their use compared to their fixed, traditional counterparts [
5]. Traditionally, they are classified depending on their shape: box type, pontoon type, frame type, mat type, tethered floating type, and horizontal-plate type [
6]. Considering their wave attenuation mechanism, floating breakwaters are mainly represented by reflective and dissipative types [
7]. Reflective breakwaters reflect the incoming wave and are often rigid structures that do not deform under the wave load. Dissipative breakwaters dissipate wave energy through turbulence, friction, and inelastic deformation. Thanks to their easy building process and durability, floating breakwaters have recently captured the attention of wave energy operators interested in developing and integrating their solutions over reliable and economic substructures, even in low-energy seas [
8,
9,
10]. Currently, hybrid FBs are categorized based on the WEC-type system, as discussed in a recent review by Zhao et al., 2019 [
11].
With the oscillating water column type WEC, a typical hollow-shaped structure is present. Examples of these devices can be found in [
12,
13,
14,
15], implementing one or more air chambers (each one equipped with an air turbine) to produce electricity. These studies demonstrated the possibility for these devices to function as WECs, but due to very low energetic performances, their main purpose remains coastal protection. In Michailides and Angelides, 2011 [
16], a flexible floating breakwater consisting of several modules was proposed. The adjacent modules were connected by the power take-off (PTO hereinafter) system, which is driven by the relative motion of the modules.
With the “wave-activated bodies” or “oscillating bodies” type of WEC, some box-type breakwaters reached the stage of engineering application [
17]. Pile-restrained floating breakwaters, modified with the insertion of a PTO system [
18], have also been investigated. The performances of these devices were evaluated through linear potential flow theory by [
19,
20]. Another WEC-type coupled with pile-restrained breakwater is represented by the piezoelectric wave energy converter (PWEC), proposed in [
21]. A hydro-elastic model has been developed to investigate the influence of width and submergence of the PWEC, showing that with increasing submergence, a shift towards large wave frequency occurs [
22]. Their technological readiness level is lower, although the potential to be adapted for double use seems higher. However, long wave attenuation in operational conditions represents a crucial disadvantage.
A simple solution could arise by coupling WECs on the weather side of FBs [
23,
24,
25,
26,
27]. In these cases, higher efficiency could be reached, and often arrays of WECs are used, making the modular WEC smaller in size compared to the breakwater behind it. Moreover, a significant increment in the efficiency of the WEC array can be observed due to the existence of the rear breakwater, reflecting the incoming waves, and amplifying the motion of the WECs [
28]. It is noteworthy that, for specific frequencies, devices positioned on the weather side of a breakwater may experience zero energy efficiency due to Bragg resonance [
29]: however, a proper triggering of the system can have a constructive effect [
30,
31].
The innovative hybrid FB-WEC analyzed in this paper has been proposed, simultaneously drawing inspiration from both Salter’s duck [
32] and traditional naval hull architecture [
33,
34]. The duck falls under a class of WECs known as terminators. A terminator is oriented perpendicularly to the direction of the wave. For the twofold function, a terminator is the best solution since it acts by destroying the waves it faces, leaving an almost calmer sea on the lee side. The updates proposed for the novel device act in accordance with the principles of versatility and cost-effectiveness.
In this paper, results derived from an experimental campaign on the hybrid device are analyzed on a 1:10 Froude-scaled module. The investigation mainly aimed at evaluating the dynamic behaviour of the device, the mooring loads, as well as its hydraulic performances in terms of wave transmission. The role of the draft parameter in determining the dual functioning is examined. In particular, in
Section 2, the innovative device is accurately described, as well as the entire experimental setup.
Section 3 reports the main results obtained and is followed by
Section 4, where a discussion on the feasibility of the dual function of the module is reported. Conclusions and future research lines on the module are described in
Section 5.
2. Materials and Methods
In the first part of this section (
Section 2.1), the concept, geometric properties, and inertial characteristics of the hybrid module are described. Following that, a brief overview of the physical model is provided in
Section 2.2, outlining the properties and layout of the Floater and mooring. Subsequently, in
Section 2.3, information about the facility, instruments, and the generation and acquisition system is presented. The final part,
Section 2.4, offers a summary of the experimental test program.
2.1. Description of the Device
Transitioning from existing solutions that integrate a floating breakwater and a wave energy converter, we present an innovative hybrid system. The primary feature of the device is its adjustable submergence, enabling a dual function as both a passive breakwater and a wave energy harvester. Depending on sea-state conditions, the floater’s draft is altered to modify overall stability.
In extreme and severe sea states, the device strictly functions as a passive breakwater, absorbing incoming waves and safeguarding the devices installed inside the archipelago. Conversely, in more frequent mild sea states, the floating breakwater acts as a wave energy converter (WEC), contributing to the energy production of the archipelago. In the latter case, maximum energy is harvested when the floating module moves in resonance with the waves. Water pumps inside the module facilitate displacement modification. In breakwater functionality, the module is almost fully submerged, ensuring (i) significant device stability and (ii) substantial reflection and dissipation of incoming waves. However, when the module operates as a WEC, a lower displacement is required, allowing for greater instability and device motion. Although the overtopping volume behind the structure may be higher when the device is almost fully submerged, this aspect does not significantly impact wave transmission, as the device is designed for offshore applications where there are no sensitive structures in close proximity to the breakwater.
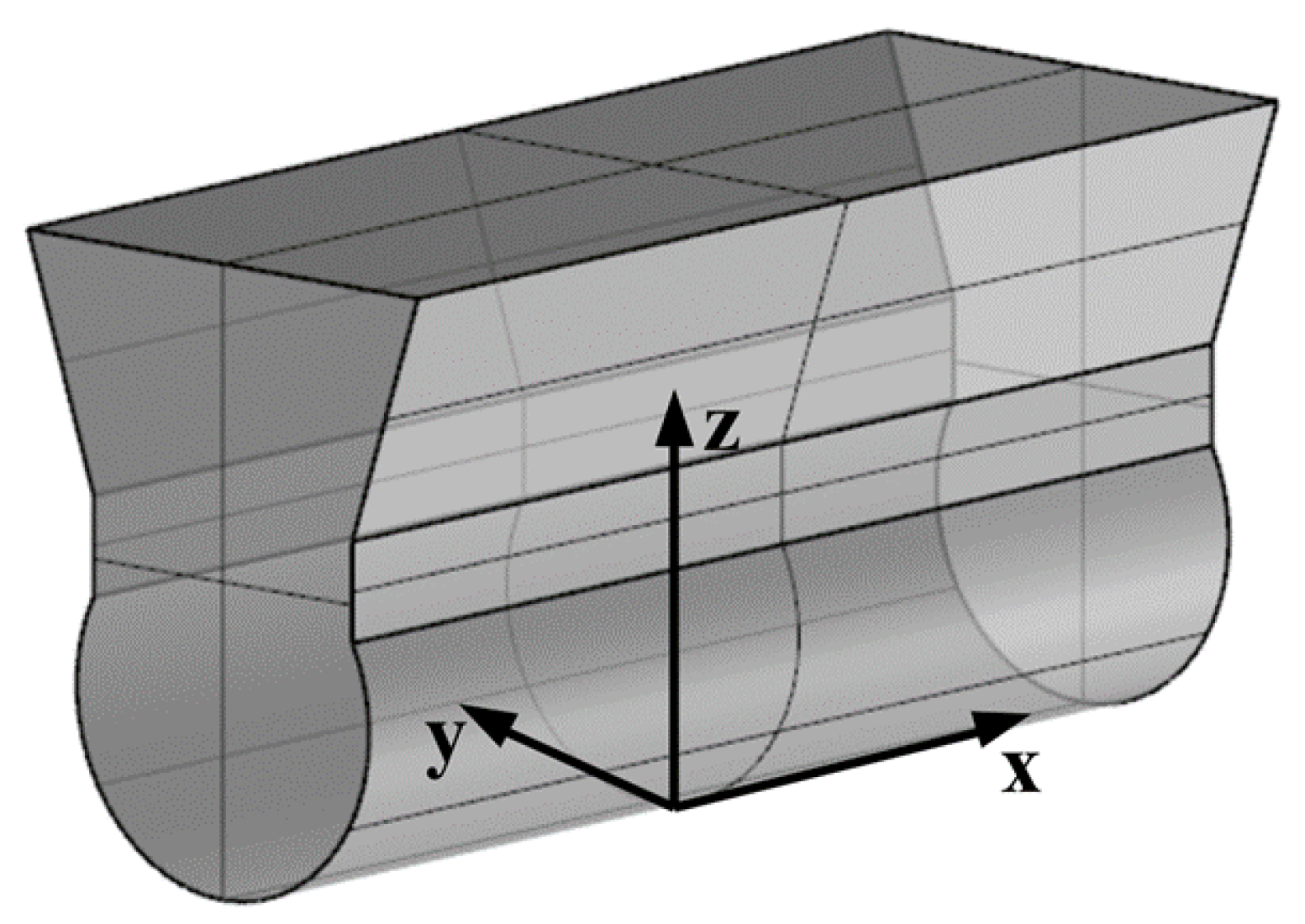
The preliminary concept of the proposed floating breakwater-wave energy converter (FB-WEC) has been designed as a truncated lower cylinder, developing longitudinally and connected to an upper trapezoid. In WEC conditions, only the lower part of the module directly interacts with waves, and the choice of the cylinder is influenced by the expectation of achieving maximum motion exploitation. Experimental and numerical studies [
35,
36] comparing three different geometries demonstrated that the cylinder configuration exhibited large peak-to-peak roll amplitudes, associated with the smallest values of added mass moment of inertia [
37]. In breakwater conditions, the enlargement of the body surface interacting with waves ensures greater stability. The reference system is centred on the keel line of the device, as illustrated in
Figure 1, with the free surface tangent to the keel. When varying the draft, the free surface is envisioned as moving along the positive z-axis.
Different operational conditions were analyzed by considering four drafts, as shown in
Figure 2. The device was gradually filled with water and consequently, its draft increased, aiming to provide rising stability.
The most important stability parameter was the transverse metacentric height, denoted as
, and defined as the distance between the vertical centre of gravity and the metacentre [
38]. As shown in
Figure 3, where the transversal section of a generic floater is represented, the metacentre is denoted as
. It is a fictitious point intersecting the vertical lines passing, respectively, from the centre of gravity,
G, and the centre of buoyancy,
B. For small heel angles, up to 10, the
was assumed constant and followed Equation (
1):
where
is the distance from the metacentre to the centre of buoyancy
B, also called metacentric radius;
is the distance from the keel to the centre of buoyancy; and
is the distance from the keel to the centre of gravity
G. These parameters depended on the shape of the hull and the weight’s amount and distribution. When varying the draft,
D, they changed because the weight changed, and so did the submerged volume (hereinafter displacement ∇). Considering the double functioning of the device, the choice of the metacentric height fell into the values of 0.2 m for the WEC behaviour and 0.6 for protection purposes. Then, the centre of gravity was derived using Equation (
1).
In
Table 1 the main parameters for each configuration are reported. It is worth noting that the four values of
D were chosen as follows:
= 1.25 m: in this case, the sea level reached half of the lower cylinder;
= 2.50 m: referring to a condition in which the sea level embraced the whole cylinder;
= 3.50 m: an intermediate condition, with the device submerged until the changing section;
= 4.75 m: when the device was almost fully submerged.
Table 1.
Parametric properties for different operational conditions.
Table 1.
Parametric properties for different operational conditions.
| D [m] | [m] | [m] | ∇ [m3] |
|---|
| 1.25 | 0.20 | 1.30 | 27.83 |
| 2.50 | 0.20 | 1.41 | 63.42 |
| 3.50 | 0.60 | 1.50 | 90.77 |
| 4.75 | 0.60 | 2.34 | 133.36 |
These conditions suggest that the first two are associated with WEC behaviour, while the last two are indicative of breakwater performances.
In the full-scale scenario, the geometric characteristics of the device are detailed in
Table 2. Here
L represents the length in the x-direction,
B is the overall beam,
is the waterline beam,
R is the radius of the lower cylinder,
H is the overall height and
D is the draft. Additionally,
,
,
represent, respectively, the roll, pitch and yaw radius of gyration.
2.2. Experimental Setup
To accurately simulate the module’s behaviour in mild and frequent sea states, a 1:10 scale model was constructed following Froude’s law. The model (depicted in
Figure 4a,b) was assembled using four shaped PVC sheets (density,
): two for the side profiles, two for the trapezoidal forms and a cylindrical section with a 4 mm thickness. The sheets were secured by riveting slender steel profiles on the edges and siliconized for waterproofing. The upper part utilized the PVC sheet covering only one-third of the available surface for ease of manual ballasting/de-ballasting and to control inertia. Perforated bars on the side sheets served as connections for the anchoring system.
Dynamic testing was crucial to understand the effectiveness of the module, especially concerning resonance with waves, allowing for optimal energy harnessing. Attenuation performances were evaluated to determine effectiveness as a breakwater. Three draft values were explored: = 0.125 m, = 0.25 m, = 0.35 m.
The main geometric and inertial characteristics of the floating platform are summarized in
Table 3.
Four gravity anchors were used for the device, each connected to a mooring line, whose characteristics are reported in
Table 4. The module was securely fastened with four lines—two in the front and two behind the model. As depicted in
Figure 5, each line comprised an inextensible rope of 1 m length, further connected to a system of four springs [
39]. This arrangement was followed by a load cell, ultimately connected to the model through a 0.70 m long soft steel cable.
2.3. Test Facility and Instrumentation
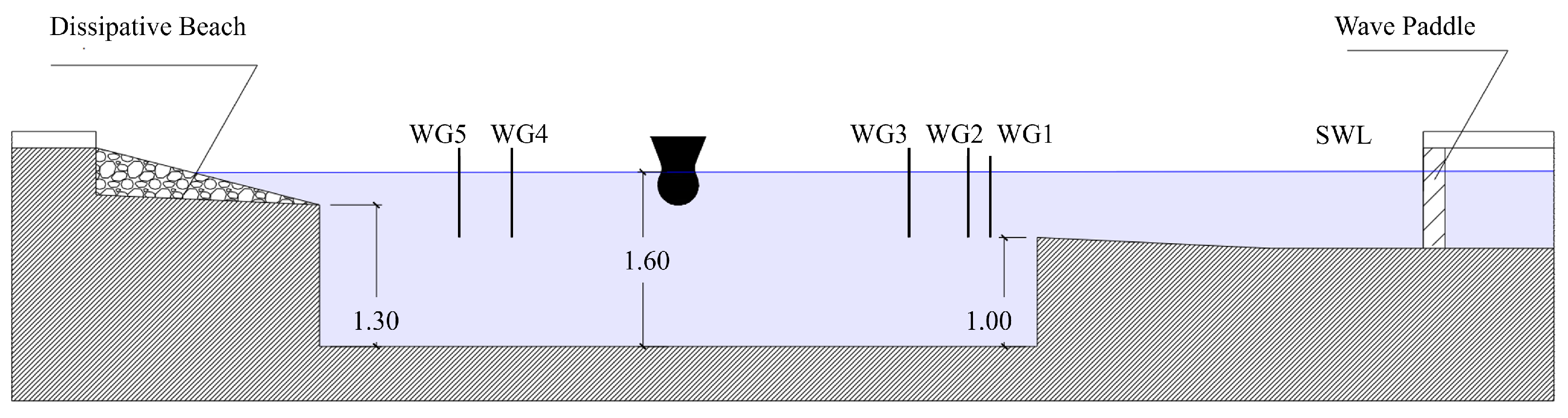
The experimental campaign was conducted in a 3D tank measuring 16 m parallel to the wave paddle and 12 m in the other direction, with a depth range varying from 0.9 m to 0.43 m, resulting in a slope of 1:22. The tank was equipped with a dissipative beach in the final section, while a deeper area was constructed in the middle, measuring 5.50 m by 6.50 m parallel and orthogonal to the wavefront, with depths ranging from 1 m to 1.30 m. When the tank was filled with water, the pit had an average depth of 1.4–1.8 m.
The experimental campaign had two main objectives: evaluating the dynamics of the device and assessing its hydraulic performance in waves. The dynamics were examined using an inertial measurement unit (IMU), capturing accelerations, angular velocities, and inclinations around the three axes [
40]. Additionally, submersible in-line load cells were strategically placed on each mooring line to measure tension resulting from wave forces [
41].
To record the wave profile, six resistive wave gauges were employed: three positioned in front of the model to measure reflection through the Mansard and Funke method [
42], two behind the model for assessing transmission, and one outside the PIT to compare internal and external measurements. The arrangement of the probes and their coordinates with respect to the pit reference system is shown in (
Figure 6) and detailed in
Table 5.
Regular and irregular waves were generated using the AwaSys 5 software [
43], developed at the Hydraulics and Coastal Engineering Laboratory of the University of Aalborg (Denmark). For data acquisition, three different software programs were utilized: “WaveLab2” to record the elevation of the wave profile [
44], the code provided with the IMU sensor to capture the movements of the device, and a LabVIEW (Laboratory Virtual Instrumentation Engineering Workbench, available at [
45]) code to record the tension in the mooring anchors through the load cells. All acquired data, with a sampling frequency of 20 Hz, were synchronized, processed, and analyzed in MATLAB 2022b.
2.4. Experimental Test Program
The first part of the experimental test program was related to the calibration of the model. With the model properly identified, their behaviour under wave loads could be examined, in terms of dynamic by means of the response amplitude operators, in terms of loads on the mooring system, and in terms of attenuation performances through transmission coefficients.
2.4.1. Model Calibration
To achieve the desired properties of the model in terms of draft,
, mass, and inertia, the model underwent several steps. Initially, it was weighed without ballast, and its centre of gravity and natural period in pitch and roll were determined (
Figure 7a). Subsequently, preliminary tests were conducted in water to ascertain the model’s properties, including static draft, trim, and heel. Inclining tests (
Figure 7b) were performed for each draft value to establish the transverse metacentric height
involving the measurement of the inclination angle recorded when moving a known mass
m into different known positions
. The stability parameter was determined by solving Equation (
2). Once the model achieved the correct values of draft, trim, heel, and design weight, roll inertia was assessed by measuring the angular frequency in water using Equation (
3).
To evaluate the restoring properties of the moored model, static tests were performed. Each mooring was pre-tensioned at 0.7 kg while the model was in the mean position. Subsequently, the model underwent a series of quasi-static displacements, evenly distributed along the positive and negative y-axis, and the corresponding mooring tensions were recorded.
2.4.2. Decay Test
Free oscillation tests were conducted on the moored model in the six degrees of freedom (surge, sway, heave, roll, pitch, yaw) to determine the natural periods and damping coefficients. The natural period
for each j-DoF was obtained by averaging the n-th cycles taken by the device to decay (Equation (
4)). The damping coefficients
a and
b were found using the exponentially decaying sinusoidal equation (Equation (
5)). Additionally, the damping ratio was determined using the logarithmic decrement method as a function of two response amplitudes
and
, according to Equations (
6) and (
7) [
46]. In addition, the linear
and quadratic
damping coefficients were determined using a common method applied in the offshore industry [
47], which involves linearly interpolating the left-hand side of Equation (
8) over the coefficient multiplying
.
2.4.3. Response under Wave Loads
Regular and irregular wave tests were conducted to assess the dynamic characteristics and attenuation performance of the device in all configurations. Specifically, the dynamic response was evaluated by defining the response amplitude operators (
) of the motions, as shown in Equation (
9), where
represents the j-th DoF depending on the angular frequency
, and
a denotes the wave amplitude. The mooring response was assessed in terms of maximum and mean tensions
T, along with their response amplitude operator, as described in Equation (
10). On the other hand, the attenuation performances were appraised through the transmission coefficient
given in Equation (
11), where, respectively,
and
represent the transmitted and incident wave heights. In the case of irregular waves, these wave heights are replaced by the corresponding spectral wave heights.
Table 6 provides an overview of the test matrix for the regular wave tests conducted on the model, involving three distinct wave steepness values denoted by
. To further investigate the impact of draft variation on wave-module interaction, irregular wave tests were conducted. These irregular waves were generated using a JONSWAP spectrum [
48] with a peak enhancement factor
= 3.3 (
Table 7).
5. Conclusions
This paper presents an innovative hybrid floating breakwater-wave energy converter, proposed and tested in the wave tank of the Department of Engineering of the University of Campania “Luigi Vanvitelli”. The novelty of this hybrid device is the optimization of both functionalities, wave energy harvester and floating breakwater, by varying its draft. In fact, although it has been already demonstrated the possibility for hybrid floating breakwaters to convert some wave energy into electricity, their main purpose remains the protection against storm waves. On the other hand, there exist few WECs for which attenuation performances (mainly aimed at coastal protection) have been assessed. Even in this case, the breakwater functioning is an added feature. The performances of the proposed device have direct implications on the practical possibility of creating an offshore energy hub, as it should reduce the wave agitation under severe wave conditions. Otherwise, in more frequent mild sea states, the floating module should behave as WEC, contributing to the energy production of the archipelago.
The experimental campaign examined a 1:10 Froude-scaled model, exploring three draft values exposed to a series of regular and irregular waves. The primary objectives were to assess the dynamic response under wave action, focusing on motions and tensions in the mooring lines, and to evaluate the hydraulic performances in terms of transmission coefficient.
The initial findings concern the dynamic and attenuation performances. The assessment of heave and roll motion response amplitude operators reveals that, for both, the peak of the response occurs for wave periods close to the corresponding heave and roll natural periods of the structure. This suggests the potential exploitation of one or both of these DoFs to produce energy: however, the selection of a Power-Take-Off (PTO) system becomes crucial to determine the module’s effectiveness. Analyzing the efficiency and operating mechanisms of various existing PTOs seems to incline the decision towards the use of a gyroscopic system [
51] or an integrated sloshing/OWC system [
52]. This choice is fundamental since, depending on the energy conversion mechanism, the dynamics of the device, as well as its energy efficiency, could vary significantly.
Continuing within the domain of response amplitude operators, those of the mooring tensions, calculated by dividing tension by wave amplitude, exhibit a subtle increase with wavelength for all drafts, both in the starboard and rear lines. The curves show a gradual rise due to the anticipated peak in mooring response in proximity to the sway natural period, which has been intentionally designed to be significantly higher than wave periods, escalating from to . In terms of maximum tensions, mooring lines experience heightened strain with increasing wavelength, assuming very similar values for the case of and , while markedly increasing for . Conversely, mean tensions reach their peak for the case, attributed to the higher waterline beam.
The estimation of the transmission coefficient on the model revealed a substantial dependency on the natural period of the structure. The coefficient exhibited an increasing trend as it approached the roll and heave resonance periods, reaching peak values of 0.87 for , 0.92 for , and 0.63 for , followed by a subsequent decrease to a consistent minimum of approximately 0.45. Notably, a distinct behaviour was observed for the first draft value, where the transmission coefficient was maximal for the lowest value and decreased with its increase. This behaviour was qualitatively explained by considering the wave generation capability of the floater. Specifically, for = 0.125 m, the module’s limited ability to impede incoming waves passing underneath, attributed to its small draft, contributed to the observed maximum at < 10. Conversely, for and cases, the transmission coefficient aligned with the heave and roll damping evolution, indicating a significant contribution from waves generated by floater motions. Overall, the third draft exhibited the lowest values of highlighting its effectiveness as a breakwater.
Excluding values corresponding to the resonance periods, transmission coefficients are relatively low, even lower considering irregular waves. However, considering that the maximum relative wavelength
is around 20 (i.e.,
≈ 6 m), this result is expected, as floating breakwaters are known to function optimally in short waves. For this reason, a smaller-scale module properly arranged in an optimal layout should be tested. In fact, while optimizing the spacing could result in a significant reduction in the wave energy entering the archipelago when the module works as a breakwater, on the other hand, considering the wave energy converter behaviour, choosing a particular value of the spacing could enhance the effectiveness of the first line in producing energy. The back line could function as a wave maker, as the reflected wave combines with the incident wave [
53,
54].
In general, this study on an innovative floating breakwater-WEC confirms its potential in protecting multi-use offshore platforms, reducing the wave loads on each component, and supplying electricity to the platform by converting wave energy.