Modeling the Transport of Inorganic Arsenic Species through Field Soils: Irrigation and Soil Structure Effect
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Description, Sampling and Characterization
2.2. Leaching Experiments
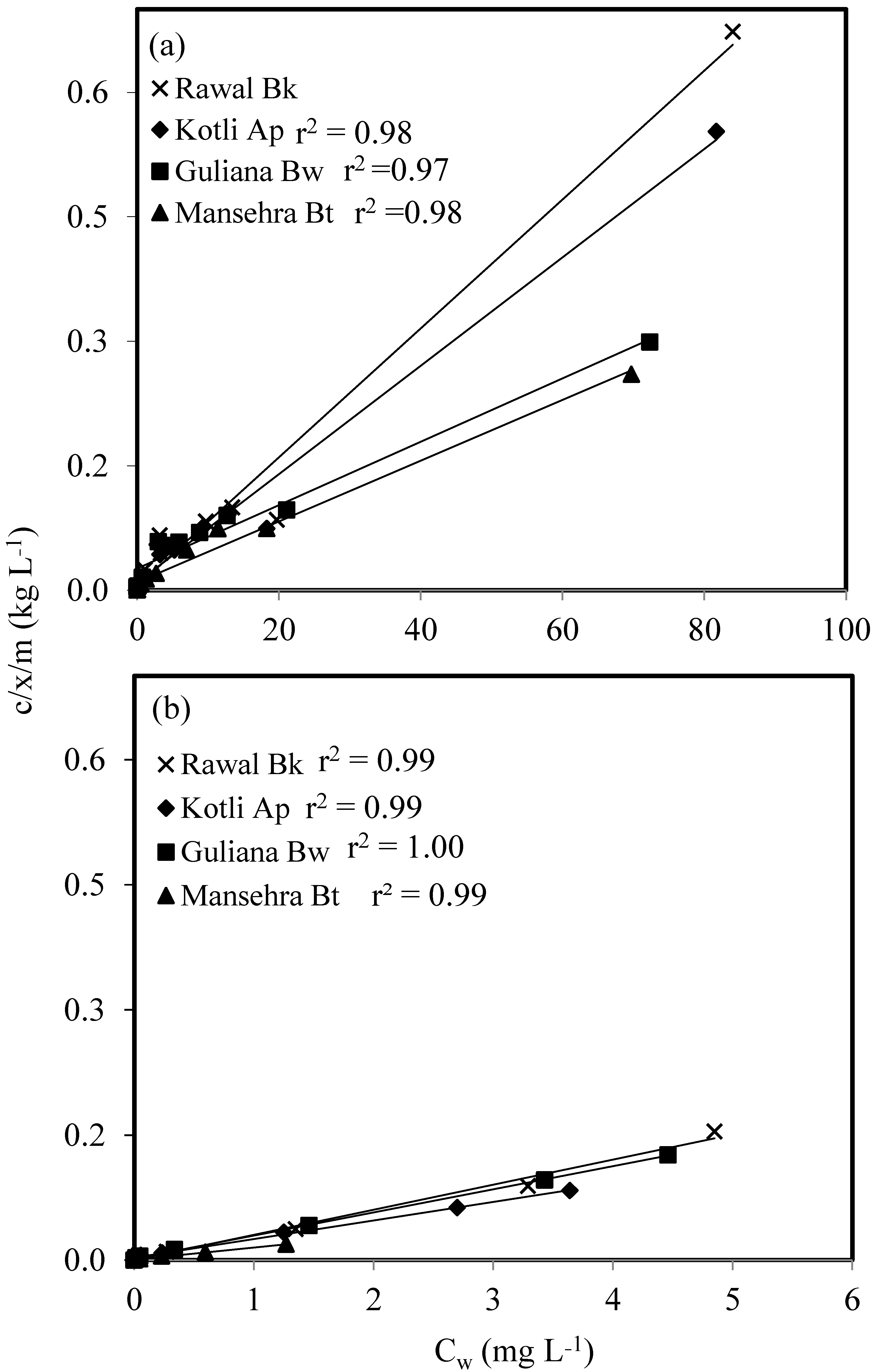
2.3. Batch Experiment for As(V) and As(III) Sorption
2.4. Analysis
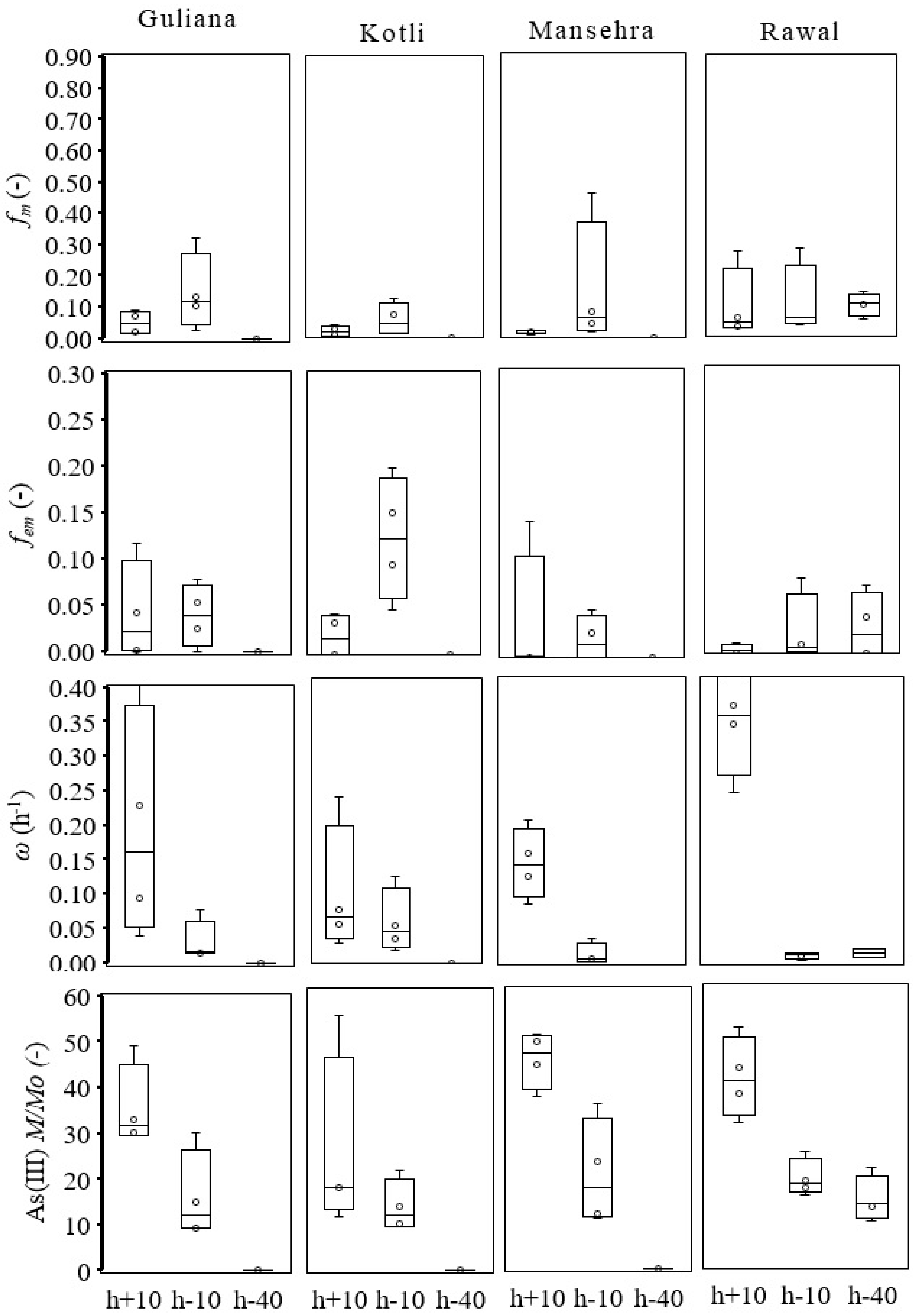
2.5. Parameter Estimation
2.6. Statistical Analysis
3. Results
3.1. Flow Path Marking
3.2. Non-Adsorbing Solute (Cl) Breakthrough Curves
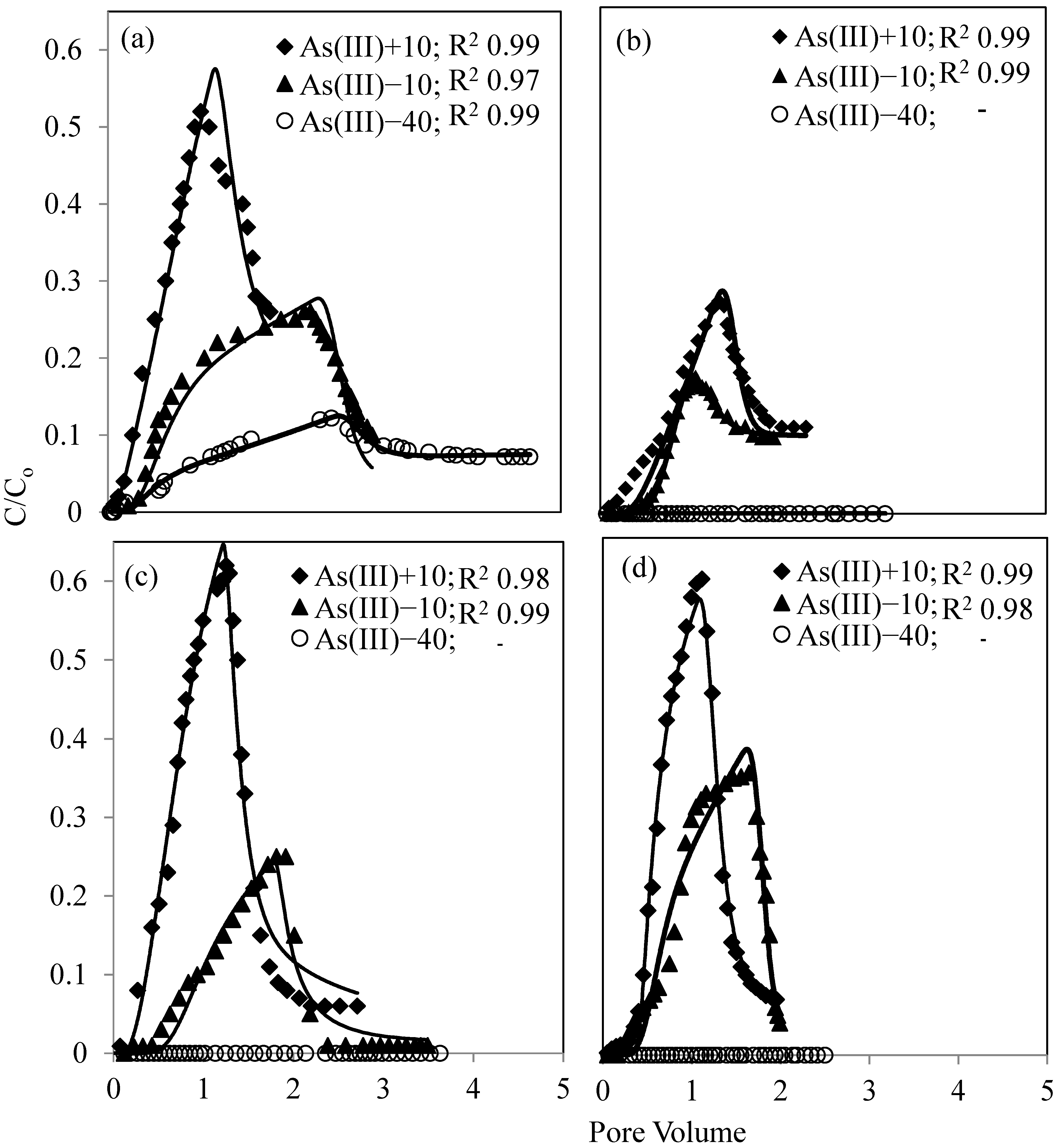
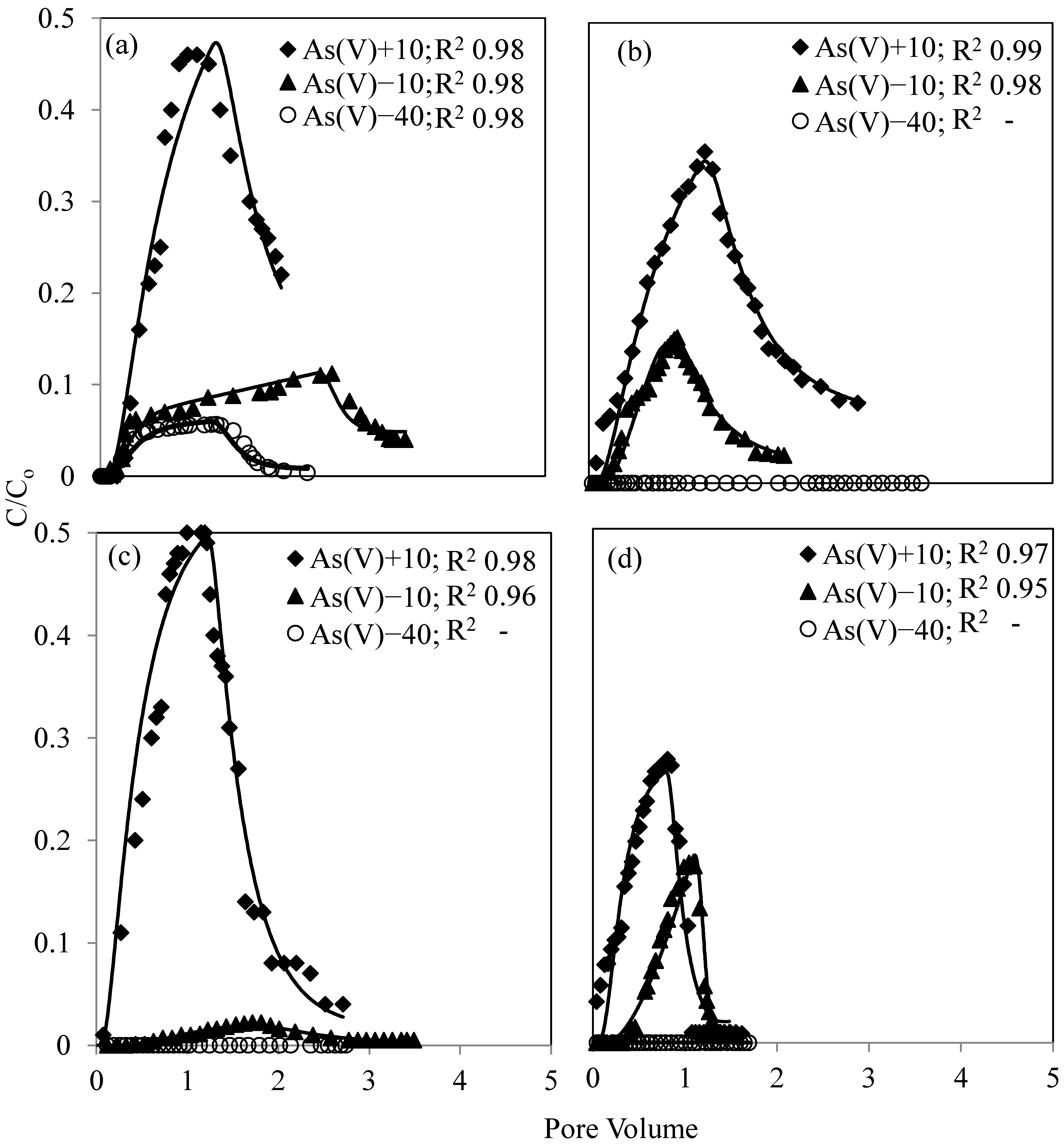
3.3. As(V) and As(III) Breakthrough
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization (WHO). Guidelines for Drinking-Water Quality, 3rd ed.; WHO: Geneva, Switzerland, 2004; Volume 1. [Google Scholar]
- FAO. Arsenic Contamination of Irrigation Water, Soil and Crops in Bangladesh: Risk Implications for Sustainable Agriculture and Food Safety in Asia; Heikens, A., Ed.; Regional Office for Asia and The Pacific, Rap Publication 2006/2020; Food and Agriculture Organization of the United Nation: Bangkok, Thailand, 2006. [Google Scholar]
- Vasile, G.G.; Tenea, A.G.; Dinu, C.; Iordache, A.M.M.; Gheorghe, S.; Mureseanu, M.; Pascu, L.F. Bioavailability, accumulation and distribution of toxic metals (As, Cd, Ni and pb) and their impact on sinapis alba plant nutrient metabolism. Int. J. Environ. Res. Public Health 2021, 18, 12947. [Google Scholar] [CrossRef] [PubMed]
- Strawn, D.G. Review of interactions between phosphorus and arsenic in soils from four case studies. Geochem. Trans. 2018, 19, 10. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.J.; Steenhuis, T.S.; Nam, K. Movement of heavy metals in soil through preferential flow paths under different rainfall intensities. Clean Soil Air Water 2008, 36, 984–989. [Google Scholar] [CrossRef]
- Sayyad, G.; Afyuni, M.; Mousavi, S.F.; Abbaspour, K.C.; Richards, B.K.; Schulin, R. Transport of Cd, Cu, Pb and Zn in a calcareous soil under wheat and safflower cultivation—A column study. Geoderma 2009, 154, 311–320. [Google Scholar] [CrossRef]
- Alzahrani, Y.; Alshehri, F.; El-Sorogy, A.S.; Alzahrani, H. Environmental assessment of heavy metals in soils around Al-Janabeen Dam, southwest Saudi Arabia. J. King Saud Univ. Sci. 2023, 35, 102503. [Google Scholar] [CrossRef]
- Daneshyar, S.K.; Dalalian, M.; Shahmohammadi-Kalalagh, S.; Sabbaghtazeh, E.; Saedi, S. Numerical and Analytical Simulation of Transport of Cd, Ni and Zn in Disturbed and Undisturbed Saturated Loamy Soil Columns. Iran. J. Chem. Chem. Eng. 2023, in press. [CrossRef]
- Hashem, M.A.; Takaki, M.; Jodai, T.; Toda, K. Measurements of arsenite and arsenate contained in mining river waters and leached from contaminated sediments by sequential hydride generation flow injection analysis. Talanta 2011, 84, 1336–1341. [Google Scholar] [CrossRef] [PubMed]
- Tabelin, C.; Sasaki, R.; Igarashi, T.; Park, I.; Tamoto, S.; Arima, T.; Ito, M.; Hiroyoshi, N. Simultaneous leaching of arsenite, arsenate, selenite and selenate, and their migration in tunnel-excavated sedimentary rocks: I. Column experiments under intermittent and unsaturated flow. Chemosphere 2017, 186, 558–569. [Google Scholar] [CrossRef]
- Abdelaal, A.; Abdelkader, A.I.; Alshehri, F.; Elatiar, A.; Almadani, S.A. Assessment and Spatiotemporal Variability of Heavy Metals Pollution in Water and Sediments of a Coastal Landscape at the Nile Delta. Water 2022, 14, 3981. [Google Scholar] [CrossRef]
- Melamed, R.; Jurinak, J.J.; Dudley, L.M. Effect of adsorbed phosphate on transport of arsenate through an oxisol. Soil Sci. Soc. Am. J. 1995, 59, 1289–1294. [Google Scholar] [CrossRef]
- Elizibeth, L.W.; Mark, O.B.; Timothy, A.K.; Jeol, G.M. Adsorption and Transport of Arsenic (V) in Experimental Subsurface Systems. J. Environ. Qual. 2003, 32, 841–850. [Google Scholar] [CrossRef]
- Kuhlmeier, P.D. Sorption and desorption of arsenic from sandy soils: Column studies. J. Soil Contam. 1997, 6, 21–36. [Google Scholar] [CrossRef]
- Darland, J.E.; Inskeep, W.P. Effect of pore water velocity on the transport of arsenate. Environ. Sci. Technol. 1997, 31, 704–709. [Google Scholar] [CrossRef]
- Radu, T.; Subacz, J.L.; Phillippi, J.M.; Barnett, M.O. Effects of dissolved carbonate on arsenic adsorption and mobility. Environ. Sci. Technol. 2005, 39, 7875–7882. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Selim, H.M. Modeling the transport and retention of arsenic (V) in soils. Soil Sci. Soc. Am. J. 2006, 70, 1677–1687. [Google Scholar] [CrossRef]
- Zhang, H.; Selim, H.M. Second-order modeling of arsenite transport in soils. J. Contam. Hydrol. 2011, 126, 121–129. [Google Scholar] [CrossRef] [PubMed]
- Das, I.; Ghosh, K.; Das, D.K.; Sanyal, S.K. Transport of arsenic in some affected soils of Indian subtropics. Soil Res. 2014, 52, 822–832. [Google Scholar] [CrossRef]
- Avili, F.G.; Makaremi, M. Predicting Model of Arsenic Transport and Transformation in Soil Columns and Ground Water Contamination (Case study: Gorgan Plain, Iran). Anthropog. Pollut. 2020, 4, 57–64. [Google Scholar]
- Chotpantarat, S.; Amasvata, C. Influences of pH on transport of arsenate (As5+) through different reactive media using column experiments and transport modeling. Sci. Rep. 2020, 10, 3512. [Google Scholar] [CrossRef]
- Gerke, H.H.; van Genuchten, M.T. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media. Water Resour. Res. 1993, 29, 305–319. [Google Scholar] [CrossRef]
- Gupta, A.; Destouni, G.; Jensen, M.B. Modelling tritium and phosphorous transport by preferential flow in structured soil. J. Contam. Hydrol. 1999, 35, 389–407. [Google Scholar] [CrossRef]
- Akhtar, M.S.; Stüben, D.; Norra, S.; Memon, M. Soil structure and flow rate-controlled molybdate, arsenate and chromium (III) transport through field columns. Geoderma 2011, 161, 126–137. [Google Scholar] [CrossRef]
- Seyfried, M.S.; Rao, P.S. Solute transport in undisturbed columns of an aggregated tropical soil: Preferential flow effects. Soil Sci. Soc. Am. J. 1987, 45, 837–842. [Google Scholar] [CrossRef]
- Rukh, S.; Akhtar, M.S.; Mehmood, A.; Haghooghi, N.; Radcliffe, D.E. Evaluating nonequilibrium solute transport through four soils of Pakistan using a HYDRUS model and nonparametric indices. Soil Sci. Soc. Am. J. 2018, 82, 1071–1084. [Google Scholar] [CrossRef]
- Fortin, J.; Gagnon-Bertrand, E.; Vézina, L.; Rompé, M. Preferential bromide and pesticide movement to tile drains under different cropping practices. J. Environ. Qual. 2002, 31, 1940–1952. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Martin, M.J.; Lorenzo, L.F.; Sanchez-Camazano, M. Leaching of Cd, Zn, Pb, and Cu in packed and undisturbed columns of soils affected by the spill from a pyrite mine in the South of Spain. Soil Sediment Contam. 2001, 10, 359–373. [Google Scholar] [CrossRef]
- Jaynes, D.B.; Ahmed, S.I.; Kung, K.J.S.; Kanwar, R.S. Temporal Dynamics of preferential flow to subsurface drain. Soil Sci. Soc. Am. J. 2001, 65, 1368–1376. [Google Scholar] [CrossRef]
- Van Genuchten, M.T.; Wierenga, P.J. Mass transfer studies in sorbing porous media, I. Analytical solutions. Soil Sci. Soc. Am. J. 1976, 40, 473–481. [Google Scholar] [CrossRef]
- Šimůnek, J.; Jarvis, N.J.; van-Genuchten, M.T.; Gardenas, A. Review and comparison of models for describing nonequilibrium and preferential flow and transport in the vadose zone. J. Hydrol. 2003, 272, 14–35. [Google Scholar] [CrossRef]
- Šimůnek, J.; Sejna, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One Dimensional Movement of Water, Heat, and Multiple Solutes in Variable Saturated Media; Version 4.xx; USDA-ARS, U.S. Salinity Laboratory: Riverside, CA, USA, 1998. [Google Scholar]
- Flury, M.; Flühler, H. Brilliant Blue FCF as a dye tracer for solute transport studies-a toxicological overview. J. Environ. Qual. 1994, 23, 1108–1112. [Google Scholar] [CrossRef]
- Maqsood, H.R.; Rukh, S.; Imran, M.; Mehmood, A.; Ahmad, W.; Matloob, A.; Ahmad, H.S.; Khan, A.; Butt, S.A. Evaluation of laterite as a filter media to remove arsenic from groundwater. J. Serb. Chem. Soc. 2021, 86, 195–207. [Google Scholar] [CrossRef]
- Rukh, S.; Akhtar, M.S.; Mehmood, A.; Hassan, S.; Khan, K.S.; Naqvi, S.M.S.; Imran, M. Arsenate and arsenite adsorption in relation with chemical properties of alluvial and loess soils. J. Serb. Chem. Soc. 2017, 82, 943–954. [Google Scholar] [CrossRef]
- Welsh, E.P.; Crook, J.G.; Sanzolone, R. Trace-level determination of arsenic and selenium using continuous-flow hydride generation atomic absorption spectrophotometry (HG-AAS). In Quality Assurance Manual for the Branch of Geochemistry; Arbogast, B.F., Ed.; US Geol Survey: Denver, CO, USA, 1990; pp. 38–45. [Google Scholar]
- Moreda-Pineiro, C.; Moscoso-Perez, P.; Lopez-Mahia, S.; Muniategui-Lorenzo, E.; Fernandez-Fernandez Rodriguez, D.P. Multivariate optimisation of hydride generation procedures for single element determinations of As, Cd, Sb, and Se in natural waters by electrothermal atomic absorption spectrometry. Talanta 2001, 53, 871–883. [Google Scholar] [CrossRef] [PubMed]
- Glaubig, R.A.; Goldberg, S. Determination of inorganic arsenic (III) and arsenic (III plus V) using automated Hydride-Generation Atomic-Absorption Spectrometry. Soil Sci. Soc. Am. J. 1988, 52, 536–537. [Google Scholar] [CrossRef]
- Anthemidis, A.N.; Zachariadis, G.A.; Stratis, J.A. Determination of arsenic(III) and total inorganic arsenic in water samples using an on-line sequential insertion system and hydride generation atomic absorption spectrometry. Anal. Chim. Acta 2005, 547, 237–242. [Google Scholar] [CrossRef]
- Hipp, B.W.; Langdale, G.W. Use of solid-state chloride electrode for chloride determinations in soil extracts. Commun. Soil Sci. Plant Anal. 1971, 2, 237–240. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Navidpour, A.H.; Ahmed, M.B.; Mojiri, A.; Huang, Y.; Zhou, J.L. Adsorption and desorption behavior of arsenite and arsenate at river sediment-water interface. J. Environ. Manag. 2022, 317, 115497. [Google Scholar] [CrossRef] [PubMed]
- Šimůnek, J.; van Genuchten, M.T. Modeling nonequilibrium flow and transport using HYDRUS. Vadose Zone J. 2008, 7, 782–797. [Google Scholar] [CrossRef]
- SAS Institute Inc. SAS/STAT® Software, version 9.4, System for Windows; SAS Institute Inc.: Cary, NC, USA, 2002.
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. B 1964, 26, 211–234. [Google Scholar] [CrossRef]
- Wierenga, P.J.; Young, M.H.; Mancino, C.F. Large weighing lysimeters for water use and deep percolation studies. Soil Sci. 1996, 161, 491–501. [Google Scholar]
- Vervoort, R.W.; Radcliffe, D.E.; West, L.T. Soil structure development and preferential solute flow. Water Resour. Res. 1999, 35, 913–928. [Google Scholar] [CrossRef]
- Mooney, S.J.; Morris, C. A morphological approach to understanding preferential flow using image analysis with dye tracers and X-ray computed tomography. Catena 2008, 73, 204–211. [Google Scholar] [CrossRef]
- Gerke, H.H.; Köhne, J.M. Estimating hydraulic properties of soil aggregate skins from sorptivity and water retention. Soil Sci. Soc. Am. J. 2002, 66, 26–36. [Google Scholar] [CrossRef]
- Ketelsen, H.; Meyer-Windel, S. Adsorption of brilliant blue FCF by soils. Geoderma 1999, 90, 131–145. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, Z.; Hou, F.; Cheng, J. Characterizing Preferential Flow Paths in Texturally Similar Soils under Different Land Uses by Combining Drainage and Dye-Staining Methods. Water 2021, 13, 219. [Google Scholar] [CrossRef]
- Li, M.; Yao, J.; Cheng, J. Study on the Preferential Flow Characteristics under Different Precipitation Amounts in Simian Mountain Grassland of China. Water 2020, 12, 3489. [Google Scholar] [CrossRef]
- Sondal, J.; Singh, D.; Sikka, R. Comparative evaluation of arsenate sorption–desorption in two soils of North India. Environ. Earth Sci. 2016, 75, 249–253. [Google Scholar] [CrossRef]
- Ghorbanzadeh, N.; Jung, W.; Halajnia, A.; Lakzian, A.; Kabra, A.N.; Jeon, B. Removal of arsenate and arsenite from aqueous solution by adsorption on clay minerals. Geosyst. Eng. 2015, 18, 302–311. [Google Scholar] [CrossRef]
- Feng, Q.; Zhang, Z.; Chen, Y.; Liu, L.; Zhengjie, Z.; Chen, C. Adsorption and desorption of characteristics of arsenic on soils: Kinetic, equilibrium, and effect of Fe(OH)3 colloid, H2SiO3 colloid and phosphate. Procedia Environ. Sci. 2013, 18, 26–36. [Google Scholar] [CrossRef]
- Wauchope, R.D. Fixation of arsenical herbicides, phosphate, and arsenate in alluvial soils. J. Environ. Qual. 1975, 4, 355–358. [Google Scholar] [CrossRef]
- Huang, J.H.; Voegelin, A.; Pombo, S.A.; Lazzaro, A.; Zeyer, J.; Kretzschmar, R. Influence of arsenate adsorption to ferrihydrite, goethite, and boehmite on the kinetics of arsenate reduction by Shewanella putrefaciens strain CN-32. Environ. Sci. Technol. 2011, 45, 7701–7709. [Google Scholar] [CrossRef]
- Grafe, M.; Eick, M.; Grossl, P. Adsorption of arsenate (V) and arsenite (III) on goethite in the presence and absence of dissolved organic carbon. Soil Sci. Soc. Am. J. 2001, 65, 1680–1687. [Google Scholar] [CrossRef]
- Redman, A.; Macalday, D.; Ahmann, D. Natural organic matter affects arsenic speciation and sorption onto hematite. Environ. Sci. Technol. 2002, 36, 2889–2896. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Zhang, S.; Shan, X.; Feng, M.; Zhu, Y.; McLaren, R. Adsorption of arsenate on soils. Part 1. Laboratory batch experiments using 16 Chinese soils with different physcochemical properties. Environ. Pollut. 2005, 138, 285–289. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Zhang, S.; Shan, X.; Feng, M.; Zhu, Y.; McLaren, R. Adsorption of arsenate on soils. Part 2. Modeling the relationship between adsorption capacity and soils physcochemical properties using 16 Chinese soils. Environ. Pollut. 2005, 138, 278–284. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; De Cristofaro, A.; Violante, A. Effect of pH, phosphate and oxalate on the adsorption/desorption of arsenate on/from goethite. Soil Sci. 2001, 166, 197–2008. [Google Scholar] [CrossRef]
- Bonis, M.L.; Echevarria, G.; Thiry, Y.; Simonnot, M.O. Arsenic sorption properties in a chronosequence of soils derived from clay parent material. In Proceedings of the 5th International Congress on Arsenic in the Environment, Buenos Aires, Argentina, 11–16 May 2014; Marta, I., Hugo, B.L., Martin, N., Natalia, M., Jochen, Q., Prosun, B., Naidu, B.R., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 295–297. [Google Scholar] [CrossRef]
- Sø, H.U.; Postma, D.; Jakobsen, R.; Larsen, F. Sorption and desorption of arsenate and arsenite on calcite. Geochim. Cosmochim. Acta 2008, 72, 5871–5884. [Google Scholar] [CrossRef]
- Rumynin, V.G. Conceptual transport models for adsorbable solutes. In Subsurface Solute Transport Models and Case Histories with Applications to Radionuclide Migration; Springer: Dordrecht, The Netherlands, 2011; Volume 25, pp. 585–614. [Google Scholar] [CrossRef]
- Padilla, I.Y.; Yeh, T.C.J.; Conklin, M.H. The effect of water content on solute transport in unsaturated porous media. Water Res. 1999, 35, 3303–3313. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, Q.J. Effect of pore water velocities and solute input methods on chloride transport in the undisturbed soil columns of loess plateau. Appl. Water Sci. 2016, 6, 1–8. [Google Scholar] [CrossRef]
- Avila, M.A.S.; Breiter, R. Modelling the competitive sorption process of multiple solutes during their transport in porous media. Environ. Model. Assess. 2009, 14, 615–629. [Google Scholar] [CrossRef]
- Köhne, J.M.; Köhne, S.; Simunek, J. A review of model applications for structured soils: b) pesticide transport. J. Contam. Hydrol. 2009, 104, 36–60. [Google Scholar] [CrossRef]
- Ladu, J.L.C.; Zhang, D. Modeling atrazine transport in soil columns with HYDRUS-1D. Water Sci. Eng. 2011, 4, 258–269. [Google Scholar] [CrossRef]



| Horizon | Depth | As(V) | As(III) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| b † | k † | Kd ‡ | Retardation for Three Heads § | b | k | Kd | Retardation for Three Heads § | ||||||
| cm | mg kg−1 | L mg−1 | L kg−1 | +10 mm | −10 mm | −40 mm | mg kg−1 | L mg−1 | L kg−1 | +10 mm | −10 mm | −40 mm | |
| Rawal soil series; silty, mixed, hyperthermic Typic Hapludalfs | |||||||||||||
| A | 0–10 | 307 (19) | 0.07 (0.01) | 21 (0.4) | 58 (7) | 75 (7) | 85 (1) | 22 (2) | 9 (5) | 50 (3) | 132 (16) | 174 (14) | 197 (10) |
| Bw | 10–18 | 248 (9) | 0.14 (0.01) | 34 (0.3) | 108 (9) | 133 (17) | 145 (26) | 36 (1.3) | 6 (1.5) | 86 (5) | 271 (25) | 337 (48) | 370 (77) |
| Bt | 18–30 | 275 (9) | 0.16 (0.01) | 42 (3) | 138 (6) | 171 (20) | 193 (28) | 43 (1) | 14 (3) | 104 (6) | 341 (39) | 422 (51) | 476 (60) |
| Bk | 30–46 | 131 (10) | 0.57 (0.05) | 67 (1.2) | 248 (118) | 319 (197) | 350 (224) | 37 (2) | 22 (9) | 79 (15) | 264 (52) | 331 (70) | 364 (80) |
| Kotli soil series; fine, mixed, hyperthermic, Entic Haplusterts | |||||||||||||
| Ap | 0–10 | 153 (1.4) | 0.43 (0.00) | 61 (0.1) | 255 (125) | 310 (132) | 502 (220) | 42 (1.5) | 10 (3) | 104 (5) | 290 (42) | 357 (47) | 580 (142) |
| Bw | 10–18 | 227 (5) | 0.20 (0.01) | 44 (3.4) | 144 (26) | 163 (34) | 205 (84) | 42 (0.3) | 14 (2) | 101 (2) | 357 (4.3) | 404 (26) | 500 (143) |
| C | 18+ | 234 (35) | 0.24 (0.05) | 52 (3.5) | 209 (26) | 227 (47) | 286 (52) | 54 (1.0) | 50 (20) | 78 (21) | 304 (88) | 332 (124) | 417 (146) |
| Guliana soil series; silty, mixed, hyperthermic Udic Haplustalfs | |||||||||||||
| Ap | 0–10 | 235 (27) | 0.18 (0.04) | 41 (5.1) | 94 (11) | 103 (16) | 111 (17) | 39 (0.75) | 10 (0.75) | 96 (11) | 257 (16) | 280 (32) | 301 (38) |
| Bw | 10–20 | 256 (26) | 0.18 (0.03) | 44 (11) | 113 (21) | 118 (12) | 125 (11) | 39 (1.3) | 12 (1.3) | 96 (7) | 264 (91) | 273 (74) | 288 (75) |
| Bt1 | 20–30 | 248 (28) | 0.32 (0.12) | 71 (17) | 233 (22) | 242 (44) | 260 (47) | 61 (4) | 38 (4.4) | 100 (6) | 336 (54) | 344 (27) | 370 (40) |
| Bt2 | 30–50 | 231 (13) | 0.45 (0.05) | 95 (4) | 315 (83) | 316 (31) | 345 (32) | 62 (0.5) | 53 (0.51) | 83 (1.3) | 273 (27) | 300 (34) | 290 (42) |
| Mansehra soil series; silty, mixed, thermic Typic Hapludalfs | |||||||||||||
| Ap | 0–20 | 262 (27) | 0.17 (0.04) | 43 (5) | 108 (25) | 148 (34) | 179 (75) | 40 (0.5) | 7 (0.35) | 97 (0.9) | 243 (41) | 330 (48) | 397 (132) |
| Bw | 20–40 | 204 (11) | 0.34 (0.09) | 65 (12) | 287 (157) | 318 (124) | 407 (115) | 50 (0.4) | 13 (1.7) | 120 (2) | 411 (19) | 478 (63) | 640 (193) |
| Bt | 40–70 | 290 (21) | 0.37 (0.04) | 100 (5) | 459 (240) | 475 (252) | 545 (258) | 70 (0.6) | 25 (4) | 142 (10) | 485 (37) | 501 (30) | 583 (42) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rukh, S.; Akhtar, M.S.; Alshehri, F.; Mehmood, A.; Malik, K.M.; Almadani, S.; Khan, A.; Shahab, M. Modeling the Transport of Inorganic Arsenic Species through Field Soils: Irrigation and Soil Structure Effect. Water 2024, 16, 386. https://doi.org/10.3390/w16030386
Rukh S, Akhtar MS, Alshehri F, Mehmood A, Malik KM, Almadani S, Khan A, Shahab M. Modeling the Transport of Inorganic Arsenic Species through Field Soils: Irrigation and Soil Structure Effect. Water. 2024; 16(3):386. https://doi.org/10.3390/w16030386
Chicago/Turabian StyleRukh, Shah, Mohammad Saleem Akhtar, Fahad Alshehri, Ayaz Mehmood, Kouser Majeed Malik, Sattam Almadani, Ahmad Khan, and Muhammad Shahab. 2024. "Modeling the Transport of Inorganic Arsenic Species through Field Soils: Irrigation and Soil Structure Effect" Water 16, no. 3: 386. https://doi.org/10.3390/w16030386
APA StyleRukh, S., Akhtar, M. S., Alshehri, F., Mehmood, A., Malik, K. M., Almadani, S., Khan, A., & Shahab, M. (2024). Modeling the Transport of Inorganic Arsenic Species through Field Soils: Irrigation and Soil Structure Effect. Water, 16(3), 386. https://doi.org/10.3390/w16030386






