Estimating the Maximum Depth of Andean Lakes: A Comparative Analysis Using Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. The Study Area
2.2. Satellite Imagery
2.3. True Lake Bathymetry and Selection of Bathymetric Target Values
2.4. Selection of Bathymetric Targets (Ztl,j) and Multispectral Observations (Btl,j) of the Different LANDSAT 8 (L8) Bands
2.5. Modelling the Lake’s Maximum Depth (Zmax) Using Ztl,j and Btl,j
2.5.1. Splitting the Total Observations into Training and Validation Data Sets (Split-Sample Test)
2.5.2. Modelling Methods
2.5.3. Statistics for the Evaluation of the Performance of the Zmax Multispectral Models
2.5.4. Test for the Evaluation of the Performance of the Zmax Multispectral Models
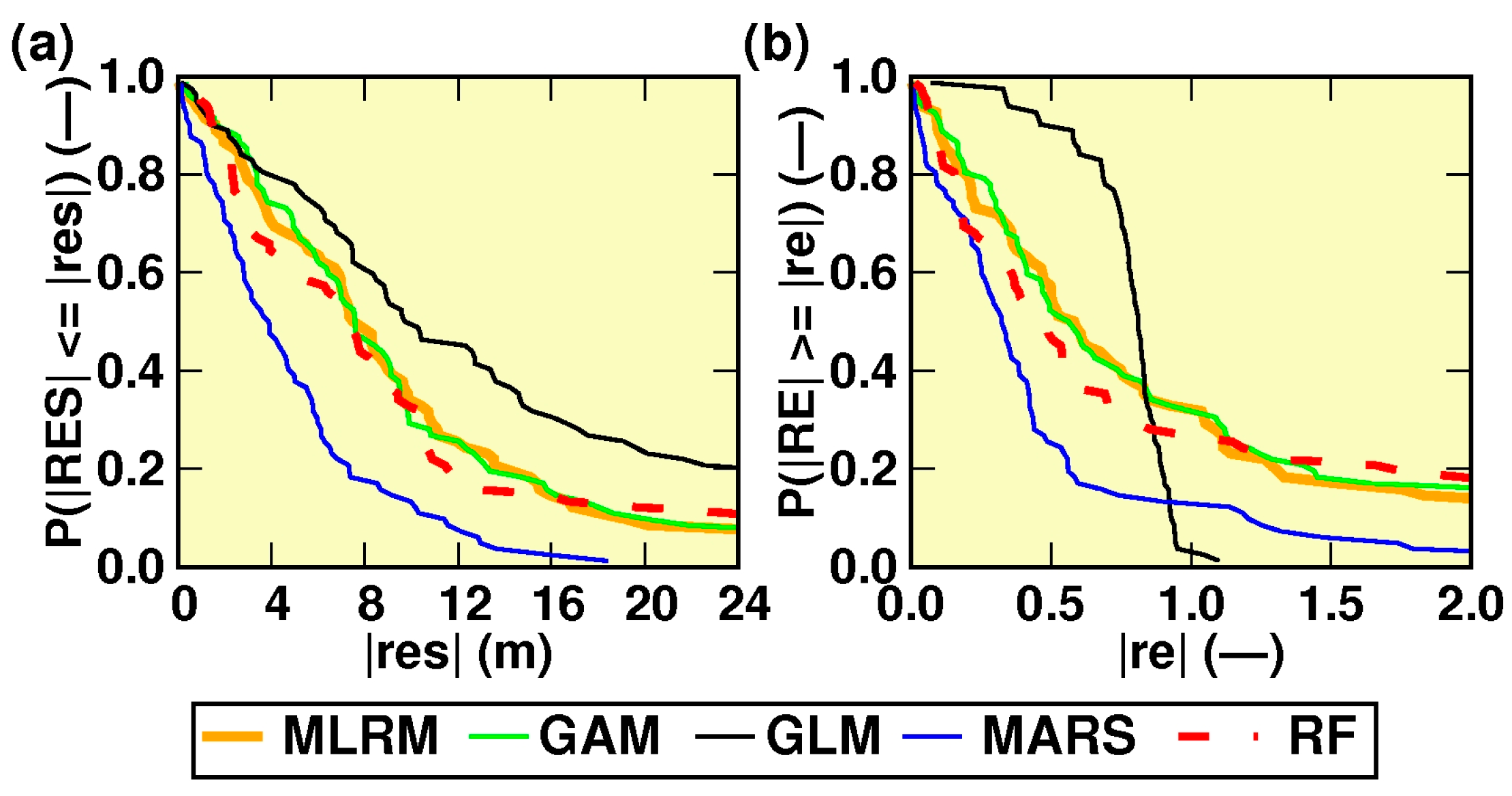
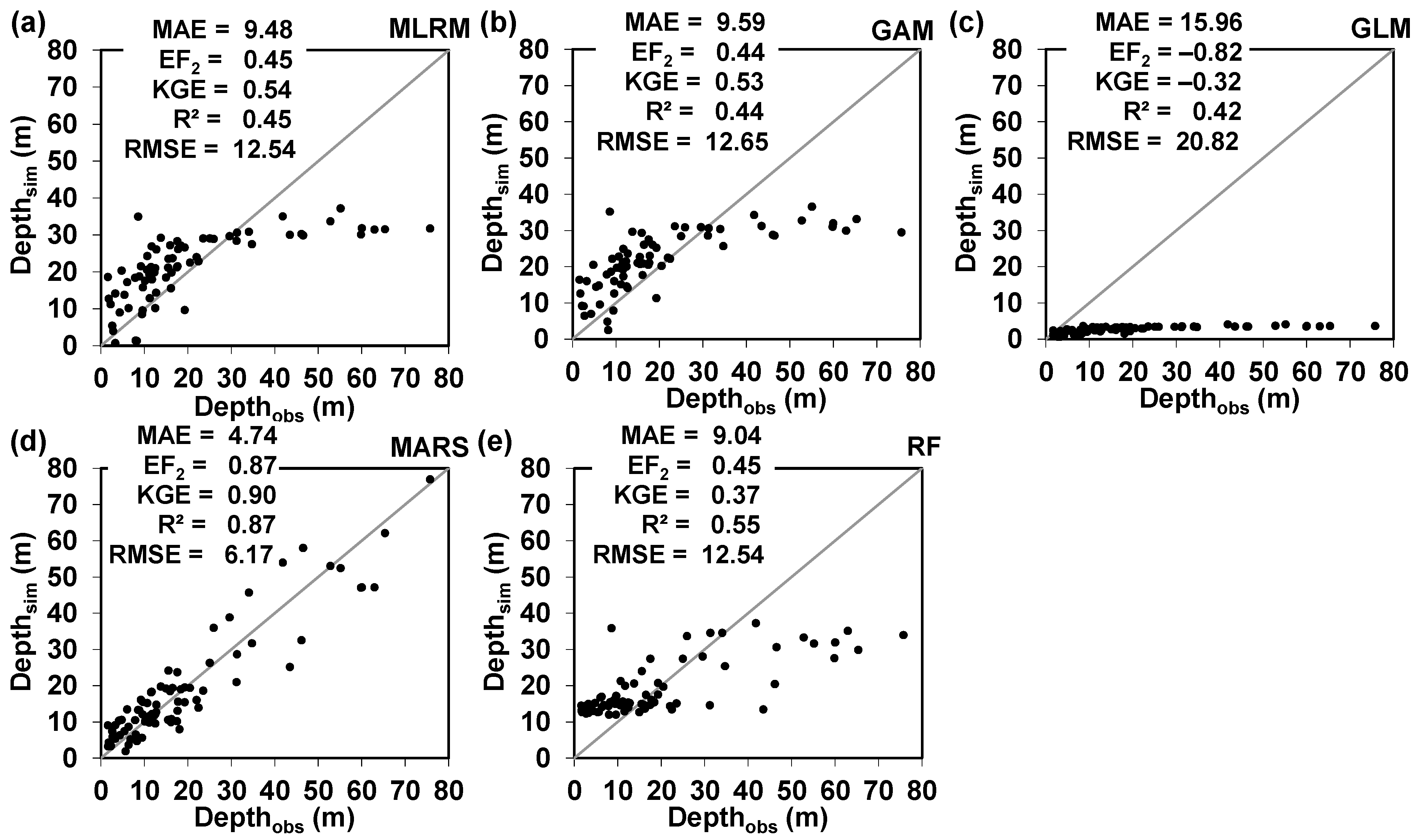
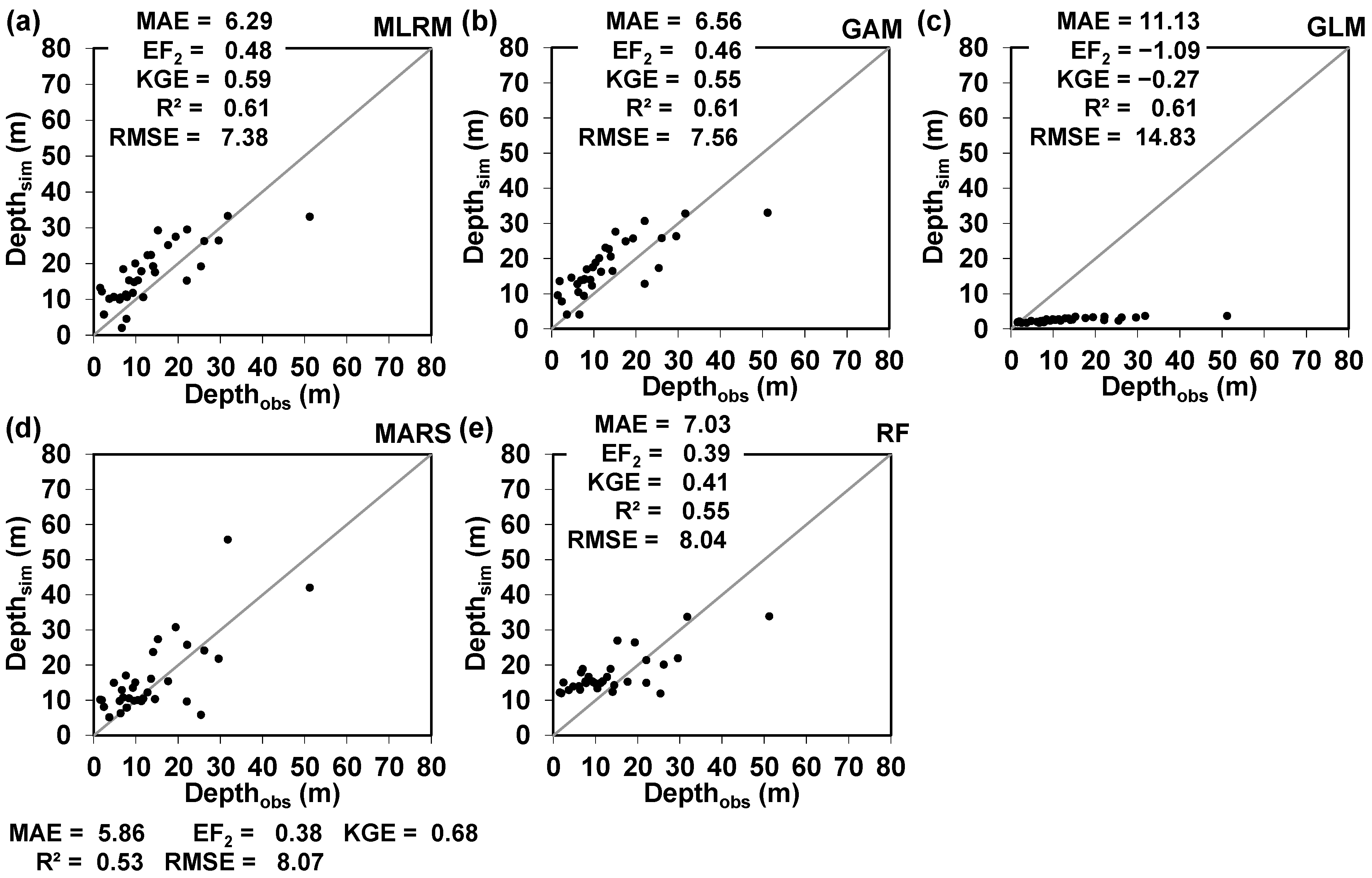
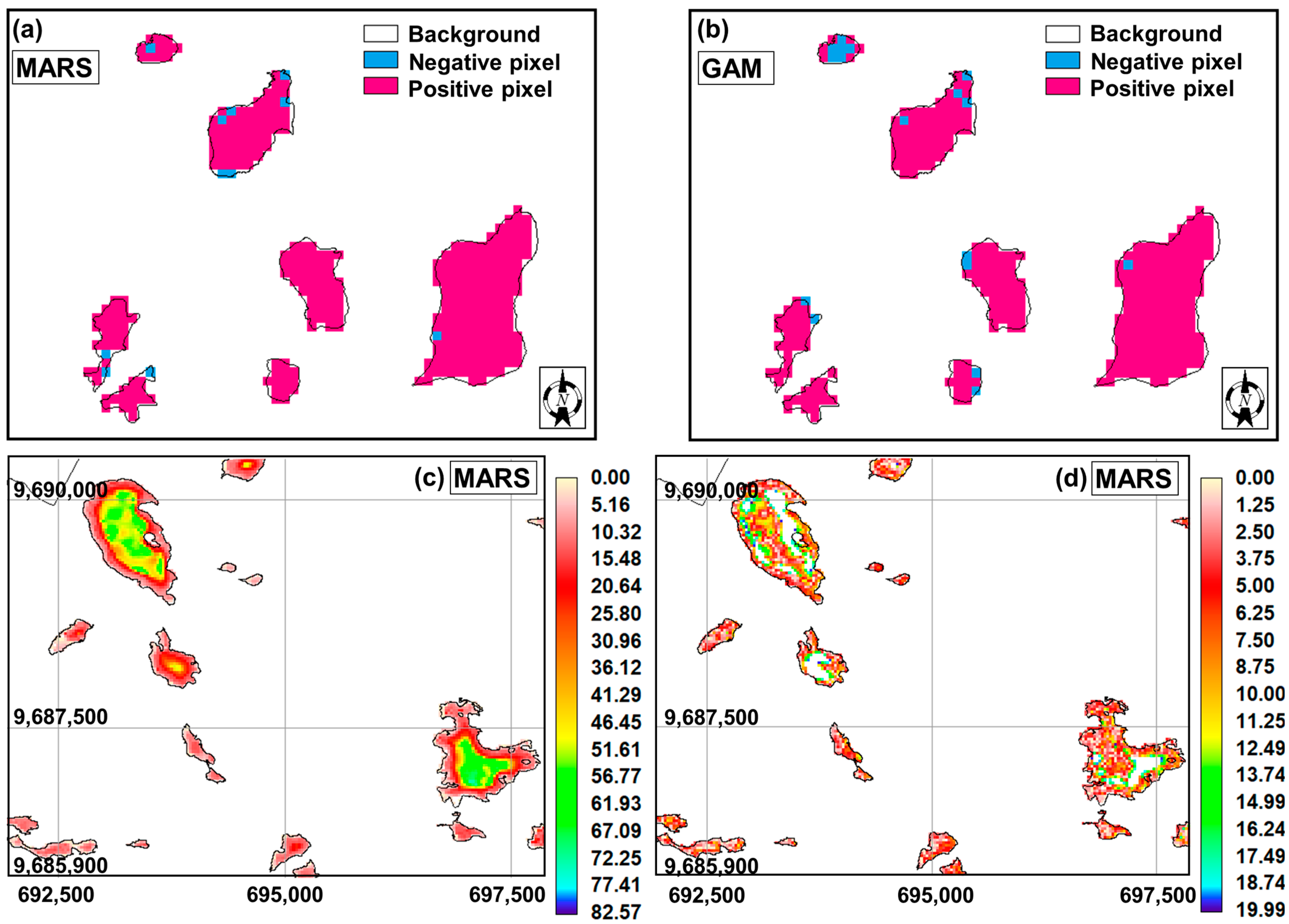
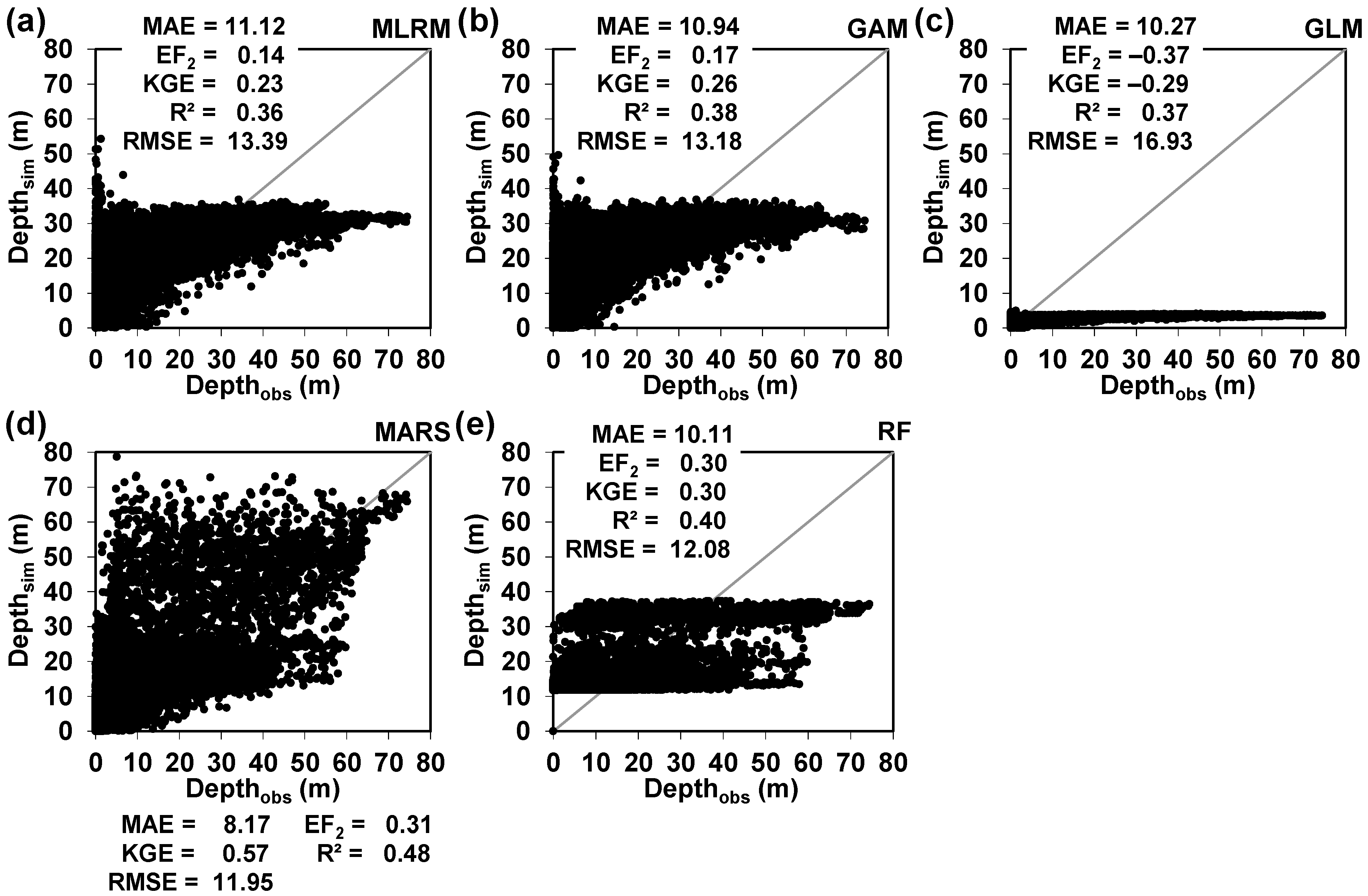
3. Results
Modelling the Lake’s Maximum Depth (Zmax) Based on the Use of Bathymetric Targets and Multispectral Observations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mosquera, P.V.; Hampel, H.; Vázquez, R.F.; Alonso, M.; Catalan, J. Abundance and morphometry changes across the high-mountain lake-size gradient in the tropical Andes of Southern Ecuador. Water Resour. Res. 2017, 53, 7269–7280. [Google Scholar] [CrossRef]
- Sotomayor, G.; Hampel, H.; Vázquez, R.F.; Forio, M.A.E.; Goethals, P.L.M. Selection of an adequate functional diversity index for stream assessment based on biological traits of macroinvertebrates. Ecol. Indic. 2023, 151, 110335. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Mosquera, P.V.; Hampel, H. Bathymetric Modelling of High Mountain Tropical Lakes of Southern Ecuador. Water 2024, 16, 1142. [Google Scholar] [CrossRef]
- Lyon, S.W.; Hickman, S.; Mosquera, P.V.; Vázquez, R.F.; Hampel, H. Stable water isotopic composition and evaporation to inflow ratios for high-mountain tropical Ecuadorian lakes. Hydrol. Sci. J. 2024, 69, 1523–1538. [Google Scholar] [CrossRef]
- Mosquera, P.V.; Hampel, H.; Vázquez, R.F.; Catalan, J. Water chemistry variation in tropical high-mountain lakes on old volcanic bedrocks. Limnol. Oceanogr. 2022, 67, 1522–1536. [Google Scholar] [CrossRef]
- Duarte, C.R.; de Miranda, F.P.; Landau, L.; Souto, M.V.S.; Sabadia, J.A.B.; Neto, C.Â.d.S.; Rodrigues, L.I.d.C.; Damasceno, A.M. Short-time analysis of shoreline based on RapidEye satellite images in the terminal area of Pecém Port, Ceará, Brazil. Int. J. Remote Sens. 2018, 39, 4376–4389. [Google Scholar] [CrossRef]
- Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Scheihing, K.; Tröger, U. Local climate change induced by groundwater overexploitation in a high Andean arid watershed, Laguna Lagunillas basin, northern Chile. Hydrogeol. J. 2018, 26, 705–719. [Google Scholar] [CrossRef]
- Li, Y.; Gao, H.; Zhao, G.; Tseng, K.-H. A high-resolution bathymetry dataset for global reservoirs using multi-source satellite imagery and altimetry. Remote Sens. Environ. 2020, 244, 111831. [Google Scholar] [CrossRef]
- Hassan, M.H.; Nadaoka, K. Assessment of machine learning approaches for bathymetry mapping in shallow water environments using multispectral satellite images. Int. J. Geoinform. 2017, 13, 1–15. [Google Scholar]
- Li, J.; Knapp, D.E.; Lyons, M.; Roelfsema, C.; Phinn, S.; Schill, S.R.; Asner, G.P. Automated Global Shallow Water Bathymetry Mapping Using Google Earth Engine. Remote Sens. 2021, 13, 1469. [Google Scholar] [CrossRef]
- Gholamalifard, M.; Kutser, T.; Esmaili-Sari, A.; Abkar, A.A.; Naimi, B. Remotely Sensed Empirical Modeling of Bathymetry in the Southeastern Caspian Sea. Remote Sens. 2013, 5, 2746–2762. [Google Scholar] [CrossRef]
- Pope, A.; Scambos, T.A.; Moussavi, M.; Tedesco, M.; Willis, M.; Shean, D.; Grigsby, S. Estimating supraglacial lake depth in West Greenland using Landsat 8 and comparison with other multispectral methods. Cryosphere 2016, 10, 15–27. [Google Scholar] [CrossRef]
- Vinayaraj, P.; Raghavan, V.; Masumoto, S. Satellite-Derived Bathymetry using Adaptive Geographically Weighted Regression Model. Mar. Geod. 2016, 39, 458–478. [Google Scholar] [CrossRef]
- Kim, M.; Danielson, J.; Storlazzi, C.; Park, S. Physics-Based Satellite-Derived Bathymetry (SDB) Using Landsat OLI Images. Remote Sens. 2024, 16, 843. [Google Scholar] [CrossRef]
- Gholamalifard, M.; Esmaili Sari, A.; Abkar, A.; Naimi, B. Bathymetric Modeling from Satellite Imagery via Single Band Algorithm (SBA) and Principal Components Analysis (PCA) in Southern Caspian Sea. Int. J. Environ. Res. 2013, 7, 877–886. [Google Scholar]
- Genuer, R.; Poggi, J.-M. Random Forests with R; Springer Nature: Cham, Switzerland, 2020; p. 98. [Google Scholar]
- Chang, N.-B.; Bai, K. Multisensor Data Fusion and Machine Learning for Environmental Remote Sensing; Taylor & Francis Group, LLC: Abingdon, UK, 2018; p. 508. [Google Scholar]
- Manessa, M.D.M.; Kanno, A.; Sekine, M.; Haidar, M.; Yamamoto, K.; Imai, T.; Higuchi, T. Satellite-derived Bathymetry using Random Forest algorithm and Worldview-2 Imagery. Geoplan. J. Geomatics Plan. 2016, 3, 117–126. [Google Scholar] [CrossRef]
- Mabula, M.J.; Kisanga, D.; Pamba, S. Application of machine learning algorithms and Sentinel-2 satellite for improved bathymetry retrieval in Lake Victoria, Tanzania. Egypt. J. Remote Sens. Space Sci. 2023, 26, 619–627. [Google Scholar] [CrossRef]
- Xie, C.; Chen, P.; Zhang, Z.; Pan, D. Satellite-derived bathymetry combined with Sentinel-2 and ICESat-2 datasets using machine learning. Front. Earth Sci. 2023, 11, 1111817. [Google Scholar] [CrossRef]
- Hassan, M.H.; Negm, A.; Nadaoka, K.; Abdelaziz, T.; Elsahabi, M. Comparative study of approaches to bathymetry detection in Nasser/Nubia Lake using multispectral SPOT-6 satellite imagery. Hydrol. Res. Lett. 2016, 10, 45–50. [Google Scholar] [CrossRef]
- Hassan, M.H.; Negm, A.; Zahran, M.; Saavedra, O.C. Bathymetry Determination from High Resolution Satellite Imagery Using Ensemble Learning Algorithms in Shallow Lakes: Case Study El-Burullus Lake. Int. J. Environ. Sci. Dev. 2016, 7, 295–301. [Google Scholar]
- Ashphaq, M.; Srivastava, P.K.; Mitra, D. Satellite-Derived Bathymetry in Dynamic Coastal Geomorphological Environments Through Machine Learning Algorithms. Earth Space Sci. 2024, 11, e2024EA003554. [Google Scholar] [CrossRef]
- Getirana, A.; Jung, H.C.; Tseng, K.-H. Deriving three dimensional reservoir bathymetry from multi-satellite datasets. Remote Sens. Environ. 2018, 217, 366–374. [Google Scholar] [CrossRef]
- Qin, X.; Wu, Z.; Luo, X.; Shang, J.; Zhao, D.; Zhou, J.; Cui, J.; Wan, H.; Xu, G. MuSRFM: Multiple scale resolution fusion based precise and robust satellite derived bathymetry model for island nearshore shallow water regions using sentinel-2 multi-spectral imagery. ISPRS J. Photogramm. Remote Sens. 2024, 218, 150–169. [Google Scholar] [CrossRef]
- Borja, P.; Cisneros, P. Estudio edafológico. In Informe del II año del Proyecto “Elaboración de la Línea Base en Hidrología de los Páramos de Quimsacocha y su Área de Influencia; Programa para el Manejo del Agua y del Suelo (PROMAS), Universidad de Cuenca: Cuenca, Ecuador, 2009; p. 104. [Google Scholar]
- Hungerbühler, D.; Steinmann, M.; Winkler, W.; Seward, D.; Egüez, A.; Peterson, D.E.; Helg, U.; Hammer, C. Neogene stratigraphy and Andean geodynamics of southern Ecuador. Earth-Sci. Rev. 2002, 57, 75–124. [Google Scholar] [CrossRef]
- Arcusa, S.; Schneider, T.; Mosquera, P.; Vogel, H.; Kaufman, D.; Szidat, S.; Grosjean, M. Late Holocene tephrostratigraphy from Cajas National Park, southern Ecuador. Andean Geol. 2020, 47, 508–528. [Google Scholar] [CrossRef]
- Ramsay, P.M.; Oxley, E.R.B. The growth form composition of plant communities in the ecuadorian páramos. Plant Ecol. 1997, 131, 173–192. [Google Scholar] [CrossRef]
- Alvites, C.; Battipaglia, G.; Santopuoli, G.; Hampel, H.; Vázquez, R.F.; Matteucci, G.; Tognetti, R.; De Micco, V. Dendrochronological analysis and growth patterns of Polylepis reticulata (Rosaceae) in the Ecuadorian Andes. IAWA J. 2019, 40, S331–S335. [Google Scholar] [CrossRef]
- Vuille, M.; Bradley, R.S.; Keimig, F. Climate Variability in the Andes of Ecuador and Its Relation to Tropical Pacific and Atlantic Sea Surface Temperature Anomalies. J. Clim. 2000, 13, 2520–2535. [Google Scholar] [CrossRef]
- Young, N.E.; Anderson, R.S.; Chignell, S.M.; Vorster, A.G.; Lawrence, R.; Evangelista, P.H. A survival guide to Landsat preprocessing. Ecology 2017, 98, 920–932. [Google Scholar] [CrossRef]
- Yunus, A.P.; Dou, J.; Song, X.; Avtar, R. Improved Bathymetric Mapping of Coastal and Lake Environments Using Sentinel-2 and Landsat-8 Images. Sensors 2019, 19, 2788. [Google Scholar] [CrossRef] [PubMed]
- USGS. Landsat 8 (L8) Data Users Handbook; U.S. Geological Survey: Sioux Falls, SD, USA, 2019; p. 106.
- Pannatier, Y. VARIOWIN. Software for Spatial Data Analysis in 2D; Springer: New York, NY, USA, 1996. [Google Scholar]
- Wang, Y.; Liu, D.; Tang, D. Application of a generalized additive model (GAM) for estimating chlorophyll-a concentration from MODIS data in the Bohai and Yellow Seas, China. Int. J. Remote Sens. 2017, 38, 639–661. [Google Scholar] [CrossRef]
- Wei, C.; Zhao, Q.; Lu, Y.; Fu, D. Assessment of Empirical Algorithms for Shallow Water Bathymetry Using Multi-Spectral Imagery of Pearl River Delta Coast, China. Remote Sens. 2021, 13, 3123. [Google Scholar] [CrossRef]
- Abdul Gafoor, F.; Al-Shehhi, M.R.; Cho, C.-S.; Ghedira, H. Gradient Boosting and Linear Regression for Estimating Coastal Bathymetry Based on Sentinel-2 Images. Remote Sens. 2022, 14, 5037. [Google Scholar] [CrossRef]
- Elshazly, R.E.; Elshemy, M.M.; Zeidan, B.A.; Armanuos, A.M. Modeling of bathymetry for lake Manzala using remote sensing and GIS. In Proceedings of the Twenty-Second International Water Technology Conference, IWTC22 Ismailia, Ismailia, Egypt, 12–13 September 2019; pp. 113–124. [Google Scholar]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Wicki, A.; Parlow, E. Multiple Regression Analysis for Unmixing of Surface Temperature Data in an Urban Environment. Remote Sens. 2017, 9, 684. [Google Scholar] [CrossRef]
- Monteys, X.; Harris, P.; Caloca, S.; Cahalane, C. Spatial Prediction of Coastal Bathymetry Based on Multispectral Satellite Imagery and Multibeam Data. Remote Sens. 2015, 7, 13782–13806. [Google Scholar] [CrossRef]
- Ma, L.; Yan, X.; Qiao, W. A Quasi-Poisson Approach on Modeling Accident Hazard Index for Urban Road Segments. Discret. Dyn. Nat. Soc. 2014, 2014, 489052. [Google Scholar] [CrossRef]
- Ver Hoef, J.M.; Boveng, P.L. Quasi-Poisson vs. negative binomial regression: How should we model overdispersed count data? Ecology 2007, 88, 2766–2772. [Google Scholar] [CrossRef]
- Lopatin, J.; Dolos, K.; Hernández, H.J.; Galleguillos, M.; Fassnacht, F.E. Comparing Generalized Linear Models and random forest to model vascular plant species richness using LiDAR data in a natural forest in central Chile. Remote Sens. Environ. 2016, 173, 200–210. [Google Scholar] [CrossRef]
- Emamgolizadeh, S.; Bateni, S.M.; Shahsavani, D.; Ashrafi, T.; Ghorbani, H. Estimation of soil cation exchange capacity using Genetic Expression Programming (GEP) and Multivariate Adaptive Regression Splines (MARS). J. Hydrol. 2015, 529, 1590–1600. [Google Scholar] [CrossRef]
- Conoscenti, C.; Ciaccio, M.; Caraballo-Arias, N.A.; Gómez-Gutiérrez, Á.; Rotigliano, E.; Agnesi, V. Assessment of susceptibility to earth-flow landslide using logistic regression and multivariate adaptive regression splines: A case of the Belice River basin (western Sicily, Italy). Geomorphology 2015, 242, 49–64. [Google Scholar] [CrossRef]
- Zhang, W.G.; Goh, A.T.C. Multivariate adaptive regression splines for analysis of geotechnical engineering systems. Comput. Geotech. 2013, 48, 82–95. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T.C.; Zhang, Y.; Chen, Y.; Xiao, Y. Assessment of soil liquefaction based on capacity energy concept and multivariate adaptive regression splines. Eng. Geol. 2015, 188, 29–37. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Brito, J.E.; Hampel, H.; Birkinshaw, S. Assessing the Performance of SHETRAN Simulating a Geologically Complex Catchment. Water 2022, 14, 3334. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Feyen, J. Assessment of the effects of DEM gridding on the predictions of basin runoff using MIKE SHE and a modelling resolution of 600 m. J. Hydrol. 2007, 334, 73–87. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of ‘goodness-of-fit’ measures in hydrological and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Feyen, J. Rainfall-runoff modelling of a rocky catchment with limited data availability: Defining prediction limits. J. Hydrol. 2010, 387, 128–140. [Google Scholar] [CrossRef]
- Ye, Z.; Liu, H.; Chen, Y.; Shu, S.; Wu, Q.; Wang, S. Analysis of water level variation of lakes and reservoirs in Xinjiang, China using ICESat laser altimetry data (2003–2009). PLoS ONE 2017, 12, e0183800. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Clark, M.P.; Vogel, R.M.; Lamontagne, J.R.; Mizukami, N.; Knoben, W.J.M.; Tang, G.; Gharari, S.; Freer, J.E.; Whitfield, P.H.; Shook, K.R.; et al. The Abuse of Popular Performance Metrics in Hydrologic Modeling. Water Resour. Res. 2021, 57, e2020WR029001. [Google Scholar] [CrossRef]
- Hong, H.P.; Li, S.H. Plotting positions and approximating first two moments of order statistics for Gumbel distribution: Estimating quantiles of wind speed. Wind Struct. 2014, 19, 371–387. [Google Scholar] [CrossRef]





| Machine Learning Method | ||||||
|---|---|---|---|---|---|---|
| Analysis | Number of Lakes | MLRM | GAM | GLM | MARS | RF |
| Global | 114 | 0.84 | 0.85 | 0.14 | 0.88 | 0.87 |
| Shallow | 15 | 0.40 | 0.40 | 1.00 | 0.33 | 0.00 |
| Deep | 99 | 0.91 | 0.92 | 0.01 | 0.96 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vázquez, R.F.; Mejía, D.; Mosquera, P.V.; Hampel, H. Estimating the Maximum Depth of Andean Lakes: A Comparative Analysis Using Machine Learning. Water 2024, 16, 3570. https://doi.org/10.3390/w16243570
Vázquez RF, Mejía D, Mosquera PV, Hampel H. Estimating the Maximum Depth of Andean Lakes: A Comparative Analysis Using Machine Learning. Water. 2024; 16(24):3570. https://doi.org/10.3390/w16243570
Chicago/Turabian StyleVázquez, Raúl F., Danilo Mejía, Pablo V. Mosquera, and Henrietta Hampel. 2024. "Estimating the Maximum Depth of Andean Lakes: A Comparative Analysis Using Machine Learning" Water 16, no. 24: 3570. https://doi.org/10.3390/w16243570
APA StyleVázquez, R. F., Mejía, D., Mosquera, P. V., & Hampel, H. (2024). Estimating the Maximum Depth of Andean Lakes: A Comparative Analysis Using Machine Learning. Water, 16(24), 3570. https://doi.org/10.3390/w16243570






