An Adaptive Process-Wise Fitting Approach for Hydrological Modeling Based on Streamflow and Remote Sensing Evapotranspiration
Abstract
1. Introduction
2. Study Areas and Methods
2.1. Study Areas
2.2. Methods
2.3. Modeling Hydrological System Using Directed Graphs
2.3.1. Graph-Based Representation of Hydrological Processes and Interdependencies
2.3.2. Quantifying Parameter Influences on Hydrological Processes
- Strong Association: Solely related to the currently calibrated process, with no links to any preceding processes in the graph.
- Moderate Association: Not related to the currently calibrated process but associated with its preceding processes.
- Weak Association: Related to both the currently calibrated process and preceding processes.
- Unrelated: No relation to any preceding or current processes.
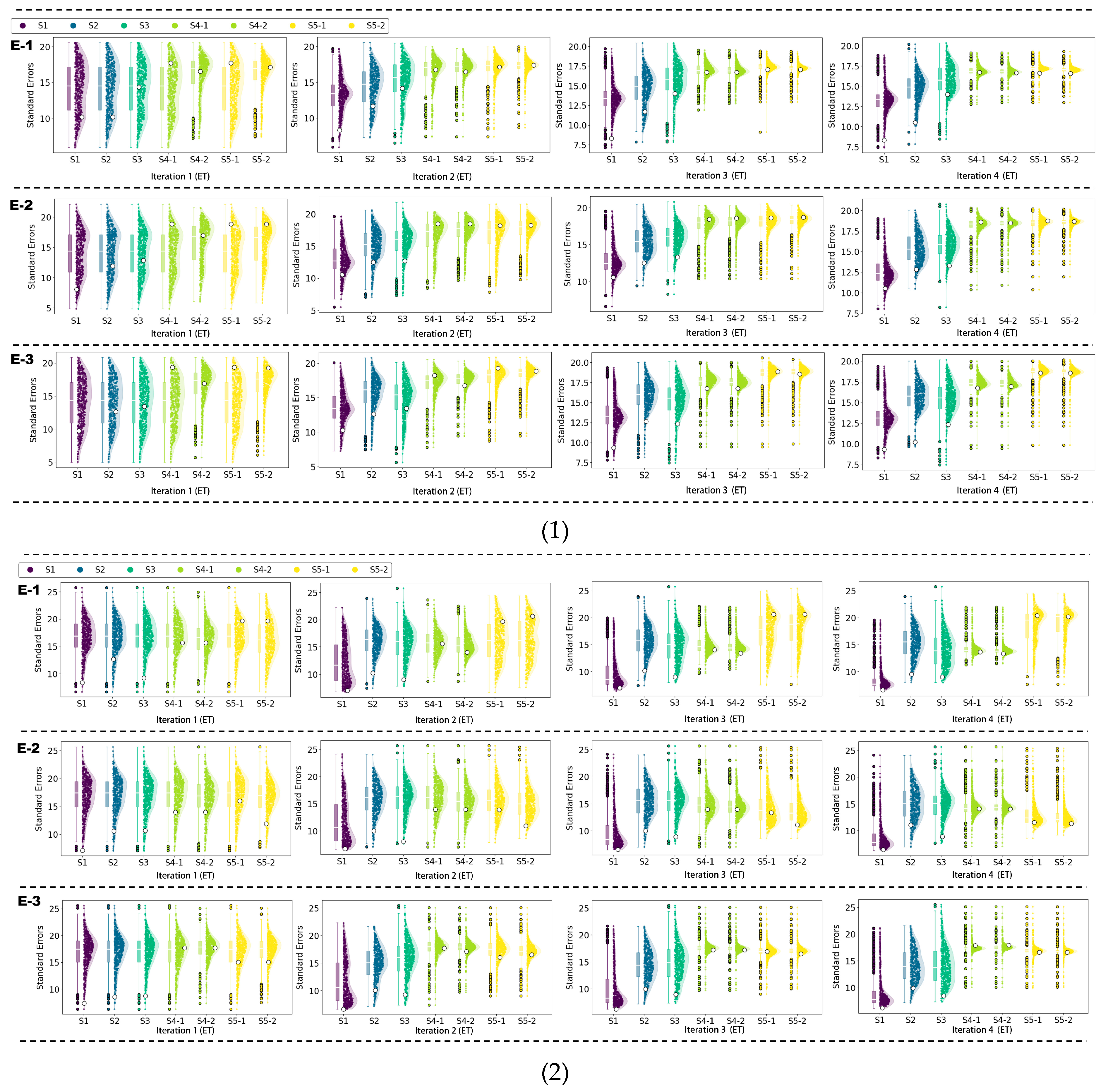
2.4. Process-Specific Simulation Evaluation Using Data with Inherent Uncertainties
2.5. Parameter Updating by Improved PSO with Learning Rates
2.6. Experimental Design
2.6.1. Experimental Setup
2.6.2. Parameter–Process Relations
2.7. Experimental Data
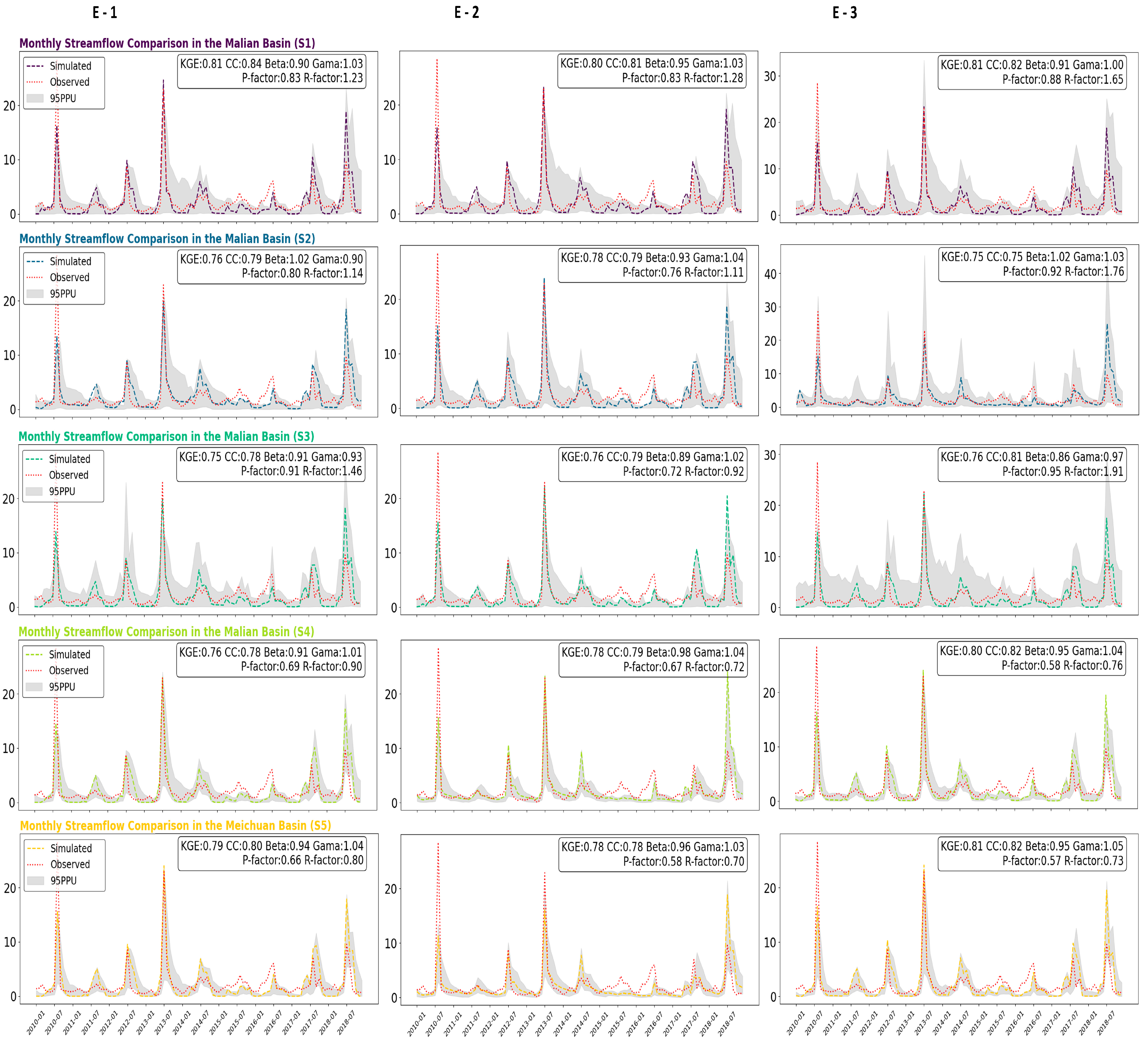
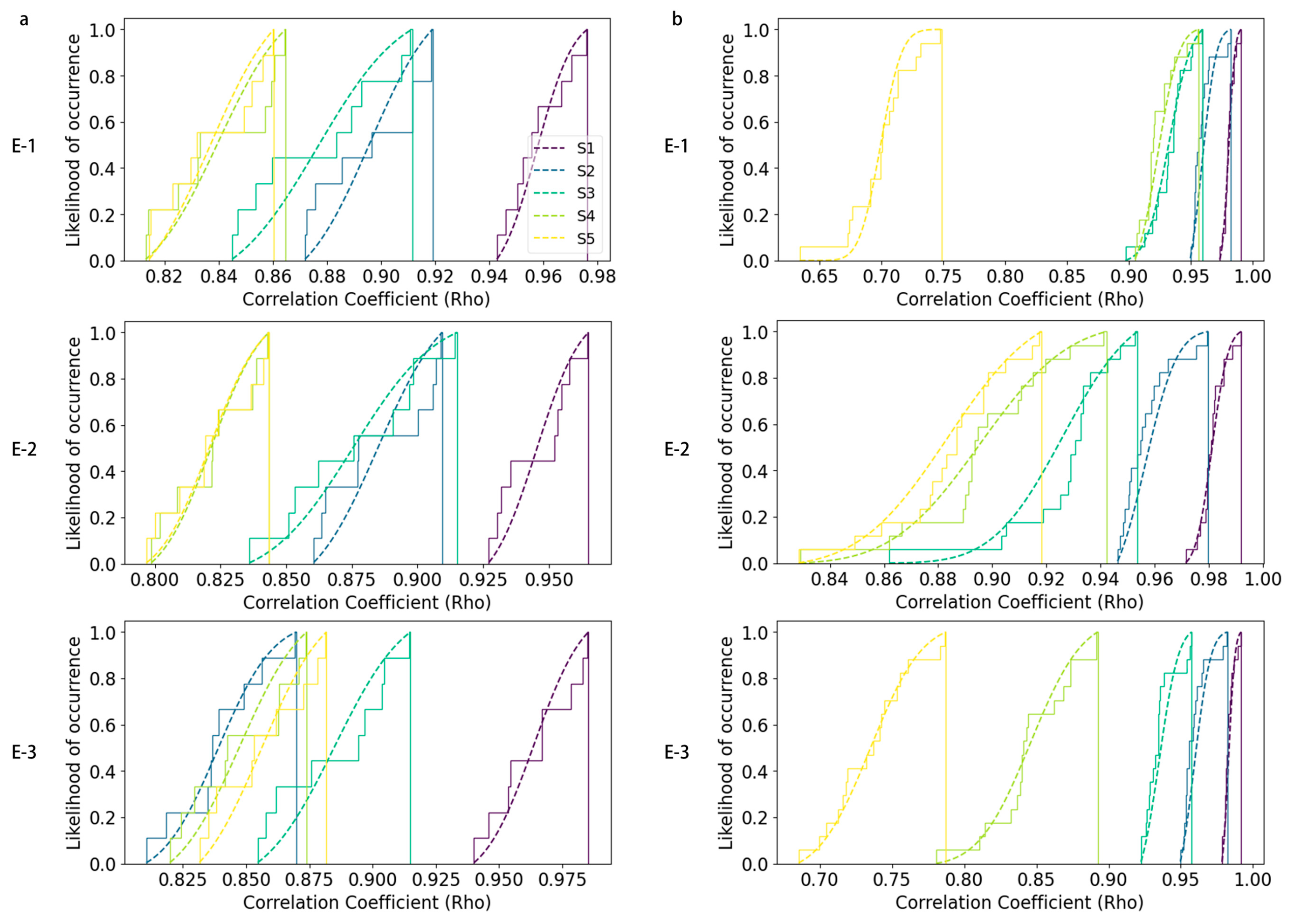
3. Results
3.1. Simulated Streamflow at Gauge Stations
3.2. Simulated ET in Sub-Basins
4. Discussion
4.1. Are the ETC-Estimated Metrics More Effective than Traditional Evaluation Methods?
4.2. Is the Optimization of Parameters Across Processes with the Learning Rate More Effective than the Traditional Method?
4.3. Limitations and Future Works
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Zhao, Y.; Ma, Q.; Wang, P.; Ge, Y.; Yu, W. A parallel computing-based and spatially stepwise strategy for constraining a semi-distributed hydrological model with streamflow observations and satellite-based evapotranspiration. J. Hydrol. 2021, 599, 126359. [Google Scholar] [CrossRef]
- Shen, H.; Tolson, B.A.; Mai, J. Time to Update the Split-Sample Approach in Hydrological Model Calibration. Water Resour. Res. 2022, 58, e2021WR031523. [Google Scholar] [CrossRef]
- Becker, R.; Koppa, A.; Schulz, S.; Usman, M.; aus der Beek, T.; Schüth, C. Spatially distributed model calibration of a highly managed hydrological system using remote sensing-derived ET data. J. Hydrol. 2019, 577, 123944. [Google Scholar] [CrossRef]
- Hasan, H.M.; Hosseini-Moghari, S.-M.; Döll, P.; Güntner, A. Multi-variable Pareto optimal calibration of the global hydrological model WaterGAP for 1500 major drainage basins around the globe. In Proceedings of the Copernicus Meetings, Vienna, Austria, 24–28 April 2023. [Google Scholar]
- Chlumsky, R.; Mai, J.; Craig, J.R.; Tolson, B.A. Simultaneous calibration of hydrologic model structure and parameters using a blended model. Water Resour. Res. 2021, 57, e2020WR029229. [Google Scholar] [CrossRef]
- Ougahi, J.H.; Rowan, J.S. Combining Hydrological Models and Remote Sensing to Characterize Snowpack Dynamics in High Mountains. Remote Sens. 2024, 16, 264. [Google Scholar] [CrossRef]
- Lan, T.; Lin, K.; Xu, C.-Y.; Tan, X.; Chen, X. Dynamics of hydrological-model parameters: Mechanisms, problems and solutions. Hydrol. Earth Syst. Sci. 2020, 24, 1347–1366. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, Y.; Li, J.; Xu, H.; Zhang, C.; Deng, L.; Wang, Y.; Peng, M. Improving CMIP6 atmospheric river precipitation estimation by cycle-consistent generative adversarial networks. J. Geophys. Res. Atmos. 2024, 129, e2023JD040698. [Google Scholar] [CrossRef]
- Li, Z.; He, M.-Y.; Li, B.; Wen, X.; Zhou, J.; Cheng, Y.; Zhang, N.; Deng, L. Multi-isotopic composition (Li and B isotopes) and hydrochemistry characterization of the Lakko Co Li-rich salt lake in Tibet, China: Origin and hydrological processes. J. Hydrol. 2024, 630, 130714. [Google Scholar] [CrossRef]
- Mao, H.; Wang, C.; He, Y.; Song, X.; Ma, R.; Li, R.; Duan, Z. Advancing SWAT Model Calibration: A U-NSGA-III-Based Framework for Multi-Objective Optimization. Water 2024, 16, 3030. [Google Scholar] [CrossRef]
- Rajib, A.; Evenson, G.R.; Golden, H.E.; Lane, C.R. Hydrologic model predictability improves with spatially explicit calibration using remotely sensed evapotranspiration and biophysical parameters. J. Hydrol. 2018, 567, 668–683. [Google Scholar] [CrossRef]
- Wambura, F.J.; Dietrich, O.; Lischeid, G. Improving a distributed hydrological model using evapotranspiration-related boundary conditions as additional constraints in a data-scarce river basin. Hydrol. Process. 2018, 32, 759–775. [Google Scholar] [CrossRef]
- Ningthoujam, V.; Romeji, N. SWAT Model Calibration and Validation with Remotely Sensed Evapotranspiration data in Maklang-Tuyungbi-Taret lok Ungauged Basin in Manipur, India. Iran. J. Sci. Technol. Trans. Civ. Eng. 2024, 1–17. [Google Scholar] [CrossRef]
- Herman, M.R.; Nejadhashemi, A.P.; Abouali, M.; Hernandez-Suarez, J.S.; Daneshvar, F.; Zhang, Z.; Anderson, M.C.; Sadeghi, A.M.; Hain, C.R.; Sharifi, A. Evaluating the role of evapotranspiration remote sensing data in improving hydrological modeling predictability. J. Hydrol. 2018, 556, 39–49. [Google Scholar] [CrossRef]
- Rajib, M.A.; Merwade, V.; Yu, Z. Multi-objective calibration of a hydrologic model using spatially distributed remotely sensed/in-situ soil moisture. J. Hydrol. 2016, 536, 192–207. [Google Scholar] [CrossRef]
- Zejun, L.; Pan, L.; Maoyuan, F.; Xueqing, C.; Ping, H.; Caijun, W.; Jingwen, Z. Evaluating the Effect of Transpiration in Hydrologic Model Simulation through Parameter Calibration. J. Hydrol. Eng. 2020, 25, 123944. [Google Scholar]
- van Griensven, A.; Ndomba, P.; Yalew, S.; Kilonzo, F. Critical review of SWAT applications in the upper Nile basin countries. Hydrol. Earth Syst. Sci. 2012, 16, 3371–3381. [Google Scholar] [CrossRef]
- Ochege, F.U.; Shi, H.; Li, C.; Ma, X.; Igboeli, E.E.; Luo, G. Assessing Satellite, Land Surface Model and Reanalysis Evapotranspiration Products in the Absence of In-Situ in Central Asia. Remote Sens. 2021, 13, 5148. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- McColl, K.A.; Vogelzang, J.; Konings, A.G.; Entekhabi, D.; Piles, M.; Stoffelen, A. Extended triple collocation: Estimating errors and correlation coefficients with respect to an unknown target. Geophys. Res. Lett. 2014, 41, 6229–6236. [Google Scholar] [CrossRef]
- Chen, F.; Crow, W.T.; Bindlish, R.; Colliander, A.; Burgin, M.S.; Asanuma, J.; Aida, K. Global-scale evaluation of SMAP, SMOS and ASCAT soil moisture products using triple collocation. Remote Sens. Environ. 2018, 214, 1–13. [Google Scholar] [CrossRef]
- Jia, Y.; Li, C.; Yang, H.; Yang, W.; Liu, Z. Assessments of three evapotranspiration products over China using extended triple collocation and water balance methods. J. Hydrol. 2022, 614, 128594. [Google Scholar] [CrossRef]
- Khan, M.S.; Liaqat, U.W.; Baik, J.; Choi, M. Stand-alone uncertainty characterization of GLEAM, GLDAS and MOD16 evapotranspiration products using an extended triple collocation approach. Agric. For. Meteorol. 2018, 252, 256–268. [Google Scholar] [CrossRef]
- Yin, G.; Park, J. The use of triple collocation approach to merge satellite-and model-based terrestrial water storage for flood potential analysis. J. Hydrol. 2021, 603, 127197. [Google Scholar] [CrossRef]
- Rajib, M.A.; Merwade, V. Improving soil moisture accounting and streamflow prediction in SWAT by incorporating a modified time-dependent Curve Number method. Hydrol. Process. 2016, 30, 603–624. [Google Scholar] [CrossRef]
- Abbas, S.A.; Bailey, R.T.; White, J.T.; Arnold, J.G.; White, M.J.; Čerkasova, N.; Gao, J. A framework for parameter estimation, sensitivity analysis, and uncertainty analysis for holistic hydrologic modeling using SWAT+. Hydrol. Earth Syst. Sci. 2024, 28, 21–48. [Google Scholar] [CrossRef]
- Eini, M.R.; Massari, C.; Piniewski, M. Satellite-based soil moisture enhances the reliability of agro-hydrological modeling in large transboundary river basins. Sci. Total Env. 2023, 873, 162396. [Google Scholar] [CrossRef]
- Odusanya, A.E.; Schulz, K.; Biao, E.I.; Degan, B.A.S.; Mehdi-Schulz, B. Evaluating the performance of streamflow simulated by an eco-hydrological model calibrated and validated with global land surface actual evapotranspiration from remote sensing at a catchment scale in West Africa. J. Hydrol. Reg. Stud. 2021, 37, 100893. [Google Scholar] [CrossRef]
- Yang, Y.; Guan, K.; Peng, B.; Pan, M.; Jiang, C.; Franz, T.E. High-resolution spatially explicit land surface model calibration using field-scale satellite-based daily evapotranspiration product. J. Hydrol. 2021, 596, 125730. [Google Scholar] [CrossRef]
- Demirel, M.C.; Koch, J.; Rakovec, O.; Kumar, R.; Mai, J.; Müller, S.; Thober, S.; Samaniego, L.; Stisen, S. Tradeoffs between temporal and spatial pattern calibration and their impacts on robustness and transferability of hydrologic model parameters to ungauged basins. Water Resour. Res. 2024, 60, e2022WR034193. [Google Scholar] [CrossRef]
- Herman, M.R.; Hernandez-Suarez, J.S.; Nejadhashemi, A.P.; Kropp, I.; Sadeghi, A.M. Evaluation of Multi- and Many-Objective Optimization Techniques to Improve the Performance of a Hydrologic Model Using Evapotranspiration Remote-Sensing Data. J. Hydrol. Eng. 2020, 25, 04020006. [Google Scholar] [CrossRef]
- Gan, Y.; Liang, X.Z.; Duan, Q.; Choi, H.I.; Dai, Y.; Wu, H. Stepwise sensitivity analysis from qualitative to quantitative: Application to the terrestrial hydrological modeling of a Conjunctive Surface-Subsurface Process (CSSP) land surface model. J. Adv. Model. Earth Syst. 2015, 7, 648–669. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT calibration and uncertainty programs. A User Man. 2015, 103, 17–66. [Google Scholar]
- Singh, A.; Jha, S.K. Identification of sensitive parameters in daily and monthly hydrological simulations in small to large catchments in Central India. J. Hydrol. 2021, 601, 126632. [Google Scholar] [CrossRef]
- Niraula, R.; Meixner, T.; Norman, L.M. Determining the importance of model calibration for forecasting absolute/relative changes in streamflow from LULC and climate changes. J. Hydrol. 2015, 522, 439–451. [Google Scholar] [CrossRef]
- Dangol, S.; Zhang, X.; Liang, X.-Z.; Anderson, M.; Crow, W.; Lee, S.; Moglen, G.E.; McCarty, G.W. Multivariate calibration of the SWAT model using remotely sensed datasets. Remote Sens. 2023, 15, 2417. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.-z.; Zhang, X.-c.; Zheng, F.-l. Impacts of land use change and climate variability on hydrology in an agricultural catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Zhao, F.; Wu, Y.; Qiu, L.; Sun, Y.; Sun, L.; Li, Q.; Niu, J.; Wang, G. Parameter Uncertainty Analysis of the SWAT Model in a Mountain-Loess Transitional Watershed on the Chinese Loess Plateau. Water 2018, 10, 690. [Google Scholar] [CrossRef]
- Zhang, L.; Podlasly, C.; Feger, K.-H.; Wang, Y.; Schwärzel, K. Different land management measures and climate change impacts on the runoff—A simple empirical method derived in a mesoscale catchment on the Loess Plateau. J. Arid Environ. 2015, 120, 42–50. [Google Scholar] [CrossRef]
- Huo, J.; Liu, L. Evaluation method of multiobjective functions’ combination and its application in hydrological model evaluation. Comput. Intell. Neurosci. 2020, 2020, 8594727. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, G.; Huang, F.; Qin, H.; Wang, B.; Yi, L. Directed graph deep neural network for multi-step daily streamflow forecasting. J. Hydrol. 2022, 607, 127515. [Google Scholar] [CrossRef]
- Fenicia, F.; Savenije, H.H.; Matgen, P.; Pfister, L. Understanding catchment behavior through stepwise model concept improvement. Water Resour. Res. 2008, 44, 1–13. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Arsenault, R.; Brissette, F.P. Continuous streamflow prediction in ungauged basins: The effects of equifinality and parameter set selection on uncertainty in regionalization approaches. Water Resour. Res. 2014, 50, 6135–6153. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity analysis for importance assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Bonyadi, M.R.; Michalewicz, Z. Particle swarm optimization for single objective continuous space problems: A review. Evol. Comput. 2017, 25, 1–54. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- MCKAY, M. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Sobol, I.M. Uniformly distributed sequences with an additional uniform property. USSR Comput. Math. Math. Phys. 1976, 16, 236–242. [Google Scholar] [CrossRef]
- Mai, J. Ten strategies towards successful calibration of environmental models. J. Hydrol. 2023, 620, 129414. [Google Scholar] [CrossRef]
- Fritz, C.O.; Morris, P.E.; Richler, J.J. Effect size estimates: Current use, calculations, and interpretation. J. Exp. Psychol. Gen. 2012, 141, 2. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Parteli, E.J.; Xia, Q.; Yin, X.; Shao, Y. A regional hydrological model for arid and semi-arid river basins with consideration of irrigation. Environ. Model. Softw. 2022, 157, 105531. [Google Scholar] [CrossRef]
- Ma, T.; Duan, Z.; Li, R.; Song, X. Enhancing SWAT with remotely sensed LAI for improved modelling of ecohydrological process in subtropics. J. Hydrol. 2019, 570, 802–815. [Google Scholar] [CrossRef]
- Robert, W.M.; Gene, Y.; Claire, B.; Margaret, W.G.; Zhiming, Q.; Devendra, M.A.; Prem, B.P.; James, V.B.; Timothy, R.G. Parameterization Guidelines and Considerations for Hydrologic Models. Trans. ASABE 2015, 58, 1681–1703. [Google Scholar] [CrossRef]
- Vaezi, A.R. Modeling Runoff from Semi-Arid Agricultural Lands in Northwest Iran. Pedosphere 2014, 24, 595–604. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Beven, K. Prophecy, reality and uncertainty in distributed hydrological modelling. Adv. Water Resour. 1993, 16, 41–51. [Google Scholar] [CrossRef]
- Larose, M.; Heathman, G.; Norton, L.; Engel, B. Hydrologic and atrazine simulation of the Cedar Creek watershed using the SWAT model. J. Environ. Qual. 2007, 36, 521–531. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Foulon, É.; Rousseau, A.N. Equifinality and automatic calibration: What is the impact of hypothesizing an optimal parameter set on modelled hydrological processes? Can. Water Resour. J. Rev. Can. Des Ressour. Hydr. 2018, 43, 47–67. [Google Scholar] [CrossRef]
- Pan, M.; Fisher, C.K.; Chaney, N.W.; Zhan, W.; Crow, W.T.; Aires, F.; Entekhabi, D.; Wood, E.F. Triple collocation: Beyond three estimates and separation of structural/non-structural errors. Remote Sens. Environ. 2015, 171, 299–310. [Google Scholar] [CrossRef]
- Ling, L.; Trümmer, M.R. Multiquadric collocation method with integralformulation for boundary layer problems. Comput. Math. Appl. 2004, 48, 927–941. [Google Scholar] [CrossRef]
- He, Y.; Wang, C.; Hu, J.; Mao, H.; Duan, Z.; Qu, C.; Li, R.; Wang, M.; Song, X. Discovering Optimal Triplets for Assessing the Uncertainties of Satellite-Derived Evapotranspiration Products. Remote Sens. 2023, 15, 3215. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Crow, W.T. Evaluation of assumptions in soil moisture triple collocation analysis. J. Hydrometeorol. 2014, 15, 1293–1302. [Google Scholar] [CrossRef]
- Shi, C.; Xie, Z.; Qian, H.; Liang, M.; Yang, X. China land soil moisture EnKF data assimilation based on satellite remote sensing data. Sci. China Earth Sci. 2011, 54, 1430–1440. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H. Significance of the China meteorological assimilation driving datasets for the SWAT model (CMADS) of East Asia. Water 2017, 9, 765. [Google Scholar] [CrossRef]
- Tachikawa, T.; Hato, M.; Kaku, M.; Iwasaki, A. Characteristics of ASTER GDEM version 2. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 3657–3660. [Google Scholar]
- Abrams, M.; Crippen, R.; Fujisada, H. ASTER global digital elevation model (GDEM) and ASTER global water body dataset (ASTWBD). Remote Sens. 2020, 12, 1156. [Google Scholar] [CrossRef]
- Zanaga, D.; Van De Kerchove, R.; Daems, D.; De Keersmaecker, W.; Brockmann, C.; Kirches, G.; Wevers, J.; Cartus, O.; Santoro, M.; Fritz, S. ESA WorldCover 10 m 2021 v200. 2022. Available online: https://worldcover2021.esa.int/download (accessed on 21 April 2023).
- Gong, P.; Liu, H.; Zhang, M.; Li, C.; Wang, J.; Huang, H.; Clinton, N.; Ji, L.; Li, W.; Bai, Y. Stable classification with limited sample: Transferring a 30-m resolution sample set collected in 2015 to mapping 10-m resolution global land cover in 2017. Science Bulletin 2019, 64, 370–373. [Google Scholar] [CrossRef]
- Running, S.; Mu, Q.; Zhao, M. Mod16a2 modis/terra net evapotranspiration 8-day l4 global 500m sin grid v006. NASA EOSDIS Land Processes DAAC 2017, 6. [Google Scholar]
- He, S.; Zhang, Y.; Ma, N.; Tian, J.; Kong, D.; Liu, C. A daily and 500 m coupled evapotranspiration and gross primary production product across China during 2000–2020. Earth Syst. Sci. Data Discuss. 2022, 2022, 5463–5488. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Hong, Y.; Fisher, J.B.; Zhang, N.; Chen, J.; Cheng, J.; Zhao, S.; Zhang, X. Bayesian multimodel estimation of global terrestrial latent heat flux from eddy covariance, meteorological, and satellite observations. J. Geophys. Res. Atmos. 2014, 119, 4521–4545. [Google Scholar] [CrossRef]
- Senay, G.B. Satellite psychrometric formulation of the Operational Simplified Surface Energy Balance (SSEBop) model for quantifying and mapping evapotranspiration. Appl. Eng. Agric. 2018, 34, 555–566. [Google Scholar] [CrossRef]













| Type | Resolution | Source |
|---|---|---|
| Observed Streamflow | Daily (2006–2018) | Chinese Hydrological Yearbook |
| Observed ET | Daily (2006–2018) | China national agro-ecosystem databases Changwu station |
| Climate | Daily (2006–2018) | CMADS https://www.cmads.org/, accessed on 15 April 2023 |
| ET | 500 m/1 km (2006–2018) | PMLv2, GLASS https://data.tpdc.ac.cn, accessed on 20 August 2022 http://www.glass.umd.edu/, accessed on 24 August 2022 |
| DEM | 30 m | ASTER GDEM https://lpdaac.usgs.gov/products/ast14demv003/, accessed on 10 October 2022 |
| Land Use | 10 m | ESA WorldCover https://esa-worldcover.org/en, accessed on 15 October 2022 |
| Soil | 1 km | 1:1,000,000 soil type map https://www.resdc.cn/Default.aspx, accessed on 10 March 2023 |
| 30 m | China high-resolution national soil attribute dataset http://soil.geodata.cn, accessed on 21 March 2023 |
| Type | Resolution | Source |
|---|---|---|
| Observed Streamflow | Daily (2006–2018) | Yangtze River Basin Hydrological Yearbook |
| Observed ET | Daily (2006–2018) | China national agro-ecosystem databases Qianyanzhou station |
| Climate | Daily (2006–2018) | CMADS https://www.cmads.org/, accessed on 15 April 2023 |
| ET | 500 m/1 km (2006–2018) | PMLv2, GLASS https://data.tpdc.ac.cn, accessed on 20 August 2022 http://www.glass.umd.edu/, accessed on 24 August 2022 |
| DEM | 30 m | ASTER GDEM https://lpdaac.usgs.gov/products/ast14demv003/, accessed on 10 October 2022 |
| Land Use | 10 m | FROM-GLC https://data-starcloud.pcl.ac.cn/zh, accessed on 22 October 2022 |
| Soil | 1 km | 1:1,000,000 soil type map https://www.resdc.cn/Default.aspx, accessed on 10 March 2023 |
| 30 m | China high-resolution national soil attribute dataset http://soil.geodata.cn, accessed on 21 March 2023 |
| Experiment | E-1 | E-2 | E-3 | |
|---|---|---|---|---|
| Scheme | ||||
| S1 | 0.81 | 0.80 | 0.80 | |
| S2 | 0.76 | 0.78 | 0.75 | |
| S3 | 0.75 | 0.76 | 0.76 | |
| S4 | 0.76 | 0.78 | 0.80 | |
| S5 | 0.79 | 0.78 | 0.81 | |
| Experiment | E-1 | E-2 | E-3 | |
|---|---|---|---|---|
| Scheme | ||||
| S1 | 0.92 | 0.93 | 0.94 | |
| S2 | 0.83 | 0.92 | 0.87 | |
| S3 | 0.75 | 0.85 | 0.78 | |
| S4 | 0.76 | 0.78 | 0.80 | |
| S5 | 0.89 | 0.81 | 0.85 | |
| Parameters | CH_K2 | EPCO | ALPHA_BF | SOL_AWC | |
|---|---|---|---|---|---|
| Processes (Variable) | |||||
| Evapotranspiration (ET) | Unrelated [0] | Strong [2] | Moderate [1.5] | Weak [0.5] | |
| Channel routing (Streamflow) | Strong [2] | Unrelated [0] | Unrelated [0] | Weak [0.5] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Mao, H.; Nemoto, T.; He, Y.; Hu, J.; Li, R.; Wu, Q.; Wang, M.; Song, X.; Duan, Z. An Adaptive Process-Wise Fitting Approach for Hydrological Modeling Based on Streamflow and Remote Sensing Evapotranspiration. Water 2024, 16, 3446. https://doi.org/10.3390/w16233446
Wang C, Mao H, Nemoto T, He Y, Hu J, Li R, Wu Q, Wang M, Song X, Duan Z. An Adaptive Process-Wise Fitting Approach for Hydrological Modeling Based on Streamflow and Remote Sensing Evapotranspiration. Water. 2024; 16(23):3446. https://doi.org/10.3390/w16233446
Chicago/Turabian StyleWang, Chen, Huihui Mao, Tatsuya Nemoto, Yan He, Jinghao Hu, Runkui Li, Qian Wu, Mingyu Wang, Xianfeng Song, and Zheng Duan. 2024. "An Adaptive Process-Wise Fitting Approach for Hydrological Modeling Based on Streamflow and Remote Sensing Evapotranspiration" Water 16, no. 23: 3446. https://doi.org/10.3390/w16233446
APA StyleWang, C., Mao, H., Nemoto, T., He, Y., Hu, J., Li, R., Wu, Q., Wang, M., Song, X., & Duan, Z. (2024). An Adaptive Process-Wise Fitting Approach for Hydrological Modeling Based on Streamflow and Remote Sensing Evapotranspiration. Water, 16(23), 3446. https://doi.org/10.3390/w16233446








