Assessment of Drainage Network Configuration Using Gibbs’ Model with Increased Number of Flow Directions
Abstract
1. Introduction
2. Application of Gibbs’ Model
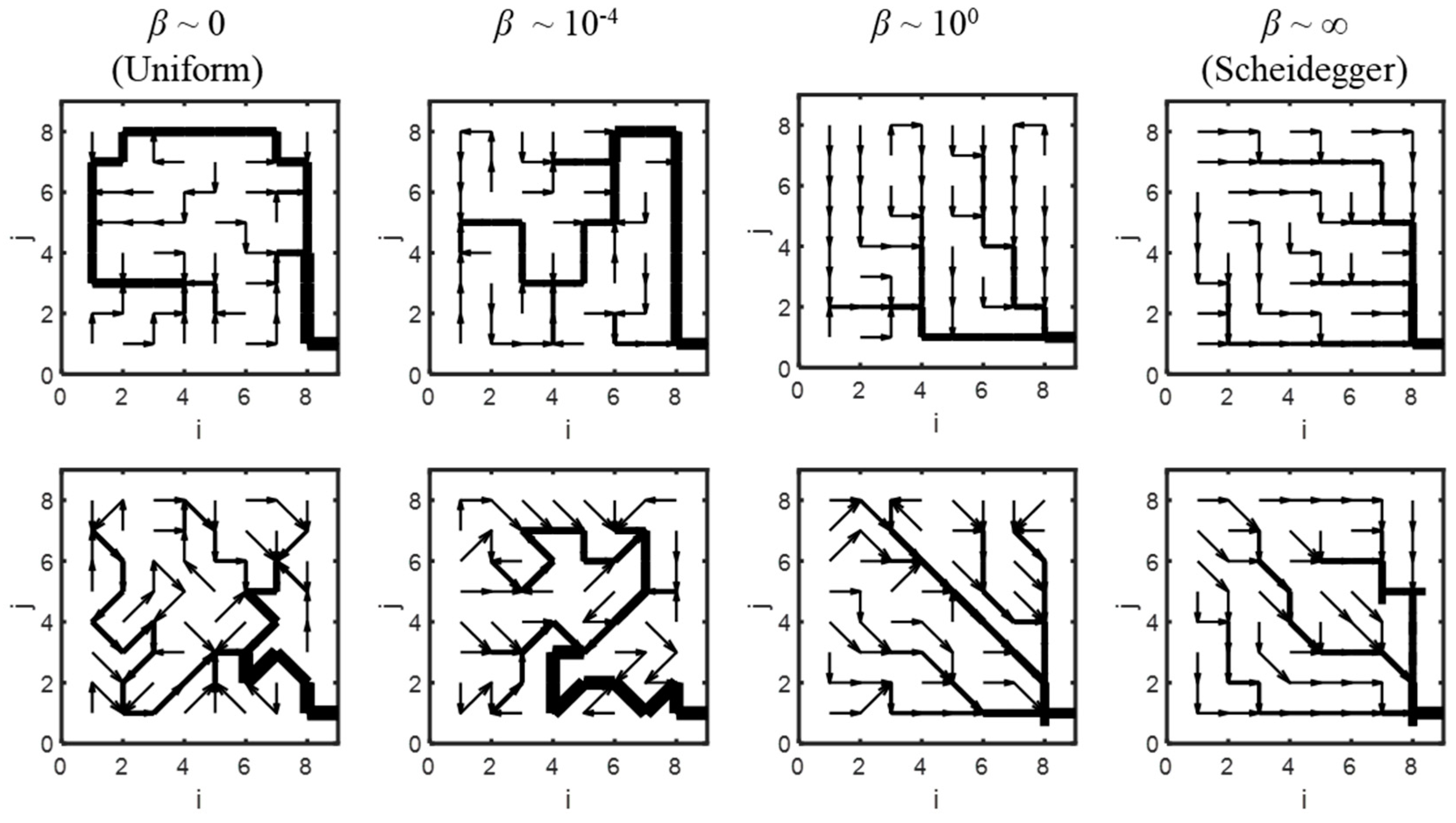
2.1. Uniform, Scheidegger and Gibbs’ Model
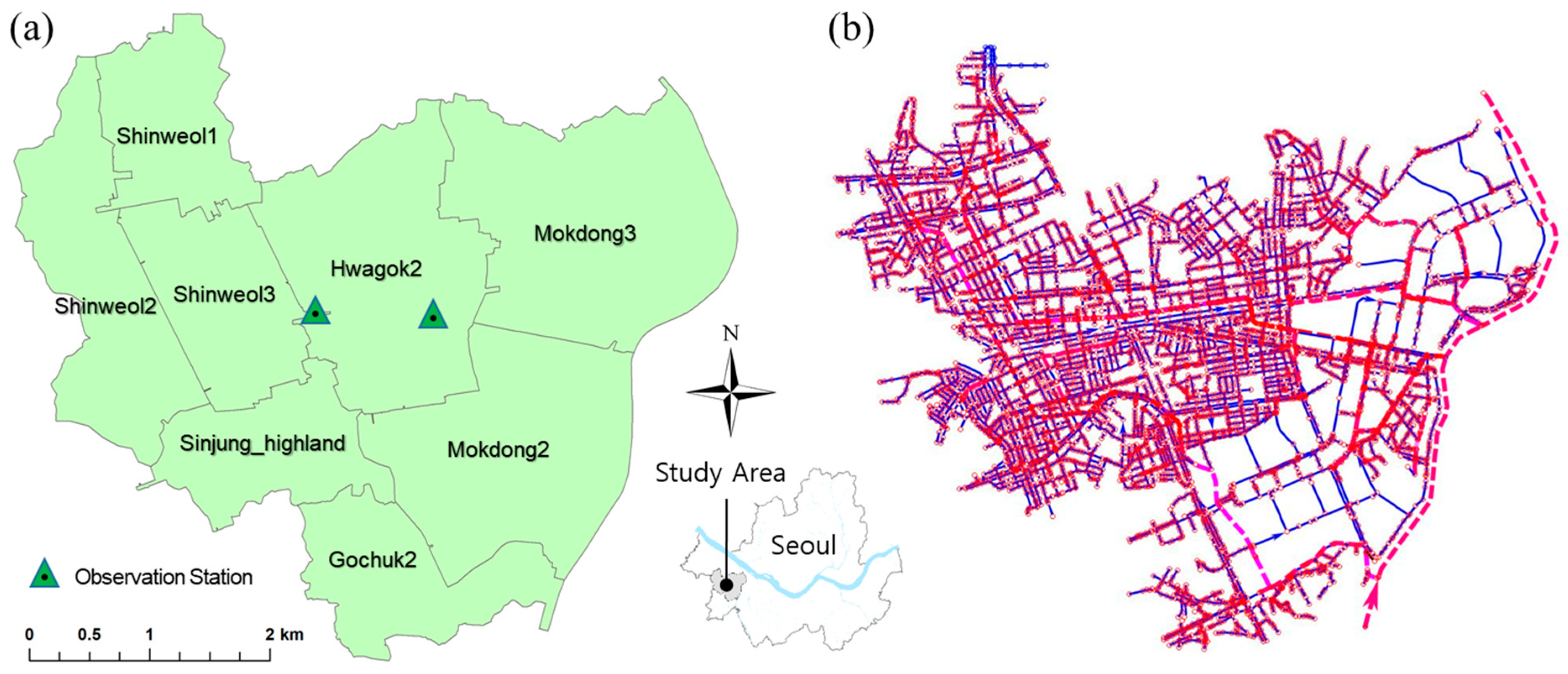
2.2. Study Area for Application of Gibbs’ Model
3. Results and Discussion
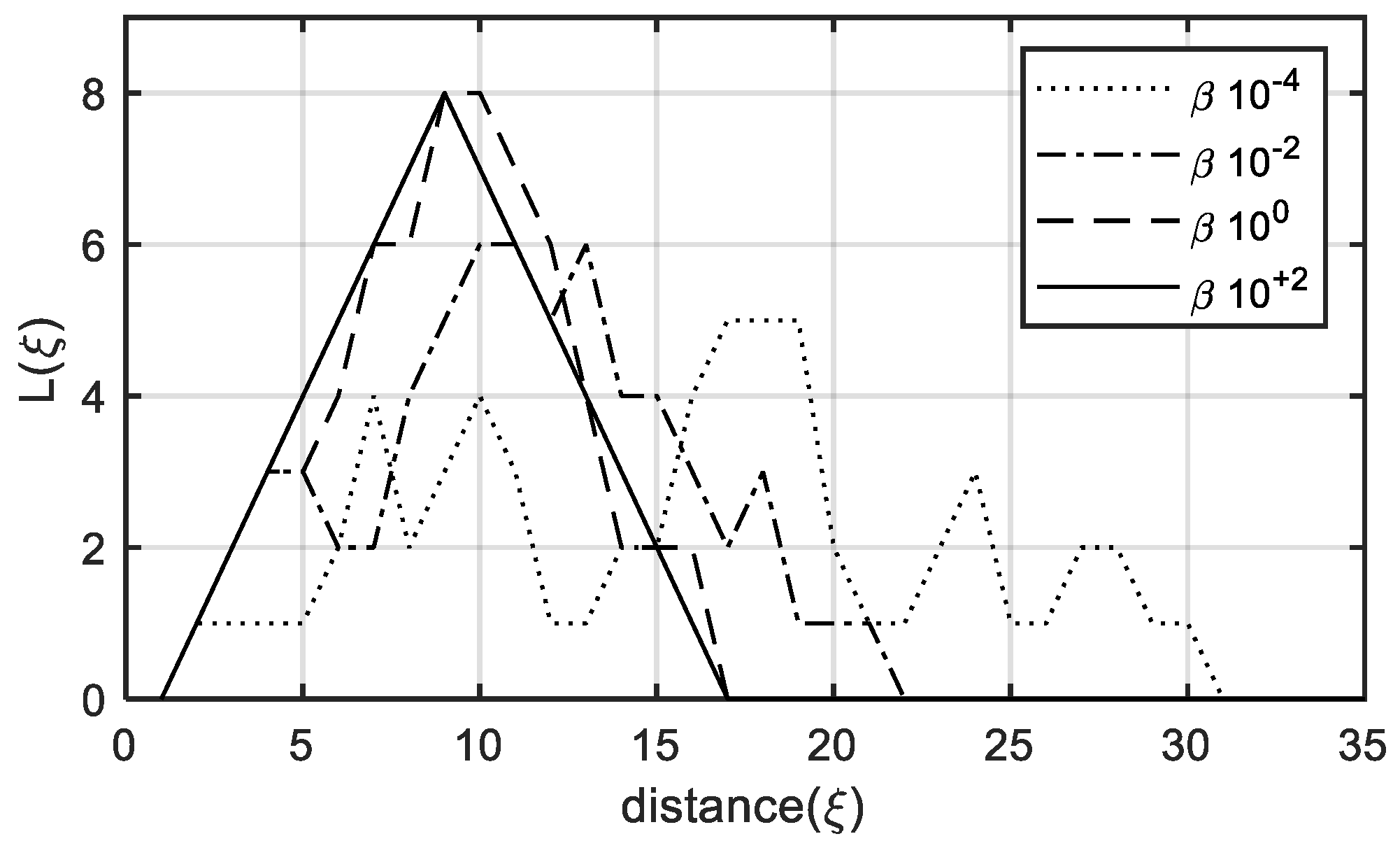
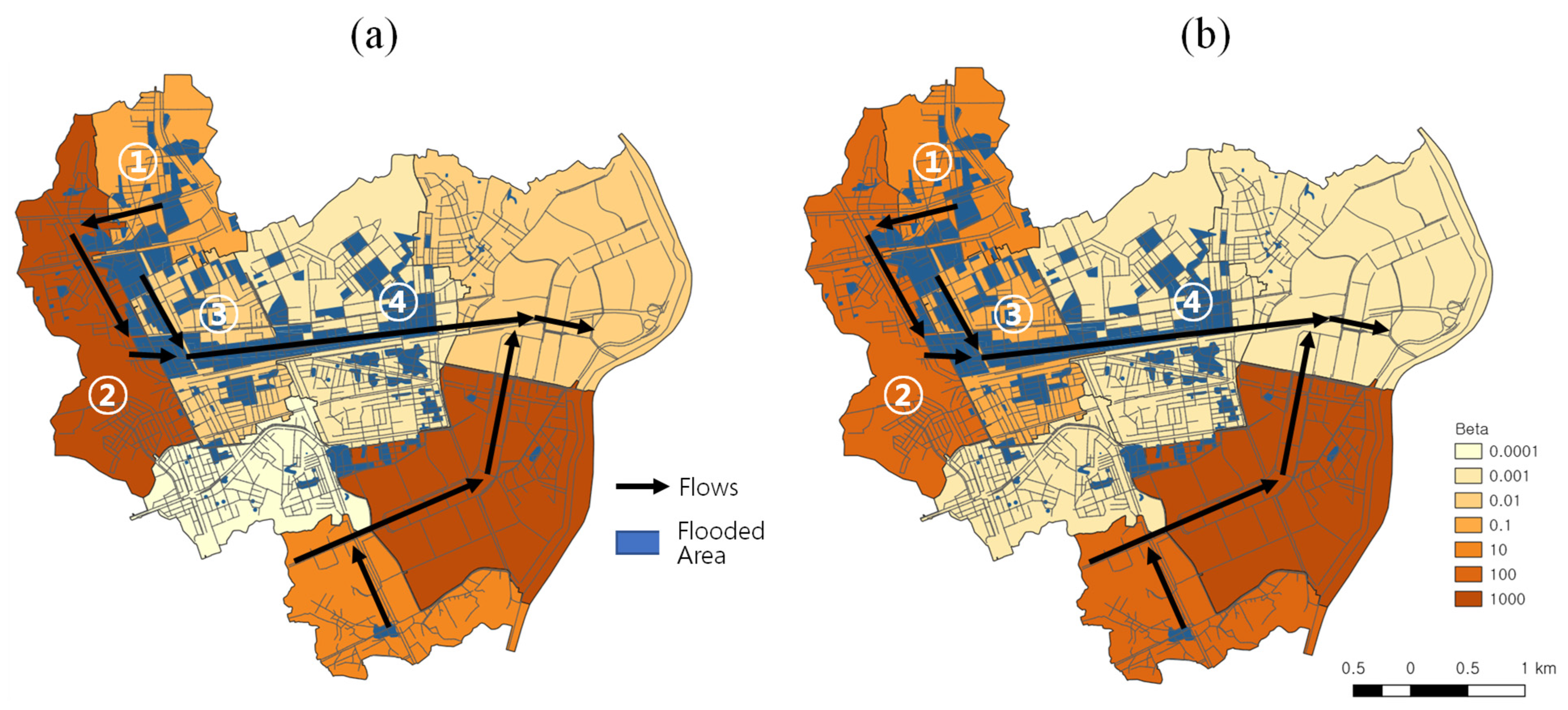
3.1. Assessment of Drainage Network Configuration Using Gibbs’ Model
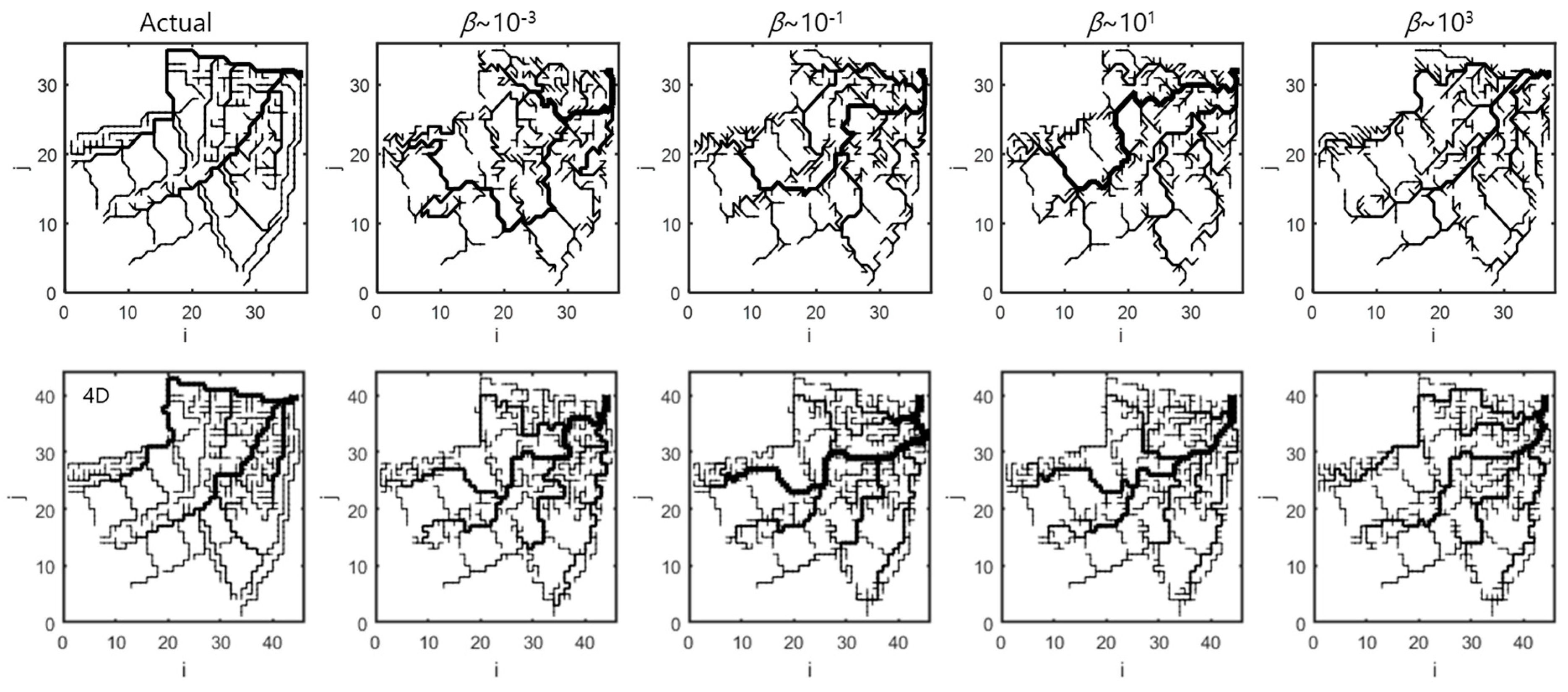
3.2. Procedures to Estimate β of the Shinewoel Watershed Using Gibbs’ Model
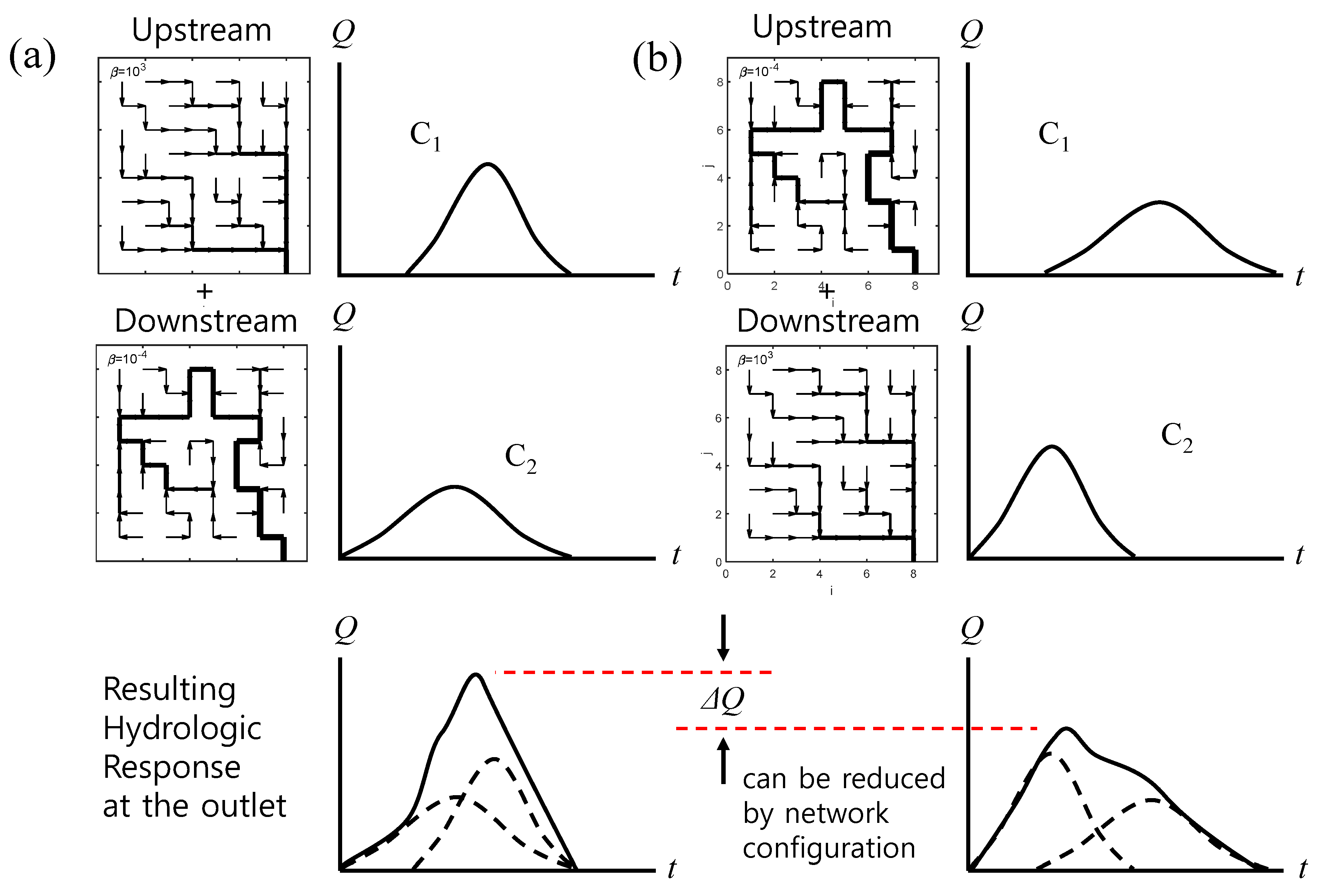
3.3. Importance of Network Configuration in Floods
3.4. Application to a Study Area for Flow Estimation Using the Width Function-Based IUH
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, F.; Simon, K.S.; Perry, G.L.W. River networks: An analysis of simulating algorithms and graph metrics used to quantify topology. Methods Ecol. Evol. 2022, 13, 1374–1387. [Google Scholar] [CrossRef]
- Xingyuan, Z.; Fawen, L.; Yong, Z. Impact of changes in river network structure on hydrological connectivity of watersheds. Ecol. Indic. 2023, 146, 109848. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E. Stochastic Methods in Hydrology: Rain, Landforms, and Floods: CIMAT, Guanajuato, Mexico, March 25–28, 1996; World Scientific: Singapore; River Edge, NJ, USA, 1998. [Google Scholar]
- Zhang, Y.; Wang, E.; Gong, Y. A Structural Optimization of Urban Drainage Systems: An Optimization Approach for Mitigating Urban Floods. Water 2024, 16, 1696. [Google Scholar] [CrossRef]
- Ren, H.; Liu, S.; Li, M.; Zhang, H.; Wang, H.; Hao, X.; Cui, J. Topological Analysis and Application of Urban Drainage Network. Water 2022, 14, 3732. [Google Scholar] [CrossRef]
- Ngamalieu-Nengoue, U.A.; Martínez-Solano, F.J.; Iglesias-Rey, P.L.; Mora-Meliá, D. Multi-Objective Optimization for Urban Drainage or Sewer Networks Rehabilitation through Pipes Substitution and Storage Tanks Installation. Water 2019, 11, 935. [Google Scholar] [CrossRef]
- Dodds, P.S.; Rothman, D.H. Scaling, universality, and geomorphology. Annu. Rev. Earth Planet. Sci. 2000, 28, 571–610. [Google Scholar] [CrossRef]
- Zoccatelli, D.; Borga, M.; Chirico, G.B.; Nikolopoulos, E. The relative role of hillslope and river network routing in the hydrologic response to spatially variable rainfall fields. J. Hydrol. 2015, 531, 349–359. [Google Scholar] [CrossRef]
- Perron, J.T.; Richardson, P.W.; Ferrier, K.L.; Lapotre, M. The root of branching river networks. Nature 2012, 492, 100–103. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Sun, T. A stochastic model for the formation of channel networks in tidal marshes. Geophys. Res. Lett. 2004, 31, L21503. [Google Scholar] [CrossRef]
- Dodds, P.S.; Rothman, D.H. Geometry of river networks. III. Characterization of component connectivity. Phys. Rev. E 2001, 63, 016117. [Google Scholar] [CrossRef]
- Terui, A.; Ishiyama, N.; Urabe, H.; Ono, S.; Finlay, J.C.; Nakamura, F. Metapopulation stability in branching river networks. Proc. Natl. Acad. Sci. USA 2018, 115, E5963–E5969. [Google Scholar] [CrossRef]
- Mantilla, R. Physical Basis of Statistical Scaling in Peak Flows and Stream Flow Hydrographs for Topologic and Spatially Embedded Random Self-similar Channel Networks. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 2012. [Google Scholar]
- Mantilla, R.; Gupta, V.K.; Troutman, B.M. Scaling of peak flows with constant flow velocity in random self-similar networks. Nonlinear Process. Geophys. 2011, 18, 489–502. [Google Scholar] [CrossRef]
- Gupta, V.K.; Mantilla, R.; Troutman, B.M.; Dawdy, D.; Krajewski, W.F. Generalizing a nonlinear geophysical flood theory to medium-sized river networks. Geophys. Res. Lett. 2010, 37, L11402. [Google Scholar] [CrossRef]
- Mandapaka, P.V.; Krajewski, W.F.; Mantilla, R.; Gupta, V.K. Dissecting the effect of rainfall variability on the statistical structure of peak flows. Adv. Water Resour. 2009, 32, 1508–1525. [Google Scholar] [CrossRef]
- Leopold, L.B.; Langbein, W.B. The Concept of Entropy in Landscape Evolution; US Geological Survey Professional Paper 500A; US Government Printing Office: Washington, DC, USA, 1962.
- Abrahams, A.D. Channel networks—A geomorphological perspective. Water Resour. Res. 1984, 20, 161–188. [Google Scholar] [CrossRef]
- Karlinger, M.R.; Troutman, B.M. A random spatial network model based on elementary postulates. Water Resour. Res. 1989, 25, 793–798. [Google Scholar] [CrossRef]
- Troutman, B.M.; Karlinger, M.R. Gibbs distribution on drainage networks. Water Resour. Res. 1992, 28, 563–577. [Google Scholar] [CrossRef]
- Kindermann, R.; Snell, J.L. Markov Random Fields and Their Applications; American Mathematical Society: Providence, RI, USA, 1980. [Google Scholar]
- Scheidegger, A.E. A stochastic model for drainage patterns into an intramontane trench. Int. Assoc. Sci. Hydrol. Bull. 1967, 12, 15–20. [Google Scholar] [CrossRef]
- Karlinger, M.R.; Troutman, B.M. Fat fractal scaling of drainage networks from a random spatial network model. Water Resour. Res. 1992, 28, 1975–1981. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Valdes, J.B. Geomorphologic structure of hydrologic response. Water Resour. Res. 1979, 15, 1409–1420. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E. On the formulation of an analytical approach to hydrologic response and similarity at the basin scale. J. Hydrol. 1983, 65, 95–123. [Google Scholar] [CrossRef]
- Seo, Y.; Schmidt, A.R. Application of Gibbs’ model to urban drainage networks: A case study in southwestern Chicago, USA. Hydrol. Process. 2014, 28, 1148–1158. [Google Scholar] [CrossRef]
- Seo, Y.; Schmidt, A.R. The effect of rainstorm movement on urban drainage network runoff hydrographs. Hydrol. Process. 2012, 26, 3830–3841. [Google Scholar] [CrossRef]
- Seo, Y.; Hwang, J.; Noh, S.J. Analysis of Urban Drainage Networks Using Gibbs’ Model: A Case Study in Seoul, South Korea. Water 2015, 7, 4129–4143. [Google Scholar] [CrossRef]
- Semadeni-Davies, A.; Hernebring, C.; Svensson, G.; Gustafsson, L.-G. The impacts of climate change and urbanisation on drainage in Helsingborg, Sweden: Suburban stormwater. J. Hydrol. 2008, 350, 114–125. [Google Scholar] [CrossRef]
- Willems, P.; Olsson, J.; Arnbjerg-Nielsen, K.; Beecham, S.; Pathirana, A.; Gregersen, I.B.; Madsen, H.; Nguyen, V.T.V. Impacts of Climate Change on Rainfall Extremes and Urban Drainage Systems; IWA Publishing: London, UK, 2012. [Google Scholar]
- Seo, Y.; Park, S.Y.; Schmidt, A.R. Implication of the flow resistance formulae on the prediction of flood wave propagation. Hydrol. Sci. J. 2016, 61, 683–695. [Google Scholar] [CrossRef]
- Moussa, R. What controls the width function shape, and can it be used for channel network comparison and regionalization? Water Resour. Res. 2008, 44, W0845. [Google Scholar] [CrossRef]
- Seo, Y.; Choi, N.J.; Schmidt, A.R. Contribution of directly connected and isolated impervious areas to urban drainage network hydrographs. Hydrol. Earth Syst. Sci. 2013, 17, 3473–3483. [Google Scholar] [CrossRef]
- Van de Nes, T.J. Linear Analysis of a Physically Based Model of a Distributed Surface Runoff System; Wageningen University and Research: Wageningen, The Netherlands, 1973. [Google Scholar]
- Lashermes, B.; Foufoula-Georgiou, E.; Dietrich, W.E. Channel network extraction from high resolution topography using wavelets. Geophys. Res. Lett. 2007, 34, L23S04. [Google Scholar] [CrossRef]
- Lee, M.T.; Delleur, J.W. A variable source area model of the rainfall-runoff process based on the Watershed Stream Network. Water Resour. Res. 1976, 12, 1029–1036. [Google Scholar] [CrossRef]
- Seo, Y.; Schmidt, A.R. Network configuration and hydrograph sensitivity to storm kinematics. Water Resour. Res. 2013, 49, 1812–1827. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E.; Wang, C.T. A representation of an instantaneous unit-hydrograph from geomorphology. Water Resour. Res. 1980, 16, 855–862. [Google Scholar] [CrossRef]
- Naden, P.S. Spatial variability in flood estimation for large catchments—The exploitation of channel network structure. Hydrol. Sci. J.-J. Des. Sci. Hydrol. 1992, 37, 53–71. [Google Scholar] [CrossRef]
- Franchini, M.; OConnell, P.E. An analysis of the dynamic component of the geomorphologic instantaneous unit hydrograph. J. Hydrol. 1996, 175, 407–428. [Google Scholar] [CrossRef]
- Da Ros, D.; Borga, M. Use of digital elevation model data for the derivation of the geomorphological instantaneous unit hydrograph. Hydrol. Process. 1997, 11, 13–33. [Google Scholar] [CrossRef]





| Subcatchment | β | Nash–Sutcliffe Efficiency (E) | ||
|---|---|---|---|---|
| 4D | 8D | 4D | 8D | |
| Shinweol1 | 10−1 | 101 | 0.852 | 0.934 |
| Shinweol2 | 103 | 103 | 0.546 | 0.785 |
| Shinweol3-1 | 10−3 | 101 | 0.799 | 0.804 |
| Shinweol3-2 | 10−1 | 10−2 | 0.931 | 0.935 |
| Mokdong2 | 10−2 | 10−3 | 0.682 | 0.674 |
| Hwagok2 | 10−3 | 10−3 | 0.889 | 0.932 |
| Mokdong3 | 103 | 103 | 0.836 | 0.933 |
| Shinjeong_highland | 10−4 | 10−3 | 0.544 | 0.503 |
| Gochuk2 | 101 | 102 | 0.735 | 0.879 |
| Flow Directions | Gage Station 1 | Gage Station 2 | ||
|---|---|---|---|---|
| 2 July 2013 | 12 July 2013 | 2 July 2013 | 12 July 2013 | |
| 4D | 0.83 | 0.84 | 0.84 | 0.68 |
| 8D | 0.83 | 0.84 | 0.89 | 0.75 |
| SWMM | 0.81 | 0.83 | 0.87 | 0.78 |
| Flow Directions | Gage Station 1 | Gage Station 2 | ||
|---|---|---|---|---|
| 2 July 2013 | 12 July 2013 | 2 July 2013 | 12 July 2013 | |
| 4D | 9.38 | 14.85 | 14.75 | 22.06 |
| 8D | 9.83 | 15.19 | 16.41 | 24.29 |
| SWMM | 11.19 | 17.38 | 16.43 | 24.66 |
| Observed | 8.13 | 16.28 | 17.51 | 29.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, Y.; Hwang, J.; Woo, D.K. Assessment of Drainage Network Configuration Using Gibbs’ Model with Increased Number of Flow Directions. Water 2024, 16, 3442. https://doi.org/10.3390/w16233442
Seo Y, Hwang J, Woo DK. Assessment of Drainage Network Configuration Using Gibbs’ Model with Increased Number of Flow Directions. Water. 2024; 16(23):3442. https://doi.org/10.3390/w16233442
Chicago/Turabian StyleSeo, Yongwon, Junshik Hwang, and Dong Kook Woo. 2024. "Assessment of Drainage Network Configuration Using Gibbs’ Model with Increased Number of Flow Directions" Water 16, no. 23: 3442. https://doi.org/10.3390/w16233442
APA StyleSeo, Y., Hwang, J., & Woo, D. K. (2024). Assessment of Drainage Network Configuration Using Gibbs’ Model with Increased Number of Flow Directions. Water, 16(23), 3442. https://doi.org/10.3390/w16233442







