Abstract
This study aims to detect changes in rainfall variability caused by climate change for various scenarios in the CMIP6 (Coupled Model Intercomparison Project Phase 6) multi-model ensemble. Projected changes in rainfall unevenness in terms of different timescale indices using three categories, namely WD50 (number of wettest days for half annual rainfall), SI (seasonality index), and DWR (ratio of dry-season to wet-season rainfall) are analyzed in Zengwen Reservoir watershed, southern Taiwan over near future (2021–2040) and midterm future (2041–2060) relative to the baseline period (1995–2014) under SSP2-4.5 and SSP5-8.5 scenarios. The projected rainfall for both baseline and future periods is derived from 25 GCMs (global climate models). The results indicate that noticeably deteriorated rainfall unevenness is projected in the Zengwen Reservoir watershed over future periods, which include decreased WD50, increased SI, and decreased DWR. Though there were noticeable differences in the rainfall projections by the different GCMs, the overall consensus reveals that uncertainties in future rainfall should not be ignored. In addition, WD50 has the greatest deviated relative change in mean, which implies that the short-timescale rainfall unevenness index is easily affected by climate change in the study area. Distributional changes in rainfall unevenness determined by simultaneously considering alterations in relative changes in mean and standard deviation indicated that there was no single dominant category. However, the top two categories, with summed frequencies exceeding 0.5, characterize different properties of rainfall unevenness indices. The top two categories of WD50 and SI commonly have decreased mean and increased mean, respectively, but nearly equal frequencies of the top two categories in DWR exhibit opposite variations. The proposed rainfall unevenness change detection approach provides a better understanding of the impacts of climate change on rainfall unevenness, which is useful for preparing adaptive mitigation measures for coping with disasters induced by climate change.
1. Introduction
There is increasing evidence that anthropogenic warming has induced modification of the global hydrologic cycle, which has been revealed and documented in many studies [1,2,3,4,5,6]. Significant alterations in rainfall spatiotemporal variability, as well as the magnitude and frequency of rainfall extremes caused by such intensification, have far-reaching impacts on human socioeconomic activities and natural systems. Quantifying how climate change would affect rainfall regimes is receiving growing concerns and has become a top priority in water resources planning and management over recent decades, since altered rainfall regimes threaten future water availability.
ETCCDI (Expert Team on Climate Change Detection and Indices) [7] is a popular approach to assess changes in rainfall regimes based on daily rainfall data. The ETCCDI indices are not only used in assessing global/regional variations in historical rainfall data [8,9,10,11,12,13,14,15] but also in evaluating future climate projections [16,17,18,19,20,21,22,23]. The increasing magnitude and frequency of rainfall extremes lead to further exacerbation of daily rainfall unevenness. However, quantifying changes in daily rainfall unevenness with global warming is seldom addressed in the literature until recently [24]. Chen (2020) [25] provided detailed reviews of the measures of rainfall unevenness. For example, the Gini and Schutz indices, widely used indices for measuring income inequality, have been used as measures to evaluate rainfall unevenness based on hourly/daily rainfall data [26,27,28,29]. Rajah et al. (2014) [26] also developed the wet-day Gini index to measure uneven rainfall spreads across the wet days during a year. Another newly developed daily rainfall-based measure to assess rainfall unevenness is to calculate the number of wettest days that constitute half of the annual total rainfall [24]. This measure has gained popularity in characterizing rainfall unevenness in observed/projection rainfall and regional/global scales [24,25,30,31,32,33].
Taiwan approximately ranges between 21.9°–25.3° N and 120°–122° E (the western edge of the Pacific Ocean) and is characterized by prevalent monsoon climate and summer tropical cyclones. The average annual rainfall of nearly 2500 mm, but with high spatiotemporal fluctuation, is received in this 36,000 km2 island, which results in Taiwan being vulnerable to frequent floods and droughts. The way in which climate change would affect the magnitude and frequency of such natural hazards. How climate change affects the magnitude and frequency of climatic extremes is of increasing concern recently since it may worsen flooding and drought problems in the future. In this regard, a number of studies have been conducted in the past. For example, Huang et al. (2012) [34] investigated the impacts of climate change on frequencies of the maximum consecutive dry days and maximum 1-, 2-, and 3-day rainfall under scenario A1B. Tung et al. (2016) [35] evaluated projected changes in the annual daily maximum precipitation over Taiwan using 16 CMIP5 models under scenarios RCP4.5 and RCP8.5. Chen et al. (2021) [36] assessed the changes in rainfall intensity-duration-frequency characteristics of 21 stations in Taiwan under scenarios RCP2.6 and RCP8.5. Tung et al. (2022) [37] used nine ETCCDI indices to evaluate long-term trends of rainfall extremes using 1960–2017 daily gridded rainfall data in Taiwan. These previous studies all focus on rainfall extremes in Taiwan since damaging catastrophes have frequently occurred in the past. Projected changes in rainfall unevenness are rarely addressed in Taiwan. The main aim of this study is thus to investigate projected changes in rainfall unevenness in southern Taiwan under climate change. Different timescales (daily, monthly, and semi-annual) indices are adopted to evaluate changes in rainfall unevenness under climate change in the Zengwen Reservoir watershed located in southern Taiwan. Two scenarios (SSP2-4.5 and SSP5-8.5) of the CMIP6 (Coupled Model Intercomparison Project Phase 6) multi-model ensemble over the near future (2021–2040) and midterm future (2041–2060) are used to evaluate climate change’s impacts on rainfall unevenness in this study.
The rest of this study is organized as follows. Section 2 briefly introduces the used data and methods, which include the study area of Zengwen Reservoir watershed, daily gridded rainfall data from 25 CMIP6 GCMs (global climate models), rainfall unevenness indices, and a simplified method used to evaluate distributional changes in rainfall indices. Results of the projected changes in rainfall unevenness indices for future periods under various scenarios are presented in Section 3, which is followed by Section 4 outlining conclusions.
2. Data and Methods
2.1. Study Area
The largest alluvial plain (Chianan Plain) and the second high-tech industrial district (Southern Taiwan Science Park), located in southern Taiwan, lead to flourishing agricultural and blooming industrial activities in this region. Stable water supplies to maintain socioeconomic activities in this region heavily depend on reservoirs to regulate the highly fluctuating streamflow. Zengwen Reservoir, with the greatest capacity of 506.1 × 106 m3 (measured in 2023) in Taiwan, is the most important water resources facility in this region for supplying domestic, agricultural, and industrial water requirements. Finished in 1973, the initial design purpose of Zengwen Reservoir was to increase irrigation water supplies for the Chianan Plain through the joint operation of the nearby Wushantou Reservoir. With rapid population growth and the development of high-tech industrial districts in this region, water competition between agricultural and industrial water demands has become intense recently. Although a new Nanhua Reservoir was built in 1982 to expand domestic and industrial water supply capability, water shortage problems in this region have been frequently met in the past decades. In addition, newly planned industrial districts in the near future would further stress water supply problems. Evaluating reservoir yields under climate change in the future receives growing concern and ranks as a top priority in water resources planning and management.
Several recent studies [38,39,40,41] thus explore the impacts of climate change on rainfall and hydrologic characteristics, water resources, and flooding risk in the Zengwen Reservoir watershed. The location of Zengwen Reservoir associated with its watershed is shown in Figure 1. Spatially averaged daily rainfall in the watershed of Zengwen Reservoir is evaluated to detect projected changes in rainfall unevenness under various emission scenarios.
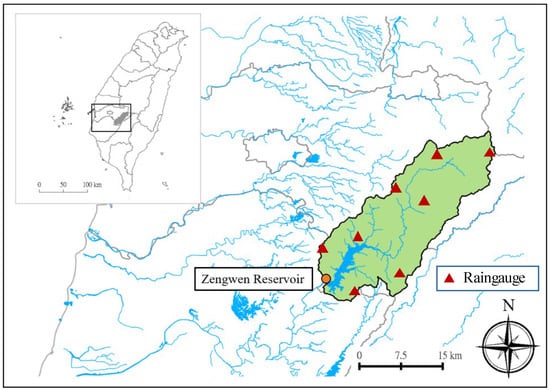
Figure 1.
Location of Zengwen Reservoir and its watershed in southern Taiwan.
2.2. Climate Models and Scenarios
Data used in this study comprise daily rainfall for a baseline period from 1995 to 2014 and also from projections for the near future (2021 to 2040) and midterm future (2041 to 2060) using projections from 25 GCMs [32,42], which are listed in Table 1. Many studies [16,43,44] indicated that a multi-model ensemble outperforms a single model and is an efficient approach to reducing model-specific uncertainties [45,46,47,48,49]. Daily simulated rainfall data from 25 CMIP6 GCMs for various scenarios are considered in this study in order to reduce model-specific uncertainties. Due to the coarse resolution used in GCMs, the daily rainfall used in this study is statistically downscaled and bias-corrected by the TCCIP (Taiwan Climate Change Projection Information and Adaptation Knowledge Platform) [50]. The retrieved daily rainfall data are grid-based data with a spatial resolution of 5 km × 5 km. The spatial mean daily rainfall series of Zengwen Reservoir serves as a basis for analyzing the impacts of climate change on rainfall unevenness.

Table 1.
The 25 CMIP6 GCMs used in this study.
The new scenarios in CMIP6 integrate the shared socioeconomic pathways (SSPs) [51,52] and forcing levels of the representative concentration pathways (RCPs) [53] to better address the impacts of climate policies [54]. Two scenarios, including SSP2-4.5 and SSP5-8.5 from Tier 1 scenarios [55], are used in this study to evaluate climate change-induced projected alterations on rainfall unevenness for near future (NF) of 2021–2040 and midterm future (MF) of 2041–2060 relative to the baseline (BL) period of 1995–2014 in southern Taiwan. The grid-based rainfall data from the period 1995–2014 are also simulated using GCMs. That is, the rainfall in the baseline period used as a reference may not be exactly the same as the actual measured rainfall. The obtained rainfall unevenness based on simulated rainfall is, therefore, different from the actual measured data-derived indices.
2.3. Rainfall Unevenness Indices
Projected changes in rainfall unevenness caused by climate change in the Zengwen Reservoir watershed are evaluated at three temporal scales: daily, monthly, and semi-annual rainfalls. The daily timescale rainfall unevenness index considered in this study is the number of wettest days that constitute half of annual total rainfall WD50 [24] or the wet days for the top 50% of annual rainfall [31]. This daily rainfall unevenness index is denoted as WD50 [33] in this study and calculated as
where R(i) denotes the ith greatest daily rainfall in descending rainfall series within a year; PRCPTOT is the annual total wet-day rainfall. The threshold to distinguish a wet (or rain) day and a dry day in this study is 1 mm per day.
Determining values of WD50 starts by sorting the daily rainfall series from wettest to driest and then counting the number of wet days with cumulative rainfall exceeding half of the annual total rainfall for each year. The smaller WD50 indicates a higher degree of unevenness of daily rainfall.
The seasonality index (SI) [56,57] is used to assess rainfall unevenness at a monthly timescale, which is calculated as
where Rj denotes the monthly rainfall in month j, j = 1, 2, …, 12. The values of SI range between 0 (complete uniformity of equal rainfall in all months) and 1.83 (maximum disparity of total annual rainfall occurred in one month). Thus, the greater the SI, the greater the uneven distribution of monthly rainfall.
The half-year timescale-rainfall-unevenness index used in this study is the ratio of dry-season rainfall to wet-season rainfall, denoted as DWR, and calculated as
where PRCPWS (precipitation in the wet season) and PRCPDS (precipitation in the dry season) represent wet-season (May–October) and dry-season (January–April and November–December) rainfall, respectively. The values of DWR range between 0 (no rainfall in the dry season) to 100% (equal rainfall in wet and dry seasons). The smaller the DWR, the greater the uneven semi-annual rainfall distribution. The DWR > 100% represents dry-season rainfall exceeding wet-season rainfall, which is not considered in this study because of reversed wet and dry seasons.
2.4. Measures of Rainfall Variability Changes
The proposed three rainfall unevenness indices are calculated each year over the baseline period (1995–2014) and two future periods (2021–2040 and 2041–2060) under two emission scenarios for 25 GCMs. The temporal mean over each 20-year period is then served as a basis to evaluate climate change impacts on rainfall unevenness. Changes in temporal means of rainfall indices for two future periods relative to those in the baseline period are expressed as the relative change in rainfall indices [23], which is calculated as
where RIf and RIb denote the statistical properties of 20 years for each rainfall unevenness index in the future and baseline periods, respectively.
This relative change measure is used to evaluate alterations in mean and standard deviation of future 20-year periods for each rainfall unevenness index, which are denoted as RCM (relative changes of mean) and RCSD (relative change of standard deviation), respectively. Changes in RCM represent a shift of the center of the rainfall unevenness distribution. Positive and negative RCMs reveal increased and decreased means or right-shifted and left-shifted distributions, respectively. On the other hand, changes in RCSD denote variation in the dispersion within the distribution. Positive and negative RCSDs denote increased and decreased standard deviations or flattened and sharpened distributions, respectively. Simultaneous changes in RCM and RCSD reveal projected distributional changes in rainfall unevenness for the future periods relative to the baseline periods under climate change. In order to systematically summarize distributional changes in rainfall unevenness, a simplified nine-category distributional changes, proposed by Shiau and Huang (2015) [58], is used if changes in RCM and RCSD are categorized into increase, no change, and decrease. The absolute values of RCM and RCSD are less than 1%, representing minor alterations, and are considered as no changes in RCM and RCSD in this study. This qualitative description of shift and shape changes in distributions, summarized in Table 2, can comprehensively evaluate differences in distributions between future and baseline periods of proposed rainfall unevenness indices.

Table 2.
Summaries of nine-category distributional changes.
3. Results and Discussion
3.1. Relative Changes of Means for Rainfall Unevenness
Figure 2 illustrates the box plots associated with the 20-year temporal means (red nods) of 25 GCMs for three rainfall unevenness indices over the baseline period (BL: 1995–2014) and future periods (NF: 2021–2040 and MF: 2041–2060) under scenarios SSP2-4.5 and SSP5-8.5 in Zengwen Reservoir watershed, southern Taiwan. Diverse variations among 25 GCMs are observed for these three rainfall unevenness indices in Figure 2. For simplicity, the following description thus focuses on the 20-year temporal means of each GCM. Figure 2a shows greater percentages of decreased WD50 in MF (76% and 72%) than those in NF (56% and 60%) for SSP2-4.5 and SSP5-8.5, respectively. The ensemble mean of 25 GCMs for WD50 is 11.3 days in BL and becomes 10.8 days under both scenarios in NF and 10.8 and 10.7 days for SSP2-4.5 and SSP5-8.5 in MF, respectively. The decline in WD50s over future periods reveals that more daily rainfall extremes are projected in the future, which is approximately short of 0.5–0.6 days, to reach half of the annual total rainfall.
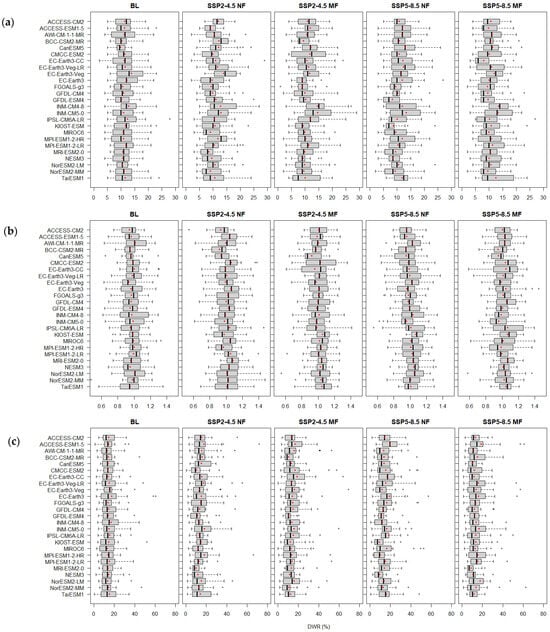
Figure 2.
Box plots of (a) WD50, (b) SI, and (c) DWR of 25 GCMs over the baseline period (1995–2014) and future periods (NF: 2021–2040 and MF: 2041–2060) under scenarios SSP2-4.5 and SSP5-8.5.
The inherently uneven monthly rainfall distribution in southern Taiwan leads to high SI in BL and becomes greater in NF and MF. For example, the ensemble mean of 25 GCMs for SI is 0.97 in BL (Figure 2b). Slightly increased SIs are observed when time evolves into future periods. The SIs of 1.01 and 1.00 in NF and 1.01 and 1.02 in MF for SSP2-4.5 and SSP5-8.5 are noted, respectively. In addition, consistent variations in increased trend among 25 GCMs are observed in NF and MF. For instance, 72% and 84% of GCMs have increased SIs for SSP2-4.5 and SSP5-8.5 in NF and 88% and 84% for SSP2-4.5 and SSP5-8.5 in MF, respectively. Figure 3 shows the monthly rainfall distributions in BL, NF, and MF under scenarios SSP2-4.5 and SSP5-8.5. Clearly, worse unevenness is observed in NF and MF due to noticeably increased PRCPWS (approximately 3.8% increase relative to BL) when compared to the nearly unchanged PRCPDS with a relative change of −0.2%. This phenomenon is in line with the decline in WD50, which shows that more extreme daily rainfall occurs in wet seasons.
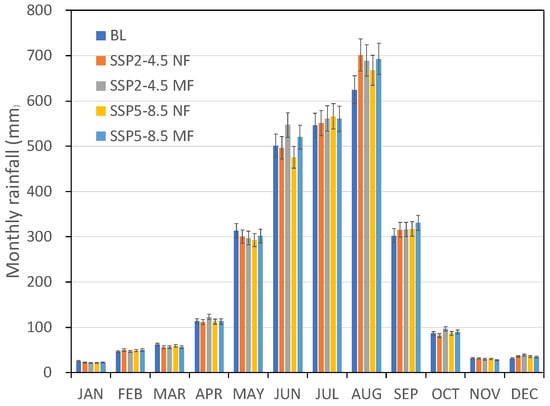
Figure 3.
Monthly rainfall distribution in baseline periods (BL: 1995–2014) and future periods (NF: 2021–2040 and MF: 2041–2060) under scenarios SSP2-4.5 and SSP5-8.5.
Half of GCMs (52%) exhibit slightly declined DWR (Figure 2c) from BL to NF for both scenarios. The percentages of declined DWRs become 64% and 72% from BL to MF for SSP2-4.5 and SSP5-8.5, respectively. The ensemble mean for DWR is 14.9% in BL and decreases to 14.6% and 14.4% under SSP2-4.5 and SSP5-8.5 in NF and 14.1% and 13.8% under SSP2-4.5 and SSP5-8.5 in MF, respectively. Noticeably increased wet-season rainfall in future periods (Figure 3) not only results in higher SI but also leads to lower DWR in NF and MF. However, diverse variations among GCMs indicate that certain percentages of GCMs exhibit increased DWR, although the ensemble means show a declining trend. For example, 48% and 52% of GCMs have increased and decreased DWR from BL to NF for both scenarios, respectively, and mean DWRs are 14.9% and 14.6% in BL and NF, respectively.
Figure 4 illustrates the box plots of RCM of 25 GCMs for three rainfall unevenness indices in NF and MF under SSP2-4.5 and SSP5-8.5. Diverse RCMs, from negative to positive, are observed among 25 GCMs for all rainfall indices. However, the ensemble means of 25 GCMs show a consistent trend over future periods for these rainfall indices. That is, the decreased RCMs of WD50 and DWR associated with the increased RCM of SI reveal that rainfall variability becomes pronounced over future periods, especially in MF. For example, WD50s have decreased RCMs in NF and MF, and the least RCM of −5.1% was estimated in MF under SSP5-8.5. DWRs also have declined RCMs in NF and MF. Reduced RCMs of −4.0% and −5.9% are noted in MF for SSP2-4.5 and SSP5-8.5, respectively. Positive RCMs of SIs represent more uneven monthly rainfall distribution over future periods, and the greatest value of 4.8 is noted under SSP5-8.5 in MF.
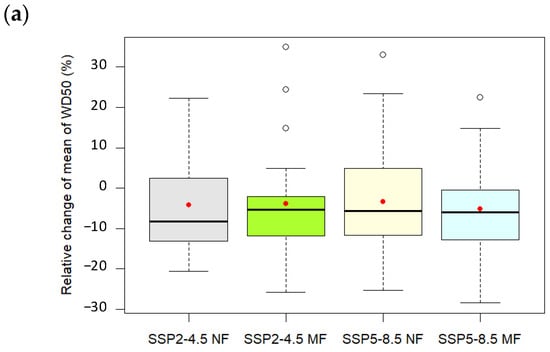
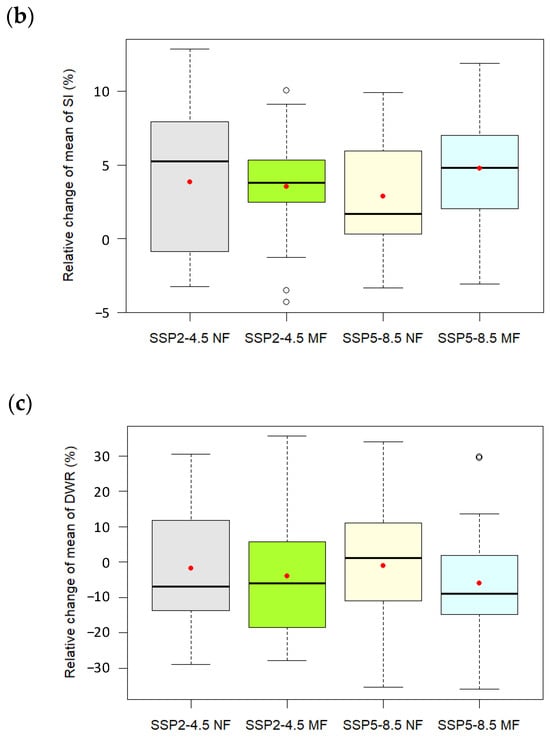
Figure 4.
Box plots of RCMs of (a) WD50, (b) SI, and (c) DWR for future periods (NF: 2021–2040 and MF: 2041–2060) under scenarios SSP2-4.5 and SSP5-8.5. The red dot indicates the mean value.
3.2. Relative Changes of Standard Deviations and Distributional Changes for Rainfall Unevenness
The increased interquartile range of each GCM from BL to NF and MF for three rainfall indices, shown in Figure 2, reveals that greater standard deviations of rainfall unevenness are projected over future periods. That is, values of rainfall unevenness indices spread greater ranges in NF and MF than those in BL. For instance, the ensemble mean of the standard deviation of WD50 is 4.34 days and then increases to 4.48 and 4.55 days in NF and 4.55 and 4.63 days in MF under SSP2-4.5 and SSP5-8.5, respectively.
The box plots of RCSD of 25 GCMs over NF and MF under scenarios SSP2-4.5 and SSP5-8.5 for three rainfall unevenness indices are shown in Figure 5. The values of RCSDs also spread from negative to positive and have much greater ranges than those of RCMs. This phenomenon indicates that significant dispersion in rainfall unevenness distributions caused by climate change should not be ignored over future periods. Positive deviated RMSDs prevalent in WD50 and DWR lead to greater ensemble means of RCSD for WD50 (7.7%–10.8%) and DWR (9.9%–16.1%) in NF and MF. The ensemble mean of RCSD for SI is offset by positive and negative deviated RMSDs and results in a near-zero ensemble mean of RCSD (−0.8% to 4.4%) over future periods.
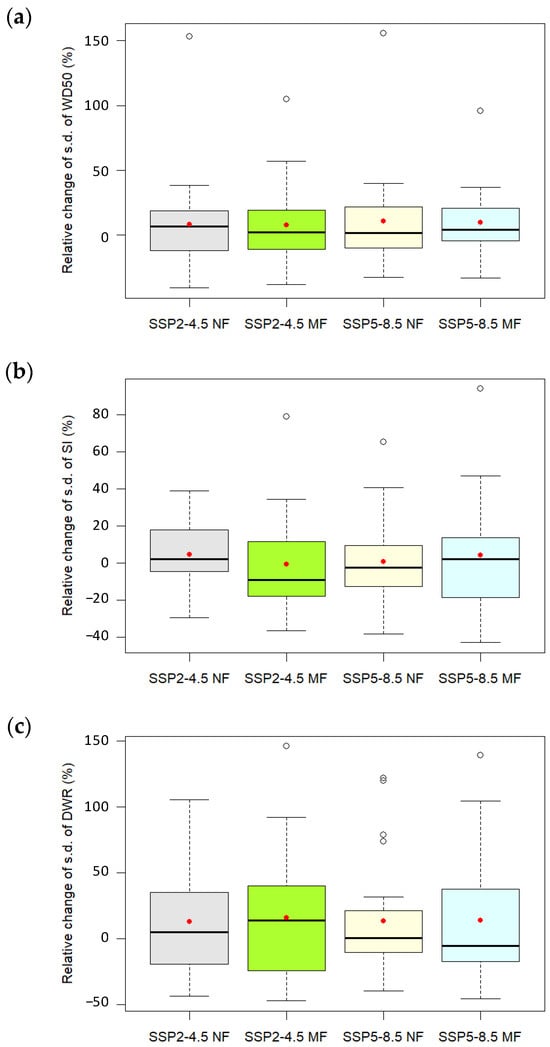
Figure 5.
Box plots of RCSDs of (a) WD50, (b) SI, and (c) DWR for future periods (NF: 2021–2040 and MF: 2041–2060) under scenarios SSP2-4.5 and SSP5-8.5. The red dot indicates the mean value.
Figure 6a–c shows the histograms of WD50, SI, and DWR for BL, NF, and MF under scenarios SSP2-4.5 and SSP5-8.5, which are outcomes of MIROC6, EC-Earth3-CC, and INM-CM5-0, respectively. These histograms clearly demonstrate that alterations in rainfall unevenness include not only changes in mean but also changes in distribution. Using the histogram in BL as the reference, Figure 6a shows that the histograms of WD50 over NF and MF under two scenarios all have negative-shifted means and narrower ranges (standard deviation). The SI histograms in NF under two scenarios (Figure 6b) have a negative-shifted mean and greater range relative to the histogram in BL. However, SI histograms in MF have different variations, with a negative-shifted mean and narrower range for SSP2-4.5 and a positive-shifted mean and greater range for SSP5-8.5. The DWR histograms in NF and MF under two scenarios (Figure 6c) demonstrate a positive-shifted mean and greater range.
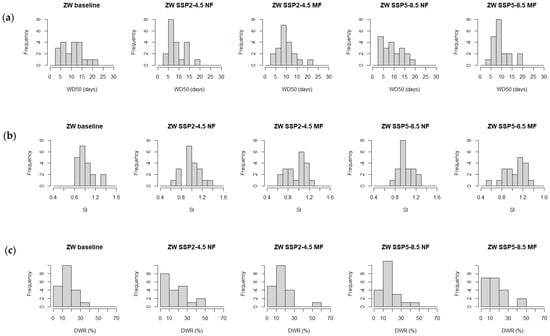
Figure 6.
Histograms of (a) DWR of INM-CM5-0, (b) SI of EC-Earth3-CC, and (c) WD50 of MIROC6 over BL and NF and MF under SSP2-4.5 and SSP5-8.5.
Figure 6 reveals diverse distributional changes in various rainfall unevenness indices, GCMs, future periods, and emission scenarios. In order to systematically assess climate change-induced distributional changes in rainfall unevenness, the simplified nine-category distributional changes proposed by Shiau and Huang (2015) [58] (summarized in Table 2) is adopted in this study. This approach simultaneously considers RCM and RCSD in NF and MF for various scenarios relative to the RCM and RCSD in BL. Table 3 reports the frequencies of nine categories for 25 GCMs with various future periods and scenarios. No single dominant category is observed for these three rainfall unevenness indices because of diverse distributional changes existing among GCMs. However, the top two categories in each index not only have frequencies exceeding 0.5 but also characterize differences among the three rainfall unevenness indices. Categories I and VII are the top two categories for WD50 with summed frequencies of 0.56 and 0.76 in NF and 0.56 and 0.60 in MF for SSP2-4.5 and SSP5-8.5, respectively. The top two categories for SI are III and IX, which have summed frequencies of 0.52 and 0.76 in NF and 0.68 and 0.76 in MF for SSP2-4.5 and SSP5-8.5, respectively. The summed frequencies of categories I and IX for DWR are 0.64 and 0.68 in NF and 0.72 and 0.72 in MF for SSP2-4.5 and SSP5-8.5, respectively.

Table 3.
Frequencies of distributional change category for rainfall indices.
These top two categories in each index reflect different characteristics of changes in rainfall unevenness. For example, WD50 has the top two categories of I (decreased RCM and decreased RCSD) and VII (decreased RCM and RCSD), which have decreased mean in common. Categories III (increased RCM and decreased RCSD) and IX (increased RCM and increased RCSD) are the top two categories for SI and have commonly increased mean. However, the top two categories of DWR, categories I (decreased RCM and decreased RCSD) and IX (increased RCM and increased RCSD), have totally different variations. Differences in frequency between categories I (0.36) and IX (0.33) are not significant, which implies that opposite variations (increased RCM vs. decreased RCM and increased RCSD vs. decreased RCSD) are equally likely in DWR.
3.3. Discussion
The above multiple temporal scales rainfall unevenness analyses reveal that rainfall variability would become pronounced in the Zengwen Reservoir watershed for future rainfall projection. Projected alterations in rainfall unevenness in the Zengwen Reservoir watershed can be generally summarized as decreased WD50, increased SI, and decreased DWR, although opposite variations are also noted among GCMs. Close relationships among these three rainfall unevenness indices are also detected. Decreased WD50 indicates that more daily rainfall extremes occur in wet-season months for future periods, which leads to more uneven monthly rainfall distribution. Increased wet-season rainfall results in increased SI and then decreases DWR.
Based on mean RCMs of various future periods and scenarios, the WD50 has the greatest deviated RCM of 4.16% (absolute mean of −4.26%, −3.40%, −3.83%, and −5.13% for SSP2-4.5 and SSP5-8.5 in NF and MF), then followed the SI of 3.76% (mean of 3.86%, 2.89%, 3.52%, and 4.77%), and the DWR has the least deviated RCM of 3.19% (absolute mean of −1.83%, −1.06%, −3.95%, and −5.93%). This phenomenon implies that the rainfall unevenness index with a shorter temporal scale is easily affected by climate change in the Zengwen Reservoir watershed. In addition, WD50 and SI have consistent variations between various periods and scenarios. In contrast, DWR has greater deviated RCMs in MF (−3. 95% and −5.93%) than those in NF (−1.83% and −1.06%).
Noticeably deteriorated rainfall unevenness is projected over future periods in the Zengwen Reservoir watershed. A special situation of wetter wet seasons and drier dry seasons caused by climate change receives growing concerns in southern Taiwan since it possibly induces frequent flooding in wet seasons and limited water availability in dry seasons. Decreased DWR associated with increased SI detected in the Zengwen Reservoir watershed may not provide sufficient information to answer whether wetter wet seasons and drier dry seasons occur in this watershed.
Variations of PRCPWS and PRCPDS in a GCM can be classified into four types, i.e., increased PRCPWS and increased PRCPDS, increased PRCPWS and decreased PRCPDS, decreased PRCPWS and increased PRCPDS, and decreased PRCPWS and decreased PRCPDS. Table 4 reports the relative frequencies of these four types of PRCPWS–PRCPDS variations for various scenarios and periods. Some specific properties of frequencies for various types are observed in Table 4. For example, the frequency of increased PRCPWS and increased PRCPDS is highest in scenario SSP2-4.5 MF (0.44), the frequency of decreased PRCPWS and decreased PRCPDS is highest in scenario SSP5-8.5 NF (0.48), and lower frequencies of decreased PRCPWS and increased PRCPDS are noted in both scenarios and periods (0.04–0.20).

Table 4.
Frequencies of different categories of variations in PRCPWS and PRCPDS for various scenarios and periods.
The combined frequencies of future periods and scenarios indicate that the frequency of increased PRCPWS and decreased PRCPDS rank third (0.25) since it is lower than those of increased PRCPWS and increased PRCPDS (0.31) and decreased PRCPWS and decreased PRCPDS (0.31). This fact implies that the wetter wet season and drier dry season (increased PRCPWS and decreased PRCPDS) are not prevalent in the Zengwen Reservoir watershed. It is worth noting that there are minor differences in frequencies between increased PRCPWS and decreased PRCPDS and the other top two types. This phenomenon indicates that diverse PRCPWS–PRCPDS variations existed in the Zengwen Reservoir watershed.
Although no similar studies for detecting changes in rainfall unevenness in Taiwan induced by climate change are conducted in the literature, similar findings about the impacts of climate change on rainfall characteristics over Taiwan are observed between previous studies and this work. For instance, Huang et al. (2012) [30] indicated that increased 1- and 2-day rainfalls over the future (2080–2099) will be observed in southern Taiwan based on five GCMs under the A1B scenario. Tung et al. (2016) [31] indicated that the annual daily maximum precipitation would increase by 10% by 2065 and 14% at the end of the 21st century using 16 CMIP5 GCMs under the RCP8.5 scenario. Chen et al. (2021) [36] concluded that projected rainfall intensities of 24-h duration increase in southern Taiwan using two RCPs (RCP2.6 and RCP8.5) and five GCMs. Increased short durations, such as 1–2 days of extreme rainfall, would reduce WD50, which is in line with the results of this study. In addition, Li et al. (2020) [59] suggested that rainfall tends to increase in winter and decrease in summer in the future based on three GCMs under scenarios A1B, A2, and B1. Although decreased PRCPWS and increased PRCPDS are not prevalent in the Zengwen Reservoir watershed, the low probability of 0.13 reveals that it is possible to occur in this situation in the future. Huang et al. (2019) [60] showed that future extreme precipitation during Mei-Yu seasons (May and June) is projected to become more frequent and intense over western Taiwan under the RCP8.5 scenario. Chang et al. (2022) [61] showed that 24- and 48-h rainfall with a 100-year recurrence interval is expected to increase by 10–40% across four river basins in Taiwan based on d4PDF +4K experiments.
Various affected rainfall indices have different impacts on water resources planning and management. For example, decreased WD50 over the projected future periods caused by increases in daily rainfall extremes raise concerns about flash flooding and drainage problems. Alterations of greater temporal scales rainfall unevenness, such as decreased DWR and increased SI, imply projected water availability problems between wet and dry seasons in the future. Growing concerns about projected increases in extreme short-duration rainfall in the future are noted in many studies since it may result in catastrophic disasters. It is necessary to prepare mitigation measures well to cope with such extreme events caused by global warming in the future.
4. Conclusions
In this study, multiple temporal scales of rainfall unevenness are simultaneously evaluated in the Zengwen Reservoir watershed, southern Taiwan, under climate change. The results indicate that noticeably deteriorated rainfall unevenness is detected over future periods, especially in MF (2041–2060). Climate change-induced deteriorated rainfall unevenness generally includes decreased WD50, increased SI, and decreased DWR, although opposite variations are also noted among GCMs. Projected increases in daily rainfall extremes not only reduce WD50 but also increase SI and decrease DWR. In addition, the WD50 has the greatest absolute mean RCM and the DWR has the least deviated RCM, which implies that the rainfall unevenness index with a shorter temporal scale is easily affected by climate change.
Distributional changes in rainfall unevenness indices determined by simultaneous consideration of RCM and RCSD are also explored in this study. The results indicate that no single category of distributional change is prevalent among GCMs, future periods, and scenarios. However, the frequencies of the top two categories exceed 0.5 and characterize differences among the three rainfall unevenness indices. The top two distributional change categories in DWR are I (decreased RCM and decreased RCSD) and IX (increased RCM and increased RCSD), which are totally opposite. This phenomenon implies that diverse variations in DWR and two opposite distributional change categories have a nearly equal likelihood. Increased RCM and decreased RCM are prevalent in SI and WD50, respectively.
Evaluating the impacts of climate change on rainfall unevenness over southern Taiwan receives increasing concerns since it would deteriorate frequent flooding and drought problems met in the past. Quantifying the impacts of climate change for various scenarios and uncertainties from GCMs is necessary to prepare mitigation measures to cope with such changing environments caused by global warming in the future. However, the lack of quantitative measures to detect similarity or dissimilarity between two distributions is the limitation of the currently used approach. In addition to quantitatively evaluating projected distributional changes in rainfall indices, evaluating impacts on rainfall variability for the period of 2061–2100, assessing projected changes in streamflow, and developing adaptive operation rules of reservoirs for coping with climate change have become more important than ever. Such tasks in southern Taiwan remain topics of future studies.
Author Contributions
Conceptualization, J.-T.S.; methodology, J.-T.S.; software, C.-C.L. and H.-W.T.; formal analysis, J.-T.S., C.-C.L. and H.-W.T.; data curation, H.-W.T. and S.-T.C.; writing—original draft preparation, J.-T.S.; writing—review and editing, J.-T.S., H.-W.T. and S.-T.C.; funding acquisition, J.-T.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science and Technology Council, Taiwan, ROC, grant number NSTC 112-2221-E-006-147.
Data Availability Statement
The authors do not have permission to share the TCCIP data.
Conflicts of Interest
The authors declare no competing financial interests or personal relationships that could influence this work.
References
- Trenberth, K.E. Conceptual framework for changes of extreme of the hydrological cycle with climate change. Clim. Chang. 1999, 42, 327–399. [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.A.; O’Gorman, P.A.; Maher, N. More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Chang. 2016, 6, 508–513. [Google Scholar] [CrossRef]
- Madakumbura, G.D.; Kim, H.; Utsumi, N.; Shiogama, H.; Fischer, E.M.; Seland, Ø.; Scinocca, J.F.; Mitchell, D.M.; Hirabayashi, Y.; Oki, T. Event-to-event intensification of the hydrologic cycle from 1.5 °C to 2 °C warmer world. Sci. Rep. 2019, 9, 3483. [Google Scholar] [CrossRef]
- Allan, R.P.; Barlow, M.; Byrne, M.P.; Cherchi, A.; Douville, H.; Fowler, H.J.; Gan, T.Y.; Pendergrass, A.G.; Rosenfeld, D.; Swann, A.L.S.; et al. Advances in understanding large-scale responses of the water cycle to climate change. Ann. N. Y. Acad. Sci. 2020, 1472, 49–75. [Google Scholar] [CrossRef]
- Pratap, S.; Markonis, Y. The response of the hydrological cycle to temperature changes in recent and distant climatic history. Prog. Earth Planet. Sci. 2022, 9, 30. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev.–Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 11, D05109. [Google Scholar] [CrossRef]
- Hong, Y.; Ying, S. Characteristics of extreme temperature and precipitation in China in 2017 based on ETCCDI indices. Adv. Clim. Chang. Res. 2018, 9, 218–226. [Google Scholar]
- Gebrechorkos, S.H.; Hülsmann, S.; Bernhofer, C. Changes in temperature and precipitation extremes in Ethiopia, Kenya, and Tanzania. Int. J. Climatol. 2019, 39, 18–30. [Google Scholar] [CrossRef]
- Gbode, I.E.; Adeyeri, O.E.; Menang, K.P.; Intsiful, J.D.K.; Ajayi, V.O.; Omotosho, J.A.; Akinsanola, A.A. Observed changes in climate extremes in Nigeria. Meteorol. Appl. 2019, 26, 642–654. [Google Scholar] [CrossRef]
- Cooley, A.K.; Chang, H. Detecting change in precipitation indices using observed (1977–2016) and modeled future climate data in Portland, Oregon, USA. J. Water Clim. Chang. 2021, 12, 1135–1153. [Google Scholar] [CrossRef]
- Shiau, J.T.; Wu, P.S. Nonstationary distributional changes of annual rainfall indices in Taiwan. Asia-Pac. J. Atmos. Sci. 2021, 57, 435–450. [Google Scholar] [CrossRef]
- Moraglia, G.; Brattich, E.; Carbone, G. Precipitation trends in North and South Carolina, USA. J. Hydrol. Reg. Stud. 2022, 44, 101201. [Google Scholar] [CrossRef]
- López, J.J.; Ayuso-Muñoz, J.L.; Goñi, M.; Gimena, F.N. Analysis of the effect of climate change on the characteristics of rainfall in Igeldo-Gipuzkoa (Spain). Water 2023, 15, 1529. [Google Scholar] [CrossRef]
- Silmann, J.; Kharin, V.V.; Zhang, X.; Zwiers, F.W.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part1. Model evaluation in present climate. J. Geophys. Res. Atmos. 2013, 118, 1716–1733. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, W.; Xu, J.; Li, L. Extreme precipitation indices over China in CMIP5 Models. Part I: Model evaluation. J. Clim. 2015, 28, 8603–8619. [Google Scholar] [CrossRef]
- Akinsanola, A.A.; Kooperman, G.J.; Reed, K.A.; Pendergrass, A.G.; Hannah, W.M. Projected changes in seasonal precipitation extremes over the United States in CMIP6 simulations. Environ. Res. Lett. 2020, 15, 104068. [Google Scholar] [CrossRef]
- Srivastava, A.; Grotjahn, R.; Ullrich, P.A. Evaluation of historical CMIP6 model simulations of extreme precipitation over contiguous US regions. Weather Clim. Extrem. 2020, 29, 100268. [Google Scholar] [CrossRef]
- Rojpratak, S.; Supharatid, S. Regional extreme precipitation index: Evaluations and projections from the multi-model ensemble CMIP5 over Thailand. Weather Clim. Extrem. 2022, 37, 100475. [Google Scholar] [CrossRef]
- de Medeiros, F.J.; de Oliveira, C.P.; Avila-Diaz, A. Evaluation of extreme precipitation climate indices and their projected changes for Brazil: From CMIP3 to CMIP6. Weather Clim. Extrem. 2022, 38, 100511. [Google Scholar] [CrossRef]
- Lei, X.; Xu, C.; Liu, F.; Song, L.; Cao, L.; Suo, N. Evaluation of CMIP6 models and multi-model ensemble for extreme precipitation over arid Central Asia. Remote Sens. 2023, 15, 2376. [Google Scholar] [CrossRef]
- Zhao, J.; Gan, T.Y.; Zhang, G.; Zhang, S. Projected changes of precipitation extremes in North America using CMIP6 multi-climate model ensembles. J. Hydrol. 2023, 621, 129598. [Google Scholar] [CrossRef]
- Pendergrass, A.G.; Knutti, R. The uneven nature of daily precipitation and its change. Geophys. Res. Lett. 2018, 45, 11980–11988. [Google Scholar] [CrossRef]
- Chen, Y. Increasing uneven intra-seasonal distribution of daily and hourly precipitation over Eastern China. Environ. Res. Lett. 2020, 15, 104068. [Google Scholar] [CrossRef]
- Rajah, K.; O’Leary, T.; Turner, A.; Petrakis, G.; Leonard, M.; Westra, S. Changes to the temporal distribution of daily precipitation. Geophys. Res. Lett. 2014, 41, 8887–8894. [Google Scholar] [CrossRef]
- Zhang, Y.; Fueglistaler, S. Mechanism for increasing tropical rainfall unevenness with global warming. Geophys. Res. Lett. 2019, 46, 14836–14843. [Google Scholar] [CrossRef]
- Zou, S.; Abuduwaili, J.; Duan, W.; Ding, J.; De Maeyer, P.; De Voorde, T.V.; Ma, L. Attribution of changes in the trend and temporal non-uniformity of extreme precipitation events in Central Asia. Sci. Rep. 2021, 11, 15032. [Google Scholar] [CrossRef]
- Nguyen, D.Y.; Chen, S.T. Generating continuous rainfall series of high temporal resolution using stochastic rainfall generator with copula and modified Huff rainfall curves. Water 2022, 14, 2123. [Google Scholar] [CrossRef]
- Wu, G.; Li, Y.; Li, T.; Ma, Z.; Shi, C.G. The unevenness in observed daily precipitation in mainland China. Theor. Appl. Climatol. 2021, 146, 1031–1041. [Google Scholar] [CrossRef]
- Han, J.; Miao, C.; Duan, Q.; Wu, J.; Gou, J.; Zheng, H. Changes in unevenness of wet-day precipitation over China during 1961–2020. J. Geophys. Res. Atmos. 2021, 126, e2020JD034483. [Google Scholar] [CrossRef]
- Ahn, M.S.; Ullrich, P.A.; Gleckler, P.J.; Lee, J.; Ordonez, A.C.; Pendergrass, A.G. Evaluating precipitation distributions at regional scales: A benchmarking framework and application to CMIP5 and 6 models. Geosci. Model Dev. 2023, 16, 3927–3951. [Google Scholar] [CrossRef]
- Goffin, B.D.; Kansara, P.; Lakshmi, V. Intensification in the wettest days to 50 percent of annual precipitation (WD50) across Europe. Geophys. Res. Lett. 2024, 51, e2023GL107403. [Google Scholar] [CrossRef]
- Huang, W.C.; Chiang, Y.; Wu, R.Y.; Lee, J.L.; Lin, S.H. The impact of climate change on rainfall frequency in Taiwan. Terr. Atmos. Ocean. Sci. 2012, 23, 553–564. [Google Scholar] [CrossRef]
- Tung, Y.S.; Chen, C.T.; Min, S.K.; Lin, L.Y. Evaluating extremes rainfall changes over Taiwan using a standardized index. Terr. Atmos. Ocean. Sci. 2016, 27, 705–715. [Google Scholar] [CrossRef]
- Chen, P.Y.; Tung, C.P.; Tsao, J.H.; Chen, C.J. Assessing future rainfall intensity-duration-frequency characteristics across Taiwan using the k-nearest neighbor method. Water 2021, 13, 1521. [Google Scholar] [CrossRef]
- Tung, Y.S.; Wang, C.Y.; Weng, S.P.; Yang, C.D. Extremes index trend of daily gridded rainfall dataset (1960–2017) in Taiwan. Terr. Atmos. Ocean. Sci. 2022, 33, 8. [Google Scholar] [CrossRef]
- Tung, C.P. Climate change impacts on water resources of the Tsengwen Creek watershed in Taiwan. J. Am. Water Resour. Assoc. 2001, 37, 167–176. [Google Scholar] [CrossRef]
- Kimura, N.; Chiang, S.; Wei, H.P.; Su, Y.F.; Chu, J.L.; Cheng, C.T.; Liou, J.J.; Chen, Y.M.; Lin, L.Y. Tsengwen Reservoir watershed hydrological flood simulation under global climate change using the 20 km mesh Meteorological Research Institute Atmospheric General Circulation Model (MRI-AGCM). Terr. Atmos. Ocean. Sci. 2014, 25, 449–461. [Google Scholar] [CrossRef]
- Wei, H.P.; Yeh, K.C.; Liou, J.J.; Chen, Y.M.; Cheng, C.T. Estimating the risk of river flow under climate change in the Tsengwen River basin. Water 2016, 8, 81. [Google Scholar] [CrossRef]
- Teng, T.Y.; Liu, T.M.; Tung, Y.S.; Cheng, K.S. Converting climate change gridded daily rainfall to station daily rainfall—A case study at Zengwen Reservoir. Water 2021, 13, 1516. [Google Scholar] [CrossRef]
- Wang, Y.C.; Hsu, H.H.; Chen, C.A.; Tseng, W.L.; Hsu, P.C.; Lin, C.W.; Chen, Y.L.; Jiang, L.C.; Lee, Y.C.; Liang, H.C.; et al. Performance of the Taiwan Earth System Model in simulating climate variability compared with observations and CMIP6 model simulations. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002353. [Google Scholar] [CrossRef]
- Gleckler, P.J.; Taylor, K.E.; Doutriaux, C. Performance metrics for climate models. J. Geophys. Res. 2008, 113, D06194. [Google Scholar] [CrossRef]
- Baker, N.C.; Taylor, P.C. A framework for evaluating climate model performance metrics. J. Clim. 2016, 29, 1773–1782. [Google Scholar] [CrossRef]
- Peng, S.; Wang, C.; Li, Z.; Mihara, K.; Kuramochi, K.; Toma, Y.; Hatano, R. Climate change multi-model projections in CMIP6 scenarios in Central Hokkaido, Japan. Sci. Rep. 2023, 13, 230. [Google Scholar] [CrossRef]
- Bosshard, T.; Carambia, M.; Goergen, K.; Kotlarski, S.; Krahe, P.; Zappa, M.; Schär, C. Quantifying uncertainty sources in an ensemble of hydrological climate-impact projections. Water Resour. Res. 2013, 49, 1523–1536. [Google Scholar] [CrossRef]
- Addor, N.; Rössler, O.; Köplin, N.; Huss, M.; Weingartner, R.; Seibert, J. Robust changes and sources of uncertainty in the projected hydrological regimes of Swiss catchments. Water Resour. Res. 2014, 50, 7541–7562. [Google Scholar] [CrossRef]
- Hattermann, F.F.; Vetter, T.; Breuer, L.; Su, B.; Daggupati, P.; Donnelly, C.; Fekete, B.; Flörke, F.; Gosling, S.N.; Hoffmann, P.; et al. Sources of uncertainty in hydrological climate impact assessment: A cross-scale study. Environ. Res. Lett. 2018, 13, 015006. [Google Scholar] [CrossRef]
- Chegwidden, O.S.; Nijssen, B.; Rupp, D.E.; Arnold, J.R.; Clark, M.P.; Hamman, J.J.; Kao, S.C.; Mao, Y.; Mizukami, N.; Mote, P.W.; et al. How do modeling decisions affect the spread among hydrologic climate change projections? Exploring a large ensemble of simulations across a diversity of hydroclimates. Earth’s Future 2019, 7, 623–637. [Google Scholar] [CrossRef]
- Lin, L.Y.; Lin, C.T.; Chen, Y.M.; Cheng, C.T.; Li, H.C.; Chen, W.B. The Taiwan Climate Change Projection Information and Adaptation Knowledge Platform: A decade of climate research. Water 2022, 14, 358. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Kriegler, E.; Ebi, K.L.; Kemp-Benedict, E.; Riahi, K.; Rothman, D.S.; van Ruijven, B.J.; van Vuuren, D.P.; Birkmann, J.; Kok, K.; et al. The roads ahead: Narratives for shared socioeconomic pathways describing world futures in the 21st century. Glob. Environ. Chang. 2017, 42, 169–180. [Google Scholar] [CrossRef]
- Riahi, K.; van Vuuren, D.P.; Kriegler, E.; Edmonds, J.; O’Neill, B.C.; Fujimori, S.; Bauer, N.; Calvin, K.; Dellink, R.; Fricko, O.; et al. The shared socioeconomic pathways and their energy, land use, and greenhouse gas emissions implications: An Overview. Glob. Environ. Chang. 2017, 42, 153–168. [Google Scholar] [CrossRef]
- van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.-F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Simpkins, G. Progress in climate modelling. Nat. Clim. Chang. 2017, 7, 684–686. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Tebaldi, C.; van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Pryor, S.C.; Schoof, J.T. Changes in the seasonality of precipitation over the contiguous USA. J. Geophys. Res. 2008, 113, D21108. [Google Scholar] [CrossRef]
- Imteaz, M.; Hossain, I. Climate change impacts on ‘seasonality index’ and its potential implications on rainwater savings. Water Resour. Manag. 2023, 37, 2593–2606. [Google Scholar] [CrossRef]
- Shiau, J.T.; Huang, W.H. Detecting distributional changes of annual rainfall indices in Taiwan using quantile regression. J. Hydro-Environ. Res. 2015, 9, 368–380. [Google Scholar] [CrossRef]
- Li, C.Y.; Lin, S.S.; Chuang, C.M.; Hu, Y.L. Assessing future rainfall uncertainties of climate change in Taiwan with a bootstrapped neural network-based downscaling model. Water Environ. J. 2020, 34, 77–92. [Google Scholar] [CrossRef]
- Huang, W.R.; Huang, P.H.; Chang, Y.H.; Cheng, C.T.; Hsu, H.H.; Tu, C.Y.; Kitoh, A. Dynamical Downscaling Simulation and Future Projection of Extreme Precipitation Activities in Taiwan during the Mei-Yu Seasons. J. Meteorol. Soc. Jpn. 2019, 97, 481–499. [Google Scholar] [CrossRef]
- Chang, J.; Tanaka, T.; Tachikawa, Y. Frequency Analysis of Past and Future Extreme Rainfall Events in Taiwan Using d4PDF. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2022, 78, I_457–I_462. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).