Real-Time Analysis and Digital Twin Modeling for CFD-Based Air Valve Control During Filling Procedures
Abstract
1. Introduction
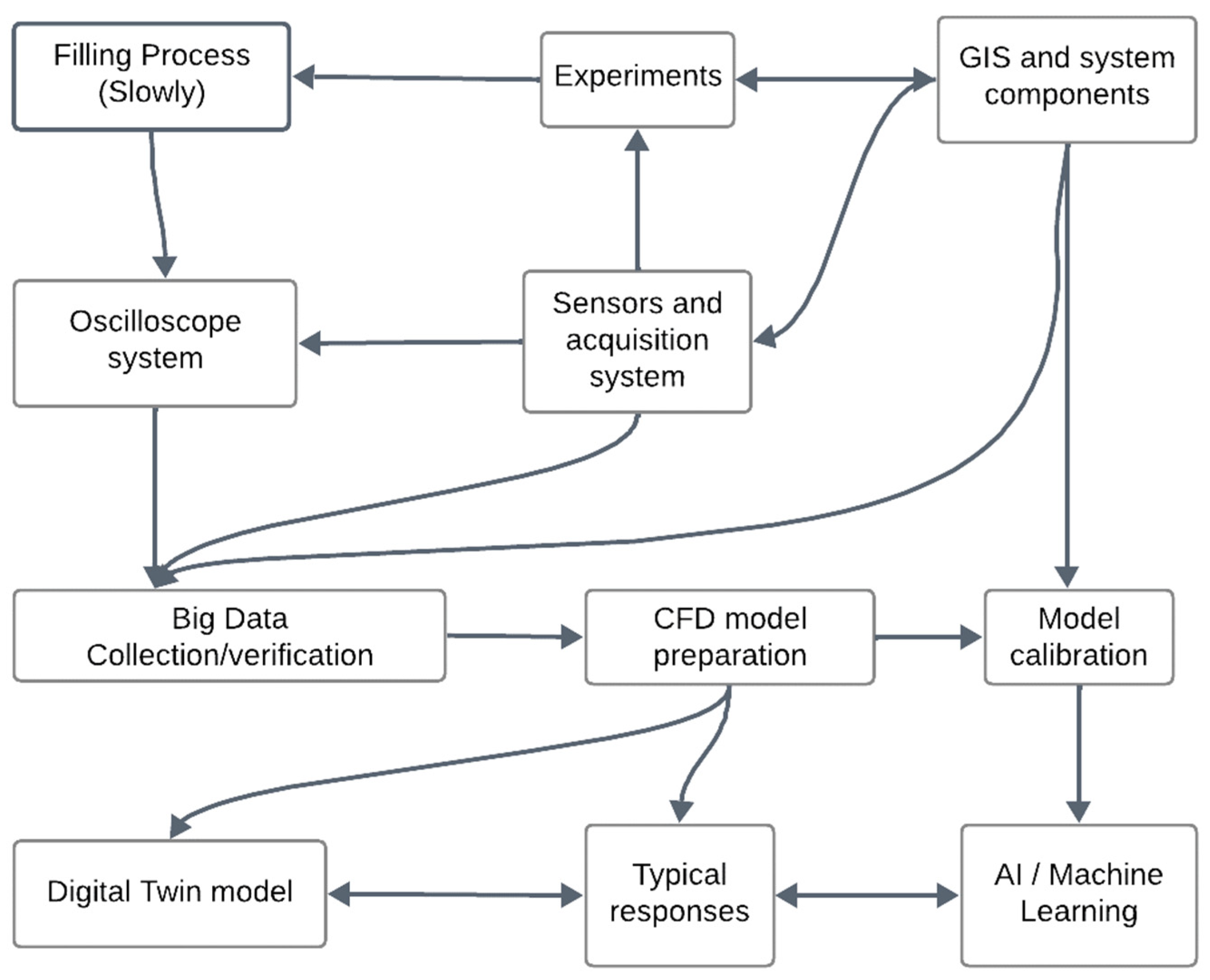
2. Methodology
2.1. Digital Twin
2.2. Big Data Platform
3. Digital Twin—CFD Model
3.1. Numerical Approach
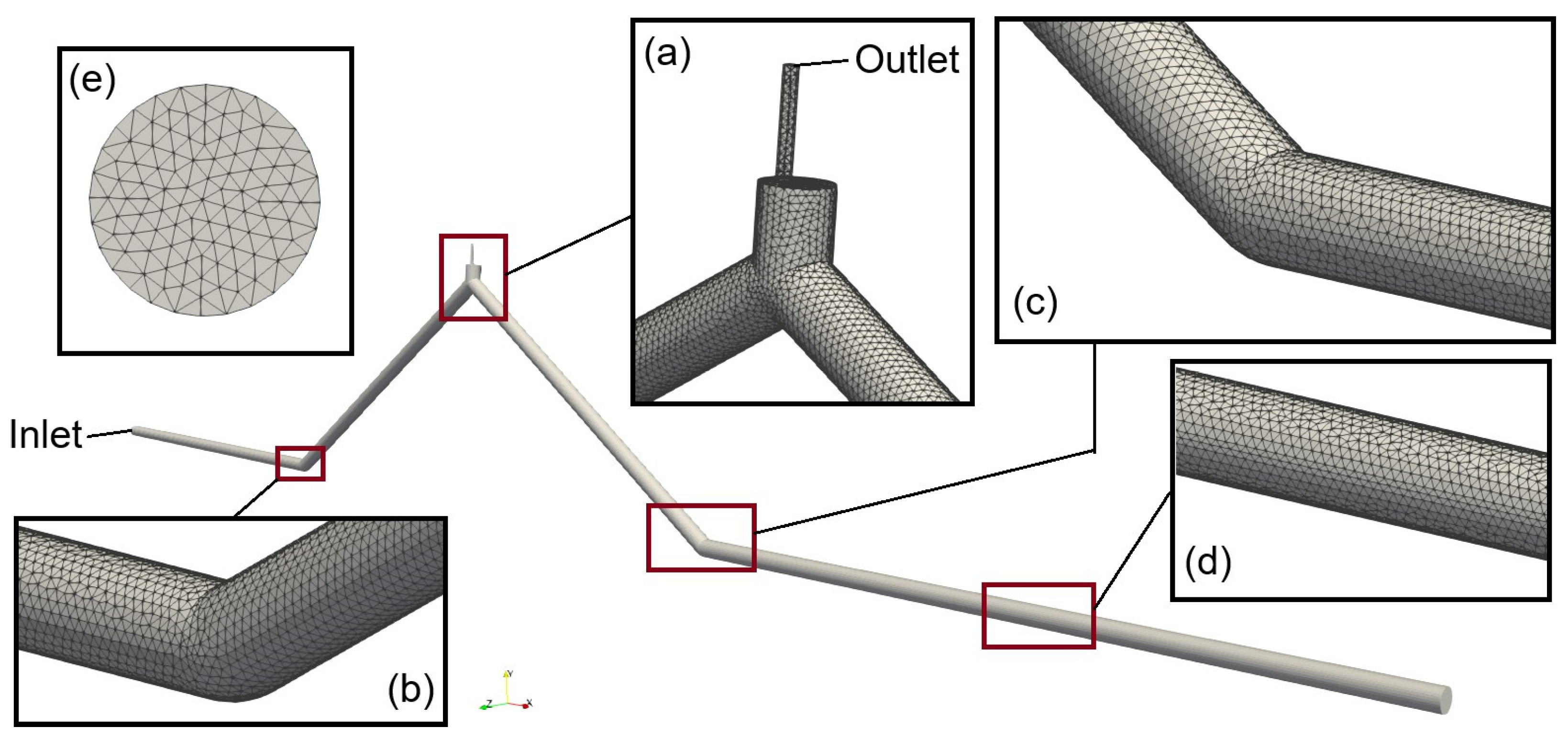
3.2. Geometry and Mesh
- The electro-pneumatic valve opens from the instant t = 0.0 s, and the effect of the opening is negligible.
- The ball valve in the experimental setup’s right sector is closed. Therefore, this element needs to be addressed in the geometry of the CFD model.
- The effect of the air valve is represented by a small pipe with a nominal diameter of one inch (1″) and an orifice with a diameter of 3.175 mm, corresponding to the discharge orifice of the S050 air valve.
3.3. Boundary Conditions
3.4. Computational Process
4. Analysis of Results and Discussion
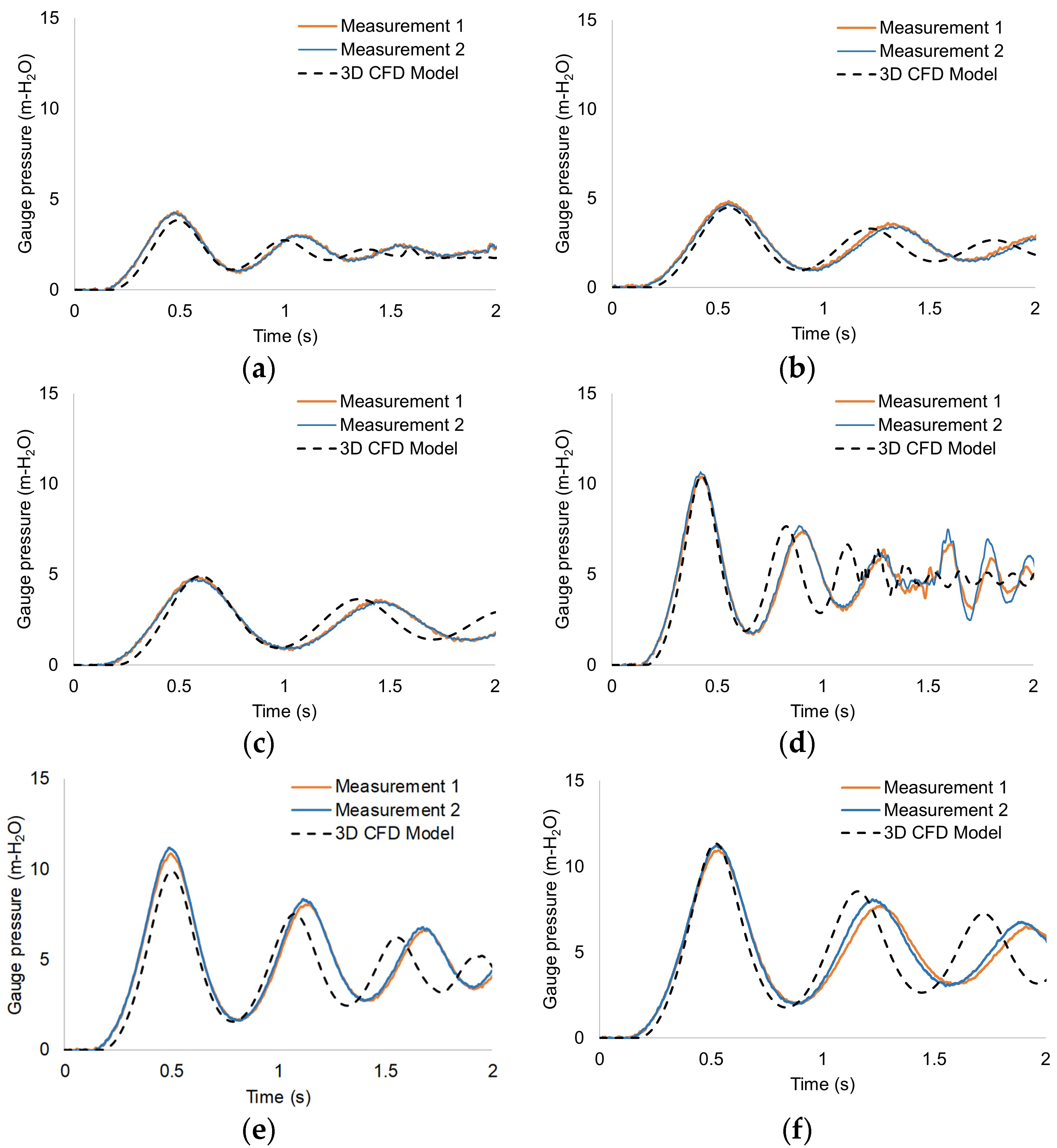
4.1. Numerical Validation of CFD Model
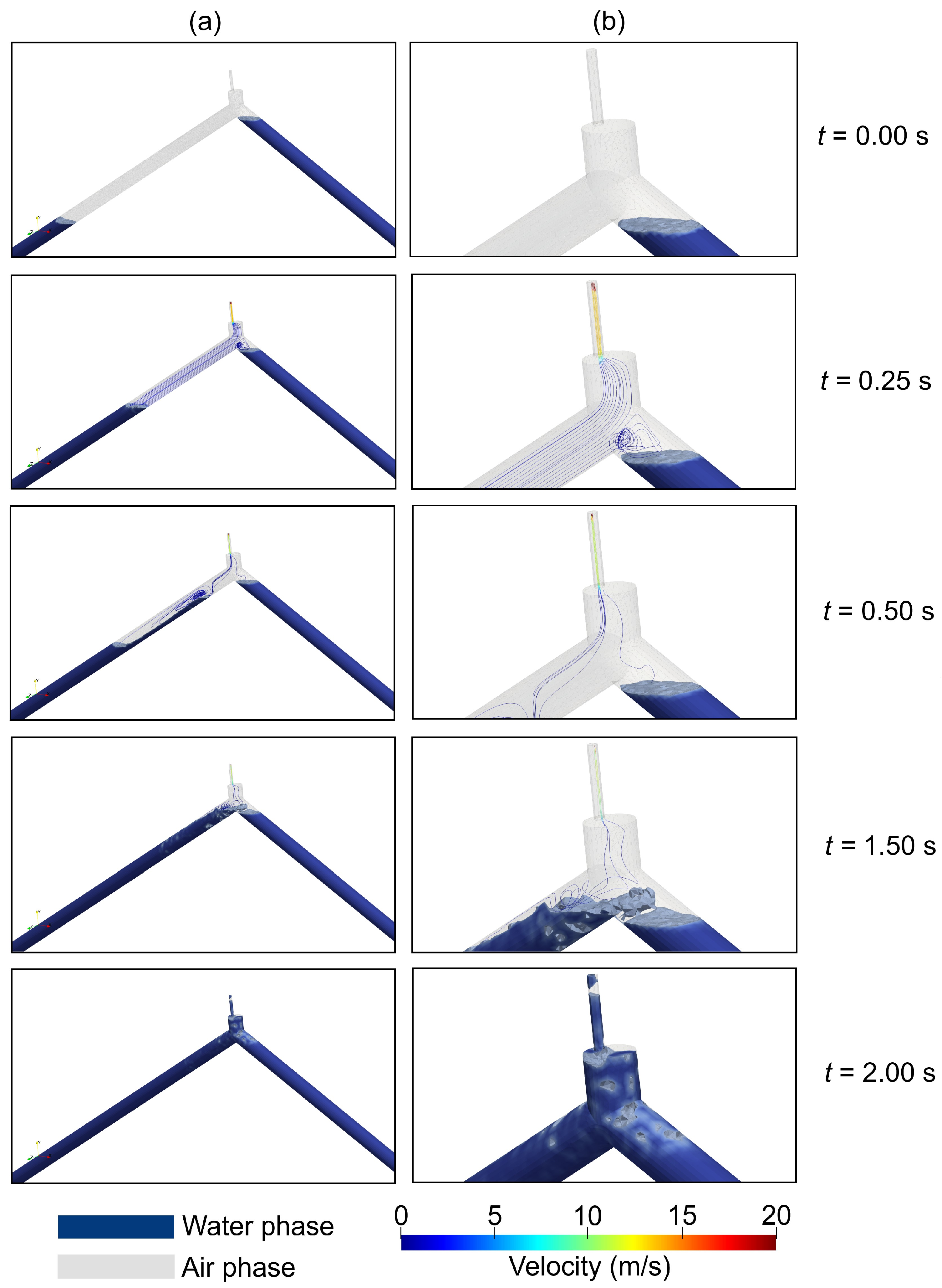
4.2. Validation of Air-Water Interaction
- t = 0.00 s: At that instant, the pipe contains an initial air pocket at atmospheric conditions, and the water column is at rest since the filling process has not yet started.
- t = 0.25 s: The water column at the left branch gradually rises due to the hydro-pneumatic tank pumping, and the air-water interface starts to exhibit a different shape. In addition, the location of the air-water interface in the frame of the CFD model and the experimental one is similar.
- t = 0.50 s: The water column returns slightly in the opposite direction of flow, and the air-water interface collapses, generating a transition from pressurized flow to free surface flow, which occurs in the CFD model and the experiment facility.
- t = 1.54 s: The water column has reached the upper end of the pipe, thus displacing part of the air volume that the air valve S050 has expelled. At this stage, a moderate mixing of air bubbles with the water phase begins to be generated, evident in the CFD model frame and the experiment’s video frame.
- t = 2.00 s: Much of the pipe’s air volume is expelled at this experiment stage. In that sense, the pipe is almost entirely occupied by water. Small bubbles are observed due to the mixing of air and water at the high point of the pipe and are evident experimentally and numerically through the contours of the CFD model.
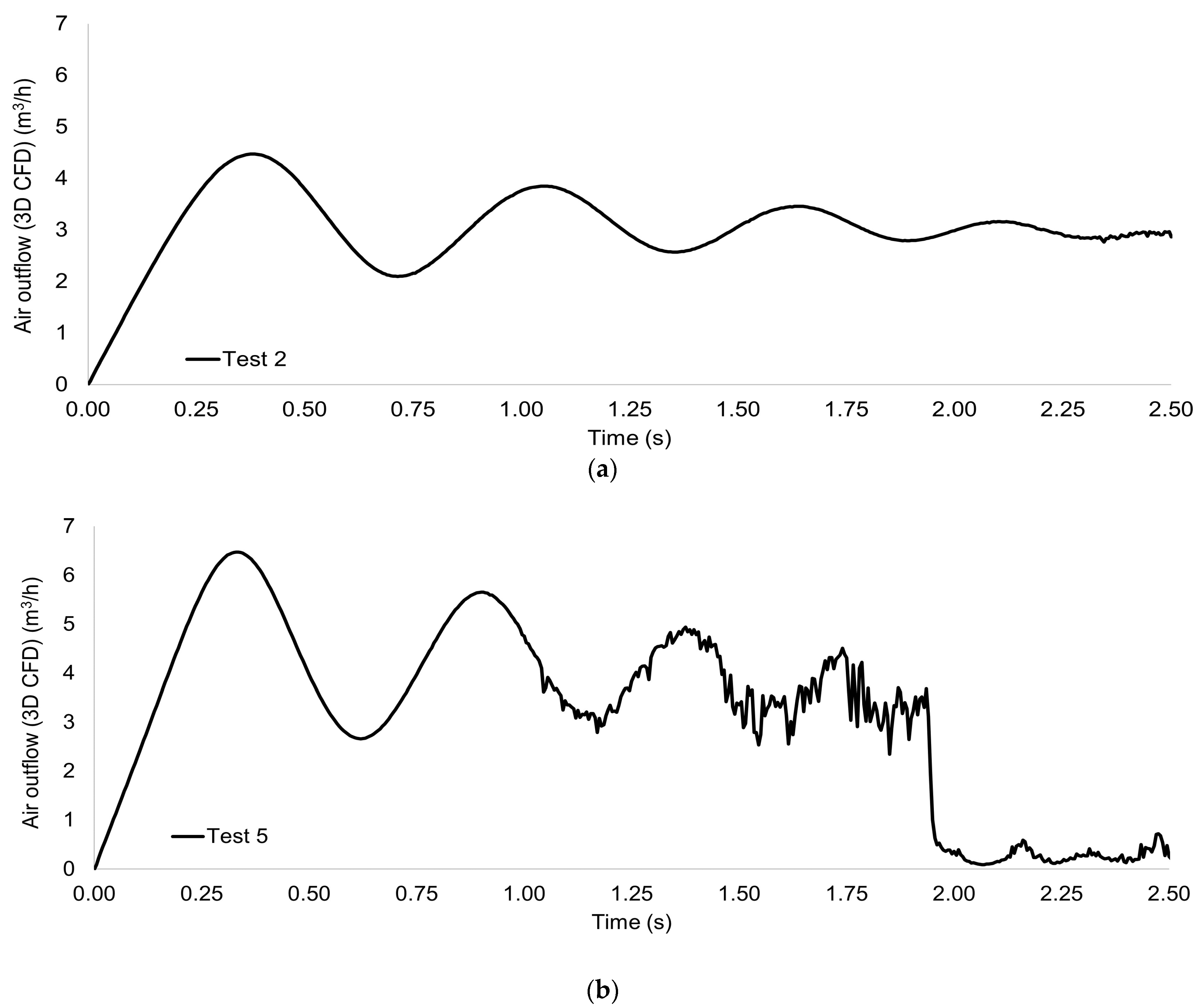
4.3. Dynamic of Air Expulsion from Pipelines
- t = 0.00 s: There are no air streamlines at this instant due to the hydraulic system being at rest.
- t = 0.25 s: At this instant, air streamlines parallel the pipe axis with a velocity between 0 and 5 m/s. These are located between the initial air-water interface, up to the upper end of the pipe, where there is a vorticity at the corner. On the other hand, the air streamlines increase in velocity at the end of the air valve to values between 10 and 15 m/s. At the discharge orifice, the velocity increases to a value higher than 20 m/s, according to the observed contours.
- t = 0.50 s: The air streamlines in the air valve zone decrease in velocity magnitude due to the number of streamlines, while vortices occur in the air pocket as a result of the transient event, in which the air pocket releases energy after compressing in the first oscillation. Velocity contours are the same at time instant t = 0.25 s.
- t = 1.50 s: At this instant, the air streamlines are chaotically distributed in the upper zone of the pipe without being traced in the air valve structure. At this time, the airflow velocity is less than 5 m/s.
- t = 2.00 s: The filling process ends, so it is not easy to visualize the tracing of the air streamlines.
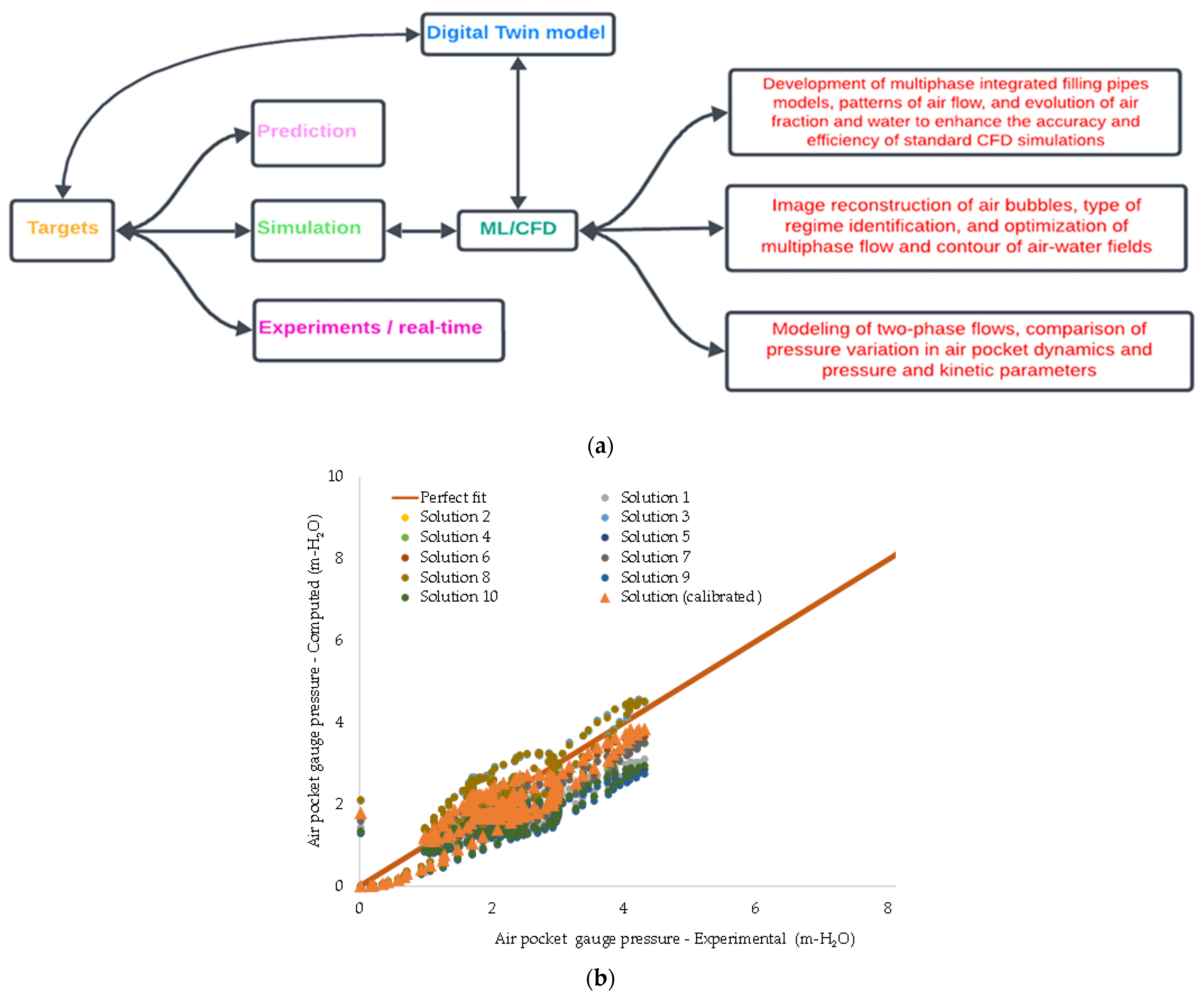
5. Conclusions
- This study contributes to developing an integrated system for real-time monitoring of pipeline operations. It includes the three-dimensional representation from computational fluid dynamics tools that allows the identification of the air-water interaction from this study scenario and the detailed evolution of fluid parameters such as pressure, velocity–velocity, and temperature spatially and temporally.
- This study represents a breakthrough in the simulation of the filling process with entrapped air and air valves in three dimensions, going beyond 2D CFD simulation that relied on discharge orifices to approximate air ejection effects.
- The integration of CFD models and Digital Twins has several limitations: data sources, interpretability of results, robustness of the integrated model, phenomenon complexity, machine learning efficiency, and extrapolation of results. However, this research also faced several challenges and opportunities: analysis of results, discussion, and future directions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| : | thermal conductivity (W/m/°K); |
| : | roughness constant (-); |
| : | closure coefficient (-); |
| : | specific internal energy (J/kg); |
| : | pipe diameter (m); |
| : | diffusion term for (m2/s); |
| : | diffusion term for (m2/s); |
| : | blending function (–); |
| : | surface tension force (N/m2); |
| : | roughness function parameter (–); |
| : | gravitational acceleration vector (m/s2); |
| : | turbulent kinetic energy generation (m2/s3); |
| : | turbulence kinetic energy (m2/s2); |
| : | pipe absolute roughness (m); |
| : | sand-grain roughness height (–); |
| and : | length of left and right pipe branches (m); |
| : | initial air pocket length (m); |
| : | energy source term (Nm); |
| : | hydro-pneumatic gauge pressure (Pa); |
| : | atmospheric pressure (Pa); |
| : | surface heat flux (W/m2); |
| : | air pocket pressure (N/m2); |
| : | temperature (°K); |
| : | universal gas constant (J/°K/mol); |
| : | velocity vector (m/s); |
| : | velocity field associated with the air phase (m/s); |
| : | shear velocity (m/s); |
| : | turbulent kinematic viscosity (m2/s); |
| : | kinematic viscosity of fluid in a near-wall cell (m2/s); |
| : | specific turbulence dissipation rate (1/s); |
| : | time (s); |
| : | volume fraction (-); |
| : | mixing density (kg/m3); |
| : | dynamic viscosity (Ns/m2); |
| : | initial air pocket size (m); |
| , , , and : | constants of the turbulence model (-). |
| Subscripts | |
| : | refers to the water phase |
| : | refers to the air phase |
Appendix A. Governing Equations of the 3D CFD Model
References
- Ramos, H.M.; Fuertes-Miquel, V.S.; Tasca, E.; Coronado-Hernández, O.E.; Besharat, M.; Zhou, L.; Karney, B. Concerning Dynamic Effects in Pipe Systems with Two-Phase Flows: Pressure Surges, Cavitation, and Ventilation. Water 2022, 14, 2376. [Google Scholar] [CrossRef]
- John, H.B., Jr.; Dechant, D.A. Current Proposed Changes to AWWA M11 Steel Pipe: A Guide for Design and Installation. In Proceedings of the Pipelines 2014: From Underground to the Forefront of Innovation and Sustainability, Portland, OR, USA, 3–6 August 2014; pp. 2221–2228. [Google Scholar] [CrossRef]
- Boulos, P.F.; Karney, B.W.; Wood, D.J.; Lingireddy, S. Hydraulic Transient Guidelines for Protecting Water Distribution Systems. J. Am. Water Work. Assoc. 2005, 97, 111–124. [Google Scholar] [CrossRef]
- Crabtree, A.; Oliphant, K. Resistance of PE4710 Piping to Pressure Surge Events in Force Main Applications. 2012. Available online: https://conduitcalc.plasticpipe.org/pdf/resistance-of-pe4710-piping-to-pressure-surge-evnets-in-force-main-applications.pdf (accessed on 10 September 2024).
- Hussam, F.; Tarek, Z. Hierarchical Fuzzy Expert System for Risk of Failure of Water Mains. J. Pipeline Syst. Eng. Pr. 2010, 1, 53–62. [Google Scholar] [CrossRef]
- Ramezani, L.; Karney, B.; Malekpour, A. Encouraging Effective Air Management in Water Pipelines: A Critical Review. J. Water Resour. Plan. Manag. 2016, 142, 4016055. [Google Scholar] [CrossRef]
- Lauchlan, C.; Escarameia, M.; May, R.; Burrows, R.; Gahan, C. Air in Pipelines—A Literature Review. 2005. Available online: https://eprints.hrwallingford.com/551/1/SR649.pdf (accessed on 10 September 2024).
- Zhou, L.; Cao, Y.; Karney, B.; Bergant, A.; Tijsseling, A.S.; Liu, D.; Wang, P. Expulsion of Entrapped Air in a Rapidly Filling Horizontal Pipe. J. Hydraul. Eng. 2020, 146, 4020047. [Google Scholar] [CrossRef]
- Malekpour, A.; Shahroodi, A. What Is a Safe Filling Velocity in Water and Wastewater Pipelines? In Proceedings of the Pipelines 2023, San Antonio, TX, USA, 12–16 August 2023; pp. 301–312. [Google Scholar] [CrossRef]
- Tasca, E.S.A.; Karney, B. Improved Air Valve Selection through Better Device Characterization and Modeling. J. Hydraul. Eng. 2023, 149, 4023019. [Google Scholar] [CrossRef]
- Ramezani, L.; Karney, B.; Malekpour, A. The Challenge of Air Valves: A Selective Critical Literature Review. J. Water Resour. Plan. Manag. 2015, 141, 4015017. [Google Scholar] [CrossRef]
- García-Todolí, S.; Iglesias-Rey, P.L.; Mora-Meliá, D.; Martínez-Solano, F.J.; Fuertes-Miquel, V.S. Computational Determination of Air Valves Capacity Using CFD Techniques. Water 2018, 10, 1433. [Google Scholar] [CrossRef]
- Zhou, F.; Hicks, F.E.; Steffler, P.M. Transient Flow in a Rapidly Filling Horizontal Pipe Containing Trapped Air. J. Hydraul. Eng. 2002, 128, 625–634. [Google Scholar] [CrossRef]
- De Martino, G.; Fontana, N.; Giugni, M. Transient Flow Caused by Air Expulsion through an Orifice. J. Hydraul. Eng. 2008, 134, 1395–1399. [Google Scholar] [CrossRef]
- Carlos, M.; Arregui, F.J.; Cabrera, E.; Palau, C.V. Understanding Air Release through Air Valves. J. Hydraul. Eng. 2011, 137, 461–469. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; López-Jiménez, P.A.; Martínez-Solano, F.J.; López-Patiño, G. Numerical Modelling of Pipelines with Air Pockets and Air Valves. Can. J. Civ. Eng. 2016, 43, 1052–1061. [Google Scholar] [CrossRef]
- Coronado-Hernández, Ó.E.; Besharat, M.; Fuertes-Miquel, V.S.; Ramos, H.M. Effect of a Commercial Air Valve on the Rapid Filling of a Single Pipeline: A Numerical and Experimental Analysis. Water 2019, 11, 1814. [Google Scholar] [CrossRef]
- Zhou, L.; Pan, T.; Wang, H.; Liu, D.; Wang, P. Rapid Air Expulsion through an Orifice in a Vertical Water Pipe. J. Hydraul. Res. 2019, 57, 307–317. [Google Scholar] [CrossRef]
- Romero, G.; Fuertes-Miquel, V.S.; Coronado-Hernández, Ó.E.; Ponz-Carcelén, R.; Biel-Sanchis, F. Analysis of Hydraulic Transients during Pipeline Filling Processes with Air Valves in Large-Scale Installations. Urban. Water J. 2020, 17, 568–575. [Google Scholar] [CrossRef]
- Li, L.; Zhu, D.Z.; Huang, B. Analysis of Pressure Transient Following Rapid Filling of a Vented Horizontal Pipe. Water 2018, 10, 1698. [Google Scholar] [CrossRef]
- Chan, S.N.; Cong, J.; Lee, J.H.W. 3D Numerical Modeling of Geyser Formation by Release of Entrapped Air from Horizontal Pipe into Vertical Shaft. J. Hydraul. Eng. 2018, 144, 04017071. [Google Scholar] [CrossRef]
- Wang, J.; Vasconcelos, J.G. Investigation of Manhole Cover Displacement during Rapid Filling of Stormwater Systems. J. Hydraul. Eng. 2020, 146, 4020022. [Google Scholar] [CrossRef]
- Fang, H.; Zhou, L.; Cao, Y.; Cai, F.; Liu, D. 3D CFD Simulations of Air-Water Interaction in T-Junction Pipes of Urban Stormwater Drainage System. Urban. Water J. 2022, 19, 74–86. [Google Scholar] [CrossRef]
- Aguirre-Mendoza, A.M.; Paternina-Verona, D.A.; Oyuela, S.; Coronado-Hernández, O.E.; Besharat, M.; Fuertes-Miquel, V.S.; Iglesias-Rey, P.L.; Ramos, H.M. Effects of Orifice Sizes for Uncontrolled Filling Processes in Water Pipelines. Water 2022, 14, 888. [Google Scholar] [CrossRef]
- American Water Works Association (AWWA). Air-Release, Air/Vacuum, and Combination Air Valves: M51; American Water Works Association (AWWA): Denver, CO, USA, 2001; Volume 51. [Google Scholar]
- Paternina-Verona, D.A.; Coronado-Hernández, O.E.; Espinoza-Román, H.G.; Arrieta-Pastrana, A.; Tasca, E.; Fuertes-Miquel, V.S.; Ramos, H.M. Attenuation of Pipeline Filling Over-Pressures through Trapped Air. Urban. Water J. 2024, 21, 698–710. [Google Scholar] [CrossRef]
- Martins, N.M.C.; Delgado, J.N.; Ramos, H.M.; Covas, D.I.C. Maximum Transient Pressures in a Rapidly Filling Pipeline with Entrapped Air Using a CFD Model. J. Hydraul. Res. 2017, 55, 506–519. [Google Scholar] [CrossRef]


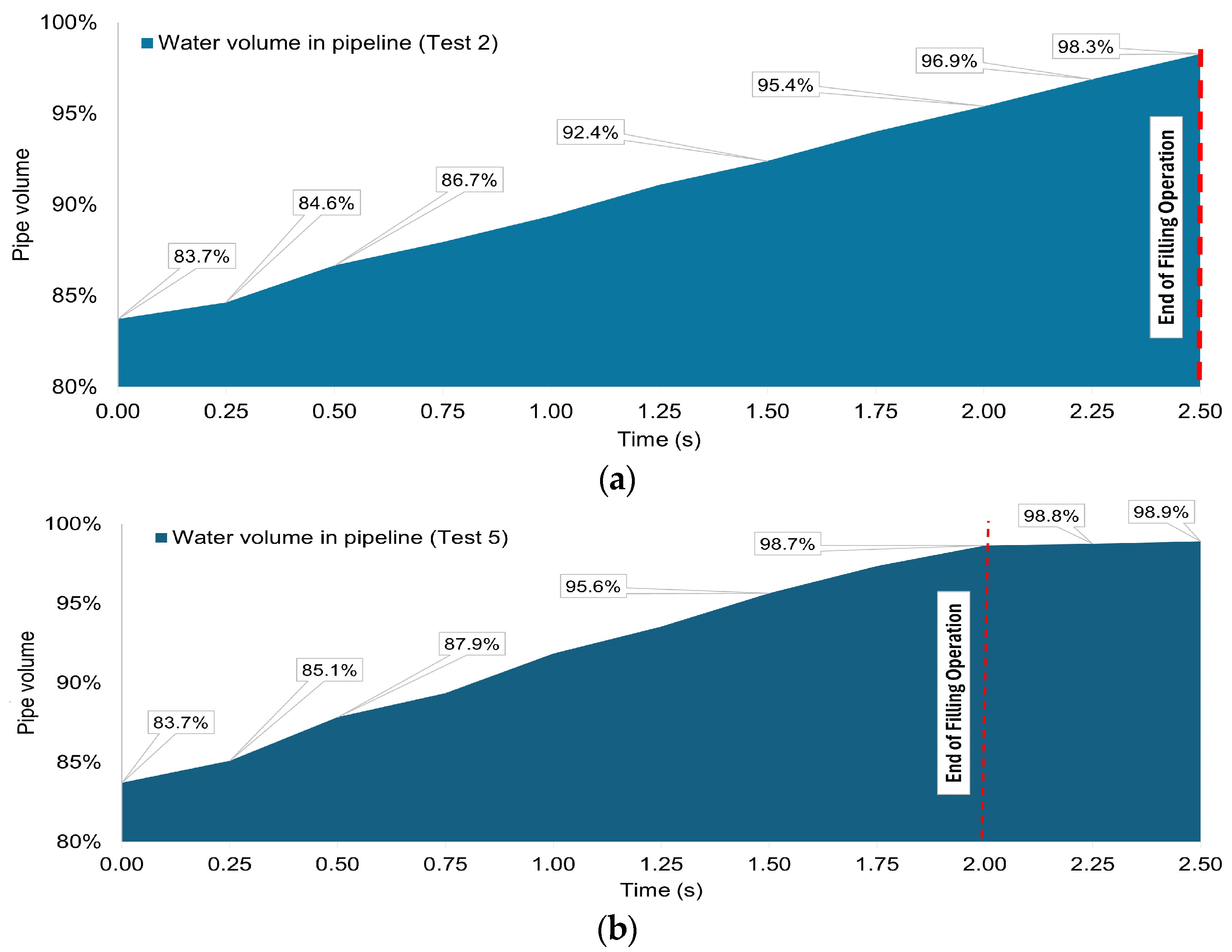
| Test No. | (kPa) | (m) |
|---|---|---|
| 1 | 20 | 0.46 |
| 2 | 20 | 0.96 |
| 3 | 20 | 1.36 |
| 4 | 50 | 0.46 |
| 5 | 50 | 0.96 |
| 6 | 50 | 1.36 |
| Test No. | (m) | (m) | (%) |
|---|---|---|---|
| 1 | 4.29 | 3.84 | 10.0% |
| 2 | 4.67 | 4.48 | 4.1% |
| 3 | 4.71 | 4.78 | 2.4% |
| 4 | 10.53 | 10.42 | 1.0% |
| 5 | 11.05 | 9.90 | 10.0% |
| 6 | 11.34 | 11.10 | 2.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paternina-Verona, D.A.; Coronado-Hernández, O.E.; Pérez-Sánchez, M.; Ramos, H.M. Real-Time Analysis and Digital Twin Modeling for CFD-Based Air Valve Control During Filling Procedures. Water 2024, 16, 3015. https://doi.org/10.3390/w16213015
Paternina-Verona DA, Coronado-Hernández OE, Pérez-Sánchez M, Ramos HM. Real-Time Analysis and Digital Twin Modeling for CFD-Based Air Valve Control During Filling Procedures. Water. 2024; 16(21):3015. https://doi.org/10.3390/w16213015
Chicago/Turabian StylePaternina-Verona, Duban A., Oscar E. Coronado-Hernández, Modesto Pérez-Sánchez, and Helena M. Ramos. 2024. "Real-Time Analysis and Digital Twin Modeling for CFD-Based Air Valve Control During Filling Procedures" Water 16, no. 21: 3015. https://doi.org/10.3390/w16213015
APA StylePaternina-Verona, D. A., Coronado-Hernández, O. E., Pérez-Sánchez, M., & Ramos, H. M. (2024). Real-Time Analysis and Digital Twin Modeling for CFD-Based Air Valve Control During Filling Procedures. Water, 16(21), 3015. https://doi.org/10.3390/w16213015









