Abstract
To enhance the efficiency of solving the optimal operation model for cascade reservoirs, this paper first constructed an optimal operation model of cascade reservoirs. The model comprehensively considered the ecological flow, the guaranteed output of hydroelectric power plants, and the relaxation constraints of the water level at the end of water supply and storage period. The relaxation constraints refer to two relaxation variable constraints, which are used to ensure that the water levels decline in the water supply period and rise in the water storage periods. At the same time, to avoid the challenges of “dimension disaster” and susceptibility to local optima commonly encountered in existing optimization algorithms when resolving the above model, a novel optimization algorithm, M-IWO-ODDDP, derived from the optimization principles of the Invasive Weed Optimization (IWO) and Discrete Differential Dynamic Programming (DDDP) algorithms, was proposed in this paper. The 11 cascade hydropower stations in the Wujiang River basin were used as a case study, and the results showed that the water-level dispatching process exhibited a high degree of conformity with the actual dispatching process during both the water supply and storage periods. Furthermore, the output calculation results based on the M-IWO-ODDDP algorithm were 3.94% and 0.30% higher than the actual output and ODDDP calculation results, respectively, while reducing water abandonment by 21.58% and 4.07%.
1. Introduction
In recent years, China’s hydropower industry has developed rapidly and 13 major hydropower stations have been planned and constructed. Currently in China, hydropower has the largest share of installed capacity for renewable energy sources. Fully exploiting multi-reservoir joint power generation holds significant importance for enhancing the utilization rate of hydropower resources and attaining carbon peak and carbon neutrality objectives [1,2,3]. With the improvement of our understanding of the benefits of power generation, as well as the operational safety and ecological protection of hydropower stations, the operational processes of cascade reservoirs are becoming more complicated. In addition to the conventional reservoir dispatching constraints, ecological flow constraints and guaranteed output constraints are also taken into account in the construction of an optimal operation model for cascade hydropower stations.
However, due to the distinctive attributes of the optimal operation model of cascade hydropower stations, such as being high-dimensional, nonlinear, and subject to multiple constraints, the construction and resolution of the model have emerged as prominent and challenging issues in contemporary research [4,5,6,7].
Currently, the techniques used for resolving reservoir optimization operation problems mainly fall into two categories: traditional optimization algorithms and swarm intelligence optimization algorithms. Among them, traditional optimization algorithms mainly include linear programming and its improved forms, nonlinear programming, and dynamic programming and its improved algorithms. For example, a linear programming model has been established to address the issue of flood control compensation and regulation in reservoirs, and the linear coupling between reservoir dispatch and river flow has been effectively mapped in this model [8]. Regarding algorithms used for nonlinear programming, a hedging model for the economic optimization of hydropower stations has been formulated and resolved using nonlinear programming techniques [9]. In the field of dynamic programming and its improved algorithms, when applying the above algorithms to solve a hydropower optimal scheduling model, it is evident from the results that these three methods exhibit limited efficiency in addressing high-dimensional multi-constraint problems [10]. Numerous studies have consistently demonstrated that conventional optimization algorithms, such as dynamic programming and its enhanced variants, often encounter “dimension disaster” when addressing the joint optimization scheduling problem in large-scale reservoir systems [11,12,13,14,15].
To solve the “dimension disaster” problem faced by traditional optimization algorithms, swarm intelligence optimization algorithms have been rapidly developed and widely applied in reservoir optimization. For example, Afshar employed Particle Swarm Optimization (PSO) for resolving an optimization operation model for water supply and power generation in Iran’s DEZ reservoir, and the study’s findings indicated that the convergence of the PSO algorithm was relatively reliable [16]. Azizipour et al. employed the Invasive Weed Optimization (IWO) algorithm for resolving the optimization operation model of power generation in a single reservoir and verified its applicability in reservoir operation optimization [17]. Fang et al. took Liujiaping Hydropower Station as their research object and employed the NSGA-II algorithm to improve an operational model of the reservoir, using multiple objectives for optimization [18]. Li et al. used a genetic algorithm (GA) for addressing the operational model for the multi-objective optimization of Huangzangsi Reservoir, providing a theoretical reference for the scheduling and operational management of the reservoir [19]. However, previous research has shown that swarm intelligence optimization algorithms have the drawbacks of premature convergence and falling into local optima when addressing optimization problems of significant scale and high dimensionality [20].
Based on the principle of orthogonal testing, scholars have proposed an Orthogonal Discrete Differential Dynamic Programming (ODDDP) algorithm that effectively addresses computational dimensionality and optimally solves large-scale reservoir scheduling problems [21]. Through orthogonal experiments, the ODDDP algorithm greatly reduces the number of scheme components, and greatly improves the convergence speed without affecting the optimization results. Moreover, compared with swarm intelligence optimization algorithms, the biggest advantage of ODDDP is that it solves the problem of unstable optimization results (that is, poor reproducibility of results) of swarm intelligence optimization algorithms. Under the condition of the same initial conditions, its optimization results are fixed and unique each time. However, this algorithm has limitations related to its reliance on the quality of the initial solutions and susceptibility to local optima convergence. To address this issue, the present study examined the optimization principle of the ODDDP algorithm and drew insights from the spatial diffusion mechanism of the IWO algorithm. Consequently, novel IWO-ODDDP and M-IWO-ODDDP algorithms were designed and proposed. By using the 11-stage mixed-model reservoir in the Wujiang River basin as a case study, this research thoroughly analyzed and validated the efficacy of the enhanced ODDDP algorithm for tackling intricate high-dimensional nonlinear optimization problems.
The subsequent sections of this document are structured in the following manner. Section 2 formulates the optimal operation model for cascade reservoirs, taking into account the constraints of the relaxation variables. Section 3 introduces the ODDDP algorithm and its enhancement strategy by analyzing the convergence and robustness of the improved ODDDP algorithm based on test functions. Additionally, a methodology is presented to solve the cascade reservoir optimal operation model using the enhanced ODDDP algorithm. Following that, Section 4 presents and analyzes the case study along with its findings. The subsequent section, Section 5, is dedicated to formulating conclusions.
2. Optimal Operation Model of Cascade Reservoirs
2.1. Objective Function
The guaranteed output reflects the power generation capacity of a hydropower station to a certain extent. Reducing the damage to the guaranteed output is vital for ensuring the safe operation of a power grid and demonstrating the level of reservoir dispatching. Therefore, a maximum generation model of cascade hydropower stations that takes into account the constraint of guaranteed output is proposed in this paper.
In this model, “year” is taken to mean the whole scheduling period, and “month” is taken to mean the calculation period. The model’s objective function is formulated as follows:
where F represents the objective function expression, T represents the length of the scheduling interval, M represents the count of reservoirs, represents the output of reservoir i at period t, and represent penalty coefficients, and represents a positive integer. is the guaranteed output of reservoir i; is the overall output coefficient of reservoir i; and are the flow of power generation and the generating head of reservoir i at period t, respectively; and is the ternary logical variable at period t, and its value is as follows:
where mod is a function that takes the remainder. And in this paper, the value of is set to 1.
2.2. Constraints
2.2.1. Conventional Constraints
To ensure the safety of the reservoir, power station, and flood control equipment, the conventional constraints are set in the model of reservoir optimal operation. Moreover, the conventional constraints of the cascade reservoir optimal operation model mainly include the water balance constraint, water level of the reservoir constraint, discharge flow constraint, output of the hydropower plant constraint, generating flow constraint, generating head constraint, and runoff coupling constraint between two adjacent reservoirs. The specific expression of each constraint is as follows:
When the scheduling plan does not satisfy any of the constraints listed in Table 1, it is penalized by setting the objective function value of the plan to a certain minimum value. And this allows the solution to be discarded during the sorting process as a nonoptimized solution.

Table 1.
The conventional constraints of optimal operation model for cascade reservoirs.
2.2.2. Model-Specific Constraints
- (1)
- Ecological Flow Constraint
With the promotion of ecological construction in China, ecological flow has become an important constraint in the process of reservoir operation. That is, the minimum discharge flow of the reservoir should not be less than the ecological flow. The expression of ecological flow constraint is as follows:
where represents the ecological flow of reservoir i at period t.
- (2)
- Relaxation constraints of water level
The model solution results obtained via directly adopting the aforementioned objective function and constraint conditions often exhibit inconsistencies with real-world scenarios. This is primarily due to the model’s tendency to prioritize maintaining high water levels for maximizing power generation during dispatch periods, disregarding uncertainties associated with incoming water, particularly during flood seasons. Such an oversight could potentially intensify reservoir flood control pressures and increase the risk of water abandonment. Therefore, to ensure alignment between the solution results of the model and the actual dispatching operation of the reservoir group, flexible constraints on relaxation variables are proposed for the termination of both the water supply and storage periods. The method of relaxation variable constraint control used for the termination of the water supply period is presented in Equation (4), while Equation (5) illustrates the corresponding control for the termination of the water storage period.
where and are the outputs of reservoir i during the termination of the water supply and storage periods, considering the constraints imposed by relaxation variables; and are the outputs of reservoir i during the termination of the water supply and storage periods, considering the constraints imposed by relaxation variables; and are reservoir i’s water levels during the termination of the water supply and storage periods, respectively; and are the upper limits of reservoir i’s water levels during the termination of the water supply and storage periods, respectively; and are the lower thresholds for reservoir i’s water levels at the termination of the water supply and storage periods, respectively; and and are the relaxation control coefficients during the termination of the water supply and storage periods, respectively.
3. Methodology
3.1. ODDDP Algorithm
Dynamic programming (DP) is the most commonly used optimization algorithm to solve the optimal dispatching problem of a single reservoir, and it has the problem of “dimension disaster” when solving the optimal dispatching problem of a cascade reservoir with more than two reservoirs. The Discrete Differential Dynamic Programming (DDDP) is an improved algorithm of DP, which is mainly used to solve the optimal scheduling problem of cascade reservoirs. However, it still has the problem of “dimension disaster” when solving the optimal scheduling problem of a large number of cascade reservoirs. Therefore, the ODDDP algorithm based on orthogonal experiment came into being. Moreover, a cascade reservoir optimization scheduling model containing 4 reservoirs was built by the author of the algorithm, and the ODDDP and DDDP algorithms were used to solve the model respectively. The results showed that there was no significant difference between the optimization results of the ODDDP and DDDP. However, the DDDP takes nearly 700 times longer than the ODDDP algorithm [21].
The ODDDP algorithm built on the foundations of the DDDP algorithm via orthogonal experiments for dimensionality reduction. An orthogonal experiment is an experimental plan that targets multiple factors and levels, adopting the principle of “uniform dispersion, uniformity, and comparability” to select representative experimental plans, in an effort to minimize the quantity of experiments while ensuring the reliability of experimental results or conclusions. Although the ODDDP algorithm greatly reduces the number of scheme combinations in the DDDP algorithm, it does not change the discrete increment generation method of the DDDP algorithm, thus failing to overcome the shortcomings related to the DDDP algorithm’s dependence on initial solution quality and easy convergence to local optimal solutions.
At present, the DDDP algorithm utilizes two methods for generating discrete increments: the fixed increment [21] and variable increment [10] methods. The fixed increment method uses a fixed and invariant discrete increment for optimization during the algorithm iteration process. The variable increment method uses a larger discrete increment in the early stage of iteration and a smaller discrete increment in the subsequent iteration phase to shift the algorithm from global to local optimization. Related studies have shown that the DDDP algorithm’s optimization effect with variable increment implementation is better than that with fixed increment implementation [22]. Equation (6) is one of the calculation methods used for determining the discrete increment.
where represents the discrete increment of time period t for reservoir i during each iteration of the algorithm, iter represents the current quantity of iterations of the algorithm, and represents the upper limit of iterations that can be performed.
As demonstrated in Equation (6), the discrete increment in the ODDDP algorithm gradually decreases as the number of iterations grows, achieving a global-to-local optimization process. However, when the initial optimization process deviates far from the global optimal solution, the ODDDP algorithm often falls into local optima in the later optimization process. Therefore, this article introduced Gaussian random variables to perturb the discrete increments during the algorithm iteration process to enhance the algorithm’s capacity for achieving global optimization.
The flowchart of the ODDDP algorithm for optimization is shown in Figure 1.
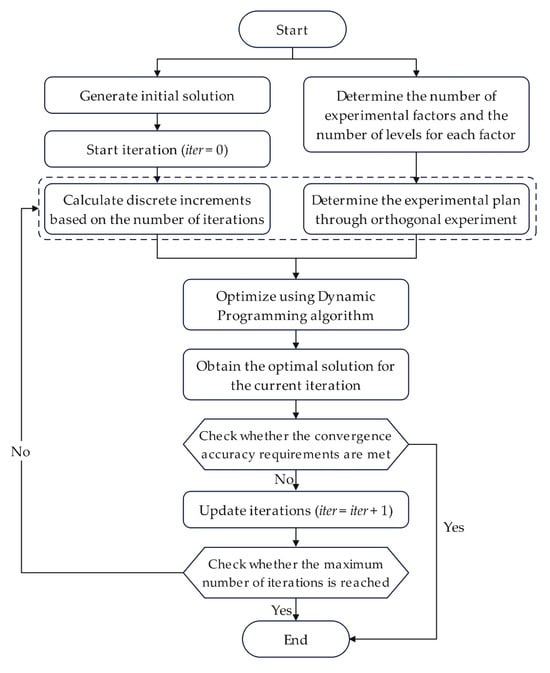
Figure 1.
The flowchart of the ODDDP algorithm.
3.2. Improvement Strategy for the ODDDP Algorithm
Drawing inspiration from the mechanism used for the spatial diffusion of seeds around parent individuals in the Invasive Weed Optimization (IWO) algorithm [23], the IWO-ODDDP algorithm was proposed, and its discrete increment generation method is shown in Equation (7):
where and represent the standard deviations of reservoir i at the onset and culmination of iteration, respectively, with ; represents the nonlinear harmonic index, with a value of 3; and represents a random variable that conforms to a Gaussian distribution.
As shown in Equation (7), the IWO-ODDDP algorithm and the variable increment optimization method in the ODDDP algorithm are consistent, and both can achieve a one-time optimization process that shifts from global to local. However, due to the disturbance of random Gaussian variables, the IWO-ODDDP algorithm has a strictly nonmonotonic “global–local” optimization characteristic, unlike the ODDDP algorithm. The optimization process diagram of the IWO-ODDDP algorithm and ODDDP algorithm is depicted in Figure 2. The data presented in Figure 2 illustrate that the optimization mode of the ODDDP algorithm implements a strategy of global-to-local optimization based on strict monotonic characteristics. Compared with the optimization mode of the ODDDP algorithm, the IWO-ODDDP algorithm can improve the breadth and depth of optimization in the initial iteration, theoretically improving the algorithm’s global convergence ability.
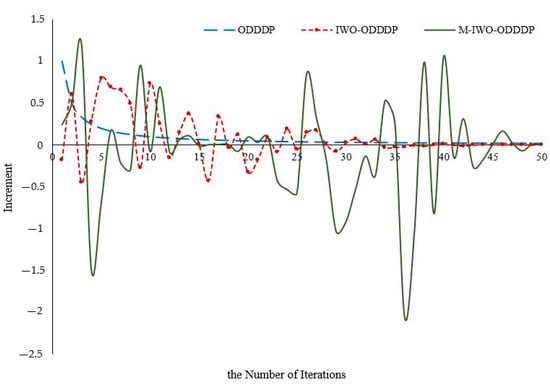
Figure 2.
A schematic representation of three algorithms for optimization.
Several scholars have highlighted the fact that the single “global–local” optimization mode has the drawback of easily falling into local optimal solutions [24]. To further increase the optimization breadth and depth of the algorithm, based on the periodic properties of trigonometric functions, this paper proposed the M-IWO-ODDDP algorithm by modifying Equation (7) to reflect the form shown in Equation (8) (where n is an integer):
The schematic diagram of the M-IWO-ODDDP algorithm optimization process is also depicted in Figure 2.
The information depicted in Figure 2 demonstrates that the optimization method of the M-IWO-ODDDP algorithm can achieve the reciprocating optimization characteristic of “global–local–global–local···”. It could potentially determine the local optimal solution through subsequent “global–local” optimization when “global–local” optimization becomes trapped in a suboptimal solution specific to the locality and cannot be completed, thereby increasing the algorithm’s global search ability and search depth. Moreover, it could enhance the algorithm’s capacity to achieve global convergence.
As shown in Equation (8), for a specific value of n, it is necessary to increase the number of iterations as much as possible to reduce the range of discrete variables between adjacent iterations, potentially decreasing the probability of the algorithm “crossing” the optimal solution during the optimization process. When n remains constant, increasing the maximum threshold for the iteration count enhances the likelihood of convergence towards the global optimal solution. Simultaneously, with an increase in the upper limit of the iterations, there will be a significant rise in the program’s computational duration, leading to the algorithm having low optimization efficiency. Taking into account both the algorithm’s optimization quality and operational efficiency, this article recommended taking n as 1, and then Equation (8) is transformed into the following:
3.3. Convergence and Robustness Analysis of the Enhanced ODDDP Algorithm
3.3.1. Convergence Analysis of the Enhanced ODDDP Algorithm
The Schaffer and Shubert functions are widely employed as benchmark test functions to evaluate the optimization capabilities of intelligent algorithms [25]. The Schaffer and Shubert functions are two-dimensional complex entities. The independent variables of Schaffer and Shubert fall within the range of [−10, 10]. The Schaffer function attains its minimum value of 0 at the coordinate (0, 0), while the Schubert function achieves its minimum value of −186.7309 at the coordinate (−1.42513, 0.80032). The convergence of ODDDP, IWO-ODDDP, and M-IWO-ODDDP was examined in this study using Schaffer and Shubert functions.
In the process of resolving the Schaffer and Shubert functions using the ODDDP, IWO-ODDDP, and M-IWO-ODDDP algorithms, we initialized the independent variable coordinates at (5, 5) as the first proposed resolution and set the upper limit of iterations to 2000. The standard deviation was initialized at 5 and finally reduced to 0.0001 when using the IWO-ODDDP and M-IWO-ODDDP to optimize and solve the aforementioned two test functions. The optimization process and the resulting optimizations of the algorithm are depicted in Figure 3 and Table 2, respectively.
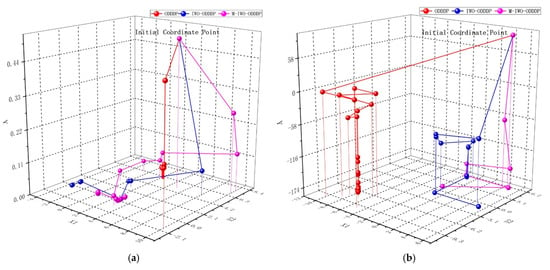
Figure 3.
The optimization process diagram of an intelligent algorithm for test functions: (a) Schaffer function optimization process; (b) Shubert function optimization process.

Table 2.
The optimization results of an intelligent algorithm for test functions.
The findings presented in Figure 3 and Table 2 demonstrate the following: ① The improved ODDDP algorithm had a significantly better convergence effect than the ODDDP algorithm. ② The M-IWO-ODDDP improvement method exhibited a higher likelihood of surpassing the constraints imposed by local optimal solutions and converging or approximating towards the global optimal solution than the IWO-ODDDP improvement method.
3.3.2. Robustness Analysis of M-IWO-ODDDP
Based on the convergence analysis results of the improved ODDDP algorithm, we observed that the M-IWO-ODDDP algorithm had a better convergence effect than the ODDDP and IWO-ODDDP algorithms. To analyze the robustness of the M-IWO-ODDDP algorithm, this paper took the Schaffer function as an example and analyzed its impact on optimization results based on two aspects: different initial solutions and different parameter values.
- (1)
- The influence of diverse initial solutions on optimization results
Within the range of independent variable values in the Schaffer function, 100 sets of initial solutions were randomly generated, and the remaining parameter values were the same as those in the convergence analysis of the improved ODDDP algorithm. The outcomes of the optimization process can be observed in Figure 4. In the figure, the pink points represent the initial solution, and the purple points represent the global optimal solution.
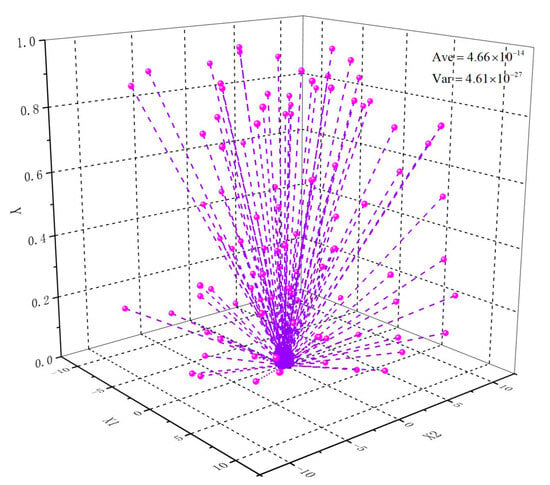
Figure 4.
The optimization results with different initial solutions.
The information depicted in Figure 4 shows that the M-IWO-ODDDP algorithm had no significant dependence on the initial solution. This improvement method could converge towards the globally optimal solution under different initial solution conditions. The above results demonstrate that the M-IWO-ODDDP algorithm has a robust convergence effect.
- (2)
- The impact of varying parameter values on the outcomes of optimization
The M-IWO-ODDDP algorithm mainly involves two parameters: the initial and the final values of the standard deviation. The initial standard deviation value mainly reflects the algorithm’s global optimization performance, while the final standard deviation value reflects the algorithm’s local optimization performance. Therefore, the initial standard deviation value was considered a larger value in the search space, and the final standard deviation value was considered a smaller value. The impact of varying parameter values on the outcomes of optimization was analyzed by randomly generating 100 groups of parameter values within the intervals of [2, 10] and [0, 0.01] for the initial and final standard deviations. The outcomes of the optimization can be observed in Figure 5.
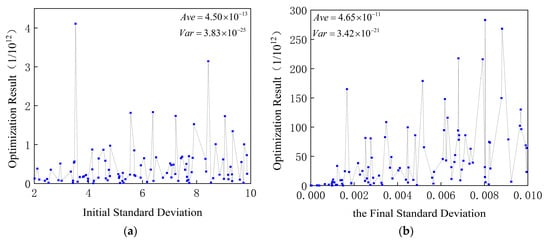
Figure 5.
The optimization results with different initial and final standard deviations: (a) results with different initial standard deviation; (b) results with different final standard deviation.
The information depicted in Figure 5 reveals that under different initial and final standard deviation conditions, the M-IWO-ODDDP algorithm can converge or approximately achieve the most favorable outcome on a global scale. Moreover, the convergence effect of the M-IWO-ODDDP algorithm was relatively stable, as shown by the consistent variation in the optimization results. Furthermore, by comparing the optimization results under different initial and final standard deviation values, it can be seen that the impact of changes in the initial standard deviation value on the convergence effect was smaller than that of the ultimate measure of variability. Based on the optimization results under different standard deviation terminal values, it can be seen that as the standard deviation terminal value increased, the optimization effect gradually deteriorated. When the standard deviation terminal value takes a smaller value, the optimization results converge or approximately converge towards the globally optimal solution, and the convergence effect is stable.
The optimization results under different initial solutions, various initial standard deviation measurements, and diverse final values of standard deviation demonstrate the robustness of the M-IWO-ODDDP algorithm as a comprehensive approach. Regarding the specific impacts of different parameter values on the optimization results, the sensitivity of the optimization results to the initial solution value was smallest, followed by the initial standard deviation value, and the sensitivity of the final standard deviation value was highest.
3.4. Improved ODDDP Algorithm Application in Cascade Hydropower Station Optimal Operation Model
Due to the superior optimization effect of the M-IWO-ODDDP compared to IWO-ODDDP, this study utilized the former to address the optimal operational model used for a series of interconnected hydroelectric power plants. The solution flow chart of the cascade reservoir optimization operation model based on the M-IWO-ODDDP algorithm was consistent with the ODDDP algorithm (as shown in Figure 1). The following are the precise measures taken:
Step 1: Generate the initial solution. Due to the fact that the M-IWO-ODDDP algorithm is not affected by the quality of the initial solution, the initial reservoir water-level scheduling process line for cascade reservoirs was generated using either the equal flow method or the random method.
Step 2: Reframe the orthogonal test plan. Orthogonal test combination schemes were generated using allpairs software, taking into account the quantity of cascade reservoirs engaged in the process of regulation and the quantity of the discrete states. Let m represent the quantity of reservoirs participating in regulation and n represent the quantity of distinct states (where n is an odd number). Consequently, we aimed to determine the total count M of the orthogonal test scheme combinations at each moment during the dispatching period. The matrix A was constructed by amalgamating the aforementioned M orthogonal test schemes.
where is the element value corresponding to the i-level reservoir of the j-th state combination scheme in the orthogonal experimental scheme combination matrix A, and is an integer.
Step 3: Generate the state combination scheme. The cascade reservoir water-level dispatching process for each combination scheme was established according to the initial water-level dispatching process and orthogonal test combination scheme matrix. This process is defined in Equations (11) and (12).
where represents reservoir i’s water level at time t in state combination scheme j, and represents the standard deviation of reservoir i calculated via the algorithm in the iter iteration.
Step 4: Dynamic programming optimization. Given that there were M orthogonal test scheme combinations at each time point throughout the scheduling period, the overall count of possible arrangements for schemes throughout the scheduling period was MT−1 + 2M. Moreover, the optimal scheduling process in all current combinations of scheduling schemes was determined using the dynamic programming algorithm by calculating their target fitnesses.
Step 5: Iterative calculation. was used as the new initial scheduling solution. Moreover, we reiterated Steps 3~4 until the condition iter = itermax was met. Finally, the ultimate optimization strategy was presented.
4. Case Study
4.1. Study Area
This study was centered on the Wujiang River basin, located in the province of Guizhou in China. The research subject of this study comprised a total of 11 reservoirs situated in the Wujiang River basin, constituting a cascade system. Based on this, we developed a comprehensive power generation model for the Wujiang River cascade reservoirs that takes into account both medium- and long-term factors. The runoff data from the actual Wujiang Reservoir Group in 2018 were utilized as inputs for the model. Our objective was to assess and exhibit the dependability of the M-IWO-ODDDP algorithm for optimizing cascade reservoir dispatching through model resolution. Furthermore, the feasibility of the proposed improved optimal dispatching model for cascade hydropower stations was verified in this paper. In the cascade reservoirs of Wujiang River, four reservoirs, namely Suofengying, Geliqiao, Silin, and Shatuo, are operated on a daily basis, while the remaining reservoirs are managed on an annual or multi-year basis. The medium- and long-term dispatching processes of the daily regulation reservoir were simulated through a balanced approach to inflow and outflow. That is, the outflow of the daily regulated reservoir was simulated as equivalent to its inflow. The spatial topological relationship between the 11 reservoirs within the Wujiang River basin is depicted in Figure 6.
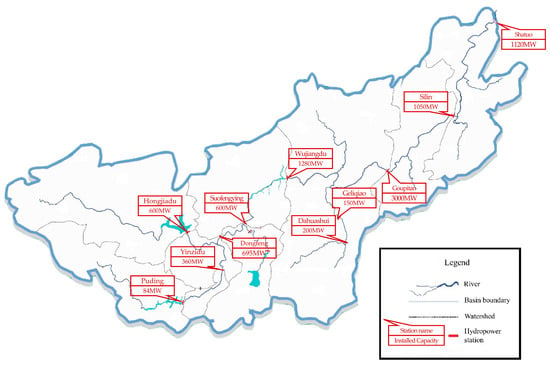
Figure 6.
The spatial topological relationship between the 11 reservoirs in the Wujiang River Basin.
The initial solution of the Wujiang cascade reservoir’s maximum power generation model was generated using the equal flow method. In the course of resolving the model, the discrete state number was taken as 3, and a seven-factor, three-level orthogonal table was constructed using allpairs software to generate 18 orthogonal experimental schemes. The final value of the standard deviation in the M-IWO-ODDDP algorithm was 0.0001, and the initial value of the standard deviation was as follows:
where is the initial standard deviation value at time t of the i-th reservoir.
4.2. Results and Discussion
By setting different maximum iteration times, the ODDDP algorithm and M-IWO-ODDDP algorithm were used to solve the medium- and long-term optimization scheduling model of the Wujiang cascade reservoirs. Drawing from the outcomes of the proposed solution, the ability of the M-IWO-ODDDP algorithm to perform optimization scheduling modeling of a series of interconnected hydroelectric power plants was analyzed. The optimization results of the two algorithms under different maximum iteration times are displayed in Figure 7.
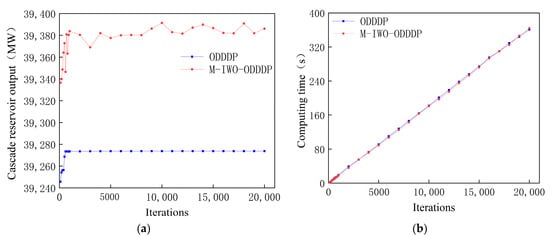
Figure 7.
The optimization results of the ODDDP and M-IWO-ODDDP algorithms under different maximum iteration times: (a) output of the cascade reservoirs; (b) time consumption of calculation.
As depicted in Figure 7, the following conclusions were drawn in terms of optimization results: (1) Overall, the M-IWO-ODDDP algorithm was more prone to overcoming the local optimal solution limitation and achieving a global optimal solution, unlike the ODDDP algorithm. (2) When itermax was small, the ODDDP algorithm’s optimization results improved as itermax increased, but as the itermax value continued to increase, the optimization results stabilized. By comparing the optimization results with those of the M-IWO-ODDDP algorithm, it was seen that they only converged to a certain local optimal solution. (3) The M-IWO-ODDDP algorithm exhibited significant instability in its optimization results due to the randomness of Gaussian variables when itermax was small. As the itermax value increased, although the optimization results stabilized, they still exhibited instability.
In terms of computational time, there was little disparity between the M-IWO-ODDDP algorithm and the ODDDP algorithm under the same itermax conditions, and there was a notable linear relationship between the duration of computation and the itermax value, indicating that the computational time was only affected by the maximum number of iterations and had no significant relationship with the generation method of discrete variables in the ODDDP algorithm.
Furthermore, a comparative examination of the optimization results of the two algorithms was also conducted in this paper by examining the optimal scheduling schemes for cascade reservoirs optimized using the ODDDP and M-IWO-ODDDP algorithms. The output and abandoned water flows of cascade reservoirs optimized by the ODDDP and M-IWO-ODDDP algorithms are shown in Table 3.

Table 3.
The optimal solution scheme for the optimization of the ODDDP and M-IWO-ODDDP algorithms.
According to the results presented in Table 3 for the output and abandoned water flow of cascade reservoirs in the Wujiang River, it can be observed that both the optimized ODDDP and M-IWO-ODDDP algorithms yielded higher calculated outputs compared to the actual values, while the calculated abandoned water was lower than the actual amount. The optimization scheme resolved by the M-IWO-ODDDP algorithm reduced the unused water capacity of the cascade reservoirs, improved the rate at which water resources were used, and increased the output of the series of interconnected hydroelectric power plants in comparison with the ODDDP algorithm. Furthermore, according to the output of Wujiang hydroelectric power plants, it is evident that the difference in output between the two algorithm optimization results mainly manifested in the Puding and Dahuashui reservoirs. Their reservoir water-level regulation process is depicted in the diagram provided in Figure 8.
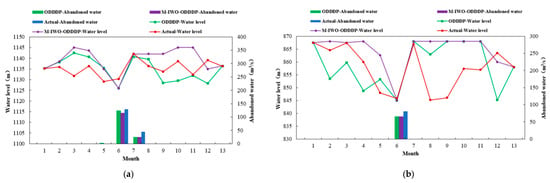
Figure 8.
The dispatching strategy for the Puding and Dahuashui reservoirs: (a) Puding reservoir; (b) Dahuashui reservoir.
The information depicted in Figure 8 indicates the following: (1) The water-level dispatching process calculated via the enhanced cascade reservoir optimal dispatch model was highly consistent with the actual dispatch process during water supply and storage periods. This finding highlights that the optimization scheme proposed in this study is more suitable for practical dispatching scenarios compared to traditional models. (2) The overall water-level scheduling schemes of Puding and Dahuashui reservoirs optimized via the M-IWO-ODDDP algorithm were better than those optimized by the ODDDP algorithm, indicating that the optimization results of the M-IWO-ODDDP algorithm fully utilized the head efficiency, reduced the rate at which water was consumed for generating power, enhanced the efficiency of water resource utilization, and enhanced electricity production within the timeframe of reservoir management in the “water-to-electricity” scheduling mode. (3) The Puding and Dahuashui reservoirs did not abandon water before June, and in early June, the reservoirs’ water levels all decreased to the lower boundary of the reservoir water level, indicating that the optimization results of the M-IWO-ODDDP and ODDDP algorithms both reduced the abandoned water volume during the flood period by reinforcing the flow of power generation and reducing the reservoir water level before the flood period, as well as pre-releasing the reservoir in advance. (4) For the Puding reservoir, by the end of June, the M-IWO-ODDDP optimization scheme’s water level reached the flood period limit water level (i.e., the upper limit of the flood season water-level constraint), which was better than the ODDDP algorithm’s optimization result, resulting in a greater amount of abandoned water being present in June. This indicates that in the later stage of optimization, the ODDDP algorithm failed to overcome the local optimal limit due to the reduced search range, causing the reservoir water level to not converge to the upper limit of the flood season water-level constraint by the end of June, so it failed to achieve the most favorable outcome on a worldwide scale.
To analyze the impact of the number of reservoirs, size of the reservoirs, and other factors on the calculation time of the M-IWO-ODDDP algorithm, we took Hongjiadu, Puding, Hongjiadu–Dongfeng (H-D), Hongjiadu–Dongfeng–Suofengying–Wujiangdu (H-D-S-W), and Hongjiadu–Dongfeng–Suofengying–Wujiangdu–Goupitan (H-D-S-W-G) as research objects, respectively, by setting different orthogonal experimental level numbers, and using the M-IWO-ODDDP algorithm to solve the model. The results are shown in Table 4 and Figure 9.

Table 4.
The computing time of M-IWO-ODDDP algorithm under different conditions.
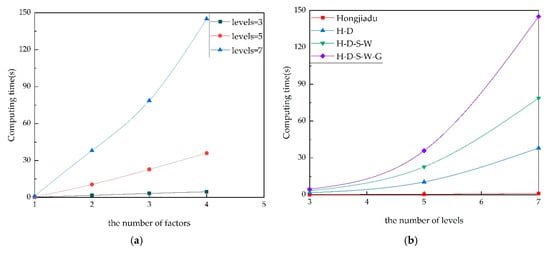
Figure 9.
The effects of varying quantities and levels of different factors on the computing time of M-IWO-ODDDP: (a) the impact of factor quantity; (b) the impact of factor level numbers.
Analysis of Table 4 and Figure 9 reveals the following: (1) For a specific reservoir or cascade reservoirs, an increase in the number of levels results in an exponential growth in computing time. (2) The computing times for HJD and PD reservoirs indicate that, when the number of levels is constant, reservoirs with larger capacity exhibit longer calculation times. (3) At a given level number, as the quantity of reservoirs (primarily reflecting factor count) increases, the calculation time also escalates, demonstrating a transition from linear growth (with fewer factors) to exponential growth (as factor count increases).
5. Conclusions
By considering the ecological flow, guaranteed output, and relaxation constraints of the water level at the end of the water supply and storage periods, a maximum generation model of cascade hydropower stations that takes into account the constraint of guaranteed output was proposed in this paper. Moreover, by drawing on the spatial diffusion mechanism of the IWO algorithm, the IWO-ODDDP and M-IWO-ODDDP algorithms were proposed. By analyzing the improved ODDDP algorithm’s convergence and resilience, as well as considering the Wujiang cascade reservoirs to be the research object, a study was carried out, the findings of which are outlined below:
- (1)
- In comparison to the conventional optimal operation model of cascade reservoirs, the results of the model constructed in this paper show that the reservoir water level was lowered in advance of the flood season and rose during the flood season, which aligned with the actual scheduling patterns observed in cascade reservoir systems.
- (2)
- The convergence performance of the improved ODDDP algorithm surpassed that of its original algorithm, and the M-IWO-ODDDP improvement method can more easily overcome the local optimal solution limit than the IWO-ODDDP improvement method and achieve the globally optimal solution through convergence.
- (3)
- The M-IWO-ODDDP improvement method has no significant dependence on the initial solution quality, and different parameter values in the algorithm have limited impacts on the convergence effect. The algorithm also has good robustness.
- (4)
- For the same maximum number of iterations, there was little disparity in computation time between the M-IWO-ODDDP and ODDDP algorithms. The stability of the M-IWO-ODDDP optimization results was lower than that of the ODDDP algorithm due to the influence of random variable perturbations for different maximum iteration times.
- (5)
- The computing time of the M-IWO-ODDDP is influenced by the number of cascade reservoirs, reservoir size, and the levels of factors. As the quantity of reservoirs, storage capacity, and factor levels increase, there is a corresponding rise in the algorithm’s computing time.
In summary, the optimal operation model of cascade reservoirs constructed in this paper is consistent with the actual scheduling law of reservoirs. The M-IWO-ODDDP algorithm proposed in this paper can greatly improve the solving efficiency of the optimal operation model of cascade reservoirs, and the research results can provide guiding value for cascade reservoirs scheduling practice.
Despite this, the M-IWO-ODDDP algorithm does not demonstrate computational superiority over the ODDDP algorithm; thus, further investigation is warranted to enhance its computational efficiency through the application of computer parallel technology.
Author Contributions
Conceptualization, C.W. and Z.W.; methodology, C.W. and P.Y.; software, P.Y. and Z.L.; validation, Z.L. and Y.W.; resources, C.W. and Z.W.; data curation, P.Y.; writing—original draft preparation, C.W.; writing—review and editing, C.W.; visualization, C.W.; funding acquisition, C.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R & D Program of China (Grant No. 2023YFC3206700), the Funded Projects of Special Funds for Basic Scientific Research Operating Expenses of Yellow River Institute of Hydraulic Research (Grant No. HuangKeFa202218 & Grant No. HuangKeFa202304).
Data Availability Statement
The data used to support the findings of this study are included within the article.
Acknowledgments
We would like to acknowledge the reviewers and editors for their valuable comments and suggestions.
Conflicts of Interest
Author Peng Yue is employed by the company, Qinghai Sanjiang Hydropower Development Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Li, X.; Liu, P.; Wang, Y.; Yang, Z.; Gong, Y.; An, R.; Huang, K.; Wen, Y. Derivation of operating rule curves for cascade hydropower reservoirs considering the spot market: A case study of the China’s Qing River cascade-reservoir system. Renew. Energy 2022, 182, 1028–1038. [Google Scholar] [CrossRef]
- Thiha, S.; Shamseldin, A.; Melville, B. Correction to: Improving the summer power generation of a hydropower reservoir using the modified multistep ahead timevarying hedging rule. Water Resour. Manag. 2022, 36, 2889. [Google Scholar] [CrossRef]
- Ren, P.; Zhou, J.; Mo, L.; Zhang, Y. Comprehensive study on cascade hydropower stations in the lower reaches of yalong river for power generation and ecology. Energy Sustain. Dev. 2023, 73, 236–246. [Google Scholar] [CrossRef]
- Schultz, G.A.; Plate, E.J. Developing optimal operating rules for flood protection reservoirs. J. Hydrol. 1976, 28, 245–264. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, C.; Peng, Y.; Fu, G.; Zhou, H. A two stage Bayesian stochastic optimization model for cascaded hydropower systems considering varying uncertainty of flow forecasts. Water Resour. Res. 2014, 50, 9267–9286. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Wang, S.; Cheng, C.; Jiang, Z.; Qin, H.; Liu, Y. Developing a successive linear programming model for head-sensitive hydropower system operation considering power shortage aspect. Energy 2018, 155, 252–261. [Google Scholar] [CrossRef]
- Babamiri, O.; Marofi, S. A multi-objective simulation–optimization approach for water resource planning of reservoir–river systems based on a coupled quantity–quality model. Environ. Earth Sci. 2021, 80, 389. [Google Scholar] [CrossRef]
- Chen, S.; Li, D.; Tao, X.; Huang, Y. Development and application of a compensative regulationlinear programming model for reservoir flood-control. Adv. Water Sci. 2017, 28, 507–514. [Google Scholar]
- Wang, J.; Cheng, C.; Wu, X.; Shen, J.; Cao, R. Optimal Hedging for Hydropower Operation and End-of-Year Carryover Storage Values. J. Water Resour. Plan. Manag. 2019, 145, 04019003. [Google Scholar] [CrossRef]
- Shen, J.; Zhu, W.; Cheng, C.; Zhong, H.; Jiang, Y.; Li, X. Method for high-dimensional hydropower system operations coupling random sampling with feasible region identification. J. Hydrol. 2021, 599, 126357. [Google Scholar] [CrossRef]
- Zhao, T.; Cai, X.; Lei, X.; Wang, H. Improved Dynamic Programming for Reservoir Operation Optimization with a Concave Objective Function. J. Water Resour. Plan. Manag. 2012, 138, 590–596. [Google Scholar] [CrossRef]
- Heidari, M.; Chow, V.; Kokotović, P.; Meredith, D. Discrete Differential Dynamic Programing Approach to Water Resources Systems Optimization. Water Resour. Res. 1971, 7, 273–282. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Cheng, C. Optimizing electrical power production of hydropower system by uniform progressive optimality algorithm based on two-stage search mechanism and uniform design. J. Clean. Prod. 2018, 190, 432–442. [Google Scholar] [CrossRef]
- Raso, L.; Bader, J.; Weijs, S. Reservoir Operation Optimized for Hydropower Production Reduces Conflict with Traditional Water Uses in the Senegal River. J. Water Resour. Plan. Manag. 2020, 146, 05020003. [Google Scholar] [CrossRef]
- Mousavi, S.; Zanoosi, A.; Afshar, A. Optimization and simulation of a multiple reservoir system operation. J. Water Supply Res. Technol. AQUA 2004, 53, 409–424. [Google Scholar] [CrossRef]
- Afshar, M. Large scale reservoir operation by Constrained Particle Swarm Optimization algorithms. J. Hydro Environ. Res. 2012, 6, 75–87. [Google Scholar] [CrossRef]
- Azizipour, M.; Ghalenoei, V.; Afshar, M.; Solis, S. Optimal Operation of Hydropower Reservoir Systems Using Weed Optimization Algorithm. Water Resour. Manag. 2016, 30, 3995–4009. [Google Scholar] [CrossRef]
- Fang, G.; Ding, Z.; Huang, X.; Dai, L. Optimization of hydropower reservoir operation considering river ecological protection. J. Hydroelectr. Eng. 2018, 37, 1–9. [Google Scholar]
- Li, Y.; Chen, Z.; Yang, J.; Tang, N.; Dong, G. Study on Optimal Operation of Heihe Huangzangsi Water Control Project. Yellow River 2021, 43, 140–146. [Google Scholar]
- Suwal, N.; Huang, X.; Kuriqi, A.; Chen, Y.; Pandey, K.; Bhattarai, K. Optimisation of cascade reservoir operation considering environmental flows for different environmental management classes. Renew. Energy 2020, 158, 453–464. [Google Scholar] [CrossRef]
- Feng, Z.; Liao, S.; Niu, W.; Cheng, C.; Tang, J.; Su, H. Orthogonal discrete differential dynamic programming for mid-long term optimal operation of cascade hydropower system. Proc. CSEE 2015, 35, 4635–4644. [Google Scholar]
- Feng, Z.; Niu, W.; Cheng, C.; Lund, J. Optimizing hydropower reservoirs operation via an orthogonal progressive optimality algorithm. J. Water Resour. Plan. Manag. 2018, 144, 4018001. [Google Scholar] [CrossRef]
- Mehrabian, A.; Lucas, C. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inform. 2006, 1, 355–366. [Google Scholar] [CrossRef]
- Fang, G.; Wu, C.; Liao, T.; Huang, X.; Qu, B. A two-layer improved invasive weed optimization algorithm for optimal operation of cascade reservoirs. Water Supply 2020, 20, 2311–2323. [Google Scholar] [CrossRef]
- Fozooni, A.; Kamari, O.; Pourtalebiyan, M.; Gorgich, M.; Khalilzadeh, M.; Valizadeh, A. An Analysis of the Operation Factors of Three PSO-GA-ED Meta-Heuristic Search Methods for Solving a Single-Objective Optimization Problem. Comput. Intell. Neurosci. 2022, 2022, 2748215. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).