Features and Constitutive Model of Hydrate-Bearing Sandy Sediment’s Triaxial Creep Failure
Abstract
1. Introduction
2. Materials and Methods
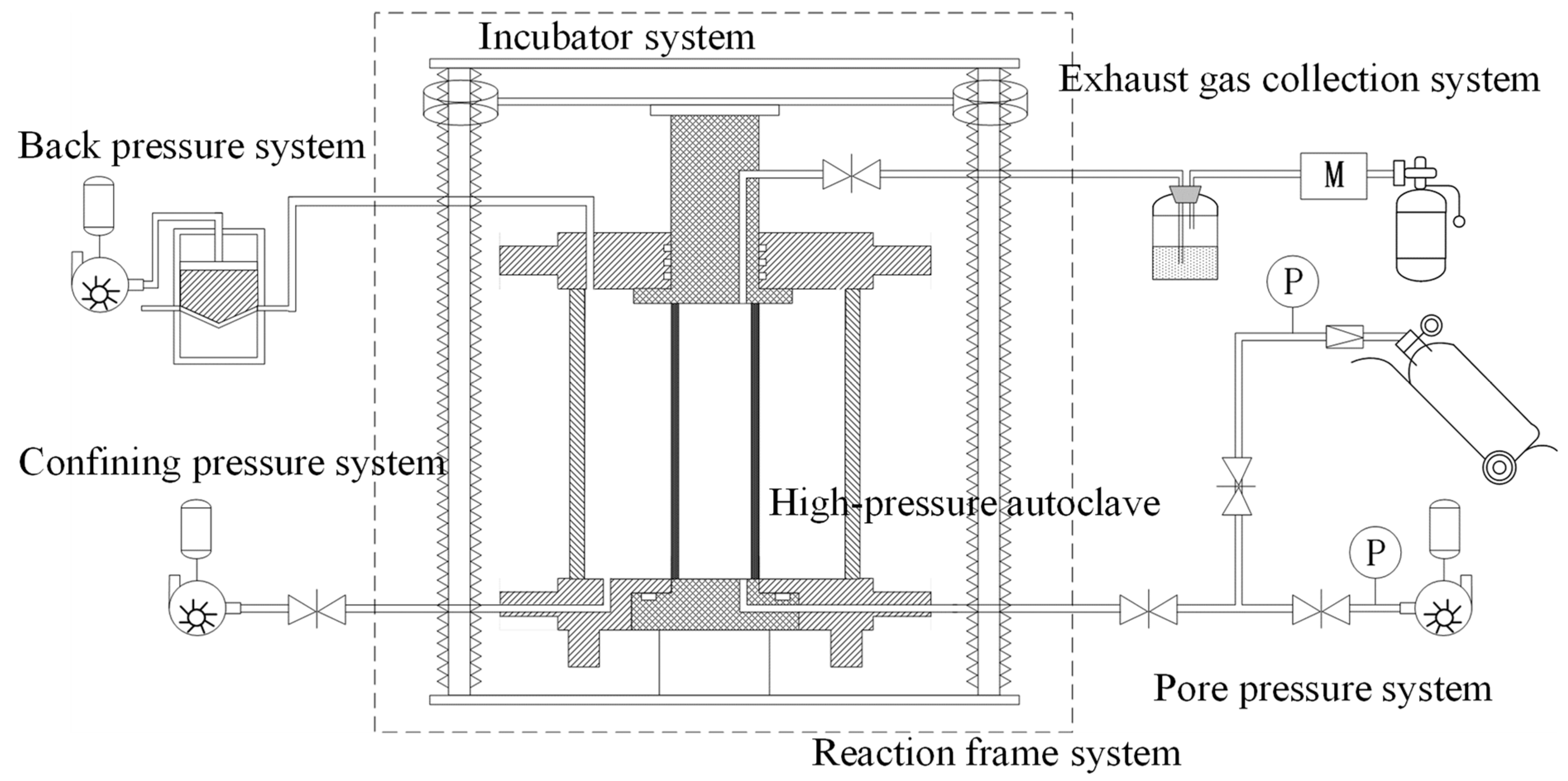
2.1. Experimental Instruments
2.2. Experimental Condition
3. Results and Discussion
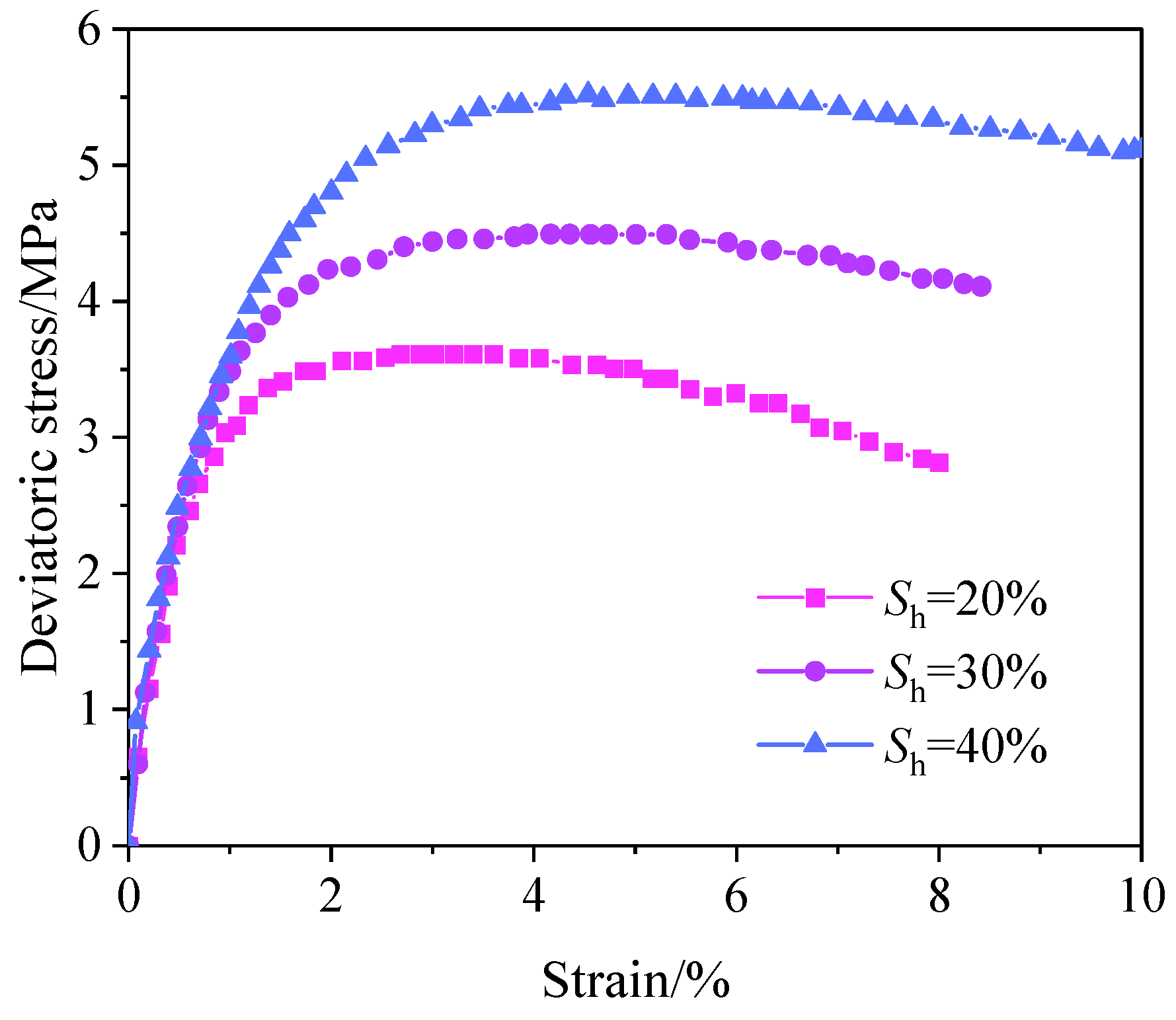
3.1. Conventional Triaxial Experiment Results
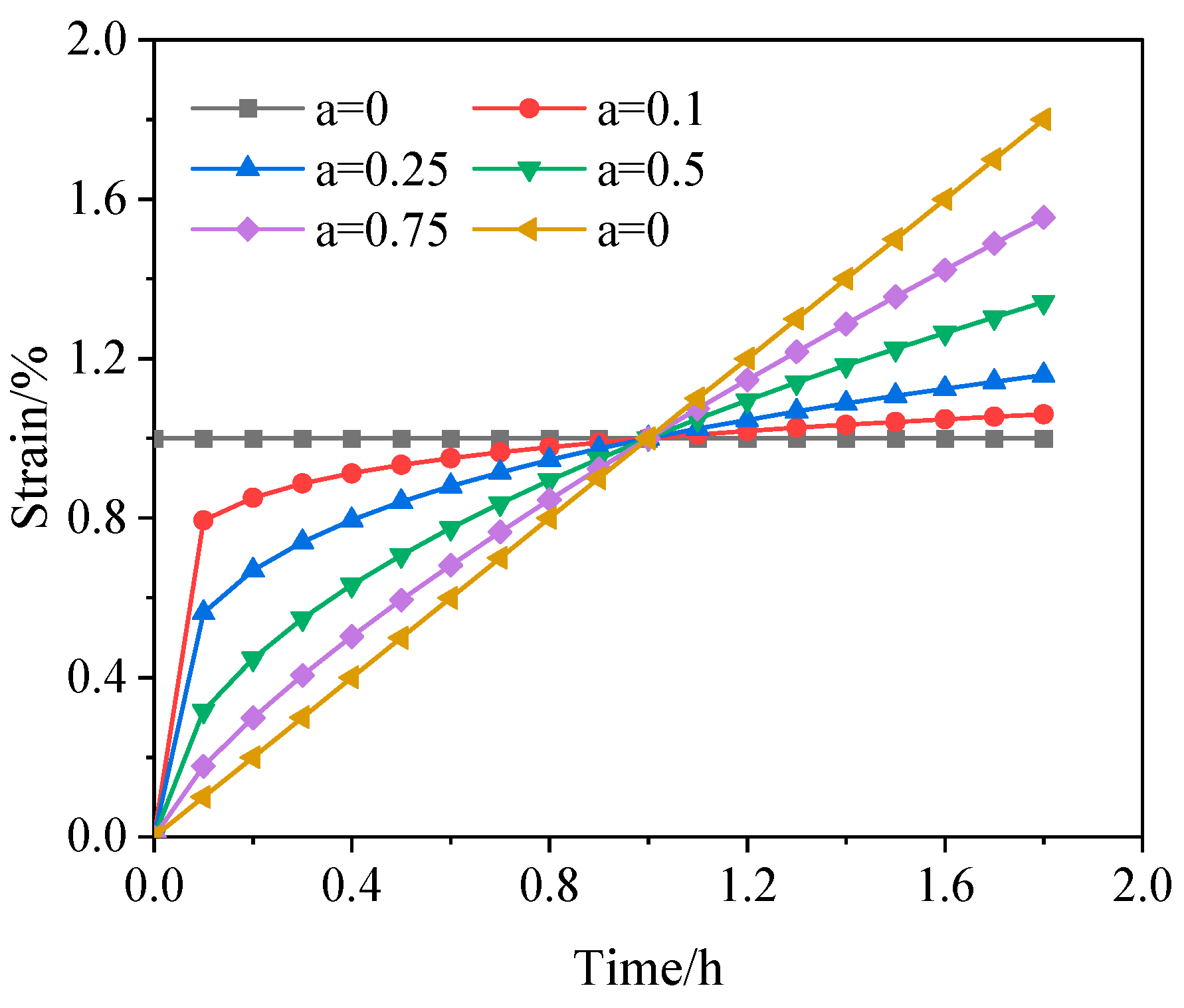
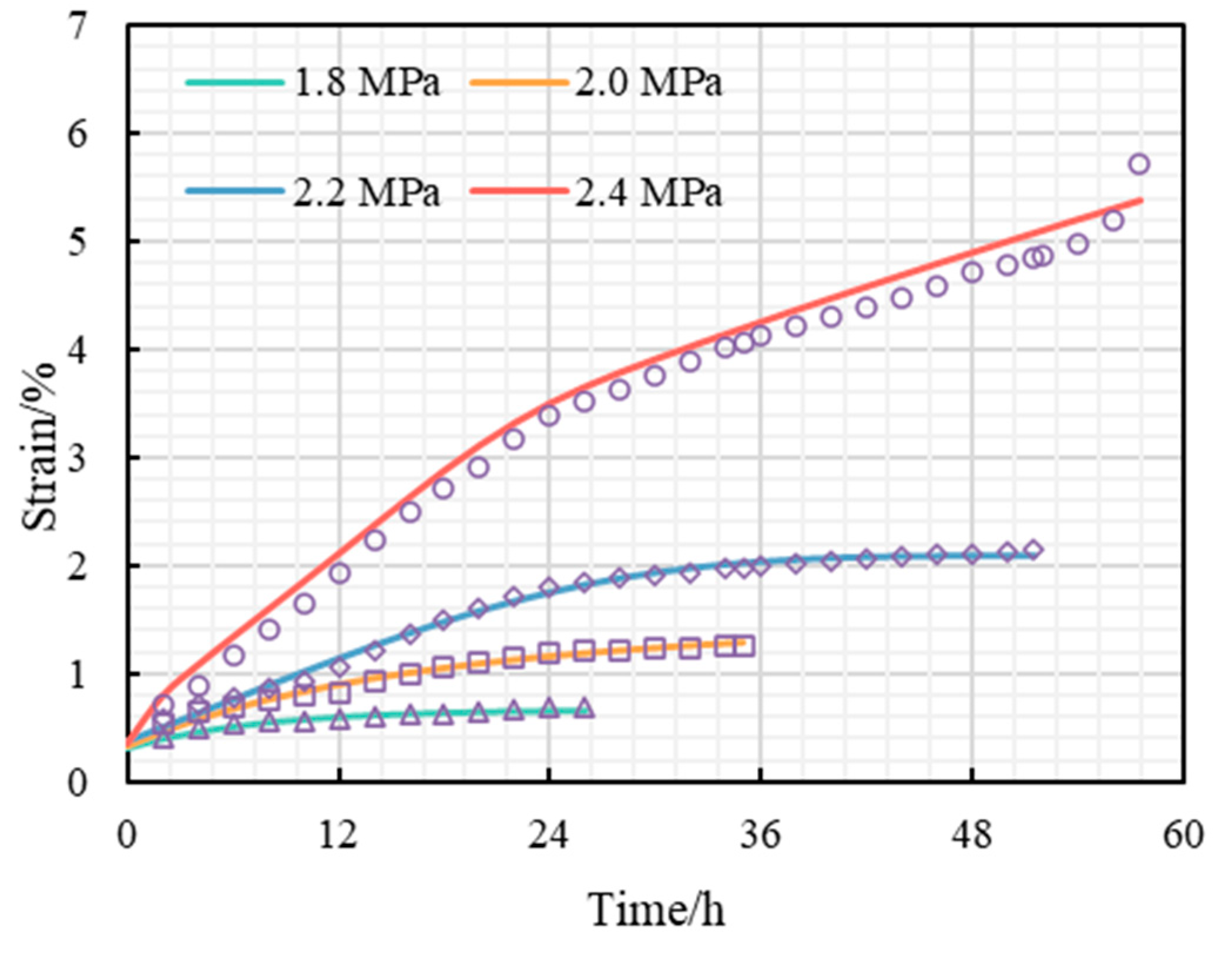
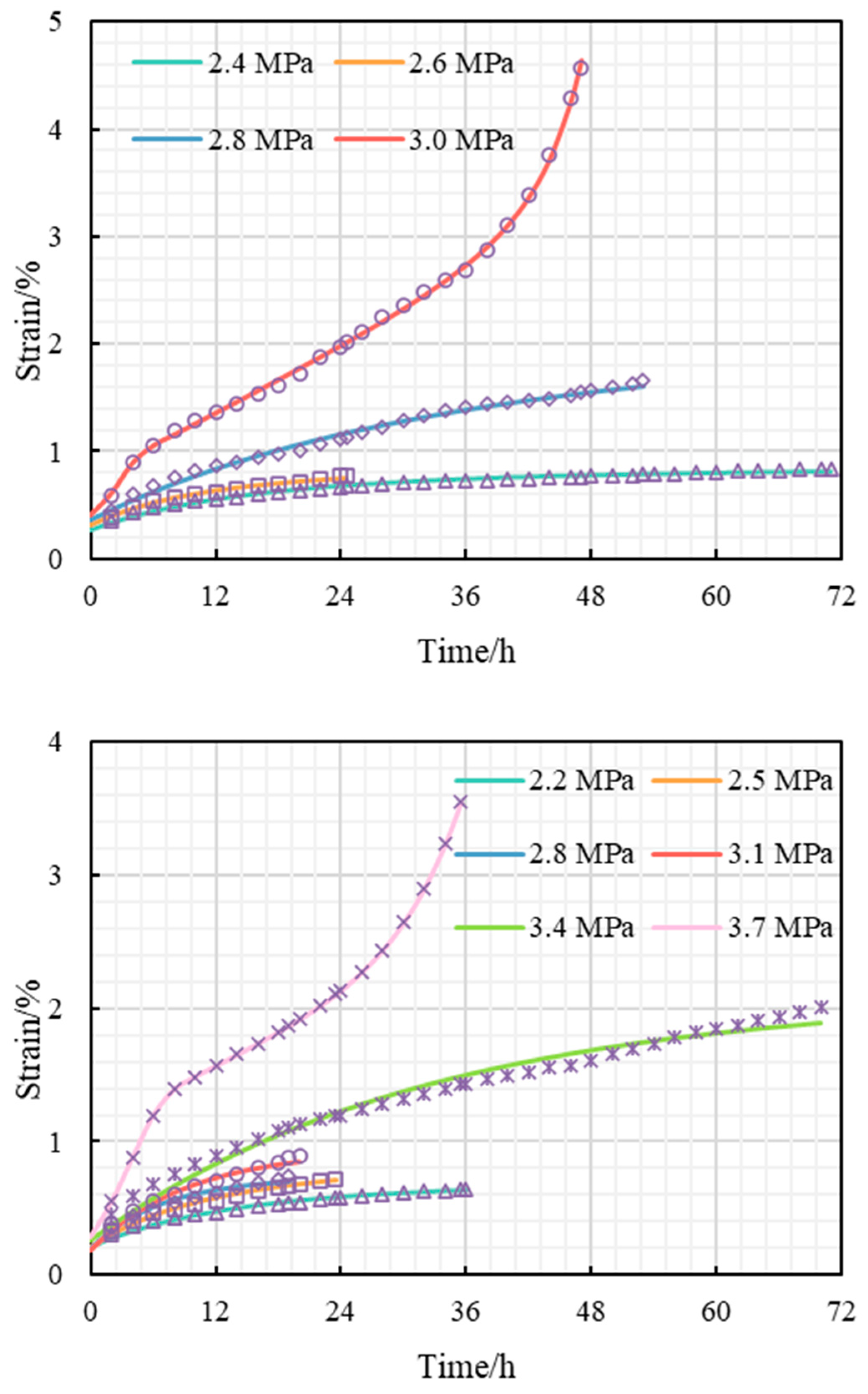
3.2. Triaxial Creep Test Results
3.3. Long-Term Strength
4. Description of Full Creep Regions in HBSS: A New Creep Constitutive Model
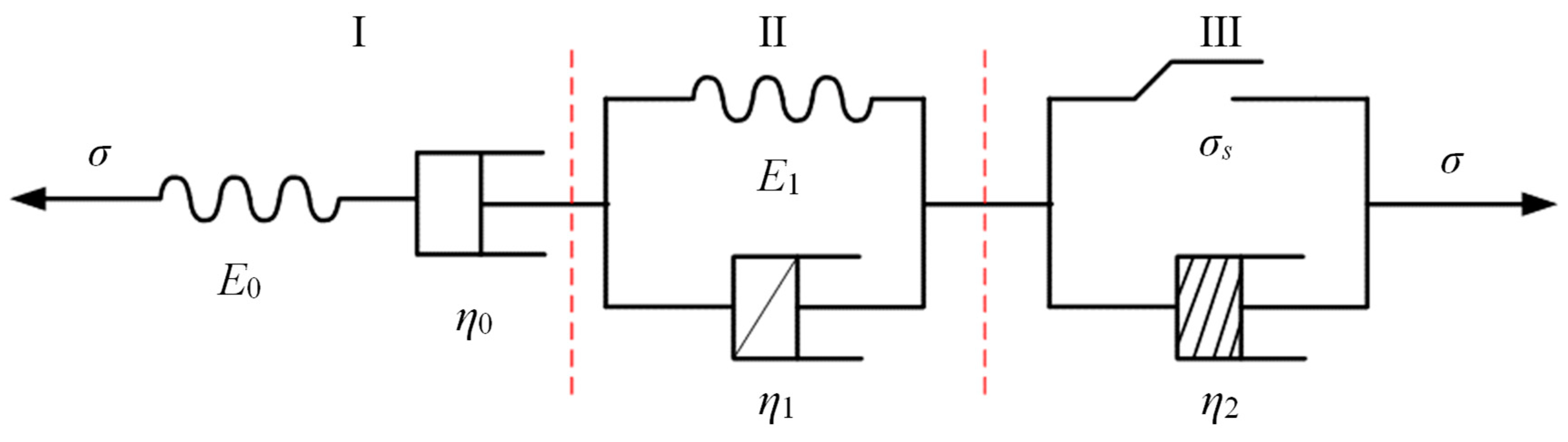
4.1. One-Dimensional Creep Constitutive Model
4.1.1. Fractional-Order Viscoplastic Body Models
4.1.2. Nonlinearisation of Viscous Elements
4.1.3. Fractional-Order Nonlinear Creep Modelling
4.2. Three-Dimensional Creep Constitutive Model
4.3. Model Parameter Identification
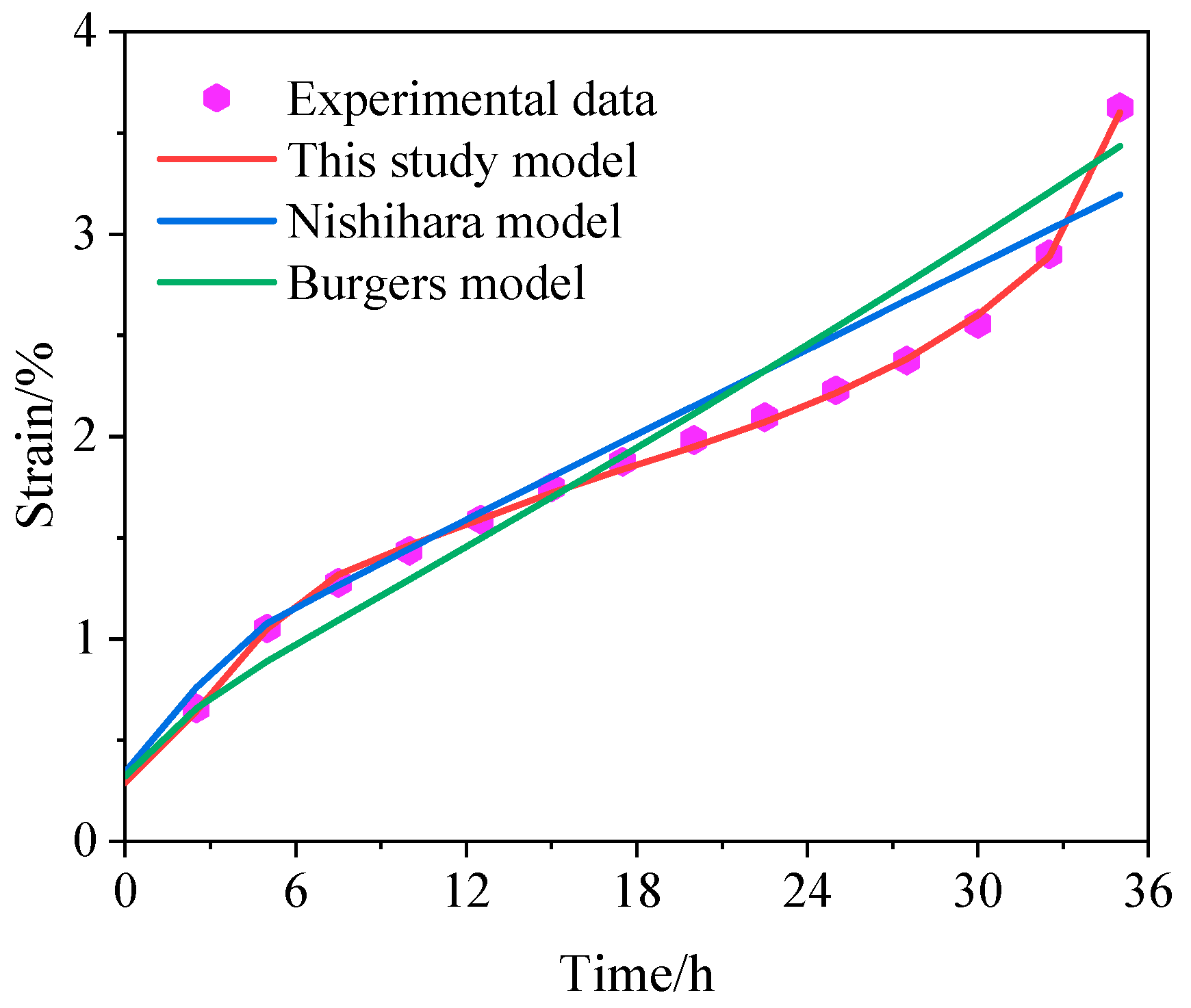
4.4. Model Verification
5. Conclusions and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, A.; Deng, H.; Zhang, H.; Jiang, M.; Liu, H.; Xiao, Y.; Wen, J. Developing a Two-Step Improved Damage Creep Constitutive Model Based on Soft Rock Saturation-Loss Cycle Triaxial Creep Test. Nat. Hazards 2021, 108, 2265–2281. [Google Scholar] [CrossRef]
- Li, Y.; Liu, L.; Jin, Y.; Wu, N. Characterization and Development of Marine Natural Gas Hydrate Reservoirs in Clayey-Silt Sediments: A Review and Discussion. Adv. Geo-Energy Res. 2021, 5, 75–86. [Google Scholar] [CrossRef]
- Wu, P.; Li, Y.; Wang, L.; Wang, L.; Sun, X.; Liu, W.; Song, Y. Triaxial Tests on the Overconsolidated Methane Hydrate-Bearing Clayey-Silty Sediments. J. Pet. Sci. Eng. 2021, 206, 109035. [Google Scholar] [CrossRef]
- Dong, L.; Li, Y.; Liao, H.; Liu, C.; Chen, Q.; Hu, G.; Liu, L.; Meng, Q. Strength Estimation for Hydrate-Bearing Sediments Based on Triaxial Shearing Tests. J. Pet. Sci. Eng. 2020, 184, 106478. [Google Scholar] [CrossRef]
- Li, J.; Ye, J.; Qin, X.; Qiu, H.; Wu, N.; Lu, H.; Xie, W.; Lu, J.; Peng, F.; Xu, Z.; et al. The First Offshore Natural Gas Hydrate Production Test in South China Sea. China Geol. 2018, 1, 5–16. [Google Scholar] [CrossRef]
- Priest, J.A.; Hayley, J.L. Strength of Laboratory Synthesized Hydrate-Bearing Sands and Their Relationship to Natural Hydrate-Bearing Sediments. JGR Solid. Earth 2019, 124, 12556–12575. [Google Scholar] [CrossRef]
- Sun, X.; Yao, D.; Qu, J.; Sun, S.; Qin, Z.; Tao, L.; Zhao, Y. A Novel Transient Hole Cleaning Algorithm for Horizontal Wells Based on Drift-Flux Model. Geoenergy Sci. Eng. 2024, 233, 212517. [Google Scholar] [CrossRef]
- Morshedifard, A.; Masoumi, S.; Abdolhosseini Qomi, M.J. Nanoscale Origins of Creep in Calcium Silicate Hydrates. Nat. Commun. 2018, 9, 1785. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, C.; Luo, T.; Song, Y.; Li, Y. Creep Behaviours of Methane Hydrate-Bearing Sediments. Environ. Geotech. 2019, 9, 199–209. [Google Scholar] [CrossRef]
- Königsberger, M.; Irfan-Ul-Hassan, M.; Pichler, B.; Hellmich, C. Downscaling Based Identification of Nonaging Power-Law Creep of Cement Hydrates. J. Eng. Mech. 2016, 142, 04016106. [Google Scholar] [CrossRef]
- Sun, X.; Luo, T.; Wang, L.; Wang, H.; Song, Y.; Li, Y. Numerical Simulation of Gas Recovery from a Low-Permeability Hydrate Reservoir by Depressurization. Appl. Energy 2019, 250, 7–18. [Google Scholar] [CrossRef]
- Lei, L.; Seol, Y. Pore-Scale Investigation Of Methane Hydrate-Bearing Sediments Under Triaxial Condition. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, Y.; Zhao, X.; Wang, Z.; Li, H.; Sun, B. Risk Analysis on the Blowout in Deepwater Drilling When Encountering Hydrate-Bearing Reservoir. Ocean. Eng. 2018, 170, 1–5. [Google Scholar] [CrossRef]
- Fereidounpour, A.; Vatani, A. An Investigation of Interaction of Drilling Fluids with Gas Hydrates in Drilling Hydrate Bearing Sediments. J. Nat. Gas. Sci. Eng. 2014, 20, 422–427. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Liu, L.; Sun, J.; Liu, H.; Meng, Q. Experimental Study on Evolution Behaviors of Triaxial-Shearing Parameters for Hydrate-Bearing Intermediate Fine Sediment. Adv. Geo-Energy Res. 2018, 2, 43–52. [Google Scholar] [CrossRef]
- Miyazaki, K.; Yamaguchi, T.; Sakamoto, Y.; Aoki, K. Time-Dependent Behaviors of Methane-Hydrate Bearing Sediments in Triaxial Compression Test. Int. J. JCRM 2011, 7, 43–48. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Y.; Sun, X.; Chen, M.; Bu, Q.; Gong, B. Integrating Test Device and Method for Creep Failure and Ultrasonic Response of Methane Hydrate-Bearing Sediments. Rev. Sci. Instrum. 2023, 94, 025105. [Google Scholar] [CrossRef]
- Zhu, Z.; Luo, F.; Zhang, Y.; Zhang, D.; He, J. A Creep Model for Frozen Sand of Qinghai-Tibet Based on Nishihara Model. Cold Reg. Sci. Technol. 2019, 167, 102843. [Google Scholar] [CrossRef]
- Deng, H.; Dai, G.; Azadi, M.R.; Hu, Y. Drained Creep Test and Creep Model Evaluation of Coastal Soft Clay. Indian Geotech. J. 2021, 51, 1283–1298. [Google Scholar] [CrossRef]
- Liu, B.; Zhan, L.; Lu, H.; Zhang, J. Advances in Characterizing Gas Hydrate Formation in Sediments with NMR Transverse Relaxation Time. Water 2022, 14, 330. [Google Scholar] [CrossRef]
- Wu, Q.; Lin, N.; Li, L.; Chen, F.; Zhang, B.; Wu, Q.; Xv, X.; Wang, X. Experimental Study on the Kinetics of the Natural Gas Hydration Process with a NiMnGa Micro-/Nanofluid in a Static Suspension System. Water 2022, 14, 1–17. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, X.; Wang, Y.; Yong, R.; Fan, X.; Du, S.; Zhao, Y. Improved Nonlinear Nishihara Shear Creep Model with Variable Parameters for Rock-Like Materials. Adv. Civ. Eng. 2020, 2020, 7302141. [Google Scholar] [CrossRef]
- Li, G.; Wang, Y.; Hu, Y.; Wang, D.; Yang, X.; Li, Y.; Zhou, Z.; Zhang, S. Shear Creep Mechanical Properties and Damage Model of Mudstone in Open-Pit Coal Mine. Sci. Rep. 2022, 12, 5148. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, C.P.; Han, B.B.; Duan, Z.Q. A Creep Constitutive Model for Salt Rock Based on Fractional Derivatives. Int. J. Rock Mech. Min. Sci. 2011, 48, 116–121. [Google Scholar] [CrossRef]
- Yan, B.; Guo, Q.; Ren, F.; Cai, M. Modified Nishihara Model and Experimental Verification of Deep Rock Mass under the Water-Rock Interaction. Int. J. Rock Mech. Min. Sci. 2020, 128, 104250. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, Y.; Zhou, X. Nonlinear Creep Model for Rocks Considering Damage Evolution Based on the Modified Nishihara Model. Int. J. Geomech. 2021, 21, 04021137. [Google Scholar] [CrossRef]
- Liu, J.; Wu, F.; Zou, Q.; Chen, J.; Ren, S.; Zhang, C. A Variable-Order Fractional Derivative Creep Constitutive Model of Salt Rock Based on the Damage Effect. Geomech. Geophys. Geo-Energ. Geo-Resour. 2021, 7, 46. [Google Scholar] [CrossRef]
- Chen, M.; Li, Y.; Zhang, Y.; Qi, M.; Wu, N. Recent Advances in Creep Behaviors Characterization for Hydrate-Bearing Sediment. Renew. Sustain. Energy Rev. 2023, 183, 113434. [Google Scholar] [CrossRef]
- Li, Y.; Hu, Q.; Wu, N.; Wang, H.; Sun, X.; Hu, G.; Sun, Z.; Jiang, Y. Acoustic Characterization for Creep Behaviors of Marine Sandy Hydrate-Bearing Sediment. Sci. Rep. 2023, 13, 22199. [Google Scholar] [CrossRef]
- Liu, X.; Liu, L.; Li, Z.; Yao, Z. Experimental Analysis on Creep Properties of Frozen Silty Mudstone Considering Conservation of Energy. J. Test. Eval. 2021, 49, 417–434. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, H.; Zhang, S.; Jiang, S.; Yang, L. A Nonlinear Creep Model for Surrounding Rocks of Tunnels Based on Kinetic Energy Theorem. J. Rock Mech. Geotech. Eng. 2023, 15, 363–374. [Google Scholar] [CrossRef]
- Chen, W.; Wan, W.; Xie, S.; Kuang, W.; Peng, W.; Wu, Q.; Tong, S.; Wang, X.; Tang, X. Features and Constitutive Model of Gypsum’s Uniaxial Creep Damage Considering Acidization. Geofluids 2020, 2020, 8874403. [Google Scholar] [CrossRef]
- Nguyen, N.N.; Nguyen, A.V.; Dang, L.X. The Inhibition of Methane Hydrate Formation by Water Alignment underneath Surface Adsorption of Surfactants. Fuel 2017, 197, 488–496. [Google Scholar] [CrossRef]
- Shan, R.; Bai, Y.; Ju, Y.; Han, T.; Dou, H.; Li, Z. Study on the Triaxial Unloading Creep Mechanical Properties and Damage Constitutive Model of Red Sandstone Containing a Single Ice-Filled Flaw. Rock Mech. Rock Eng. 2021, 54, 833–855. [Google Scholar] [CrossRef]
- Shukla, A.; Joshi, Y.M. Boltzmann Superposition Principle for a Time-Dependent Soft Material: Assessment under Creep Flow Field. Rheol. Acta 2017, 56, 927–940. [Google Scholar] [CrossRef]
- Qin, X.; Liang, Q.; Ye, J.; Yang, L.; Qiu, H.; Xie, W.; Liang, J.; Lu, J.; Lu, C.; Lu, H.; et al. The Response of Temperature and Pressure of Hydrate Reservoirs in the First Gas Hydrate Production Test in South China Sea. Appl. Energy 2020, 278, 115649. [Google Scholar] [CrossRef]
- Yamamoto, K.; Wang, X.-X.; Tamaki, M.; Suzuki, K. The Second Offshore Production of Methane Hydrate in the Nankai Trough and Gas Production Behavior from a Heterogeneous Methane Hydrate Reservoir. RSC Adv. 2019, 9, 25987–26013. [Google Scholar] [CrossRef]
- Liu, H.Z.; Xie, H.Q.; He, J.D.; Xiao, M.L.; Zhuo, L. Nonlinear Creep Damage Constitutive Model for Soft Rocks. Mech. Time-Depend. Mater. 2017, 21, 73–96. [Google Scholar] [CrossRef]
- Tian, Z.; Liu, Y.; Zhang, X.; Zhang, Y.; Zhang, M. Formation Mechanisms and Characteristics of the Marine Nepheloid Layer: A Review. Water 2022, 14, 678. [Google Scholar] [CrossRef]

| Sh/% | Long-Term Strength/MPa | Triaxial Strength/MPa | Strength Level |
|---|---|---|---|
| 20 | 2.2 | 3.61 | 0.61 |
| 30 | 2.8 | 4.49 | 0.62 |
| 40 | 3.4 | 5.52 | 0.62 |
| Sh/% | σ1–σ3 /MPa | G0 /MPa | K0 /MPa | H0 /MPa·h | G1 /MPa | λ /10−2 | H1 /MPa·h | H2 /MPa·h | G2 /MPa | a | R2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 1.8 | 365 | 425 | 2415 | 168 | 0.01 | 1235 | / | / | / | 0.984 |
| 2 | 456 | 431 | 1214 | 40 | −3.59 | 942 | / | / | / | 0.982 | |
| 2.2 | 429 | 426 | 1240 | 43 | 4.61 | 1159 | / | / | / | 0.995 | |
| 2.4 | 456 | 442 | 2405 | 75 | 13.15 | 4208 | 429 | 3.64 | 0.63 | 0.999 | |
| 30 | 2.4 | 1434 | 1664 | 461 | 119 | −2.82 | 2183 | / | / | / | 0.997 |
| 2.6 | 996 | 1061 | 530 | 127 | −4.39 | 1819 | / | / | / | 0.994 | |
| 2.8 | 2246 | 2063 | 328 | 39 | −1.52 | 1920 | / | / | / | 0.995 | |
| 3 | 1270 | 1060 | 1022 | 194 | 55.59 | 1232 | 132 | 7.93 | 8.01 | 0.999 | |
| 40 | 2.2 | 812 | 799 | 1375 | 71 | −5.60 | 2127 | / | / | / | 0.995 |
| 2.5 | 941 | 877 | 1727 | 103 | −4.35 | 1572 | / | / | / | 0.994 | |
| 2.8 | 1071 | 955 | 2113 | 176 | 0.01 | 1203 | / | / | / | 0.984 | |
| 3.1 | 1264 | 1099 | 2457 | 136 | 0.01 | 1277 | / | / | / | 0.990 | |
| 3.4 | 1477 | 1366 | 898 | 62 | 0.01 | 1976 | / | / | / | 0.999 | |
| 3.7 | 638 | 2400 | 1914 | 155 | 35.24 | 1754 | 249 | 5.66 | 6.43 | 0.989 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Zhang, X.; Zhou, Y. Features and Constitutive Model of Hydrate-Bearing Sandy Sediment’s Triaxial Creep Failure. Water 2024, 16, 2947. https://doi.org/10.3390/w16202947
Sun S, Zhang X, Zhou Y. Features and Constitutive Model of Hydrate-Bearing Sandy Sediment’s Triaxial Creep Failure. Water. 2024; 16(20):2947. https://doi.org/10.3390/w16202947
Chicago/Turabian StyleSun, Shihui, Xiaohan Zhang, and Yunjian Zhou. 2024. "Features and Constitutive Model of Hydrate-Bearing Sandy Sediment’s Triaxial Creep Failure" Water 16, no. 20: 2947. https://doi.org/10.3390/w16202947
APA StyleSun, S., Zhang, X., & Zhou, Y. (2024). Features and Constitutive Model of Hydrate-Bearing Sandy Sediment’s Triaxial Creep Failure. Water, 16(20), 2947. https://doi.org/10.3390/w16202947







