Evaluation of Operational Safety Risk in Wastewater Treatment Plants Based on WSR and Matter–Element Extension Theory

Abstract

Wastewater treatment plants are of significant importance in facilitating China’s urbanization process. The fundamental purpose of wastewater treatment plants is to control water pollution and protect the environment. It is therefore essential that they are operated in a safe manner in order to achieve this goal. In order to guarantee a systematic and objective assessment of the operational safety risks inherent to wastewater treatment plants, the Wuli–Shili–Renli (WSR) theory has been introduced. Accordingly, a three-dimensional evaluation index system was developed for the assessment of these risks. A combination of subjective and objective methods utilizing game theory was employed to determine comprehensive risk factor weights. Subsequently, the material–element extension theory model was implemented in a wastewater treatment plant situated in the northern region of the Changchun Development Zone. The assessment classified the plant as Level 1 (safe), although it was determined that improvements in accident prevention are necessary. This study presents a robust framework for operational safety assessment that contributes to enhanced risk management and the long-term reliability of wastewater treatment operations. The results of the sensitivity analyses provide substantial evidence of the reliability and validity of the model.

1. Introduction

Today, sewage treatment plants have emerged as crucial infrastructure in construction for China’s urbanization, exerting a significant role in the enhancement of water quality and the safeguarding of the environment. To support the nation’s extensive urbanization process, China is currently at the zenith of the construction of urban sewage treatment plants [1]. Despite the considerable improvement in water quality and the environment brought about by sewage treatment plants, they also introduce new risks related to operational safety [2]. An operational safety accident in sewage treatment plants will not only result in property losses but also readily give rise to waterborne infectious diseases, organic pollution, and the eutrophication of water bodies, directly threatening the safety of drinking water [3]. The consequent water shortage will further exacerbate China’s water shortage predicament. Hence, it is profoundly significant to evaluate the operational safety risks of sewage treatment plants, enhance their safety management level, lower the accident rate, and promote the production and development of sewage treatment plants [4].

Numerous experts have conducted substantial research on the assessment of operational safety risks in sewage treatment plants and achieved fruitful outcomes. The research on operational safety risks in sewage treatment plants primarily focuses on accident types, occurrence probabilities, and emergency measures [5]. For instance, studies have indicated that the majority of accidents in wastewater treatment plants are triggered by equipment malfunctions, human errors, or external environmental factors. Risk assessment methods such as Failure Mode and Impact Analysis (FMEA) and Fault Tree Analysis (FTA) [6] can be employed to assess the potential risks of wastewater treatment plants during operation. These methods play a significant role in analyzing the causes of accidents and formulating corresponding emergency measures. However, during the analysis process, most of these methods rely on the qualitative judgments of experts and fail to provide a multi-dimensional and comprehensive risk assessment.

In China, the evaluation of the operational safety of sewage treatment plants typically relies on qualitative assessment and empirical judgment, and there is a dearth of robust models based on data. Although some evaluation models have been proposed, due to the lack of systematic and quantitative research, a comprehensive evaluation of the operational safety of sewage treatment plants is yet to be achieved. Therefore, it is imperative to develop a structured risk assessment model that integrates multiple dimensions of the risk factors of operational safety and provides a quantitative basis for managers [7].

The innovation of this study lies in its combination of the Wuli–Shili–Renli (WSR) theory with the matter–element extension theory and proposal of a scientific and rational risk assessment model for the operational safety of sewage treatment plants. The WSR theory comprehensively encompasses the complex risk factors of sewage treatment plants through the three dimensions of Wuli, Shili, and Renli, and it allows the realization of a multi-angle analysis of safety risks.

Wuli: This commences from the safety, quality, and layout of sewage treatment plant equipment, such as the equipment’s integrity and maintenance.

Shili: This starts from the customization of technical and institutional aspects, such as safety systems and technological advancements.

Renli: This starts from personnel distribution, operational training, and personnel culture, such as literacy and technical training.

These three dimensions are interrelated and jointly constitute an index system for comprehensive risk assessment. The application of the WSR theory in the operational safety index system for sewage treatment plants allows the realization of a multi-dimensional risk analysis from a systemic perspective and provides a more comprehensive assessment than that of existing methods.

In this study, the analytic hierarchy process (AHP), the entropy weight method, and game theory are integrated to establish a multi-dimensional risk weight assessment approach. The AHP is prevalently employed in complex decision-making issues, particularly when quantitative subjective weights need to be combined with expert judgments. Its hierarchical architecture enables the decomposition of complex problems and the acquisition of the weight of each index through the subjective judgments of experts. On the contrary, the entropy weight method assigns objective weights based on the degree of data dispersion, mitigates subjective bias, and guarantees the objectivity of the evaluation. Considering the limitations of both methods, game theory was incorporated to strike a reasonable balance between subjective and objective weights. The advantage of game theory lies in its ability to handle the competition and cooperation among various weighting methods and generate more scientifically and rationally combined weights. Thus, this approach combines the advantage of expert judgment in the AHP with the advantage of objectified data in the entropy weight method and ultimately enhances the accuracy and reliability of the evaluation results through game theory. The model was applied to a sewage treatment plant located in the north of the Changchun Development Zone. The safety grade of the plant was determined with the evaluation results, and improvement suggestions were proposed for the deficiencies in its operation.

The scientific and multi-dimensional risk assessment model for sewage treatment plants proposed in this study significantly enhances the objectivity and scientific quality of the assessment compared with traditional methods. By integrating quantitative analysis with innovative approaches, the model offers a new tool for risk management in wastewater treatment plants, improving their long-term safety and operational reliability. The basic theory of the extension method and the matter–element model is introduced in Section 1. Section 2 introduces the research area and data source for this study, and Section 3 establishes the operational safety risk assessment model for the sewage treatment plant. Finally, conclusions and recommendations regarding the operational safety risks for wastewater treatment plants are outlined in Section 4.

2. Research Area and Data

2.1. Overview of the Study Area

The northern sewage treatment plant of the Changchun High-Tech Industrial Development Zone was selected. The northern sewage treatment plant is located downstream of the Yitong River, covering a total area of 32 hectares. The service area is about 1.2 million square kilometers, and the service population is 1.5 million people. Its daily sewage treatment capacity is 390,000 cubic meters; thus, it can solve the problem of sewage treatment in the northeast of Changchun City. The treated sewage is directly discharged into the Yitong River. The main treatment components include a coarse screen, grit chamber, primary sedimentation tank, modified A²/O biological tank, secondary sedimentation tank, advanced treatment, control building, and other facilities. The secondary sewage treatment of the project involves the improved A²/O process with a sludge age of 24 days. In the scheme of the advanced sewage treatment process, after the sewage is mixed in the mixing tank, it enters a V-type filter through a small-hole network reaction tank and an inclined-plate sedimentation tank. Then, chlorine is added to the clear water tank for disinfection; the treated sludge is directly concentrated and dehydrated and then transported to a sanitary landfill [8].

2.2. Data Sources

The sewage treatment plant in the northern district of Changchun Development Zone was selected as the research area. The scoring data used in this study came from a questionnaire survey. Experts from sewage treatment plants and safety supervisors rated the safety of the whole operation process of sewage treatment plants. Referring to the discussion of the safe operation of urban wastewater treatment plants [5] and WSR 2.0 [9] and following the principles of reliability and integrity, a safety risk evaluation index system for wastewater treatment plant operation was established according to physical and human management as the criterion layer, and a safety risk evaluation of the wastewater treatment plant was carried out. A specific flowchart is shown in Figure 1.

3. Methods

Based on the evaluation standards for operational management in urban sewage treatment plants, this study established an operational safety evaluation index system for sewage treatment plants for the first time by utilizing the WSR theoretical model [10]. The index system covers several key factors, such as equipment operation, operational management, and security risks. The score data were collected through a questionnaire survey distributed to sewage treatment plant experts and safety supervisors, who rated the entire operation process based on the actual operation of sewage treatment plants. In order to ensure the objectivity and scientific quality of the risk assessment, the entropy weight method was used to calculate the objective weight of each index. According to the degree of dispersion of the index data, the entropy weight method ensured that the weight distribution was not affected by subjective factors. In addition, in order to reflect the subjective judgments of the experts, the analytic hierarchy process (AHP) was used to determine the subjective weight of each indicator [11]. Since the weights calculated with different methods may conflict, we introduced game theory to combine the subjective and objective weights, balance the differences between the two, and obtain the final combined weights. This process ensures that weights are assigned while taking both the objectivity of the data and the subjective experience of the experts into account. In combination with the expert scores and game theory, matter–element extension theory was applied to construct a comprehensive risk assessment model for the operational safety of sewage treatment plants. Through this model, we accurately assessed the operational safety risk for each index and the entire sewage treatment plant, and we determined the risk levels [12].

3.1. WSR Theoretical Model

Due to the intricate, comprehensive, and interactive internal factors associated with operational safety risks in sewage treatment plants, it is feasible to establish a complete indicator system from the perspective of the WSR theoretical model [13]. This entails evaluating both the integrity of the equipment and its operational efficiency from the standpoint of Wuli, as well as assessing the effectiveness of safety measures [14]. Shili is used to evaluate the establishment of safety systems, the normal implementation of safety measures, and the rationality and effectiveness of operational management processes, such as emergency response. Renli focuses on human factors, such as the management, operational skills, safety training, and cultural development of assessors [15]. The safe operation of wastewater treatment plants can be ensured by improving the professional skills and risk prevention awareness of operators. These dimensions interact to form a comprehensive risk assessment system to better address the complex operational safety risks of wastewater treatment plants [16].

3.2. Indicator System

The operational environment of a sewage treatment plant is complex, and many uncontrollable indexes can be regarded as a complex system [17]. The WSR methodology can be used to analyze the risk indexes of operational safety in sewage treatment plants from three perspectives: ‘Wuli’, ‘Shili’, and ‘Renli’ [18]. Wuli refers to the objective existence of entities, meaning the use of existing equipment and facilities to reduce the probability of operational safety risks in sewage treatment plants and reduce losses due to disasters. It covers the integrity of equipment, maintenance, facility layout, and the surrounding environment of sewage treatment plants. Its indicators can be further subdivided into those related to water pump rooms, discharge ports, sludge treatment centers, advanced treatment systems, laboratory equipment, mechanical equipment maintenance, etc. Shili refers to the fact that when a disaster occurs during the operation and maintenance of a sewage treatment plant, the ability to take timely measures through management means and the information level while suppressing the further occurrence of disasters depends on the original equipment and environmental conditions, and this is mainly reflected in management indicators, such as safety procedures and operational management systems. Renli is mainly used to identify risks from the front end, strengthen risk management and control in the middle, and eliminate risks at the back end through the cooperation of individuals and teams; it mainly includes technical training and personnel culture level [19]. On the basis of WSR theory combined with the literature on WSR 2.0, an index system for operational safety risk evaluation of a sewage treatment plant was created, with 10 first-level indicators, namely, equipment integrity, maintenance, facility layout, surrounding environment, safety inspection, safety system, accident prevention, technical improvement, cultural level, and technical training, as the core [20], as shown in Figure 2.

3.3. Analytic Hierarchy Process (AHP)

The analytic hierarchy process is a commonly used subjective weighting method. Firstly, the decision-making objectives are determined, and a model of the hierarchical structure model is established [21]. Then, experts and the people in charge of sewage treatment plants used the evaluation scale shown in

Table 1. The scale of 1–9 used for pairwise comparisons in the AHP.

Importance Degree	Definition
1	Equal importance
3	Moderate importance of one over another
5	Strong importance of one over another
7	Very strong importance of one over another
9	Extreme importance of one over another
2, 4, 6, and 8	Intermediate values

to compare the importance of each index and form a comparison matrix. Finally, the weight of each indicator that met the coherence criterion was reasonably calculated. The consistency indicator (CI) was calculated on the basis of Equation (1), where ${\lambda }_{max}$ is the maximum characteristic value of the considered matrix. The consistency index should be 0–10%. If it is greater than 10%, the comparison matrix should be corrected, and the consistency index should be recalculated [22].

$$CI={\displaystyle \frac{{\lambda }_{max}-n}{n-1}}$$

(1)

3.4. Entropy Weight Method

This study used the entropy weight method to compute each indicator’s weight [23]. Higher entropy values indicate less variability and, hence, lower weight in the entropy weight method, which was used to quantify the degree of dispersion of the indicators. The following are the precise steps:

• Construction of an initial evaluation matrix: The original matrix is constructed with m objects and n indexes:

  $$X={⌊x_{ij}⌋}_{n\times n},$$

  (2)
• With data normalization, there are differences in the characteristics of different indicators. To remove the influence of different dimensions, the index values are normalized in this study. For a positive index, the normalization formula is as follows:

  $${\chi }_{ij}^{\prime }={\displaystyle \frac{{\chi }_{ij}-min({\chi }_{ij})}{max({\chi }_{ij})-min({\chi }_{ij})}}.$$

  (3)
  For negative indicators, the normalization formula is as follows:

  $$x_{ij}^{\prime }={\displaystyle \frac{max(x_{ij})-x_{ij}}{max(x_{ij})-min(x_{ij}),}}$$

  (4)

  where $x_{ij}$ is the original value of the jth indicator for the ith unit, and $x_{ij}^{\prime }$ is the jth indicator for the ith unit after normalization.
• Calculation of the value of information entropy $e_j$ and information utility $d_j$ of the indicator:

  $$e_j=-k[{\sum }_{i=1}^n P_{ij}\mathrm{l}\mathrm{n}(P_{ij})],$$

  (5)

  $$d_j=1-e_j.$$

  (6)
  Formally, $P_{ij}=x_{ij}^{\prime }/{\sum }_{i=1}^n x_{ij}^{\prime }$, $e_j$ is the information entropy value of the jth indicator; the smaller the entropy value e of an indicator, the larger its role in the integrated evaluation, and the smaller the entropy value, the smaller the weight. $P_{ij}$ is the jth indicator in the ith year while accounting for the proportion of the indicator [1].
• Determination of evaluation indicator weights:

  $${\omega }_j=(1-e_j)/{\sum }_{j=1}^m (1-e_j),$$

  (7)

  Formally, 0$\le {\omega }_j\le$1.

3.5. Game Theory

In response to the complexity and diversity of weighting approaches, game theory is employed to integrate different weighting methods in accordance with the characteristics of these methods. By calculating the combined coefficients and integrating the outcomes, game theory offers a more objective weighting system. In this study, the entropy weight method and the analytic hierarchy process (AHP) were utilized to calculate the individual objective weight and subjective weight of each index. The strict data format requirements of the entropy weight method and the inherent subjective bias of the analytic hierarchy process (AHP) have limitations when employed independently. Therefore, game theory was adopted to balance these methods, and the objective and subjective weights were combined to obtain the final comprehensive weight for each indicator.

The process for determining the weight of the combination was as follows.

Calculation of initial weights: Entropy weights were utilized to determine the objective weights based on data variability, while the analytic hierarchy process (AHP) was employed to derive the subjective weights from expert assessments.

Normalization of weights: Both sets of weights were normalized to guarantee comparability.

Use of combinatorial weights through game theory: Game theory was used to calculate combinatorial coefficients, balance the contributions of the two methods, and generate the final combinatorial weight for each metric [24].

Application of composite weights: Composite weights were applied in the risk assessment model to assess the importance of each indicator. In the evaluation of multi-agent problems, a variety of weighting methods can be used to obtain the weight of each index. Under the assumption that L different weighting methods are used to obtain the weight of each indicator (in this study, L = 2), L weight vectors can be obtained as follows:

$${\omega }_k=\left\{{\omega }_{k1}{\omega }_{k2}{\omega }_{k3},\cdots ,{\omega }_{km}\right\},\left[k=1,2,\cdots ,L\right].$$

(8)

Any combination of weight vectors can be expressed as

$$\omega ={\sum }_{k=1}^L {\alpha }_k·{\omega }_k^T\left[{\alpha }_k>0\right].$$

(9)

The coefficient ${\alpha }_k$ of all linear combinations in Equation (9) is optimized to minimize the dispersion between $\omega$ and different values of ${\omega }_k$. In this way, the most satisfactory weight value ${\omega }_k^{*}$ in the weight vector combination can be obtained. Further, the corresponding data model can be obtained in the following way:

$$min{\sum }_{k=1}^L {\alpha }_k·{\omega }_k^T·{\omega }_{k2}\left[\begin{array}{c}k=1,2,\dots L\end{array}\right].$$

(10)

On the basis of the properties of different matrixes, the optimal first-derivative condition of (10) can be derived with the following method:

$$\left[\begin{array}{cccc}{\omega }_1·{\omega }_1^T& {\omega }_1·{\omega }_2^T& \cdots & {\omega }_1·{\omega }_L^T\\ {\omega }_2·{\omega }_1^T& {\omega }_2·{\omega }_2^T& \cdots & {\omega }_1·{\omega }_L^T\\ ⋮& ⋮& ⋮& ⋮\\ {\omega }_L·{\omega }_1^T& {\omega }_L·{\omega }_1^T& \cdots & {\omega }_L·{\omega }_L^T\end{array}\right].$$

(11)

The coefficient of the optimized weight vector can be calculated using ${\alpha }_k^{*}$ = (${\alpha }_1^{*}{\alpha }_{2\cdots }^{*}{\alpha }_L^{*}$). The combined weight of the index can be obtained in the following way:

$${\omega }_k^{*}={\sum }_{k=1}^L {\alpha }_k^{*}·{\omega }_k^{\mathrm{T}}.$$

(12)

In the formula, ${\omega }_k^{*}$ is the combined weight.

3.6. Matter–Element Extension Theory Model

In this study, the matter–element analysis approach was employed to construct a multi-index model for evaluating the operational safety of wastewater treatment plants [25]. The matter–element analysis approach enables the quantification of various indicators, offering a comprehensive assessment of the research objects. By converting complex problems into specific models, this approach facilitates risk evaluation and decision making [26]. The application of this model allows for the identification and resolution of potential safety risks, enabling a more precise reflection of the overall safety level of a wastewater treatment plant. Additionally, the matter–element model is compatible with computer programming, facilitating efficient calculation and analysis [27].

3.6.1. Determination of Elements to Be Evaluated

The ordered triple R = (P, C, X) is used as the basic unit for describing things, and it is called the thing element. Here, P denotes the thing, C denotes the features of P, and X denotes the quantities taken by P with respect to C [8]. If a thing P is described by n features $C_1$, ${ C}_2$, …, $C_n$ and corresponding quantities $X_1$, $X_2$, …, $X_n$, it is called an n-aspect element of things and is recorded as follows [28]:

$$R=\left[\begin{array}{ccc}P& C_1,& x_1\\ & C_2,& x_2\\ & ⋮& ⋮\\ & C_n,& x_n\end{array}\right].$$

(13)

R is called an n-dimensional material element.

3.6.2. Determination Classical Domain

$$R=(N_j{C}_i{X}_{ji})=\left[\begin{array}{ccc}{N}_j& C_i& x_{j1}\\ & C_2& x_{j2}\\ & ⋮& ⋮\\ & C_i& x_{jn}\end{array}\right]=\left[\begin{array}{ccc}{N}_j& C_i& (a_{j1},b_{j1})\\ & C_2& (a_{j2},b_{j2})\\ & ⋮& ⋮\\ & C_i& (a_{jn},b_{jn})\end{array}\right],$$

(14)

where $N_j$ is the jth rank classified; $C_i$ denotes the characteristics of rank $N_j$; $X_{ji}$ is the range of quantities specified by $N_j$ with respect to $C_i$, that is, the range of values taken by each rank with respect to the corresponding characteristics [29].

3.6.3. Determination Joint Domain

$$R_P=\left(P_0,C_i,X_{pi}\right)=\left[\begin{array}{ccc}{P}_0,& C_1,& x_{p1}\\ & C_2,& x_{p2}\\ & ⋮& ⋮\\ & C_n,& x_{pn}\end{array}\right]=\left[\begin{array}{ccc}{P}_0& C_1,& \left(a_{p1};b_{p2}\right)\\ & C_2,& \left(a_{p2};b_{p2}\right)\\ & ⋮& ⋮\\ & C_n,& \left(a_{pn};b_{pn}\right)\end{array}\right],$$

(15)

where $P_0$ denotes the entirety of the rank; $X_{pi}$ is the range of quantities taken by $P_0$ with respect to $C_i$ [30].

3.6.4. Determination of the Distance of the Evaluated Matter–Element

Correlation functions are established based on topological set theory and specific conditions as follows:

$$K_j(X_i)=\left\{\begin{array}{c}{\displaystyle \frac{-\rho (x_i,x_{ji})}{\left|x_{ji}\right|}} x_i\in x_{ji}\\ {\displaystyle \frac{\rho (x_i,x_{ji})}{\rho (x,x_{pi})-\rho (x_i,x_{ji})}}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{x}_i\in x_{ji},\end{array}\right.,$$

(16)

where

$$\rho ({\chi }_i,{\chi }_{ji})=\mid {\chi }_i-{\displaystyle \frac{(a_{ji}+b_{ji})}{2}}\mid -{\displaystyle \frac{(b_{ji}-a_{ji})}{2}},$$

(17)

$$\rho ({\chi }_i,{\chi }_{pi})=\mid {\chi }_i-{\displaystyle \frac{(a_{pi}+b_{pi})}{2}}\mid -{\displaystyle \frac{(b_{pi}-a_{pi})}{2}},$$

(18)

$$\left|\begin{array}{c}{x}_{ji}\end{array}\right|=\left|\begin{array}{c}{a}_{ji}-b_{ji}\end{array}\right|,$$

(19)

$$K_j(P)={\sum }_{i=1}^n {\overline{\omega }}_i·K_j(x_i),$$

(20)

$K_j\left(P\right)$ is called the correlation of P to be evaluated with respect to rank j.

3.6.5. Determination of Risk Level

If $K_{\mathrm{a}}=\underset{j}{max} \lfloor K_j(P)\rfloor (j=1,2,\cdots ,m)$, then $R\in {\mathrm{R}}_{\mathrm{a}}$; i.e., the unit P to be evaluated belongs to class a [31].

4. Results

4.1. Modeling Application

In this study, the matter–element extension theory model was used in a sewage treatment plant in the northern district of Changchun City [32], the analytic hierarchy process was used for the determination of subjective weights, and the entropy weight method was used to determine the objective weight of each indicator. Game theory was used to calculate each indicator’s combined weight, which was then combined with expert scoring and weight data. The operational safety risk level of the sewage treatment plant was determined with the matter–element extension theory model. A wastewater treatment plant in the northern district was taken as the research object to verify the reliability of the model [8].

4.2. Risk Rating

According to the introduction of the ‘Jilin Province Sewage Treatment Plant Operation and Management Standards’, we divided the operational safety of sewage treatment plants into grades and made appropriate adjustments based on the features of the indexes and the factual situation of the research object. Finally, the selected indicators were able to fully meet the needs of the operational safety evaluation system for sewage treatment plants [5].

On this basis, the safety level of wastewater treatment plants was divided into four levels. The first level was safety, which indicated that the operation of the wastewater treatment plant was in a safe state, and there was a reliable safety guarantee for the employees in the field and the effluent quality. The second level was relatively safe, indicating that in the sewage treatment plant, there were areas that could be improved, basic operational safety could be guaranteed, and the effluent quality was in the standard state. The third level was unsafe, indicating that the operation of the wastewater treatment plant was dangerous and needed to be checked in time. There was a certain risk in the effluent quality, and production needed to be stopped immediately. The fourth level was dangerous, indicating that the sewage treatment plant had a huge safety hazard during operation and needed to be investigated immediately [16]. The details of the grading are shown in

Table 2. Values of objects to be evaluated.

Criterion	Index	Number of the Index	Correlation					Rating Value
			Level I	Level II	Level III	Level IV	Average
W Wuli	Equipment integrity	W1	1.00	0.75	0.50	0.25	0.50	0.97
	Maintenance of equipment	W2						0.96
	Facility Layout	W3						0.95
	Surrounding environment	W4						0.96
S Shili	Security checks	S1						0.95
	Safety regime	S2						0.99
	Prevention of accidents	S3						0.86
	Technological improvements	S4						0.93
R Renli	Cultural level	R1						0.92
	Technical training	R2						0.89

.

4.3. The Weights of Operational Safety Risk Indexes for Sewage Treatment Plants

The weight of each indicator was determined using the entropy weight method and the analytic hierarchy process. Then, game theory was used to combine the two weighting methods and, finally, determine the combined weights of the indicators. The weight of each index is shown in

Table 3. Combined weights of operational safety risk indexes for sewage treatment plants.

Index	Determination of Subjective Weights with the Analytic Hierarchy Process ω1 (%)	Determination of Objective Weights with the Entropy Weight Method ω2 (%)	Determination of Combined Weights with Game Theory ω0 (%)
W1	5.081	8.242	7.655
W2	10.547	11.219	11.094
W3	10.547	9.557	9.741
W4	11.261	14.324	13.756
S1	11.261	15.612	14.805
S2	11.261	7.529	8.222
S3	9.832	9.337	9.429
S4	10.547	7.041	7.692
R1	9.832	8.147	8.460
R2	9.832	8.992	9.148

and Figure 3.

4.4. Construction of the Matter–Element Evaluation Model

• Establishment of a classical field: In the evaluation index system, the classical domain of quantitative indicators was set to 0–1 by the experts. The scope is assigned to four classical domains according to the risk level. The classical field with the first risk level was 1–0.75, the second risk level was 0.75–0.5, the third risk level was 0.5–0.25, and the fourth risk level was 0.25–0.
• Establishment of a controlled domain: The domain of each indicator was the total of all its classical domain values.
• Establishment of the matter–element evaluation: The detailed value of the object–element rating $R_0$ was obtained by statistically analyzing the results of the ratings of the experts and persons responsible for the Changchun City Development Zone North Wastewater Treatment Plant.

The values of the classical domain $R_1{R}_2{R}_3{R}_4$ and the object–element ratings $R_P$ after the normalization of the section domain $R_0$ and ratings were the following [32]:

$$\begin{array}{lll}{{\displaystyle R}}_1=\left[\begin{array}{ccc}{{\displaystyle N}}_1& {{\displaystyle W}}_1& (1,0.75)\\ & {{\displaystyle W}}_2& (1,0.75)\\ & {{\displaystyle W}}_3& (1,0.75)\\ & {{\displaystyle W}}_4& (1,0.75)\\ & {{\displaystyle S}}_1& (1,0.75)\\ & {{\displaystyle S}}_2& (1,0.75)\\ & {{\displaystyle S}}_3& (1,0.75)\\ & {{\displaystyle S}}_4& (1,0.75)\\ & {{\displaystyle R}}_1& (1,0.75)\\ & {{\displaystyle R}}_2& (1,0.75)\end{array}\right]& {{\displaystyle R}}_2=\left[\begin{array}{ccc}{{\displaystyle N}}_2& {{\displaystyle W}}_1& (0.75,0.5)\\ & {{\displaystyle W}}_2& (0.75,0.5)\\ & {{\displaystyle W}}_3& (0.75,0.5)\\ & {{\displaystyle W}}_4& (0.75,0.5)\\ & {{\displaystyle S}}_1& (0.75,0.5)\\ & {{\displaystyle S}}_2& (0.75,0.5)\\ & {{\displaystyle S}}_3& (0.75,0.5)\\ & {{\displaystyle S}}_4& (0.75,0.5)\\ & {{\displaystyle R}}_1& (0.75,0.5)\\ & {{\displaystyle R}}_2& (0.75,0.5)\end{array}\right]& {{\displaystyle R}}_3=\left[\begin{array}{ccc}{{\displaystyle N}}_3& {{\displaystyle W}}_1& (0.5,0.25)\\ & {{\displaystyle W}}_2& (0.5,0.25)\\ & {{\displaystyle W}}_3& (0.5,0.25)\\ & {{\displaystyle W}}_4& (0.5,0.25)\\ & {{\displaystyle S}}_1& (0.5,0.25)\\ & {{\displaystyle S}}_2& (0.5,0.25)\\ & {{\displaystyle S}}_3& (0.5,0.25)\\ & {{\displaystyle S}}_4& (0.5,0.25)\\ & {{\displaystyle R}}_1& (0.5,0.25)\\ & {{\displaystyle R}}_2& (0.5,0.25)\end{array}\right]{{\displaystyle R}}_4=\left[\begin{array}{ccc}{{\displaystyle N}}_4& {{\displaystyle W}}_1& (0.25,0)\\ & {{\displaystyle W}}_2& (0.25,0)\\ & {{\displaystyle W}}_3& (0.25,0)\\ & {{\displaystyle W}}_4& (0.25,0)\\ & {{\displaystyle S}}_1& (0.25,0)\\ & {{\displaystyle S}}_2& (0.25,0)\\ & {{\displaystyle S}}_3& (0.25,0)\\ & {{\displaystyle S}}_4& (0.25,0)\\ & {{\displaystyle R}}_1& (0.25,0)\\ & {{\displaystyle R}}_2& (0.25,0)\end{array}\right]\\ {{\displaystyle R}}_P=\left[\begin{array}{ccc}{{\displaystyle N}}_P& {{\displaystyle W}}_1& (0,1)\\ & {{\displaystyle W}}_2& (0,1)\\ & {{\displaystyle W}}_3& (0,1)\\ & {{\displaystyle W}}_4& (0,1)\\ & {{\displaystyle S}}_1& (0,1)\\ & {{\displaystyle S}}_2& (0,1)\\ & {{\displaystyle S}}_3& (0,1)\\ & {{\displaystyle S}}_4& (0,1)\\ & {{\displaystyle R}}_1& (0,1)\\ & {{\displaystyle R}}_2& (0,1)\end{array}\right]& {{\displaystyle R}}_0=\left[\begin{array}{ccc}{{\displaystyle N}}_0& {{\displaystyle W}}_1& 0.966\\ & {{\displaystyle W}}_2& 0.959\\ & {{\displaystyle W}}_3& 0.947\\ & {{\displaystyle W}}_4& 0.959\\ & {{\displaystyle S}}_1& 0.951\\ & {{\displaystyle S}}_2& 1\\ & {{\displaystyle S}}_3& 0.857\\ & {{\displaystyle S}}_4& 0.928\\ & {{\displaystyle R}}_1& 0.922\\ & {{\displaystyle R}}_2& 0.889\end{array}\right]& \end{array}$$

4.5. Correlation and Weight Coefficients

Using Formulas (16)–(19), the degree of correlation of each indicator with the four levels was calculated [33], and the scores obtained from the questionnaire were calculated using the entropy weight method. Finally, the weight of each index was obtained. Using Formula (20), the safety level of the wastewater treatment plant was obtained [8], as shown in

Table 4. Evaluation of matter-element analysis and indicator weighting results in sewage treatment plants.

Criterion	Index	Number of the Index	Correlation				Weights (%)
			Level I	Level II	Level III	Level IV
W Wuli	Equipment integrity	W1	0.134	−0.866	−0.933	−0.955	7.655
	Maintenance of equipment	W2	0.162	−0.838	−0.919	−0.946	11.094
	Facility layout	W3	0.211	−0.789	−0.894	−0.930	9.741
	Surrounding environment	W4	0.163	−0.837	−0.918	−0.946	13.756
S Shili	Security check	S1	0.193	−0.807	−0.903	−0.936	14.805
	Safety regime	S2	4.000	−0.960	−0.980	−0.987	8.222
	Prevention of accidents	S3	0.429	−0.429	−0.714	−0.810	9.429
	Technological improvements	S4	0.286	−0.714	−0.857	−0.905	7.692
R Renli	Cultural level	R1	0.311	−0.689	−0.844	−0.896	8.460
	Technical training	R2	0.442	−0.558	−0.779	−0.853	9.148

.

4.6. Comprehensive Correlation Calculation

On the basis of Formula (20), the degree of relatedness of the comprehensive indexes could be calculated. Based on the principle of maximum subordination, the risk rank of each object to be evaluated could be judged. The evaluation results are shown in

Table 5. Results of the calculation of the comprehensive correlation of sewage treatment plants.

Object	Criterion	Correlation				Risk Rating
		Level I	Level I	Level I	Level I
Changchun North District Wastewater Treatment Plant	W Wuli	0.169	−0.831	−0.916	−0.944	Level I
	S Shili	0.268	−0.732	−0.866	−0.911
	R Renli	0.380	−0.621	−0.811	−0.874

[8].

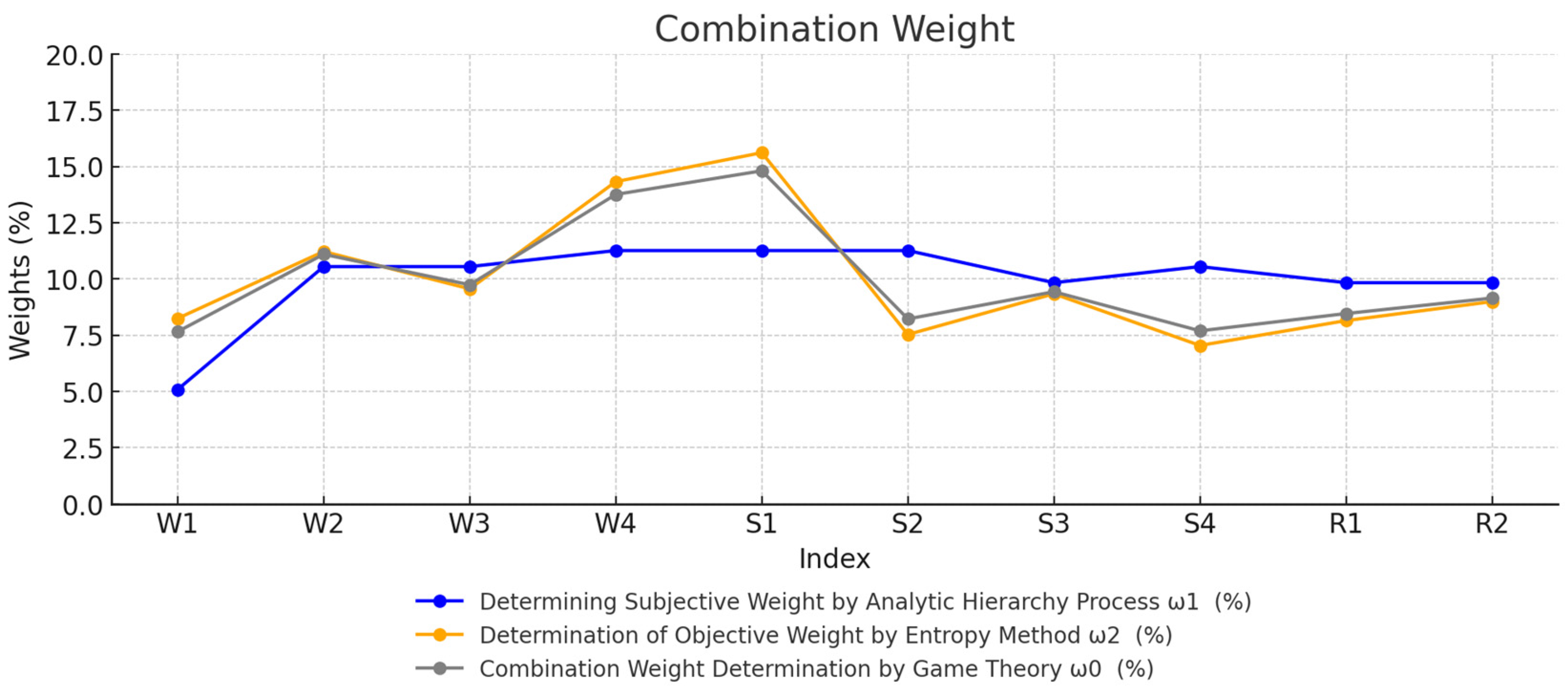
• According to the combined weights calculated using game theory, it was not difficult to see that different indicators had different impacts on the operational safety of sewage treatment plants, and in the weight calculation, the larger the weight value of the indicators, the greater the impact on operational safety. The weights of the 10 indicators in the whole evaluation index system can be seen in Table 3, in which safety inspection (S1) had the largest weight in safety risks in sewage treatment plants, and equipment integrity (W1) had the smallest weight. Safety inspection is a key factor in the operational safety of wastewater treatment plants. The weights of the indicators were different, and they were ranked as follows in descending order: S1 > W4 > W2 > W3 > S3 > R2 > R1 > S2 > S4 > W1. It was concluded that the weight ratio of safety inspection (S1) was the largest, which indicated that it could reflect the safety risk characteristics of the WWTP. In comparison with the other indicators, if a wastewater treatment plant can be improved in terms of safety inspection (S1), the operational safety of the whole plant can be significantly improved.
• According to the weight calculation in the previous section, the values of all evaluation indicators were ranked. The results showed that the operational safety correlations of the wastewater treatment plant were ranked in the following order: S2 > W1 > W2 > W4 > W3 > S1 > S4 > R1 > R2 > S3. All indicators were at the first level of safety, which indicated that the operation of the wastewater treatment plant was in a safe environment. The wastewater treatment plant did the best on the S2 indicator and received the highest rating. In terms of accident prevention (S3), the wastewater treatment plant needed further strengthening, in addition to accumulating experience in relevant aspects and making adjustments to accident prevention policies and measures, which would help improve its operational safety.
• According to the evaluation results, the operational safety risk of the WWTP was at a safe level (level 1). It was able to ensure the quality of effluent water while preventing casualties in the process of sewage treatment and preventing pollution of the surrounding environment. S1 and S3 were the most heavily weighted indicators and those that were rated the lowest; therefore, the wastewater treatment plant needs to be further developed and perfected so as to ensure that the discharge of effluent water can effectively reduce the environmental risk of water pollution and increase the degree of guaranteed safety of the aquatic environment.

4.7. Sensitivity Analysis

A sensitivity analysis was conducted based on the system of risk indicators for the operational safety of wastewater treatment plants. Three different combination weighting methods were used to evaluate the sensitivity of the operational safety risk assessment system for wastewater treatment plants: the arithmetic weighting method, the variance-based combination weighting method, and the limit minimization method. The sensitivity was analyzed by varying the combination weighting coefficient γ with values of 0.5, 0.913, 0.8, 0.2, and 0.1. The results are shown in Figure 4.

As can be seen in Figure 4, when the combination weighting coefficient γ exceeded 0.5, the indicators W1, W4, S1, S2, and S4 showed significant deviations, with the most pronounced deviation being observed in indicator S1. This suggested that these indicators were more sensitive to changes in the weighting coefficients, especially S1, which had a significant impact on the overall system. In contrast, the remaining indicators showed relatively small deviations and low sensitivity to changes in weighting.

Despite the significant deviations observed for several key indicators (W1, W4, S1, S2, and S4), the overall level of operational safety risk of the STPs remained relatively stable. When all ten indicators were considered together, it could be seen that although certain indicators showed high sensitivity, the overall risk level of the system remained largely unaffected by variations in the combination weighting coefficient. Thus, the overall sensitivity of the system was low, indicating that the operational safety risk of the STPs was not significantly affected by changes in the weighting scheme.

In conclusion, although some key indicators (such as S1) were highly sensitive to changes in the weighting coefficients, the system showed considerable robustness, with only small variations in the overall risk level. For the assessment of the operational safety of wastewater treatment plants, the low sensitivity of the model can be considered an advantage. This means that the model’s results remain reliable in the face of uncertainty or noisy data, and they are suitable for use in realistic and variable environments [34].

5. Conclusions

Wastewater treatment plants are an effective way to control water pollution and alleviate water shortages. Their role depends on guaranteeing their operation. At the same time, they have played a timely role in curbing water shortage crises, so the sewage treatment business has become a key area in the development of China’s environmental protection. Therefore, the operational safety of wastewater treatment plants is of great significance.

This study established a risk evaluation index system for the operational safety of sewage treatment plants using Wuli, Shili, and Renli, which resulted in a combination of the oriental literature and traditional cultural understanding to extend the exploration and thinking of the operational safety of sewage treatment plants. The entropy weight method was used for the determination of objective weights, and the analytic hierarchy process was used for the determination of subjective weights. Finally, game theory was utilized to calculate the combined weights of each index. The entropy weight method was utilized to combine the focuses of different weighting methods, solve the weighting problem from another perspective, and improve the accuracy of the weight value. On this basis, a risk assessment method based on the matter–element extension model was established. The feasibility of the model was proved through the analysis of arithmetic examples, which provided a method for solving similar problems. This will provide theoretical support for the evaluation of the operational safety risk in urban sewage treatment plants. According to the evaluation results, the operational safety risk of the wastewater treatment plant was at level 1 (safe). However, the score for accident prevention (S3) was low, indicating that it was necessary to strengthen the management and develop corresponding policies.

A similar theoretical model was also used to address sustainability in the shale gas sector. A multidimensional comprehensive analysis of the sustainability of shale gas was conducted using an index system established with the WSR theoretical model. Specific recommendations for improvement were made for cities with weak sustainability of shale gas, which has greatly aided in those cities’ energy development. A comparable theoretical model was also utilized in an article on the risk assessment of urban power grid planning in China. An example was analyzed to demonstrate the model’s viability, offering a fresh approach to tackling related issues. Through these two examples, it is not difficult to see the universality and feasibility of the matter–element extension model based on WSR theory. To assess the strengths of the model proposed in this study, we compared the results with those of other risk assessment methods used in wastewater treatment plants and similar systems. In their discussion of the safe operation of municipal wastewater treatment plants, Fangwen Li et al. adopted a traditional qualitative approach that focused on expert judgments and the manual assessment of safety risks [35]. In contrast, our model combined subjective (AHP) and objective (entropy weight method) approaches and optimized the weight combinations through game theory, thus providing a more balanced data-driven assessment. Ji et al. used a fuzzy comprehensive evaluation method and the Delphi method in bridge risk assessment, highlighting the importance of multi-criteria decision-making in complex systems [36]. While their fuzzy approach handled uncertainty well, ours provides a more structured framework that combines subjective with objective assessments and is able to quantify risk more precisely. Finally, Xiantao Qin et al. adopted a model combining gray system theory with fuzzy logic in bridge safety assessment, which allowed them to deal with uncertainties in data [36]. However, by integrating game theory, we were able to better deal with the connections between different weighting methods and provide a more flexible and comprehensive evaluation model. By comparing these three methods, it can be seen that although other methods provide help in evaluation, the accuracy and reliability of the risk assessment model that we proposed were significantly improved.

Currently, there are few reports on the operational safety of wastewater treatment plants, and the scope of safe operation given is narrow, as it is mostly limited to one aspect, such as the production process, equipment operation safety, and laboratory safety. This may cause incorrect judgments of the operational safety of WWTPs, resulting in the pollution of water resources. Therefore, based on the results of the evaluation in this study, the following suggestions are provided for reference.

• For accident prevention (S3), it is recommended that a comprehensive risk assessment be carried out regularly to identify potential hazards and formulate appropriate preventive measures to effectively prevent accidents in wastewater treatment plants and safeguard the safety of personnel and facilities. For example, regular safety drills, especially simulation drills in the areas of equipment failure and accident prevention, can improve the speed and accuracy of employees’ response in the event of an accident. At the same time, it is recommended to introduce a real-time monitoring system for the continuous monitoring of the safety of critical equipment and processes to ensure that potential risks can be detected and prevented in time when they are elevated. These measures, combined with the strengthening of equipment maintenance, operational practices, and staff training, are expected to effectively reduce the risk of accidents in the operation of wastewater treatment plants and ensure the long-term stability and safety of the system.
• For safety inspection (S1), which has the largest weight value, it is recommended to strengthen the physical security measures in facilities, such as installing a sufficient number of monitoring cameras and setting up a high-standard lighting system. Biosecurity procedures should be reinforced, such as by frequently cleaning the working environment and installing high-efficiency air filtration systems in locations that are prone to creating dangerous biological aerosols. By taking these precautions, the risk of accidents can be reduced while also safeguarding the environment and personnel.
• It is recommended that a comprehensive safety management system be established with detailed safety management policies and procedures covering all operational aspects. A full-time safety management department should be established to oversee the day-to-day implementation of safety. The safety inspection system should be continuously updated and improved to adapt to the ever-changing work environment and technological advances.