The Coupled Application of the DB-IWHR Model and the MIKE 21 Model for the Assessment of Dam Failure Risk

Abstract

The phenomenon of global climate change has led to an increase in the frequency of extreme precipitation events, an acceleration in the melting of glaciers and snow cover, and an elevation of the risk of flooding. In this study, the DB-IWHR model was employed in conjunction with the MIKE 21 hydrodynamic model to develop a simulation system for the dam failure flow process of an earth and rock dam. The study concentrated on the KET reservoir, and 12 dam failure scenarios were devised based on varying design flood criteria. The impact of reservoir failures on flood-risk areas was subjected to detailed analysis, with consideration given to a range of potential failure scenarios and flood sizes. It was determined that under identical inflow frequency conditions, the higher the water level, the more rapid the breakout process and the corresponding increase in flood peak discharge. Conversely, for a given frequency of incoming water, an elevated water level results in a transient breach process, accompanied by a reduction in flood peak flow. Moreover, for a given water level, an increase in water frequency results in a reduction in breaching time, an extension of flood duration, and an increase in flood peak flow. The observed trend of flood spreading is generally north-south, and this process is highly compatible with the topographic and geomorphological features, demonstrating good adaptability.

1. Introduction

The trend of global warming has contributed to the frequent occurrence of extreme rainfall events and accelerated the melting process of glaciers and snow packs. This accelerated melting not only has serious impacts on ecosystems, but also further exacerbates the risk of flooding, with investigations revealing that more than half of all dam failures are due to flood-induced failures of earth and rock dams, which poses a significant threat to human settlements and agricultural production.

Regarding the study of numerical simulation of flood dam failure, Fondelli et al. [1] used an adaptive mesh technique to simulate the dam failure process using Volume of Fluid (VOF) simulation. The VOF method is an advanced computational fluid dynamics technique specifically designed to track the dynamic motion of two or more immiscible fluids at an interface and is often combined with the Navier–Stokes equations to enable accurate modelling of such flow behaviour. Using this approach, they successfully demonstrated the high accuracy and reliability of numerical simulation of free surface flow; Niu et al. [2] used the SPH method to simulate the violent interactions between the free surface of the dam failure and the objects, which improved the computational accuracy, and verified the stability and accuracy of the ISPH scheme; He et al. [3] proposed a depth-averaged two-dimensional model of dam-breaking flows in moving beds and vegetated beds, and studied and analysed the effect of the presence or absence of vegetation on dam breakage; Seyedashraf et al. [4] proposed a numerical format for finite element methods with full variance attenuation properties capable of masking errors during sudden changes in flow conditions; Subklay et al. [5] proposed implicit and explicit methods applicable to water quality modelling of long-term flooding scenarios; Ali et al. [6] carried out sediment transport of solid particles contained in river valleys during flood transit modelling and applied to the Hamiz dam failure event; Elmiloud et al. [7] used the Radial Basis Function Meshless Method (RBFM) to solve the two-dimensional diving equations and simulated the dam failure flow over irregular, frictionally wet and dry terrain; Kojima et al. [8] modelled the flood water flow after the Tokyo earthquake; Li et al. [9] established a dam failure model and a computer program for a non-viscous homogeneous dam and verified it in an actual dam failure event; Wang et al. [10] proposed a simulation method for complex terrain downstream of a tailings dam breach by using unmanned aerial photogrammetry (UAV) and smooth particle hydrodynamics (SPH) numerical methods; Thu et al. [11] investigated the effects of the initial water level and the dam breach width on the peak three-dimensional force intensity calculation results; Alibek et al. [12] proposed an improved numerical model to simulate the water flow transferred from different heights of mud layer during dam breaching; Sadegh et al. [13] analysed the propagation of dam-break water flow over a step by using a new semi-implicit method of weakly compressible moving particles; Chen et al. [14] developed an innovative e-computing spreadsheet for simulating the flood dam failure process line by leveraging its superior computational capabilities and integrating VBA (Visual Basic for Applications) programming on the Excel interface, and proposed the DB-IWHR spreadsheet model for flood dam failure analysis; Shen et al. [15] proposed an improved model for the tailings pond dam failure impact analysis, proposed an improvement of the DB-IWHR model; in recent years, Danish academics developed MIKE ZERO for use in numerical analyses of dam failure. MIKE 21 [16,17,18], HEC-RAS [19] and a host of other models have also been widely used for reservoir assessment and mitigation measures. A study used the DB-IWHR and HEC-RAS models to simulate the breaching process of the Tangjiashan weir, and explored in depth the techniques for calculating and predicting weir breach floods. The study analysed in detail the effects of key parameters such as water level height, reservoir capacity curve and breach flow on the breaching process.

At present, numerical simulation techniques are still in a stage of continuous research and development in the field of dam failure research, especially for the dam failure of earth and rock dams in reservoirs located in flat areas. In order to predict and simulate the dam failure process more accurately, the coupling technique between models becomes an important means to improve the prediction accuracy. At the international level, several organisations and institutions have proposed standards and regulations on dam failure simulation. For example, the International Commission on Large Dams (ICOLD) has clearly stated in its guidelines that dam failure simulations should take into account the combined effects of water velocity and flood height. In addition, the United States Army Corps of Engineers (USACE) has proposed corresponding calculation methods and safety standards. This study focuses on the phenomenon of overtopping failure, but in addition to overtopping failures, there is an equally important aspect that should not be overlooked when exploring the mechanisms of dam damage: tubification failure, a type of dam failure that usually occurs when the reservoir level rises dramatically and the flow of water passes through the defects or cracks in the dam structure, creating a high-velocity flow of water, which in turn erodes the building materials. This type of failure usually occurs when the water flows through the defects or cracks of the dam structure, resulting in a high-velocity flow that erodes the construction materials, and ultimately causes the dam structure to collapse. In this study, only the overtopping damage is investigated. A typical reservoir is selected as the research object, and a two-dimensional coupled hydrodynamic model of DB-IWHR and MIKE 21 is successfully constructed. By using this coupled model, key risk indicators such as water depth and flow rate of flood inundation after dam failure can be accurately assessed, which in turn provides more solid data support for flood risk management.

2. Model and Methods

2.1. DB-IWHR Model

DB-IWHR model integrates a flood process line calculation program into VBA to obtain flood process lines using parameters such as flow depth, shear stress and embankment material to predict the characteristics of the breach and flow characteristics.

2.1.1. Flow and Velocity at the Breach Section

The flow at the outlet of the breach is calculated according to the free outflow theory, i.e., without considering the contraction of the flow in the vertical direction, only the lateral contraction is considered, and the wide-roofed weir formula is used to estimate the flow at the breach section.

$$Q=CB{(H-z)}^{3/2}=m_b{m}_q\sqrt{2g}B{(H-z)}^{3/2}$$

(1)

$$C=m_b{m}_q\sqrt{2g}$$

(2)

where m_b is the flow coefficient of the wide top weir, m_q is the side contraction coefficient. C is the combined flow coefficient [20,21], the theoretical value of 1.7 m^1/2/s, which can be selected in the range of 1.3 to 1.7 m^1/2/s. In the study of Fread [22], it was found that when the damage is close to the completion of the reservoir level close to the tailing level, a drop coefficient needs to be considered.

The velocity of flow in the breach section is determined by the following formula:

$$V={\displaystyle \frac{Q}{Bh}}=C{\displaystyle \frac{{(H-z)}^{\frac{3}{2}}}{h}}=C{m}^{-1}\sqrt{(H-z)}$$

(3)

$$CB{(H-z)}^{\frac{3}{2}}=-{\displaystyle \frac{\Delta W}{\Delta H}}{\displaystyle \frac{\Delta H}{\Delta t}}+q$$

(4)

where q is the incoming flow rate.

2.1.2. Scour Model

A hyperbolic model was developed for the scour model, i.e., the relationship curve between erosion rate and shear stress:

$$\dot{z}=\mathsf{\Phi }(\tau )={\displaystyle \frac{\nu }{a+b\nu }}$$

(5)

where v is the shear stress after deducting the critical shear stress.

$$\nu =k(\tau -{\tau }_c)$$

(6)

where k is the unit transformation factor for the range of shear stresses in which τ is allowed to approach z_ult. z_ult represents the asymptotic value of the curve, i.e., the limiting value of the erosion rate. Specifically, as the velocity v tends to infinity, the asymptote value of the curve, z_ult, tends to 1/b. In the model setup, the constant k is set to 100, and the parameter 1/a represents the initial slope of the curve when the velocity v is zero. The construction of the model is based on an in-depth analysis of the erosion resistance of the soil material whose ‘strength’ should not be regarded as infinite. Based on the model parameters, we determined a = 1.1, b = 0.0003, and shear stress τ_c = 30 Pa. With these settings, the calculated value of z_ult is 3.333 mm/s.

2.1.3. Modelling of Lateral Extension of Breach

As the bottom of the breach is continuously scoured and deepened, the slopes on both sides gradually collapse and lose stability, leading to the continuous expansion of the breach flanks. The model adopts circular sliding surface analysis to reasonably reproduce the rock slope failure process caused by the downcutting of the slope angle, and the hyperbolic model is used to calculate the inclination change Δβ of the trapezoidal flanks.

$$B=B_0+2\Delta z+2h\tan \left(\beta -{\displaystyle \frac{\pi }{2}}\right)$$

(7)

$$\beta ={\beta }_0+\Delta \beta ={\beta }_0+{\displaystyle \frac{\Delta z}{m_1\Delta z+m_2}}$$

(8)

where 1/m₁ and 1/m₂ denote the initial tangent and asymptote of the hyperbola, respectively.

2.2. MIKE 21 Model

MIKE 21 model is based on numerically solved two-dimensional shallow water equations and incompressible Reynolds-averaged Navier–Stokes equations integrated along the water depth, and is capable of simulating changes in water levels and currents induced by a variety of forcings, as well as any two-dimensional free-surface flow ignoring laminar partitioning.

2.2.1. Governing Equation

The two-dimensional non-constant flow calculation module of MIKE 21 follows the Reynolds mean stress equation for two-dimensional incompressible fluids, using both the Busiennesk assumption and the hydrostatic pressure assumption.

Water flow continuity equation:

$${\displaystyle \frac{\partial h}{\partial t}}+{\displaystyle \frac{\partial h\overline{u}}{\partial x}}+{\displaystyle \frac{\partial h\overline{v}}{\partial y}}=hs$$

(9)

where t is time; u and v are velocity components in the x and y directions.

The lateral stress term T_ij is accurately estimated by applying an eddy viscosity formulation based on mean bathymetric flow velocity gradients, including viscous friction, turbulent friction and differential advection.

$$T_{xx}=2A{\displaystyle \frac{\partial \overline{u}}{\partial x}}, T_{xy}=A({\displaystyle \frac{\partial \overline{u}}{\partial y}}+{\displaystyle \frac{\partial \overline{v}}{\partial x}}), T_{yy}=2A{\displaystyle \frac{\partial \overline{v}}{\partial y}}$$

(10)

2.2.2. Discrete Equation in Space

The spatial discretisation of the computational region adopts the finite volume method based on the Riemannian solution, which achieves an accurate simulation of fluid dynamics by partitioning the continuous fluid domain into non-overlapping triangular or quadrilateral cells, transforming the continuous physical equations into discrete algebraic equations, and further improves the simulation by dividing the region into fine mesh cells with physical parameters and boundary conditions imposed on each cell accuracy and reliability.

Shallow water system of equations:

$${\displaystyle \frac{\partial U}{\partial t}}+\nabla ·F(U)=S(U)$$

(11)

where U is a conserved physical vector; F is a flux vector; and S is a source term. Both first-order and second-order solutions can be used for spatial discrete solving. To achieve fitting accuracy, the MIKE 21 model is constructed as a second-order computational model using the TVD-constrained least-squares method, and the hyperbolic equations are solved in the flux difference splitting (FDS) format proposed by Roe [23].

2.2.3. Time Integral

Low-order explicit Euler methods:

$$U_{n+1}=U_n+\Delta tG(U_n)$$

(12)

where Δt is the time step.

2.2.4. Boundary Condition

The open boundary is the flow boundary, the closed boundary is the land boundary, all variables flowing perpendicular to the boundary are zero, and the momentum equation reaches full stability at the land boundary.

In conclusion, the models and methods employed in this study are elucidated in comprehensive detail. For a detailed schematic of the research process, please refer to the attached Figure 1.

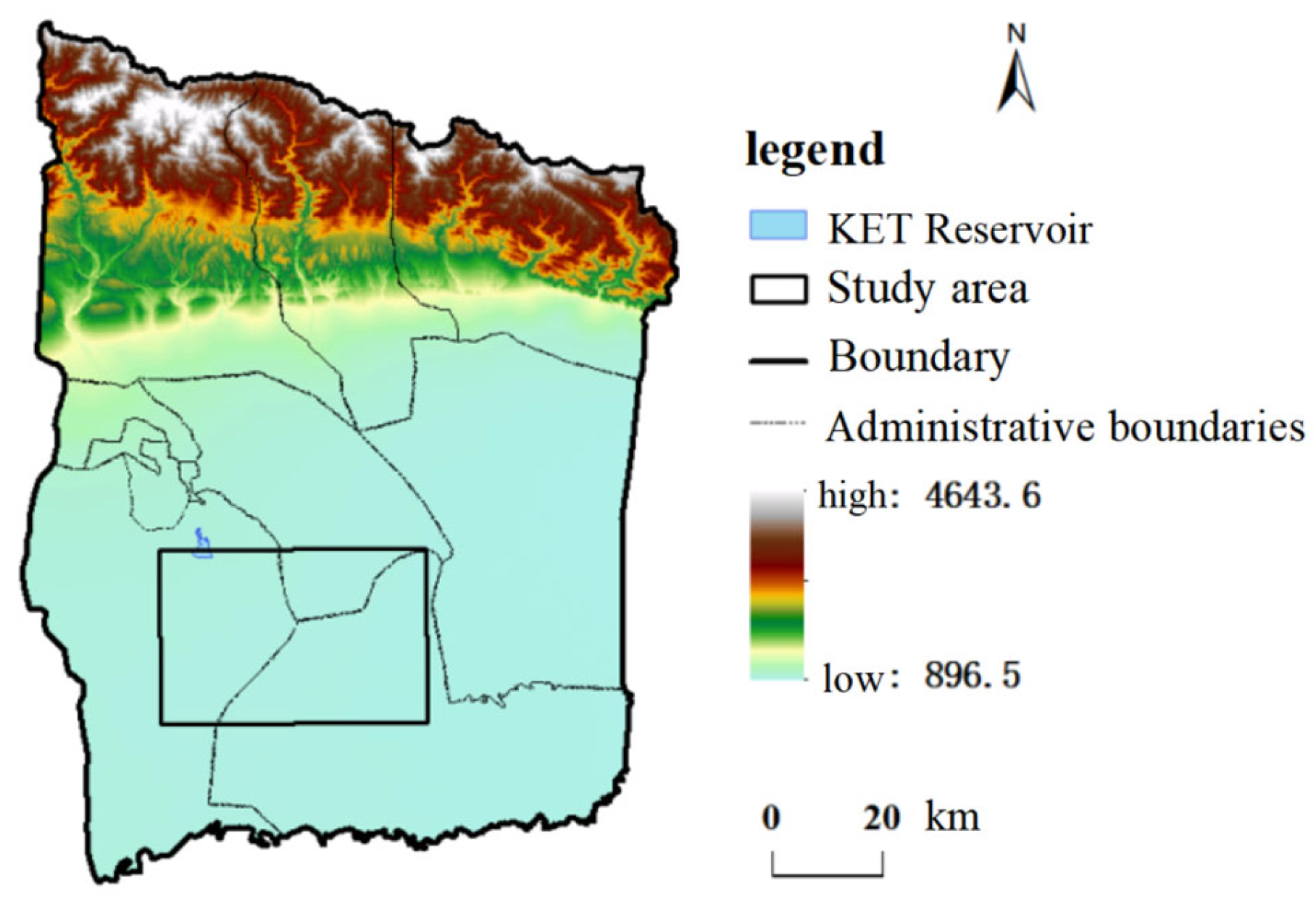
3. Condition Study

This paper takes the KET reservoir as its research object. The dam body is a homogeneous earth dam, mainly composed of silt soil and silty clay. In order to ensure the safety of the dam, the management station closely monitors key parameters such as seepage from the dam body and dam base, and reservoir level, as required for monitoring. To this end, flow meters have been installed to accurately monitor water flow dynamics, and pressure tubes are used to make detailed observations of the seepage lines of the dam. Automatically registered water level gauges were also installed to monitor changes in reservoir levels in real time. Water volume monitoring has been carried out downstream of the river to provide an overall picture of the hydrological dynamics of the dam. The scope of the study is determined by the breach of the reservoir in different conditions and the distribution of the infrastructure, villages and other key areas under the reservoir. The area in question is 624 km², comprising a north-south span of approximately 25 km and an east-west span of approximately 34 km. It extends from the KET reservoir dam site to the south of the range along the Desert Road. The location of the KET reservoir is shown in Figure 2.

3.1. Analysis of Breach Locations and Breach Flow Processes

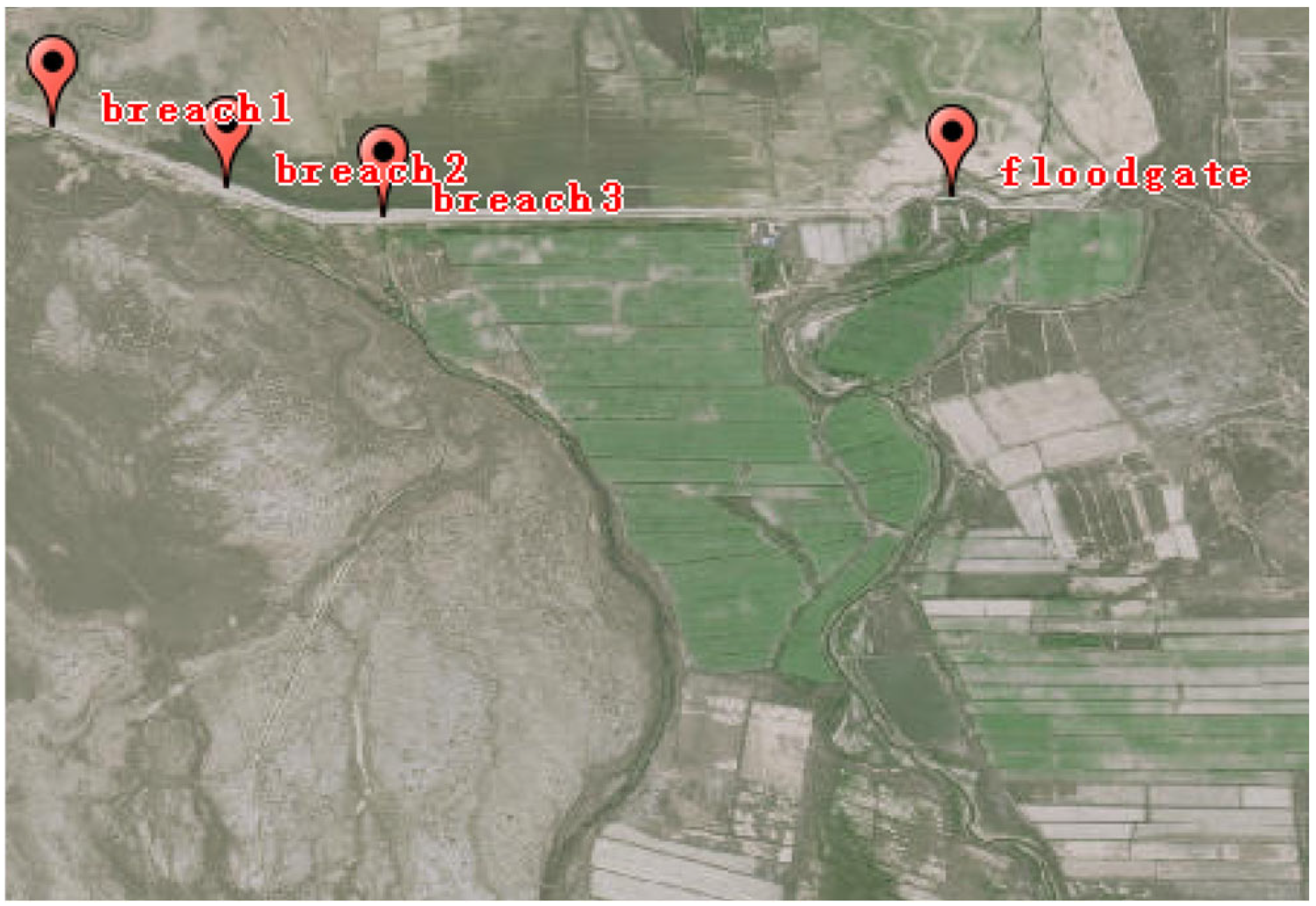
3.1.1. Determination of the Location of the Breach

Combined with the characteristics of the plain reservoir to analyse the dam body of the reservoir in the study area, the dam body of the KET reservoir is a homogeneous earth dam and is very likely to occur in the areas of damage, including the following: ① landslides: the dam body of the water-facing slopes and the piles of rock berms are not well drained, resulting in landslides and thus leading to local failure; ② seepage: the various parts of the body of the earth dam; ③ pipe surges: the site of the dam filtration of the water; ④ floodgates: the deformation of the gate, the destruction of the component caused by the reservoir cannot be normal venting of the flood water, making the development of the above disasters accelerated. The above disasters are accelerated due to the failure of the reservoir to discharge flood water properly as a result of the deformation of the gate and the damage of the gate components.

The axial lengths of the earth dam sections are all large, so the gradual breaching of the earth dam sections is considered, and the possible locations of breaching are identified as Breach 1, Breach 2 and Breach 3, as shown in Figure 3.

3.1.2. Analysis of Routed Flow Processes

The crest elevation is 949.7 m, the length of the dam is 3.16 km, the upstream slope of the dam body is 1:2.5, and the downstream slope of the dam body is 1:2. These figures have been determined according to the range of influence of the flow process. The DB-IWHR model simplifies the calculation process by using a linear slip surface and considering the main soil parameters involving friction angle f, cohesion c, nonlinear friction angle f₁, nonlinear cohesion c₁, dry gravity γ_d, saturated gravity γ_sat, and pore water pressure R_u. The parameters of the dam body of the KET Reservoir are shown in

Table 1. Dam Parameters Information.

f (°)	c (kPa)	f1 (°)	c1 (kPa)	γd (kN/m3)	γsat (kN/m3)	Ru
26.5	18	0	0	1.95	22.00	0

. After detailed site investigation, it was found that the thickness of the silt soil layer was approximately between 1.1 and 3.2 m, with a soil yellow to yellow-brown colour, loose structure and moderate moisture content, while the thickness of the pulverised clay layer was between 0.3 and 0.7 m, with a yellow colour and the same moderate moisture content. In order to further understand its particle size composition, we conducted a particle analysis test and obtained

Table 2. Distribution of particle size content of dam fill soil.

Sampling Location	Sampling Depth (m)	Grain Size (mm)							Unevenness Coefficient	Curvature Coefficient	Define Name
		>1	1 ~ 0.5	0.5 ~ 0.25	0.25 ~ 0.1	0.1 ~ 0.075	0.075 ~ 0.05	<0.05
		Content (%)
1	1.0	0.0	0.2	2.0	10.8	29.7	39.0	18.3	2.0	1.1	silt soil
2	1.2	0.0	0.3	2.1	10.0	16.0	49.0	22.6	1.5	1.5	silt soil
3	0.8	0.0	0.0	0.2	1.9	23.1	58.7	16.1	1.5	1.5	silt soil
4	0.9	0.0	0.0	0.6	8.8	18.3	59.3	13.0	1.5	1.5	silt soil
5	0.5	0.0	0.0	0.3	3.9	20.9	24.8	50.1	1.5	0.7	silt soil
Average number		0.0	0.1	1.0	7.1	21.6	46.2	24.0
1	2.5	0.0	0.0	0.3	7.1	14.5	67.6	10.5	1.5	1.5	silty clay
2	2.0	0.0	0.2	0.9	4.7	12.7	69.0	12.5	1.5	1.5	silty clay
3	3.5	0.6	0.7	9.4	8.7	3.5	64.3	12.8	1.5	1.5	silty clay
4	2.5	0.0	0.3	2.4	12.3	18.0	58.0	9.0	1.0	1.0	silty clay
5	1.8	0.0	0.0	1.7	3.6	12.0	70.9	11.8	1.5	1.5	silty clay
Average number		0.1	0.2	2.9	7.3	12.1	66.0	11.3

based on the compilation of the test results.

As the water level continued to rise, the water pressure inside the dam body increased dramatically. Concurrently, the shear strength of the structural materials of the dam body failed to meet the requisite standards, resulting in erosion and scouring of the dam materials. This phenomenon resulted in a reduction in the stability of the dam body, which in turn led to the localised sliding of the soil and the formation of landslides. At the weak points of the dam body, the erosive action of the water flow was particularly significant, rapidly leading to the formation of an initial breach. As the breach continues to expand, it reaches a critical size at which the rapid loss of dam material triggers a significant outflow of water from the reservoir, ultimately leading to a dam failure. According to different design flood standards, 12 different flood dam failure scenarios are set up, as shown in Figure 4.

(a) When Breach 1 encountered P = 5% flood, the floodgate for some reason cannot open and close normally, the reservoir reaches the calibration flood level (i.e., Condition 1-1) followed by a dam failure, the total flood volume is 61.03 million m³, the final width of the breach is 37.78 m, the height of the breach is 8.1 m, the breach lasted for 4.35 h, the flow rate reaches a maximum of 19,940 m³/s in the third 3.13 h, and the downstream flow rate reaches a stable of 150~200 m³/s until the end of incoming flood;

(b) When Breach 1 encountered P = 2% flood, the floodgate for some reason cannot open and close normally, the reservoir reaches the calibration flood level (i.e., Condition 2-1), followed by a dam failure, the total flood volume is 76,330,000 m³, the final width of the breach is 37.78 m, the height of the breach is 8.1 m, the collapse of the dam lasted for 4.03 h, the flow rate reaches a maximum of 2939 m³/s at the second 48 h, and the discharge flow rate reaches a stable of 150–250 m³/s until the end of the incoming flood.

A variety of flood process lines have been demonstrated above, and two of them have been analysed. From the many simulation data, it can be concluded that the higher the starting level of the simulated flood, the shorter the duration of the dam failure, and the larger the maximum discharge flow.

3.2. Modelling the Evolution of Dam Failure Floods

3.2.1. Confirmation of Modelling Scope

According to the situation of the breach flow process under different operating conditions of the reservoir, combined with the distribution of infrastructure, villages and other key areas downstream of the reservoir area, it was determined through trial calculations that from the dam site of the reservoir, along the highway to the south, the north-south direction is about 25 km, the east-west direction is about 34 km, with a total area of 624 km². A schematic diagram of the modelling scope is shown in Figure 5.

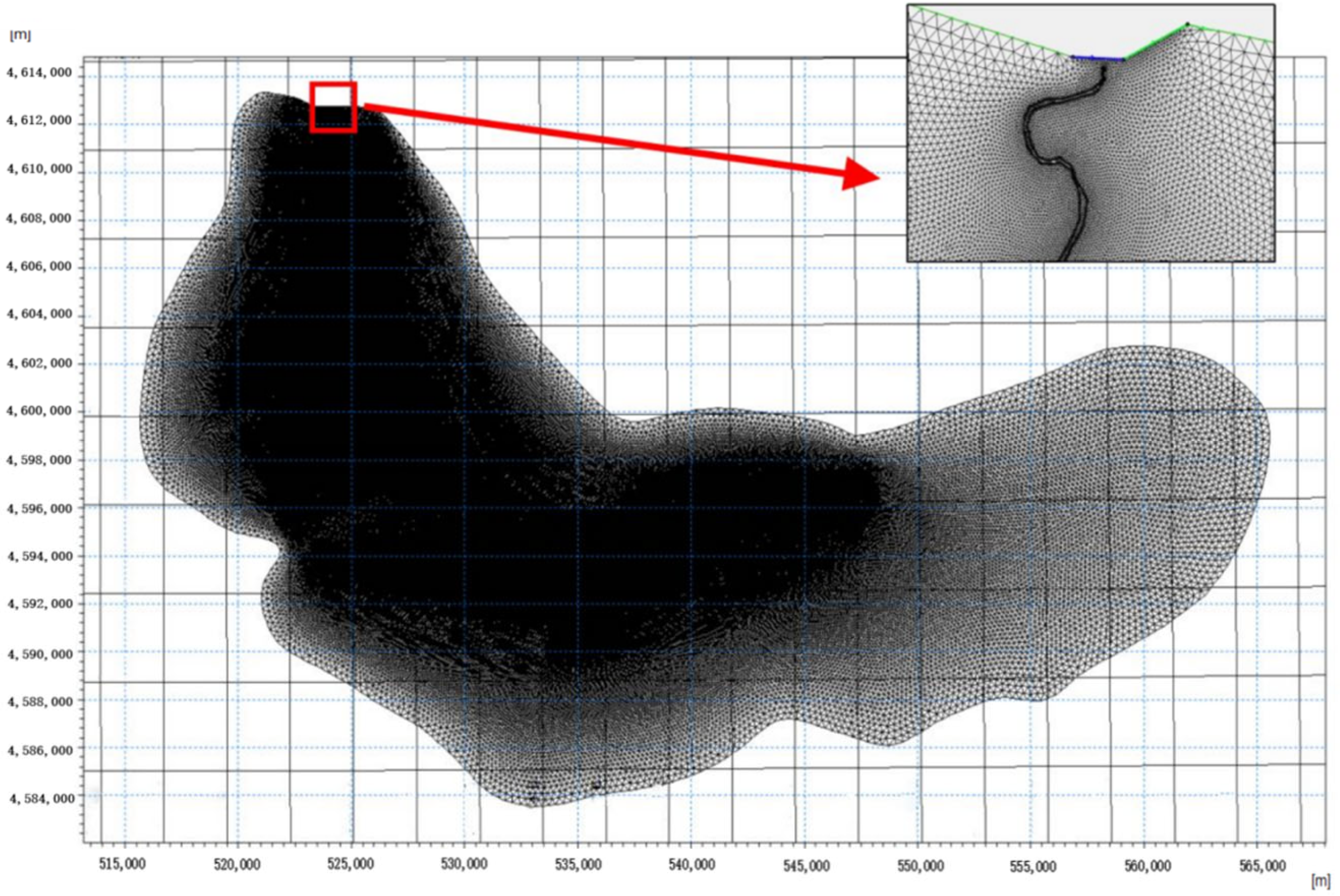
3.2.2. Grid Construction

Grid quality is the key to the accuracy of the results of the two-dimensional hydrodynamic model, and the simulation area is divided into a finite number of grid cells. This flood analysis, according to the topography, geomorphology and digital elevation model (DEM), and other basic information, according to the “Flood Dam Failure Simulation Technical Regulations” [24] requirements to determine the grid size, focus on the region or the terrain and features of large changes in the region, the grid is encrypted, the terrain is flat, the magnitude of the change of the region grid size is relaxed accordingly, and the average grid size is not more than 0.05 km².

In order to optimise the grid arrangement, the grids in the downstream area of the KET reservoir are all triangular non-structural grids with a minimum angle of not less than 30°, and the grids on both sides of the river and along the highway downstream of the dam site are appropriately encrypted to ensure that there is a corresponding water-blocking effect for the highway and other building structures.

The simulation area downstream of the KET reservoir is 624 km², and the number of grids is 537,244. In order to improve the accuracy of flood calculation, the maximum area of a single grid along the river and important roads is not more than 0.01 km², and the downstream of the reservoir area is obtained for the grid section and local grid as shown in Figure 6.

After grid processing, DEM elevation scatter interpolation was performed to obtain the topographic cloud map as shown in Figure 7.

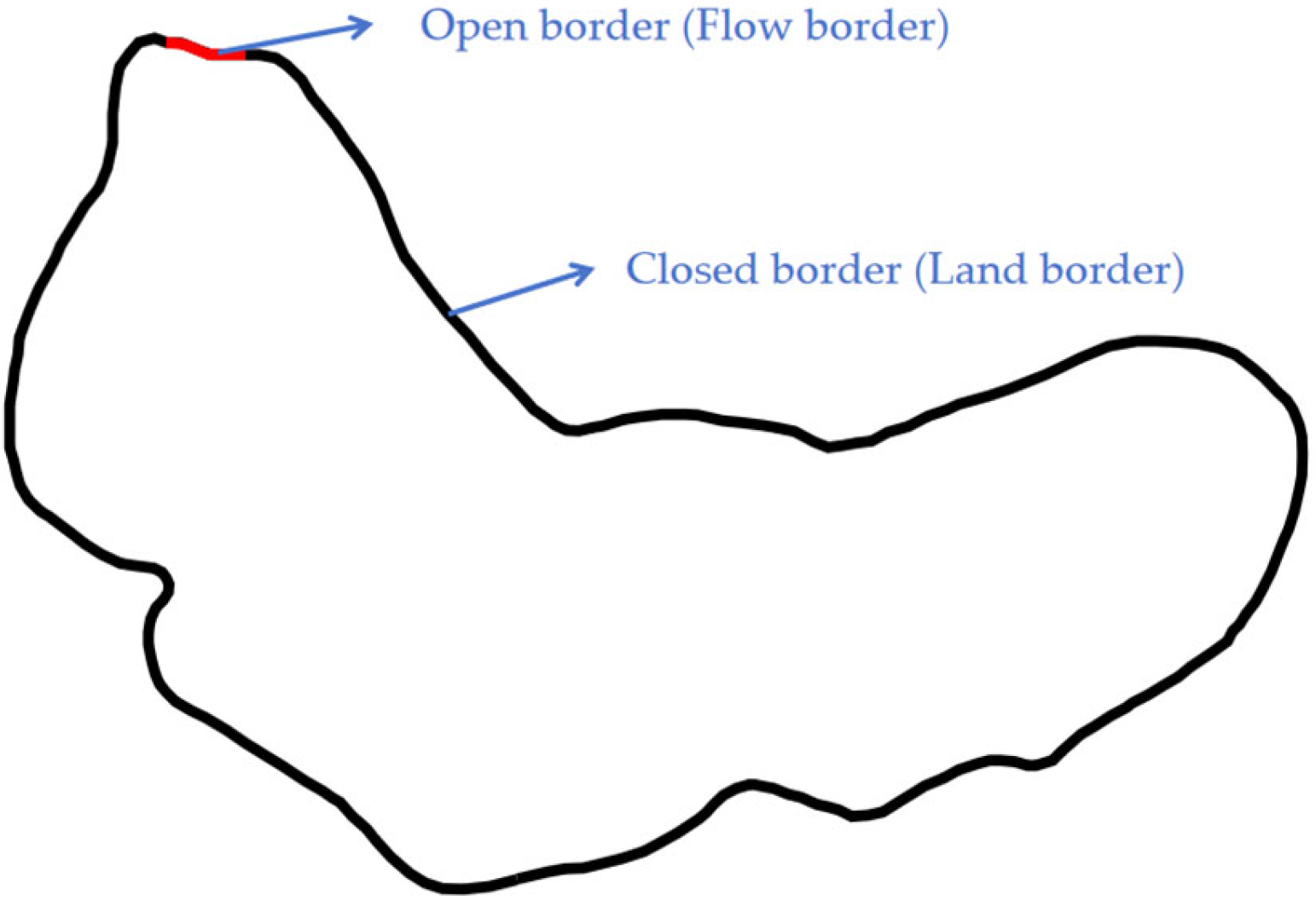
3.2.3. Boundary Condition Setting

In conjunction with the actual engineering situation of flood evolution calculations for KET Reservoir, two types of boundaries are defined for each flood evolution calculation scheme for the downstream flood protection zone, which are the flow boundary and the land boundary (zero flow velocity).

(1)

Open boundary

The locations of Breach 1 (R4 + 140), Breach 2 (R3 + 678) and Breach 3 (R3 + 256) are the inlet boundaries, i.e., the open boundaries for the model calculations.

(2)

Closed boundary

Except for the open boundary, all other locations on the periphery of the calculation area are land boundaries that will not be traversed during flood evolution. A schematic of the boundary condition setup is shown in Figure 8.

3.2.4. Selection of Model Parameters

The main parameters to be set in this model are simulation time and time step, roughness, dry and wet boundaries, wind field and eddy viscosity coefficient. Risk elements such as inundation depth and flood flow rate are extracted, and the parameters that have no obvious influence on the calculation results are assigned default values. The parameters are set as follows:

(1)

Simulation time and time step

The simulation time and time step are important parameters affecting the model calculation. To ensure the model can run accurately and stably, the simulation time and time step of the model are set to 30 s.

(2)

Roughness

Roughness is an important model parameter in MIKE 21. In this simulation, the topography, geomorphology, and vegetation conditions in the subarea were considered in combination with the field investigation and remote sensing image data, and different roughness values were assigned to different sublayers according to the Guidelines for the Preparation of Flood Risk Maps [25], Hydraulic Calculation Manual and other information as shown in

Table 3. Ground Roughness Values in the KET Flood Protection Area.

Type Name	Element	Roughness (n)	Manning Value (1/n)
Residential area	Neighbourhoods	0.060	16.67
	General housing	0.070	14.29
	Squares, open spaces	0.060	16.67
Rivers and lakes	Rivers and canals	0.023	43.48
	Gully	0.027	37.04
Land with vegetation cover	Grassland	0.030	33.33
	Woodland	0.070	14.29
Land without vegetation cover	Grassed gravel, saline areas	0.050	20.00
	Shoreline	0.035	28.57
	Gobi desert	0.040	25.00

. The cloud map of roughness values in the study area is shown in Table 3 and Figure 9.

3.2.5. Build the Model

A two-dimensional hydrodynamic model of the KET reservoir study area was established, and the parameters, initial conditions and non-constant flow boundary conditions were entered sequentially to construct a mathematical model of flood evolution. The flood evolution of Breach 1 was simulated when encountering P = 5% and P = 2% occurrence of the breach and the flood risk elements were obtained.

KET Reservoir is located in the plain area, the terrain downstream of the dam site is flat, the river channel from the downstream of the spillway gate to the desert highway section is curved and slender, the terrain on both sides of the river is relatively flat, and the river channel begins to diverge after crossing the desert highway.

When the reservoir in Breach 1 encountered P = 5% and P = 2% flood, the peak flow was 1940 m³/s and 2939 m³/s, respectively. From the inundation situation, the flood water flowed into the downstream channel. Due to the influence of topography, the river channel initially according to the influence of the terrain has a certain over-flow capacity. Most of the flood water in the river channel, thereafter, by the influence of the topography of the flood is roughly divided into the east and the west directions, with the flood water to the highway evolving. The highway blocks part of the flood water, the water level rises locally, and the flood flow rate and inundation depth in the inundation area gradually level off. The terrain of KET Reservoir Flood Protection Zone shows high north and low south, high west and low east, and the flood water evolves to the south in the form of dispersion, as shown in Figure 10 and Figure 11.

3.3. Analysis of Inundation under Different Flood Conditions

Numerical simulation of reservoir dam failure was carried out according to different flood conditions to obtain important risk element information such as inundation depth, flood flow rate, etc. Statistical analysis was carried out using ArcGIS, and the calculation results are detailed in

Table 4. Flood Risk Element Information Outcome.

Breach Location	Serial Number	Working Condition	Water Frequency	Peak Flow (m3/s)	The Moment of Peak Flow (t)	Inundation Area (km2)	Max Water Depth (m)	Max Flow Velocity (m/s)
Breach 1	1	Condition 1-1	P = 5% calibrated flood level	1940.00	3.13	141.15	4.84	11.82
	2	Condition 1-2	P = 5% crest level	5005.05	3.20	167.56	4.92	20.22
	3	Condition 2-1	P = 2% calibrated flood level	2939.00	2.48	172.75	4.88	20.10
	4	Condition 2-2	P = 2% crest level	5218.00	3.11	187.44	4.93	20.70
Breach 2	5	Condition 1-1	P = 5% calibrated flood level	1892.00	2.99	148.29	4.87	14.91
	6	Condition 1-2	P = 5% crest level	5114.73	3.14	143.9	4.81	19.87
	7	Condition 2-1	P = 2% calibrated flood level	2951.00	2.49	161.27	4.85	22.03
	8	Condition 2-2	P = 2% crest level	5110.00	3.04	219.08	4.97	21.39
Breach 3	9	Condition 1-1	P = 5% calibrated flood level	1892.00	2.99	153.58	4.87	13.70
	10	Condition 1-2	P = 5% crest level	5114.73	3.14	147.99	5.39	22.61
	11	Condition 2-1	P = 2% calibrated flood level	2951.00	2.49	166.08	4.85	17.29
	12	Condition 2-2	P = 2% crest level	5110.00	3.04	224.81	5.40	22.65

.

From the simulation results in Table 2, The analyses show that the flood water arrives extremely fast, and under the same geographical location, the higher the flood frequency, the shorter its arrival time, and accordingly, the more serious the disaster impact caused. In addition, under the same flood frequency conditions, the higher the location of the dam failure, the shorter the arrival time of the flood peak, which in turn leads to more severe flood disasters. Analysing the inundation area of the three breach sites, it can be judged that the most unfavourable breach locations are Breach 3, Breach 2 and Breach 1, with inundation areas of 224.81 km², 219.08 km² and 187.44 km² in that order; when Breach 3 encounters a flood with a probability of 2%, the maximum flood flow rate reaches 22.65 m/s, which is the most seriously affected situation at this time.

3.4. Analysis of the Reasonableness of the Results

3.4.1. Grid-Independent Analysis

The grid is the basis for establishing the model, and the triangular unstructured grid modelling is used to simulate the actual terrain data. The size of the grid is the basis and prerequisite for the reasonable prediction of the flood evolution, and by adjusting the size of the grid, the impact of the parameter on the flood inundation area downstream of the reservoir can be assessed, so as to validate the reasonableness of the parameter setting.

A set of models is constructed and three different mesh size scenarios are set up for comparison while keeping all other parameters constant. Scenario I uses an unstructured mesh of 240 m, Scenario II uses an unstructured mesh of 300 m, and Scenario III uses an unstructured mesh of 360 m. The grid size of Scheme I is reduced by 20% compared to Scheme II, and the grid size of Scheme III is increased by 20% compared to Scheme II. Through calculations and analysis, it was found that the final inundation area of the floods for Scenarios I and III were 152 km² and 155.41 km², respectively. Compared with Scenario II, the inundation area of Scenario I was reduced by 1.03%, while that of Scenario III was increased by 1.2%. The variations are within the reasonable range and no significant increase or decrease is observed, indicating that the grid size selected for the model is reasonable.

3.4.2. Roughness Sensitivity Analysis

Sensitivity analysis is used to assess the impact of uncertainty in the values of model parameters on simulation results and is also the basis for constructing a hydrodynamic model and making reasonable predictions. In this study, the key parameter of the model, roughness n, was adjusted to monitor its effect on the flood inundation area, as a way to judge the reasonableness of the parameter settings and to determine realistic hydrodynamic parameters.

In order to verify the sensitivity of the roughness value, a set of analytical models is established, and three different scenarios are set up for comparison: Scenario 2 adopts the baseline roughness value of this calculation, Scenario I has a 20% higher roughness value than Scenario II, and Scenario III has a 20% lower roughness value than Scenario II. Through the analysis and calculation, the flood inundation areas of Scenarios I and III are obtained as 151.91 km² and 154.98 km², respectively. Compared with Scenario II, the flood inundation area of Scenario I decreases by 1.1%, and the flood inundation area of Scenario III increases by 0.90%. The variations are within a reasonable range and no significant increase or decrease is observed, indicating that the values of roughness selected in the modelling process are appropriate.

3.4.3. Local Flow Field Analysis

Upon encountering a design flood that occurs once in 20 years, if a breach occurs at Breach 1, the calculated flow field distribution is found to coincide with the overall elevation distribution of the digital elevation model (DEM), the breach locations, and the topographic distribution of the river channel. The greater flow velocities observed during the flood event were primarily concentrated in the narrower sections of the river channel, as well as in the vicinity of the breach and the road, particularly in the main channel and the locations of the various breaches. The localised flow changes in these areas were significant, as shown in Figure 12.

4. Discussion

In-depth discussions on the impacts of dam failure in reservoirs have provided a solid scientific basis for dam failure risk assessment. In order to effectively reduce the probability of dam failure in reservoirs, different countries have adopted different management strategies and introduced a series of related policies according to their own geographic, climatic, economic and social conditions, and established legal norms on flood prevention and control as well as safe operation and maintenance of reservoirs. In the current flood dam failure research field, the mainstream research tools include mathematical model analysis, numerical simulation and physical model test method.

This study investigates the dam failure process of an earth and rock dam in a plain reservoir under flooding conditions. The inundation extent is analysed in detail through the combination of the DB-IWHR and MIKE 21 models. This research approach is analogous to that of Yang et al. [26], who similarly employed a two-dimensional numerical model to simulate the dam failure flood evolution in the near zone of the breach and underscored the significance of the breach development process and the dam failure flood propagation characteristics. The simulation of the dam failure process revealed a close relationship between the breach flow and the rate of water level decline, a finding that corroborates the results of Ma et al. [27]. The latter group demonstrated the relationship between the breach flow and the dam failure process through a two-dimensional flood evolution numerical model coupled with the evolution of the breach, thereby emphasising the significant influence of the breach development on the flood evolution. Furthermore, the findings of this study corroborate the research conducted by Chen et al. on the simulation of earth and rock dam failure and water flow calculation [28]. It was highlighted that the failure process of earth and rock dams typically evolves gradually, with notable variations observed across different dam types. The study further corroborates this perspective through detailed condition studies, offering novel insights into the characteristics of earth and rock dam failures in plain reservoirs.

In this study, the coupled simulation technique of the DB-IWHR model and the MIKE 21 model is applied to simulate in detail the dynamic evolution of flooding of an earth and rock dam under different breach locations and different flood level failure scenarios. Comparison with existing studies reveals the complexity and influencing factors of the dam failure process. Our findings provide an important scientific basis for future dam failure risk assessment and management and highlight the importance of considering multiple factors in dam failure modelling. In addition, in-depth sensitivity analyses of the gridding and roughness parameters were conducted in this study to deepen the understanding of the flood impact mechanisms during earth and rock dam failure. These comprehensive analyses provide a scientific basis for predicting the potential impacts of flooding on the downstream area after an earth and rock dam failure, thus providing an important reference for flood risk prediction and the formulation of emergency response plans. These results not only help to safeguard people’s lives and properties but also effectively reduce the losses caused by flood disasters.

5. Conclusions

In this paper, the numerical simulation of the dam failure of an earth and rock dam in a plain reservoir under the action of a flood is thoroughly discussed, and the DB-IWHR model is used to predict the dam failure process. The process line of the flood flow during the dam failure of the reservoir is successfully obtained, which is further combined with the MIKE 21 model to provide a detailed analysis of the flood dam failure of the reservoir and its inundation range. The main conclusions of the study are as follows:

(1)

A new coupled model for predicting the risk of dam failure is proposed, and the coupled analysis of the DB-IWHR model and MIKE 21 model can effectively simulate the dam failure flood evolution process. It can be seen from the topographic map that the study area generally shows a north-high and south-low terrain, and the simulation results also show that the river channel gradually disperses downstream in a fan shape, and the flood shows a north-to-south evolution and gradually spreads to the two sides of the river, with a high degree of suitability of the flood evolution and the terrain. The flood evolution and the terrain are high, and the simulation results are good.

(2)

The dam failure flood time flow process curve law was determined, that is, in the dam failure process, the dam failure flow will be where the flood water discharge leads to the water level decline, the decline speed is faster, the flow change is larger, and the dam failure lasts for a longer time. Under the condition of the same incoming water frequency, the higher the starting water level, the shorter the duration of the dam breaching process and the smaller the peak flow; on the contrary, under the condition that the starting water level remains unchanged, the increase of the incoming water frequency will accelerate the occurrence of the dam breaching event, and the duration of the impact of the flood water is much longer, and the peak flow is also increased accordingly.

(3)

The model adapts to the shape of the complex boundary terrain, adopts an unstructured grid to analyse and calculate the study area, and determines that the simulation area downstream of the reservoir area is 624 km², the number of grids is 537,244, and the minimum angle of the triangle grids are all greater than 30°. According to the simulation results, the model parameters are reasonably configured, and it can effectively reproduce the river terrain, which indicates that the numerical model of the study area has a high degree of simulatability, thus verifying the reasonableness of the model.

(4)

The most unfavourable locations of reservoir breaches in the event of flooding have been identified as Breach 3, Breach 2, and Breach 1. On this basis, a more efficient contingency plan will be formulated in a targeted manner to ensure that rapid response measures can be taken in the event of a dam failure. The plan will specify the flood avoidance and transfer routes and emergency measures for the affected population so as to minimise casualties and property damage and to safeguard the lives and property of the people.