Abstract
The rise in shallow groundwater levels is typically triggered by precipitation recharge, exhibiting a certain lag relative to precipitation changes. Therefore, identifying the response mechanism of shallow groundwater levels to precipitation is crucial for clarifying the interaction between precipitation and groundwater. However, the response mechanism of groundwater levels to precipitation is complex and variable, influenced by various hydrogeological and geographical conditions, and often exhibits significant nonlinear characteristics. To address this issue, this study employs methods such as continuous wavelet transform, cross wavelet transform, and wavelet coherence to analyze the response patterns of groundwater levels to precipitation at different wavelet scales in the Datong Basin from 2013 to 2022: (i) At short wavelet scales (10.33~61.96 d), the groundwater level dynamics respond almost instantaneously to extreme rainfall; (ii) At medium wavelet scales(61.96~247.83 d), the precipitation-groundwater recharge process shows characteristics of either rapid recovery or significant delay; (iii) At long wavelet scales (247.83~495.67 d), three potential groundwater processes were identified in the Datong Basin, exhibiting long-term lag responses throughout this study period, with lag times of 11.18 days, 148.75 days, and 151.49 days, respectively. Furthermore, the results indicate that the lag response time of shallow groundwater levels to precipitation is not only related to the wavelet scale but also to the identified depth conditions of different groundwater regions, groundwater extraction intensity, precipitation intensity, and aquifer lithology. This study distinguishes the temporal and spatial response mechanisms of shallow groundwater to precipitation at different wavelet scales, and this information may further aid in understanding the interaction between precipitation and groundwater levels.
1. Introduction
Groundwater has long been one of the primary water resources for various domestic, agricultural, and industrial uses, particularly in regions where surface water resources are limited [1], climate change worsens the water resource shortage issue [2,3,4], and causes unfavorable ecological effects [5,6]. Precipitation infiltration is a key pathway for local groundwater recharge, and its variability is directly related to the recharge process, making it the most critical climatic factor influencing groundwater resources [7]. Therefore, understanding the response mechanism of groundwater systems to precipitation is crucial, as it aids in the management and sustainable utilization of groundwater.
Current methods for assessing the relationship between aquifer responses and precipitation include physically based simulation models, statistical analysis, and wavelet analysis. Among these, physically based simulation models simulate the recharge and infiltration processes of groundwater systems through physical models. For example, the WetSpass model is a spatially distributed hydrological model based on physical principles. Its core concept involves estimating groundwater recharge, surface runoff, and actual evapotranspiration losses through multiple input parameters. Researchers have applied the WetSpass model to analyze the impact of changes in climate, land use, and soil parameters on 18 different natural groundwater recharge scenarios in Qatar. The results indicate that precipitation is the primary factor influencing natural groundwater recharge in arid regions [8]. Although simulation is one of the most effective tools for conducting such analyses, its implementation requires extensive data, including various hydrogeological factors such as land use, topography, and soil type, as well as climatic factors like precipitation, temperature, and evapotranspiration. However, acquiring these data on a large scale poses significant challenges [9]. Additionally, detailed analysis of the water system is required, and in the absence of sufficient data and expertise, various assumptions are often needed to simplify the physical models, making their application challenging.
Statistical methods are employed to explore the empirical relationships and temporal trends between groundwater and precipitation response processes [10]. These methods include time series analysis and linear regression, the Mann–Kendall test, autocorrelation analysis, and cross-correlation analysis. Notably, time series analysis, linear regression, and the Mann–Kendall test are commonly used to reveal trends and abrupt changes in hydrological sequences [11,12]. Some researchers have employed cross-correlation analysis to analyze the temporal relationships between dependent and independent variables by calculating cross-correlation coefficients at different time lags, thereby determining their lag periods [13]. However, the cross-correlation analysis method has the following major limitations: (1) It is only applicable to stationary and ergodic sequences; (2) It cannot reveal cross-correlation relationships within different time scale ranges [14]. However, due to the combined effects of natural and anthropogenic factors, groundwater dynamics often exhibit significant randomness and non-stationarity in time series [15].
Wavelet analysis is an effective tool for analyzing non-stationary signals across different time scales. It includes continuous wavelet analysis, cross wavelet analysis, and wavelet coherence analysis, providing joint distribution information of time series in both the time domain and frequency domain, enabling a clear description of the relationship between time and signal frequency [16,17]. Various hydrological studies have applied wavelet analysis to examine significant deviations from stationarity in hydrological processes, analyzing the persistence and periodicity of aquifers and the interactions between precipitation and groundwater levels, further extracting the lag response time between precipitation and groundwater levels [18,19,20].
In summary, wavelet analysis, as an effective tool, provides strong support for a deeper understanding of the interaction between precipitation and groundwater levels. In reality, precipitation and groundwater level time series often exhibit complex characteristics such as non-stationarity and multi-time scale variability [21], resulting in multi-scale response relationships between precipitation and groundwater levels. However, most existing studies have mostly focused on the relationship between precipitation and groundwater levels at a single wavelet scale without thoroughly exploring the response processes at different wavelet scales. Therefore, this paper aims to clarify the lag response times of groundwater levels to precipitation at different wavelet scales based on wavelet analysis and to reveal the multi-scale response relationships between precipitation and groundwater levels. Furthermore, this method is applied to analyze the long-term time series of precipitation and groundwater levels in the Datong Basin of Shanxi Province from 2013 to 2022. Using continuous wavelet transform, this research analyzes the multi-scale periodic characteristics of changes in precipitation and groundwater levels. Additionally, cross wavelet transform and wavelet coherence analysis are used to investigate the lagged response of groundwater levels to precipitation at various wavelet scales.
2. Materials
2.1. Study Area
The Datong Basin is located in northern Shanxi Province, China, spanning from 39°05′ to 40°33′ N latitude and 112°15′ to 114°17′ E longitude. It encompasses seven counties and cities, including Datong City, Datong County, Huairen County, Shanyin County, Ying County, Hunyuan County, and Shuozhou City, with a total plain area of approximately 8700 km2. The Datong Basin has a semi-arid continental climate characterized by dryness, low precipitation, frequent wind, and dust. The long-term average temperature ranges from 6.5 °C to 7.5 °C, and the long-term average annual precipitation is between 377 mm and 419.4 mm. The long-term average annual evaporation in the region is 1882.8 mm, with the evaporation in the winter and spring seasons being 9.7 to 21.4 times higher than the precipitation, making these seasons particularly dry. Spring droughts are another notable climatic feature of this area. Geomorphologically, the basin is relatively simple and can be divided into two main landform types: the piedmont alluvial inclined plain and the alluvial plain. The piedmont alluvial inclined plain is characterized by depositional landforms with relatively gentle slopes, ranging from 3° to 15°, sloping towards the plains, with elevations between 1100 m and 1200 m, and predominantly featuring gravel layers. The alluvial plain refers mainly to the central part of the basin, also a depositional type, with flat terrain and slight inclines towards major rivers, with elevations between approximately 950 m and 1100 m. The saline-alkali land is uniformly distributed across this area, and the terrain slope is less than one-thousandth both longitudinally and laterally, with sediments mainly composed of fine-grained materials [22].
To investigate the response patterns between precipitation and groundwater levels at different wavelet scales, this study collected long-term time series data of groundwater levels and precipitation from groundwater monitoring stations and meteorological stations in the Datong Basin, Shanxi Province. The observation period for this dataset spans from 2013 to 2022. The spatial distribution of groundwater monitoring stations and meteorological stations is shown in Figure 1.
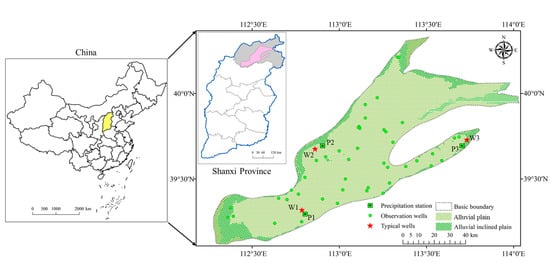
Figure 1.
Overview of this study area.
2.2. Dataset
This study collected groundwater level observation data from 50 wells in the Datong Basin for the period from 2013 to 2022, provided by the Hydrological and Water Resources Survey Station of Shanxi Province. The observation interval is 5 days, with measurements taken on the 1st, 6th, 11th, 16th, 21st, and 26th of each month over the ten years from 2013 to 2022. Daily precipitation data for 50 stations in the Datong Basin from 2013 to 2022 were obtained from the fifth-generation atmospheric reanalysis dataset (ERA5) provided by ECMWF (European Centre for Medium-Range Weather Forecasts), covering global climate data from January 1950 to the present (https://cds.climate.copernicus.eu (accessed on 13 October 2024)). To ensure that the precipitation and groundwater level data had the same frequency and time scale, the daily precipitation data were aggregated into 5-day totals for analysis. This study selected three shallow groundwater monitoring wells, W1, W2, and W3, located in the alluvial plain and the piedmont alluvial inclined plain, which are part of Datong City and Shuozhou City in terms of administrative divisions. Since the alluvial plain covers a larger area compared to the piedmont alluvial inclined plain, two typical groundwater monitoring wells, W1 and W2, were selected from the alluvial plain. Detailed information on each monitoring well is provided in Table 1.

Table 1.
Information on monitoring well locations.
3. Method
Wavelet transform is a technique used to obtain time-frequency information from time series data. In wavelet transform analysis, a small “wave” that traverses the time domain is employed to decompose the time series, capturing the time-frequency information of the series across different wavelet scales [23]. In this study, a continuous wavelet transform is employed to analyze the multi-scale periodic characteristics of precipitation and groundwater level time series. Additionally, cross wavelet transform and wavelet coherence analysis are used to interpret the lagged response relationship between the two time series across various wavelet scales. Furthermore, the Morlet wavelet is employed as the basis wavelet in this research due to its optimal balance between the time and frequency domains and its widespread recommendation for primary signal extraction tasks [24].
3.1. Continuous Wavelet Transform (CWT)
Continuous Wavelet Transform (CWT) is a signal processing technique used to analyze how the frequency characteristics of a signal change over time. Before analyzing the relationships between time series, CWT generates a power spectrum for each time series by applying wavelet functions to transform the signal from the time domain into the wavelet domain. The CWT produces a two-dimensional representation known as the wavelet time-frequency spectrum, which displays the frequency characteristics of the signal at different scales and times [25]. By analyzing the wavelet time-frequency spectrum, one can gain insights into how the frequency characteristics of the signal evolve over different time periods, thereby revealing the local features and structures of the signal. This study employs the Morlet wavelet, which provides a good balance between time and frequency localization, as the mother wavelet , which exhibits an excellent balance in time and frequency localization. By adjusting two key parameters of the Morlet wavelet, namely the Fourier factor and scale, we can flexibly adapt to the requirements of different frequency and temporal resolutions. The Fourier factor affects the frequency characteristics of the wavelet, while the scale determines the size of the wavelet. The flexible adjustment of these two parameters allows us to customize the Morlet wavelet to better fit the different frequency components of the signal. Specifically, the adjustment mechanism of the Morlet wavelet we employed can be described by the relationship between period and scale, i.e., period = fourier_factor × scale. This equation reveals the interaction between the Fourier factor and scale, enabling us to precisely control the wavelet’s period for effective analysis of the signal’s various frequency features. Therefore, in this research, we fully utilize the flexibility of the Morlet wavelet, making it a powerful tool to meet complex signal analysis needs. By calculating the Fourier transform of the Morlet wavelet, we can obtain numerical results for the Fourier factor. This process can be accomplished using mathematical software or specialized wavelet analysis tool kits. The experimental results indicate that the selected Fourier factor of the Morlet wavelet is 1.033. Hence, we derive scale = 0.9681 × period, which provides an important theoretical basis for subsequent signal analysis and offers practical reference. The Morlet wavelet function is as follows:
In the formula, represents the dimensionless frequency, and η denotes the dimensionless time, . The essence of continuous wavelet transform (CWT) is the convolution of the time series with the Morlet wavelet. For a given mother wavelet and a time series , the wavelet transform is expressed as follows:
In the formula, represents the uniform time step, and denotes the wavelet scale. The wavelet transform involves translating the wavelet function along the localized time t and adjusting the wavelet scale to compute the wavelet coefficients , which describe the contribution of scale at different time positions to the time series . In this study, we apply wavelet transform to the time series of precipitation and groundwater levels to explore their dynamic changes across different time scales. In practical applications of continuous wavelet transform (CWT), the Discrete Fourier Transform (DFT) is commonly used for convolution computations. However, a limitation of Fourier transform is its assumption of periodic data, which introduces localized wavelet power spectrum estimation errors at the start and end of the time series, known as edge effects. To mitigate edge effects, two main approaches are employed. One approach is to extend the signal to include additional data beyond the region of interest, which does not affect the analysis of the region of interest. Another method is to zero-pad the signal before performing the wavelet transform, extending the total length to the next power of two, and then removing the zero-padding afterward. This approach reduces edge effects, but it is important to note that zero-padding introduces discontinuities that can amplify the signal amplitude near the edges and introduce more zero-value data at larger scales, further diminishing the signal amplitude. The region affected by zero-padding is known as the Cone of Influence (COI), where the wavelet power decreases to of its maximum value at the edges. Consequently, areas below the COI are more susceptible to edge effects, while regions beyond the COI are considered negligible [26,27].
3.2. Cross Wavelet Transform (XWT)
To understand how changes in precipitation affect groundwater level variations, we employed bivariate wavelet analysis to examine the relationship between the precipitation time series and the groundwater level time series in the time-frequency domain. This analysis also aims to explore how the phase angle represents the causal and physical mechanisms between the time series. In bivariate wavelet analysis, the Cross Wavelet Transform (XWT) has been developed to identify the cross wavelet spectrum between two time series. This method, which builds upon the continuous wavelet transform, effectively examines the multi-scale relationships between the two series in the time-frequency domain. For the two time series and , which represent precipitation and groundwater levels, respectively, the form of XWT is defined as:
In the formula, represents the wavelet transform of the precipitation time series at scale s, represents the wavelet transform of the groundwater level time series at scale , and denotes the complex conjugate of the wavelet transform of the groundwater level time series . The c ross-wavelet spectrum can be expressed as:
The cross wavelet power represents the cross wavelet power spectrum, and the phase angle indicates the lag between the precipitation and groundwater level time series at time on the wavelet scale . The time lag between precipitation and groundwater level at a specific wavelet scale can be calculated as , where is the period corresponding to the specific wavelet scale. The theoretical probability distribution of the cross wavelet power relative to the background power spectra of the two-time series can be expressed as:
Here, represents the confidence level associated with the probability of the probability distribution function, which is defined as the square root of the product of two distributions. and denote the Fourier spectra of the time series and at scale , respectively, and and are the variances of the respective time series.
3.3. Wavelet Coherence Analysis (WTC)
Research has shown that Cross Wavelet Transform (XWT) may yield misleadingly significant results, particularly when one of the time series has a pronounced peak in its spectrum, even if there is no true correlation between the two-time series. This occurs because the XWT does not account for the normalization of wavelet power during its computation [28]. To address this issue, a normalized measure known as Wavelet Coherence (WTC) has been proposed to assess the relationship between the precipitation time series and groundwater level time series . Similar to the definition of a correlation coefficient, wavelet coherence is used to quantify the correlation between a pair of time series as a function of frequency, with values ranging from 0 to 1. An ideal wavelet coherence can be defined as:
To estimate wavelet coherence, it is necessary to apply some smoothing to the estimates of the single wavelet spectra and the cross wavelet spectrum in advance. This can be expressed as:
In this context, represents the smoothing operator, which is defined as , where denotes smoothing along the wavelet scale axis and denotes smoothing in the time domain. The wavelet coherence ranges between 0 and 1, indicating no relationship and a linear relationship between the precipitation time series and the groundwater level time series at scale , respectively.
In addition, a conceptual framework of this research procedure was presented in Figure 2 to illustrate the analytical design of this study.

Figure 2.
Flowchart of this research process.
4. Results
4.1. Temporal Variation Characteristics of Precipitation and Groundwater Levels
Based on the analysis of precipitation data, as shown in Figure 3, the annual precipitation recorded at the three meteorological stations indicates that the average annual precipitation for P1, P2, and P3 is 441.74 mm, 537.29 mm, and 606.45 mm, respectively. The ratios of the maximum to minimum annual precipitation for P1, P2, and P3 are 1.31, 1.46, and 1.52, respectively. Additionally, intense precipitation events at P1, P2, and P3 mainly occur in the summer and autumn, while winter and spring experience fewer precipitation events. As illustrated in Figure 4, the intra-annual variation shows that precipitation is highest from June to September, accounting for 70% to 80% of the total annual precipitation. The remaining months contribute only 20% to 30% of the annual precipitation. This indicates that there are certain differences in the distribution of precipitation both within the year and between years in the Datong Basin.
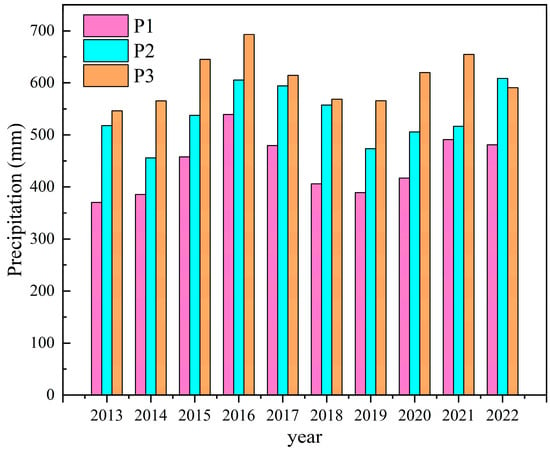
Figure 3.
Annual precipitation statistics for meteorological stations.
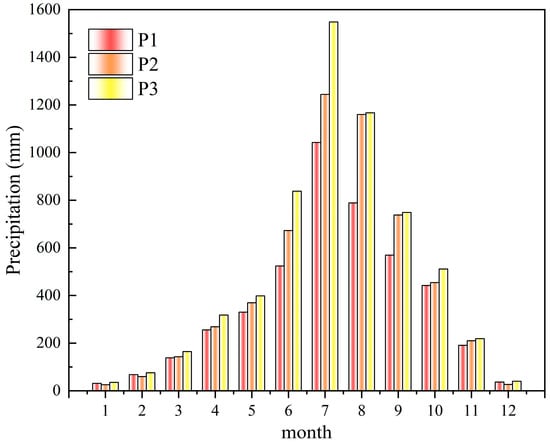
Figure 4.
Monthly precipitation statistics for meteorological stations.
Using the observed precipitation data from three meteorological stations (P1, P2, P3) to evaluate the relationship with groundwater level data from three monitoring stations (W1, W2, W3). As shown in Figure 5b,c, the overall fluctuation trends of groundwater levels in wells W2 and W3 are similar. When precipitation occurs, there is a delayed response in the rise of groundwater levels, which appears some time after the rainfall event. The timing of the highest and lowest groundwater levels does not coincide with the timing of maximum and minimum precipitation. Instead, the groundwater level increases with the rise in maximum precipitation during the rainy season until it reaches a peak. It is noteworthy that the groundwater levels in wells W2 and W3 reach their lowest points during the high-water periods each year and their highest points during the low-water periods, indicating a significant lagged response to precipitation. In contrast, Figure 5a shows that the groundwater level in well W1 closely follows the fluctuation trend of precipitation at P1. The groundwater level in W1 rises quickly with increased precipitation and decreases as precipitation declines, demonstrating that W1 is highly sensitive to changes in precipitation. Compared to W2 and W3, the groundwater level in W1 exhibits a more rapid dynamic response to precipitation.
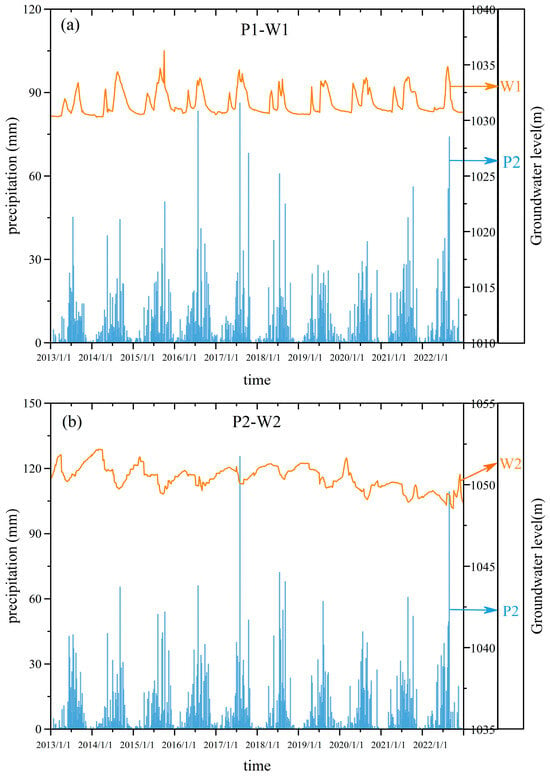
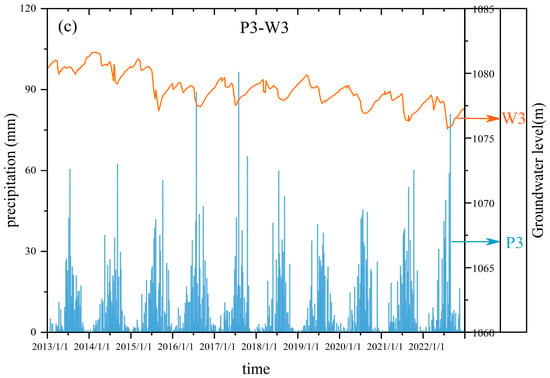
Figure 5.
Precipitation and groundwater level time series: (a) P1-W1; (b) P2-W2; (c) P3-W3.
4.2. Multi-Scale Periodic Characteristics of Precipitation and Groundwater Levels
The continuous wavelet transform (CWT) was used to extract the periodic scale characteristics of groundwater levels and precipitation in this study area, revealing the main time-frequency patterns of groundwater and precipitation processes. Before performing the CWT, this study data were standardized to ensure comparability of time-frequency features between different time series in the wavelet analysis and to minimize the impact of amplitude on the results. Since the precipitation and groundwater level data are finite time series, “boundary effects” may occur at the ends of the time series. To eliminate or reduce these boundary effects near the endpoints of the series, symmetric extension of the data at both ends was conducted. After the wavelet transform was performed, the wavelet transform coefficients corresponding to the extended data at both ends were removed, retaining only the wavelet coefficients within the original data series. After standardization and symmetric extension, the precipitation and groundwater level monitoring data were subjected to continuous wavelet transform to identify their periodic characteristics and significant time intervals. The continuous wavelet power spectrum and wavelet variance plots for precipitation and groundwater levels are shown in Figure 6. Yellow and blue represent the peak and trough values of energy density, respectively, reflecting the locality and dynamic characteristics of the main oscillation components in time-frequency variations. The color intensity indicates the relative changes in energy density. The black thick solid contour encloses values that have passed the 95% confidence level of the red noise test, while the region beneath the black thin solid line is the cone of influence (COI), indicating areas where the edge effects of the continuous wavelet transform data are more significant.
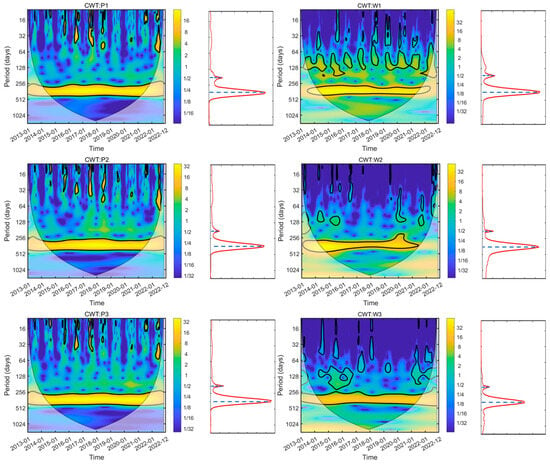
Figure 6.
Continuous wavelet transform spectra of precipitation and groundwater levels, with the wavelet variance plot right side of each subplot.
From the continuous wavelet power spectrum, it can be observed that significant oscillatory periods in the precipitation data from all meteorological stations and the groundwater level data from monitoring wells are present in the range of 256–512 days. This period has passed the 95% red noise test from June 2015 to December 2020, indicating high temporal power density as confirmed by the red noise test. The wavelet variance plot further shows that, during this study period, both precipitation and groundwater levels exhibit peak values within the wavelet scales of 61.96 to 247.83 d (64 × 0.9681~256 × 0.9681) and 247.83 to 495.67 d (256 × 0.9681~512 × 0.9681). This suggests that both the precipitation and groundwater level data in this study area exhibit similar significant multiscale periodic characteristics.
From the continuous wavelet power spectrum of precipitation, it is evident that the energy spectrum for precipitation data at meteorological stations P1, P2, and P3 shows discontinuous variation within the wavelet scale range of 7.74 to 61.96 d (8 × 0.9681~64 × 0.9681), with a relatively short duration. In contrast, within the wavelet scale range of 247.83 to 495.67 d (256 × 0.9681~512 × 0.9681), the variation is continuous and exhibits higher energy density. For the continuous wavelet power spectrum of groundwater levels, significant periodicities at the 95% confidence level through red noise testing are not consistent across the monitoring wells. Wells W1, W2, and W3 all show oscillations in groundwater levels within the wavelet scale ranges of 7.74 to 61.96 d (8 × 0.9681~64 × 0.9681), 61.96 to 247.83 d (64 × 0.9681~256 × 0.9681), and 247.83 to 495.67 d (256 × 0.9681~512 × 0.9681). However, compared to W2 and W3, Well W1 exhibits a significant seasonal periodicity within the wavelet scale range of 61.96 to 247.83 d (64 × 0.9681~256 × 0.9681), with higher wavelet energy density, indicating that groundwater fluctuations in W1 are more pronounced within this periodic range. Additionally, Well W3 demonstrates the longest duration within the wavelet scale range of 247.83 to 495.67 d (256 × 0.9681~512 × 0.9681) compared to W1 and W2, showing more pronounced long-period characteristics.
In summary, during this study period, both precipitation and groundwater levels exhibit two main oscillatory periodic time scales: 61.96 to 247.83 d (64 × 0.9681~256 × 0.9681) and 247.83 to 495.67 d (256 × 0.9681~512 × 0.9681). This indicates that within the same time domain, precipitation and groundwater levels show significant responsive variations. At smaller time scales, the temporal response of both precipitation and groundwater levels is discontinuous and exhibits larger variations. In contrast, at larger time scales, the temporal response of precipitation and groundwater levels is relatively continuous and exhibits smaller variations. Therefore, precipitation is the primary driver of groundwater level changes, with its impact being more pronounced at larger time scales.
4.3. Analysis of Groundwater Level Response to Precipitation
To analyze the phase relationship and time-lag response characteristics between precipitation and groundwater levels in the time-frequency domain, cross wavelet transforms were performed for three representative wells (W1, W2, W3) and their corresponding meteorological stations (P1, P2, P3). The phase angles were used to interpret the time intervals between fluctuations in the two series. In Figure 7, the color scale bar on the right indicates the cross wavelet power spectral density. Blue and yellow represent the troughs and peaks of energy density, respectively. The direction of the arrows shows the phase relationship between the two series: arrows pointing to the right signify that the two series are in phase, while arrows pointing to the left indicate an out-of-phase relationship.
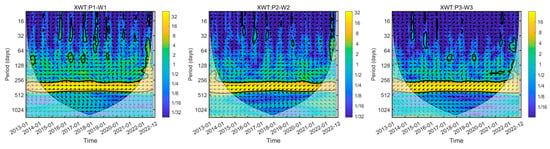
Figure 7.
Cross wavelet transform spectra of precipitation and groundwater levels.
Based on the Cross Wavelet Transform (XWT) results for P1-W1, P2-W2, and P3-W3, it was identified that precipitation and groundwater levels exhibit a common periodicity of 256 to 512 days. The dynamic relationship between groundwater levels and precipitation within this period passed the 95% red noise test throughout this study period from January 2013 to December 2022, with these regions enclosed by black thick solid lines, indicating that the groundwater response to precipitation occurs over a period of 256 to 512 days. Additionally, locally significant intervals of resonance were identified; for instance, P1-W1, P2-W2, and P3-W3 exhibited resonance periods in shorter cycles (0~64 days, 64~128 days) during periods such as April 2016 to June 2016, June 2022 to July 2022, May 2014 to June 2016, and March 2017 to June 2017. However, the power density during these periods was relatively low. These features indicate that precipitation has a significant impact on groundwater level changes across different time scales. At longer periods (256~512 days), the response of groundwater levels to precipitation is more pronounced and consistent. In contrast, at shorter periods (0~64 days, 64~128 days), although resonance occurs, its impact is relatively weaker. This suggests that groundwater level responses to precipitation can exhibit multi-scale characteristics within the same study period.
To further analyze the response characteristics between precipitation and groundwater levels, Wavelet Coherence (WTC) is introduced. While the Cross Wavelet Transform (XWT) is limited to detecting regions of high resonance energy between two time series, significant correlations might still exist even in regions of low resonance energy. The wavelet coherence spectrum not only measures the significant correlation in low-power regions of the cross wavelet transform but also maintains a similar phase relationship to that of the significant time-frequency domain in the XWT. This addresses some of the limitations of the cross wavelet transform. In Figure 8, the color scale bar on the right side represents the coherence between the two time series (ranging from 0 to 1). Higher WTC values indicate a stronger correlation between the power spectra of the two variables at the corresponding time and frequency, while lower values indicate a weaker correlation.
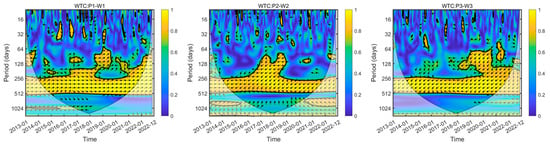
Figure 8.
Wavelet coherence spectrum of precipitation and groundwater levels.
Based on the Wavelet Coherence (WTC) analysis of groundwater levels and precipitation over this study period, a high-coherence spectral band was observed in the 256 to 512-day range, consistent with the results from the Cross-Wavelet Transform (XWT). Specifically, in addition to the significant oscillatory period of 256 to 512 days revealed by both XWT and WTC, various local correlations were also identified. For instance, the P1-W1 pair exhibited periodic resonance in the 20 to 50 days and 64 to 256 days ranges, particularly during the periods of 2015–2016 and 2016–2018. However, the phase angles of these local resonance phenomena differed from those in the significant periodic regions (256~512 days) throughout this study period, indicating that precipitation is not the primary driver of this periodic response. Similarly, P2-W2 and P3-W3 showed 64 to 256-day cycles during the periods of 2016–2019 and 2018–2021, respectively. Additionally, significant wavelet coherence in the short periods for P1-W1, P2-W2, and P3-W3 displayed discontinuous patches with varying phase behaviors. This suggests that local factors such as circulation patterns and soil moisture might influence short-period seasonal variations.
In summary, the response characteristics of groundwater levels to precipitation in the Datong Basin are evident not only at the annual wavelet scale throughout this study period but also at various local wavelet scales. Therefore, this study averaged the wavelet coherence values over the entire time domain for each wavelet scale to obtain the variation of the average wavelet coherence value with wavelet scale. Figure 9 illustrates the relationship between the average wavelet coherence values (R2) for groundwater levels and precipitation at the meteorological stations P1-W1, P2-W2, and P3-W3 as a function of time scale. Overall, at wavelet scales of 10 to 61.96 d (10.33 × 0.9681~64 × 0.9681), the R2 values are relatively low, fluctuating within the range of 0.2 to 0.4. This indicates that short-term precipitation fluctuations do not significantly affect groundwater levels at these scales. However, at wavelet scales of 61.96 to 123.92 d (64 × 0.9681~128 × 0.9681) and 247.83 to 348.52 d (256 × 0.9681~360 × 0.9681), the correlation values R2 show an increasing trend. The average wavelet coherence reaches its maximum at wavelet scales of 123.92 to 247.83 d (128 × 0.9681~256 × 0.9681) and 247.83 to 495.67 d (256 × 0.9681~512 × 0.9681). This indicates that the cumulative effect of precipitation significantly impacts groundwater levels at these scales, with the peak wavelet coherence value nearing 1 in the 247.83 to 495.67 d (256 × 0.9681~512 × 0.9681) range. This highlights a pronounced annual periodic response characteristic between precipitation and groundwater levels.
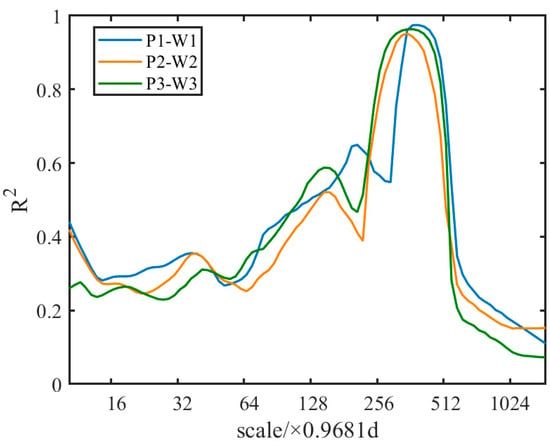
Figure 9.
Variation of average wavelet coherence values between precipitation and groundwater levels with wavelet scale.
4.4. Multi-Scale Response Patterns between Precipitation and Groundwater Levels
To gain a deeper understanding of the multi-scale response patterns between precipitation and groundwater levels, we analyzed the variation of average wavelet coherence values (R2) with time scale, as shown in Figure 8. Based on this, we categorized the wavelet scales into short-term scales 10~61.96 d (10.33 × 0.9681~64 × 0.9681), mid-term scales 61.96~247.83 d (64 × 0.9681~256 × 0.9681), and long-term scales 247.83~495.67 d (256 × 0.9681~512 × 0.9681). Among these three types of wavelet scales, we selected three representative scales for detailed analysis: 11.89 d (12.29 × 0.9681) for the short-term scale, 134.56 d (138.99 × 0.9681) for the mid-term scale, and 359.22 d (371.06 × 0.9681) for the long-term scale. While the primary focus of this study is on these three representative scales, similar trends were observed across other wavelet scales, which further supports the robustness of our findings.
Figure 10 illustrates the original signals of groundwater levels and precipitation at various wavelet scales, as well as the time-varying signals of groundwater levels and precipitation reconstructed through the Inverse Continuous Wavelet Transform (Inverse CWT). Additionally, based on the results of Cross Wavelet Transform (XWT), the phase angle variations between the two signals during this study period were analyzed. In wavelet analysis, shorter wavelet scales correspond to higher signal frequencies. Thus, in the Datong Basin shown in Figure 10a, a short wavelet scale of 11.89 d represents high-frequency signals, which are typically associated with intense precipitation events. It can be observed from the figure that the phase angle ranges of P1-W1, P2-W2, and P3-W3 vary from −180° to 180° (with groundwater lagging behind precipitation by −6.15 to 6.15 days), showing significant variability in phase angles, especially during intense rainfall events. These intense events may trigger higher infiltration trends, which decrease as soil moisture increases and approaches saturation. For instance, the phase angle of P1-W1 changed from −150° to 150° in 2017. This indicates that higher-frequency signals may exhibit greater phase angle variability, usually related to extreme precipitation. From Figure 10b, it is evident that when the wavelet scale is 134.56 d, the reconstructed signals of precipitation and groundwater levels, along with their phase angle changes, show substantial fluctuations at W1-P1, W2-P2, and W3-P3 monitoring points in different years, reflecting instability in groundwater system responses. Overall, the range of these phase angles is from −180° to 180° (lag of −67.28 to 67.28 days). Specifically, during 2013 to 2014, the phase angles were generally smaller, indicating a rapid response of groundwater levels to precipitation. However, from 2015 to 2017, the phase angles increased significantly, reflecting an enhanced delay in the response. Since 2018, the phase angles at each monitoring point have shown significant fluctuations, sometimes recovering rapidly and other times experiencing considerable delays. This phenomenon may be closely related to changes in soil moisture and human activities, which can significantly affect groundwater recharge processes and infiltration rates [29], leading to phase angle variability. Furthermore, the appearance of negative phase angles in Figure 10a,b may be due to changes in groundwater occurring prior to precipitation infiltration reaching groundwater levels. Compared to the phase angle variation patterns between short wavelet scales of 11.89 d and intermediate wavelet scales of 134.56 d, the long wavelet scale of 359.22 d shows stable phase angles between precipitation and groundwater levels, as depicted in Figure 10c. The average phase angles between W1-P1, W2-P2, and W3-P3 are 10.85°, 144.32°, and 146.97°, respectively. Based on the average phase angles, the time lags of groundwater levels relative to precipitation changes were calculated and detailed in Table 2. The time lag responses from precipitation to groundwater levels for W1-P1, W2-P2, and W3-P3 are 11.18 days, 148.75 days, and 151.49 days, respectively.
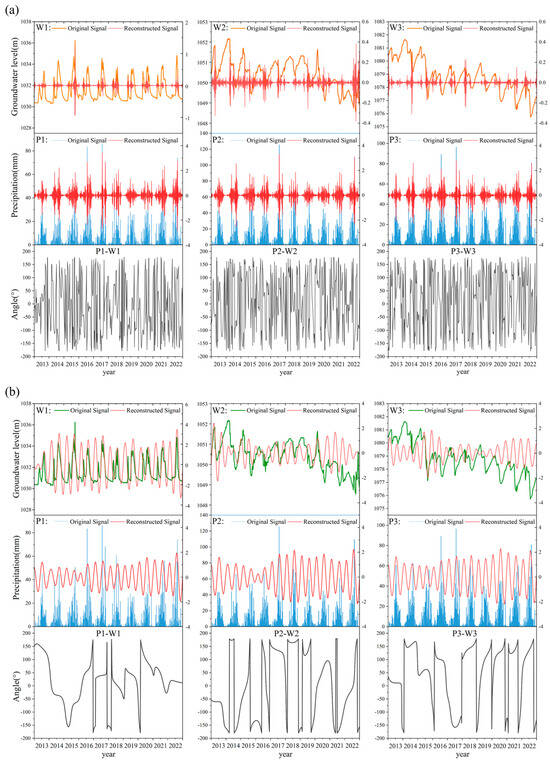
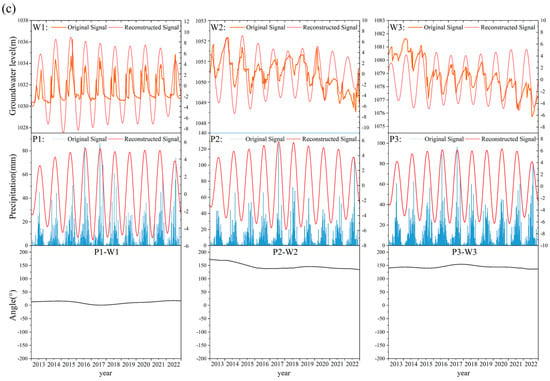
Figure 10.
Original signals of groundwater levels and precipitation, their respective reconstructed signals, and the phase angles between them: (a) Wavelet scale of 11.89 d (period of 12.29 days); (b) Wavelet scale of 134.56 d (period of 138.99 days); (c) Wavelet scale of 359.22 d (period of 371.06 days).

Table 2.
Phase angles and time lags between precipitation and groundwater levels at a wavelet scale of 359.22 d (period of 371.06 days).
This study results indicate that groundwater levels exhibit different spatiotemporal response patterns to precipitation across various wavelet scales. The amplitude information of groundwater level and precipitation, as well as the phase angles, is detailed in Table 3. Specifically, when the wavelet scale is small, corresponding to periods of intense rainfall, the amplitude of groundwater signals is relatively smaller compared to the high-amplitude signals observed during rainfall events. Additionally, the phase relationship between precipitation and groundwater changes is non-stationary, with groundwater levels responding more rapidly to precipitation. However, as the wavelet scale increases, the amplitude of groundwater signals becomes larger, while the amplitude during rainfall remains relatively smaller. Consequently, the phase angle between precipitation and groundwater changes tends to stabilize, reflecting a long-term lag between precipitation and groundwater levels. This suggests that the contribution of extreme events to groundwater recharge is limited, while sustained rainfall plays a more significant role in the recharge process.

Table 3.
The amplitude information and the phase angles of groundwater level and precipitation.
5. Discussion
Based on the cross wavelet transform and wavelet coherence analysis, different spatiotemporal response patterns between groundwater levels and precipitation in the Datong Basin at various wavelet scales have been identified. The results indicate that the lag relationship between precipitation and groundwater levels exhibits significant variations across different spatiotemporal scales. In fact, the lag time between groundwater levels and precipitation is influenced not only by complex natural factors but also by human activities.
5.1. Groundwater Level Depth
The cross wavelet transform reveals the long-term lag relationship between groundwater levels and precipitation at different monitoring sites in the Datong Basin over the entire study period, as shown in Figure 7 and Figure 11. The depth of the groundwater table is a significant factor affecting the lag time between precipitation and groundwater recharge. As shown in Table 4, there is a positive correlation between lag time and groundwater depth. Specifically, as the groundwater depth increases, the lag time also increases. For example, among the monitoring wells located in the alluvial plain area, well W1 has the smallest groundwater depth and the shortest lag time of approximately 11 days. Conversely, in monitoring wells situated in the alluvial inclined plain, well experience significant effects from precipitation with the shortest lag time of 41.53 days. This phenomenon indicates that in areas with deeper groundwater tables, the impact of rainfall on groundwater levels takes a longer time to manifest. This could be attributed to the fact that deeper groundwater implies longer flow paths and higher resistance from soil and rock layers, resulting in a slower response to groundwater level changes. Conversely, in regions with shallower groundwater tables, changes in groundwater levels in response to rainfall are observed more quickly due to shorter flow paths and higher soil permeability.
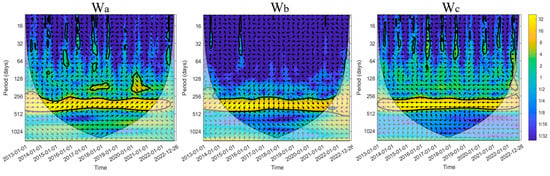
Figure 11.
Cross wavelet transform spectra of precipitation and groundwater levels at different spatial locations.

Table 4.
Lag response time of groundwater levels to precipitation at different spatial locations.
5.2. Precipitation Intensity
Precipitation is one of the most important sources of groundwater. Even minor variations in precipitation intensity can lead to significant changes in groundwater dynamics [30,31]. For monitoring wells, under the same extraction conditions, a smaller amount of precipitation recharge results in a slower rate of groundwater level rise. Additionally, the response time of groundwater levels to precipitation can be significantly prolonged [32]. Figure 10a shows the original signals of groundwater levels and precipitation during heavy rainfall events for monitoring wells W1, W2, and W3, as well as the time-varying signals of groundwater levels and precipitation reconstructed through the Inverse Continuous Wavelet Transform (Inverse CWT). Taking the wet period from July to September 2016 as an example, the lag time between groundwater levels and precipitation for wells W1, W2, and W3 was approximately 7 days, indicating that groundwater levels responded relatively quickly to precipitation during the wet period, with a shorter lag time. Therefore, during periods of high precipitation intensity, groundwater levels are more responsive to precipitation, further highlighting that high-intensity precipitation is a major driving factor for groundwater recharge [33].
5.3. Groundwater Exploitation Intensity
The Datong Basin is a crucial part of China’s Yan-Tong small economic zone, which is also a key area for grain production in the region. However, agricultural production conditions in the Datong Basin are poor, with low agricultural productivity. The main reasons for this are water scarcity, with an average annual precipitation of only about 400 mm, leading to the region’s reputation for frequent droughts. Additionally, less than 20% of the arable land is irrigated, with over 80% being dry land. Currently, the primary method for meeting agricultural irrigation needs is groundwater extraction [34]. As shown in Figure 12, the total groundwater extraction in the Datong Basin increased from 3.6 × m3 in 2001 to 4.9 × m3 in 2019. In fact, this large-scale groundwater exploitation has become one of the main methods of groundwater discharge [35]. However, excessive exploitation has severely disrupted the natural balance of groundwater, leading to significant changes in groundwater dynamics. If the amount of groundwater exploitation equals the recharge amount, although the groundwater level will be below the original average level, the fluctuations in groundwater level will not continue to decline. However, when exploitation exceeds the recharge capacity, the groundwater level will continue to decline, leading to an increase in the thickness of the unsaturated zone and thereby delaying the response time of groundwater levels to precipitation. As illustrated in Figure 13, there is no common period between the groundwater level changes in monitoring well W and precipitation P. This is because the monitoring well is located in an over-extraction area, where the pumping rate exceeds the natural recharge rate of the groundwater.
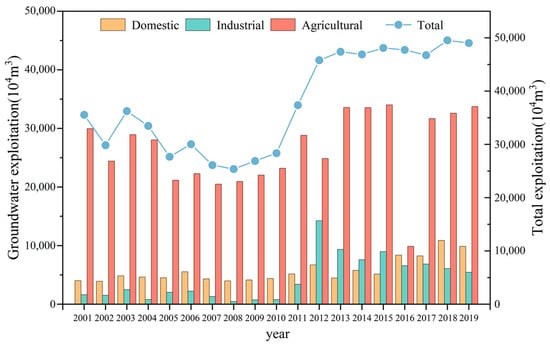
Figure 12.
Total groundwater extraction in the Datong Basin from 2001 to 2019.
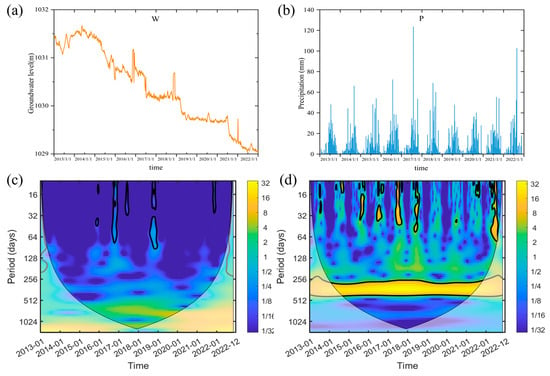
Figure 13.
(a) Characteristics of the groundwater level time series at monitoring well locations; (b) Characteristics of the precipitation time series; (c) Continuous wavelet transform spectrum of the groundwater level time series; (d) Continuous wavelet transform spectrum of the precipitation time series.
5.4. Lithology of Aquifers
The lithology of aquifers is another important factor influencing the response of groundwater levels to precipitation [36,37]. Different aquifer lithologies typically exhibit distinct hydrogeological parameters, such as hydraulic conductivity [38], specific yield [39], and precipitation infiltration coefficients [40]. As a result, the temporal lag of groundwater level dynamics in response to precipitation demonstrates varying patterns spatially. In the Datong Basin, the genesis of loose layers varies, and the distribution and burial conditions differ accordingly. The shallow aquifer lithology in the Datong Basin is primarily composed of fine to medium sand, while the alluvial inclined plain surrounding the basin features gravel layers, with hydraulic conductivities generally ranging from 100 to 300 m3/d and specific yields between 300 and 1000 m3/d. In contrast, the sediment in the central alluvial plain area of the basin consists mostly of fine-grained materials. Due to the low topography and phreatic lag, the hydraulic conductivity here is only 10 to 100 m3/d, with specific yields less than 300 m3/d. The cross wavelet transform reveals the long-term lag relationship between groundwater levels and precipitation at the and monitoring sites in the Datong Basin throughout the entire study period, as shown in Figure 14. A comparison of monitoring wells and further indicates that, despite their proximity, the lag time between precipitation and groundwater levels at in the alluvial inclined plain is approximately 12 days, whereas it extends to 38 days at in the alluvial plain area. Detailed information is presented in Table 5. This phenomenon clearly illustrates that under similar conditions, the better the lithology of the aquifer, the higher its hydrological response sensitivity, and consequently, the shorter the lag time.
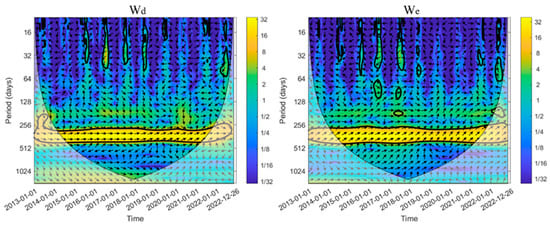
Figure 14.
Cross wavelet transform spectra of precipitation and groundwater levels at well locations Wd and We.

Table 5.
Lag response time of groundwater levels to precipitation at well locations Wd and We.
5.5. Limitations
Numerous and complex factors influence the response time of groundwater to precipitation. Previous studies have shown that the characteristics of aquifer media between wells, the connectivity of the groundwater system [41], and preferential flow pathways [42] can significantly influence the lag time in groundwater response to precipitation. In this study, we focused on analyzing the effects of rainfall intensity, groundwater depth, and groundwater exploitation intensity, while not considering other critical factors such as geological conditions and aquifer boundaries. In reality, these factors do not exist in isolation; rather, they interact and influence each other within diverse geological and geographical contexts. Given the lack of detailed hydrological data in the Datong Basin, our research aims to reveal the multi-scale response patterns of groundwater levels to rainfall through the comprehensive application of wavelet methods. Future research efforts must delve deeper into the hydrological and geological conditions of the region to gain a more comprehensive understanding of the complexity of groundwater systems. Specifically, there is a need to enhance the investigation of potential influencing factors, including geological structures, soil types, and land cover, which will contribute to uncovering more information regarding the intricate interactions between groundwater and precipitation.
6. Conclusions
This study combines continuous wavelet analysis, cross wavelet transform, and wavelet coherence analysis to explore the complex relationship between shallow groundwater levels and their response patterns to precipitation. Continuous wavelet analysis identifies the main periodic characteristics of groundwater levels and precipitation, while cross wavelet transform and wavelet coherence analysis reveal their nonlinear response patterns. We performed continuous wavelet transform, cross wavelet transform, and wavelet coherence analysis on the five-day groundwater levels and precipitation data from three representative monitoring wells in the Datong Basin for the period 2013–2022, clarifying the response mechanisms of groundwater levels to precipitation across different temporal and spatial scales. The main conclusions of this study are as follows:
- (1)
- We analyzed the continuous wavelet inverse transforms of groundwater level and precipitation signals at short, medium, and long wavelet scales (11.89 d, 134.56 d, and 359.22 d, respectively) and investigated the temporal phase angle changes between precipitation and groundwater levels during this study period. By analyzing the response relationships between rainfall and groundwater signals at different wavelet scales, we identified response patterns under varying precipitation conditions. Notably, groundwater level changes at the short wavelet scale are highly correlated with intense rainfall events, and the phase angle exhibits significant temporal variations. During each intense rainfall event, the phase angle increases over time, indicating that rainfall recharge is significantly dependent on prior conditions, and the groundwater level response to intense rainfall is almost instantaneous. At the medium wavelet scale, the phase angle differences between precipitation and groundwater levels in the Datong Basin are relatively small. The response patterns at monitoring wells W1-P1, W2-P2, and W3-P3 show characteristics of both rapid recovery and significant delays. At the long wavelet scale, the phase angles between precipitation and groundwater levels tend to be consistent. Throughout this study period, the phase angles of precipitation-groundwater level signals at wells W1-P1, W2-P2, and W3-P3 were approximately 10.85°, 144.32°, and 146.97°, respectively, with precipitation-groundwater level time lags of 11.18 days, 148.75 days, and 151.49 days. This indicates that the lag time of groundwater response to precipitation can vary across different spatiotemporal scales.
- (2)
- Key factors influencing the lag time between precipitation and groundwater recharge include groundwater depth, precipitation intensity, groundwater extraction intensity, as well as the spatial distribution and monitoring frequency of the wells.
- (3)
- Although these factors may introduce some uncertainty in assessing groundwater level responses, the combined use of continuous wavelet transform, cross wavelet transform, and wavelet coherence analysis remains highly effective. Particularly in regions with limited hydrological and geological data, these methods provide a multi-scale view of the response patterns of groundwater levels to precipitation in the Datong Basin.
It is important to note that in studying the response mechanisms of shallow groundwater levels to precipitation, the sensitivity of research parameters and system uncertainty are critical aspects that cannot be overlooked. First, the selection of wavelet scales plays a crucial role in the analysis. Different wavelet scales can capture variations at different frequencies, thereby revealing the complex dynamic relationship between groundwater levels and precipitation. By appropriately selecting wavelet scales, researchers can more effectively analyze time series data, identify potential periodicities and trends, and gain deeper insights into hydrological processes. Secondly, data quality is equally important in this research process. Accurate groundwater level and precipitation data form the foundation of any quantitative analysis, and the reliability of the data directly impacts the credibility of these research findings. Therefore, ensuring high-quality data collection, processing, and storage is a prerequisite for conducting relevant studies. Additionally, the selection of model parameters is a core factor contributing to uncertainty. The application of different wavelet functions may lead to significant discrepancies in results, resulting in inconsistent research conclusions. Consequently, future studies should emphasize these factors to enhance the accuracy and reliability of analyses.
Author Contributions
H.Z. and Y.Z. conceived these research methods and wrote the manuscript; W.S. and Y.R. conducted data collection; X.R. supervised this research project; W.X. and C.G. reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under contract No. 42376180 and the Shanxi Province Water Conservancy Science and Technology Research and Promotion Project under contract No. 2023ZF17.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors are deeply grateful to the editors and reviews for their contributions to improve the original version of this manuscript.
Conflicts of Interest
Author Y.Z. was employed by the company North Information Control Research Academy Group Co., LTD. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zektser, I.S.; Everett, L.G. Groundwater and the Environment: Applications for the Global Community; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Xu, F.; Qu, Y.; Bento, V.A.; Song, H.; Qiu, J.; Qi, J.; Wan, L.; Zhang, R.; Miao, L.; Zhang, X. Understanding Climate Change Impacts on Drought in China over the 21st Century: A Multi-Model Assessment from CMIP6. Npj Clim. Atmos. Sci. 2024, 7, 32. [Google Scholar] [CrossRef]
- Wan, L.; Bento, V.A.; Qu, Y.; Qiu, J.; Song, H.; Zhang, R.; Wu, X.; Xu, F.; Lu, J.; Wang, Q. Drought Characteristics and Dominant Factors across China: Insights from High-Resolution Daily SPEI Dataset between 1979 and 2018. Sci. Total Environ. 2023, 901, 166362. [Google Scholar] [CrossRef] [PubMed]
- Zeng, J.; Zhou, T.; Qu, Y.; Bento, V.A.; Qi, J.; Xu, Y.; Li, Y.; Wang, Q. An Improved Global Vegetation Health Index Dataset in Detecting Vegetation Drought. Sci. Data 2023, 10, 338. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Qi, J.; Leng, S.; Wang, Q. Long-Term Vegetation Phenology Changes and Responses to Preseason Temperature and Precipitation in Northern China. Remote Sens. 2022, 14, 1396. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, R.; Bento, V.A.; Leng, S.; Qi, J.; Zeng, J.; Wang, Q. The Effect of Drought on Vegetation Gross Primary Productivity under Different Vegetation Types across China from 2001 to 2020. Remote Sens. 2022, 14, 4658. [Google Scholar] [CrossRef]
- Tashie, A.M.; Mirus, B.B.; Pavelsky, T.M. Identifying Long-term Empirical Relationships between Storm Characteristics and Episodic Groundwater Recharge. Water Resour. Res. 2016, 52, 21–35. [Google Scholar] [CrossRef]
- Ajjur, S.B.; Di Lorenzo, E. Sensitivity of Groundwater Recharge Assessment to Input Data in Arid Areas. Hydrology 2024, 11, 28. [Google Scholar] [CrossRef]
- Ntona, M.M.; Busico, G.; Mastrocicco, M.; Kazakis, N. Modeling Groundwater and Surface Water Interaction: An Overview of Current Status and Future Challenges. Sci. Total Environ. 2022, 846, 157355. [Google Scholar] [CrossRef] [PubMed]
- Nanditha, H.S.; Reshmidevi, T.V.; Simha, L.U.; Kunhikrishnan, P. Statistical Analysis of Rainfall and Groundwater Interaction in Bhadra Catchment. Environ. Dev. Sustain. 2023, 26, 16267–16287. [Google Scholar] [CrossRef]
- Abebe, S.A.; Qin, T.; Zhang, X.; Yan, D. Wavelet Transform-Based Trend Analysis of Streamflow and Precipitation in Upper Blue Nile River Basin. J. Hydrol. Reg. Stud. 2022, 44, 101251. [Google Scholar] [CrossRef]
- Pal, L.; Ojha, C.S.P.; Chandniha, S.K.; Amit Kumar, A.K. Regional Scale Analysis of Trends in Rainfall Using Nonparametric Methods and Wavelet Transforms over a Semi-Arid Region in India. Intl J. Climatol. 2019, 39, 2737–2764. [Google Scholar] [CrossRef]
- Sharif, M.A.; Jafari, H. Estimation of Groundwater Recharge Lag Time in Mashhad-Chenaran Aquifer Using Cross-Correlation Method. Water Soil 2021, 35, 489–504. [Google Scholar]
- Sun, Q.; Liu, T.; Han, Z.; Liu, H.; Dong, H.; Qin, C. Multitemporal Scale Response of Vegetation Cover to Climate Change in Northern Tianshan by Remote Sensing Analysis. Trans. Chin. Soc. Agric. Eng. 2014, 30, 248–255. [Google Scholar]
- He, L.; Hou, M.; Chen, S.; Zhang, J.; Chen, J.; Qi, H. Construction of a Spatio-Temporal Coupling Model for Groundwater Level Prediction: A Case Study of Changwu Area, Yangtze River Delta Region of China. Water Supply 2021, 21, 3790–3809. [Google Scholar] [CrossRef]
- Guo, T.; Zhang, T.; Lim, E.; Lopez-Benitez, M.; Ma, F.; Yu, L. A Review of Wavelet Analysis and Its Applications: Challenges and Opportunities. IEEe Access 2022, 10, 58869–58903. [Google Scholar] [CrossRef]
- Grobbelaar, M.; Phadikar, S.; Ghaderpour, E.; Struck, A.F.; Sinha, N.; Ghosh, R.; Ahmed, M.Z.I. A Survey on Denoising Techniques of Electroencephalogram Signals Using Wavelet Transform. Signals 2022, 3, 577–586. [Google Scholar] [CrossRef]
- Wang, C.; Dai, F.; Liu, Y.; Wang, Y.; Li, H.; Qu, W. Shallow Groundwater Responses to Rainfall Based on Correlation and Spectral Analyses in the Heilonggang Region, China. Water 2023, 15, 1100. [Google Scholar] [CrossRef]
- Niu, S.; Shu, L.; Li, H.; Xiang, H.; Wang, X.; Opoku, P.A.; Li, Y. Identification of Preferential Runoff Belts in Jinan Spring Basin Based on Hydrological Time-Series Correlation. Water 2021, 13, 3255. [Google Scholar] [CrossRef]
- Yang, T.; Wang, G. Periodic Variations of Rainfall, Groundwater Level and Dissolved Radon from the Perspective of Wavelet Analysis: A Case Study in Tengchong, Southwest China. Environ. Earth Sci. 2021, 80, 492. [Google Scholar] [CrossRef]
- Yanfang, S.; Zhonggen, W.; Changming, L.I.U. Research Progress on the Time Series Analysis Methods in Hydrology. Prog. Geogr. 2013, 32, 20–30. [Google Scholar] [CrossRef]
- Liu, A.; Xu, Y.; Liu, C.; Ercheng, P. Geological Characteristics and Tectonic Evolution of Datong Basin. Geoscience 2021, 35, 1296. [Google Scholar]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Rezaei, A.; Gurdak, J.J. Large-Scale Climate Variability Controls on Climate, Vegetation Coverage, Lake and Groundwater Storage in the Lake Urmia Watershed Using SSA and Wavelet Analysis. Sci. Total Environ. 2020, 724, 138273. [Google Scholar] [CrossRef]
- Cazelles, B.; Chavez, M.; Berteaux, D.; Ménard, F.; Vik, J.O.; Jenouvrier, S.; Stenseth, N.C. Wavelet Analysis of Ecological Time Series. Oecologia 2008, 156, 287–304. [Google Scholar] [CrossRef]
- Nazari-Sharabian, M.; Karakouzian, M. Relationship between Sunspot Numbers and Mean Annual Precipitation: Application of Cross-Wavelet Transform—A Case Study. J—Multidiscip. Sci. J. 2020, 3, 67–78. [Google Scholar] [CrossRef]
- Maraun, D.; Kurths, J. Cross Wavelet Analysis: Significance Testing and Pitfalls. Nonlinear Process. Geophys. 2004, 11, 505–514. [Google Scholar] [CrossRef]
- Yu, H.-L.; Lin, Y.-C. Analysis of Space–Time Non-Stationary Patterns of Rainfall–Groundwater Interactions by Integrating Empirical Orthogonal Function and Cross Wavelet Transform Methods. J. Hydrol. 2015, 525, 585–597. [Google Scholar] [CrossRef]
- Zheng, W.; Wang, S.; Tan, K.; Shen, Y.; Yang, L. Rainfall Intensity Affects the Recharge Mechanisms of Groundwater in a Headwater Basin of the North China Plain. Appl. Geochem. 2023, 155, 105742. [Google Scholar] [CrossRef]
- Cai, P.; Li, R.; Guo, J.; Xiao, Z.; Fu, H.; Guo, T.; Wang, T.; Zhang, X.; Song, X. Spatiotemporal Dynamics of Groundwater in Henan Province, Central China and Their Driving Factors. Ecol. Indic. 2024, 166, 112372. [Google Scholar] [CrossRef]
- Venkatesan, G.; Subramani, T.; Karunanidhi, D.; Sathya, U.; Li, P. Impact of Precipitation Disparity on Groundwater Fluctuation in a Semi-Arid Region (Vellore District) of Southern India Using Geospatial Techniques. Environ. Sci. Pollut. Res. 2021, 28, 18539–18551. [Google Scholar] [CrossRef] [PubMed]
- Boas, T.; Mallants, D. Episodic Extreme Rainfall Events Drive Groundwater Recharge in Arid Zone Environments of Central Australia. J. Hydrol. Reg. Stud. 2022, 40, 101005. [Google Scholar] [CrossRef]
- Brookfield, A.E.; Zipper, S.; Kendall, A.D.; Ajami, H.; Deines, J.M. Estimating Groundwater Pumping for Irrigation: A Method Comparison. Groundwater 2024, 62, 15–33. [Google Scholar] [CrossRef]
- Ruud, N.; Harter, T.; Naugle, A. Estimation of Groundwater Pumping as Closure to the Water Balance of a Semi-Arid, Irrigated Agricultural Basin. J. Hydrol. 2004, 297, 51–73. [Google Scholar] [CrossRef]
- Entezari, M.; Karimi, H.; Gholam Heidari, H.; Jafari Aghdam, M. Estimation of Groundwater Recharge Level in Karstic Aquifers Using Modified APLIS Model. Arab. J. Geosci. 2020, 13, 198. [Google Scholar] [CrossRef]
- Nagaraj, S.; Purushothaman, P. Assessment of Influencing Level of Rainfall and Physical Factors on Groundwater Level for a Semi-Arid Flat Terrain Watershed Using Grid-Based Geospatial Analysis: A Case Study from Lower Palar Basin, Tamil Nadu, India. Environ. Monit. Assess. 2023, 195, 1159. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, M.A.A.; Szabó, N.P.; Szűcs, P. Exploring Hydrogeological Parameters by Integration of Geophysical and Hydrogeological Methods in Northern Khartoum State, Sudan. Groundw. Sustain. Dev. 2023, 20, 100891. [Google Scholar] [CrossRef]
- Zheng, G.; Cao, J.R.; Cheng, X.S.; Ha, D.; Wang, F.J. Experimental Study on the Artificial Recharge of Semiconfined Aquifers Involved in Deep Excavation Engineering. J. Hydrol. 2018, 557, 868–877. [Google Scholar] [CrossRef]
- Analysis of Rainfall Infiltration and Its Influence on Groundwater in Rain Gardens|Environmental Science and Pollution Research. Available online: https://link.springer.com/article/10.1007/s11356-019-05622-z (accessed on 3 October 2024).
- Han, X.; Liu, J.; Srivastava, P.; Mitra, S.; He, R. Effects of Critical Zone Structure on Patterns of Flow Connectivity Induced by Rainstorms in a Steep Forested Catchment. J. Hydrol. 2020, 587, 125032. [Google Scholar] [CrossRef]
- Schiavo, M. Entropy, Fractality, and Thermodynamics of Groundwater Pathways. J. Hydrol. 2023, 623, 129824. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).