Abstract
To address the complexity and high computational burden in the design of drip irrigation networks, the Jaya algorithm is utilized to study factors affecting project costs, including equipment and pipeline depreciation and the operation and management costs of the irrigation area. A mathematical model of synchronization optimal design of pipe layout and pipe diameter selection in a drip irrigation network system with constraints on pipe diameter, flow velocity, and pipe pressure is established. Using an irrigation district in Xinjiang, China, as an example, the Jaya algorithm optimization design program was run independently 50 times, and the relative deviation of each optimization result from the optimal solution was calculated. The results show that the annual cost per unit area o is reduced to 635.99 RMB/hm2, a 25.34% reduction compared to the original engineering program, and the investment-saving effect is obvious. The relative deviation is controlled within 3%, which shows that the algorithm has stable convergence performance and can meet the requirements of actual engineering design. The Jaya algorithm eliminates the need for parameter tuning, and it excels in cost savings, algorithm stability, and computational accuracy, making it an effective method for the single-objective optimization design of drip irrigation networks.
1. Introduction
Water scarcity is considered one of the greatest global risks in the coming decade [1], seriously threatening global food security, ecological safety, and economic growth [2,3]. Water resources are scarce in China, particularly in Northwest China [4], where agriculture is highly dependent on irrigation and agricultural water resources are a key factor in local agricultural development [5]. In recent years, sub-film drip irrigation technology has been widely used in oasis irrigation areas in Northwest China and the extension area has expanded rapidly due to its advantages of saving water, saving labor, increasing yield, and high efficiency [6,7,8]. However, as the area of oasis agricultural irrigation areas in Xinjiang and Gansu continues to expand, the scale and complexity of drip irrigation piping network systems also increase. Therefore, how to optimize the piping layout and design of drip irrigation systems has become an important issue to be solved.
Currently, the layout and pipe diameter selection in drip irrigation systems primarily relies on the experience of designers, lacking systematic optimization, which results in complex and time-consuming hydraulic calculations. Since the flow and pressure parameters of pipes at all levels interact, any adjustment of pipe diameter or hydraulic parameters requires recalculation of the whole system. This situation not only increases labor and time costs but also may lead to a non-optimized design scheme for the pipe network, which in turn increases the construction and operation costs of the project [9].
With the progress in computer technology, it has become possible to use computer programs to carry out the optimal design of drip irrigation pipe network systems. Through computer-aided design, it can effectively optimize the layout mode and pipe diameter selection of the pipe network, thus reducing the investment cost, reducing the waste of resources, and promoting the popularization and application of water-saving irrigation technology, which is of great practical significance. However, most current pipe network optimization design models focus primarily on the one-time project investment [9,10], ignoring factors such as operation and management costs, as well as water use efficiency. Therefore, there is an urgent need to construct a more comprehensive mathematical model to improve the overall efficiency of pipe network systems.
Traditional optimization design methods include linear programming [11], nonlinear programming [12], and dynamic programming [13]. Linear and nonlinear programming methods are generally suitable for simple and medium-sized problems, but they have certain limitations when dealing with complex and discrete variable problems. Dynamic programming has significant advantages in handling complex and discrete variable issues; however, it experiences a substantial increase in computational complexity and storage requirements when faced with large-scale problems, making the solution difficult and limiting its application range. Therefore, although dynamic programming overcomes some of the limitations of linear and nonlinear programming, there is still a need to seek new optimization methods to improve efficiency when solving complex large-scale problems.
In recent years, heuristic algorithms have been widely applied in pipeline network optimization design, such as genetic algorithms [14], artificial fish swarm algorithms [15], optimization algorithms [16], atomic search algorithms [17], and hybrid algorithms [18]. These algorithms are effective at solving complex, nonlinear problems, but their parameter settings are complicated, and they are prone to getting stuck in local optimal solutions.
The Jaya algorithm, as a parameter-free heuristic optimization algorithm, addresses these challenges and demonstrates significant advantages across various fields due to its simplicity, ease of use, and lack of need for parameter tuning [19,20]. Its unique search mechanism, which relies on guiding solutions towards superior outcomes while avoiding inferior ones, enhances both exploration and exploitation, resulting in improved convergence rates and solution quality.
Research has shown that the Jaya algorithm often outperforms traditional optimization techniques, especially in complex nonlinear scenarios, showcasing superior convergence characteristics and solution precision. Furthermore, its computational efficiency allows for its application in large-scale problems without the prohibitive resource demands of other methods.
However, studies exploring the application of the Jaya algorithm specifically in drip irrigation network optimization remain rare. Therefore, it is crucial to investigate its applicability in this domain. This research aims to analyze the effectiveness and advantages of the Jaya algorithm, particularly in comparison with traditional methods such as genetic algorithms and dynamic programming. By highlighting its potential, this study seeks to provide insights that may pave the way for future applications of Jaya in both drip irrigation networks and other relevant areas.
This study establishes a mathematical model for the synchronization optimization of pipe layout and pipe diameter selection, aiming for the lowest annual cost per unit area, for a large-scale drip irrigation pipe network system in the pressurized irrigation area of an oasis in Northwest China. Based on the Jaya algorithm, the optimization design is carried out for a drip irrigation pipe network system in a specific region of Xinjiang, China, to verify the effectiveness and superiority of the Jaya algorithm in this type of optimization design field.
2. Materials and Methods
2.1. Problem Description
2.1.1. System Overview
The drip irrigation network system studied includes a pump house and field drip irrigation network. The pump house includes water pumps and ancillary equipment, while the field drip irrigation pipe network includes main pipes, sub-main pipes, branch pipes, lateral pipes, and water valves. This system is widely used in Xinjiang, China, characterized by large farmland areas and machine-leveled land. The “comb-type” layout, where lateral pipes are arranged bilaterally along both sides of the branch pipes according to crop rows, is commonly adopted [9,17], as shown in Figure 1.
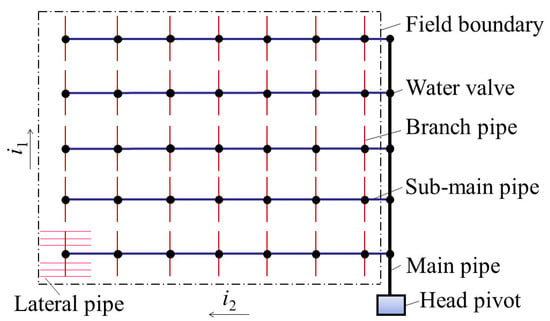
Figure 1.
Schematic diagram of the “comb-type” pipe network layout. In the drip irrigation pipe network system, different pipe layouts and pipe diameter choices directly affect the along-stream head loss of water flow, which leads to different project investment costs. Therefore, the goal of optimizing the drip irrigation pipe network system is to achieve economic optimization, i.e., to minimize the project investment cost and operation cost under the premise of meeting the irrigation requirements. However, how to reasonably and quickly obtain the most economical piping layout and pipe diameter scheme for drip irrigation network systems has become an urgent problem to be solved [17].
2.1.2. Objective
The goal of this study is to minimize the investment and operational costs of the drip irrigation network while ensuring optimal irrigation performance. This involves determining the most economical pipe layout and diameter configuration.
2.1.3. Assumptions and Simplifications
To solve the above problems, the following simplified assumptions and methods were designed for the pressurized drip irrigation network system in this study: (1) Simplification of the irrigation system: a continuous irrigation system is used on the main pipe, and a rotational irrigation system is used on the sub-main pipe and branch pipe. The number of branch pipes working in each irrigation rotation is determined by the design irrigation cycle and irrigation duration, and each sub-main pipe generally has a maximum of two branch pipes working at the same time. (2) Regularization of field shape: for irregularly shaped fields, the field shape is regularized to a rectangle, and the slope is a uniform slope along the two length directions of the rectangle.
2.2. Mathematical Model
This study considers both the construction cost of the irrigation area and the operation and management cost after its completion. The synchronization optimization model of the pipeline layout and pipe diameter selection of the drip irrigation network system was established with the objective of the lowest annual cost per unit area.
2.2.1. Objective Function
The annual cost per unit area is given by the following:
Annual cost per unit area = (annual depreciation of fixed assets + annual operating and management costs)/irrigated area.
- (1)
- Annual depreciation of fixed assets
The total fixed assets of the irrigation project include both the fixed assets of the head pivot and the pipe network project. The fixed assets of the head pivot include the construction costs of the pumping station and its supporting equipment, and the construction costs of the supporting equipment of the pumping station include the costs of filters and fertilizer tanks.
where F is the annual depreciation of fixed assets (RMB); K is the residual value of fixed assets (RMB), taking 3% of the total fixed assets of the irrigation project; and r is the depreciable life of fixed assets; the depreciable life of fixed assets r is divided into the depreciable life of the head pivot equipment r1 and the depreciable life of the pipeline network r2.
The total fixed assets of the irrigation project W (RMB):
where W1 is the fixed assets of the head pivot of the project (RMB); W2 is the fixed assets of the pipe network project (RMB).
The fixed assets of the head pivot of the project:
where W11 is the construction costs of the pumping station (RMB); W12 is the construction costs of the supporting equipment of the pumping station (RMB); FP is the investment per unit of installed capacity of the pumping station (RMB/kW); WP is the installed capacity of the pumping station (kW); WG is the cost of a filter to match the irrigated area (RMB); and WF is the cost of fertilizer storage tanks to match the irrigated area (RMB).
The fixed assets of the pipe network project:
where θ is the proportion of piping accessories to piping costs, taken to be 0.1; τ is the proportion of direct costs such as labor and machinery costs to pipeline costs, taken to be 0.2; n is the total number of pipe sections; Di is the inner diameter of the ith pipe section (mm); Li is the length of the ith pipe section (m); and A, B, and c are coefficients related to the pipeline cost, which are obtained by fitting the pipeline inner diameter and the pipeline cost.
- (2)
- Annual operating and management costs
The annual operating and management costs mainly include electricity, water, and other costs. Other costs include project repair and maintenance costs and personnel expenses. Other costs are estimated in proportion to the total fixed assets of the irrigation project.
Annual operating and management costs:
where G is the annual operation and management costs (RMB); C is the electricity cost (RMB); O is the water fee (RMB); and λ is the operation cost coefficient, taken to be 0.1.
where E is the unit price of electricity (RMB/kWh); TZ is the annual operating hours of the pump (h); e is the unit price of water (RMB/m3); m1 is the combined gross irrigation quota (m3/ hm2); and S is the irrigated area (hm2).
- (3)
- Annual cost per unit area
Organizing Equations (1)–(10), the annual cost per unit area P can be obtained as follows:
2.2.2. Restrictive Condition
To make the optimized scheme meet the requirements of system operation and maintain a certain degree of feasibility and practicality, reasonable constraints must be set to constrain the optimization calculation process.
- (1)
- Pipe diameter constraint
Throughout the network, the diameter of the next level’s pipe must be no greater than that of the previous level.
where Dj is the diameter of the upper pipe of Dj+1 (mm).
In addition, the pipe diameter selected must be the standardized commercial pipe diameter provided by the irrigation district project construction:
where D is the pipe diameter of optional pipes (mm); N is the number of standard pipe diameters.
- (2)
- Flow velocity constraint
To ensure the stability and reliability of the pipe network system and to extend the pipeline’s service life, the water flow velocity in the pipeline should be no less than the minimum allowable flow velocity and no greater than the maximum allowable flow velocity.
where vi is the flow velocity of the ith pipe section (m/s); vmin is the minimum allowable flow velocity of the ith pipe section (m/s); and vmax is the maximum allowable flow rate of the ith pipe section (m/s).
- (3)
- Pipeline pressure capacity constraints
To ensure that the pipe network system can withstand the expected pressure during normal operation, and to safeguard the safety and reliability of the system, the maximum pressure during the operation of the pipe network should be less than the pressure that the pipe material can withstand.
where Pi,max is the maximum pressure during operation of the ith pipe section (MPa); Pi,c is the pressure-bearing capacity of the ith pipe section (MPa).
- (4)
- Nodal pressure constraints
Ensure that the pressure at each node in the pipe network is maintained within reasonable limits for proper operation and stability of the system. The pressure at each node in the pipe network should be satisfied:
where E0 is the water source elevation (m); H1 is the pump head (m); h is the sum of the head loss at the head pivot (m); M (j) is the set of all pipe segments that the water source passes through to node j; α is the localized head loss coefficient; f, m, and b are pipe correlation coefficients; Qi is the flow of the ith pipe section (L/h); Ej is the jth node for the ground elevation (m); and Hj,min is the minimum head that must be satisfied at node j (m).
- (5)
- Constraint on the allowable head deviation in the irrigation district
To meet the requirements for irrigation uniformity, the design flow deviation of the irrigators within the irrigation area should not exceed the allowable design flow deviation.
where qv is the irrigator design flow deviation rate (%); qmax is the irrigator maximum flow (L/h); qmin is the irrigator minimum flow (L/h); qd is the irrigator design flow (L/h); and [qv] is the irrigator design allowable flow deviation rate (%).
- (6)
- Constraint on the number of rotational irrigation groups
Irrigation should be completed within the maximum irrigation cycle in order to meet the needs of crop growth.
where N is the number of actual rotational irrigation groups; Nmax is the maximum number of rotational irrigation groups; td is the water supply time (h/day); Tmax is the design irrigation cycle (days); and t is the duration of one irrigation (h).
2.2.3. Optimization Design Method of Drip Irrigation Network Based on Jaya Algorithm
The Jaya algorithm is based on the principle of continuous improvement, and its core idea is that the offspring individuals are constantly approaching the excellent individuals while moving away from the worst individuals, thus continuously improving the quality of the solution. Compared with other heuristic optimization algorithms, the Jaya algorithm has simple parameters, and only the population size and the maximum number of iterations need to be set; it is easier to understand and implement, and is very suitable for solving global optimization and engineering design optimization problems; and it has the oriented characteristics of converging to the best and avoiding the worst [21,22].
The algorithmic process in this study is divided into the following four stages.
- (1)
- Initialize the population.
Set the population size and the maximum number of iterations, and randomly generate the pipe diameter selection scheme to form the initial population to start the iteration.
- (2)
- Update Individuals.
The updated iteration equation is as follows:
where Xj,k,i is the ith pipe diameter variable of the kth individual in the jth iteration process; Xj,best,i is the ith pipe diameter variable of the individual with the best value of the objective function in the jth iteration process; Xj,worst,i is the ith pipe diameter variable of the individual with the worst value of the objective function in the jth iteration process; |Xj,k,i| is the absolute value of Xj,k,I; r1,j,i and r2,j,i are a random number between 0 and 1; and X’j,k,i is the updated value of Xj,k,i.
- (3)
- Greedy selection.
In the jth iteration, update the ith pipe diameter variable of the kth individual according to the iteration equation, and if the generated new individual has a better economy than the original one, the new individual is used to replace the original one; otherwise, it is not replaced. After all individuals have been updated, the next iteration is calculated.
- (4)
- Output optimal solution.
Repeating the two phases of updating individuals and greedy selection until the number of iterations reaches the maximum set number of times to output the optimal solution.
The flowchart for the optimized design of the drip irrigation network based on the Jaya algorithm is shown in Figure 2.
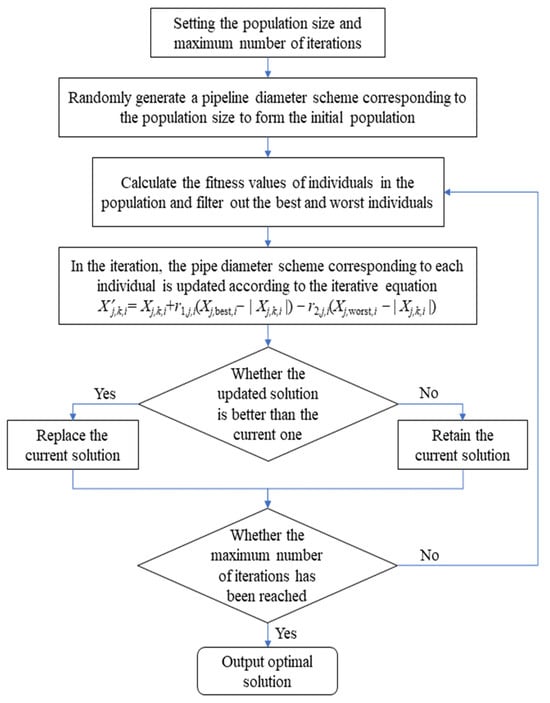
Figure 2.
Flow chart of drip irrigation network optimization design based on Jaya algorithm.
3. Case Study
3.1. Overview of Project Areas
This case study selects a drip irrigation district in Shihezi City, Xinjiang, China, as the study area, located at 44°18′ N latitude and 86°4′ E longitude, with a mid-temperate continental semi-arid climate. The main irrigation method is under-membrane drip irrigation, and the primary crop is cotton.
The controlled area of the drip irrigation network system in the irrigation area is 31.1 hm2, with an irrigation quota of 28.89 mm; the soil capacity is 1.5 g/cm3, the land in the project area has been leveled, the terrain slope in the direction of the main pipe is I1 = 1/1000, and the terrain slope in the direction of the sub-main pipe is I2 = 1/1000. Based on local test data, the design water consumption intensity is 6.5 mm/d; the planned soil wetting layer depth is 0.5 m; the field water holding rate is 24%; the upper and lower limits of soil water content are calculated as 90% and 65% of the field water holding capacity, respectively; the coefficient of irrigation water utilization is 0.9; and the maximum water consumption intensity is 6.5 mm/day, with an effective rainfall of 0 mm/day due to low rainfall and high evaporation in the area.
Based on factors such as the project’s climate, crop types, planting mode, and soil conditions, the lateral pipe used is a single-wing labyrinth drip irrigation belt with a design flow of 2.1 L/h, a diameter of 16 mm, a working pressure of 10 m, and an allowable design head deviation of 20%. The distance between irrigators is 0.3 m. The main pipe and sub-main pipe are laid in the form of 0.4 MPa PVC pipes buried in the ground, while the branch pipes are laid on the ground surface with thin-walled PE pipes, and each part of the pipes is connected to the pipe network through the pipe fittings.
In the hydraulic calculation for the drip irrigation pipe network, the calculations of irrigation quota, irrigation continuation, head loss along the pipeline, system design flow, and pressure are based on the recommended formulas in “Technical standard for micro irrigation engineering” [23] and “Technical standard for water-saving irrigation project” [24].
The program was debugged multiple times, with the population size of the Jaya algorithm set to 500 and the maximum number of iterations set to 15. To mitigate the impact of the inherent randomness of the algorithm on the evaluation of its solution performance, the optimization design program was run independently 50 times. The optimal results and the relative deviations of each run from the optimal results were recorded.
The design parameters of the drip irrigation network system are provided in Table 1, and the unit prices of the PVC and PE pipes are listed in Table 2.

Table 1.
Design parameters of drip irrigation network system.

Table 2.
Unit prices for PVC and PE pipes.
3.2. Optimization Design of Drip Irrigation System Based on Jaya Algorithm
3.2.1. Optimization Results and Analysis
Table 3 shows the design results based on the Jaya algorithm and the original project. The annual cost per unit area based on the Jaya algorithm is 635.99 RMB/hm2, which is 25.34% lower than the original design cost of 851.89 RMB/hm2. The drip irrigation network system in the original project includes 4 main pipes, 40 sub-main pipes, and 80 branch pipes, whereas the optimized system based on the Jaya algorithm includes 3 main pipes, 24 sub-main pipes, and 48 branch pipes. The number of pipes in the drip irrigation network system optimized based on the Jaya algorithm is significantly reduced compared to the original project, and the diameter of the pipes is smaller than that of the original project. Due to the reduction in the number of pipes and the pipe diameter, the annual cost per unit area is reduced. Figure 3 shows the layout of the original project’s drip irrigation network system (a) and the layout of the optimized drip irrigation network system based on the Jaya algorithm (b).

Table 3.
Design results based on the Jaya algorithm and the original project.
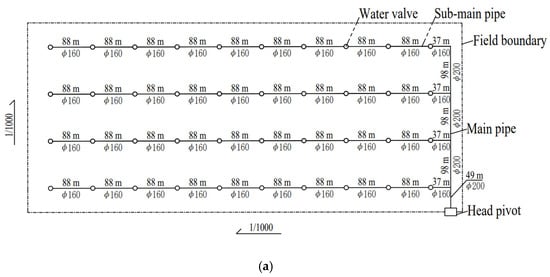
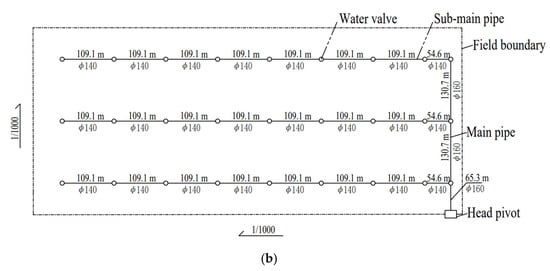
Figure 3.
Layout of the drip irrigation network system. (a) Layout of the drip irrigation network system of the original project. (b) Layout of the drip irrigation network system obtained by the optimization design based on the Jaya algorithm.
3.2.2. Relative Deviation Rate of Optimization Results
Table 4 shows the statistics of the relative deviation of the results from 50 runs compared to the optimal results, including the number of occurrences within each deviation range. The probability that the relative deviation of the optimization results is less than 0.5% is 92%, and the probability that it is less than 3% is 100%. This indicates that the Jaya algorithm exhibits good convergence and stability for this research problem, meeting the requirements for stable convergence in the synchronization optimization of the drip irrigation network.

Table 4.
Number of occurrences of relative deviation within each range.
In this study, the optimal solution was filtered from the results of 50 independent runs. In theory, if a globally optimal solution (or a solution obtained with sufficiently stringent constraints) can be determined for a problem, the solution is considered as the true solution. However, for complex optimization problems, finding the global optimal solution is often extremely challenging. At the same time, there is usually a certain range in the setting of constraints. As a result, the optimal solution obtained is usually the best estimate provided by efficient algorithms or theoretical analyses, and may not be the true global optimal solution. The statistics of relative deviations not only assess the convergence and stability of the algorithm, but also provide a range of acceptable results. Optimization results with a relative deviation of less than 5% can be considered excellent for system performance.
4. Discussion
This study demonstrated the effectiveness and superiority of the Jaya algorithm in the optimal design of a drip irrigation network system in Xinjiang, China. This was achieved by establishing a mathematical model aimed at minimizing the annual cost per unit area and employing the Jaya algorithm for the system’s optimization.
The optimization results indicate that the Jaya algorithm reduced the annual cost per unit area compared to traditional methods. The primary reasons for these cost savings are the following: (1) The Jaya algorithm effectively identifies optimal pipe layouts that minimize water distribution losses and enhance flow efficiency, leading to reduced operational costs. (2) By systematically evaluating various pipe diameters, the Jaya algorithm ensures that the chosen diameters balance hydraulics and economic feasibility, thus lowering material costs without compromising performance. (3) The flexibility of the Jaya algorithm allows it to accommodate various design constraints and local conditions, which leads to more customized and efficient solutions for specific scenarios.
This study provides an effective method. The method optimizes the pipe layout and pipe diameter selection of the drip irrigation system through synchronization. However, some limitations still exist: (1) This study examines a comb-type pipe network system with lateral pipes arranged bidirectionally along the branch pipes. However, there are other configurations, such as comb-type systems with unilateral lateral pipe arrangements and Fengzi-type layouts with bidirectional lateral pipes, as well as irregular pipe network arrangements. Further investigation is needed to assess the applicability of the Jaya algorithm to these different network layout patterns. (2) The plots in this study are artificially regularized into rectangular shapes with uniform slopes in both length directions. However, real plots have varied shapes and complex topography, which increases the difficulty of the study and necessitates further research. (3) The head pivots in this study are located at the corners of the pipe network system. Different locations of the head pivots can affect the most economical layout pattern of the system, and further research is needed to explore these variations. (4) In this study, rotational irrigation groups operate as follows: Branches at the ends of the farthest and nearest sub-main pipes are prioritized for irrigation. If the number of branches in a rotational irrigation group exceeds the branches in the sub-main pipe, the excess branches are distributed to other branches at the ends of the sub-main pipes until all branches are included in the group. If the number of branches in a rotational group exceeds twice the number of branches in the sub-main pipe, the penultimate node is treated as the last branch. Excess branches are then irrigated rotationally, based on the farthest and nearest branches at the ends of the sub-main pipes. This process continues until all branches are assigned. Further research is needed if a random rotational irrigation group scheme is to be employed. (5) The annual cost per unit area calculated in this study includes only the costs related to the investment in the pipeline network system. There remains a discrepancy between this and the actual project costs. Therefore, the annual cost per unit area presented here serves as a reference. Further research is needed to refine the calculation and better align it with actual investment costs by incorporating additional cost factors and improving the cost formula.
To address the limitations of this study and enhance the optimization of drip irrigation network systems, future research should consider incorporating more complex field shapes and terrain slope models to improve realism and accuracy. For instance, methods such as Geographic Information Systems (GISs) and Digital Elevation Models (DEMs) can be utilized to create more detailed terrain representations. Additionally, exploring multi-objective optimization algorithms, such as Non-dominated Sorting Genetic Algorithm II (NSGA-II) or Multi-Objective Particle Swarm Optimization (MOPSO), could lead to more comprehensive designs. These algorithms can balance trade-offs between various objectives, such as head loss and crop yield, providing more holistic solutions. Moreover, including factors such as head and yield in the optimization objectives could enhance the practical applicability of the designs. Continuous improvement and refinement will result in a more scientific and efficient design of drip irrigation networks, offering stronger support for sustainable agricultural development and water resource management. In summary, the integration of specific advanced techniques and methodologies in future research will not only strengthen the design aspects but also contribute to more effective water resource management strategies.
5. Conclusions
This study established a mathematical model for the synchronization optimization of piping layout and diameter selection in a drip irrigation network. The objective was to minimize the annual cost per unit area by accounting for equipment and piping depreciation costs, as well as operation and management costs. A single-objective optimization design was performed using the Jaya algorithm. The synchronization optimization of a drip irrigation system in an irrigation area in Shihezi City, Xinjiang, China, was carried out, and the annual cost per unit area of the optimized drip irrigation system was reduced by 25.34% compared with the original project. In addition, the relative deviation rates of the optimization design results are kept within 3%, indicating that Jaya’s algorithm shows stable convergence and high computational accuracy in the optimal design of the drip irrigation network. Therefore, the Jaya algorithm is an effective method for the synchronization optimal design of pipe layout and pipe diameter selection in drip irrigation network systems.
The successful application of the Jaya algorithm in this study not only improves cost-effectiveness but also enhances resource efficiency, which is important for sustainable agricultural practices. Its potential impact in the field of agriculture and water management highlights the importance of advanced optimization techniques in coping with water scarcity and enhancing crop yields.
Author Contributions
Conceptualization, K.F. and W.W.; methodology, K.F. and W.W; software, K.F., X.Y. and T.Z.; validation, Y.P., X.H. (Xuefei Huo) and D.R; formal analysis, K.F.; investigation, X.H. (Xiaotao Hu) and W.W; resources, K.F.; data curation, K.F.; writing—original draft preparation, K.F.; writing—review and editing, D.R., Y.P., X.H. (Xuefei Huo) and Y.W.; visualization, X.H. (Xuefei Huo); supervision, W.W.; project administration, W.W. and X.H. (Xiaotao Hu); funding acquisition, W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program (2022YFD1900402), and the Xinjiang Uygur Autonomous Region Major Science and Technology Special Project (2023A02002).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
Many thanks to W.W., X.T.H and D.R. for their help and support!
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, F.; Bo, Y.; Ciais, P.; Dumas, P.; Tang, Q.; Wang, X.; Liu, J.; Zheng, C.; Polcher, J.; Yin, Z.; et al. Deceleration of China’s human water use and its key drivers. Proc. Natl. Acad. Sci. USA 2020, 117, 7702–7711. [Google Scholar] [CrossRef] [PubMed]
- Rich, D.; Andiroglu, E.; Gallo, K.; Ramanathan, S. A review of water reuse applications and effluent standards in response to water scarcity. Water Secur. 2023, 20, 100154. [Google Scholar] [CrossRef]
- Gajghate, P.W.; Mirajkar, A.; Shaikh, U.; Bokde, N.D.; Yaseen, Z.M. Optimization of layout and pipe sizes for irrigation pipe distribution network using steiner point concept. Math. Probl. Eng. 2021, 2021, 6657459. [Google Scholar] [CrossRef]
- Shu, R.; Cao, X.C.; Wu, M.Y. Clarifying regional water scarcity in agriculture based on the theory of blue, green and grey water footprints. Water Resour. Manag. 2021, 35, 1101–1118. [Google Scholar] [CrossRef]
- Hui, G.; Sien, L. A review of drip irrigation’s effect on water, carbon fluxes, and crop growth in farmland. Water 2024, 16, 2206. [Google Scholar] [CrossRef]
- Hiremath, D.; Makadia, J.J.; Rudrapur, S. Economic impact and decomposition analysis of income change vis-a-vis drip and conventional irrigation technology in bananas: A case study of the south gujarat region in India. J. Irrig. Drain. Eng. 2023, 149, 04023029. [Google Scholar] [CrossRef]
- Yang, P.; Cheng, M.H.; Wu, L.F.; Fan, J.L.; Li, S.; Wang, H.D.; Qian, L. Review on drip irrigation: Impact on crop yield, quality, and water productivity in China. Water 2023, 15, 1733. [Google Scholar] [CrossRef]
- Rao, F.P.; Abudikeranmu, A.; Shi, X.P.; Heerink, N.; Ma, X.L. Impact of participatory irrigation management on mulched drip irrigation technology adoption in rural Xinjiang, China. Water Resour. Econ. 2021, 33, 100170. [Google Scholar] [CrossRef]
- Zhao, R.; He, W.; Lou, Z.; Nie, W.; Ma, X. Synchronization optimization of pipeline layout and pipe diameter selection in a self-pressurized drip irrigation network system based on the genetic algorithm. Water 2019, 11, 489. [Google Scholar] [CrossRef]
- Li, Z.; Lin, Z.J.; Lyu, S.L.; Wei, Z.W.; Huang, H.Q. Tree-type irrigation pipe network planning and design method using ICSO-ASV. Water 2020, 12, 1985. [Google Scholar] [CrossRef]
- Alperovits, E.; Shamir, U. Design of optimal water distribution systems. Water Resour. Res. 1977, 13, 885–900. [Google Scholar] [CrossRef]
- Dandy, G.C.; Hassanli, A.M. Optimum design and operation of multiple subunit drip irrigation systems. J. Irrig. Drain. Eng. 1996, 122, 265–275. [Google Scholar] [CrossRef]
- Giménez, J.L.; Calvet, J.; Alonso, A. A two-level dynamic programming method for the optimal design of sewerage networks. IFAC Proc. Vol. 1995, 28, 537–542. [Google Scholar] [CrossRef]
- Liu, R.; Guo, F.; Sun, W.; Wang, Y.; Zhang, Z.; Ma, X. A new method for optimization of water distribution networks while considering accidents. Water 2021, 13, 1651. [Google Scholar] [CrossRef]
- Liu, Y.; Tao, Z.P.; Yang, J.; Mao, F. The modified artificial fish swarm algorithm for least-cost planning of a regional water supply network problem. Sustainability 2019, 11, 4121. [Google Scholar] [CrossRef]
- Ezzeldin, R.M.; Djebedjian, B. Optimal design of water distribution networks using whale optimization algorithm. Urban Water J. 2020, 17, 14–22. [Google Scholar] [CrossRef]
- Duan, X.; He, W.; Wang, Y.; Liu, Q.; Tian, Y.; Shi, X. Optimization design method of a large-scale multilevel gravity drip irrigation pipe network system based on atom search optimization. J. Irrig. Drain. Eng. 2022, 148, 04022023. [Google Scholar] [CrossRef]
- Batmaz, V.; Kayaalp, N. Optimization of water distribution networks using hybrid BBO-IWO algorithm. Urban Water J. 2023, 20, 205–222. [Google Scholar] [CrossRef]
- Buddala, R.; Mahapatra, S.S. Improved teaching–learning-based and JAYA optimization algorithms for solving flexible flow shop scheduling problems. J. Ind. Eng. Int. 2018, 14, 555–570. [Google Scholar] [CrossRef]
- Yu, K.J.; Liang, J.J.; Qu, B.Y.; Chen, X.; Wang, H.S. Parameters identification of photovoltaic models using an improved JAYA optimization algorithm. Energy Manag. 2017, 150, 742–753. [Google Scholar] [CrossRef]
- Venkata Rao, R. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar] [CrossRef]
- Rao, R.V.; Saroj, A. A self-adaptive multi-population based Jaya algorithm for engineering optimization. Swarm Evol. Comput. 2017, 37, 1–26. [Google Scholar]
- GB/T 50485—2020; Technical Standard for Micro Irrigation Engineering. China Planning Press: Beijing, China, 2020. (In Chinese)
- GB/T 50363—2018; Technical Standard for Water-Saving Irrigation Project. China Planning Press: Beijing, China, 2018. (In Chinese)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).