Mechanical Response Study of a Cross-Fault Water Conveyance Tunnel under the Combined Action of Faulting Dislocation and Seismic Loading
Abstract
1. Introduction
2. Shear Tests of Wall Rock–Lining Contact Surfaces
2.1. Test Procedure
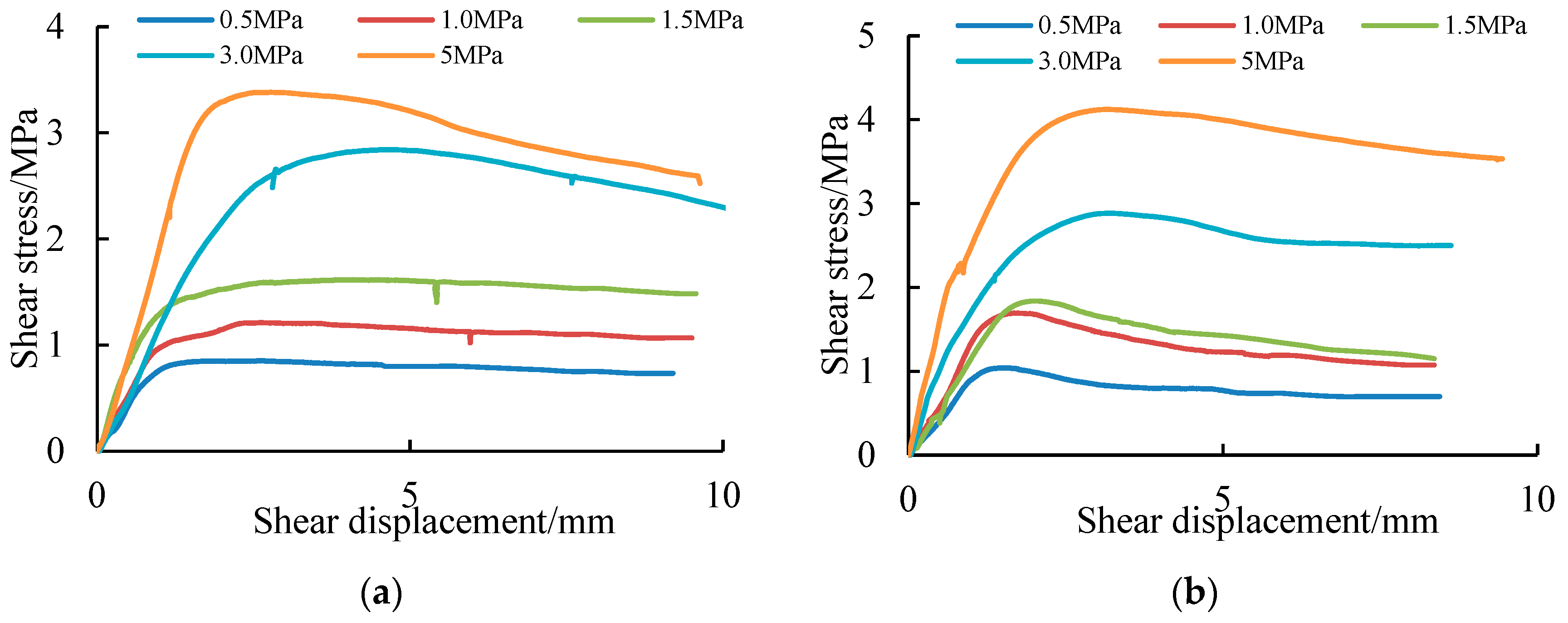
2.2. Test Results
3. Numerical Simulation Test of the Wall Rock–Lining Interface
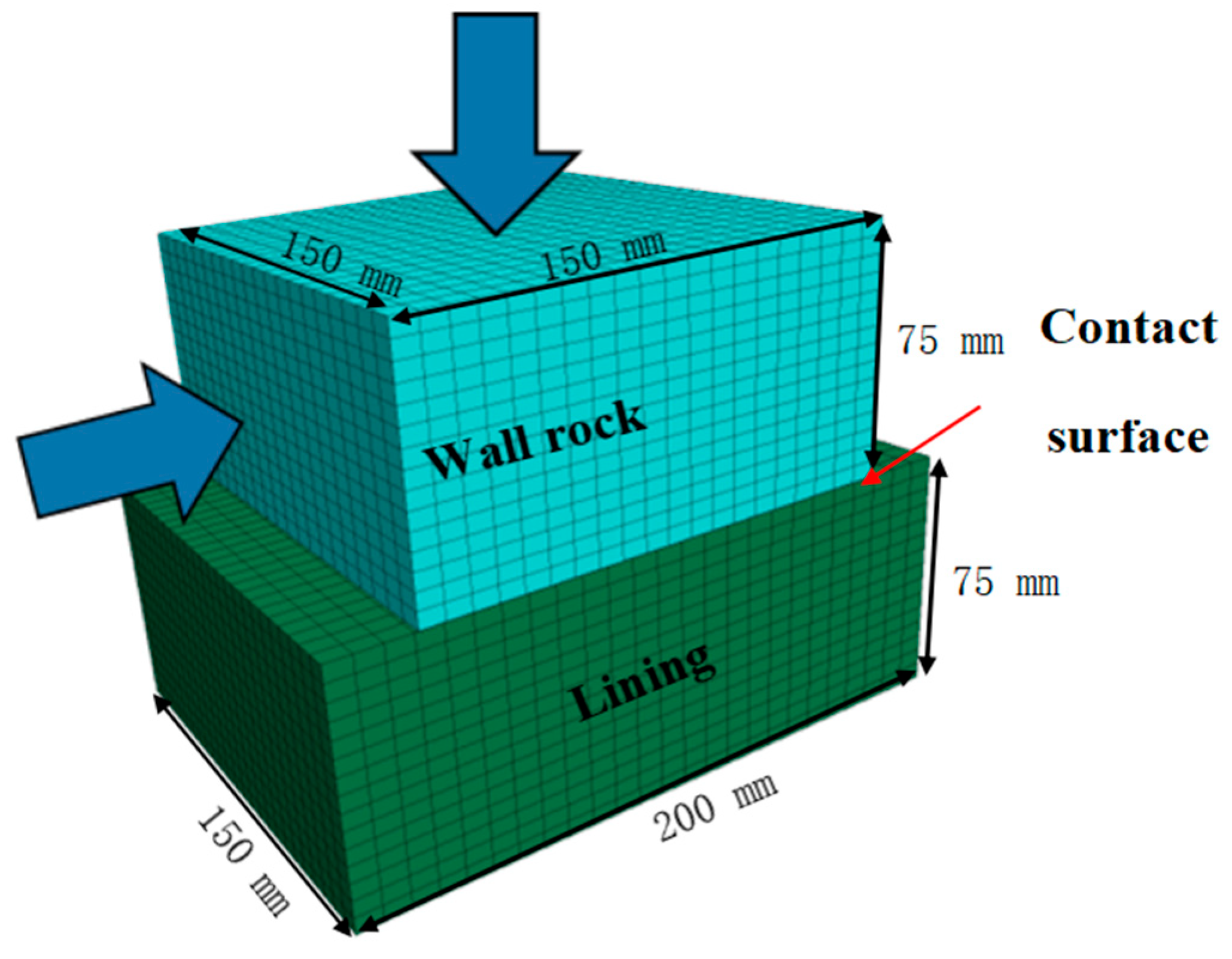
3.1. Numerical Simulation Model
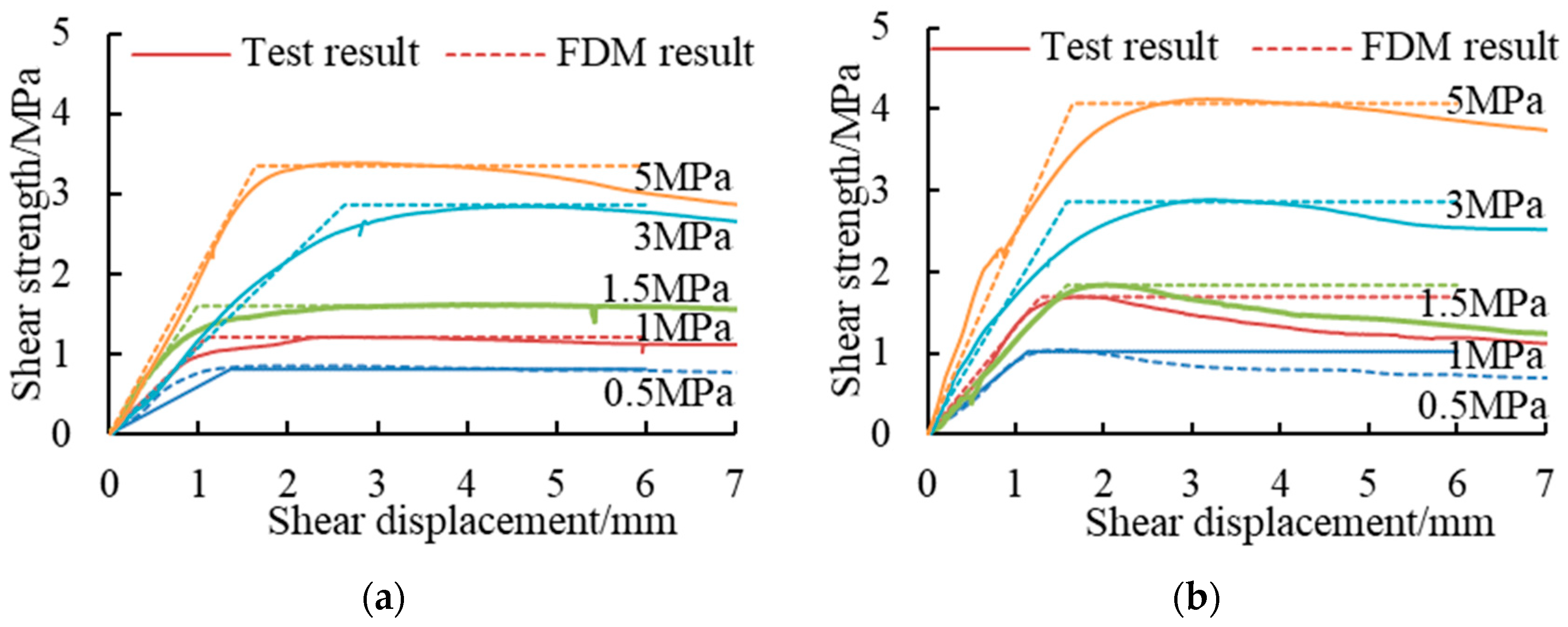
3.2. Numerical Simulation Test Results
4. Mechanical Response of a Cross-Fault Tunnel in Consideration of the Wall Rock–Lining Interaction
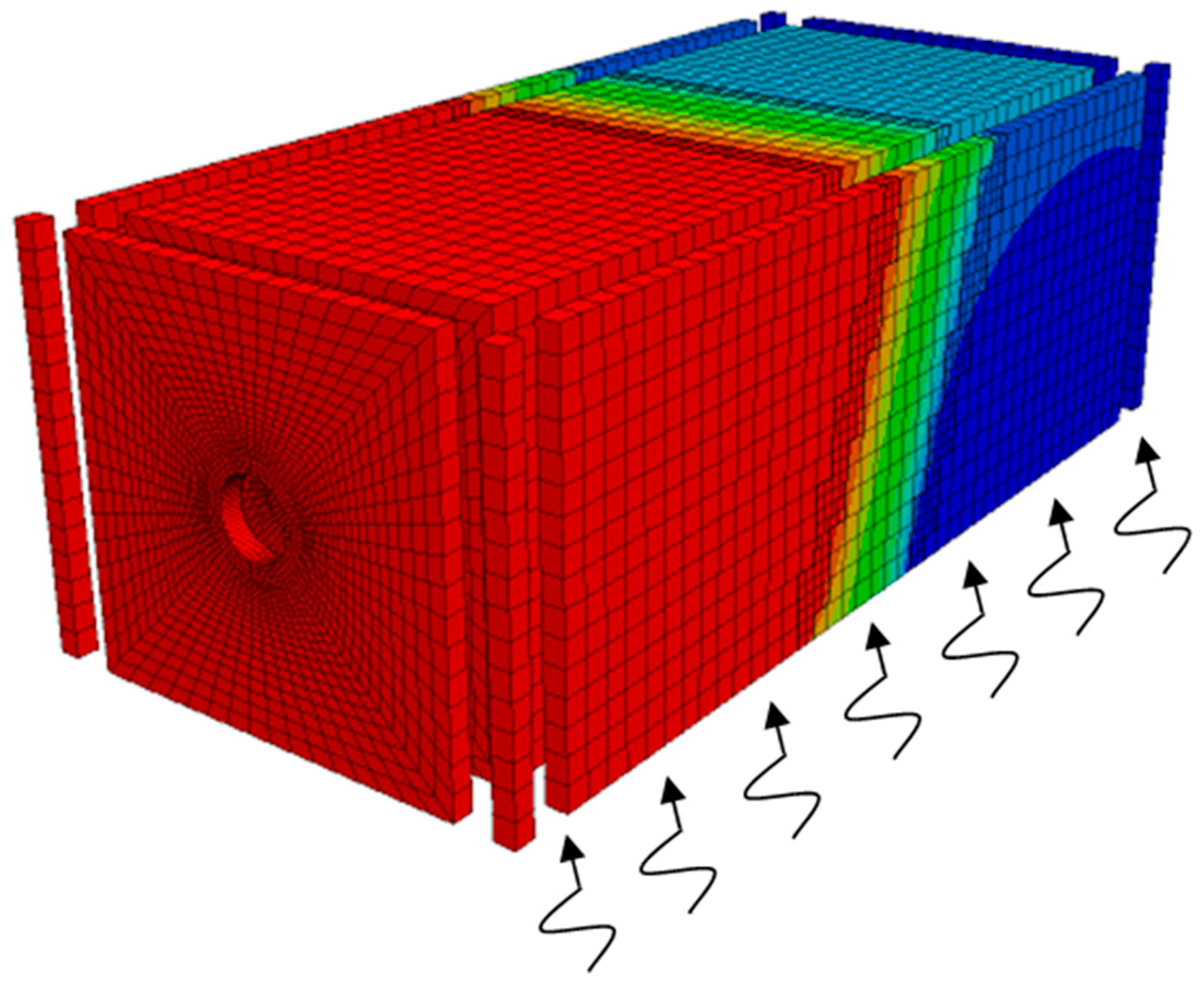
4.1. Establishment of the Numerical Model of the Cross-Fault Tunnel
4.2. Numerical Analysis Procedure of the Cross-Fault Tunnel under the Combined Action of Faulting and Seismic Loading
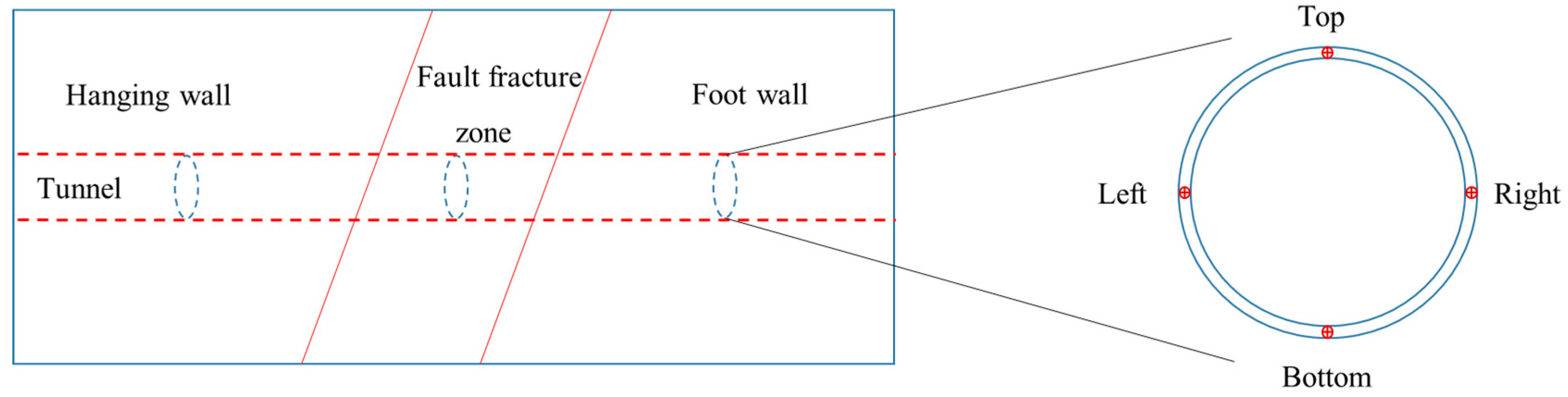
4.3. Mechanical Response Monitoring Scheme of the Cross-Fault Tunnel
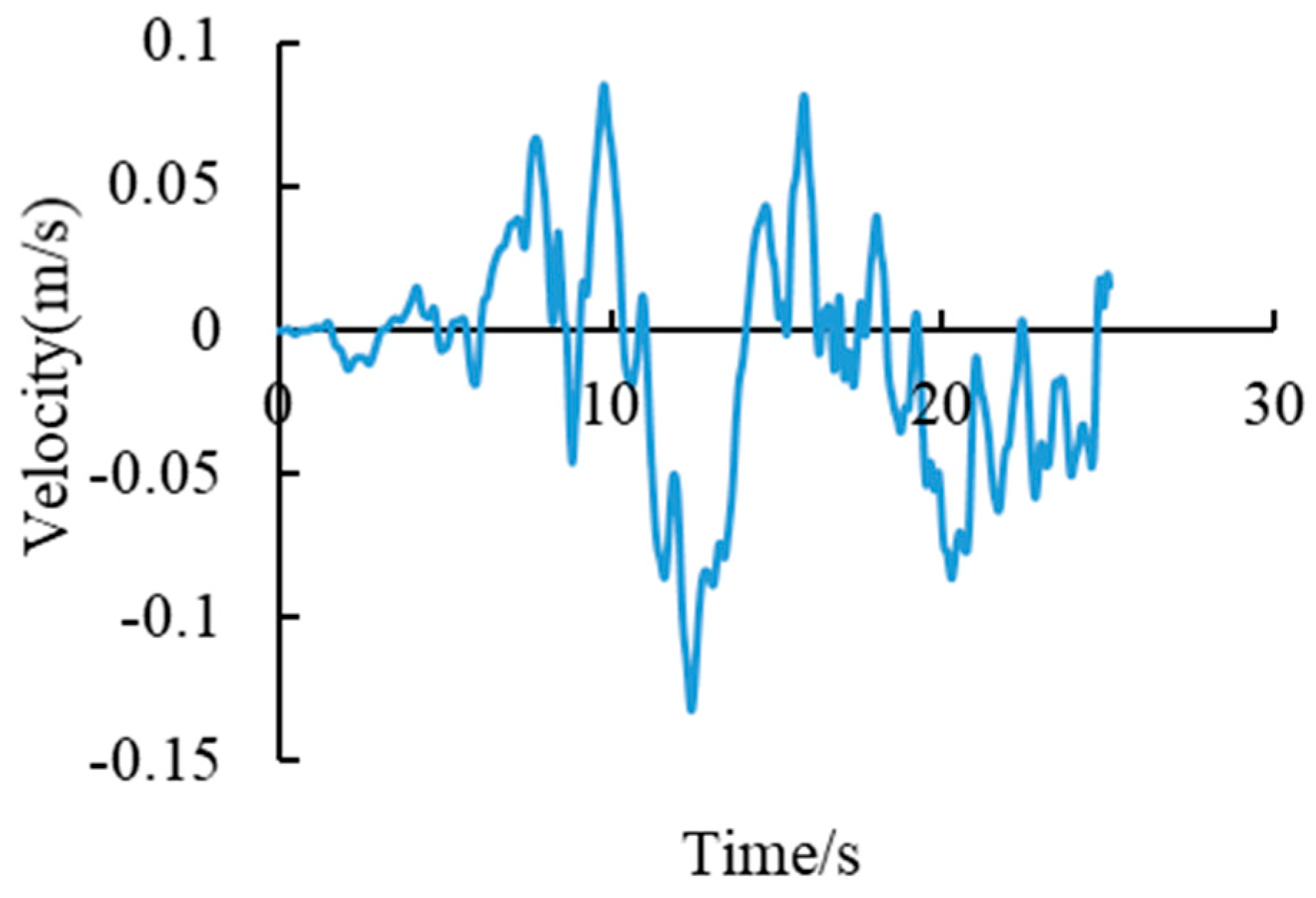
4.4. Mechanical Response of a Cross-Fault Tunnel under the Combined Action of Faulting Dislocation and Seismic Loading
4.5. Dynamic Response Analysis of the Wall Rock–Lining Contact Surface
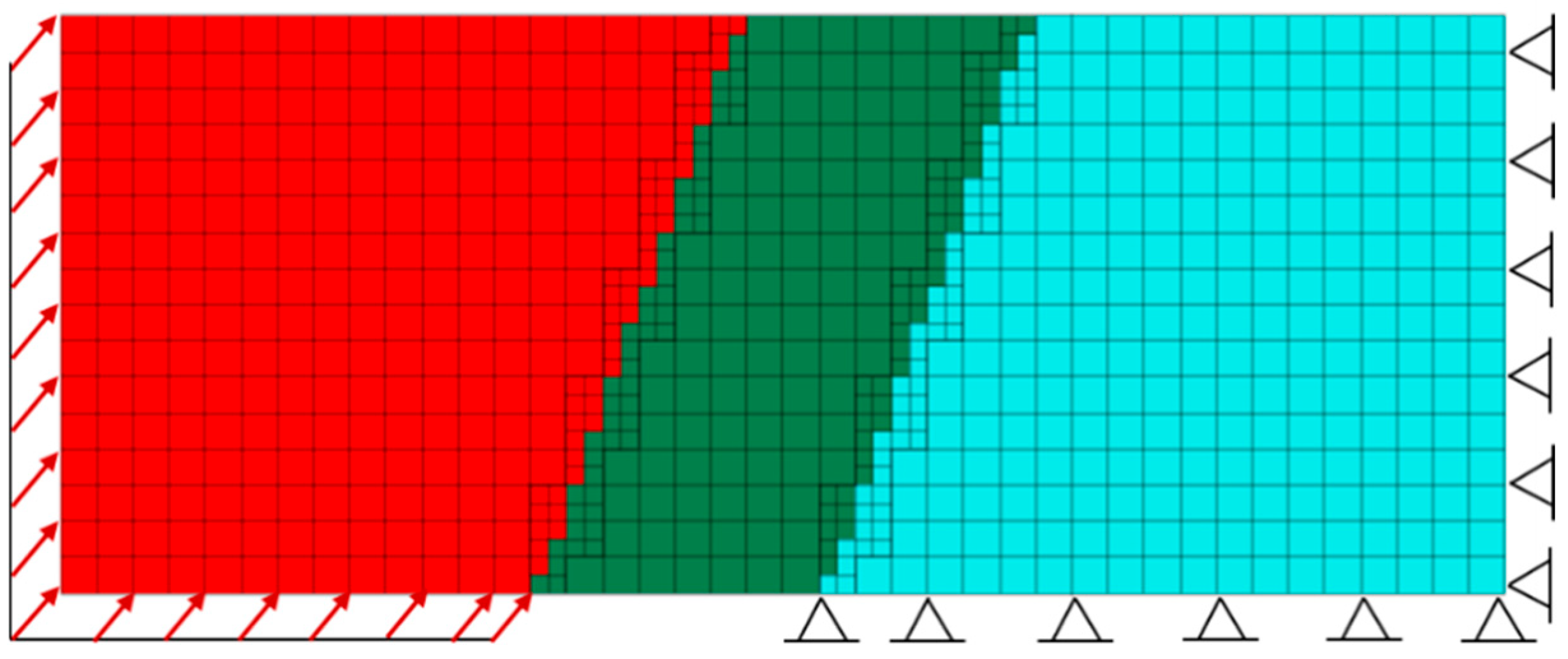
4.5.1. Effect of Different Fault Modes on the Dynamic Response of the Cross-Fault Tunnel
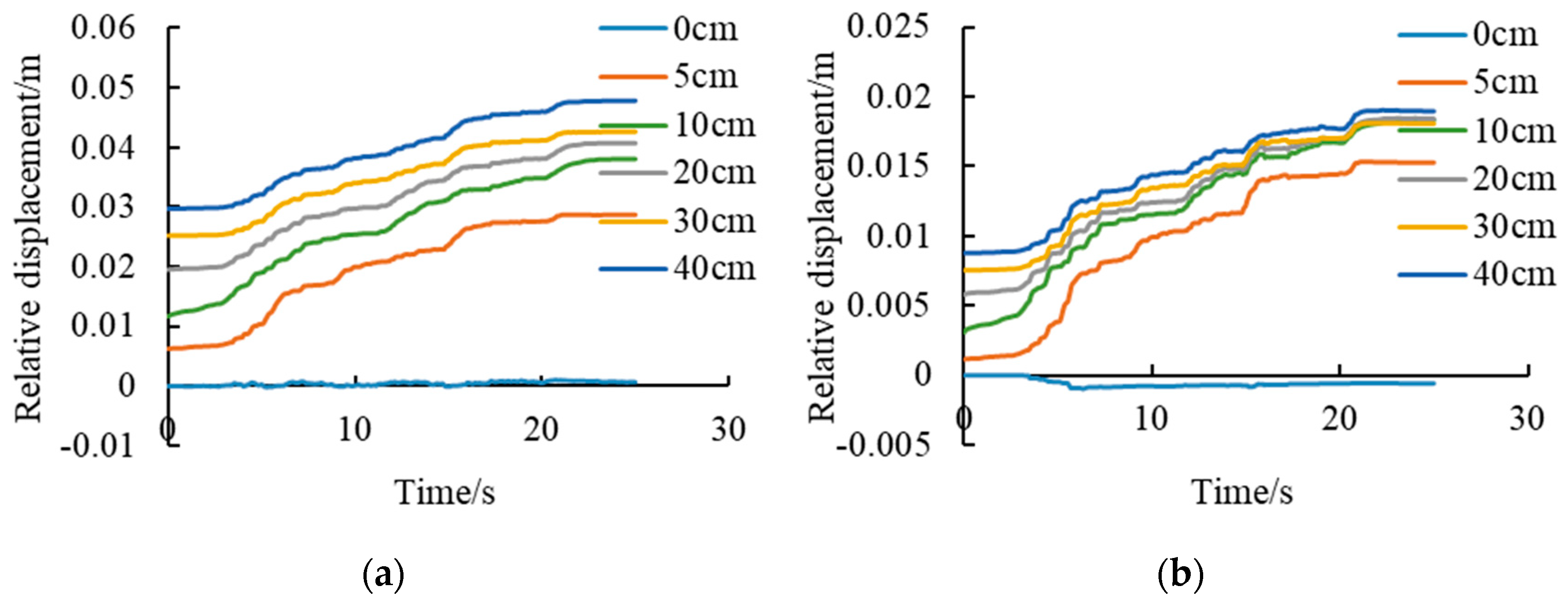
4.5.2. Effect of Different Initial Faulting Distances on the Seismic Response of the Cross-Fault Tunnel
4.6. Seismic Response of the Cross-Fault Tunnel after Initial Faulting Deformation
5. Conclusions
- (1)
- Numerical simulations with FDM software can reproduce the shear test of the wall rock–lining interface. The Coulomb model can better simulate the shear mechanical behavior of the wall rock–lining interface. Linear fitting of the pre-peak curve and simulation of the peak intensity are achieved.
- (2)
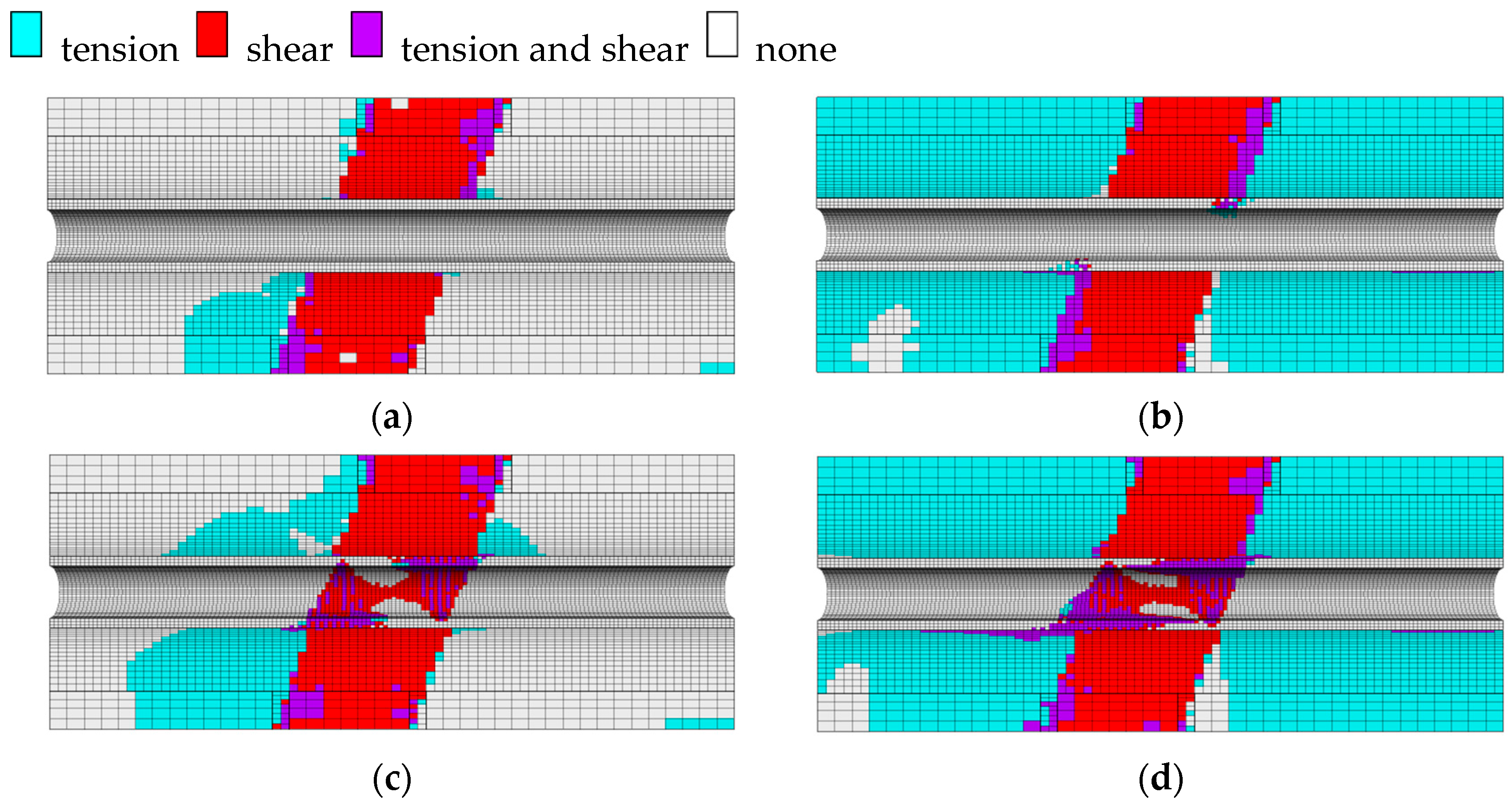
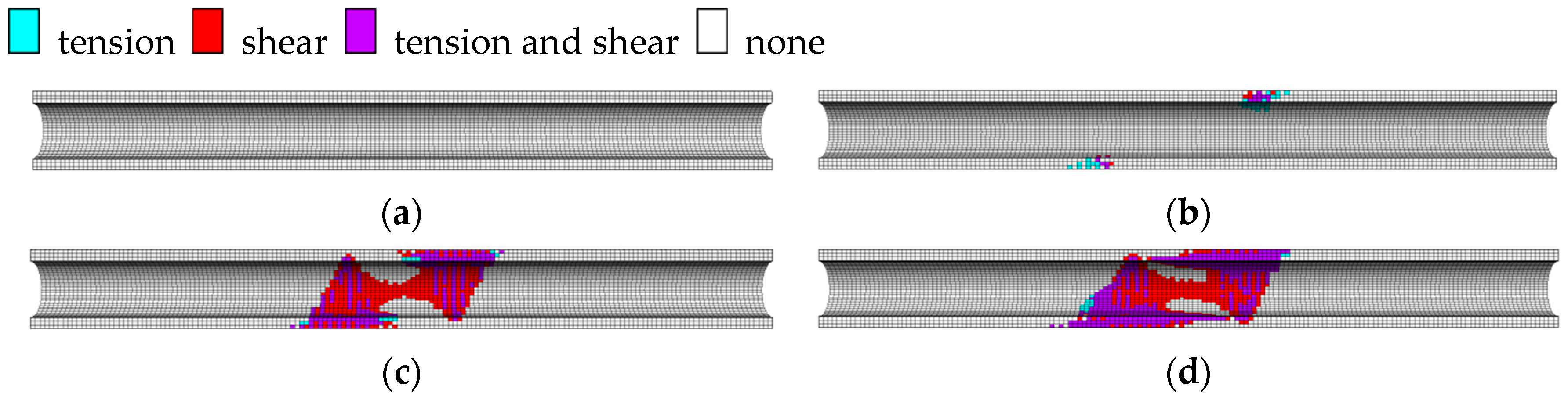
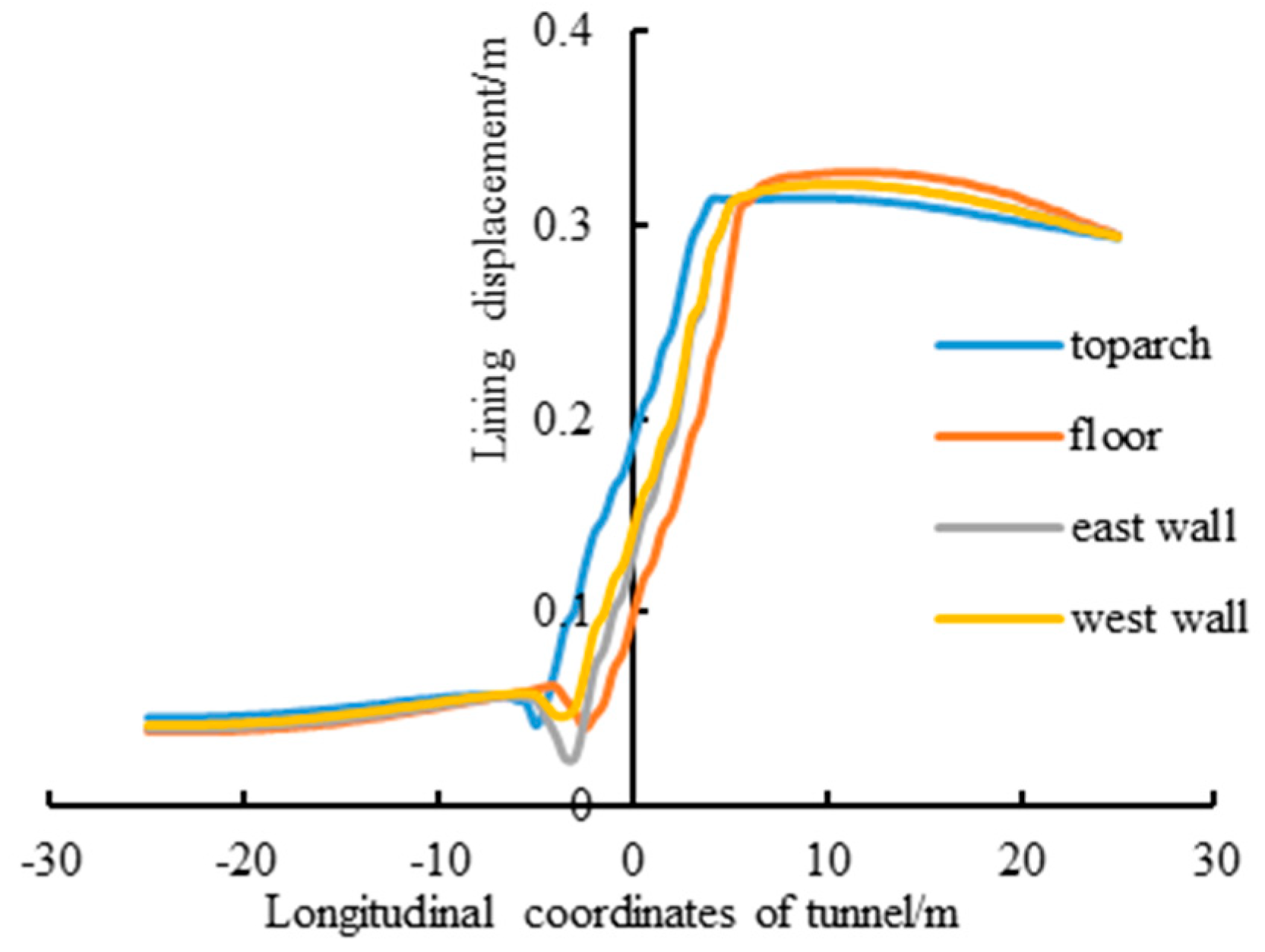
- In the seismic response of a cross-fault tunnel under the action of faulting dislocation and seismic loading, the magnitude of the initial faulting dislocation exhibits a significant effect on the relative deformation of the tunnel. The larger the initial faulting distance, the larger the permanent relative deformation and the more serious the tunnel damage. In addition, the responses of different parts of the tunnel are different. The failure of the concrete lining is mainly concentrated in the range of the fault fracture zone, and the main failure mode of the lining is shear failure. At the boundary between the fault fracture zone and the hanging and foot walls, the failure modes of the concrete lining are tensile and shear failure.
- (3)
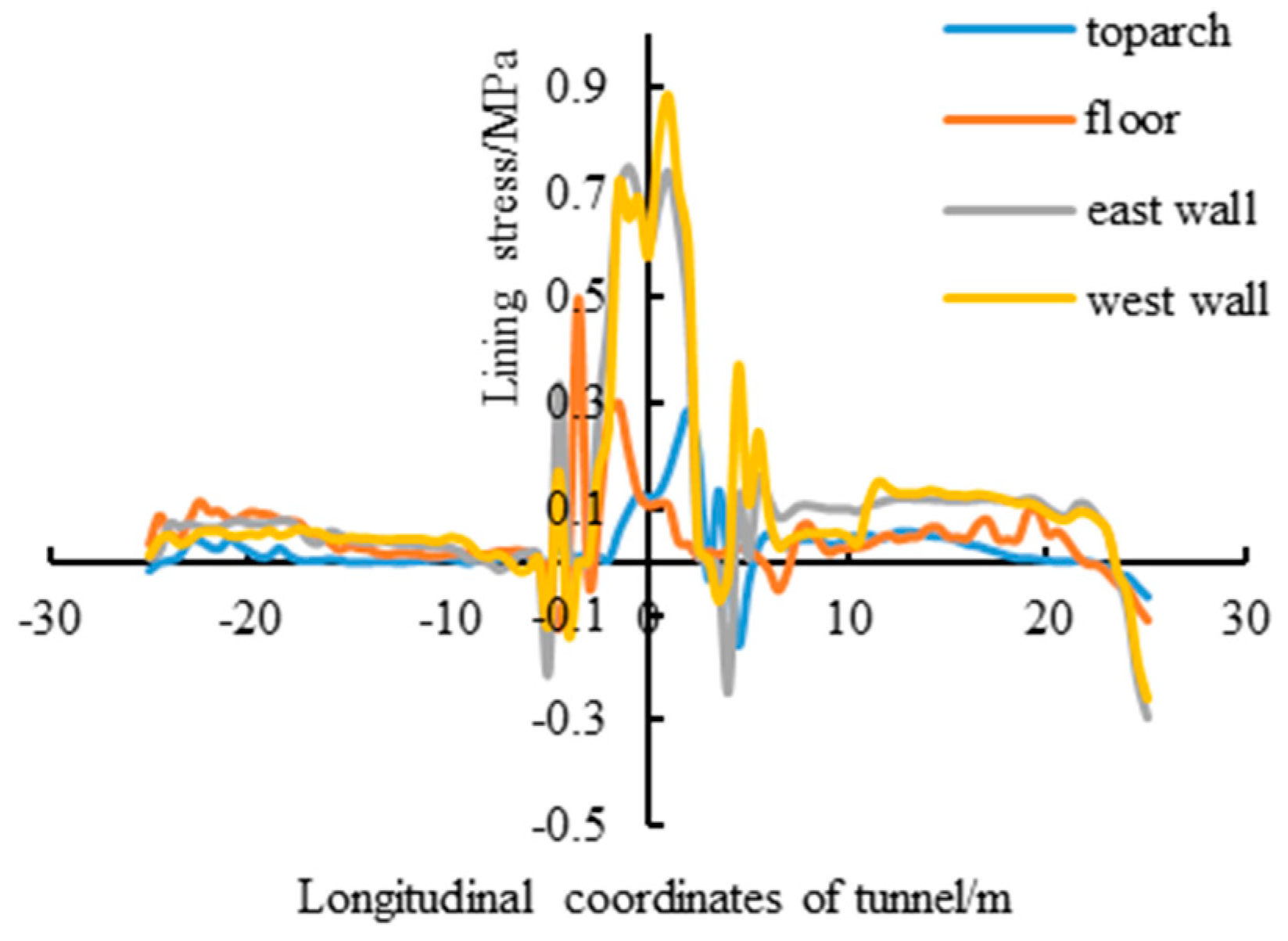
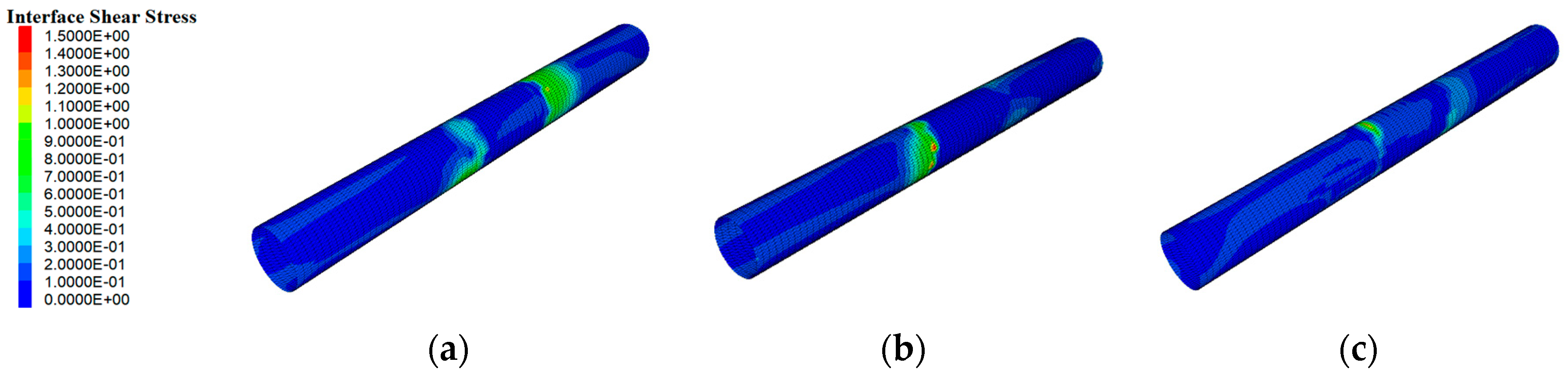
- The position of the maximum shear stress on the interface of the wall rock and tunnel lining is related to the fault mode. The maximum value of the shear stress is concentrated on the tunnel near the active fault side. The shear stress of the interface is smallest in the normal fault mode, and the shear stress in the reverse fault and strike–slip fault modes is larger. Considering the initial faulting damage, the relative deformation of the deformation of the tunnel located in the fault fracture zone increases with an increasing earthquake time.
- (4)
- The initial faulting dislocation of an active fault demonstrates an impact on the seismic performance of the lining structures. Therefore, in the region of the active fault distribution and areas with frequent earthquakes, it is necessary to consider the initial damage caused by the active fault and then carry out relevant seismic resistance studies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cui, Z.; Sheng, Q.; Leng, X.L. Control effect of a large geological discontinuity on the seismic response and stability of underground rock caverns: A case study of the Baihetan #1 surge chamber. Rock Mech. Rock Eng. 2016, 49, 2099–2114. [Google Scholar]
- Zhang, X.H.; Fu, P.; Yin, J.M.; Liu, K.Y. In-situ stress characteristics and active tectonic response of Xianglushan tunnel of Middle Yunnan Water Diversion Project. Chin. J. Geotech. Eng. 2021, 43, 130–139. [Google Scholar]
- Si, J.Z.; Zeng, Y.C.; Liu, J.B. Challenges and some thoughts on open-TBM construction in a railway tunnel with complex geologies. Tunn. Constr. 2021, 41, 433–440. [Google Scholar]
- Wang, R.B.; Wang, X.Y.; Zhang, W.Q.; Xu, W.Y.; Lu, J.B.; Xiang, T.B. Physical model experiment of external water pressure in lining surrounding rock of a deep tunnel with cross fault. J. Tsinghua Univ. (Sci. Technol.) 2024, 64, 1179–1192. [Google Scholar]
- Wang, W.D.; Li, J.Y.; Han, Z. Comprehensive assessment of geological hazard safety along railway engineering using a novel method: A case study of the Sichuan-Tibet railway, China. Geomat. Nat. Hazards Risk 2020, 11, 1–21. [Google Scholar] [CrossRef]
- Zhu, Y.T.; Niu, X.Q.; Tian, J.Z. A machine vision-based intelligent segmentation method for dam underwater cracks using swarm optimization algorithm and deep learning. Comput.-Aided Civ. Infrastruct. Eng. 2024, 1–13. [Google Scholar] [CrossRef]
- Shi, W.; Wang, R.; Wang, Q.Y. Research review of the response displacement method for aseismic design of underground structures. Sci. Technol. Eng. 2024, 24, 61–71. [Google Scholar]
- Zhuang, H.Y.; Wang, R.; Shi, P.X.; Chen, G.X. Seismic response and damage analysis of underground structures considering the effect of concrete diaphragm wall. Soil Dyn. Earthq. Eng. 2019, 116, 278–288. [Google Scholar] [CrossRef]
- Aygar, E.B.; Gokceoglu, C. Problems encountered during a railway tunnel excavation in squeezing and swelling materials and possible engineering measures: A case study from Turkey. Sustainability 2020, 12, 1166. [Google Scholar] [CrossRef]
- Hashimoto, S.; Fujino, Y.; Abe, M. Damage analysis of hanshin expressway viaducts during 1995 kobe earthquake. II: Damage mode of single reinforced concrete piers. J. Bridge Eng. 2005, 10, 54–60. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Gao, B.; Jiang, Y.J.; Yuan, S. Investigation and assessment on mountain tunnels and geotechnical damage after the Wenchuan earthquake. Sci. China Ser. E Technol. Sci. 2009, 52, 546–558. [Google Scholar] [CrossRef]
- Roy, N.; Sarkar, R. A review of seismic damage of mountain tunnels and probable failure mechanisms. Geotech. Geol. Eng. 2017, 35, 1–28. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Shi, C.; Li, T.B.; Yuan, Y. Damage characteristics and influence factors of mountain tunnels under strong earthquakes. Nat. Hazards 2012, 61, 387–401. [Google Scholar] [CrossRef]
- Tao, S.J.; Gao, B.; Wen, Y.M.; Zhou, X. Investigation and analysis on the seismic damage of mountain tunnels subjected to Wenchuan earthquake. Appl. Mech. Mater. 2011, 99–100, 273–281. [Google Scholar] [CrossRef]
- Xiong, W.; Fan, W.; Peng, J.B.; Deng, L.S.; Yan, F.Y. Numerical analysis of effect of normal fault activity on road mountain tunnel project. Chin. J. Rock Mech. Eng. 2014, 29 (Suppl. S1), 2845–2852. [Google Scholar]
- Caulfield, R.J.; Kieffer, D.S.; Tsztoo, D.F.; Cain, B. Seismic design measures for the retrofit of the Claremont tunnel. In Rapid Excavation and Tunneling Conference Proceedings; Society for Mining Metallurgy & Exploration: Englewood, CO, USA, 2005; pp. 1128–1138. [Google Scholar]
- Shahidi, A.R.; Vefaeian, M. Analysis of longitudinal profile of the tunnels in the active faulted zone and designing the flexible lining (for Koohrang-III tunnel). Tunn. Undergr. Space Technol. 2005, 20, 213–221. [Google Scholar] [CrossRef]
- Anastasopoulos, I.; Gerolymos, N.; Drosos, V.; Georgarakos, T.; Kourkoulis, R.; Gazetas, G. Behaviour of deep immersed tunnel under combined normal fault rupture deformation and subsequent seismic shaking. Bull. Earthq. Eng. 2008, 6, 213–239. [Google Scholar] [CrossRef]
- Mahsa, G.V.; Aliakbar, G.; Sina, M. Analysis of cylindrical tunnels under combined primary near fault seismic excitations and subsequent reverse fault rupture. Acta Geodyn. Geomater. 2017, 14, 5–26. [Google Scholar]
- Yang, Z.H.; Lan, H.X.; Zhang, Y.S.; Gao, X.; Li, L.P. Nonlinear dynamic failure process of tunnel-fault system in response to strong seismic event. J. Asian Earth Sci. 2013, 64, 125–135. [Google Scholar] [CrossRef]
- Zhou, J.Q.; Zhou, C.B.; Feng, Q.G.; Gao, T. Analytical model for load-transfer mechanism of rock-socketed drilled piles: Considering bond strength of the concrete-rock interface. Int. J. Geomech. 2020, 20, 04020059. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, C.; Zhao, C.F.; Wang, Y.B.; Fei, Y. Effect of grout conditions on the mechanical behaviors of unloading sand-concrete interface for reinforcing bored pile foundation. Constr. Build. Mater. 2020, 243, 118218. [Google Scholar] [CrossRef]
- Min, G.J.; Fukuda, D.; Oh, S.W.; Chung, M.; Cho, S.H. A numerical study on shear behavior of the interface between blasted rock and concrete. Explos. Blasting 2019, 37, 26–35. [Google Scholar]
- GB/T 50266-2013; Standard for Test Methods of Engineering Rock Mass. China Planning Press: Beijing, China, 2013.
- Xu, W.L.; Niu, X.Q.; Zhu, Y.T. Deformation behavior and damage evaluation of fly ash-slag based geopolymer concrete under cyclic tension. J. Build. Eng. 2024, 86, 108664. [Google Scholar] [CrossRef]
- GB/T 50218-2014; Standard for Engineering Classification of Rock Masses. China Planning Press: Beijing, China, 2014.
- GB/T 50010-2010; Code for Design of Concrete Structures. China Planning Press: Beijing, China, 2010.
- Zhang, C.Q.; Cui, G.J.; Deng, L.; Zhou, H.; Lu, J.J.; Dai, F. Laboratory investigation on shear behaviors of bolt-grout interface subjected to constant normal stiffness. Rock Mech. Rock Eng. 2020, 53, 1333–1347. [Google Scholar] [CrossRef]
- Mei, X.C.; Sheng, Q.; Cui, Z.; Zhang, M.C.; Chen, L.J. Seismic responses of an underground tunnel considering rock–tunnel interaction. Geotech. Eng. 2023, 176, 434–452. [Google Scholar] [CrossRef]
- Wu, L.T.; Gao, G.L.; Yu, J.; Zhou, F.T.; Yang, Y.; Wang, T.F. PDD: Partitioning DAG-Topology DNNs for Streaming Tasks. IEEE Internet Things J. 2024, 11, 9258–9268. [Google Scholar] [CrossRef]
- Oh, J.; Moon, T. Seismic design of a single bored tunnel: Longitudinal deformations and seismic joints. Rock Mech. Rock Eng. 2018, 51, 893–910. [Google Scholar] [CrossRef]






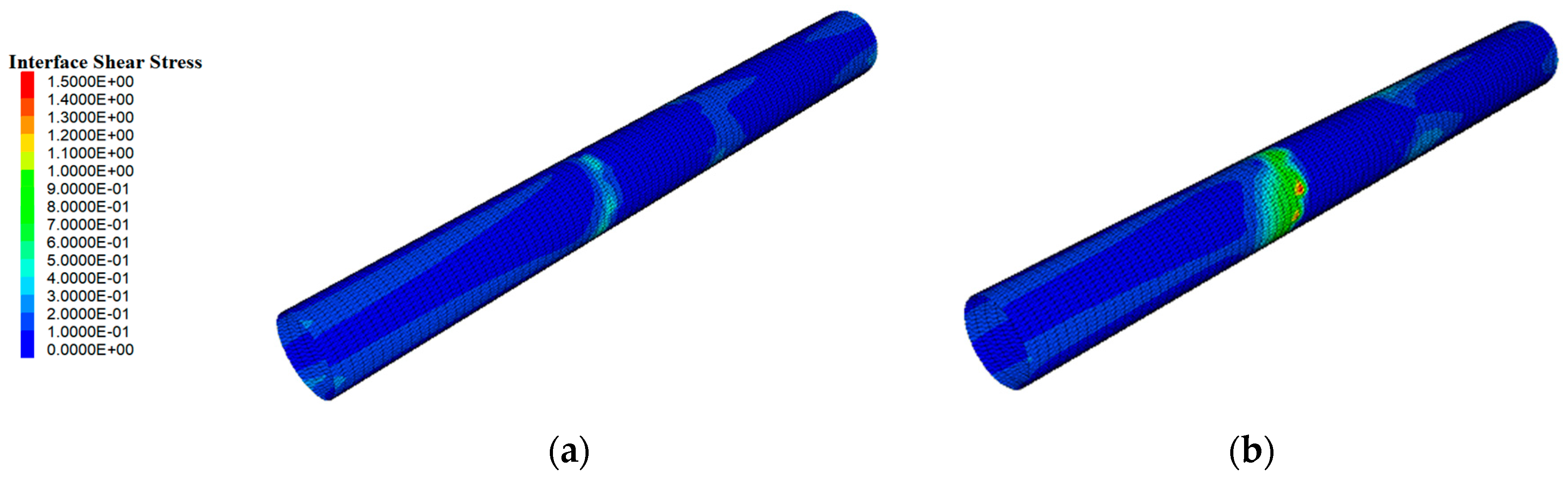
| Materials | Density (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Friction Angle (°) | Cohesion (MPa) | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|
| The wall rock | 1990 | 1.22 | 0.19 | 22 | 0.1 | 0.15 |
| The lining | 2324 | 23.77 | 0.18 | 54.9 | 3.16 | 2.0 |
| Specimen Type | (MPa) | (Tested) (MPa) | (MPa/mm) | (MPa/mm) | (Calculated) (MPa) |
|---|---|---|---|---|---|
| J1 | 0.5 | 0.85 | 1.53 | 0.20 | 0.85 |
| 1.0 | 1.21 | 3.05 | 0.26 | 1.21 | |
| 1.5 | 1.62 | 4.58 | 0.38 | 1.60 | |
| 3 | 2.84 | 9.15 | 0.26 | 2.86 | |
| 5 | 3.38 | 15.25 | 0.48 | 3.35 | |
| J2 | 0.5 | 1.04 | 1.92 | 0.21 | 1.20 |
| 1.0 | 1.69 | 3.84 | 0.31 | 1.69 | |
| 1.5 | 1.84 | 5.76 | 0.27 | 1.84 | |
| 3 | 2.88 | 11.52 | 0.43 | 2.86 | |
| 5 | 4.12 | 19.20 | 0.58 | 4.07 |
| Materials | Density (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Friction Angle (°) | Cohesion (MPa) | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|
| Hanging wall | 2650 | 3.0 | 0.3 | 37.26 | 0.55 | 0.25 |
| Foot wall | 2300 | 1.5 | 0.33 | 28.8 | 0.5 | 0.2 |
| Fault fracture zone | 2100 | 0.5 | 0.33 | 22 | 0.1 | 0.15 |
| Tunnel | 2500 | 25 | 0.2 | 54.9 | 3.16 | 2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Yan, T.; Cui, Z.; Li, J.; Xu, R. Mechanical Response Study of a Cross-Fault Water Conveyance Tunnel under the Combined Action of Faulting Dislocation and Seismic Loading. Water 2024, 16, 2876. https://doi.org/10.3390/w16202876
Zhang M, Yan T, Cui Z, Li J, Xu R. Mechanical Response Study of a Cross-Fault Water Conveyance Tunnel under the Combined Action of Faulting Dislocation and Seismic Loading. Water. 2024; 16(20):2876. https://doi.org/10.3390/w16202876
Chicago/Turabian StyleZhang, Maochu, Tianyou Yan, Zhen Cui, Jianhe Li, and Ran Xu. 2024. "Mechanical Response Study of a Cross-Fault Water Conveyance Tunnel under the Combined Action of Faulting Dislocation and Seismic Loading" Water 16, no. 20: 2876. https://doi.org/10.3390/w16202876
APA StyleZhang, M., Yan, T., Cui, Z., Li, J., & Xu, R. (2024). Mechanical Response Study of a Cross-Fault Water Conveyance Tunnel under the Combined Action of Faulting Dislocation and Seismic Loading. Water, 16(20), 2876. https://doi.org/10.3390/w16202876






