Abstract
Accurate forecasting in hydrologic modeling is crucial for sustainable water resource management across various sectors, where predicting extreme flow phases holds particular significance due to their severe impact on the territory. Due to the inherent uncertainties in hydrologic forecasting, relying solely on a single rainfall–runoff model may not provide reliable predictions. To address this challenge, over the years, researchers have developed and applied hydrologic forecast merging (HFM) techniques that combine multiple models or ensembles to enhance forecast accuracy, reduce uncertainty, and increase confidence in the forecast. This review summarizes the progress in HFM techniques since the early 1990s and covers developments and applications in flow simulation, uncertainty analysis, monthly and seasonal streamflow predictions, ensemble forecasts, flood forecasting, and climate change analysis. The findings indicate that while HFM techniques outperform individual models regarding forecasting efficiency, their performance across applications is not uniform. Among the different methods, Bayesian model averaging (BMA) is the most popular due to its ability to reduce uncertainty and provide accurate and reliable forecasts in deterministic and probabilistic simulations. With their application simplicity, regression techniques are also robust and efficient as they perform competitively well across different model-merging applications. While specific techniques, such as model-dependent weighted averaging and neural network methods, effectively reduce forecast uncertainty, there is still room for improving forecast accuracy across different lead times. Future research can focus on advanced HFM techniques for estimating optimal weights in time-varying domains and overcoming limitations, like simulating low flows in seasonally dry catchments.
1. Introduction
Hydrological models have long been recognized as valuable tools for obtaining hydrologic variables essential for effective water resource systems management, a crucial aspect of sustainable socioeconomic development [1]. Over the years, numerous hydrologic models, ranging from conceptually lumped to physically based distributed models, have been developed and employed for streamflow simulation and flood forecasting [2]. However, it is widely acknowledged that no single model can accurately represent all the governing processes of hydrological events in a catchment system due to their structural formation [3,4]. Each model has strengths and weaknesses, and their performance varies depending on temporal and spatial contexts [5].
This limitation has motivated hydrologists to explore alternative approaches to enhance hydrological forecasts. One such approach is merging multi-model forecasts, which have improved efficiency and robustness compared to relying on a single model or switching between models [6,7]. Merging different hydrologic models formulated by different states and parameters enables the representation of more various factors in watershed hydrology than the use of a single model, in turn leading to improved forecasting efficiency and reliability [8]. By combining the strengths of different models and considering their weaknesses, merging techniques aim to systematically reduce bias, determine each model’s contribution to the merged forecast, and assess the forecast uncertainty [9]. In general, the forecast merging technique can be represented by a simplified Equation (1) [4].
where, represents the merged streamflow forecast for the ith period, and denotes the forecasted streamflow of the jth model for the same period. The function combines the individual model forecasts.
Several steps need to be followed to perform forecast merging effectively, as shown in Figure 1. Firstly, the appropriate hydrologic models need to be selected based on the characteristics of the targeted watershed, such as catchment type, topography, climatic region, and data availability. Combining models, typically up to six members, has shown significant improvements in hydrological simulations [10]. The selected models are then calibrated and validated using historical observation data, establishing relationships between model parameters and watershed to optimize the fit between simulations and observations [11]. Once the models are calibrated and validated, forecasts are generated using predicted climate variables or historical observation data. Finally, the individual model forecasts are merged using Equation (1), providing an improved and more reliable forecast.
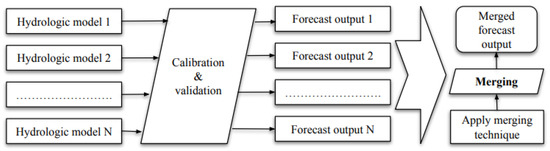
Figure 1.
Schematic diagram of the processes of hydrologic forecast merging (HFM).
Merging different hydrological model outputs has gained significant attention in the field of hydrology since the pioneering work of Cavadias and Morin in 1986 [12]. Their introduction of the merging concept using weighted averaging and multiple linear regression (MLR) methods showed improved forecast performance compared to individual models. Subsequent studies, such as McLeod et al. [13], confirmed the benefits of model output merging in streamflow forecasting. Since then, various merging techniques have been applied and compared in hydrologic applications [4,6,14,15,16,17,18,19,20]. The term “hydrologic forecasts merging (HFM)” in the literature has been used interchangeably with various expressions such as “rainfall–runoff model outputs combination”, “model combination”, “multi-model combination”, “multi-model averaging”, “multi-model ensemble averaging”, and “multi-model data fusion”. These terms all refer to combining simulations or predictions from multiple models to enhance forecast accuracy and reliability.
Five notable review papers have contributed valuable information on several HFM techniques. Jeong and Kim [21] focused on eight single-value streamflow forecast merging techniques, comparing them from theoretical and empirical perspectives to offer guidelines in technique selection. Li et al. [22] analyzed only four multi-model statistical postprocessing techniques commonly used in hydrometeorological ensemble forecasting. Han and Coulibaly [23] reviewed Bayesian forecasting systems (BFS), emphasizing advancements in Bayesian methods for flood forecasting. Zounemat-Kermani et al. [24] provided a machine-learning perspective on ensemble methods, examining their applications in various hydrological fields. Troin et al. [25] summarized and categorized model weighting approaches applied in weather and hydrological forecast aggregation without explaining their suitability for different hydrologic application purposes. However, these existing reviews did not cover the diverse hydrologic forecast merging techniques included in this review. This comprehensive review article aims to bridge several gaps left by previous review papers on HFM techniques. First, while previous reviews focused on specific subsets of HFM techniques (e.g., single-value streamflow forecast merging, Bayesian forecasting systems, machine learning perspectives, etc.), this article intends to cover a broader spectrum of HFM techniques. It aims to encompass a more diverse array of methods utilized in hydrology for merging forecasts, considering both single-value and multi-model approaches and addressing their relevance for short and long-term streamflow prediction. Second, prior reviews might have overlooked certain HFM techniques, possibly due to the evolving nature of methodologies or the limited scope of those particular reviews. This article seeks to encompass newer, emerging techniques that may not have been covered previously, ensuring a more comprehensive understanding of the range of methods available for hydrologic forecast merging. Third, while previous reviews might have discussed the methodologies and comparative analyses of techniques, this article intends to delve deeper into the practical applications of these diverse merging techniques within the field of hydrology. It aims to highlight the theoretical underpinnings or comparative analyses and the real-world applicability, advantages, limitations, and suitability of these techniques for different hydrologic forecasting purposes. Finally, besides consolidating existing knowledge, this review aims to identify and discuss emerging trends and directions in hydrologic research concerning forecast merging techniques. By doing so, it seeks to offer insights into where the field might be heading, considering advancements, innovations, or gaps that need further exploration in this domain.
For this comprehensive review, we collected published research works from 1986 to April 2023 by conducting keyword searches on the Web of Science and Scopus database. The search was refined through manual screening to focus on studies that specifically applied merging techniques to enhance streamflow predictions. In total, we reviewed 105 published research works, including 95 peer-reviewed journal articles, eight conference proceedings, one book chapter, and one thesis paper. The structure of the paper is as follows: Section 2 provides an overview of the advancement in merging techniques, highlighting their key features and developments, and a summary of the advantages and limitations of different HFM techniques, offering insights into their strengths and weaknesses. In Section 3, we present a comprehensive review of the literature on HFM applications, summarizing the studies that have utilized merging techniques to enhance streamflow predictions. Section 4 provides an overall discussion of the salient merging techniques reviewed. Finally, in Section 5, we present concluding remarks along with future research directions. For reference, a list of abbreviations used throughout the paper is provided in Abbreviations.
2. Overview of Advances in HFM Techniques from 1986 to 2023
With unprecedented advancements in computational power, the use of multi-model forecast merging has become increasingly popular as an alternative to model selection in various fields, including hydrology. Numerous techniques have been developed over the years, and different studies have categorized these techniques in different ways. Shamseldin et al. [19] noted that the HFM techniques found in the literature can be classified as linear or non-linear. Troin et al. [25] also identified two main types of weighting approaches: deterministic and probabilistic. Deterministic weighting approaches can further be classified as dynamic and static. In general, the HFM techniques can be categorized into three major groups: linear versus nonlinear, unweighted versus weighted, and point forecast versus probabilistic density forecast. Linear techniques include unweighted, weighted, and regression methods, while nonlinear techniques encompass neural networks, fuzzy theory-based systems, and genetic algorithm methods. The simple averaging method (SAM) falls under the unweighted or equally weighted category, where each available model is treated equally.
Conversely, all other techniques involve weighted averaging, with the sum of weights either constrained to unity or unconstrained [22]. The SAM and weighted averaging methods (WAMs) focus on point forecasts, whereas the Bayesian model averaging (BMA) and the quantile model averaging (QMA) methods are concerned with density predictions. BMA provides probabilistic forecasts and has been highly useful in practical applications [17]. Linear techniques are generally simpler, easier to apply, and less time-consuming than nonlinear ones. Both linear and nonlinear merging techniques have been shown to enhance the accuracy and reliability of simulated river flows [4,20,26].
The fundamental differences among HFM techniques lie in the approaches used for model weight quantification and bias removal [3,15]. For instance, techniques such as multi-model super ensemble (MMSE), modified multi-model super ensemble (M3SE), and weighted averaging assign different model weights based on their performance. In the case of weighted averaging, the constrained least-squares approach is applied to compute positive model weights [4], while MMSE and M3SE techniques estimate model weights using multiple linear regression [27]. Regarding bias correction, the weighted average does not consider any bias correction. On the other hand, MMSE and M3SE techniques remove bias by replacing the simulation mean with the observed mean or by utilizing a streamflow-frequency curve, respectively [15]. The development of HFM techniques for the past 38 years, from 1986 to 2023, is presented in Table 1. Additionally, regardless of the application types and conditions, the efficiency of different merging techniques applied for merging streamflow simulation is provided in Figure 2. This figure presents the application results from different studies in terms of non-dimensional statistical metric, Nash–Sutcliffe Efficiency (NSE).
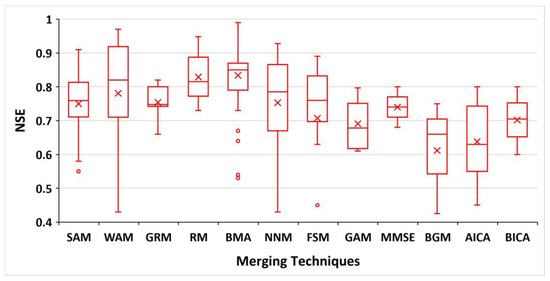
Figure 2.
The box plots of the performance of different HFM techniques. The cross signs within the box plots indicate the mean NSE value, while circles represent outliers.
2.1. Simple Averaging Method (SAM)
The SAM is a straightforward approach for merging forecasts and has been widely used in numerous studies [4,6,8,15,20,21,26,28,29,30,31,32,33,34,35,36,37]. In various studies, the SAM has been defined and implemented differently. These variations include methods such as simple arithmetic averaging [4], equal-weighted averaging (EWA) [38], and trimmed mean [39]. The simple arithmetic averaging distributes equal weights among hydrological models, mirroring the theoretical approach of EWA.

Table 1.
Summary of different categories of merging techniques and their advantages and limitations.
Table 1.
Summary of different categories of merging techniques and their advantages and limitations.
| References | HFM Categories | Method Developments 1 | Advantages | Limitations |
|---|---|---|---|---|
| [4,37] | Simple Averaging Methods | Simple arithmetic averaging or unweighted averaging: Merging without assigning any specific weight | Easy implementation and fair weights distribution among the merging models; Reduce forecast variances; At least better than the worst model | No bias correction steps; Equal treatment to all models; Ignores individual models forecast performance |
| [38] | EWA: Equal-weighted average of individual forecast | |||
| [39] | Mean: Merging without assigning any specific weight | |||
| [39] | Trimmed Mean: Trim outlier before averaging | |||
| [4] | Weighted Averaging Methods | WAM-CLS: Weighted average with unity sum of weights | Simple and understandable; High efficiency in weighting towards best models; RTMOCM suitable for real-time forecasts merging; RSWS can merge high, mid, and low flow; WAM-MOGWO can provide Pareto-optimal solutions that help uncertainty reduction | Multicollinearity and unstable weight estimates; Constrained weights lead to larger errors; Not suitable for highly correlated forecasts |
| [38] | WAM-RPS: Weighted average based on rank probability score | |||
| [40] | Granger and Newbold Methods: Weight estimation with (type 1) or without (type 2) correlations consideration | |||
| [41] | WAM-OLS: Weight estimation through multiple linear regression | |||
| [42] | RTMOCM: Linear Transfer Function Model integration | |||
| [43] | RSWM: Runoff-scale weighting with flow stages | |||
| [44] | WAM-MOGWO: Multi-objective grey wolf optimization for weighting | |||
| [41] | Granger and Ramanathan Methods | GRA: Ordinary least squares (OLS)-based weighting | Easy and quick implementation; Hedging against the use of bad model; Only GRC has bias correction steps | GRA cannot construct density forecasts; GRC sometimes produces unrealistic results |
| [41] | GRB: Weights are constrained unity | |||
| [41] | GRC: Weighting with a bias correction | |||
| [7] | Regression Methods | Constrained/Unconstrained-MLR: Based on constrained/unconstrained least square technique | Simplicity and interpretability; CCR does not need unbiased forecasts to be merged; SSE is suitable for time-varying model combination; CBP-MLR reduces attenuation bias and improves prediction over tails; Com-MLR improves forecast near median | Suffer from multicollinearity problem; Provide unstable estimates and consider no temporal dependence; CBP-MLR weights have larger variations; CBP-MLR degrades performance near the median |
| [8] | PLSR: Regression coefficient estimation using partial OLS | |||
| [31] | CCR: Bias correction with a constant term | |||
| [39] | PCR: Transfer predictor variable to orthogonal variables | |||
| [45] | SWR: Lagged forecast error and unbiased forecast | |||
| [46] | NGR: Gaussian mean as regression coefficient | |||
| [47] | CBP-MLR: Conditional bias incorporation for error reduction | |||
| [47] | Com-MLR: Weighted average of MLR and CBP-MLR | |||
| [2] | Bayesian Methods | EnBMA: Entropy-based BMA | Better performance for runoff extremes; BMA-WVC can capture different features of ensembles; Narrower uncertainty interval with CBMA; e-Bay can quantify uncertainty of deterministic forecast; QR-BMA corrects systematic biases of ensembles before merging; EnBMA is good for high flow forecasting; DSRC is suitable for error correction before merging ensembles by BMA; VR-LSTM can address the impact of ensemble types; BHMC can reduce non-systematic bias and is good for short-term forecasting | High computational complexity and long execution time; Depends on specific data distribution types and requires unbiased forecast; Provide wide and bimodal forecasts; Sometimes adds more weight to the worst performing model; Used fixed weights for merging ensemble for different forecast lead times; VB-LSTM is highly data-oriented; BMA-WVC performance is depended on specific wavelet |
| [9] | QR-BMA: Quantile regression-based BMA | |||
| [48] | BMA-LR: BMA in linear regression model | |||
| [48] | BMA-GLM: BMA in the generalized linear model | |||
| [49] | SBMC: Sequential addition of new information | |||
| [50] | BMA-WVC: BMA-based ensemble multi-wavelet Volterra coupled approach | |||
| [51] | CBMA: Copula function integrated BMA | |||
| [52] | HBMA: Hierarchical BMA for uncertainty segregation | |||
| [53] | CBP-BMA: Copula Bayesian Processor with BMA for PDF relaxation | |||
| [54] | (e-Bay) BMA: Ensemble-based dynamic Bayesian averaging | |||
| [55] | BMA-DSRC: BMA integrated with the dynamic system response curve | |||
| [56] | VB-LSTM: Regression-based Variational Bayesian Long Short-Term Memory | |||
| [57] | BHMC: Bayesian hierarchical model combination framework | |||
| [4] | Neural Network Methods | MLFFNN: Multi-layer feedforward type | Considers accuracy of each model; Maximizes the use of model information; WMLPNN uses multi-scale input data and captures temporal and spectral information; NNE can handle the non-linear nature of streamflow; ERNN is good for capturing flood peak times and peak flows | Computational complexity and time-consuming; Prone to overfitting Have limitations with non-stationary data; Limited extrapolation ability beyond training range; Highly data-oriented; Black-box in nature |
| [31] | ANN: Artificial type architecture | |||
| [58] | SNN: Simple neural network | |||
| [58] | RBFNN: Based on radial bias function | |||
| [58] | MLPNN: Based on multi-layer perceptron | |||
| [59] | WMLPNN: Wavelet-based multi-layer perceptron type | |||
| [60] | BPNN: Based on the backpropagation network | |||
| [61] | NNE: Based on an ensemble of networks | |||
| [62] | ERNN: Based on an ensemble of recurrent networks | |||
| [20] | Fuzzy System Methods | TS1: First-order Takagi-Sugeno approach | Nonlinear and flexible combination; Logical and scientific approach; ANFIS is particularly suitable for flood extreme estimation; Can handle model uncertainty | Computational complexity; Uninterpretable inside mechanism; Risk of overparameterization; Black-box in nature; Highly data-oriented |
| [34] | FSM: Possibilistic fuzzy logic approach | |||
| [34] | ANFIS: Neuro-integrated fuzzy logic approach | |||
| [36] | BFM: Bayesian integrated fuzzy logic approach | |||
| [63] | FUCEP: Fuzzy C-regression-based approach | |||
| [64] | Genetic Algorithm Methods | GEP: Gene expression-based programming | It is simple to implement, Non-linear in nature, and suitable for streamflow prediction | No guarantee of optimal solution; Difficulties with multi-objective optimization |
| [65] | GAM: Genetic algorithm-based approach | |||
| [66] | Quantile Methods | QMA: Quantile-based approach | Provide narrow, smooth, and unimodal distributions | Limitations due to number of models and sample size |
| [67] | QM: Quantile mapping based approach | |||
| [27] | MMSE | MMSE: Ordinary least square algorithm-based approach | Has bias correction and variance reduction procedure | Sometimes produce unrealistic results |
| [68] | M3SE: Bias removal step added to MMSE | |||
| [6] | Other methods | SCA: SCE-UA algorithm-based approach | Well suited for hydrological variables | Have convergence issues |
| [21] | SSE: Squared of errors-based approach | Useful to estimate time-varying average | Not suitable for operational forecasts merging | |
| [35] | InvR: Inverse variance ranking-based approach | Robustness to the peak values | Dependent on the model rank | |
| [63] | MBEM: Ensemble boosting-based approach | Good for non-linear prediction | Challenging with parameter tuning | |
| [63] | OK: Ordinary Kriging-based approach | Provides prediction uncertainty bounds | Have boundary effects | |
| [69] | BGA: Based on variance-covariance | Fair distribution of weights among ensembles | No bias correction steps | |
| [70] | AIC: Akaike information-based approach | Suitable for the multi-input averaging | Bias toward the best model and neglect of others | |
| [71] | BIC: Bayes information-based approach | Suitable for the multi-input averaging | Bias toward best model and neglect others | |
| [72] | REA: Reliability factor-based approach | Emphases on the convergent projection of the future | Provides a larger uncertainty range | |
| [73] | SGB: Stochastic boosting-based approach | Easy to implement due to regression in nature | Prone to overfitting Limiter interpretability | |
| [74] | MMA: Mallow’s criteria-based approach | Can handle model correlation | Depends on model selection criteria | |
| [75] | KDE: Kernel density-based approach | Adaptability to any number of models | Issue with proper bandwidth selection | |
| [75] | Pooled: Linear pooling-based approach | Weight adjustments among models | Sensitive to peak values | |
| [76] | BLP: Beta-based linear pooling approach | Robustness to the peak values | Have limitations with non-gaussian data distributions | |
| [77] | GCV: Cross-validation type approach | Unbiased estimation of prediction error | Consider a constant variance across all data points | |
| [78] | BM: Binomial coefficient-based approach | Weights are adjusted at each prediction moment | Numerical instability for a large number of values |
Note: 1 Elaboration of abbreviations is provided in Abbreviations.
As a result, these terms can often be used interchangeably. In the trimmed mean approach, instead of using all the available forecasts, a subset of the forecasts is selected based on certain criteria, such as excluding outliers or models with poor performance. Compared to other techniques, the SAM requires minimal effort and does not involve empirical curve fitting. It provides merged forecast outputs that are better than the worst individual forecast in terms of accuracy [21,79]. In several studies, the performance of SAM varies from 0.72 (25th percentile) to 0.82 (75th percentile) with a mean value of 0.75 in terms of NSE metric (Figure 2). The accuracy of the SAM depends on the forecasting performance of the member models included in the combination [4,80]. Consequently, applying the SAM can help avoid having the worst-performing model in the merging process when information about the members is unavailable [21].
2.2. Weighted Averaging Method (WAM)
Several studies in literature investigated the WAM for forecast merging over the past few decades [4,12,15,16,20,21,33,34,37,81]. The WAM is employed when SAM is proven inefficient due to specific individual models consistently outperforming others [82]. Compared with SAM, application results reveal a higher spread of the WAM performance with a mean NSE value of 0.77 (Figure 2). There are different approaches to determining the weights in WAM. Granger and Newbold 1977 [40] introduced two forms of weighted averaging, with or without considering correlations between the model residuals. Granger and Ramanathan [41] applied MLR using an ordinary least squares approach (WAM-OLS) to estimate weights. Shemseldin et al. [4] used the constrained least squares approach (WAM-CLS) to address the weight summation equal to 1. Additionally, there are other variations of WAM proposed in the literature. The Real-Time Model Output Combination Method (RTMOCM), introduced by Shamseldin et al. in 1999 [42], utilizes a linear transfer function model (LTFM) with an updating procedure to provide updated merged streamflow forecasts. The Runoff-Scale Weighting Method (RSWM), proposed by Hsie et al. [43], modifies the weights based on the simulated or forecasted flow scale in the hydrologic models to consider high, middle, and low flows in the merging process. Furthermore, Devineni et al. [38] proposed the WAM-RPS method, where combination weights are calculated based on the rank probability score (RPS), and Guo et al. [44] introduced the WAM-MOGWO approach, utilizing a multi-objective grey wolf optimization (MOGWO) algorithm to determine optimal weights for the combination.
2.3. Granger Ramanathan A, B, and C (GRA, GRB, and GRC) Methods
The Granger–Ramanathan A, B, and C forecast merging techniques were initially introduced in economics by Granger and Ramanathan in 1984 [41]. However, these techniques have gained significant popularity in hydrology in recent years, as evidenced by their applications in various studies [6,17,28,83]. The GRA approach utilizes the OLS method to calculate weights for merging forecasts. It aims to minimize root mean square error (RMSE) without correcting biases. On the other hand, the GRB approach also employs the OLS method to calculate weights for merging forecasts. However, in GRB, the weights are constrained to sum up to unity. This constraint ensures that the merged forecast values maintain a proportional relationship with the individual forecasts. In contrast to GRA and GRB, the GRC approach allows for unconstrained weights. Similar to previous techniques, the GRC method utilizes the OLS for weight calculation. Additionally, GRC incorporates a bias correction step to the merged forecast values. This correction helps in addressing any systematic biases present in the individual forecasts. The Granger-Ramanathan methods perform equally to SAM as their performance is comparable to each other in different applications (Figure 2).
2.4. Regression-Based Methods
Regression-based techniques have gained popularity in multi-model forecast merging due to their ease of implementation and higher performance (mean NSE value around 0.83) compared to simple or weighted averaging methods (Figure 2). One commonly used method is the MLR method, which has been widely applied in various studies [12,26,29,31,47,84]. Two variations of MLR methods are Constrained MLR and Unconstrained MLR. In Constrained MLR, the weights of individual forecasts are constrained to sum up to 1. Granger and Ramanathan [41] proposed a form of regression method called constant-coefficient regression (CCR), which incorporates a constant term to correct bias in the forecast. In CCR, it is not necessary for all individual forecasts in the combination to be unbiased [31]. Deutsch et al. [45] introduced switching regression (SR) merging techniques based on two fundamental assumptions.
The assumptions involve using lagged forecast errors from individual models and the requirement for individual forecasts to be unbiased. The non-homogeneous Gaussian regression (NGR) method [46] utilizes MLR for linear variables such as streamflow and logistic regression for binary variables to merge ensembles. In this method, the regression coefficients represent the predictive Gaussian mean, and the predictive variance is derived linearly from the variance of ensemble members. Another method, the principal component regression (PCR) [39], combines principal component analysis (PCA) and MLR. PCR addresses the issue of multicollinearity in MLR by transforming predictor variables into orthogonal variables called main components [39]. These components can be derived from linear combinations of prediction variables or through OLS regression. Another regression method, like PCR, is partial least square regression (PLSR) [8], which generates uncorrelated new predictors from original predictor variables using linear combinations to obtain a vector of estimated regression coefficients [8]. While MLR is attractive due to its simplicity and interpretability, it can have detrimental effects on extreme value estimation due to conditional bias [65]. Conditional bias-penalized MLR (CBP-MLR) and Composite MLR (Com-MLR) are techniques that can mitigate these issues [47]. CPB-MLR can reduce a linearly weighted sum of squared errors by incorporating conditional bias, while Com-MLR is defined as the linearly weighted average of MLR and CBP-MLR. Overall, regression-based techniques, including MLR and its variations, provide a straightforward approach for merging multi-model forecasts. However, care should be taken to address biases and extreme value estimation challenges.
2.5. Bayesian Methods
Bayesian methods are widely utilized as forecast merging techniques in numerous studies [8,17,22,32,35,36,51,66,67,83,85,86,87,88,89]. A prominent method within Bayesian modeling is BMA, introduced by Raftery et al. in 1997 [48]. BMA is a statistical method that provides probabilistic density forecasts, offering a more skillful and reliable description of the predictive uncertainty compared to the original ensemble members produced by individual models [32,90]. It has become immensely popular in hydrologic forecast merging. It simultaneously improves forecast efficiency and reduces uncertainty resulting from model structure. BMA determines the weights of each model using probability distribution functions (PDFs). This estimated weight can be used for both deterministic and probabilistic streamflow forecasting. The application results from several merging studies show that BMA performance varies between 0.78 and 0.86 in terms of NSE for the 25th and 75th percentile, respectively (Figure 2). In the classical BMA approach, model weights are based on posterior model probability [91,92]. However, in the mixture model, BMA calculates weights using the maximum likelihood function [90]. The expectation-maximization (EM) algorithm is commonly employed to maximize the likelihood, although global convergence is not guaranteed. To address this issue, Vrugt et al. [93] applied Differential Evolution Metropolis (DREAM), a Markov Chain Monte Carlo (MCMC) algorithm, to estimate BMA weights and variance. BMA-MCMC can handle various BMA predictive distributions. The DDS optimization algorithm has also been found to be comparable with the EM algorithm when combined with BMA [94]. One inherent characteristic of BMA is that its weight parameters are time-invariant. Moradkhani et al. [49] proposed the Sequential Bayesian Model Combination (SBMC) method, which allows for the recursive updating of models’ posterior probability by incorporating new information. Another variant, the Bayesian Hierarchical Model Combination (BHMC), introduced by Ossandon et al. [57], includes different lead times of hydrometeorological forecasts as covariates in the second layer of the hierarchy. Tsai and Elshall [52] developed hierarchical BMA (HBMA) for segregating, prioritizing, and evaluating different uncertainty sources using a BMA tree. The classical BMA assumes a Gaussian predictive distribution of forecast PDFs. Madadgar and Moradkhani [51] modified the BMA scheme by introducing CBMA, which employs the copula function, a group of multivariate functions, to postprocess hydrologic forecasts and generate streamflow probability distributions. This modification reduces reliance on parametric distribution assumptions and significantly mitigates bias in the original estimates, eliminating the need for external bias correction methods.
In 2020, Darbandsari and Coulibaly [2] proposed the entropy-based BMA (EnBMA) method, which estimates predictive distribution using entropy information gathered from individual members of multi-model streamflow forecasts. Several complex BMA-based merging methods have also been developed and applied, such as integrating BMA and data assimilation for uncertainty reduction [95], BMA-based ensemble multi-wavelet Volterra approach (BMA-WVC) for uncertainty reduction [50], Copula Bayesian Processors with BMA (CBP-BMA) for uncertainty analysis [53], Ensemble-based dynamic Bayesian averaging approach (e-Bay) for uncertainty quantification [54], Quantile regression-based BMA (QR-BMA) for bias correction and enhanced forecasting [9], Regression based Variational Bayesian Long Short-Term Memory network (VB-LSTM) to address the impact of ensemble members [56]. BMA is integrated with a dynamic system response curve (BMA-DSRC) [55]. These methods aim to further enhance the performance and capabilities of multi-model combinations using BMA.
2.6. Neural Network Methods (NNM)
Neural network methods (NNM) are powerful and widely used tools for time series prediction or pattern recognition. These methods utilize neural network (NN) structures that can map inputs to network outputs through non-linear functions. One commonly used artificial neural network (ANN) [21] structure is the multi-layer feedforward neural network (MLFFNN), which consists of three layers: an input layer, an output layer, and a single hidden layer between them. As a transfer function, logistic function, bipolar function, hyperbolic tangent function, arctan function, and scaled arctan function have been coupled with MLFFNN for merging discharge estimates [4,19]. For multi-model combination, several other neural network structures, such as simple neural network (SNN), radial bias neural network (RBNN), and multilayer perceptron neural network (MLPNN), were also introduced by Shamseldin et al. in 2007 [58]. Back-Propagation Neural Networks (BPNNs) were introduced by Li et al. in 2018 [60].
Furthermore, the MLPNN method coupled with wavelet transformation (WT) for combining the outputs of different rainfall–runoff models have been introduced by Shoaib et al. [59]. While MLFFNN and MLPNN share similarities, they differ from radial bias neural networks (RBFNN) regarding the mathematical operations of transforming neurons from the input to the output layer. RBFNN has a single hidden layer, while MLFFNN and MLPNN can have multiple hidden layers. BPNN, on the other hand, is a multi-layer-feed-forward type structure trained using both forward and error backpropagation algorithms, with each layer’s state influenced only by the state of the next layer. Another approach is the neural network ensemble (NNE) method, where the network structure is like the multi-layer-feed-forward type. However, the topology and iteration number are determined through a trial-and-error process, and a sigmoid activation function is used for the hidden and output layers [61].
Additionally, the ensemble recurrent neural network (ERNN) structure has been applied as a forecast merging technique, particularly suitable for overcoming the influence of initial conditions on model parameter optimization and reducing output uncertainty [62]. In different studies, NNMs perform differently as merging methods based on its network structure. The results presented in Figure 2 show that the 25th percentile performance of NNM is around 0.66 (in terms of NSE), although the mean value is comparable to SAM, WAM, and GRM.
2.7. Fuzzy Theory-Based Methods
Fuzzy theory has found widespread use in hydrology due to its ability to describe the properties and relationships of hydrological objects in a scientifically logical manner. Many studies [20,34,36,84,96] have employed fuzzy theory in hydrological research. Two main fuzzy approaches, the Mamdani approach [97] and the Takagi–Sugeno approach [98], are commonly used for hydrologic forecasting. The first-order Takagi–Sugeno Fuzzy system (TS1) has been tested as an HFM approach to improve forecast accuracy [20,84,96]. Hybrid techniques have been explored in search of new merging techniques for further improvement in hydrologic forecasting. For example, integrated Bayesian fuzzy logic [36] and adaptive neuro-fuzzy inference system (ANFIS) [34] have been applied. Nasseri et al. [63] proposed a fuzzy-based merging method called Fuzzy C-means ensemble based on data pattern (FUCEP). This method combines two cluster-based approaches: Fuzzy C-Regression and uncertainty estimation based on local errors and clustering. Although fuzzy methods have succeeded in many applications, their mean NSE performance is close to 0.7 (Figure 2).
2.8. Genetic Algorithm Methods (GAM)
GAM is a bioinspired calculational technique that utilizes the principle of genetics and natural evolution for optimization. GAM requires adaptive functions that include logarithmic, exponentiation, fraction, and exponential functions [81]. These adaptive functions play a crucial role in determining the fitness of each solution during the evolution process. Another approach for forecast merging is gene expression programming (GEP) [18], which is based on symbolic regression. In GEP, a genetic algorithm is applied to solve symbolic regression problems, which involve finding mathematical expressions that fit given input-output patterns [64]. A limited number of studies (e.g., [2]) utilized the GAM method in streamflow forecast merging applications because of its performance compared to other methods (Figure 2).
2.9. Quantile Methods
The QMA method was employed by Schepen and Wang [66] to merge ensemble statistical and dynamic forecasts, as well as by Muhammad et al. [67] for statistical post-processing in multi-model ensemble forecasting. In the QMA methods, the model weights are determined in such a way that they sum up to unity. These weights are estimated using a maximum posteriori approach, which can be found with a numerical search method. For instance, Schepen and Wang [66] utilized Brent’s univariate search method in their application. Another similar approach is quantile mapping (QM), which involves mapping the cumulative distribution function (CDF) of the ensemble forecasts based on the CDF of observation. However, one of the main limitations of QM is its inability to maintain the relationship between each pair of forecasts and observations.
2.10. Multi-Model Super Ensemble (MMSE) Methods
The MMSE approach, proposed by Krishnamurti et al. [27], is applied in hydrometeorological forecast merging. This approach is based on the OLS algorithm and aims to reduce bias and variance in the merged forecast streamflow from multiple member models. This method was effective, with a mean NSE value of 0.74 (Figure 2) for global streamflow simulation [10]. The modified super ensemble (M3SE) technique [68] is similar to MMSE, with the main difference lying in the bias removal step. In MMSE, bias correction is achieved by substituting the average of the simulation with the average of the observed streamflow. On the other hand, M3SE incorporates bias correction by mapping model simulation at each time step to the observed streamflow using a frequency curve. This ensures that the bias-corrected hydrologic variables are statistically in good agreement with the observations.
2.11. Other Methods
The Bates and Granger Averaging (BGA) method minimizes RMSE between model simulations and actual observations [69]. While the method uses the reciprocal of member variance to determine optimal weights, its aggregated forecast may not optimally represent ensemble information. However, its performance in hydrologic forecasting typically falls below par, with a mean NSE value of 0.61 (Figure 2). Akaike Information Criteria (AIC) [70] and Bayes Information Criteria (BIC) [71] averaging methods effectively integrate individual forecasts, considering performance and model complexity [6,17,28,82,99]. These methods combine forecasts accounting for their respective performance and complexity levels, resulting in a merged forecast that capitalizes on ensemble members’ information [83]. Utilizing a reliability factor based on historical and future convergence, the Reliability Ensemble Averaging (REA) [72] method ensures more reliable models contribute significantly to the merged forecast [86,100,101]. Particularly suitable for handling uncertainty in probabilistic forecasting, it improves forecast performance by weighting models based on their reliability [100]. Stochastic Gradient Boosting (SGB) [73], an iterative regression analysis technique, minimizes total error by merging weighted outputs. This method effectively amalgamates model predictions to obtain the ultimate predicted value. By minimizing squared error through the Mallows criterion while considering model complexity, Mallows Model Averaging (MMA) [74] strikes a balance between accuracy and complexity, optimizing the combination of different models for a merged forecast. Combining a traditional linear pool with beta transform, Beta-Transformed Linear Pool (BLP) [76] merges forecast cumulative density functions by assigning weights based on each model’s contribution. The beta transform enhances the merging process by capturing additional forecast density characteristics. Several other methods like Inverse Ranking (InvR) [35], Sum of Squared Error (SSE) [21], Kernel Density Estimator (KDE) [75], Pooled Method [75], Modified Bootstrap Ensemble Modeling (MBEM) [63], Ordinary Kriging (OK) [63], Generalized Cross Validation Score (GCV) [77], and the binomial-based method [78] have been employed to enhance hydrologic forecast performance. Their practical implementation showcases varying degrees of effectiveness, as demonstrated in specific cases, as explained in Section 3.
2.12. Advantages and Limitations of HFM Techniques
Different merging techniques in hydrologic forecasting have various performance characteristics depending on the evaluation criteria used. A report of the advantages and limitations of different HFM techniques is presented in Table 1; however, some important aspects are described in this subsection. The SAM offers benefits such as easy implementation and reduced forecast error variance [21]. However, it treats good and bad simulations equally, resulting in underperformance compared to the best individual model [10]. The WAM gives more weight to the best models and generally provides high performance [17]. Conversely, it can suffer from multicollinearity and large forecast errors when weights are constrained, and it is not suitable for highly correlated forecasts [17,21,102]. Bayesian methods (e.g., BMA) are considered reliable and accurate, particularly when ensemble member performance is low [6]. BMA can reflect wide uncertainty and bimodal bands in forecasts, while the QMA provides unimodal forecasts that are easily interpreted [66]. Nonetheless, the CBMA model (i.e., modified BMA) shows exceptional ability to remove bias and produces narrow uncertainty intervals [51]. The MLR is a simple and interpretable method but shares the multicollinearity problem with the WAM. It does not consider temporal dependence and lacks uncertainty information [47]. Regression-based techniques like MMSE and M3SE outperform individual models; however, they are vulnerable to multicollinearity and perform poorly with small sample sizes [10,15]. GRA, GRB, and GRC allow negative weights and can protect against poorly performing models [17]. GRC is considered the best overall performer among GRA, GRB, and GRC due to its ease of implementation, speed of execution, and accuracy [6].
AIC and BIC averaging techniques are also robust and efficient but perform slightly less than BMA [6]. BGA and EWA are middle-of-the-road methods that distribute weights more uniformly [10]. NNM is generally superior to linear weighting and fuzzy-based methods. It considers the accuracy of each model and yields consistent results [59,60]. However, NNM can be prone to overfitting and has limited extrapolation capabilities [6]. Fuzzy systems are effective and robust for real-time river flow forecasting but have high computational complexity and can be overparameterized [20,96]. The choice of merging methods depends on the specific requirements, data characteristics, and trade-offs between accuracy, interpretability, and computational complexity.
3. Application of the HFM Techniques: Review of the State-of-the-Art
The HFM techniques have been extensively employed in diverse catchments with varying topography, climatic regions, and worldwide landscapes. Considering the diverse and extensive applications that have been found in the literature, this chapter is categorized into six major application areas: (1) enhancing flow simulation; (2) uncertainty analysis of streamflow forecasting; (3) ensemble streamflow forecasting; (4) flood forecasting and climate change impact analysis; and (5) comparison among merging techniques. The summaries of these applications, references, and major findings are presented in Table 2, Table 3, Table 4, Table 5 and Table 6 and Section 3.1, Section 3.2, Section 3.3, Section 3.4, Section 3.5.
3.1. Enhancing Flow Simulation
Flow simulation encompasses various hydrological variables crucial for water resources management, including streamflow, water levels, ungauged flow, and reservoir in-flow. Hydrologic models, alongside preprocessing and post-processing techniques, play a vital role in improving accuracy and reliability in forecasting. Table 2 provides an overview of research papers on HFM methods for enhancing flow simulation. Shamseldin et al. [4] proposed constrained ordinary least squares weighting, a variant of the WAM, to merge rainfall–runoff model outputs. This method combined models operating in the non-updating simulation mode. To address real-time operational needs, the RTMOCM method integrated the LTFM with WAM, significantly improving discharge predictions for real-time use [42]. The WAM approach initially calculated fixed weights based on error variance and correlation during calibration. However, adopting time-varying weights (TVW) in WAM proved effective in enhancing simulated streamflow time series [103]. Ajami et al. [15] analyzed several techniques, highlighting the effectiveness of MMSE and M3SE, incorporating bias correction steps over WAM in improving accuracy. The Galway Flow Modelling and Forecasting System (GFMFS), employing SAM, WAM, and NNM, evaluated the reliability of improved river flow simulations [104].

Table 2.
Summary of HFM techniques applied for enhancing streamflow simulations and forecasts.
Table 2.
Summary of HFM techniques applied for enhancing streamflow simulations and forecasts.
| References | Key Objectives | Methods/Techniques 1 | Major Findings/Contribution |
|---|---|---|---|
| [4] | River flow simulation | MT 2: SAM, WAM, NNM | Merging enhances forecast efficiency; WAM and NNM perform similarly |
| [18] | MT: GEP system | GEP has the advantage over NNM | |
| [33] | MT: SGB, SAM, WAM | SGB fits data better than SAM and WAM | |
| [58] | MT: SNN, RBFNN, MLPNN | MLPNN merging method performs best | |
| [64] | MT: GEP, MLPNN, RBFNN | GEP performs better than NNM; Multi-model combination depends on catchment | |
| [103] | MT: Time-varying WAM | TVW improves simulated streamflow | |
| [104] | MT: SAM, WAM, NNM | NNM is best in calibration and SAM in verification | |
| [14] | River flow fore-casting | MT: SAM, NNM, Fuzzy logic | Data fusion improves river flow forecasting; NNM stable regimes, fuzzy logic volatility |
| [19] | MT: MLFFNN method with five transfer functions | Logistic function yields the best, but the Arctan function yields the worst results | |
| [20] | MT: TS1, SAM, WAM, NNM | TS1 performs similarly to WAM and NNM; TS1 efficiency depends on the best model | |
| [36] | MT: SAM, BMA, fuzzy logic, IBFL | IBFL outperforms other approaches | |
| [42] | MT: RTMOCM | RTMOCM improves discharge forecasts | |
| [43] | MT: RSWM; Objective function: FMOF | RSWM improves precision flow stages | |
| [51] | MT: BMA, Copula-BMA | CBMA is better than BMA; CBMA allows multi-modal distribution | |
| [84] | MT: TS1, SAV, linear regression models | TS1 uses linear mixture models; TS1 allows complex nonlinear mappings | |
| [96] | MT: SAM, TS1 | TS1 has lower relative error; TS1 is good for real-time forecasting | |
| [59] | Runoff simulation | MT: SMLPNN, WMLPNN | WT enhances NN merging approach |
| [105] | MT: MLPNN; KETs: Garson’s algorithm, | KETs extract knowledge from MLPNN | |
| [55] | Streamflow simulation | MT: BMA, BMA-DSRC, DSRC-BMA | BMA-DSRC multi-model combination is effective |
| [106] | MT: GRC | Multi-input averaging performs better | |
| [107] | MT: BMA with DREAM; Optimization algorithm: MCMC | Merging streamflow simulations with BMA is efficient | |
| [15] | Streamflow forecasting | MT: SAM, WAM, MMSE, M3SE | MMSE and M3SE better than WAM; M3SE more consistent in streamflow simulation |
| [47] | MT: CBP-MLR and ComMLR | CBP-MLR reduces bias and improves tails; Com-MLR is superior but degrades near median | |
| [99] | MT: AIC | AIC is better than DWT–SVR and SVR; AIC is suitable for longer lead time | |
| [28] | Regionalization and Ungauged Flow Simulation | MT: SAM, unconstrained GRA, AICA, NNM | Multi-model averaging is not consistently the best; AIC better than complex methods |
| [39] | MT: SAM, WAM | WAM best for multi-model and multi-donor ensemble | |
| [108] | MT: SAM, WAM, NNM | Conceptual model plus pooling best for regionalization; Multi-model combination does not outperform pooling | |
| [16] | Reservoir inflow forecasting | MT: WAM | WAM outperforms individual models |
| [31] | MT: SAM, CCR, SR, SSE, ANN | CCR found to be unbiased; SSE and SSE/OLC produce small RMSE | |
| [62] | MT: SAM, BMA, EANN | Merging rainfall products simulates flood hydrograph; EANN outperforms SAM and BMA | |
| [26] | Water level prediction | MT: ANFIS, ANN, MLR, SAM | SAM outperforms ANN, ANFIS, and MLR |
| [44] | Monthly streamflow prediction | MT: WAM; Optimization algorithm: MODWO | MODWO improves middle- and long-term forecasts |
| [63] | MT: MBEM, FUCEP, OK, BMA, WAM | MBEM and FUCEM better than OK, WAM, and BMA | |
| [109] | MT: BMA | BMA combination outperforms individual forecasts | |
| [8] | Seasonal streamflow forecasting | MT: SAM, BGA, GRA, GLM, PCR, PLSR, BMA- (LR, GLM, EM, MCMC) | BMA-EM performs the best; GLM is not recommended for model averaging |
| [29] | MT: SAM, MLR with monthly varying weights | Best bias-corrected model outperforms multi-model average; SAM has a smaller error reduction than MLR | |
| [30] | MT: SAM | Combined forecast useful for short-term | |
| [38] | MT: SAM, WAM | Multi-model combination reduces RPS and false alarms | |
| [66] | MT: BMA and QMA | BMA generates wide, bimodal forecasts; QMA provides narrower, unimodal forecasts | |
| [67] | MT: LR, QM, QMA, BMA | Statistical post-processing improves forecast slightly; QMA approach more promising than BMA | |
| [77] | MT: GCV, BMA, AICM, RMSE | BMA performs best in skill scores; At least three models needed for good combination | |
| [89] | MT: BMA, QMA | BMA and QMA provide similar results |
Notes: 1 Elaboration of abbreviations is provided in Abbreviations. 2 Merging Technique.
Nonlinear combination techniques addressed streamflow hydrograph complexities. The MLFFNN merged deterministic hydrologic model simulations and demonstrated robustness comparable to WAM [4]. Optimizing transfer functions within the MLFFNN structure enhanced its performance, with the logistic function yielding superior results over the arctan function [19]. Further exploration between different neural network structures favored MLFFNN or MLPNN [105] structures over SNN and RBNN [58]. Incorporating wavelet transformation into MLPNN resulted in enhanced forecast performance [59]. Fuzzy systems, like TS1, displayed efficiency similar to WAM and NNM but were influenced by the best model’s effectiveness [20,84]. Although NNM methods are suitable for stable regimes, fuzzy logic methods provide superior probabilistic results in volatile environments [14]. Fuzzy logic’s accuracy in real-time river flow forecasting in semiarid mountain regions outperformed SAM [96]. SGB, an SVM-based method, improved flood peak capture better than linear methods like SAM and WAM [33]. The RSWM with fuzzy multi-objective functions (FMOFs) enhanced forecast precision for different flow stages [43]. Combining fuzzy logic with Bayesian models, hybrid methods yielded superior outcomes [36]. The hybrid DWT–SVR method also provided improved forecasts for longer lead times [99].
Averaging schemes in HFM, classified into multi-model/multi-input, multi-model/mono-input, and mono-model/multi-input, were investigated. GRC weighting improved multi-model averaged hydrographs, showcasing improved accuracy even with varying ensemble quality [106]. BMA and DREAM optimization, employing bias-corrected satellite precipitation products, significantly enhanced streamflow accuracy [75,107]. Furthermore, DSRC, in conjunction with BMA, improved the effectiveness and robustness of the multi-model streamflow simulation [55]. Regionalization studies (e.g., [102]) found the pooling method effective for ungauged catchments [106]. Weighted and unweighted averaging techniques were compared, showcasing the superiority of multi-donor ensembles weighted by distance [37]. However, Arsenault and Brissette [28] noted inconsistent performance between multi-model averaging and the best single model for regionalization. Accurate inflow forecasts are vital for hydropower reservoir operations. WAM effectively forecasted daily reservoir inflow [16]. CCR produced unbiased forecasts for reservoir inflow, outperforming SAM, SWR, SSE, and ANN; however, in post-bias correction, SSE performed the best [31]. ERNN outperformed traditional methods for enhanced reservoir inflow forecasts [62]. Additionally, multi-model merging techniques (e.g., MLR, ANN, and ANFIS) enhanced river water level predictions, particularly during ice jam risks [26].
Seasonal streamflow prediction is crucial for water resource planning in various applications. Addressing uncertainties from diverse sources, including input data, model structures, and initial conditions, several studies have utilized ensemble or multi-model combinations to enhance forecasting accuracy [29,89]. Bohn et al. [29] explored the impact of merging techniques—SAM and MLR with monthly varying weights—on streamflow forecasting using different hydrologic models. Their study concluded that individual bias-corrected models often outperformed model averaging of biased forecasts. MLR showed superiority over SAM in reducing errors, though its performance declined with increasing lead time. In mountainous basins, probabilistic merging methods such as MBEM and FUCEM showed superior skill in seasonal water balance modeling compared to methods like OK, WAM, and BMA [63].
Similarly, comparing BMA and QMA methods, Muhammad et al. [67] suggested QMA as a promising statistical post-processing technique for seasonal ensemble streamflow forecasting, slightly enhancing forecast accuracy. Statistical models like Bayesian joint probability (BJP) were applied to seasonal streamflow forecasting in Australian catchments, and the subsequent merging of various BJP candidate models using BMA improved forecast skill, especially in scenarios dominated by noise or when multiple models influenced forecasts [89]. Mendoza et al. [77] proposed an ensemble seasonal forecasting framework and revealed that employing at least three models with BMA resulted in better correlation and bias between seasonal forecasts and observations. Their study emphasized that the choice of models and merging techniques should align with evaluation criteria for reliable probabilistic seasonal predictions. Combining several statistical methods for seasonal operation streamflow forecasting, complex BMA merging approaches (BMA-EM, BMA-GLM, BMA-MCMC, BMA-LR) showed significant improvements over individual model forecasts and other merging techniques [8]. Data-driven models have gained traction for monthly to seasonal streamflow forecasting. Merging forecasts using performance-based weighting strategies and optimization algorithms like multi-objective grey wolf optimization (MOGWO) improved forecast precision compared to individual hybrid-adaptive models [110]. CBMA exhibited narrower uncertainty intervals and higher reliability than BMA when merging monthly runoff series forecasts from Random Forest, ANN, and SVM models [87]. Additionally, applying BMA with Boruta variable preprocessing enhanced monthly runoff predictions from SVR, ANN, and MLR models in terms of continuous ranked probability skill score (CRPSS) and Kling–Gupta efficiency (KGE) metrics [109]. Studies combining statistical, dynamic, and machine learning models for seasonal forecasting revealed that techniques like CCR, BMA, and QMA provided unbiased and relatively smaller forecast errors compared to individual models, demonstrating their effectiveness in improving seasonal ensemble forecasts [31,66].
3.2. Uncertainty Analysis of Streamflow Forecasting
Uncertainty in hydrologic modeling stems from diverse sources, including climate inputs, process representation, and parameter estimation. Robust estimation of this uncertainty is vital for reliable forecasting [81]. To address this uncertainty, researchers have explored various multi-model merging techniques applied to four key areas: model structural uncertainty, input uncertainty, inherent method uncertainty, and ensemble-related uncertainty. Table 3 provides a summary of HFM applications for uncertainty analysis in streamflow forecasting. In multi-model or ensemble forecasting, BMA proved more effective than the Ensemble Kalman Filter (EnKF) in representing conceptual model uncertainty for streamflow forecasting [111]. BMA, optimized with the EM algorithm, provided reasonable uncertainty estimates [96], proving valuable for climate change assessments [112]. Additionally, BMA enhanced both deterministic and probabilistic predictions while reducing uncertainties associated with various SWAT model configurations using different precipitation input data interpolations [113]. Recent studies highlighted BMA’s effectiveness in estimating model structural uncertainty related to non-point source pollution and streamflow modeling [114]. HBMA also identified uncertainty sources among different configurations of a 1D HEC-RAS model [115]. HFM methods, such as SAM, REA, and HBMA, quantified uncertainty sources in future runoff projections using different global circulation models (GCMs) under climate change scenarios [101]. They highlighted GCMs as a primary source of uncertainty, validated by HMBA analysis. Moreover, BMA assessed uncertainties arising from inaccuracies in precipitation products and hydrologic models [116]. e-Bay and IBUNE frameworks utilizing BMA improved modeling accuracy and provided confidence intervals exceeding 95% [54,60]. SCEM-UA algorithm combined with BMA excelled in streamflow predictions and flood forecasting while reducing uncertainty [88,117]. The merging method itself can introduce uncertainty due to its structural formation. SBMC, an update over BMA, showed improved accuracy, precision, and skill scores by recursively updating models’ posterior probability with new data [49]. CBMA and CBP-BMA outperformed BMA, showcasing narrower uncertainty intervals [53,87]. Samadi et al. explored different priors in BMA, concluding that combined fixed and flexible priors provided better predictive uncertainty intervals [118]. Additionally, BMA exhibited varying levels of uncertainty based on ensemble sizes and objective estimation approaches [119,120,121]. REA method’s scenario analysis from multi-model ensembles provided more realistic uncertainty estimations under land use changes in hydrology [100].

Table 3.
Summary of HFM techniques applied for reducing uncertainty in streamflow forecasting.
Table 3.
Summary of HFM techniques applied for reducing uncertainty in streamflow forecasting.
| References | Key Objectives | Methods/Techniques 1 | Major Findings/Contribution |
|---|---|---|---|
| [20] | Uncertainty analysis | MT 2: WAM, NNM, GAM | Merging forecasts better represents hydrologic uncertainty; NNM outperforms WAM and GAM |
| [22] | MT: BMA (IBUNE); Parameter optimization: SCEM-UA | BUNE framework quantifies uncertainty sources and improves accuracy | |
| [49] | MT: BMA, SBMC | SBMC considers structural organization for uncertainty reduction | |
| [53] | MT: BMA, CBMA, CBP-BMA | CBMA and CBP-BMA outperform BMA in uncertainty metrics | |
| [54] | MT: BMA, e-Bay | e-Bay estimates uncertainty at different times and flow magnitudes | |
| [87] | MT: BMA, Copula BMA; Uncertainty analysis: Monte Carlo sampling. | CBMA provides narrow uncertainty in high-flow prediction | |
| [88] | MT: BMA; Parameter optimization: SCE-UA, SCEM-UA | SCEM-UA quantifies parameter uncertainty; BMA reduces uncertainty and improves forecast performance | |
| [111] | MT: BMA, EnKF | BMA addresses model uncertainty; EnKF outperforms BMA in terms of accuracy | |
| [113] | MT: BMA | BMA reduces uncertainty for deterministic and probabilistic prediction | |
| [114] | MT: BMA | BMA estimates model structural uncertainty interval | |
| [115] | MT: BMA, HBMA | BMA probabilistic flood maps are reliable; HBMA identifies the propagation of uncertainty sources | |
| [116] | MT: BMA | BMA improves deterministic and probabilistic prediction | |
| [118] | MT: BMA | BMA with only fixed prior shows more predictive uncertainty; BMA with fixed and flexible priors improves weighted distribution | |
| [119] | MT: BMA | BMA assesses competing models and quantifies uncertainty | |
| [120] | MT: BMA | BMA with multi-objective estimation covers more observation | |
| [121] | MT: BMA; Parameter optimization: EM | GA and BMA combination for reasonable uncertainty estimation | |
| [100] | Uncertainty analysis under LC 3 | MT: Trimmed mean, REA | REA estimates uncertainty due to model structural differences |
| [101] | Uncertainty analysis under CC 4 | MT: SAM, REA, HBMA | HBMA segregates uncertainty sources, outperforms SAM and REA |
| [112] | MT: BMA; Calibration: SCE-UA | BMA quantifies model structural uncertainty in climate change assessment |
Notes: 1 Elaboration of abbreviations is provided in Abbreviations. 2 Merging Technique. 3 Land use change. 4 Climate change.
3.3. Ensemble Streamflow Forecasting (ESF)
Ensemble methods in streamflow forecasting have gained prominence for their ability to deliver reliable and skillful predictions using diverse dynamic and data-driven models. Studies in this area have described various methods, including the widely used Bayesian Model Averaging (BMA), applied across three primary categories: real-time ensemble streamflow forecasting, BMA development, and machine learning merging methods. Table 4 summarizes studies corresponding to these HFM applications in ensemble streamflow forecasting. Real-time ensemble streamflow forecasting has gained traction for its capacity to generate reliable forecasts and minimize uncertainty. Employing BMA on 15,000 ensemble streamflow simulations driven by multiple precipitation products significantly improved accuracy and offered robust uncertainty boundaries [117,122]. Comparatively, Inverse Variance Averaging (IVA) exhibited superior performance over BMA by assigning weights based on the spread of distributions, enhancing overall forecast accuracy [35]. Additionally, the HBMC method showcased a substantial 40% improvement in forecast skill and a 28% reduction in absolute bias for short lead-time forecasting [57]. Studies focused on BMA development for ESF demonstrated enhanced findings. Comparing single-weight and multi-weight BMA approaches, multi-weight BMA exhibited superior forecast performance, especially in reducing the uncertainty associated with ensemble predictions [86]. The choice of optimization algorithms, such as EM and MCMC, impacted uncertainty reduction in streamflow forecasting [93,123]. Variations in streamflow ensembles and standard deviation types influenced BMA performance, where non-constant variance standards played a dominant role [94]. Introducing an entropy-based BMA (EnBMA) approach outperformed traditional BMA in high-flow forecasting for short to medium-range ESF [2]. Additionally, merging quantile regression-based forecasts using BMA improved forecast skills, with model diversity playing a pivotal role [9]. Machine learning methods emerged as powerful merging techniques in ensemble forecasting. BPNN showed improved simulations over single models, especially during specific flow periods [60]. However, compared to binomial-based ensemble methods, BPNN lagged in reducing water volume error and increasing the NSE value [78]. Another method, NNE, outperformed traditional approaches like SAM and WAM when merging forecasts from different machine learning models for rainfall–runoff modeling in sparsely gauged basins [61]. Regression-based VB-LSTM showed a 10–30% improvement over BMA in both deterministic and probabilistic predictions, proving its robustness in handling model structural uncertainty [56].

Table 4.
Summary of HFM techniques applied for ensemble streamflow forecasting.
Table 4.
Summary of HFM techniques applied for ensemble streamflow forecasting.
| References | Key Objectives | Methods/Techniques 1 | Major Findings/Contribution |
|---|---|---|---|
| [60] | Ensemble streamflow simulation | MT 2: BPNN | BPNN is better for low-flow and peak-flow |
| [61] | MT: SAM, WAM, NNE | NNE method performs the best | |
| [94] | MT: BMA; Optimization algorithm: EM, DDS | BMA has less impact on distribution types; BMA with non-constant variance performs differently, but data transformation improves reliability | |
| [117] | MT: BMA; Calibration algorithm: SCE-UA, SCEM-UA | BMA merged SPPs improve streamflow prediction accuracy and reduce parameter uncertainty | |
| [56] | Ensemble streamflow prediction | MT: BMA, VB-LSTM | VB-LSTM provides better probabilistic prediction |
| [86] | MT: BMA; Optimization algorithm: EM; Data transformation method: Box-Cox | BMA improves probabilistic predictions over ensembles; Multiple sets of weights BMA outperform single set | |
| [96] | MT: BMA | Multi-model ESP with BMA performs well; ESP forecasts better in non-flood season | |
| [122] | MT: BMA | BMA improves forecast quality with a lead time of 6 to 9 days | |
| [123] | MT: BMA | Grand ensemble with BMA performs best | |
| [124] | MT: DA, QM, GESP | GESP is better than individual ESP | |
| [2] | Ensemble streamflow forecasting | MT: BMA, En-BMA | BMA and En-BMA perform almost similarly; EnBMA performs better for high flow |
| [9] | MT: EWA, BMA, QR-BMA; Skill measurement: CMI | QR-BMA more skillful and reliable; QR-BMA’s skill decreases with larger ensembles | |
| [35] | MT: SAM, IVA, BMA; Inputs: Bias corrected SPPs | Multi-model averaging with SPPs improves accuracy; IVA performs better than UWA and BMA | |
| [50] | MT: BMA-WVC | BMA-WVC identifies different flow regimes; BMA-WVC is useful for longer lead times | |
| [57] | MT: BHMC | BHMC improves forecast skill, reduces bias, and provides reliable forecasts for 1 to 3 days | |
| [78] | MT: SAM, BPNN, Binomial method | Binomial-based method outperforms SAM and BPNN | |
| [93] | MT: BMA; Optimization algorithm: EM, MCMC | BMA with EM and MCMC perform similarly; BMA with MCMC handles dimensionality |
Notes: 1 Elaboration of abbreviations is provided in Abbreviations. 2 Merging Technique.
3.4. Flood Forecasting and Climate Change Impact Analysis
Climate change has become a focal point due to its impact on the hydrological cycle, altering precipitation patterns, intensifying storms, and affecting global temperatures and sea levels. These changes directly influence water resources and river flow, leading to a rise in extreme weather events and subsequent severe flooding. Table 5 summarizes the application of HFM in flood forecasting and climate change impact analysis. Gain et al. [125] investigated climate change’s impact on streamflow by merging simulations from the PCR-GLOBWB hydrological model with weather forecasts from 12 Global Climate Models (GCMs) using weighted averaging techniques. This ensemble was compared against long-term flow observations. Their findings suggested an anticipated reduction in extremely low flows but an increase in severely high flows, posing potential risks of devastating flood events. Comparatively, autoregression-based Flood Error Correction (FEC) and weighted average-based multi-model composition were evaluated against the Global Real-Time Combination Method (GRCM) for flood forecasting accuracy, where GRCM demonstrated superior performance [126]. The analysis of climate and anthropogenic changes indicated that human activities accounted for a significant portion (73–85%) of streamflow changes, with BMA predictions reducing uncertainty from both climate change (14–27%) and human activities (74–80%) [127]. Comparative assessments between BMA-EM and REA-MCMC for runoff prediction under climate change revealed that while both methods improved accuracy, REA exhibited wider uncertainty ranges due to different weighting criteria and optimization algorithms [128]. Moreover, employing BMA for ensemble averaging enhanced flood forecasting accuracy and assessed forecast uncertainties by considering measures like standard deviation and confidence intervals [32]. In enhancing flood forecast accuracy and assessing forecast uncertainties, BMA showed promising results in different contexts. For instance, it was used for preprocessing ECMWF ensemble forecasts and post-processing operational HBV model-based streamflow forecasts in Norwegian catchments. Results indicated improved forecasts up to 2–3 days with post-processing and extended predictability up to 9 days for spring floods and 3 days for autumn floods with input data preprocessing [129].

Table 5.
Summary of HFM techniques applied for flood forecasting and climate change impact assessment.
Table 5.
Summary of HFM techniques applied for flood forecasting and climate change impact assessment.
| References | Key Objectives | Methods/Techniques 1 | Major Findings/Contribution |
|---|---|---|---|
| [32] | Flood forecasting | MT 2: BMA, SAM | BMA provides robust flood forecasts |
| [126] | MT: WAM, GRCM | WAM performs better in flood forecasting; GRCM performs better for real-time application | |
| [129] | MT: BMA | BMA-based preprocessing of forcing data improves flood forecast beyond 3 days, but postprocessing of streamflow improves flood forecast for only up to 2–3 days | |
| [125] | CC 3 impact analysis | MT: WAM | Multi-model assesses climate change impacts |
| [127] | CC and human impact analysis | MT: BMA | BMA reduces uncertainties for climate and human impacts |
| [128] | CC impact analysis on runoff projection | MT: BMA, REA, EWA | REA has wider uncertainty ranges than BMA |
Notes: 1 Elaboration of abbreviations is provided in Abbreviations. 2 Merging Technique. 3 Climate change.
3.5. Comparison of Merging Techniques
Table 6 provides insights from studies that compared different merging techniques to enhance streamflow simulations and reduce uncertainty. For instance, Viney et al. [39] evaluated 10 ensemble merging techniques, with the trimmed mean performing best in terms of percent bias (PBias) of 2.7% among a subset of 4 ensemble predictions. While conditional ensembles based on flow states showed limited improvement over weighted mean ensembles, linear weighting schemes might not adequately capture the non-linear and non-stationary nature of climate variables. Constrained weight averaging resulted in larger errors than unconstrained weight averaging, with GRA offering simplicity and speed while achieving similar results to BMA and MMA [17]. Azmi et al. [130] compared five data fusion/merging methods and found K-NN to outperform others in terms of RMSE (7 m3/s) and correlation coefficient (0.92), showcasing promising error analysis considering time-varying combinations. ANFIS demonstrated superior performance with a coefficient of determination (>0.79) and RMSE (<11.97 m3/s) across different gauge stations, surpassing other methods like SAM, WAM, NNM, and FSM, even outperforming individual statistical rainfall–runoff models [34].
In merging quantile forecasts and predictive distributions of streamflow, BLP yielded slightly better results than BMA and NGR in terms of continuous rank probability score (CRPS), albeit being more time-consuming in parameter estimation, potentially resulting in suboptimal solutions that could limit its effectiveness [55]. Awol et al. [131] highlighted the superiority of forecast merging methods with nonnegative weights, such as CLS and BMA, over those without constraints, like InvR and BGA. The GRC method excelled in multi-model averaging for hydrological applications in cold regions [6,83]. Constrained MLR emerged as the best-performing multi-model ensemble method in temperate Indian catchments based on correlation coefficient (0.93) and RMSE (412 m3/s) [7]. Exploring nine averaging methods across global watersheds in diverse climate regions, Qi et al. [54] found model averaging methods to perform best in warm climatic regions, with MMSE exhibiting superior performance in most regions (67.1% catchments out of 2277) except the arctic area. Additionally, ensemble averaging showed lower efficiency for low-flow simulations (performing better in only 45% of catchments with precipitation less than 600 mm/year) but demonstrated robustness and efficiency when different objective functions were utilized [83].

Table 6.
Summary of studies on comparison of merging techniques.
Table 6.
Summary of studies on comparison of merging techniques.
| References | Key Objectives | Methods/Techniques 1 | Major Findings/Contribution |
|---|---|---|---|
| [6] | Comparison of HFM techniques | MT 2: SAM, AIC, BGA, BICA, BMA, GRA, GRB, GRC, SCA; Parameter optimization: SCE-UA | BMA fails for 18% basins out of 429; GRC performs the best in terms of NSE (0.748); Optimal combination needs less than 12 ensembles |
| [7] | MT: mean, median, trimmed mean, weighted mean, unconstrained and constrained MLR, SAM, MMSE | Constrained MLR is the best in terms of correlation coefficient (0.93) and RMSE (412 m3/s); Ensemble size of five is optimal | |
| [10] | MT: SAM, AICA, BICA, BGA, GRA, GRB, GRC, BMA, MMSE; Parameter optimization: SCE-UA | Multi-input averaging performs better than multi-model averaging; Forecast merging improves flow simulation up to six members; MMSE performs best (67.1% catchments out of 2277) except in the Arctic region | |
| [17] | MT: EWA, BGA, BMA, MMA, GRA, AICA, BICA | Unconstrained methods outperform constrained methods. In terms of RMSE (m3/s), GRA (21.38) is comparable to BMA (21.41) and MMA (21.43) | |
| [34] | MT: ANFIS, SAM, WAM, NNM, FSM | ANFIS performed the best in terms of coefficient of determination (>0.79) and RMSE (<11.97 m3/s) | |
| [39] | MT: mean, median, trimmed mean, MLR, PCR, BMA, WAM | In terms of PBias (%), trimmed mean (2.7) performs better than others; Non-stationary climate affects multi-model ensembles | |
| [83] | MT: SAM, AICA, BICA, BGA, GRA, GRB, GRC, BMA, MMSE | Model averaging is less efficient for low-flow (performs better in only 45% of catchments out of 383); GRC is the best merging method in terms of PBias; Ensemble size less than six improves forecasting | |
| [85] | MT: BMA, NGR, BLP | BLP is slightly better than BMA and NGR in terms of CRPS; BMA and BLP can be time-consuming | |
| [130] | MT: SAM, WAM, NNM, KNN | KNN outperforms conventional methods in terms of RMSE (7 m3/s) and correlation coefficient (0.92) | |
| [131] | MT: BMA, SAM, CLS, InvR, BGA, Median forecast | CLS is better in early lead times (6–18 h) in terms of RMSE (8.83 m3/s); Nonnegative weights methods (e.g., BMA and CLS) outperform others |
Notes: 1 Elaboration of abbreviations is provided in Abbreviations. 2 Merging Technique.
4. Discussion
This review examined merging techniques applied in hydrologic forecasting, mostly for streamflow simulations and forecasts. The analysis revealed that the HFM techniques were applied extensively worldwide under various topographic and climatic regions, with notable implementation observed in the United States, China, and Canada (Figure 3). The use of merging techniques in streamflow forecasting has gained popularity in the 21st century (Figure 4). Among the various merging techniques identified, the Bayesian method emerged as the most popular and highly ranked in terms of its application in various studies (Table 7). The SAM and WAM were ranked second and third, respectively. There has been a growing preference for probabilistic hydrologic forecasting using Bayesian methods over deterministic approaches in recent years. This trend has been observed among both researchers and operational forecasters. Consequently, the Bayesian method has experienced significant advancements and has become the most extensively developed merging technique in the field. Following Bayesian methods, the regression methods, weighted averaging, and neural network methods have also seen notable progress, albeit to a slightly lesser degree.
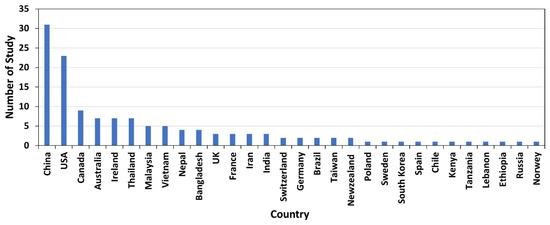
Figure 3.
Hydrologic forecast merging case study catchment locations worldwide and a number of studies conducted 1986–2023.
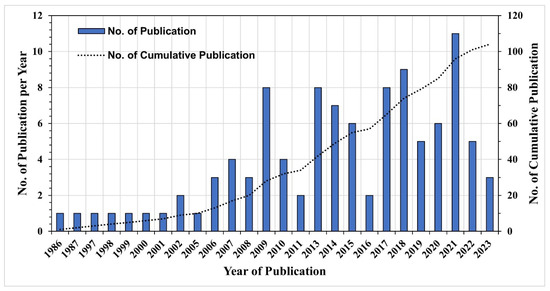
Figure 4.
Number of research works published 1986–2023 related to hydrologic forecast merging.
Multiple studies have compared different merging techniques to improve streamflow simulations and reduce uncertainty. The findings suggested that the trimmed mean performs well when considering a subset of ensemble predictions. However, linear weighting schemes commonly used in merging techniques may not effectively capture the non-linear and non-stationary nature of hydrologic variables. Weighting averaging methods have been widely used and have demonstrated significant improvements in forecast accuracy, particularly when based on regression or variance of error. Non-linear merging techniques like NNM and fuzzy systems have also proven effective in addressing the non-linear characteristics of streamflow hydrographs. Hybrid models that integrated different techniques have shown improved performance compared to simple averaging methods. Ensemble averaging methods, such as BMA and MLR, have been commonly used for river flow and streamflow prediction. BMA, in particular, has demonstrated the ability to represent conceptual model uncertainty and provide comprehensive uncertainty estimation.
Furthermore, uncertainty analysis using methods like BMA and its variations offers valuable insights into the reliability and robustness of streamflow forecasts. These methods enable better-informed decision-making in water resource management and planning by reducing uncertainty intervals and providing probabilistic predictions. Overall, Bayesian methods, nonlinear methods, and hybrid models have shown great potential to improve the accuracy and reliability of streamflow simulations and predictions.

Table 7.
Popularity rank of merging techniques in terms of application.
Table 7.
Popularity rank of merging techniques in terms of application.
| Merging Techniques 1 | Applied in Number of Studies | Rank |
|---|---|---|
| Bayesian Methods | 55 | 1 |
| Simple Averaging Methods | 43 | 2 |
| Weighted Averaging Methods | 24 | 3 |
| Neural Network Methods | 20 | 4 |
| Granger and Ramanathan Methods | 13 | 5 |
| Regression Methods | 12 | 6 |
| Fuzzy System Methods | 10 | 7 |
| AIC | 7 | 8 |
| BGA | 6 | 9 |
| MMSE, Quantile Method | 5 | 10 |
| BIC | 4 | 11 |
| REA, GAM | 3 | 12 |
| SSE | 2 | 13 |
| SGB, InvR, GLM, MMA, CCR, KDE, Pooled, MBEM, OK, GCV, SCE, IVA, NGR, BLP, BM | 1 each | 14 |
Note: 1 Elaboration of abbreviations is provided in Abbreviations.
5. Conclusions and Recommendations for Future Research
This article provides a comprehensive review of advances in multi-model or ensemble HFM techniques over the past 38 years (1986–2023) and highlights the need for further research to improve forecasting efficiency and reliability. The HFM emerged as an effective approach in producing more accurate and reliable forecasts while quantifying the associated uncertainty of rainfall–runoff models and forcing variables. The literature demonstrated the continued development of HFM techniques since the seminal work of Shamseldin et al. [4]. Notable progress has been made in enhancing hydrological modeling performance through multi-model averaging techniques. Various HFM techniques have been tested across different catchments, topographies, and climate conditions, with regression-based GRC, MMSE, and probabilistic density-based BMA showing promise in improving forecasts for different applications. Based on the findings of this comprehensive literature review on hydrologic forecast merging (HFM) techniques, several future research opportunities and directions can be suggested:
- Further research should focus on optimizing the estimation of weights used in multi-model combinations. Specifically, there is a need for comprehensive methods to calculate time-varying weights (TVWs) of member models at specific lead times, considering the dynamic nature of hydrological systems and changing forecast accuracies.
- Enhancing the efficiency of multi-model combinations, particularly for low-flow simulations and regionalization purposes, remains a challenge. Future studies could explore methodologies to better incorporate different flow stages, considering the complexities of drier catchments or ungauged basins.
- Investigating and testing the suitability and efficiency of HFM techniques for short-term forecasts, such as flash floods, is crucial. Understanding how merging techniques perform in high-impact, rapidly evolving hydrological events could significantly improve forecasting accuracy and response.
- Further exploration into the impact of member model diversity on forecast accuracy is essential. Understanding how variations in model types, structures, or input data sources affect the reliability and robustness of the merged forecasts can guide the selection and composition of the ensemble.
- Incorporating new data sources (e.g., remote sensing, crowd-sourced data) and advancing techniques (e.g., machine learning, artificial intelligence) into HFM could lead to significant improvements. Assessing the integration of these new elements within ensemble techniques for better predictive capabilities warrants exploration.
- Investigating methods to scale HFM techniques for different temporal and spatial resolutions can improve their applicability across various hydrological contexts. This involves ensuring adaptability to different scales, from local catchments to larger river basins or even regional and global applications.
- Enhancing the understanding and communication of forecast uncertainties is crucial. Future research could focus on developing methodologies to effectively quantify and communicate uncertainties associated with merged forecasts to support better decision-making.
- Exploring avenues to implement and operationalize advanced HFM techniques in real-time forecasting systems is essential. Developing frameworks or tools that enable the seamless integration of these methods into operational forecasting systems would be highly beneficial.
By addressing these future research opportunities, the field of hydrologic forecast merging can advance significantly, leading to more robust, accurate, and reliable forecasts while effectively quantifying associated uncertainties for various hydrological applications.
Author Contributions
Conceptualization, M.R.S. and P.C.; methodology, M.R.S.; formal analysis, M.R.S.; investigation, M.R.S.; writing—original draft preparation, M.R.S.; writing—review and editing, M.R.S. and P.C.; visualization, M.R.S.; supervision, P.C.; project administration, P.C.; funding acquisition, P.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Natural Science and Engineering Research Council (NSERC) of Canada, grant NSERC Canadian FloodNet (NETGP-451456).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the proprietary nature of the data.
Acknowledgments
Authors are grateful to Jongho Keum (McMaster University) for the valuable comments and analysis directions while preparing the manuscripts.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Abbreviation | Elaboration |
| AIC | Akaike information criteria |
| ANN | Artificial neural network |
| ANFIS | Adaptive neuro-fuzzy inference system |
| BGA | Bates-Granger averaging |
| BIC | Bayes information criteria |
| BJP | Bayesian joint probability |
| BLP | Beta-transformed linear pool |
| BHMC | Bayesian hierarchical model combination |
| BMA | Bayesian model averaging |
| BPNN | Back propagation neural network |
| BMA-LR | Bayesian model averaging in linear regression |
| BMA-GLM | Bayesian model averaging in a generalized linear model |
| BMA-EM | Bayesian model averaging with expectation-maximization algorithm |
| BMA-MCMC | Bayesian model averaging with MCMC |
| CBP | Copula Bayesian processor |
| CBMA | Copula Bayesian model averaging |
| CCR | Constant coefficient regression |
| CLS | Constrained least square |
| CBP-MLR | Conditional bias panelized multiple linear regression |
| CR | Containing Ratio |
| CRPS | Continuous ranked probability score |
| CRPSS | Continuous ranked probability skill score |
| Com-MLR | Composite multiple linear regression |
| DSRC | Dynamic system response curve |
| DWT-SVR | Discrete wavelets transform-support vector regression |
| EnBMA | Entropy-based Bayesian model averaging |
| ENN | Ensemble neural network |
| EnKF | Ensemble Kalman filter |
| ERNN | Ensemble recurrent neural network |
| EWA | Equal weighted averaging |
| FEC | Flood error correction |
| FIRMs | Flood Insurance Rate Maps |
| FMOF | Fuzzy multiple objective function |
| GAM | Genetic algorithm method |
| GEP | Gene expression programming |
| GRA | Granger Ramanathan Type A |
| GRB | Granger Ramanathan Type B |
| GRC | Granger Ramanathan Type C |
| GCV | Generalized cross-validation score |
| GFMFS | Galway flow modeling and forecasting system |
| GLM | Generalized linear model |
| GRCM | Global real-time combination method |
| HBMA | Hierarchical Bayesian model averaging |
| HFM | Hydrologic forecast merging |
| IBUNE | Integrated Bayesian uncertainty estimator |
| IVA | Inverse (error) variance averaging |
| InvR | Inverse rank |
| KDE | Kernel density estimator |
| IBFL | Integrated Bayesian and Fuzzy logic |
| KET | Knowledge Extraction Technique |
| K-NN | K-nearest neighbor |
| KGE | Kling–Gupta efficiency |
| LTFM | Linear transfer function model |
| MBEM | Modified Bootstrap Ensemble Modeling |
| MBWL | Maximum breakup water level |
| MLFFNN | Multi-layer feed-forward neural network |
| MLPNN | Multi-layer perceptron neural network |
| MMSE | Multi-model super ensemble |
| M3SE | Modified multi-model super ensemble |
| MLR | Multiple linear regression |
| MOGWO | Multi-objective grey wolf optimization |
| NGR | Nonhomogeneous gaussian regression |
| NNM | Neural network method |
| NSE | Nash-Sutcliffe Efficiency |
| OK | Ordinary kriging |
| OLS | Ordinary least square |
| OLC | Optimal linear correction |
| PCR | Principal component regression |
| PLSR | Partial least square regression |
| QM | Quantile mapping |
| QMA | Quantile method averaging |
| QR | Quantile regression |
| RF | Random forest |
| RBFNN | Radial basis function neural network |
| RMSE | Root mean square error |
| RSWM | Runoff scale weighted method |
| RTMOCM | Real-time model output combination method |
| SR | Switching regression |
| SAM | Simple averaging method |
| SCA | Shuffled complex averaging |
| SVM | Support vector machine |
| SCE-UA | Shuffled complex evolution-University of Arizona |
| SBMC | Sequential Bayesian model combination |
| SGB | Stochastic gradient boosting |
| SGMP | Satellite–gauge merged precipitation |
| SNN | Simple neural network |
| SSE | Sum of squared errors |
| SVR | Support vector regression |
| SWAT | Soil and water assimilation tools |
| DWT-SVR | Discrete wavelets transform support vector regression |
| TS1 | First-order Takagi-Sugeno fuzzy system |
| TVW | Time-varying weight |
| VBLSTM | Variational Bayesian Long Short-Term Memory |
| WAM | Weighted averaging method |
| WMLPNN | Wavelet multi-layer perceptron neural network |
| WVC | Wavelet Volterra approach |
References
- Chen, J.; Brissette, F.P.; Poulin, A.; Leconte, R. Overall Uncertainty Study of the Hydrological Impacts of Climate Change for a Canadian Watershed. Water Resour. Res. 2011, 47, W12509. [Google Scholar] [CrossRef]
- Darbandsari, P.; Coulibaly, P. Introducing Entropy-Based Bayesian Model Averaging for Streamflow Forecast. J. Hydrol. 2020, 591, 125577. [Google Scholar] [CrossRef]
- Ajami, N.K.; Duan, Q.; Sorooshian, S. An Integrated Hydrologic Bayesian Multimodel Combination Framework: Confronting Input, Parameter, and Model Structural Uncertainty in Hydrologic Prediction. Water Resour. Res. 2007, 43, W01403. [Google Scholar] [CrossRef]
- Shamseldin, A.Y.; O’Connor, K.M.; Liang, G.C. Methods for Combining the Outputs of Different Rainfall–Runoff Models. J. Hydrol. 1997, 197, 203–229. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H. Multi-Model Ensemble Analysis of Runoff Extremes for Climate Change Impact Assessments. J. Hydrol. 2015, 525, 352–361. [Google Scholar] [CrossRef]
- Arsenault, R.; Gatien, P.; Renaud, B.; Brissette, F.; Martel, J.-L. A Comparative Analysis of 9 Multi-Model Averaging Approaches in Hydrological Continuous Streamflow Simulation. J. Hydrol. 2015, 529, 754–767. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, R.; Jena, P.P.; Chatterjee, C.; Mishra, A. Identification of the Best Multi-Model Combination for Simulating River Discharge. J. Hydrol. 2015, 525, 313–325. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H. Ensemble Combination of Seasonal Streamflow Forecasts. J. Hydrol. Eng. 2016, 21, 04015043. [Google Scholar] [CrossRef]
- Sharma, S.; Siddique, R.; Reed, S.; Ahnert, P.; Mejia, A. Hydrological Model Diversity Enhances Streamflow Forecast Skill at Short- to Medium-Range Timescales. Water Resour. Res. 2019, 55, 1510–1530. [Google Scholar] [CrossRef]
- Qi, W.; Chen, J.; Xu, C.; Wan, Y. Finding the Optimal Multimodel Averaging Method for Global Hydrological Simulations. Remote Sens. 2021, 13, 2574. [Google Scholar] [CrossRef]
- Mizukami, N.; Rakovec, O.; Newman, A.J.; Clark, M.P.; Wood, A.W.; Gupta, H.V.; Kumar, R. On the Choice of Calibration Metrics for “High-Flow” Estimation Using Hydrologic Models. Hydrol. Earth Syst. Sci. 2019, 23, 2601–2614. [Google Scholar] [CrossRef]
- Cavadias, G.; Morin, G. The Combination of Simulated Discharges of Hydrological Models. Hydrol. Res. 1986, 17, 21–32. [Google Scholar] [CrossRef]
- McLeod, A.I.; Noakes, D.J.; Hipel, K.W.; Thompstone, R.M. Combining Hydrologic Forecasts. J. Water Resour. Plan. Manag. 1987, 113, 29–41. [Google Scholar] [CrossRef]
- Abrahart, R.J.; See, L. Multi-Model Data Fusion for River Flow Forecasting: An Evaluation of Six Alternative Methods Based on Two Contrasting Catchments. Hydrol. Earth Syst. Sci. 2002, 6, 655–670. [Google Scholar] [CrossRef]
- Ajami, N.K.; Duan, Q.; Gao, X.; Sorooshian, S. Multimodel Combination Techniques for Analysis of Hydrological Simulations: Application to Distributed Model Intercomparison Project Results. J. Hydrometeorol. 2006, 7, 755–768. [Google Scholar] [CrossRef]
- Coulibaly, P.; Haché, M.; Fortin, V.; Bobée, B. Improving Daily Reservoir Inflow Forecasts with Model Combination. J. Hydrol. Eng. 2005, 10, 91–99. [Google Scholar] [CrossRef]
- Diks, C.G.H.; Vrugt, J.A. Comparison of Point Forecast Accuracy of Model Averaging Methods in Hydrologic Applications. Stoch. Environ. Res. Risk Assess. 2010, 24, 809–820. [Google Scholar] [CrossRef]
- Fernando, A.K.; Shamseldin, A.Y.; Abrahart, R.J. Use of Gene Expression Programming for Multimodel Combination of Rainfall-Runoff Models. J. Hydrol. Eng. 2012, 17, 975–985. [Google Scholar] [CrossRef]
- Shamseldin, A.Y.; Nasr, A.E.; O’Connor, K.M. Comparison of Different Forms of the Multi-Layer Feed-Forward Neural Network Method Used for River Flow Forecasting. Hydrol. Earth Syst. Sci. 2002, 6, 671–684. [Google Scholar] [CrossRef]
- Xiong, L.; Shamseldin, A.Y.; O’Connor, K.M. A Non-Linear Combination of the Forecasts of Rainfall-Runoff Models by the first-Order Takagi-Sugeno Fuzzy System. J. Hydrol. 2001, 245, 196–217. [Google Scholar] [CrossRef]
- Jeong, D.I.; Kim, Y.-O. Combining Single-Value Streamflow Forecasts—A Review and Guidelines for Selecting Techniques. J. Hydrol. 2009, 377, 284–299. [Google Scholar] [CrossRef]
- Li, W.; Duan, Q.; Miao, C.; Ye, A.; Gong, W.; Di, Z. A Review on Statistical Postprocessing Methods for Hydrometeorological Ensemble Forecasting. WIREs Water 2017, 4, e1246. [Google Scholar] [CrossRef]
- Han, S.; Coulibaly, P. Bayesian Flood Forecasting Methods: A Review. J. Hydrol. 2017, 551, 340–351. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Batelaan, O.; Fadaee, M.; Hinkelmann, R. Ensemble Machine Learning Paradigms in Hydrology: A Review. J. Hydrol. 2021, 598, 126266. [Google Scholar] [CrossRef]
- Troin, M.; Arsenault, R.; Wood, A.W.; Brissette, F.; Martel, J. Generating Ensemble Streamflow Forecasts: A Review of Methods and Approaches Over the Past 40 Years. Water Resour. Res. 2021, 57, e2020WR028392. [Google Scholar] [CrossRef]
- Sun, W.; Trevor, B. Multiple Model Combination Methods for Annual Maximum Water Level Prediction during River Ice Breakup. Hydrol. Process. 2018, 32, 421–435. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Kishtawal, C.M.; LaRow, T.E.; Bachiochi, D.R.; Zhang, Z.; Williford, C.E.; Gadgil, S.; Surendran, S. Improved Weather and Seasonal Climate Forecasts from Multimodel Superensemble. Science 1999, 285, 1548–1550. [Google Scholar] [CrossRef]
- Arsenault, R.; Brissette, F. Multi-Model Averaging for Continuous Streamflow Prediction in Ungauged Basins. Hydrol. Sci. J. 2016, 61, 2443–2454. [Google Scholar] [CrossRef]
- Bohn, T.J.; Sonessa, M.Y.; Lettenmaier, D.P. Seasonal Hydrologic Forecasting: Do Multimodel Ensemble Averages Always Yield Improvements in Forecast Skill? J. Hydrometeorol. 2010, 11, 1358–1372. [Google Scholar] [CrossRef]
- Caiado, J. Performance of Combined Double Seasonal Univariate Time Series Models for Forecasting Water Demand. J. Hydrol. Eng. 2010, 15, 215–222. [Google Scholar] [CrossRef]
- Kim, Y.-O.; Jeong, D.; Ko, I.H. Combining Rainfall-Runoff Model Outputs for Improving Ensemble Streamflow Prediction. J. Hydrol. Eng. 2006, 11, 578–588. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, D.; Guo, Y.; Zhang, Y.; Dai, R. Application of Bayesian Model Averaging Approach to Multimodel Ensemble Hydrologic Forecasting. J. Hydrol. Eng. 2013, 18, 1426–1436. [Google Scholar] [CrossRef]
- Phukoetphim, P.; Shamseldin, A.Y. The Use of Stochastic Gradient Boosting Method for Multi-Model Combination of Rainfall-Runoff Models. In Proceedings of the International Conference on Innovations in Engineering and Technology, Bangkok, Thailand, 25–26 December 2013; pp. 275–280. [Google Scholar]
- Tareghian, R.; Bilondi, M.P. A comparative study of non-linear forecast combination of rainfall-runoff models using adaptive neuro-fuzzy inference system (ANFIS). Carpathian J. Earth Environ. Sci. 2013, 8, 41–54. [Google Scholar]
- Roy, T.; Serrat-Capdevila, A.; Gupta, H.; Valdes, J. A Platform for Probabilistic Multimodel and Multiproduct Streamflow Forecasting. Water Resour. Res. 2017, 53, 376–399. [Google Scholar] [CrossRef]
- See, L.; Openshaw, S. A Hybrid Multi-Model Approach to River Level Forecasting. Hydrol. Sci. J. 2000, 45, 523–536. [Google Scholar] [CrossRef]
- Viney, N.R.; Vaze, J.; Chiew, F.H.S.; Perraud, D.A.P.; Teng, J. Comparison of Multi-Model and Multi-Donor Ensembles for Regionalisation of Runoff Generation Using Five Lumped Rainfall-Runoff Models. In Proceedings of the 18th World IMACS Congress and MODSIM09, Cairns, Australia, 13–17 July 2009; pp. 2377–2383. [Google Scholar]
- Devineni, N.; Sankarasubramanian, A.; Ghosh, S. Multimodel Ensembles of Streamflow Forecasts: Role of Predictor State in Developing Optimal Combinations. Water Resour. Res. 2008, 44, 2006WR005855. [Google Scholar] [CrossRef] [PubMed]
- Viney, N.R.; Bormann, H.; Breuer, L.; Bronstert, A.; Croke, B.F.W.; Frede, H.; Gräff, T.; Hubrechts, L.; Huisman, J.A.; Jakeman, A.J.; et al. Assessing the Impact of Land Use Change on Hydrology by Ensemble Modelling (LUCHEM) II: Ensemble Combinations and Predictions. Adv. Water Resour. 2009, 32, 147–158. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Newbold, P. Forecasting Economic Time Series, 2nd ed.; Academic Press: San Diego, CA, USA, 1977. [Google Scholar]
- Granger, C.W.J.; Ramanathan, R. Improved Methods of Combining Forecasts. J. Forecast. 1984, 3, 197–204. [Google Scholar] [CrossRef]
- Shamseldin, A.Y.; O’Connor, K.M. A Real-Time Combination Method for the Outputs of Different Rainfall-Runoff Models. Hydrol. Sci. J. 1999, 44, 895–912. [Google Scholar] [CrossRef]
- Hsie, M.; Yan, S.-W.; Pan, N.-F. Improvement of Rainfall-Runoff Simulations Using the Runoff-Scale Weighting Method. J. Hydrol. Eng. 2014, 19, 1330–1339. [Google Scholar] [CrossRef]
- Guo, Y.; Xu, Y.-P.; Xie, J.; Chen, H.; Si, Y.; Liu, J. A Weights Combined Model for Middle and Long-Term Streamflow Forecasts and Its Value to Hydropower Maximization. J. Hydrol. 2021, 602, 126794. [Google Scholar] [CrossRef]
- Deutsch, M.; Granger, C.W.J.; Teräsvirta, T. The Combination of Forecasts Using Changing Weights. Int. J. Forecast. 1994, 10, 47–57. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E.; Westveld, A.H.; Goldman, T. Calibrated Probabilistic Forecasting Using Ensemble Model Output Statistics and Minimum CRPS Estimation. Mon. Weather Rev. 2005, 133, 1098–1118. [Google Scholar] [CrossRef]
- Jozaghi, A.; Shen, H.; Ghazvinian, M.; Seo, D.-J.; Zhang, Y.; Welles, E.; Reed, S. Multi-Model Streamflow Prediction Using Conditional Bias-Penalized Multiple Linear Regression. Stoch. Environ. Res. Risk Assess. 2021, 35, 2355–2373. [Google Scholar] [CrossRef]
- Raftery, A.E.; Madigan, D.; Hoeting, J.A. Bayesian Model Averaging for Linear Regression Models. J. Am. Stat. Assoc. 1997, 92, 179–191. [Google Scholar] [CrossRef]
- Moradkhani, H.; Hsu, K.; Sorooshian, S. Toward Improved Hydrologic Prediction with Reduced Uncertainty Using Sequential Multi-Model Combination. In World Environmental and Water Resources Congress 2008; American Society of Civil Engineers: Honolulu, HI, USA, 2008; pp. 1–10. [Google Scholar] [CrossRef]
- Rathinasamy, M.; Adamowski, J.; Khosa, R. Multiscale Streamflow Forecasting Using a New Bayesian Model Average Based Ensemble Multi-Wavelet Volterra Nonlinear Method. J. Hydrol. 2013, 507, 186–200. [Google Scholar] [CrossRef]
- Madadgar, S.; Moradkhani, H. Improved Bayesian Multimodeling: Integration of Copulas and Bayesian Model Averaging. Water Resour. Res. 2014, 50, 9586–9603. [Google Scholar] [CrossRef]
- Tsai, F.T.-C.; Elshall, A.S. Hierarchical Bayesian Model Averaging for Hydrostratigraphic Modeling: Uncertainty Segregation and Comparative Evaluation. Water Resour. Res. 2013, 49, 5520–5536. [Google Scholar] [CrossRef]
- He, S.; Guo, S.; Liu, Z.; Yin, J.; Chen, K.; Wu, X. Uncertainty Analysis of Hydrological Multi-Model Ensembles Based on CBP-BMA Method. Hydrol. Res. 2018, 49, 1636–1651. [Google Scholar] [CrossRef]
- Qi, W.; Liu, J.; Yang, H.; Sweetapple, C. An Ensemble-Based Dynamic Bayesian Averaging Approach for Discharge Simulations Using Multiple Global Precipitation Products and Hydrological Models. J. Hydrol. 2018, 558, 405–420. [Google Scholar] [CrossRef]
- Wang, J.; Bao, W.; Xiao, Z.; Si, W. Multi-Model Integrated Error Correction for Streamflow Simulation Based on Bayesian Model Averaging and Dynamic System Response Curve. J. Hydrol. 2022, 607, 127518. [Google Scholar] [CrossRef]
- Li, D.; Marshall, L.; Liang, Z.; Sharma, A. Hydrologic Multi-Model Ensemble Predictions Using Variational Bayesian Deep Learning. J. Hydrol. 2022, 604, 127221. [Google Scholar] [CrossRef]
- Ossandón, Á.; Rajagopalan, B.; Tiwari, A.D.; Thomas, T.; Mishra, V. A Bayesian Hierarchical Model Combination Framework for Real-Time Daily Ensemble Streamflow Forecasting Across a Rainfed River Basin. Earths Future 2022, 10, e2022EF002958. [Google Scholar] [CrossRef]
- Shamseldin, A.Y.; O’Connor, K.M.; Nasr, A.E. A Comparative Study of Three Neural Network Forecast Combination Methods for Simulated River Flows of Different Rainfall–Runoff Models. Hydrol. Sci. J. 2007, 52, 896–916. [Google Scholar] [CrossRef]
- Shoaib, M.; Shamseldin, A.Y.; Khan, S.; Khan, M.M.; Khan, Z.M.; Melville, B.W. A Wavelet Based Approach for Combining the Outputs of Different Rainfall–Runoff Models. Stoch. Environ. Res. Risk Assess. 2018, 32, 155–168. [Google Scholar] [CrossRef]
- Li, Z.; Yu, J.; Xu, X.; Sun, W.; Pang, B.; Yue, J. Multi-Model Ensemble Hydrological Simulation Using a BP Neural Network for the Upper Yalongjiang River Basin, China. Proc. Int. Assoc. Hydrol. Sci. 2018, 379, 335–341. [Google Scholar] [CrossRef]
- Nourani, V.; Gökçekuş, H.; Gichamo, T. Ensemble Data-Driven Rainfall-Runoff Modeling Using Multi-Source Satellite and Gauge Rainfall Data Input Fusion. Earth Sci. Inform. 2021, 14, 1787–1808. [Google Scholar] [CrossRef]
- Chiang, Y.-M.; Hao, R.-N.; Xu, Y.-P.; Liu, L. Multi-Source Rainfall Merging and Reservoir Inflow Forecasting by Ensemble Technique and Artificial Intelligence. J. Hydrol. Reg. Stud. 2022, 44, 101204. [Google Scholar] [CrossRef]
- Nasseri, M.; Zahraie, B.; Ajami, N.K.; Solomatine, D.P. Monthly Water Balance Modeling: Probabilistic, Possibilistic and Hybrid Methods for Model Combination and Ensemble Simulation. J. Hydrol. 2014, 511, 675–691. [Google Scholar] [CrossRef]
- Phukoetphim, P.; Shamseldin, A.Y.; Adams, K. Multimodel Approach Using Neural Networks and Symbolic Regression to Combine the Estimated Discharges of Rainfall-Runoff Models. J. Hydrol. Eng. 2016, 21, 04016022. [Google Scholar] [CrossRef]
- Seo, D.J. Conditional Bias-Penalized Kriging (CBPK). Stoch. Environ. Res. Risk Assess. 2013, 27, 43–58. [Google Scholar] [CrossRef]
- Schepen, A.; Wang, Q.J. Model Averaging Methods to Merge Operational Statistical and Dynamic Seasonal Streamflow Forecasts in A Ustralia. Water Resour. Res. 2015, 51, 1797–1812. [Google Scholar] [CrossRef]
- Muhammad, A.; Stadnyk, T.; Unduche, F.; Coulibaly, P. Multi-Model Approaches for Improving Seasonal Ensemble Streamflow Prediction Scheme with Various Statistical Post-Processing Techniques in the Canadian Prairie Region. Water 2018, 10, 1604. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Kishtawal, C.M.; Zhang, Z.; LaRow, T.; Bachiochi, D.; Williford, E.; Gadgil, S.; Surendran, S. Multimodel Ensemble Forecasts for Weather and Seasonal Climate. J. Clim. 2000, 13, 4196–4216. [Google Scholar] [CrossRef]
- Bates, J.M.; Granger, C.W.J. The Combination of Forecasts. J. Oper. Res. Soc. 1969, 20, 451–468. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Giorgi, F.; Mearns, L.O. Calculation of Average, Uncertainty Range, and Reliability of Regional Climate Changes from AOGCM Simulations via the “Reliability Ensemble Averaging” (REA) Method. J. Clim. 2002, 15, 1141–1158. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic Gradient Boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Hansen, B.E. Least Squares Model Averaging. Econometrica 2007, 75, 1175–1189. [Google Scholar] [CrossRef]
- Block, P.J.; Souza Filho, F.A.; Sun, L.; Kwon, H. A Streamflow Forecasting Framework Using Multiple Climate and Hydrological Models. JAWRA J. Am. Water Resour. Assoc. 2009, 45, 828–843. [Google Scholar] [CrossRef]
- Ranjan, R.; Gneiting, T. Combining Probability Forecasts. J. R. Stat. Soc. Ser. B Stat. Methodol. 2010, 72, 71–91. [Google Scholar] [CrossRef]
- Mendoza, P.A.; Rajagopalan, B.; Clark, M.P.; Cortés, G.; McPhee, J. A Robust Multimodel Framework for Ensemble Seasonal Hydroclimatic Forecasts. Water Resour. Res. 2014, 50, 6030–6052. [Google Scholar] [CrossRef]
- Wang, J.; Wang, G.; Elmahdi, A.; Bao, Z.; Yang, Q.; Shu, Z.; Song, M. Comparison of Hydrological Model Ensemble Forecasting Based on Multiple Members and Ensemble Methods. Open Geosci. 2021, 13, 401–415. [Google Scholar] [CrossRef]
- Makridakis, S.; Andersen, A.; Carbone, R.; Fildes, R.; Hibon, M.; Lewandowski, R.; Newton, J.; Parzen, E.; Winkler, R. The Accuracy of Extrapolation (Time Series) Methods: Results of a Forecasting Competition. J. Forecast. 1982, 1, 111–153. [Google Scholar] [CrossRef]
- Makridakis, S.; Winkler, R.L. Averages of Forecasts: Some Empirical Results. Manag. Sci. 1983, 29, 987–996. [Google Scholar] [CrossRef]
- Andraos, C.; Najem, W. Multi-Model Approach for Reducing Uncertainties in Rainfall-Runoff Models. In Advances in Hydroinformatics; Gourbesville, P., Caignaert, G., Eds.; Springer Water; Springer: Singapore, 2020; pp. 545–557. [Google Scholar] [CrossRef]
- Armstrong, J.S. Combining Forecasts: The End of the Beginning or the Beginning of the End? Int. J. Forecast. 1989, 5, 585–588. [Google Scholar] [CrossRef]
- Wan, Y.; Chen, J.; Xu, C.-Y.; Xie, P.; Qi, W.; Li, D.; Zhang, S. Performance Dependence of Multi-Model Combination Methods on Hydrological Model Calibration Strategy and Ensemble Size. J. Hydrol. 2021, 603, 127065. [Google Scholar] [CrossRef]
- Fiordaliso, A. A Nonlinear Forecasts Combination Method Based on Takagi–Sugeno Fuzzy Systems. Int. J. Forecast. 1998, 14, 367–379. [Google Scholar] [CrossRef]
- Bogner, K.; Liechti, K.; Zappa, M. Technical Note: Combining Quantile Forecasts and Predictive Distributions of Streamflows. Hydrol. Earth Syst. Sci. 2017, 21, 5493–5502. [Google Scholar] [CrossRef]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-Model Ensemble Hydrologic Prediction Using Bayesian Model Averaging. Adv. Water Resour. 2007, 30, 1371–1386. [Google Scholar] [CrossRef]
- Huang, H.; Liang, Z.; Li, B.; Wang, D.; Hu, Y.; Li, Y. Combination of Multiple Data-Driven Models for Long-Term Monthly Runoff Predictions Based on Bayesian Model Averaging. Water Resour. Manag. 2019, 33, 3321–3338. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Xu, C.-Y.; Liu, S.; Yuan, F.; Yang, X. Quantifying Multi-Source Uncertainties in Multi-Model Predictions Using the Bayesian Model Averaging Scheme. Hydrol. Res. 2018, 49, 954–970. [Google Scholar] [CrossRef]
- Pokhrel, P.; Wang, Q.J.; Robertson, D.E. The Value of Model Averaging and Dynamical Climate Model Predictions for Improving Statistical Seasonal Streamflow Forecasts over Australia: Statistical Dynamical Model Combination. Water Resour. Res. 2013, 49, 6671–6687. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian Model Averaging to Calibrate Forecast Ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Ibrahim, J.G. Bayesian Predictive Simultaneous Variable and Transformation Selection in the Linear Model. Comput. Stat. Data Anal. 1998, 28, 87–103. [Google Scholar] [CrossRef]
- Neuman, S.P. Maximum Likelihood Bayesian Averaging of Uncertain Model Predictions. Stoch. Environ. Res. Risk Assess. 2003, 17, 291–305. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Diks, C.G.H.; Clark, M.P. Ensemble Bayesian Model Averaging Using Markov Chain Monte Carlo Sampling. Environ. Fluid Mech. 2008, 8, 579–595. [Google Scholar] [CrossRef]
- Darbandsari, P.; Coulibaly, P. Inter-Comparison of Different Bayesian Model Averaging Modifications in Streamflow Simulation. Water 2019, 11, 1707. [Google Scholar] [CrossRef]
- Parrish, M.A.; Moradkhani, H.; DeChant, C.M. Toward Reduction of Model Uncertainty: Integration of Bayesian Model Averaging and Data Assimilation. Water Resour. Res. 2012, 48, W03519. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, W.; He, Z.; Liu, H. Application of the Takagi–Sugeno Fuzzy System for Combination Forecasting of River Flow in Semiarid Mountain Regions. Hydrol. Process. 2009, 23, 1430–1436. [Google Scholar] [CrossRef]
- Mamdani, E.H. Advances in the Linguistic Synthesis of Fuzzy Controllers. Int. J. Man-Mach. Stud. 1976, 8, 669–678. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Chen, G.; Guo, L. Evaluating a Coupled Discrete Wavelet Transform and Support Vector Regression for Daily and Monthly Streamflow Forecasting. J. Hydrol. 2014, 519, 2822–2831. [Google Scholar] [CrossRef]
- Huisman, J.A.; Breuer, L.; Bormann, H.; Bronstert, A.; Croke, B.F.W.; Frede, H.-G.; Gräff, T.; Hubrechts, L.; Jakeman, A.J.; Kite, G.; et al. Assessing the Impact of Land Use Change on Hydrology by Ensemble Modeling (LUCHEM) III: Scenario Analysis. Adv. Water Resour. 2009, 32, 159–170. [Google Scholar] [CrossRef]
- Mani, A.; Tsai, F.T.-C. Ensemble Averaging Methods for Quantifying Uncertainty Sources in Modeling Climate Change Impact on Runoff Projection. J. Hydrol. Eng. 2017, 22, 04016067. [Google Scholar] [CrossRef]
- Razavi, T.; Coulibaly, P. Improving Streamflow Estimation in Ungauged Basins Using a Multi-Modelling Approach. Hydrol. Sci. J. 2016, 61, 2668–2679. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Mathevet, T.; Perrin, C.; Michel, C. Dynamic Averaging of Rainfall-runoff Model Simulations from Complementary Model Parameterizations. Water Resour. Res. 2006, 42, 2005WR004636. [Google Scholar] [CrossRef]
- Phukoetphim, P. Multi-Model Approach for Combined Outputs of Rainfall-Runoff Models. Ph.D. Thesis, The University of Auckland, Auckland, New Zealand, 2014. [Google Scholar]
- Phukoetphim, P.; Shamseldin, A.Y.; Melvile, B.W. Knowledge Extraction from Artificial Neural Networks for Rainfall-Runoff Model Combination Systems. J. Hydrol. Eng. 2014, 19, 1422–1429. [Google Scholar] [CrossRef]
- Arsenault, R.; Essou, G.R.C.; Brissette, F.P. Improving Hydrological Model Simulations with Combined Multi-Input and Multimodel Averaging Frameworks. J. Hydrol. Eng. 2017, 22, 04016066. [Google Scholar] [CrossRef]
- Zhu, Q.; Gao, X.; Xu, Y.-P.; Tian, Y. Merging Multi-Source Precipitation Products or Merging Their Simulated Hydrological Flows to Improve Streamflow Simulation. Hydrol. Sci. J. 2019, 64, 910–920. [Google Scholar] [CrossRef]
- Goswami, M.; O’Connor, K.M.; Bhattarai, K.P. Development of Regionalisation Procedures Using a Multi-Model Approach for Flow Simulation in an Ungauged Catchment. J. Hydrol. 2007, 333, 517–531. [Google Scholar] [CrossRef]
- Abbasi, M.; Dehban, H.; Farokhnia, A.; Roozbahani, R.; Bahreinimotlagh, M. Long-Term Streamflow Prediction Using Hybrid SVR-ANN Based on Bayesian Model Averaging. J. Hydrol. Eng. 2022, 27, 05022018. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, J.; Xu, T.; Croke, B.; Jakeman, A.; Song, Y.; Yang, Q.; Lei, X.; Liao, W. Applicability Assessment and Uncertainty Analysis of Multi-Precipitation Datasets for the Simulation of Hydrologic Models. Water 2018, 10, 1611. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Treatment of Uncertainty Using Ensemble Methods: Comparison of Sequential Data Assimilation and Bayesian Model Averaging. Water Resour. Res. 2007, 43, 2005WR004838. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H.; Jung, I.W. Assessing the Uncertainties of Hydrologic Model Selection in Climate Change Impact Studies. Hydrol. Process. 2011, 25, 2814–2826. [Google Scholar] [CrossRef]
- Meira Neto, A.A.; Oliveira, P.T.S.; Rodrigues, D.B.B.; Wendland, E. Improving Streamflow Prediction Using Uncertainty Analysis and Bayesian Model Averaging. J. Hydrol. Eng. 2018, 23, 05018004. [Google Scholar] [CrossRef]
- Wang, H.; Lu, K.; Zhao, Y.; Zhang, J.; Hua, J.; Lin, X. Multi-Model Ensemble Simulated Non-Point Source Pollution Based on Bayesian Model Averaging Method and Model Uncertainty Analysis. Environ. Sci. Pollut. Res. 2020, 27, 44482–44493. [Google Scholar] [CrossRef]
- Huang, T.; Merwade, V. Uncertainty Analysis and Quantification in Flood Insurance Rate Maps Using Bayesian Model Averaging and Hierarchical BMA. J. Hydrol. Eng. 2023, 28, 04022038. [Google Scholar] [CrossRef]
- Sun, R.; Yuan, H.; Yang, Y. Using Multiple Satellite-Gauge Merged Precipitation Products Ensemble for Hydrologic Uncertainty Analysis over the Huaihe River Basin. J. Hydrol. 2018, 566, 406–420. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Hong, Y.; Yang, X.; Ma, M.; Zhang, Y.; Yuan, F. Improvement of Multi-Satellite Real-Time Precipitation Products for Ensemble Streamflow Simulation in a Middle Latitude Basin in South China. Water Resour. Manag. 2014, 28, 2259–2278. [Google Scholar] [CrossRef]
- Samadi, S.; Pourreza-Bilondi, M.; Wilson, C.A.M.E.; Hitchcock, D.B. Bayesian Model Averaging with Fixed and Flexible Priors: Theory, Concepts, and Calibration Experiments for Rainfall-Runoff Modeling. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001924. [Google Scholar] [CrossRef]
- Dong, L.; Xiong, L.; Yu, K. Uncertainty Analysis of Multiple Hydrologic Models Using the Bayesian Model Averaging Method. J. Appl. Math. 2013, 2013, 346045. [Google Scholar] [CrossRef]
- Moknatian, M.; Mukundan, R. Uncertainty Analysis of Streamflow Simulations Using Multiple Objective Functions and Bayesian Model Averaging. J. Hydrol. 2023, 617, 128961. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R.; Bosch, D. Calibration and uncertainty analysis of the SWAT model using Genetic Algorithms and Bayesian Model Averaging. J. Hydrol. 2009, 374, 307–317. [Google Scholar] [CrossRef]
- Xu, J.; Anctil, F.; Boucher, M.-A. Hydrological Post-Processing of Streamflow Forecasts Issued from Multimodel Ensemble Prediction Systems. J. Hydrol. 2019, 578, 124002. [Google Scholar] [CrossRef]
- Qu, B.; Zhang, X.; Pappenberger, F.; Zhang, T.; Fang, Y. Multi-Model Grand Ensemble Hydrologic Forecasting in the Fu River Basin Using Bayesian Model Averaging. Water 2017, 9, 74. [Google Scholar] [CrossRef]
- Dion, P.; Martel, J.-L.; Arsenault, R. Hydrological Ensemble Forecasting Using a Multi-Model Framework. J. Hydrol. 2021, 600, 126537. [Google Scholar] [CrossRef]
- Gain, A.K.; Immerzeel, W.W.; Sperna Weiland, F.C.; Bierkens, M.F.P. Impact of Climate Change on the Stream Flow of the Lower Brahmaputra: Trends in High and Low Flows Based on Discharge-Weighted Ensemble Modelling. Hydrol. Earth Syst. Sci. 2011, 15, 1537–1545. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Zhou, J.; Singh, V.P.; Guo, S.; Zhang, J. Real-Time Error Correction Method Combined with Combination Flood Forecasting Technique for Improving the Accuracy of Flood Forecasting. J. Hydrol. 2015, 521, 157–169. [Google Scholar] [CrossRef]
- Pooralihossein, S.; Delavar, M. A Multi-Model Ensemble Approach for the Assessment of Climatic and Anthropogenic Impacts on River Flow Change. Hydrol. Sci. J. 2020, 65, 71–86. [Google Scholar] [CrossRef]
- Duan, K.; Wang, X.; Liu, B.; Zhao, T.; Chen, X. Comparing Bayesian Model Averaging and Reliability Ensemble Averaging in Post-Processing Runoff Projections under Climate Change. Water 2021, 13, 2124. [Google Scholar] [CrossRef]
- Hegdahl, T.J.; Engeland, K.; Steinsland, I.; Singleton, A. Pre- and Postprocessing Flood Forecasts Using Bayesian Model Averaging. Hydrol. Res. 2023, 54, 116–135. [Google Scholar] [CrossRef]
- Azmi, M.; Araghinejad, S.; Kholghi, M. Multi Model Data Fusion for Hydrological Forecasting Using K-Nearest Neighbor Method. Iran. J. Sci. Technol. Trans. B Eng. 2010, 34, 81–92. [Google Scholar]
- Awol, F.S.; Coulibaly, P.; Tsanis, I. Identification of Combined Hydrological Models and Numerical Weather Predictions for Enhanced Flood Forecasting in a Semiurban Watershed. J. Hydrol. Eng. 2021, 26, 04020057. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).