Comparison of Machine Learning-Based Predictive Models of the Nutrient Loads Delivered from the Mississippi/Atchafalaya River Basin to the Gulf of Mexico
Abstract
1. Introduction
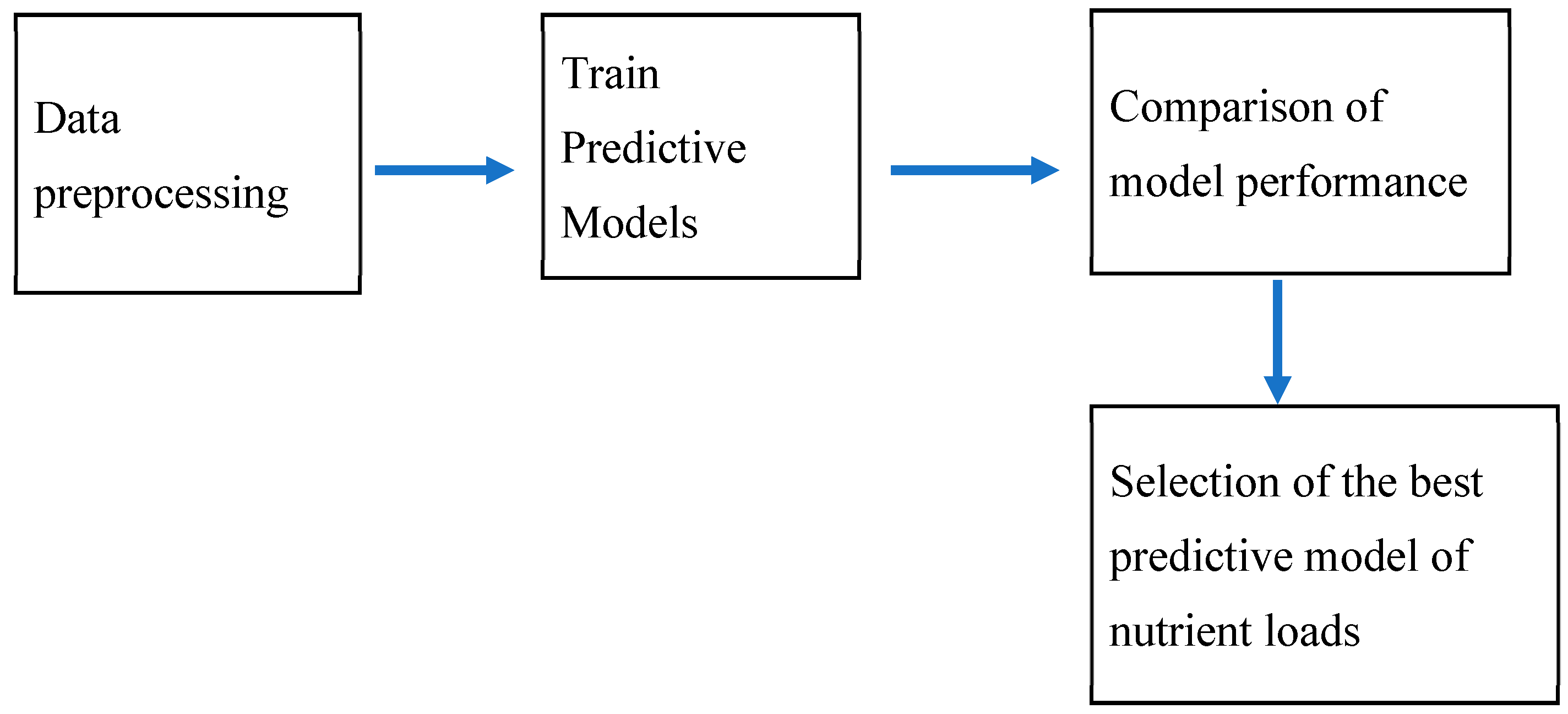
2. Materials and Methods
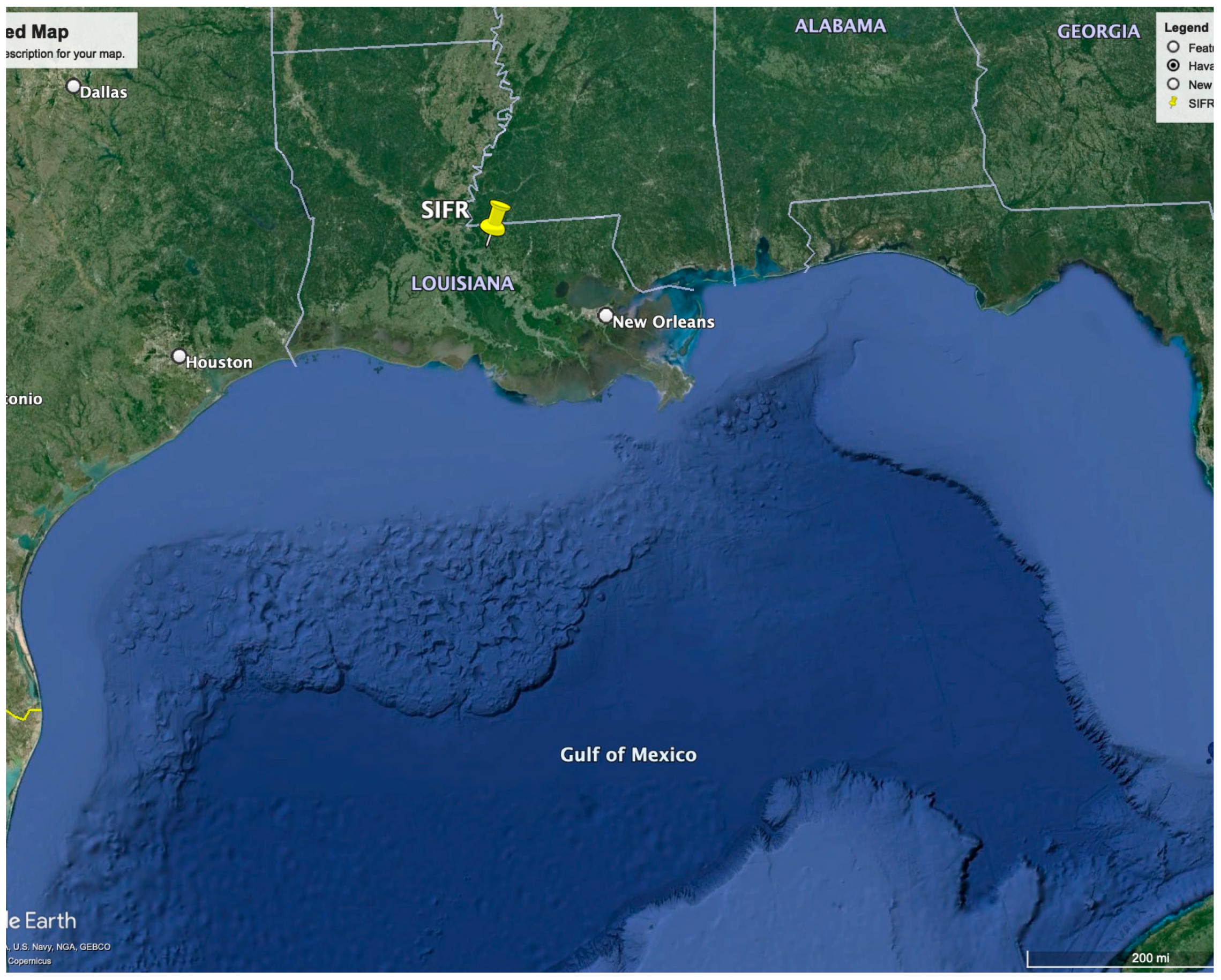
2.1. Study Site and Data
2.1.1. Data Processing
2.1.2. Assessment Metric
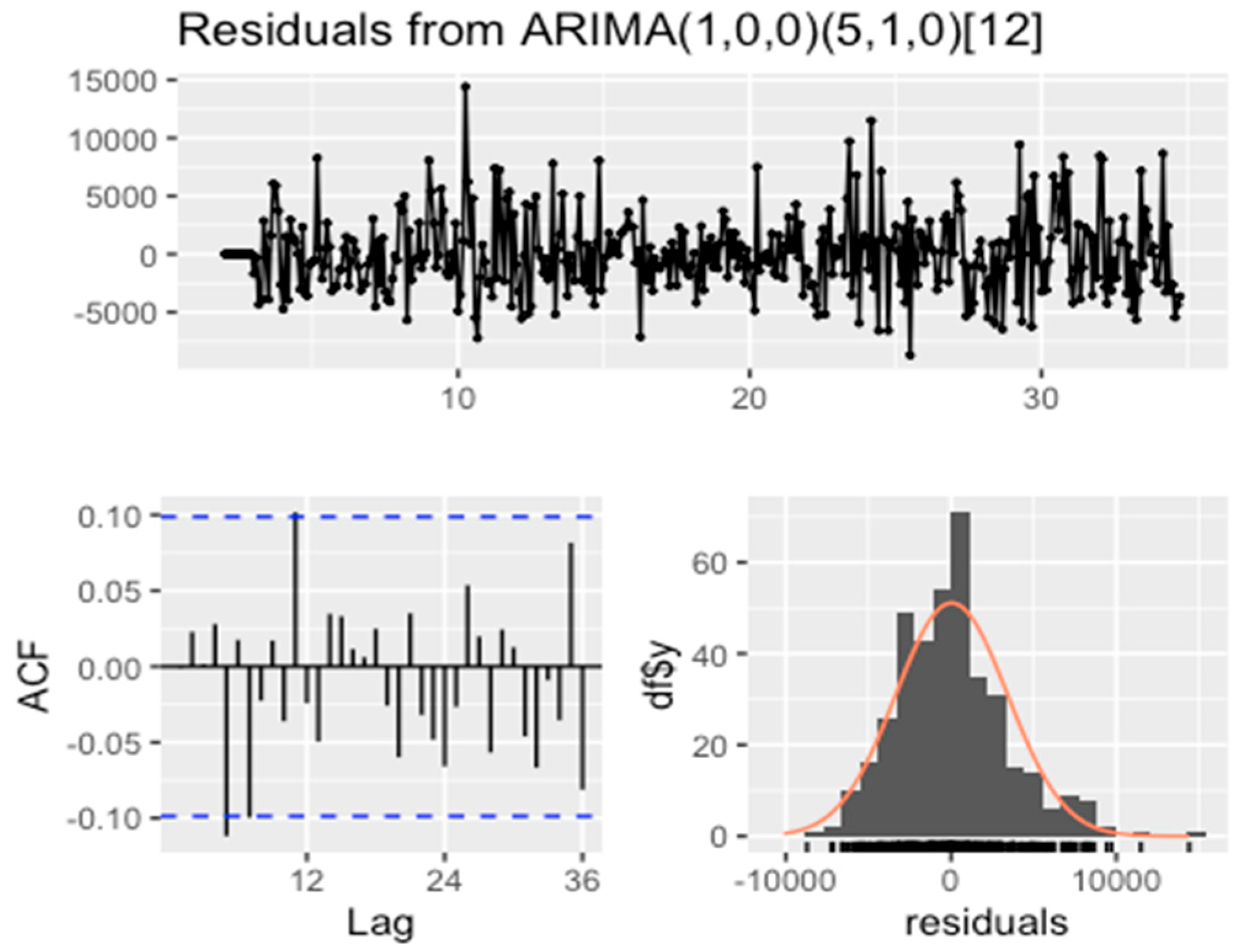
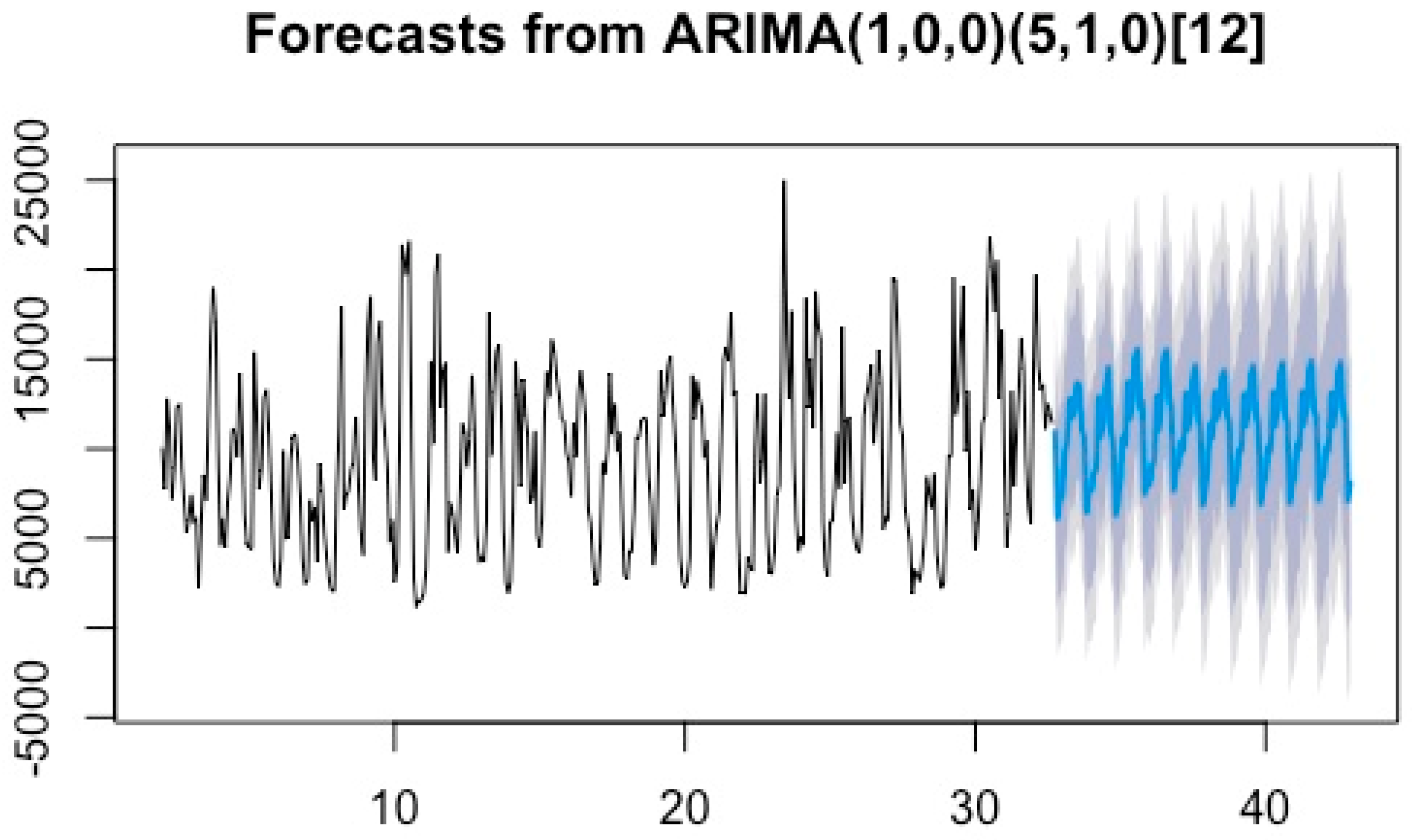
2.2. Description of the ARIMA Model
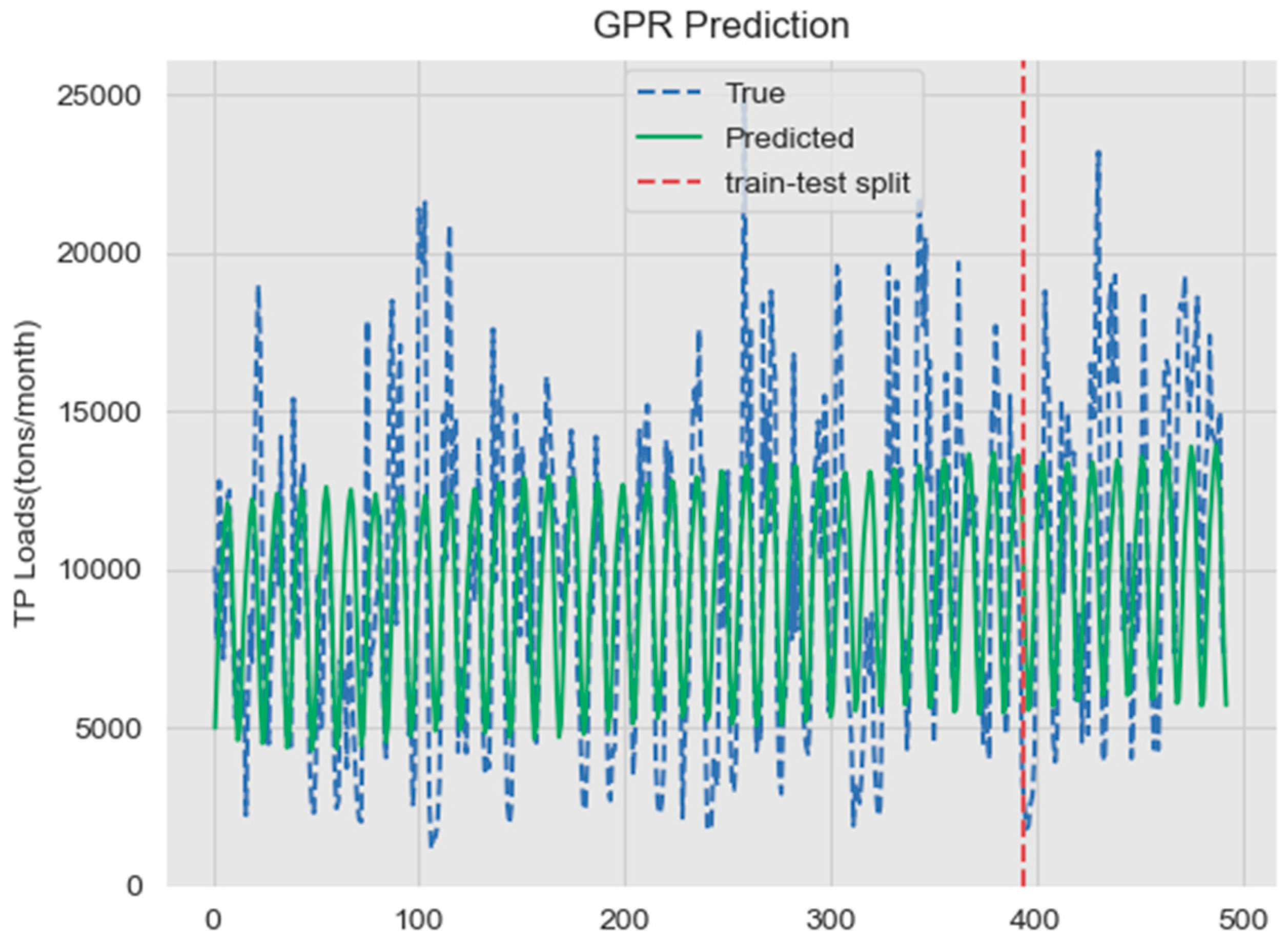
2.3. Description of the GPR Model
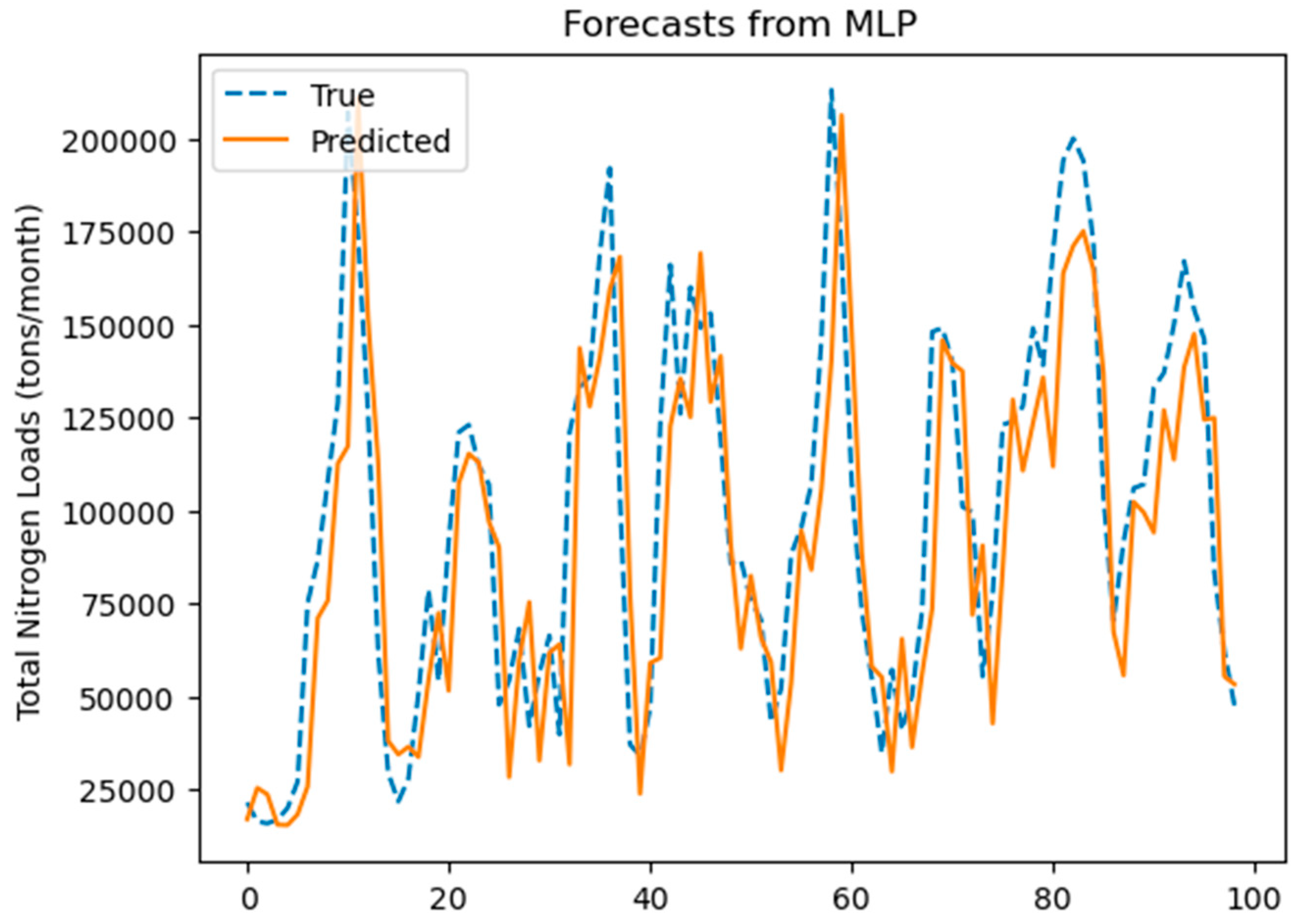
2.4. Description of the MLP Model
2.5. Description of LSTM Model
3. Results
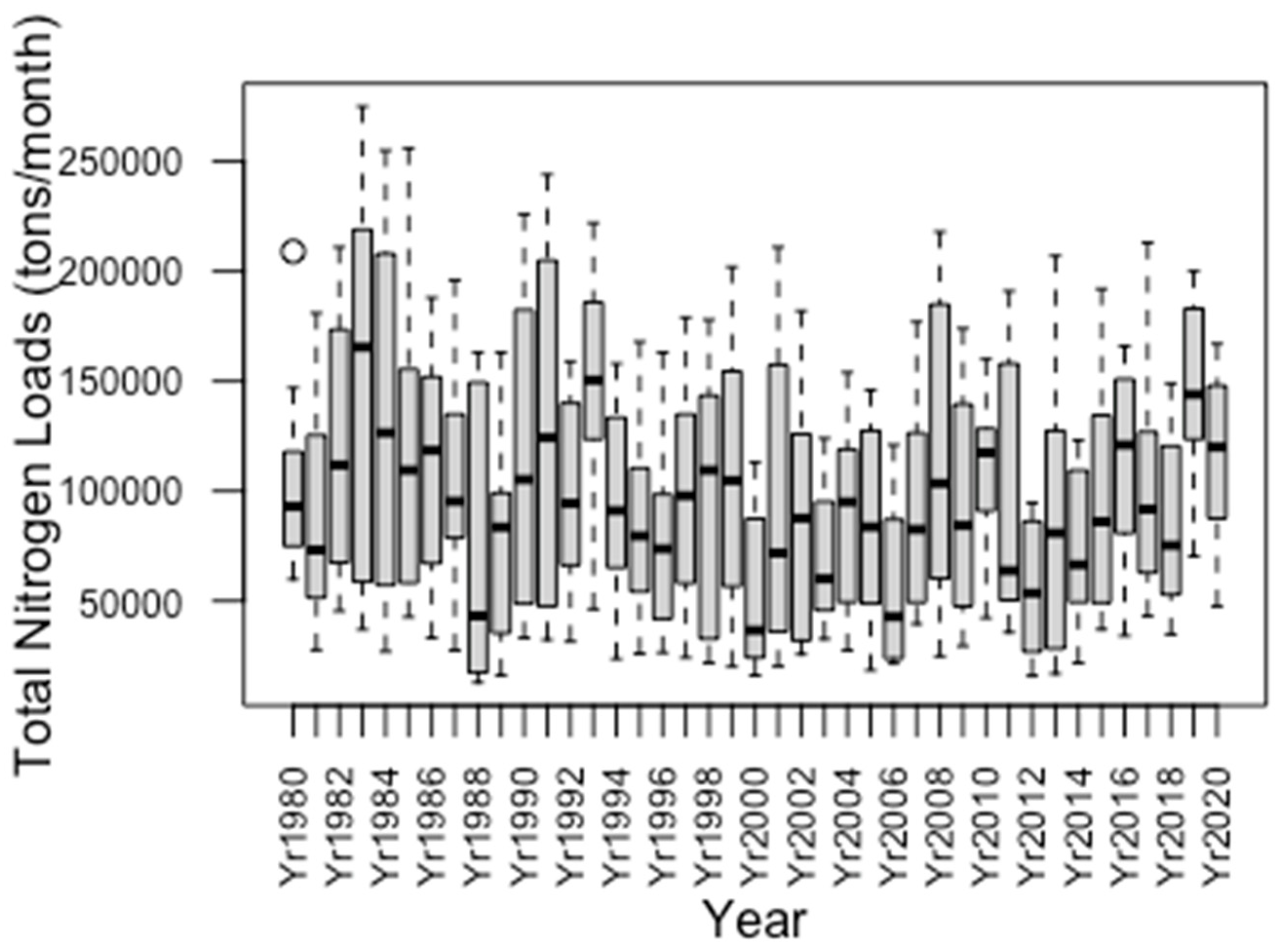
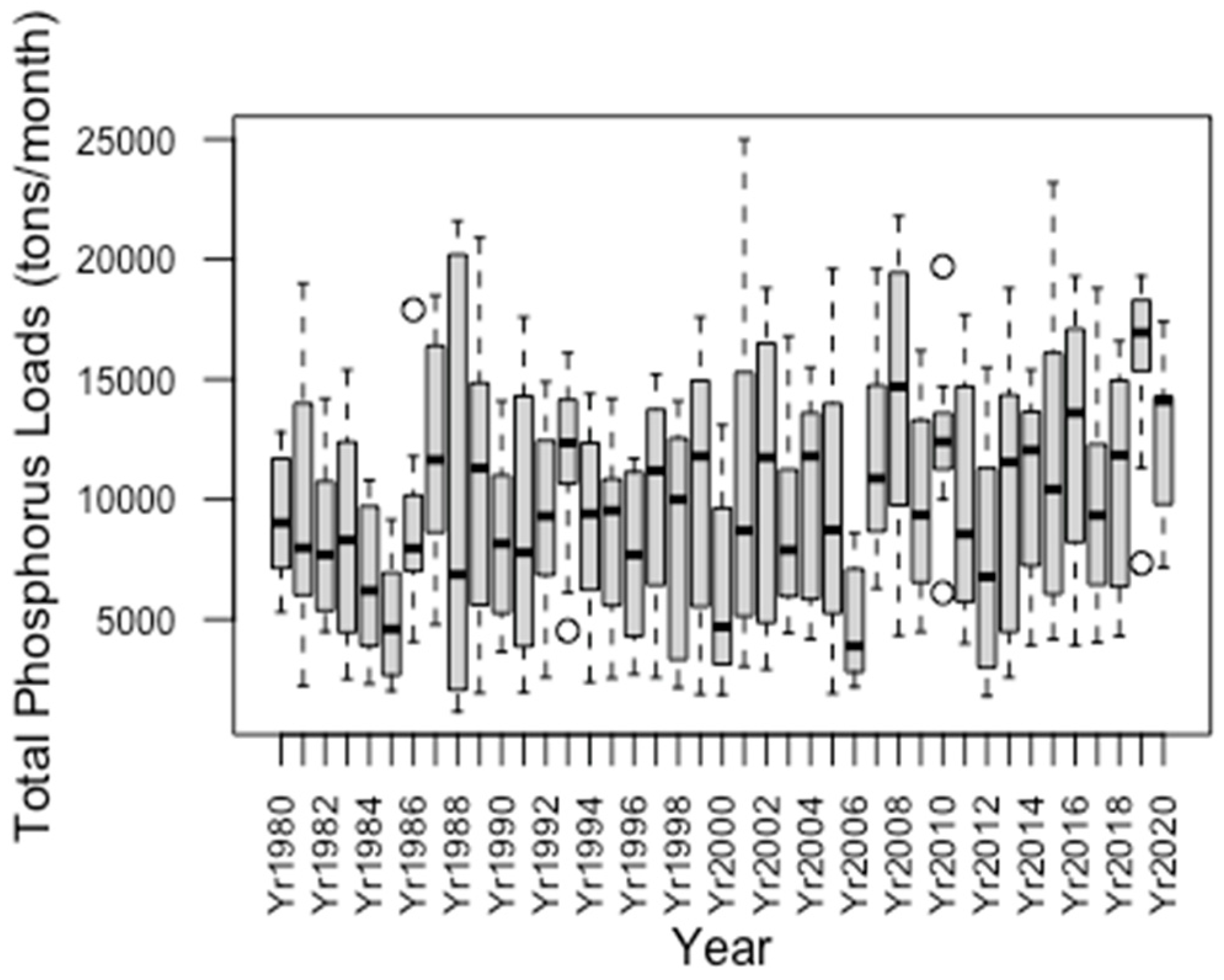
3.1. Annual Variation
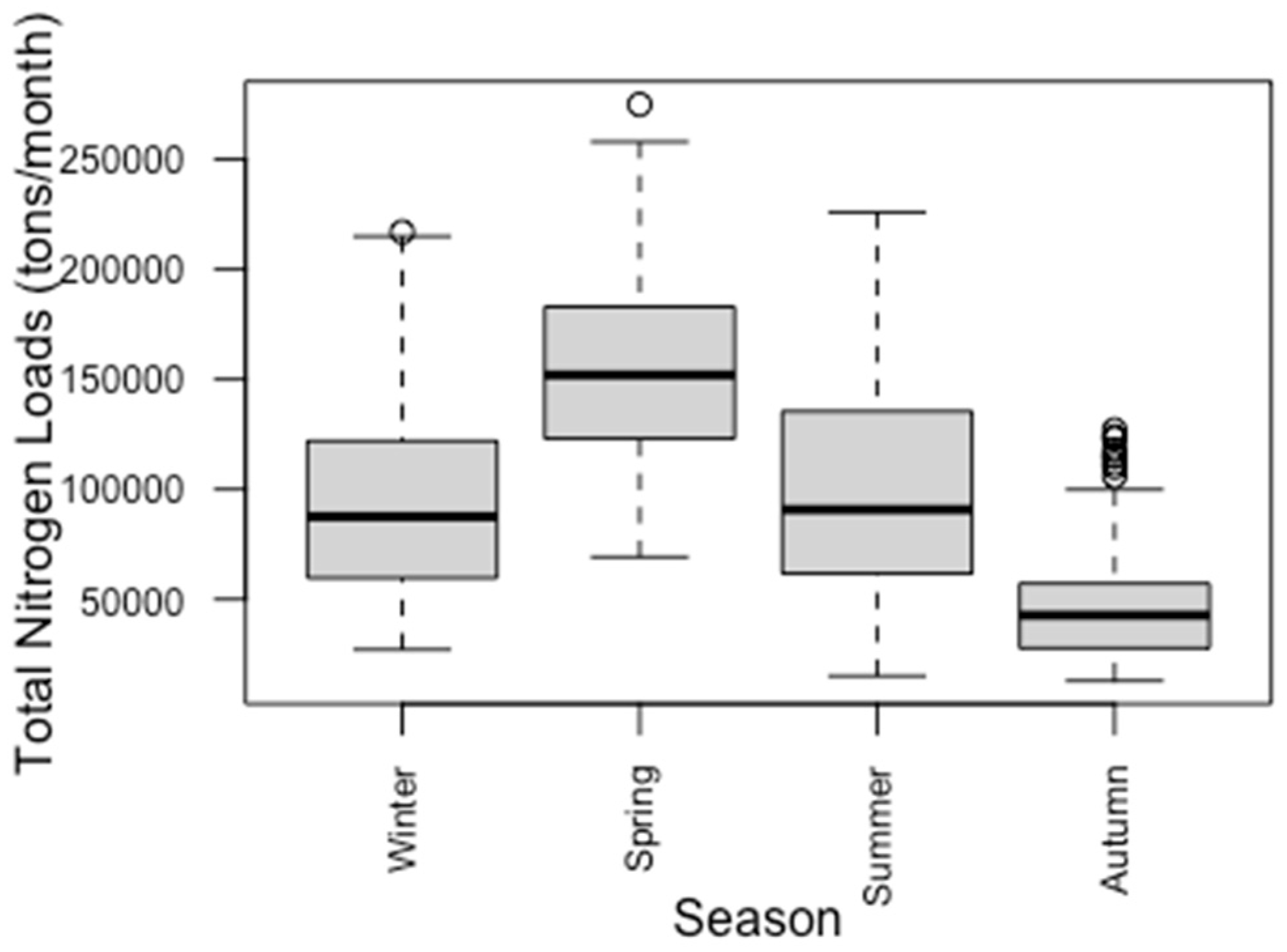
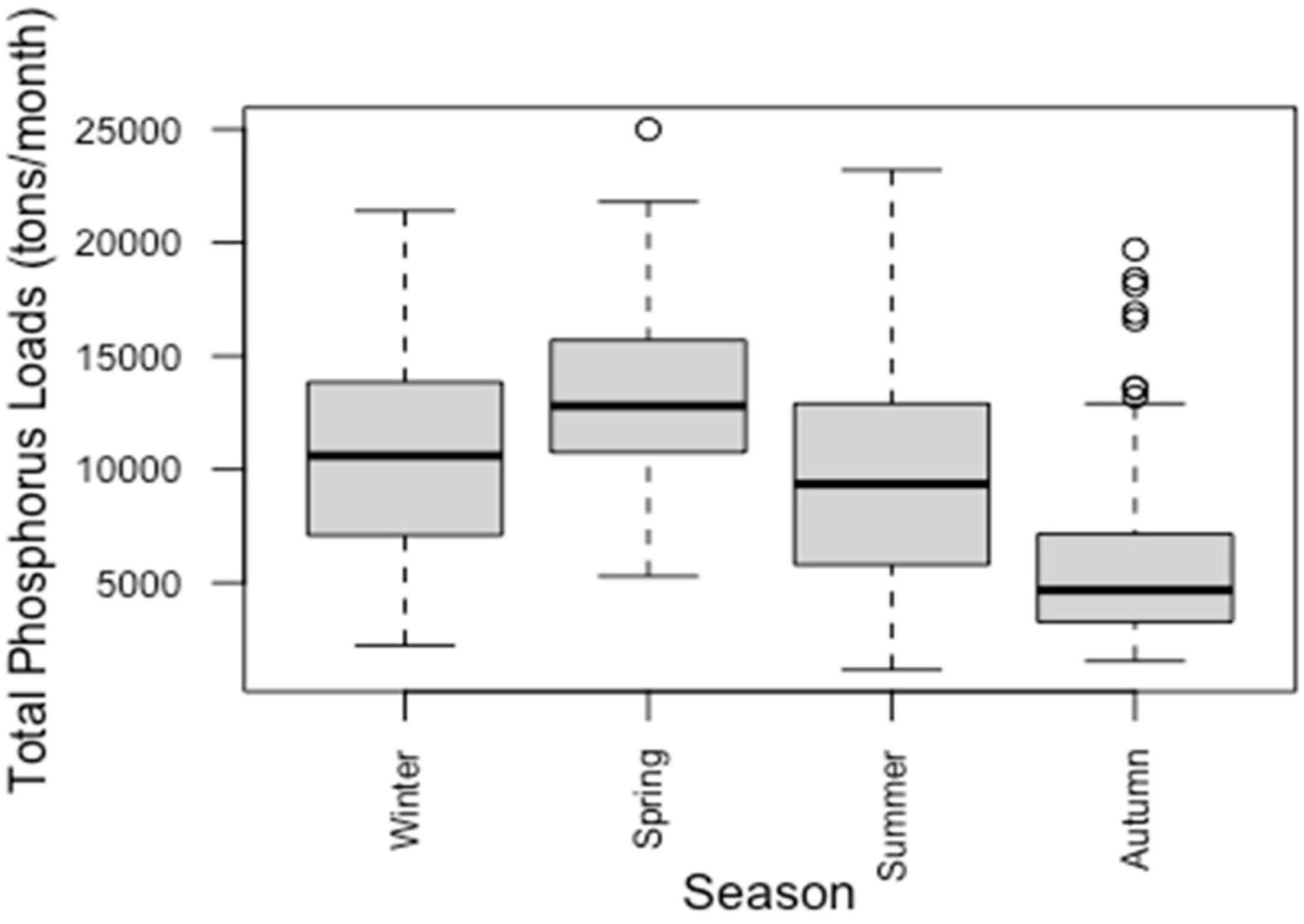
3.2. Seasonal Variations
3.3. Nutrient Loads Prediction
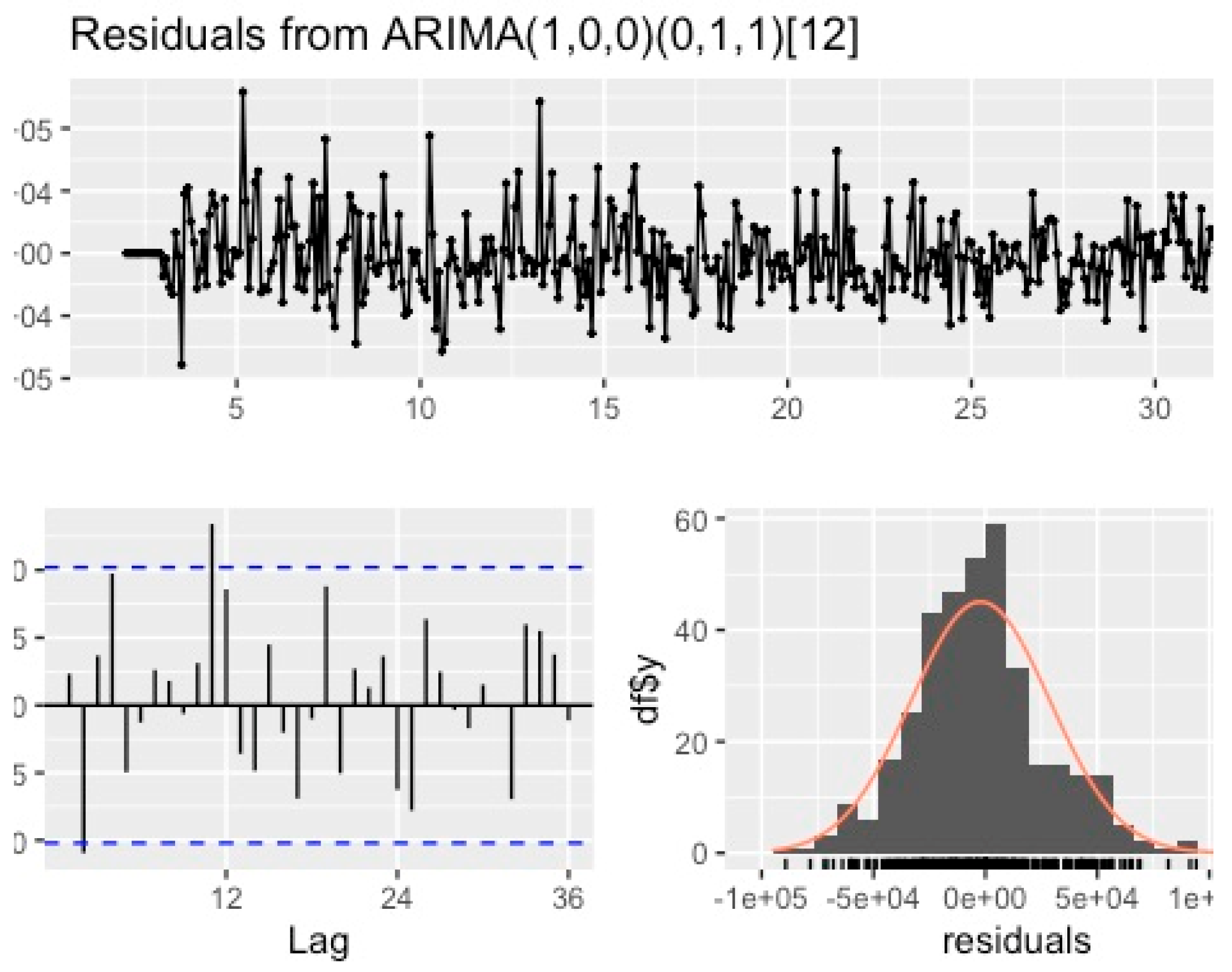
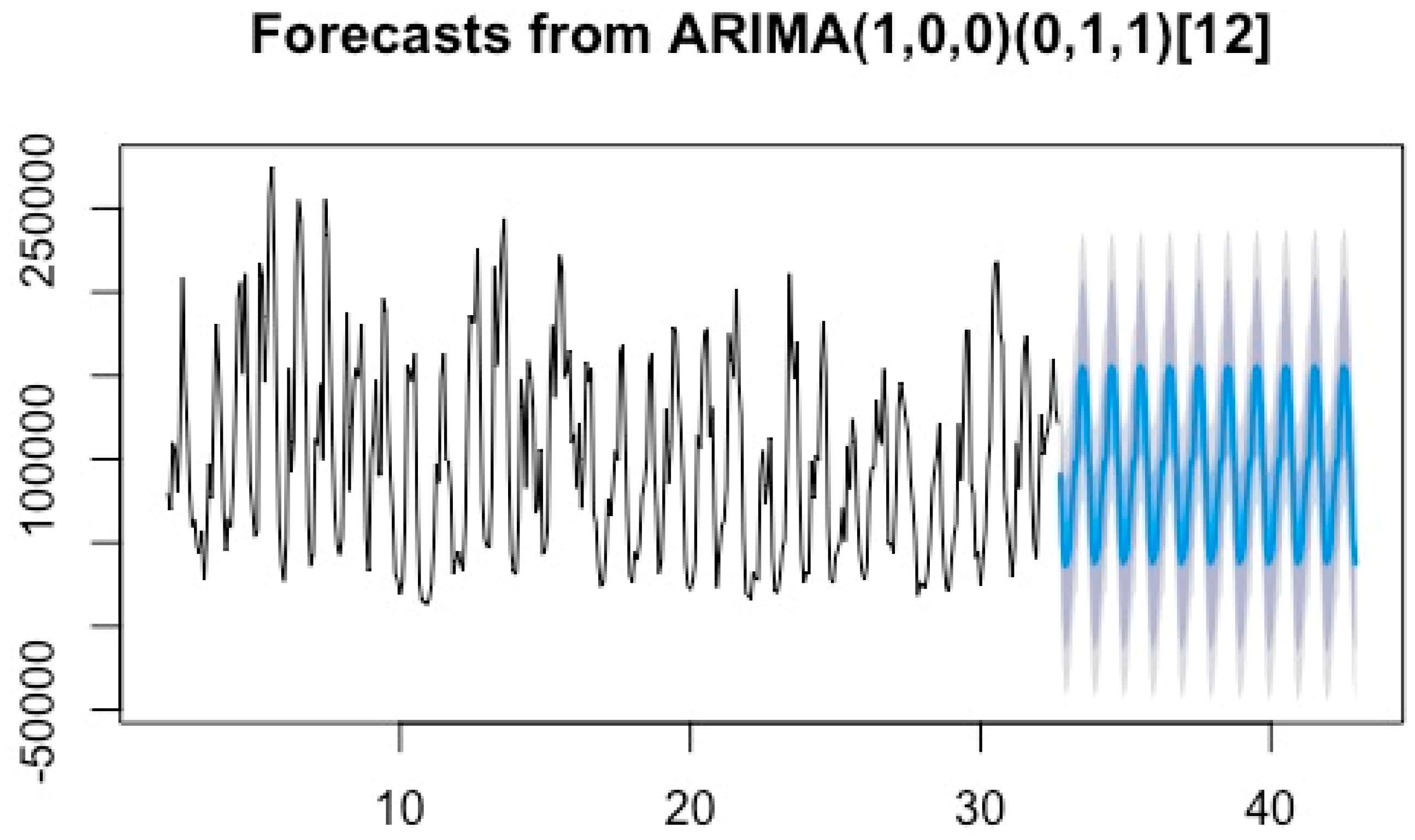
3.3.1. ARIMA Prediction
3.3.2. GPR Prediction
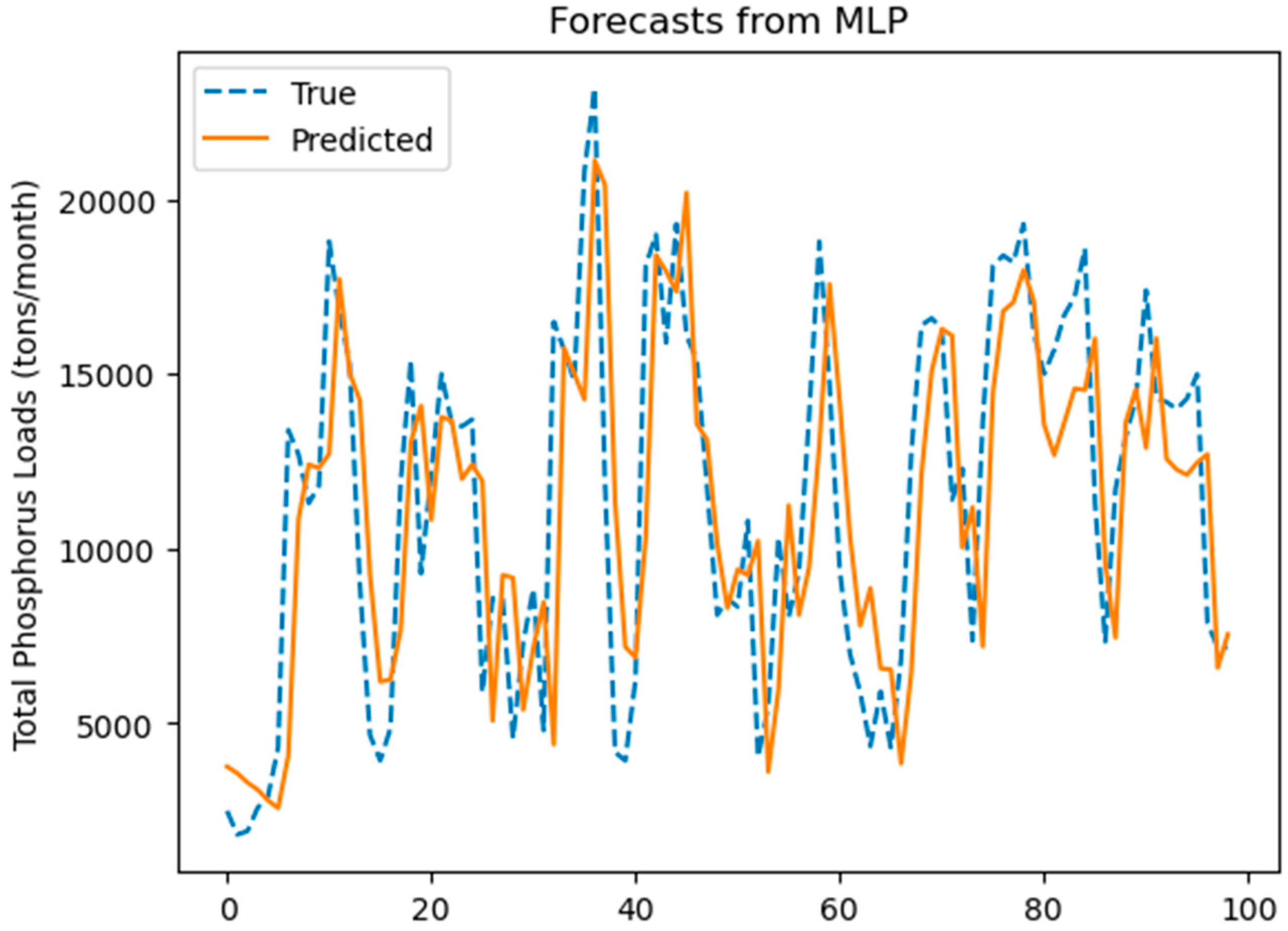
3.3.3. MLP Prediction
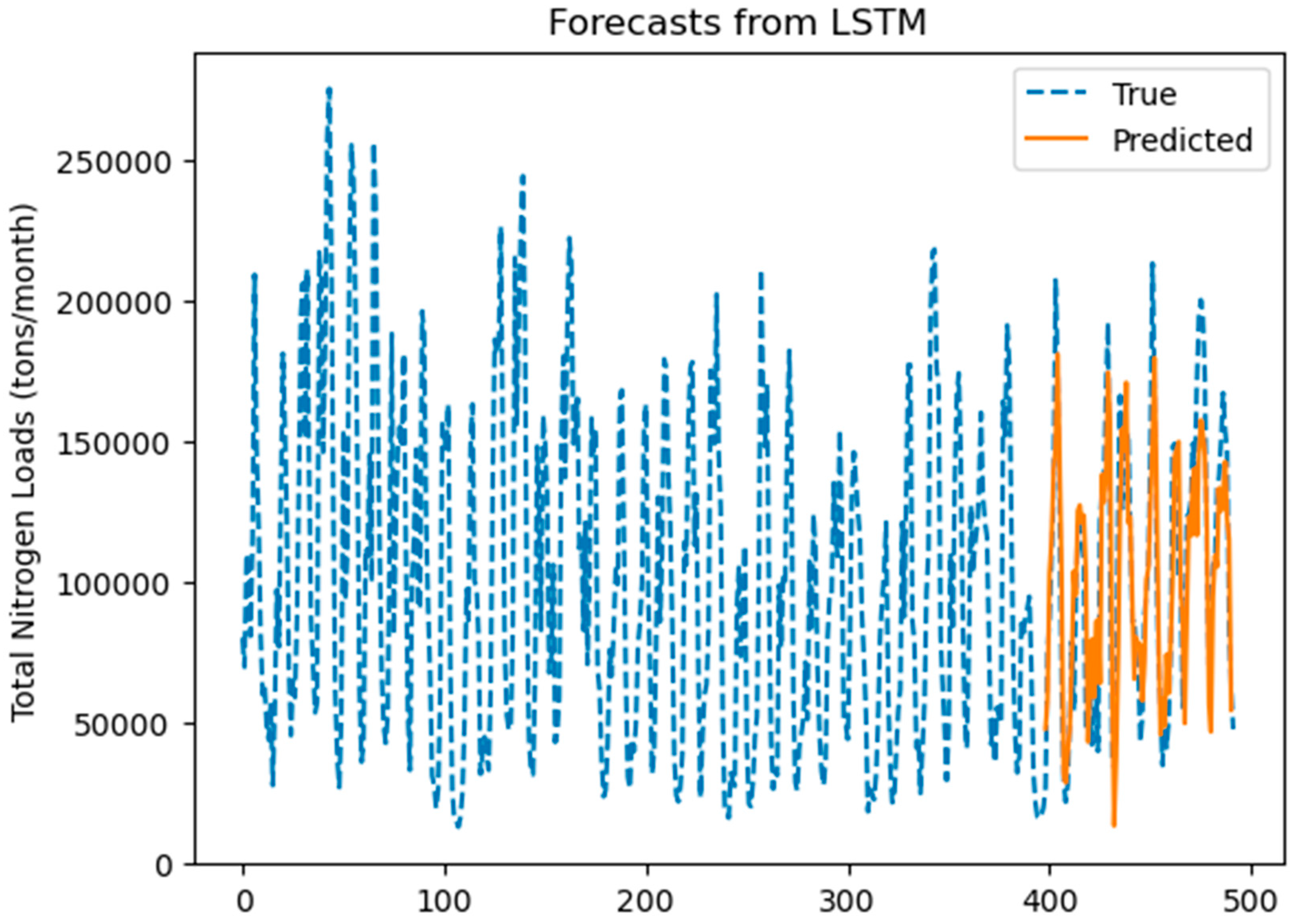
3.3.4. LSTM Prediction
3.3.5. Evaluation of Model Performance
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diaz, R.J.; Rosenberg, R. Spreading Dead Zones and Consequences for Marine Ecosystems. Science 2008, 321, 926–929. [Google Scholar] [CrossRef] [PubMed]
- U.S. Environmental Protection Agency (USEPA). Nutrient Criteria Technical Guidance Manual—Lakes and Reservoirs; U.S. Environmental Protection Agency, Office of Water: Washington, DC, USA, 2000; 232p.
- Robertson, D.M.; Schwarz, G.E.; Saad, D.A.; Alexander, R.A. Incorporating Uncertainty into the Ranking of SPARROW Model Nutrient Yields from Mississippi/Atchafalaya River Basin Watersheds. J. Am. Water Resour. Assoc. 2009, 45, 534. [Google Scholar] [CrossRef] [PubMed]
- Robertson, D.M.; Saad, D.A. Nitrogen and Phosphorus Sources and Delivery from the Mississippi/Atchafalaya River Basin: An Update Using 2012 SPARROW Models. J. Am. Water Resour. Assoc. 2021, 57, 406. [Google Scholar] [CrossRef]
- Nie, J.; Mirza, S.; Viteritto, M.; Li, Y.; Witherell, B.B.; Deng, Y.; Yoo, S.; Feng, H. Estimation of nutrient (N and P) fluxes into Newark Bay, USA. Mar. Pollut. Bull. 2023, 190, 114832. [Google Scholar] [CrossRef]
- He, S.; Chu, T.-J.; Lu, Z.; Li, D. Coupling Imports of Dissolved Inorganic Nitrogen and Particulate Organic Matter by Aquaculture Sewage to Zhangjiang Estuary, Southeastern China. Water 2024, 16, 2054. [Google Scholar] [CrossRef]
- Morales-Marín, L.A.; Chun, K.P.; Wheater, H.S.; Lindenschmidt, K.E. Trend analysis of nutrient loadings in a large prairie catchment. Hydrol. Sci. J. 2017, 62, 657. [Google Scholar] [CrossRef]
- Feng, H.; Qian, Y.; Cochran, J.K.; Zhu, Q.; Hu, W.; Yan, H.; Li, L.; Huang, X.; Chu, Y.S.; Liu, H.; et al. Nanoscale measurement of trace element distributions in Spartina alterniflora root tissue during dormancy. Sci. Rep. 2017, 7, 40420. [Google Scholar] [CrossRef]
- Antonopoulos, V.Z.; Papamichail, D.M.; Mitsiou, K.A. Statistical and trend analysis of water quality and quantity data for the Strymon River in Greece. Hydrol. Earth Syst. Sci. 2001, 5, 679. [Google Scholar] [CrossRef]
- Alexander, R.B.; Smith, R.A. Trends in the nutrient enrichment of U.S. rivers during the late 20th century and their relation to changes in probable stream trophic conditions. Limnol. Oceanogr. 2006, 51, 639. [Google Scholar] [CrossRef]
- Fernández del Castillo, A.; Yebra-Montes, C.; Verduzco Garibay, M.; de Anda, J.; Garcia-Gonzalez, A.; Gradilla-Hernández, M.S. Simple Prediction of an Ecosystem-Specifific Water Quality Index and the Water Quality Classifification of a Highly Polluted River through Supervised Machine Learning. Water 2022, 14, 1235. [Google Scholar] [CrossRef]
- Du, J.L.; Feng, H.; Nie, J.; Li, Y.; Witherell, B.B. Characterisation and assessment of spatiotemporal variations in nutrient concentrations and fluxes in an urban watershed: Passaic River Basin, New Jersey, USA. Int. J. Environ. Pollut. 2018, 63, 154. [Google Scholar] [CrossRef]
- LIoyd, C.E.M.; Freer, J.E.; Johnes, P.J.; Collins, A.L. Using hysteresis analysis of high-resolution water quality monitoring data, including uncertainty, to infer controls on nutrient and sediment transfer in catchments. Sci. Total Environ. 2016, 543, 388. [Google Scholar] [CrossRef]
- Goolsby, D.A.; Battaglin, W.A.; Lawrence, G.B.; Artz, R.S.; Aulenbach, B.T.; Hooper, R.P.; Keeney, D.R.; Stensland, G.J. Flux and Sources of Nutrients in the Mississippi-Atchafalaya River Basin: Topic 3 Report for the Integrated Assessment on Hypoxia in the Gulf of Mexico; NOAA Coastal Ocean Program Decision Analysis Series No. 17; NOAA Coastal Ocean Program: Silver Spring, MD, USA, 1999; 130p. [Google Scholar]
- David, M.B.; Drinkwater, L.E.; McIssac, G.F. Sources of Nitrate Yields in the Mississippi River Basin. J. Environ. Qual. 2010, 39, 1657. [Google Scholar] [CrossRef]
- Jacobson, L.M.; David, M.B.; Drinkwater, L.E. A Spatial Analysis of Phosphorus in the Mississippi River Basin. J. Environ. Qual. 2011, 40, 931. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Qian, Y.; Cochran, J.K.; Zhu, Q.; Heilbrun, C.; Li, L.; Hu, W.; Yan, H.; Huang, X.; Ge, M.; et al. Seasonal differences in trace element concentrations and distribution in Spartina alterniflora root tissue. Chemosphere 2018, 204, 359. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, S.G.; Schreiber, S.; Tanna, R.N.; Roberts, D.R.; Arciszewski, T.J. Statistical tools for water quality assessment and monitoring in river ecosystems—A scoping review and recommendations for data analysis. Water Qual. Res. J. 2022, 57, 40. [Google Scholar] [CrossRef]
- de Andrade Costa, D.; Soares de Azevedo, J.P.; dos Santos, M.A.; dos Santos, R. Water quality assessment based on multivariate statistics and water quality index of a strategic river in the Brazilian Atlantic Forest. Sci. Rep. 2020, 10, 22038. [Google Scholar] [CrossRef]
- Yang, W.; Zhao, Y.; Wang, D.; Wu, H.; Lin, A.; He, L. Using Principal Components Analysis and IDW Interpolation to Determine Spatial and Temporal Changes of Surface Water Quality of Xin’anjiang River in Huangshan, China. Int. J. Environ. Res. Public Health 2020, 17, 2942. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Singh, K.P.; Malik, A.; Mohan, D.; Sinha, S. Multivariate statistical techniques for the evaluation of spatial and temporal variations in water quality of Gomti River (India)—A case study. Water Res. 2004, 38, 3980. [Google Scholar] [CrossRef]
- Dutta, S.; Dwivedi, A.; SureshKumar, M. Use of water quality index and multivariate statistical techniques for the assessment of spatial variations in water quality of a small river. Environ. Monit. Assess. 2018, 190, 718. [Google Scholar] [CrossRef]
- Zhen, Y.; Feng, H.; Yoo, S. Structuring Nutrient Yields throughout Mississippi/Atchafalaya River Basin Using Machine Learning Approaches. Environments 2023, 10, 162. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Worku, T.; Khare, D.; Tripathi, S. Modeling runoff–sediment response to land use/land cover changes using integrated GIS and SWAT model in the Beressa watershed. Environ. Earth Sci. 2017, 76, 550. [Google Scholar] [CrossRef]
- Robertson, D.M.; Saad, D.A. SPARROW Models Used to Understand Nutrient Sources in the Mississippi/Atchafalaya River Basin. J. Environ. Qual. 2013, 42, 1422. [Google Scholar] [CrossRef]
- Robertson, D.M.; Saad, D.A.; Schwarz, G.E. Spatial Variability in Nutrient Transport by HUC8, State, and Subbasin based on Mississippi/Atchafalaya River Basin SPARROW models. J. Am. Water Resour. Assoc. 2014, 50, 988. [Google Scholar] [CrossRef]
- Adebiyi, A.A.; Adewumi, A.O.; Ayo, C.K. Stock Price Prediction Using the ARIMA Model. In Proceedings of the UKSim-AMSS 16th International Conference on Computer Modeling and Simulation, Cambridge, UK, 26–28 March 2014. [Google Scholar]
- Alonso, A.M.; Garcia-Martos, C. Time Series Analysis—Forecasting with ARIMA Models; Universidad Carlos III de Madrid: Madrid, Spain; Universidad Politecnica de Madrid: Madrid, Spain, 2012. [Google Scholar]
- Brownlee, J. Time Series Prediction with LSTM Recurrent Neural Networks in Python with Keras. 2016. Available online: https://machinelearningmastery.com/time-series-prediction-lstm-recurrent-neural-networks-python-keras/ (accessed on 20 May 2019).
- Box, G.; Jenkins, G. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Earnest, A.; Chen, M.I.; Ng, D.; Sin, L.Y. Using Autoregressive Integrated Moving Average (ARIMA) Models to Predict and Monitor the Number of Beds Occupied During a SARS Outbreak in a Tertiary Hospital in Singapore. BMC Health Serv. Res. 2005, 5, 36. [Google Scholar] [CrossRef] [PubMed]
- Krauss, C.; Do, X.A.; Huck, N. Deep neural networks, gradient- boosted trees, random forests: Statistical arbitrage on the S&P 500. Eur. J. Oper. Res. 2017, 259, 689. [Google Scholar] [CrossRef]
- Patterson, J.; Gibson, A. Deep Learning: A Practitioner’s Approach; O’Reilly Media: Sevastopol, CA, USA, 2017; ISBN 10 1491914254/13: 978-1491914250. [Google Scholar]
- Bhandari, H.N.; Rimal, B.; Pokhrel, N.R.; Rimal, R.; Dahal, K.R.; Khatri, R.K.C. Predicting stock market index using LSTM. Mach. Learn. Appl. 2022, 9, 100320. [Google Scholar] [CrossRef]
- Hochreiter, S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 1998, 6, 107. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; ISBN 978-0-262-18253-9. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Lebanon, IN, USA, 1994. [Google Scholar]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735. [Google Scholar] [CrossRef]


| No. of Neurons | Optimizer | No. of Epochs | Batch Size | No. of Inputs | Average Test RMSE | Average R Score | The Durbin–Watson Statistic of Residuals |
|---|---|---|---|---|---|---|---|
| 10 | Rmsprop | 50 | 1 | 6 | 29,779.76 | 0.656 | 1.7493 |
| 30 | Nadam | 50 | 1 | 5 | 29,690.46 | 0.644 | 1.6609 |
| 50 | Adam | 50 | 1 | 5 | 29,454.62 | 0.661 | 1.8440 |
| 100 | Nadam | 50 | 1 | 5 | 29,463.61 | 0.661 | 1.8209 |
| 150 | Adam | 150 | 1 | 2 | 31,195.69 | 0.619 | 1.7408 |
| 200 | Adam | 50 | 1 | 2 | 29,614.52 | 0.620 | 1.7352 |
| No. of Neurons | Optimizer | No. of Epochs | Batch Size | No. of Inputs | Average Test RMSE | Average R Score | The Durbin–Watson Statistic of Residuals |
|---|---|---|---|---|---|---|---|
| 10 | Adam | 100 | 2 | 6 | 3692.70 | 0.485 | 1.9298 |
| 30 | Adam | 100 | 1 | 5 | 3692.94 | 0.477 | 1.8508 |
| 50 | Adam | 100 | 2 | 5 | 3682.14 | 0.488 | 1.8604 |
| 100 | Adam | 50 | 4 | 5 | 3661.15 | 0.486 | 1.8574 |
| 150 | Adam | 50 | 2 | 5 | 3659.85 | 0.492 | 1.8736 |
| 200 | Nadam | 50 | 8 | 6 | 3645.58 | 0.492 | 1.8964 |
| No. of Neurons | Optimizer | No. of Epochs | Batch Size | No. Of Inputs | Average Test RMSE | Average R Score | The Durbin–Watson Statistic of Residuals |
|---|---|---|---|---|---|---|---|
| 10 | Nadam | 100 | 1 | 4 | 28,199.36 | 0.685 | 1.5490 |
| 30 | Nadam | 100 | 1 | 4 | 27,298.64 | 0.707 | 1.5024 |
| 50 | Adam | 100 | 4 | 4 | 27,560.25 | 0.710 | 1.7185 |
| 100 | Adam | 100 | 8 | 4 | 27,251.68 | 0.707 | 1.6255 |
| 150 | Adam | 100 | 1 | 4 | 28,003.56 | 0.695 | 1.6555 |
| 200 | Nadam | 100 | 1 | 4 | 28,015.95 | 0.696 | 1.7363 |
| No. of Neurons | Optimizer | No. of Epochs | Batch Size | No. of Inputs | Average Test RMSE | Average R Score | The Durbin–Watson Statistic of Residuals |
|---|---|---|---|---|---|---|---|
| 10 | Nadam | 200 | 4 | 2 | 3748.94 | 0.484 | 1.7189 |
| 30 | Nadam | 100 | 1 | 2 | 3684.78 | 0.482 | 1.5469 |
| 50 | Rmsprop | 100 | 1 | 5 | 3742.03 | 0.482 | 1.6803 |
| 100 | Rmsprop | 150 | 1 | 2 | 3734.91 | 0.469 | 1.8065 |
| 150 | Adam | 100 | 4 | 2 | 3704.34 | 0.486 | 1.5498 |
| 200 | Rmsprop | 50 | 1 | 1 | 3737.01 | 0.479 | 1.5694 |
| Model Type | Test RMSE Score | R-Squared Score |
|---|---|---|
| ARIMA | 34,710.54 | 0.760 |
| MLP | 29,454.62 | 0.661 |
| LSTM | 27,251.68 | 0.707 |
| GPR | 33,035.13 | 0.551 |
| Model Type | Test RMSE Score | R-Squared Score |
|---|---|---|
| ARIMA | 4390.63 | 0.587 |
| MLP | 3645.58 | 0.492 |
| LSTM | 3684.78 | 0.482 |
| GPR | 4367.47 | 0.136 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhen, Y.; Feng, H.; Yoo, S. Comparison of Machine Learning-Based Predictive Models of the Nutrient Loads Delivered from the Mississippi/Atchafalaya River Basin to the Gulf of Mexico. Water 2024, 16, 2857. https://doi.org/10.3390/w16192857
Zhen Y, Feng H, Yoo S. Comparison of Machine Learning-Based Predictive Models of the Nutrient Loads Delivered from the Mississippi/Atchafalaya River Basin to the Gulf of Mexico. Water. 2024; 16(19):2857. https://doi.org/10.3390/w16192857
Chicago/Turabian StyleZhen, Yi, Huan Feng, and Shinjae Yoo. 2024. "Comparison of Machine Learning-Based Predictive Models of the Nutrient Loads Delivered from the Mississippi/Atchafalaya River Basin to the Gulf of Mexico" Water 16, no. 19: 2857. https://doi.org/10.3390/w16192857
APA StyleZhen, Y., Feng, H., & Yoo, S. (2024). Comparison of Machine Learning-Based Predictive Models of the Nutrient Loads Delivered from the Mississippi/Atchafalaya River Basin to the Gulf of Mexico. Water, 16(19), 2857. https://doi.org/10.3390/w16192857








