Steady-State Shape Factor for a Slug Test in an Unconfined Aquifer
Abstract
1. Introduction
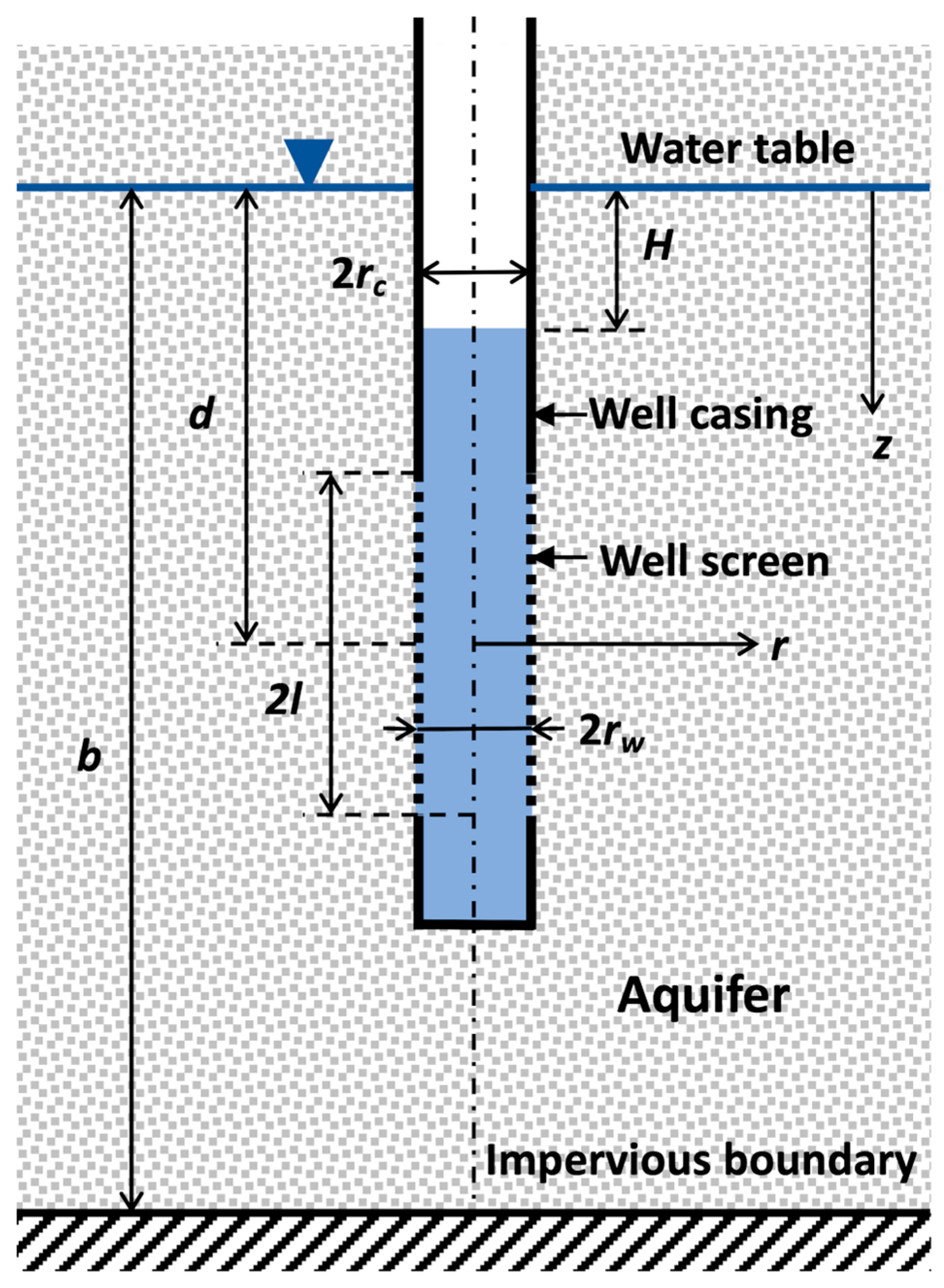
2. Materials and Methods
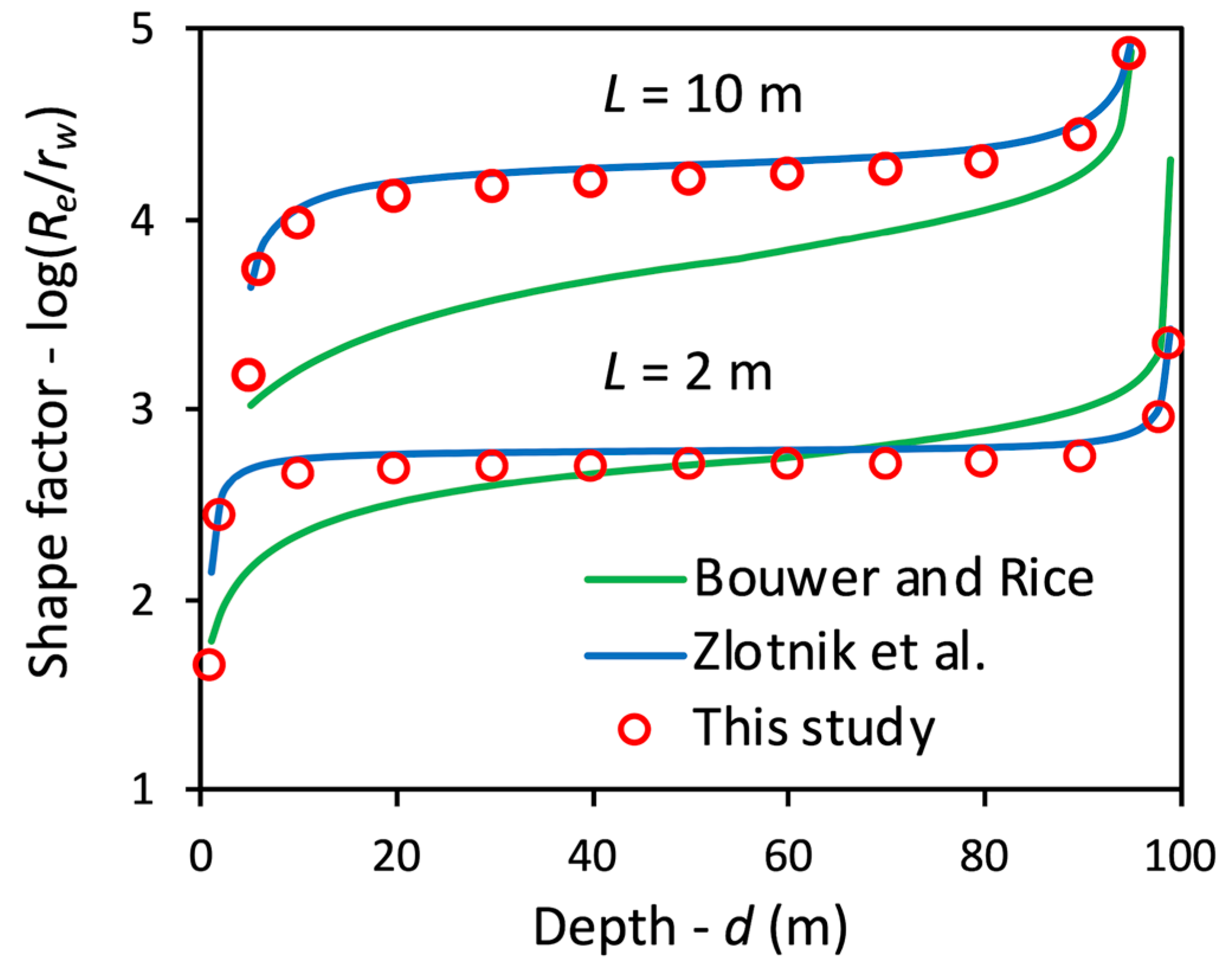
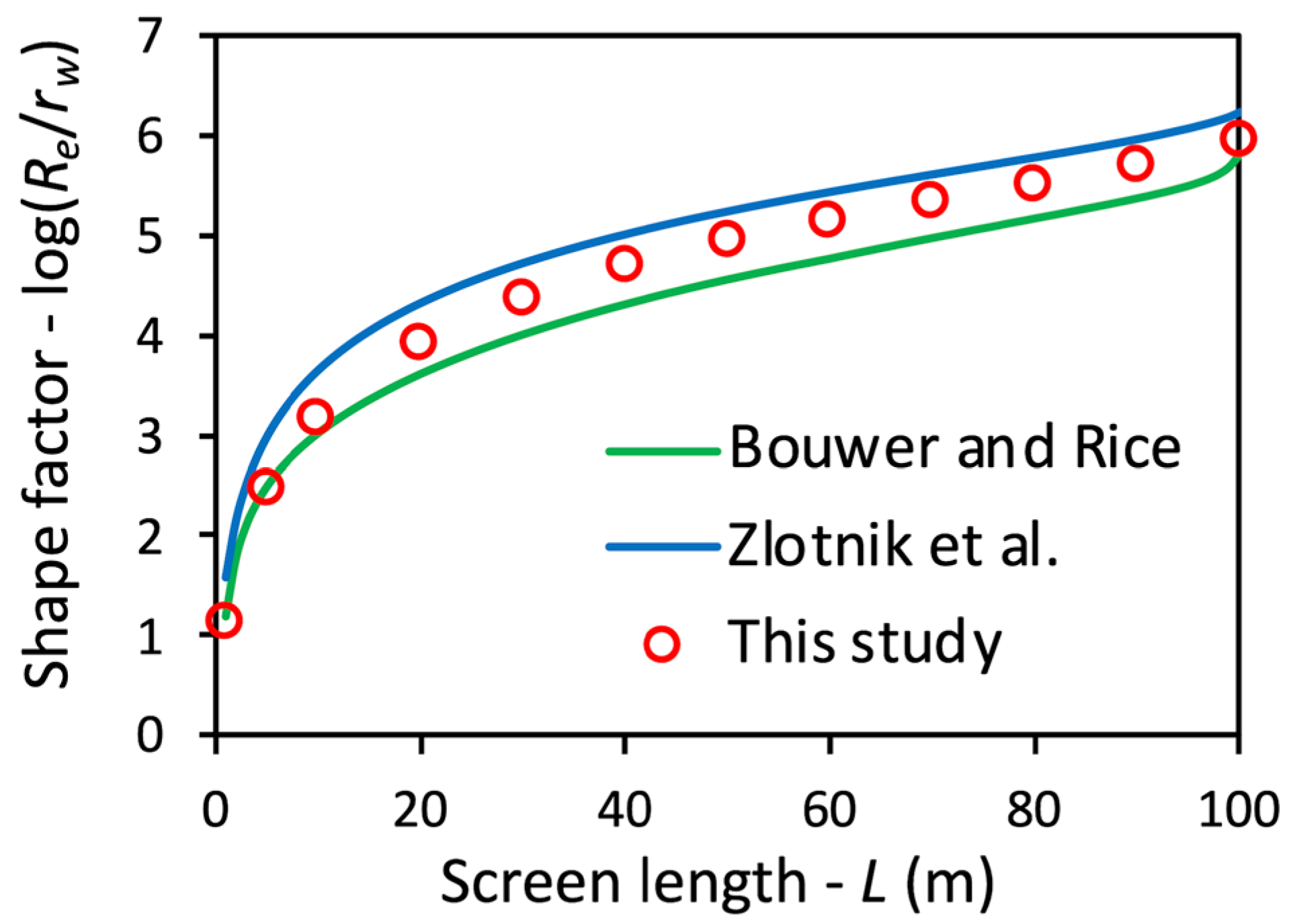
3. Results
4. Discussion
4.1. Case Studies
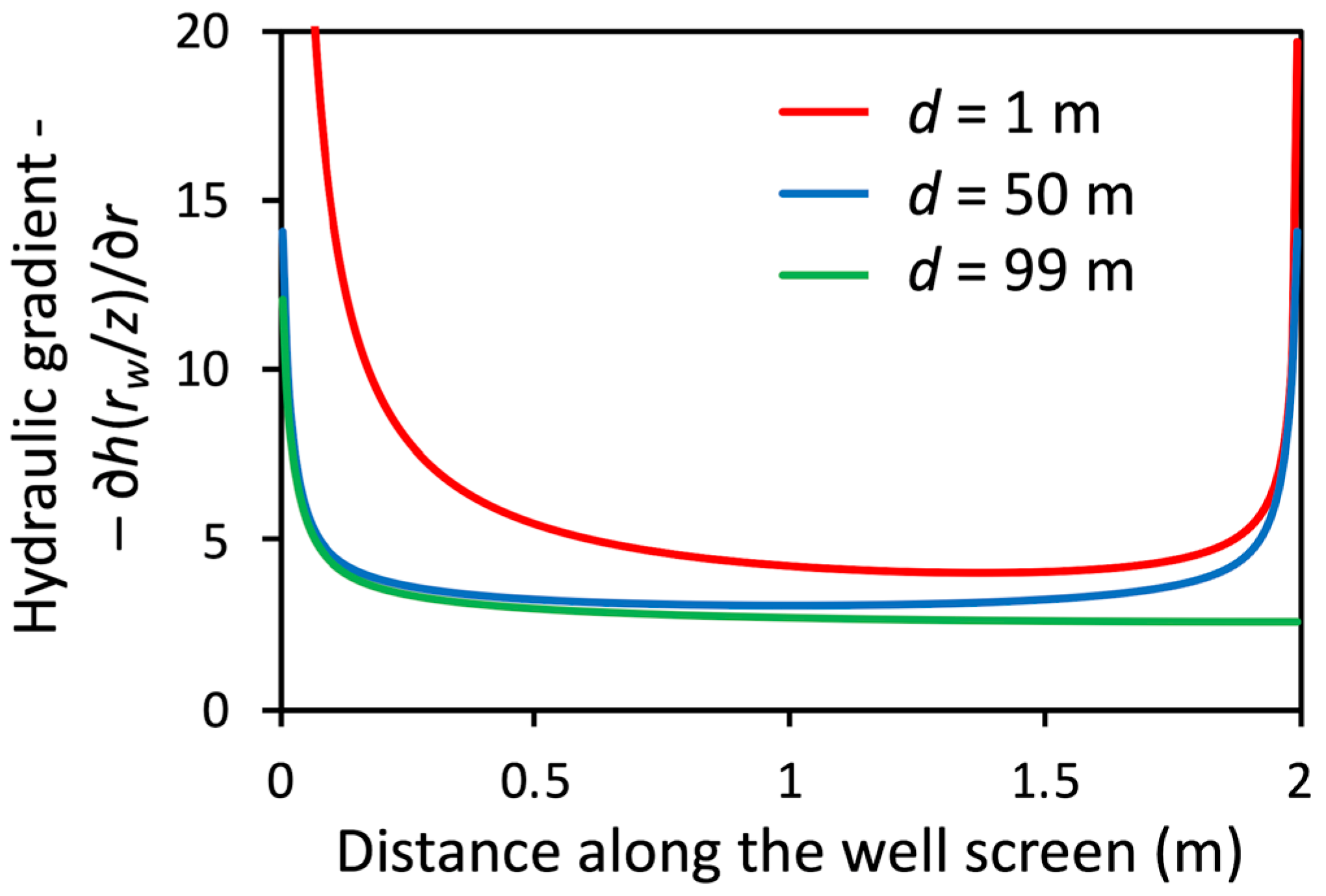
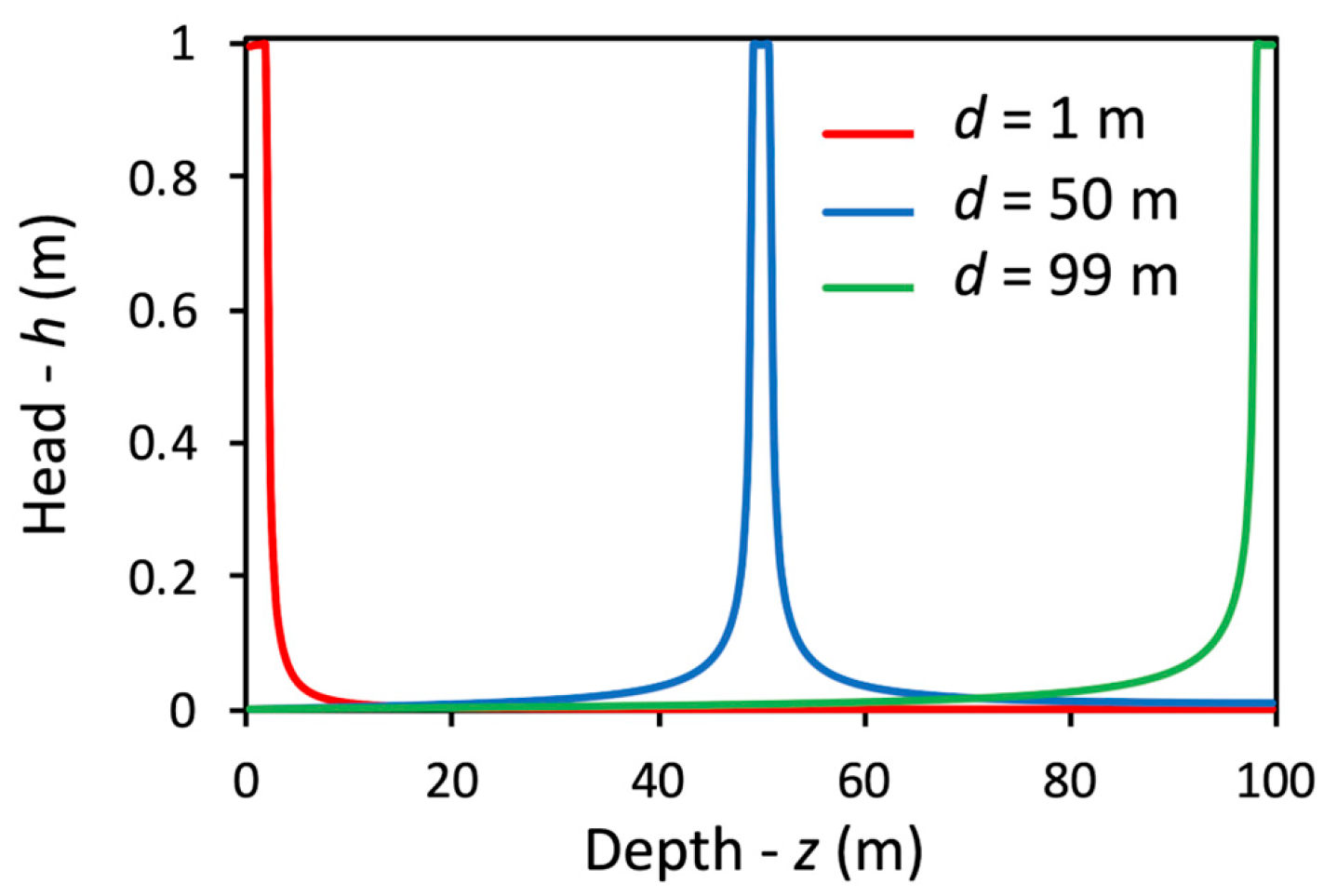
4.2. Effects of Flow Distribution at the Well Screen
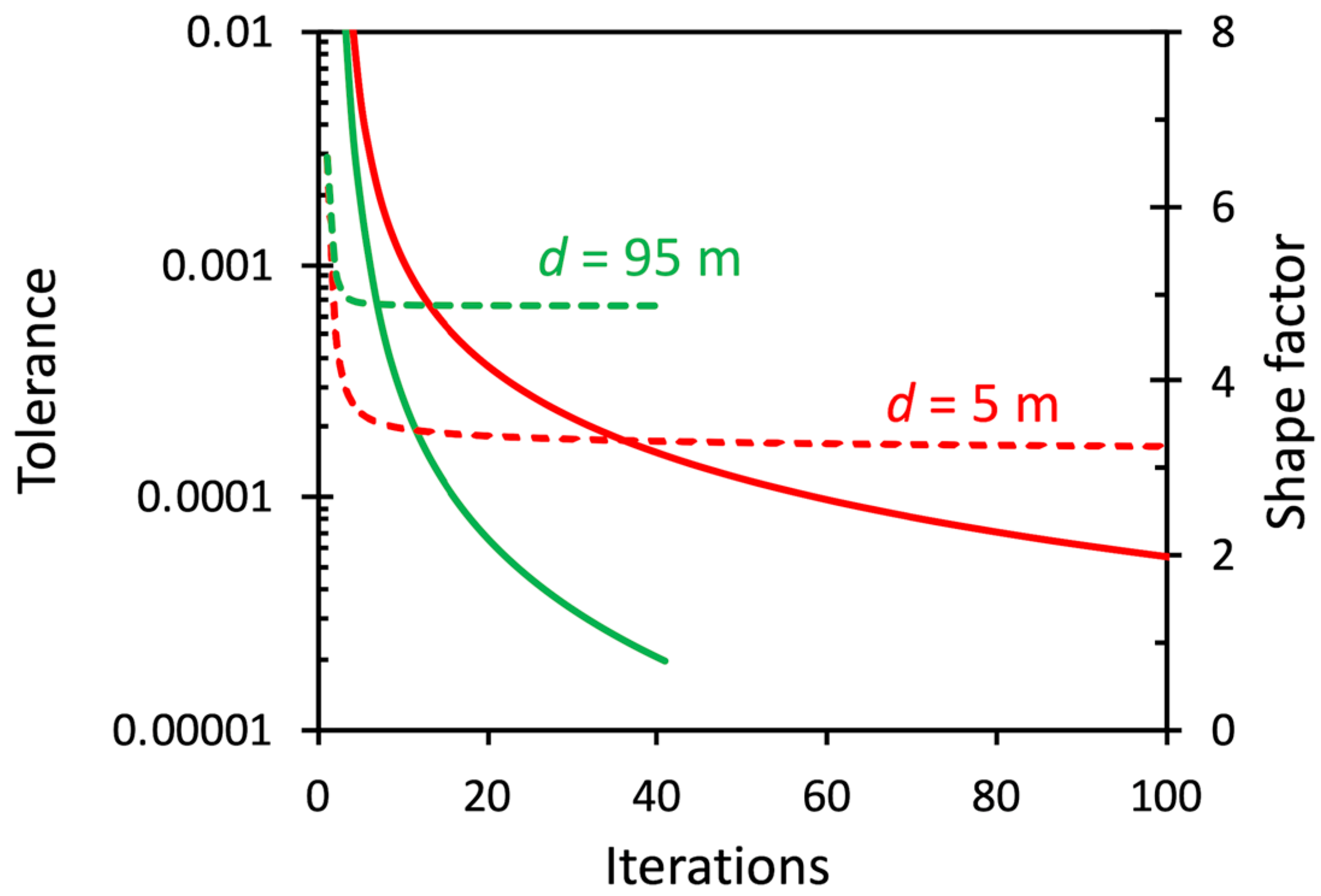
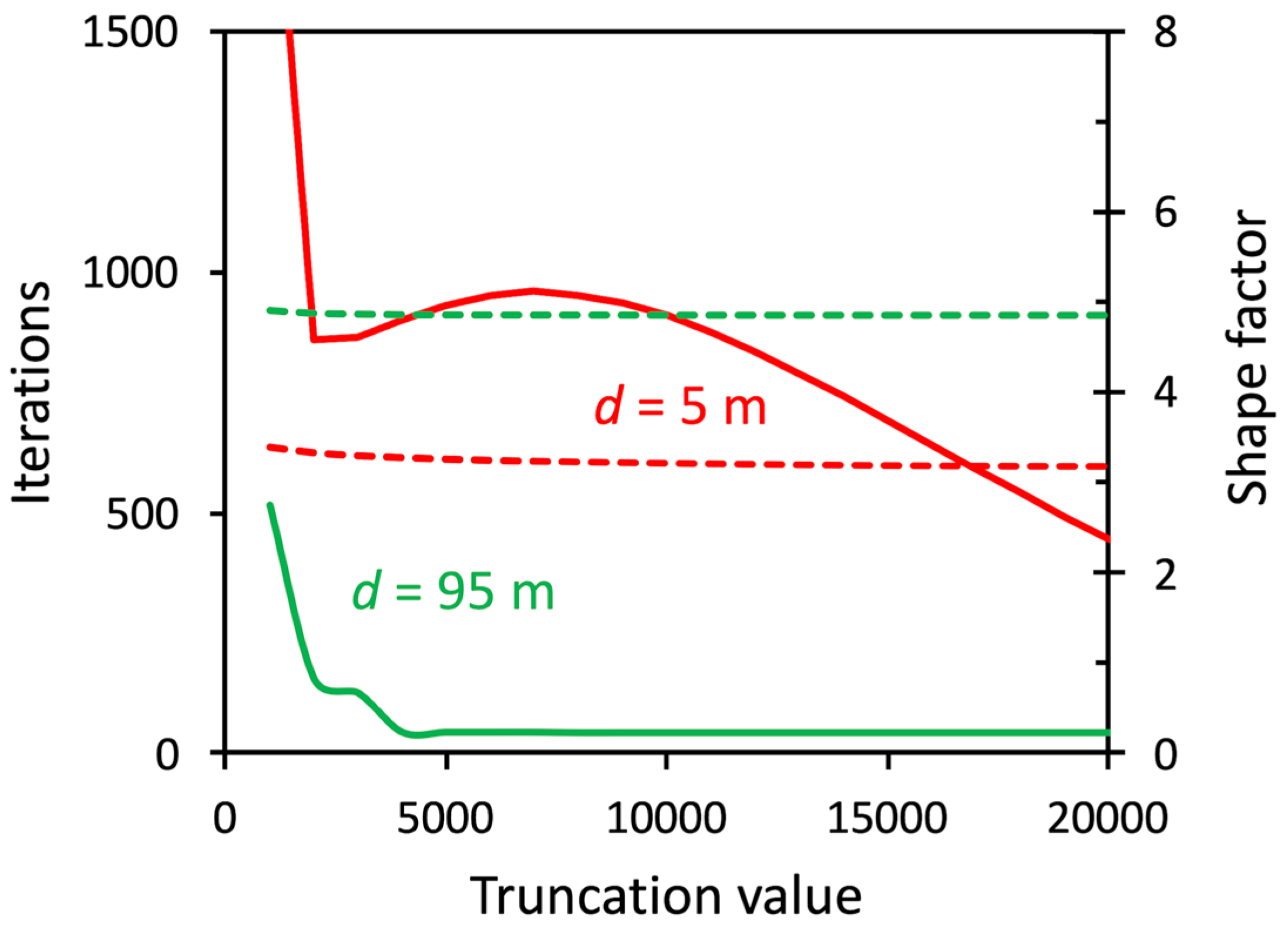
4.3. Effects of Truncation Value and Tolerance
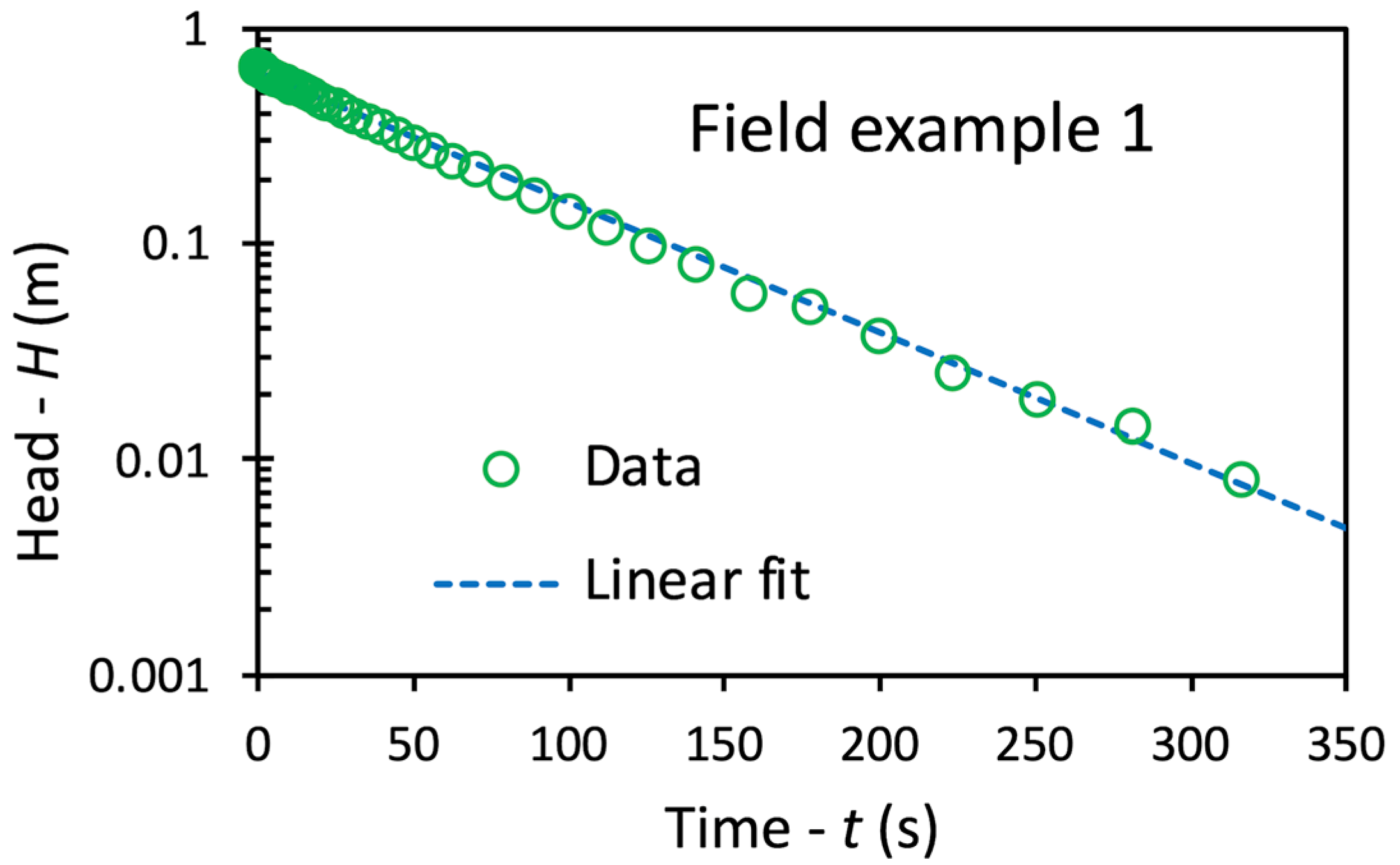
4.4. Field Examples
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- r: outer radius of the well screen or gravel pack;
- l: half-length of the well screen;
- d: depth from the water table to the center of the well screen;
- b: saturated thickness of the aquifer (depth from the water table to the impervious base);
- tol: tolerance for the maximum error in the iteration procedure;
- nmax: truncation number used in the solution procedure.
- The unit of the length parameters (r, l, d, b) must be consistent, preferably in meters.
- The program requires external functions “bessel_K0” and “bessel_K1”, which must be provided by the user.
- Instruction “parameter:: itmax = 2000” sets the maximum number of iterations of the solution procedure to 2000, but this can be changed by the user.
- The approximation “beta(n) = (1.0 − (0.5−…)” was obtained from WolframAlpha.
- Instruction “print*, it, emax, shapefactor” prints the maximum error and the shape factor during the iteration process, but it can be deleted by the user.
- Instruction “print*, ‘Maximum iterations reached’” informs the user that the maximum number of iterations has been reached before the tolerance is met, but it can be deleted by the user.
- The program needs sufficient computation time, which depends on the input parameters and the capacity of the computer.
- The user is advised to repeat calculations with different tolerance and truncation values to verify the results.
Real function shapefactor(r,l,d,b,tol,nmax) !Calculate the shape factor of a partially penetrating well !in an unconfined aquifer !22/07/2024 Florimond De Smedt !r: well filter radius !l: well filter half-lenght !d: depth to well filter center !b: aquifer thickness !tol: error tolerance !nmax: truncation number implicit none integer, intent(in) :: nmax integer :: it,n,m integer, parameter :: itmax = 2000 !Can be changed by the user real, intent(in) :: b,d,l,r,tol real :: an,beta(nmax),beta1,c(0:2*nmax),e(nmax),emax,f(nmax),q(nmax),sumq real, parameter :: pi = 4.0*atan(1.0) real :: bessel_K0,bessel_K1 !External functions provided by the user !Coefficients do n=1,nmax an = pi*(n−0.5)/b f(n) = 4.0*sin(an*d)*sin(an*l)/(an*b) q(n) = 0.0 if(an*r < 40.0) then beta(n) = bessel_K0(an*r)/(an*r*bessel_K1(an*r)) else beta(n) = (1.0-(0.5–3.0/(8.0*an*r))/(an*r))/(an*r) end if end do beta1 = beta(1) do n=1,nmax beta(n) = beta(n)/beta1 enddo c(0) = 2.0*l/b do n=1,2*nmax an = (n*pi)/b c(n) = 2.0*cos(an*d)*sin(an*l)/(an*b) end do !Iteration do it=1,itmax do n=1,nmax e(n) = f(n) do m=1,nmax e(n) = e(n)-(c(abs(n-m))-c(n+m−1))*beta(m)*q(m) end do end do emax = 0.0 sumq = 0.0 do n=1,nmax q(n) = q(n)+e(n) emax = max(abs(e(n)),emax) sumq = sumq+f(n)*q(n) end do shapefactor = 4.0*beta1*l/(b*sumq) print*,it,emax,shapefactor !Optional (can be deleted) if(emax < tol) exit end do if(it > itmax) print*,‘Maximum iterations reached’ !Optional (can be deleted) return end function shapefactor |
References
- Butler, J.J., Jr. The Design, Performance, and Analysis of Slug Tests, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2020; p. 266. [Google Scholar]
- Hvorslev, M.J. Time Lag and Soil Permeability in Ground-Water Observations; Bulletin 36; Waterways Experimental Station, Corps of Engineers, U.S. Army: Vicksburg, MS, USA, 1951; 50p. [Google Scholar]
- Bouwer, H.; Rice, R.C. A slug test for determining hydraulic conductivity of unconfined aquifers with completely or partially penetrating wells. Water Resour. Res. 1976, 12, 423–428. [Google Scholar] [CrossRef]
- Dagan, G. A note on packer, slug, and recovery tests in unconfined aquifers. Water Resour. Res. 1978, 14, 929–934. [Google Scholar] [CrossRef]
- Zlotnik, V.A.; Goss, D.; Duffield, G.M. General steady-state shape factor for a partially penetrating well. Groundwater 2010, 48, 111–116. [Google Scholar] [CrossRef] [PubMed]
- Hyder, Z.; Butler, J.J., Jr.; McElwee, C.D.; Liu, W. Slug tests in partially penetrating wells. Water Resour. Res. 1994, 30, 2945–2957. [Google Scholar] [CrossRef]
- Brand, E.W.; Premchitt, J. Shape factors of cylindrical piezometers. Géotechnique 1980, 30, 369–384. [Google Scholar] [CrossRef]
- Wilkinson, D.; Hammond, P.S. A perturbation method for mixed boundary-value problems in pressure transient testing. Transp. Porous Media 1990, 5, 609–636. [Google Scholar] [CrossRef]
- Widdowson, M.A.; Molz, F.J.; Melville, J.C. An analysis technique for multilevel and partially penetrating slug test data. Groundwater 1990, 28, 937–945. [Google Scholar] [CrossRef]
- Ratnam, S.; Soga, K.; Whittle, R.W. Revisiting Hvorslev’s intake factors with the finite element method. Géotechnique 2001, 51, 641–645. [Google Scholar] [CrossRef]
- Demir, Z.; Narasimhan, T.N. Improved interpretation of Hvorslev tests. J. Hydraul. Eng. 1994, 120, 477–494. [Google Scholar] [CrossRef]
- Mathias, S.A.; Butler, A.P. An improvement on Hvorslev’s shape factors. Géotechnique 2006, 56, 705–706. [Google Scholar] [CrossRef]
- Mathias, S.A.; Butler, A.P. Shape factors for constant-head double-packer permeameters. Water Resour. Res. 2007, 43, W06430. [Google Scholar] [CrossRef]
- Klammler, H.; Hatfield, K.; Nemer, B.; Mathias, S.A. A trigonometric interpolation approach to mixed-type boundary problems associated with permeameter shape factors. Water Resour. Res. 2011, 47, W03510. [Google Scholar] [CrossRef]
- Silvestri, V.; Abou-Samra, G.; Bravo-Jonard, C. Shape Factors of Cylindrical Piezometers in Uniform Soil. Groundwater 2012, 50, 279–284. [Google Scholar] [CrossRef] [PubMed]
- De Smedt, F. Shape Factor for Analysis of a Slug Test. Water 2023, 15, 2551. [Google Scholar] [CrossRef]
- Chapuis, R.P. Shape factors for permeability tests in boreholes and piezometers. Groundwater 1989, 27, 647–654. [Google Scholar] [CrossRef]
- Zlotnik, V.A. Interpretation of Slug and Packer Tests in Anisotropic Aquifers. Groundwater 1994, 32, 761–766. [Google Scholar] [CrossRef]
- Hyder, Z.; Butler, J.J., Jr. Slug tests in unconfined formations: An assessment of the Bouwer and Rice technique. Groundwater 1995, 33, 16–22. [Google Scholar] [CrossRef]
- Brown, D.L.; Narasimhan, T.N.; Demir, Z. An evaluation of the Bouwer Rice method of slug test analysis. Water Resour. Res. 1995, 31, 1239–1246. [Google Scholar] [CrossRef]
- Rupp, D.E.; Selker, J.S.; Simunek, J. A Modification to the Bouwer and Rice Method of Slug-Test Analysis for Large-Diameter, Hand-Dug Wells. Ground Water 2001, 39, 308–314. [Google Scholar] [CrossRef] [PubMed]
- Batu, V. Aquifer Hydraulics: A Comprehensive Guide to Hydrogeological Data Analysis; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1998; p. 727. [Google Scholar]
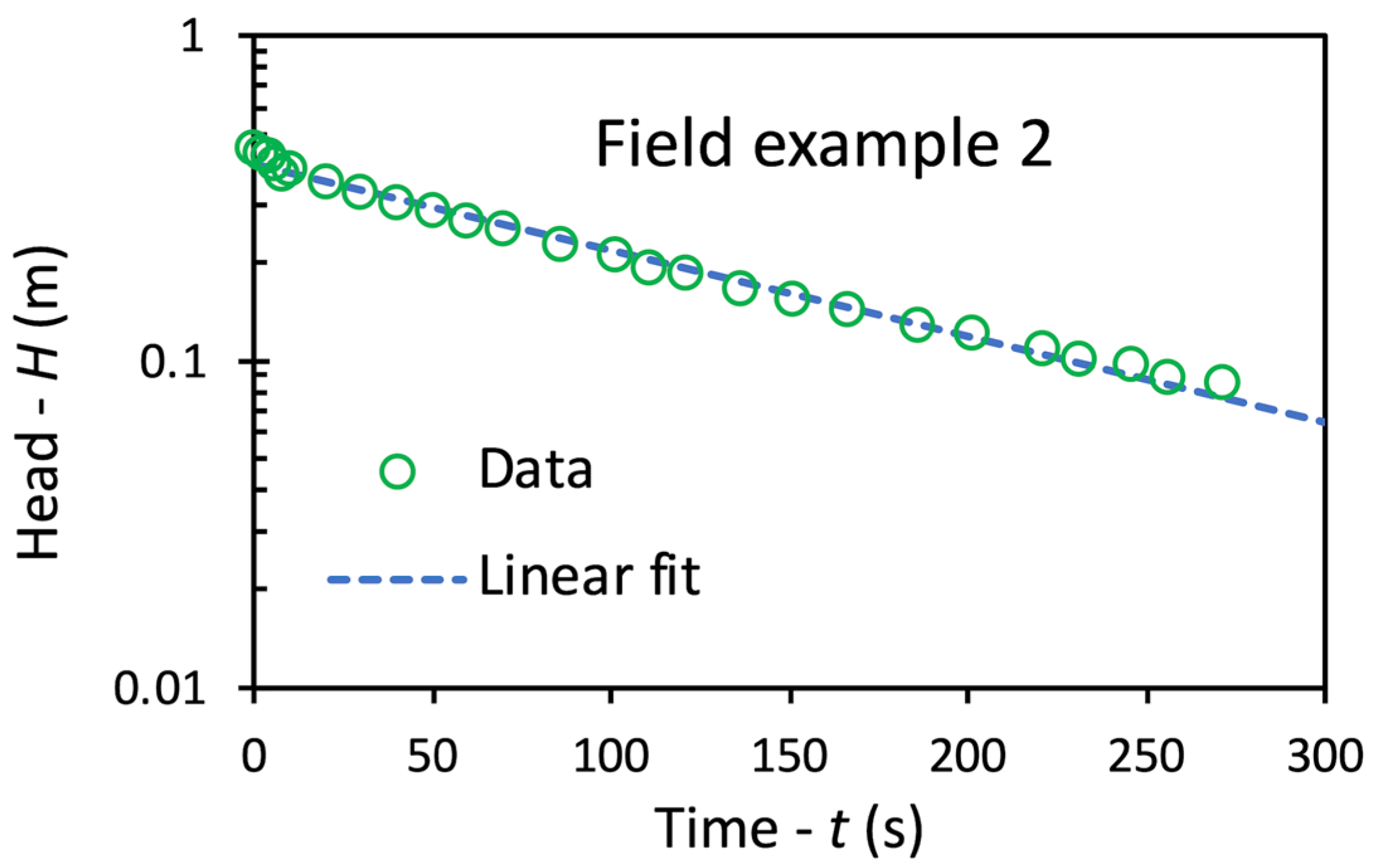
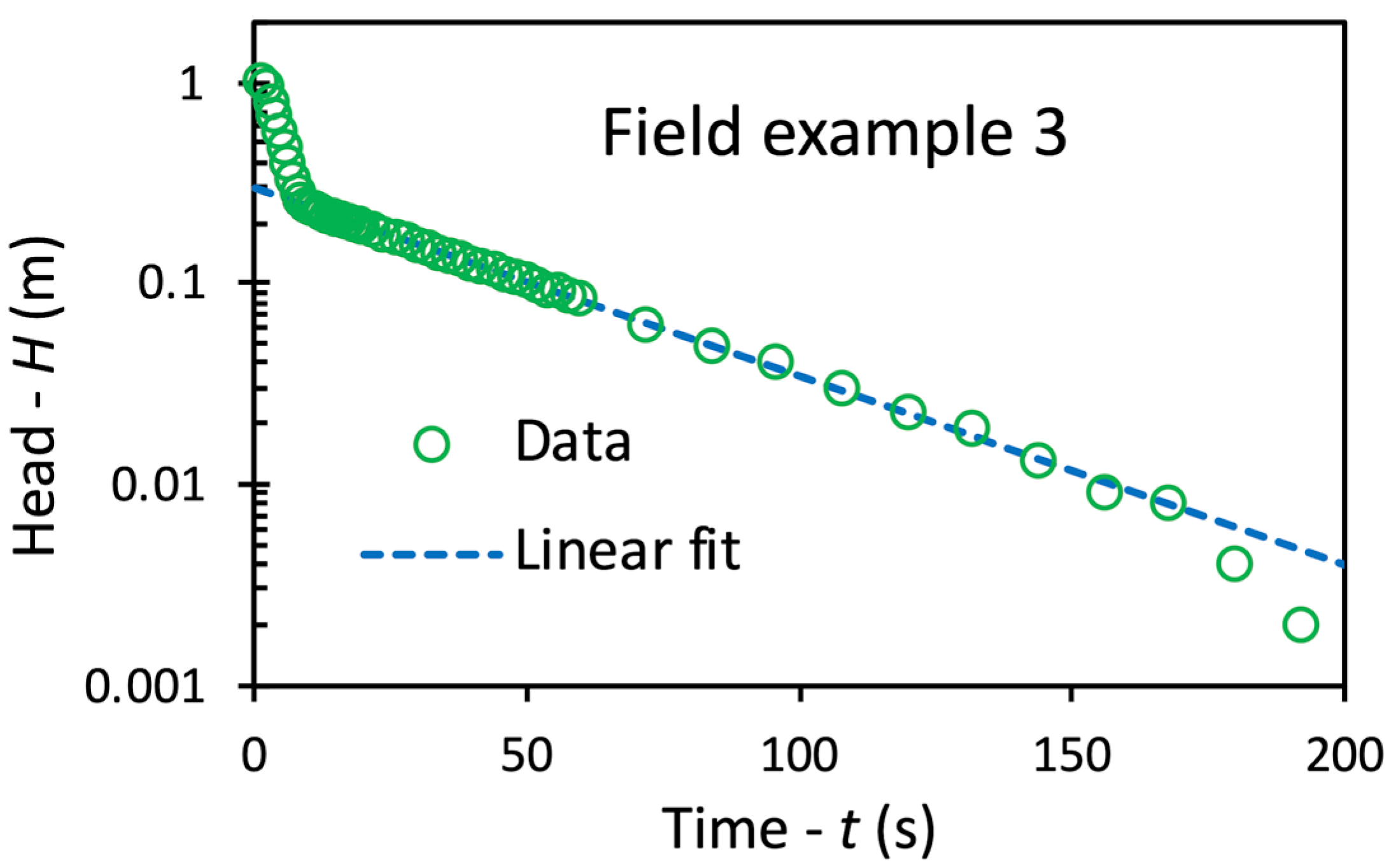
| Parameter | Field Example | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Aquifer thickness: b (m) | 50.6 | 9.93 | 2.44 |
| Screen outer radius: rw (m) | 0.125 | 0.127 | 0.105 |
| Screen inner radius: rc (m) | 0.064 | 0.052 | 0.052 |
| Screen half-length: l (m) | 0.76 | 2.10 | 1.22 |
| Screen depth: d (m) | 19.35 | 0.94 | 1.22 |
| Field Example | Method | Shape Factor | Hydraulic Conductivity K (m/day) | Difference (%) |
|---|---|---|---|---|
| 1 | This study | 2.25 | 3.68 | - |
| Bouwer and Rice [3] | 2.01 | 3.50 | –11 | |
| Zlotnik et al. [5] | 2.33 | 3.80 | 3 | |
| Hvorslev [2] | 2.50 | 4.07 | 11 | |
| De Smedt [16] | 2.28 | 3.71 | 1 | |
| 2 | This study | 2.5 | 0.73 | - |
| Bouwer and Rice [3] | 2.32 | 0.67 | –7 | |
| Zlotnik et al. [5] | 2.69 | 0.78 | 8 | |
| Hvorslev [2] | 3.50 | 1.02 | 40 | |
| De Smedt [16] | 3.22 | 0.94 | 29 | |
| 3 | This study | 1.67 | 1.73 | - |
| Bouwer and Rice [3] | 2.39 | 2.48 | 43 | |
| Zlotnik et al. [5] | 2.56 | 2.65 | 53 | |
| Hvorslev [2] | 3.15 | 3.26 | 89 | |
| De Smedt [16] | 2.88 | 2.99 | 73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Smedt, F. Steady-State Shape Factor for a Slug Test in an Unconfined Aquifer. Water 2024, 16, 2853. https://doi.org/10.3390/w16192853
De Smedt F. Steady-State Shape Factor for a Slug Test in an Unconfined Aquifer. Water. 2024; 16(19):2853. https://doi.org/10.3390/w16192853
Chicago/Turabian StyleDe Smedt, Florimond. 2024. "Steady-State Shape Factor for a Slug Test in an Unconfined Aquifer" Water 16, no. 19: 2853. https://doi.org/10.3390/w16192853
APA StyleDe Smedt, F. (2024). Steady-State Shape Factor for a Slug Test in an Unconfined Aquifer. Water, 16(19), 2853. https://doi.org/10.3390/w16192853







