Enhanced TDS Modeling Using an AI Framework Integrating Grey Wolf Optimization with Kernel Extreme Learning Machine
Abstract
1. Introduction
2. Materials and Methods
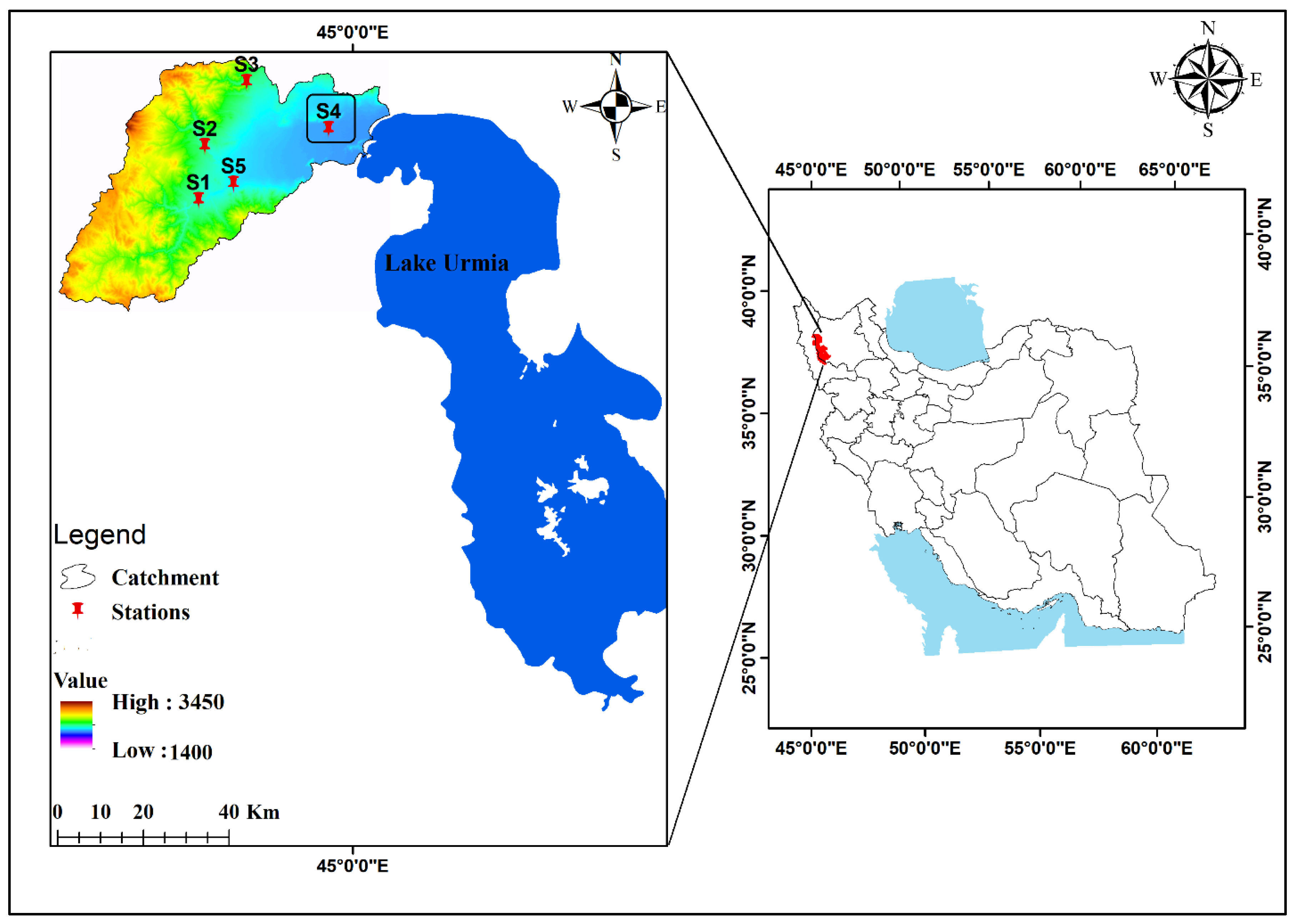
2.1. Study Area
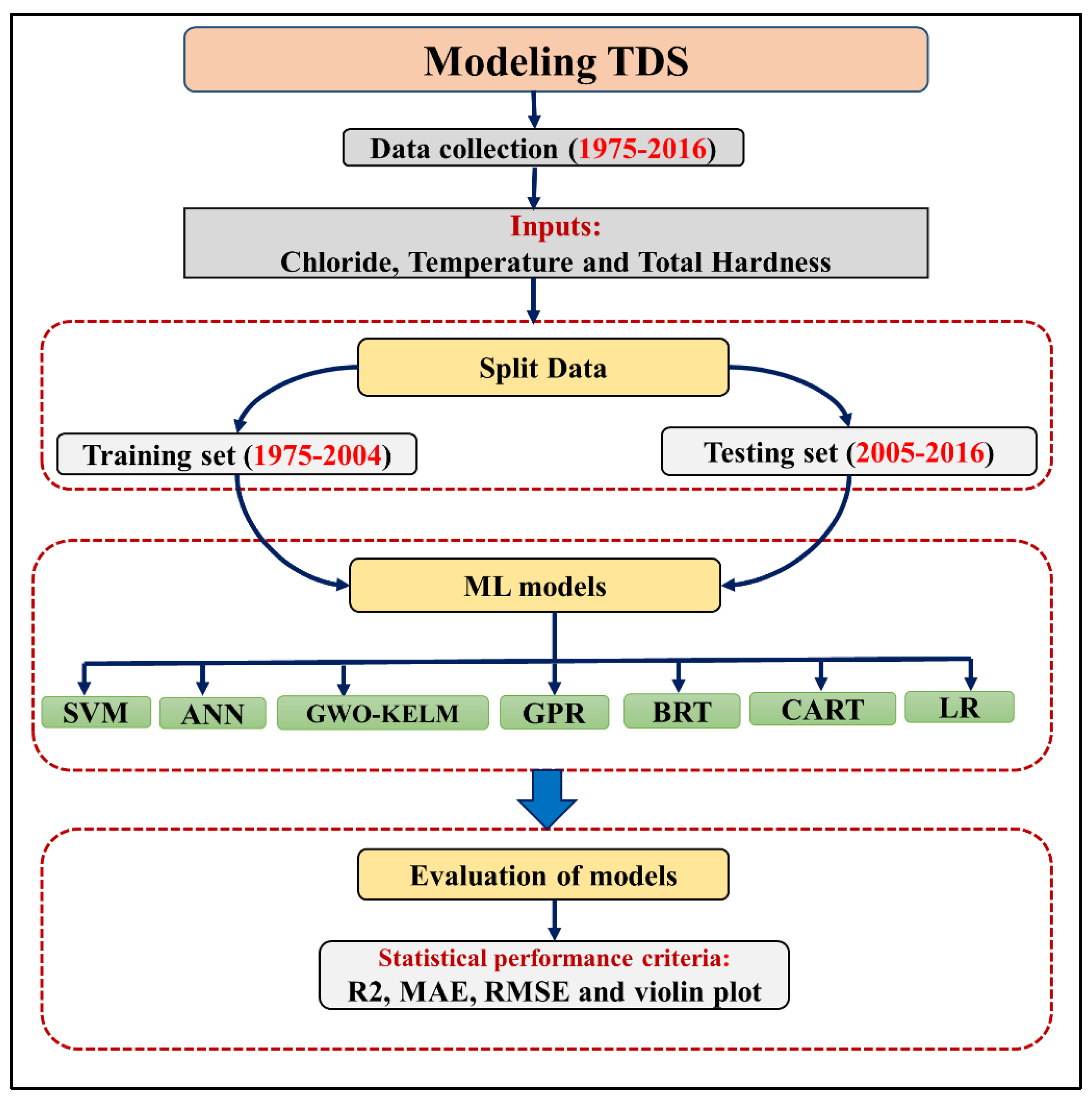
2.2. Method Development
2.2.1. Data Collection and Preparation
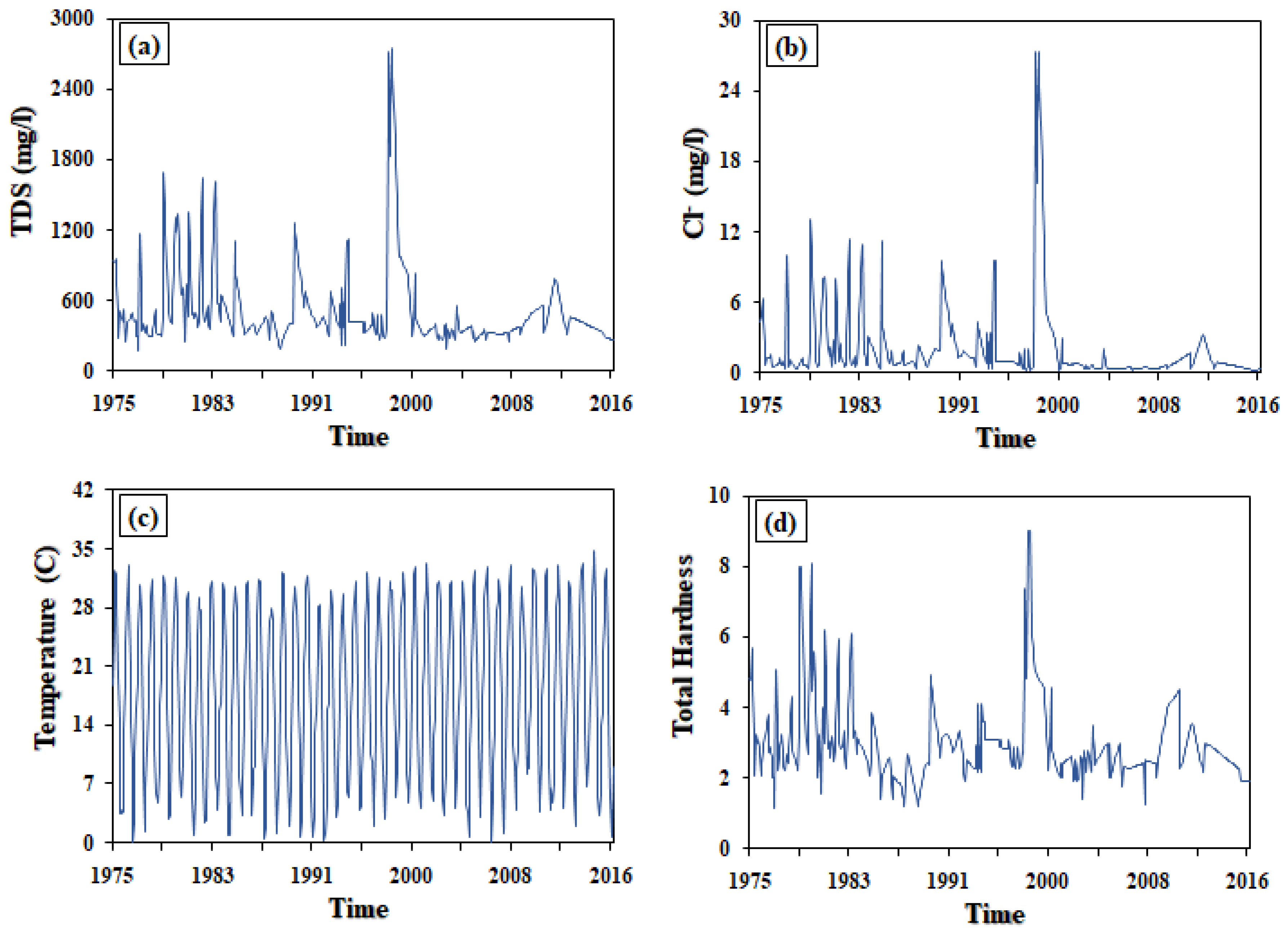
TDS
2.2.2. Driving Factors
Cl−
Temperature
Total Hardness
2.2.3. Machine Learning Algorithms
Support Vector Machine (SVM)
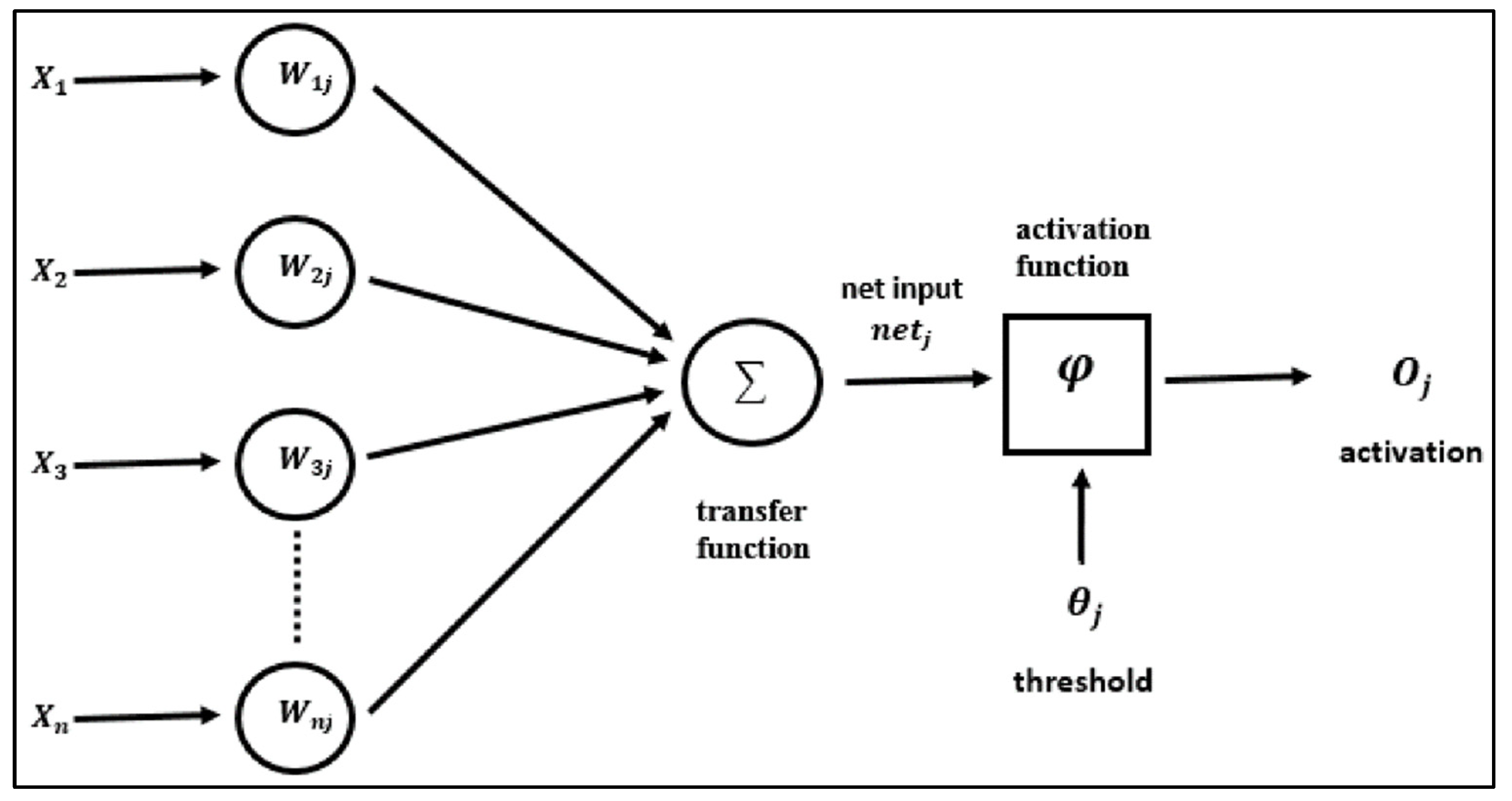
Artificial Neural Network (ANN)
Gaussian Process Regression (GPR)
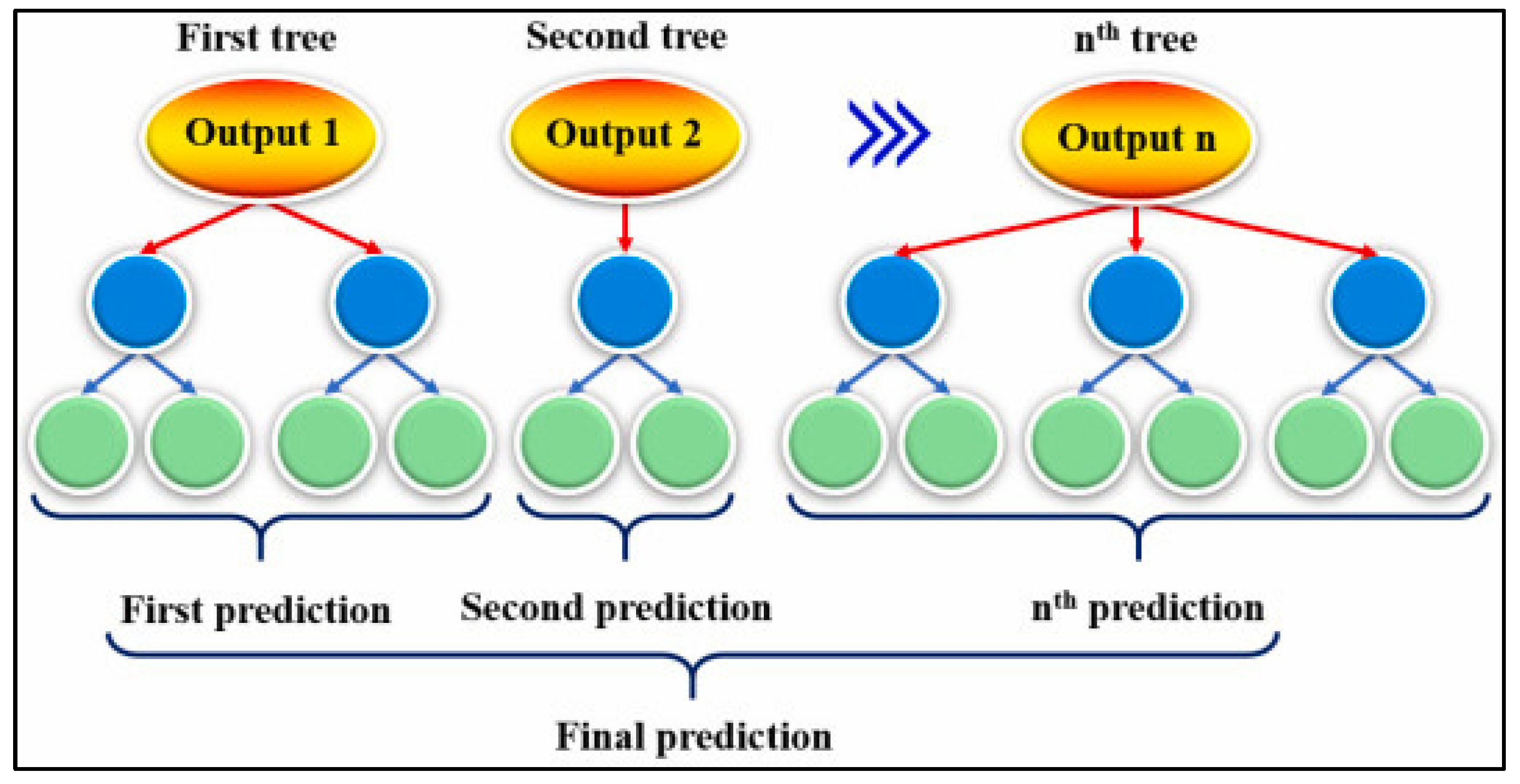
Boosted Regression Tree (BRT)
- Red circles indicate higher TDS levels in conjunction with higher chloride concentrations.
- Green circles signify moderate TDS values, corresponding to medium levels of total hardness.
- Blue circles represent lower TDS values and lower temperatures, highlighting areas with reduced solubility or changes in water chemistry.
Classification and Regression Tree (CART) Algorithm
Linear Regression (LR)
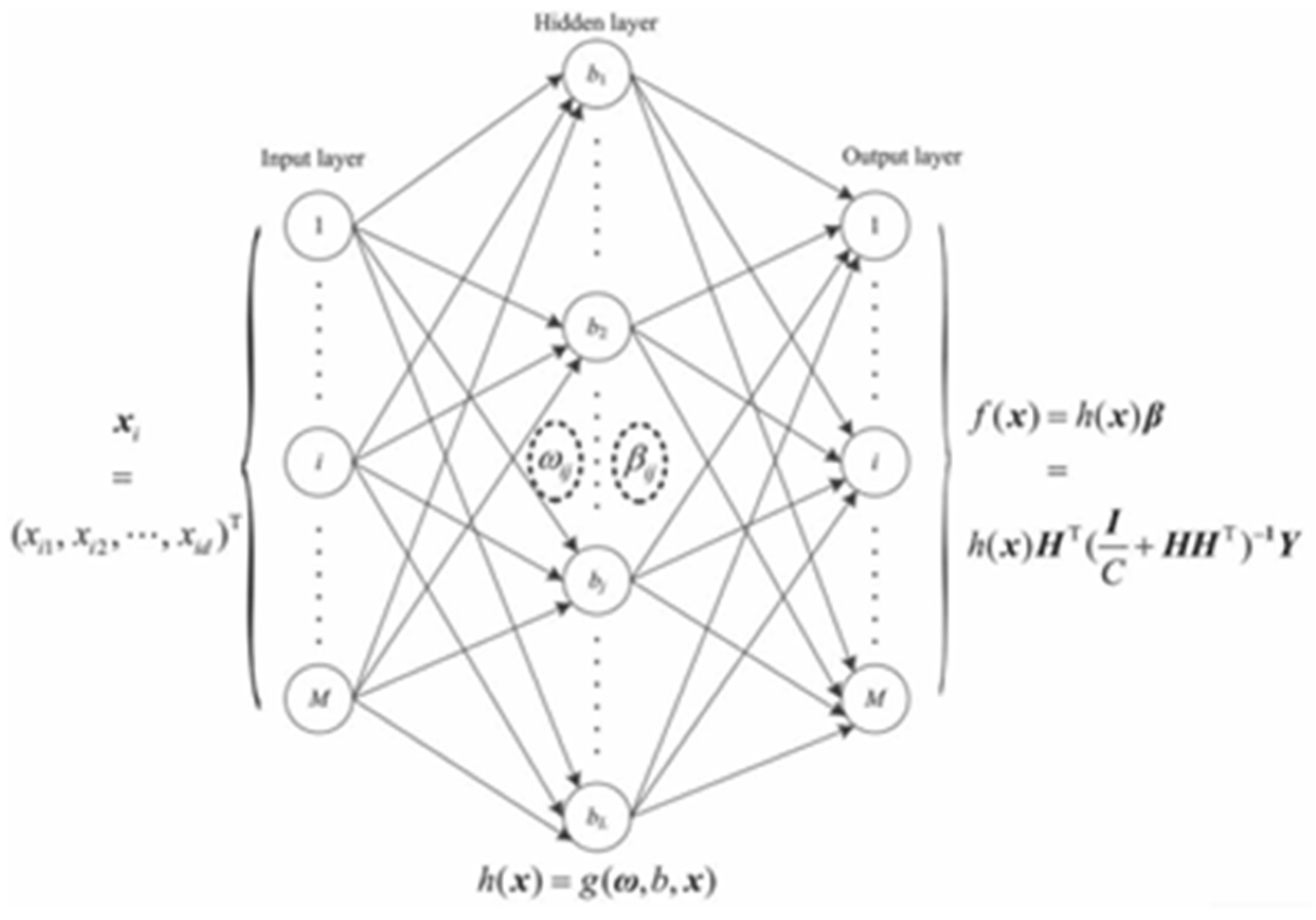
Kernel Extreme Learning Machine (KELM)
Grey Wolf Optimization (GWO)
2.2.4. Evaluation of the Machine Learning Algorithms
3. Results and Discussion
3.1. Results of ML Algorithms
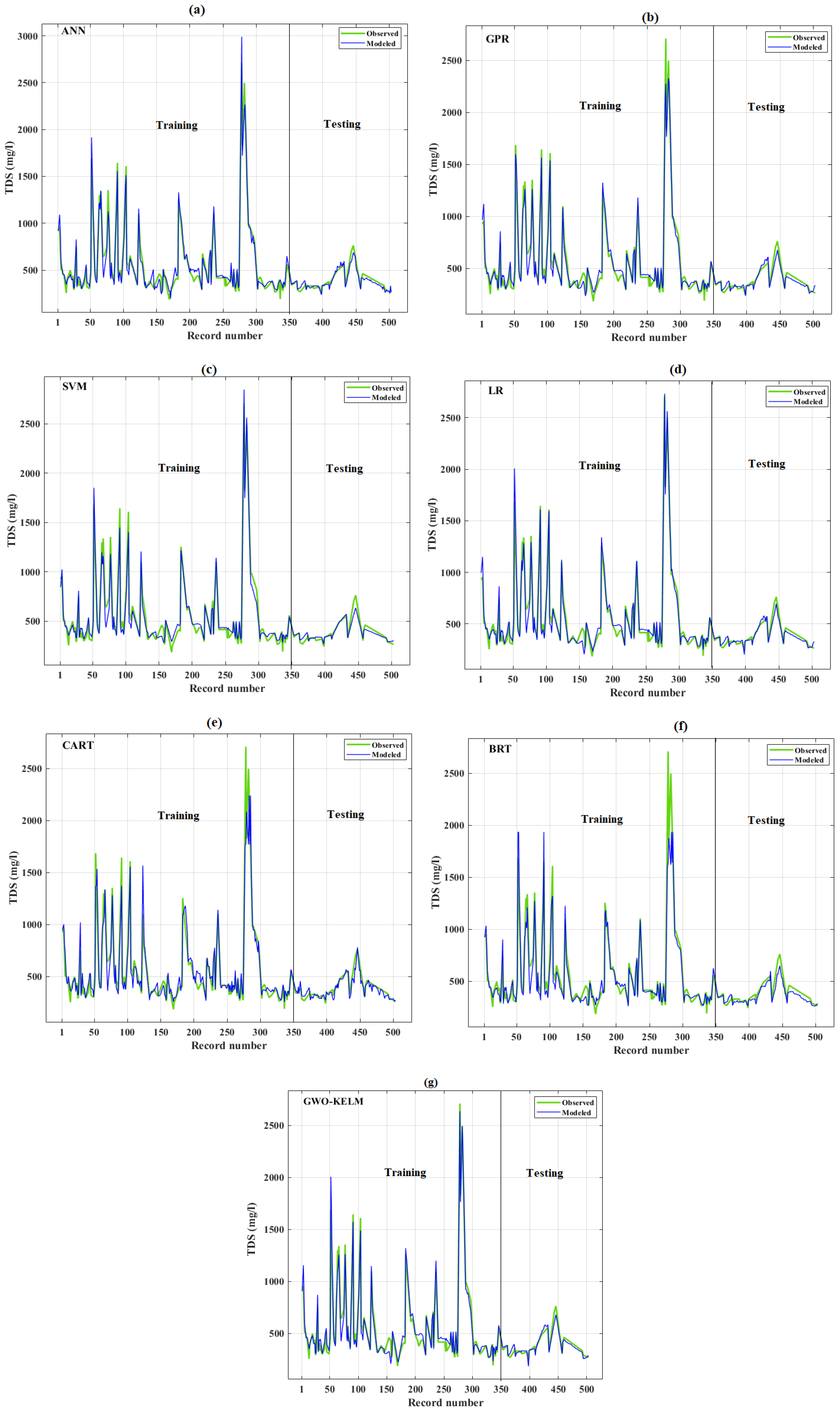
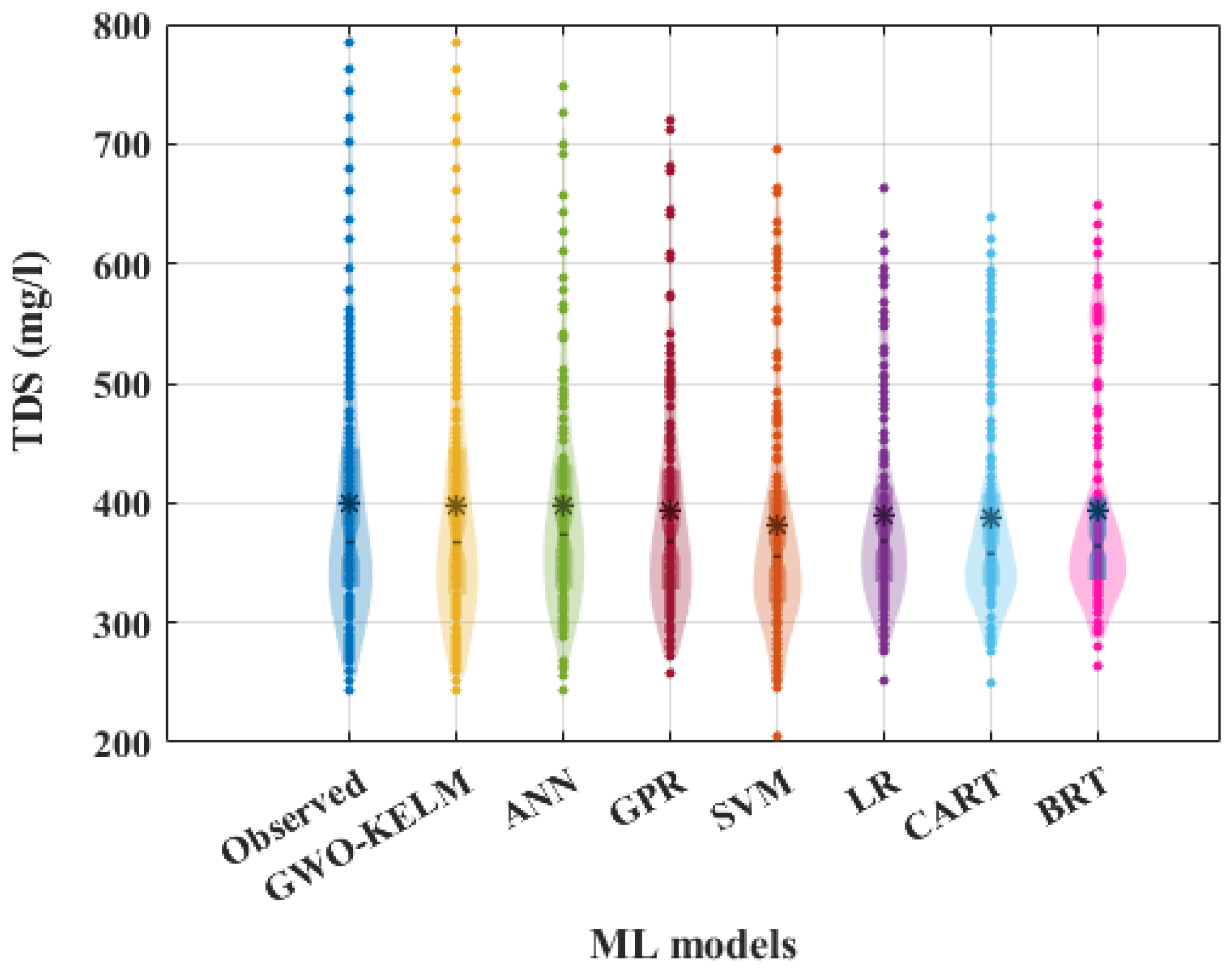
3.2. Graphical Results
3.3. Discussion of ML Algorithms’ Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations | Description |
| TDS | Total Dissolved Solids |
| GWO | Grey Wolf Optimization |
| KELM | Kernel Extreme Learning Machine |
| ELM | Extreme Learning Machine |
| ANN | Artificial Neural Network |
| GPR | Gaussian Process Regression |
| SVM | Support Vector Machine |
| LR | Linear Regression |
| CART | Classification and Regression Tree |
| BRT | Boosted Regression Tree |
| R2 | Coefficient of determination |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| ML | Machine learning |
| TH | Total hardness |
| WARWC | West Azerbaijan Regional Water Company |
| WAMO | West Azerbaijan Meteorological Organization |
| WQP | Water quality parameter |
| EPA | Environmental Protection Agency |
| SDWRs | Secondary Drinking Water Regulations |
| GP | Gaussian process |
| SWC | Soil Water Content |
References
- Karimi, S.; Amiri, B.J.; Malekian, A. Similarity metrics-based uncertainty analysis of river water quality models. Water Resour. Manag. 2019, 33, 1927–1945. [Google Scholar] [CrossRef]
- Bui, D.T.; Khosravi, K.; Tiefenbacher, J.; Nguyen, H.; Kazakis, N. Improving prediction of water quality indices using novel hybrid machine-learning algorithms. Sci. Total Environ. 2020, 721, 137612. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Rajabtabar, M.; Samadi, S.; Rezaie-Balf, M.; Ghaemi, A.; Band, S.S.; Mosavi, A. An integrated machine learning, noise suppression, and population-based algorithm to improve total dissolved solids prediction. Eng. Appl. Comput. Fluid Mech. 2021, 15, 251–271. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Seo, Y.; Kim, S.; Ghorbani, M.A.; Samadianfard, S.; Naghshara, S.; Kim, N.W.; Singh, V.P. Can decomposition approaches always enhance soft computing models? Predicting the dissolved oxygen concentration in the St. Johns River, Florida. Appl. Sci. 2019, 9, 2534. [Google Scholar] [CrossRef]
- Butler, B.A.; Ford, R.G. Evaluating relationships between total dissolved solids (TDS) and total suspended solids (TSS) in a mining-influenced watershed. Mine Water Environ. 2018, 37, 18. [Google Scholar] [CrossRef]
- Adjovu, G.E.; Stephen, H.; James, D.; Ahmad, S. Measurement of total dissolved solids and total suspended solids in water systems: A review of the issues, conventional, and remote sensing techniques. Remote Sens. 2023, 15, 3534. [Google Scholar] [CrossRef]
- Wen, Z.; Han, J.; Shang, Y.; Tao, H.; Fang, C.; Lyu, L.; Li, S.; Hou, J.; Liu, G.; Song, K. Spatial variations of DOM in a diverse range of lakes across various frozen ground zones in China: Insights into molecular composition. Water Res. 2024, 252, 121204. [Google Scholar] [CrossRef]
- Mahmoodlu, M.G.; Jandaghi, N.; Sayadi, M. Investigating the factors affecting corrosion and precipitation changes along Gorganroud River, Golestan Province. Environ. Sci. 2021, 19, 71–90. [Google Scholar] [CrossRef]
- Banadkooki, F.B.; Ehteram, M.; Panahi, F.; Sammen, S.S.; Othman, F.B.; Ahmed, E.S. Estimation of total dissolved solids (TDS) using new hybrid machine learning models. J. Hydrol. 2020, 587, 124989. [Google Scholar] [CrossRef]
- Liu, S.; Qiu, Y.; He, Z.; Shi, C.; Xing, B.; Wu, F. Microplastic-derived dissolved organic matter and its biogeochemical behaviors in aquatic environments: A review. Crit. Rev. Environ. Sci. Technol. 2024, 54, 865–882. [Google Scholar] [CrossRef]
- Sayadi, M.; Mahmoodlu, M.G. Investigation and prediction of quality parameters of Gamasyab river using multivariate method of Canonical correlation analysis and time series. J. Res. Environ. Health 2019, 5, 108–122. [Google Scholar]
- Yang, H.; Kong, J.; Hu, H.; Du, Y.; Gao, M.; Chen, F. A review of remote sensing for water quality retrieval: Progress and challenges. Remote Sens. 2022, 14, 1770. [Google Scholar] [CrossRef]
- Adjovu, G.; Ahmad, S.; Stephen, H. Analysis of Suspended Material in Lake Mead Using Remote Sensing Indices. In Proceedings of the World Environmental and Water Resources Congress 2021, Online, 7–11 June 2021; pp. 754–768. [Google Scholar]
- Dritsas, E.; Trigka, M. Efficient data-driven machine learning models for water quality prediction. Computation 2023, 11, 16. [Google Scholar] [CrossRef]
- Al-Mukhtar, M.; Al-Yaseen, F. Modeling water quality parameters using data-driven models, a case study Abu-Ziriq marsh in south of Iraq. Hydrology 2019, 6, 24. [Google Scholar] [CrossRef]
- Ewusi, A.; Ahenkorah, I.; Aikins, D. Modelling of total dissolved solids in water supply systems using regression and supervised machine learning approaches. Appl. Water Sci. 2021, 11, 13. [Google Scholar] [CrossRef]
- Panahi, J.; Mastouri, R.; Shabanlou, S. Influence of pre-processing algorithms on surface water TDS estimation using artificial intelligence models: A case study of the Karoon river. Iran. J. Sci. Technol. Trans. Civ. Eng. 2023, 47, 585–598. [Google Scholar] [CrossRef]
- Pourhosseini, F.A.; Ebrahimi, K.; Omid, M.H. Prediction of total dissolved solids, based on optimization of new hybrid SVM models. Eng. Appl. Artif. Intell. 2023, 126, 106780. [Google Scholar] [CrossRef]
- Hijji, M.; Chen, T.C.; Ayaz, M.; Abosinnee, A.S.; Muda, I.; Razoumny, Y.; Hatamiafkoueieh, J. Optimization of state of the art fuzzy-based machine learning techniques for total dissolved solids prediction. Sustainability 2023, 15, 7016. [Google Scholar] [CrossRef]
- Melesse, A.M.; Khosravi, K.; Tiefenbacher, J.P.; Heddam, S.; Kim, S.; Mosavi, A.; Pham, B.T. River water salinity prediction using hybrid machine learning models. Water 2020, 12, 2951. [Google Scholar] [CrossRef]
- Adjovu, G.E.; Stephen, H.; Ahmad, S. A machine learning approach for the estimation of total dissolved solids concentration in lake mead using electrical conductivity and temperature. Water 2023, 15, 2439. [Google Scholar] [CrossRef]
- Roushangar, K.; Aalami, M.T.; Golmohammadi, H.; Shahnazi, S. Monitoring and prediction of land use/land cover changes and water requirements in the basin of the Urmia Lake, Iran. Water Supply 2023, 23, 2299–2312. [Google Scholar] [CrossRef]
- West Azarbaijan Regional Water Company. Available online: https://www.agrw.ir/ (accessed on 10 May 2023).
- West Azerbaijan Meteorological Organization. Available online: http://www.azmet.ir/ (accessed on 10 May 2023).
- U.S. EPA. 2018 Edition of the Drinking Water Standards and Health Advisories Tables; U.S. EPA: Washington, DC, USA, 2018. Available online: https://www.epa.gov/system/files/documents/2022-01/dwtable2018.pdf (accessed on 25 May 2023).
- Rusydi, A.F. February. Correlation between conductivity and total dissolved solid in various type of water: A review. IOP Conf. Ser. Earth Environ. Sci. 2018, 118, 012019. [Google Scholar] [CrossRef]
- Das, C.R.; Das, S.; Panda, S. Groundwater quality monitoring by correlation, regression and hierarchical clustering analyses using WQI and PAST tools. Groundw. Sustain. Dev. 2022, 16, 100708. [Google Scholar] [CrossRef]
- Dewangan, S.K.; Shrivastava, S.; Kadri, M.; Saruta, S.; Yadav, S.; Minj, N. Temperature effect on electrical conductivity (EC) & total dissolved solids (TDS) of water: A review. Int. J. Res. Anal. Rev 2023, 10, 514–520. [Google Scholar]
- Chen, J.; Wu, H.; Qian, H.; Gao, Y. Assessing nitrate and fluoride contaminants in drinking water and their health risk of rural residents living in a semiarid region of Northwest China. Expo. Health 2017, 9, 183–195. [Google Scholar] [CrossRef]
- Boyd, C.E. Total hardness. In Water Quality: An Introduction; Springer: Cham, Switzerland, 2015; pp. 179–187. [Google Scholar]
- Roushangar, K.; Shahnazi, S.; Mehrizad, A. Data-intelligence approaches for comprehensive assessment of discharge coefficient prediction in cylindrical weirs: Insights from extensive experimental data sets. Measurement 2024, 233, 114673. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Roushangar, K.; Davoudi, S.; Shahnazi, S. Temporal prediction of dissolved oxygen based on CEEMDAN and multi-strategy LSTM hybrid model. Environ. Earth Sci. 2024, 83, 158. [Google Scholar] [CrossRef]
- Singh, K.P.; Malik, A.; Mohan, D.; Sinha, S. Multivariate statistical techniques for the evaluation of spatial and temporal variations in water quality of Gomti River (India)—A case study. Water Res. 2004, 38, 3980–3992. [Google Scholar] [CrossRef]
- Haykin, S. Kalman Filtering and Neural Networks; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Roushangar, K.; Shahnazi, S. Prediction of sediment transport rates in gravel-bed rivers using Gaussian process regression. J. Hydroinformatics 2020, 22, 249–262. [Google Scholar] [CrossRef]
- Kern, C.; Klausch, T.; Kreuter, F. Tree-based machine learning methods for survey research. In Survey Research Methods; NIH Public Access: Milwaukee, WI, USA, 2019; Volume 13, No. 1, p. 73. [Google Scholar]
- Jamei, M.; Karbasi, M.; Olumegbon, I.A.; Mosharaf-Dehkordi, M.; Ahmadianfar, I.; Asadi, A. Specific heat capacity of molten salt-based nanofluids in solar thermal applications: A paradigm of two modern ensemble machine learning methods. J. Mol. Liq. 2021, 335, 116434. [Google Scholar] [CrossRef]
- Lee, J.; Wang, W.; Harrou, F.; Sun, Y. Reliable solar irradiance prediction using ensemble learning-based models: A comparative study. Energy Convers. Manag. 2020, 208, 112582. [Google Scholar] [CrossRef]
- Persson, C.; Bacher, P.; Shiga, T.; Madsen, H. Multi-site solar power forecasting using gradient boosted regression trees. Sol. Energy 2017, 150, 423–436. [Google Scholar] [CrossRef]
- Said, Z.; Cakmak, N.K.; Sharma, P.; Sundar, L.S.; Inayat, A.; Keklikcioglu, O.; Li, C. Synthesis, stability, density, viscosity of ethylene glycol-based ternary hybrid nanofluids: Experimental investigations and model-prediction using modern machine learning techniques. Powder Technol. 2022, 400, 117190. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Lombardo, L. Comparative assessment using boosted regression trees, binary logistic regression, frequency ratio and numerical risk factor for gully erosion susceptibility modelling. Catena 2019, 183, 104223. [Google Scholar] [CrossRef]
- Landwehr, N.; Hall, M.; Frank, E. Logistic model trees. Mach. Learn. 2005, 59, 161–205. [Google Scholar] [CrossRef]
- Wang, Q.; Hamilton, P.B.; Xu, M.; Kattel, G. Comparison of boosted regression trees vs WA-PLS regression on diatom-inferred glacial-interglacial climate reconstruction in Lake Tiancai (southwest China). Quat. Int. 2021, 580, 53–66. [Google Scholar] [CrossRef]
- Lai, V.; Ahmed, A.N.; Malek, M.A.; Abdulmohsin Afan, H.; Ibrahim, R.K.; El-Shafie, A.; El-Shafie, A. Modeling the nonlinearity of sea level oscillations in the Malaysian coastal areas using machine learning algorithms. Sustainability 2019, 11, 4643. [Google Scholar] [CrossRef]
- Blaom, A.D.; Kiraly, F.; Lienart, T.; Simillides, Y.; Arenas, D.; Vollmer, S.J. MLJ: A Julia package for composable machine learning. arXiv 2020, arXiv:2007.12285. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees; Routledge: London, UK, 2017. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; Volume 2, pp. 1–758. [Google Scholar]
- Maulud, D.; Abdulazeez, A.M. A review on linear regression comprehensive in machine learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Ansari, M.; Akhoondzadeh, M. Mapping water salinity using Landsat-8 OLI satellite images (Case study: Karun basin located in Iran). Adv. Space Res. 2020, 65, 1490–1502. [Google Scholar] [CrossRef]
- Roushangar, K.; Shahnazi, S.; Azamathulla, H.M. Partitioning strategy for investigating the prediction capability of bed load transport under varied hydraulic conditions: Application of robust GWO-kernel-based ELM approach. Flow Meas. Instrum. 2022, 84, 102136. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, Y.; Meng, W.; Luo, Q. Functional extreme learning machine for regression and classification. Math. Biosci. Eng. 2023, 20, 3768–3792. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Roushangar, K.; Alirezazadeh Sadaghiani, A.; Shahnazi, S. Novel application of robust GWO-KELM model in predicting discharge coefficient of radial gates: A field data-based analysis. J. Hydroinformatics 2023, 25, 275–299. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. Peerj Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Kouadri, S.; Elbeltagi, A.; Islam, A.R.M.T.; Kateb, S. Performance of machine learning methods in predicting water quality index based on irregular data set: Application on Illizi region (Algerian southeast). Appl. Water Sci. 2021, 11, 190. [Google Scholar] [CrossRef]
- Infancy, K.C.; Bruntha, P.M.; Pandiaraj, S.; Reby, J.J.; Joselin, A.; Selvadass, S. Prediction of Diabetes Using ML Classifiers. In Proceedings of the 2022 6th International Conference on Devices, Circuits and Systems (ICDCS), Coimbatore, India, 21–22 April 2022; pp. 484–488. [Google Scholar]
- AbdulHussien, A.A. Comparison of machine learning algorithms to classify web pages. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 205–209. [Google Scholar]
- Ahmadi, R.; Fathianpour, N.; Norouzi, G.H. Comparison of the performance of ANN and SVM methods in automatic detection of hidden cylindrical targets in GPR images. J. Min. Eng. 2015, 10, 83–98. [Google Scholar]
- Gupta, S.; Saluja, K.; Goyal, A.; Vajpayee, A.; Tiwari, V. Comparing the performance of machine learning algorithms using estimated accuracy. Meas. Sens. 2022, 24, 100432. [Google Scholar] [CrossRef]
- Ghorbani, R.; Ghousi, R. Comparing different resampling methods in predicting students’ performance using machine learning techniques. IEEE Access 2020, 8, 67899–67911. [Google Scholar] [CrossRef]
- Sattari, M.T.; Apaydin, H.; Band, S.S.; Mosavi, A.; Prasad, R. Comparative analysis of kernel-based versus ANN and deep learning methods in monthly reference evapotranspiration estimation. Hydrol. Earth Syst. Sci. 2021, 25, 603–618. [Google Scholar] [CrossRef]

| Parameters | N | Mean | Median | Std. Error of Mean | Min | Max | Std. Deviation |
|---|---|---|---|---|---|---|---|
| TDS (mg/L) | 504 | 510.83 | 409.00 | 15.02 | 166.00 | 2752.00 | 337.31 |
| Cl (mg/L) | 504 | 2.00 | 0.87 | 0.15 | 0.20 | 27.40 | 3.36 |
| TH | 504 | 2.97 | 2.73 | 0.05 | 1.15 | 10.10 | 1.10 |
| Temperature (°C) | 504 | 17.65 | 17.74 | 0.45 | 0.00 | 34.70 | 10.05 |
| Model Type | MAE (Training) | RMSE (Training) | R2 (Training) | MAE (Testing) | RMSE (Testing) | R2 (Testing) |
|---|---|---|---|---|---|---|
| GWO-KELM | 40.73 | 58.69 | 0.972 | 34.40 | 55.75 | 0.974 |
| ANN | 40.275 | 57.46 | 0.971 | 38.25 | 60.13 | 0.969 |
| GPR | 36.26 | 52.98 | 0.976 | 40.74 | 65.38 | 0.962 |
| SVM | 40.77 | 55.75 | 0.972 | 42.97 | 69.56 | 0.959 |
| LR | 41.657 | 57.31 | 0.971 | 44.32 | 74.18 | 0.953 |
| CART | 55.361 | 94.55 | 0.924 | 56.498 | 102.064 | 0.908 |
| BRT | 51.376 | 86.633 | 0.936 | 53.828 | 108.939 | 0.895 |
| Reference | Method | Input Parameters | Best Model |
|---|---|---|---|
| Al-Mukhtar and AL-Yaseen, 2019 [15] | ANFIS, ANN, MLR | NO3, Ca+2, Mg+2, TH, SO4, Cl− | ANFIS: 0.97 |
| Banadkooki et al., 2020 [9] | ANFIS, SVM, ANN | Na, Mg, Ca, HCO3, SO4, Cl | ANFIS-MFO: 0.94 |
| Ewusi et al., 2021 [16] | GPR, BPNN, PCR | As, Cd, Hg, Cu, CN, TSS, pH, Turbidity, EC | GPR: 0.99 |
| Adjovu et al., 2023 [21] | SVM, LR, KNN, ANN, GBM, RF, ET, XGBoost | EC, Temperature | LR: 0.82 |
| Hijji et al., 2023 [19] | ANN, ELM, ANFIS, NF-GMDH-GOA NF, GMDH-PSO, GMDH | Na, Mg, Ca, HCO3 | NF-GMDH-GOA: 0.97 |
| Pourhosseini et al., 2023 [18] | SVM-CA, SVM-HS, SVM-TLBO | Na, Mg, Ca, HCO3, SO4, Cl, pH | SVM-TLBO: 0.99 |
| Panahi et al., 2023 [17] | ANN-CSA, ELM-CSA | Na, Mg, Ca, K, HCO3, SO4, Cl, pH | ELM-CSA: 0.97 |
| This study | GWO-KELM, ANN, GPR, SVM, LR, CART, BRT | Cl, TH, Temperature | GWO-KELM: 0.974 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sayadi, M.; Hessari, B.; Montaseri, M.; Naghibi, A. Enhanced TDS Modeling Using an AI Framework Integrating Grey Wolf Optimization with Kernel Extreme Learning Machine. Water 2024, 16, 2818. https://doi.org/10.3390/w16192818
Sayadi M, Hessari B, Montaseri M, Naghibi A. Enhanced TDS Modeling Using an AI Framework Integrating Grey Wolf Optimization with Kernel Extreme Learning Machine. Water. 2024; 16(19):2818. https://doi.org/10.3390/w16192818
Chicago/Turabian StyleSayadi, Maryam, Behzad Hessari, Majid Montaseri, and Amir Naghibi. 2024. "Enhanced TDS Modeling Using an AI Framework Integrating Grey Wolf Optimization with Kernel Extreme Learning Machine" Water 16, no. 19: 2818. https://doi.org/10.3390/w16192818
APA StyleSayadi, M., Hessari, B., Montaseri, M., & Naghibi, A. (2024). Enhanced TDS Modeling Using an AI Framework Integrating Grey Wolf Optimization with Kernel Extreme Learning Machine. Water, 16(19), 2818. https://doi.org/10.3390/w16192818







