Non-Intrusive Water Surface Velocity Measurement Based on Deep Learning
Abstract
1. Introduction
2. Materials and Methods
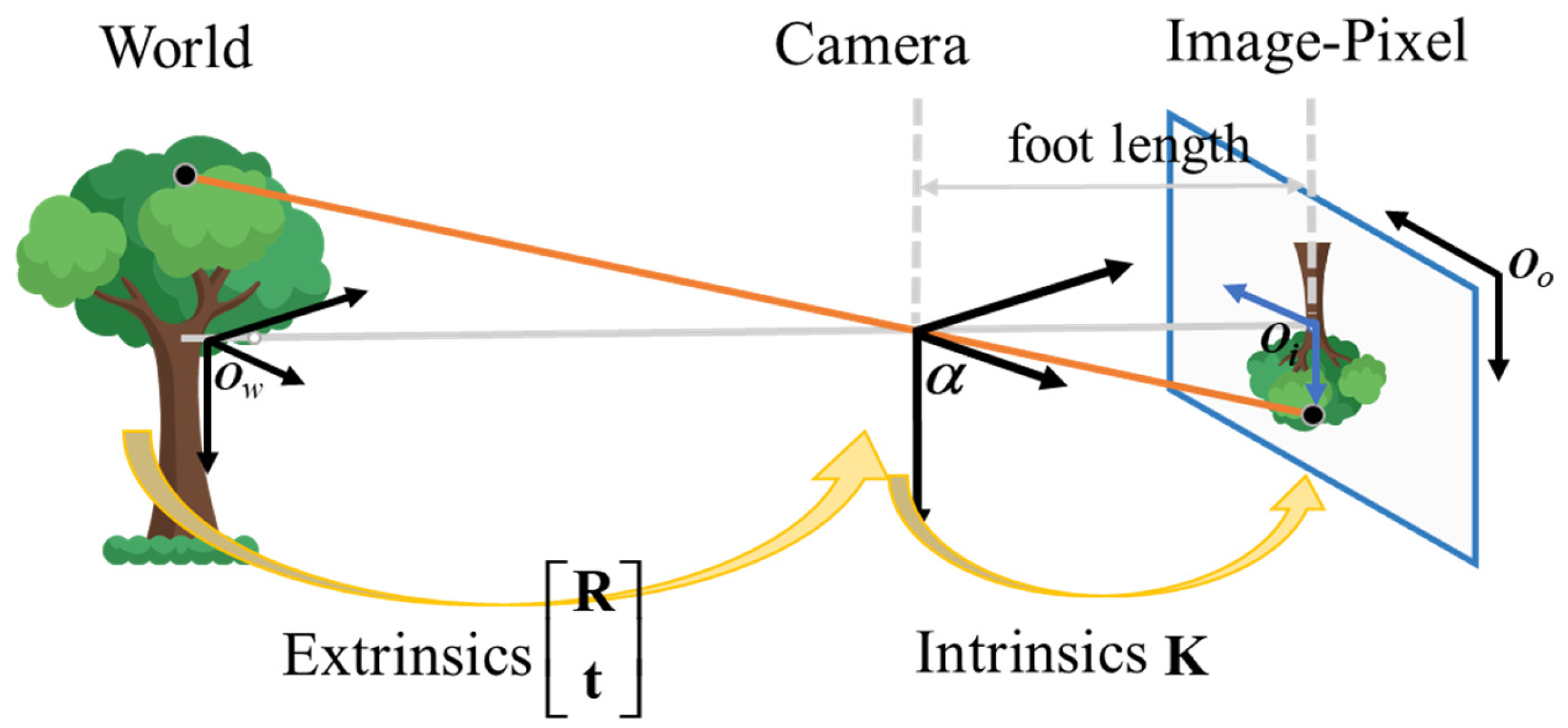
2.1. Image Correction
2.1.1. Camera Calibration
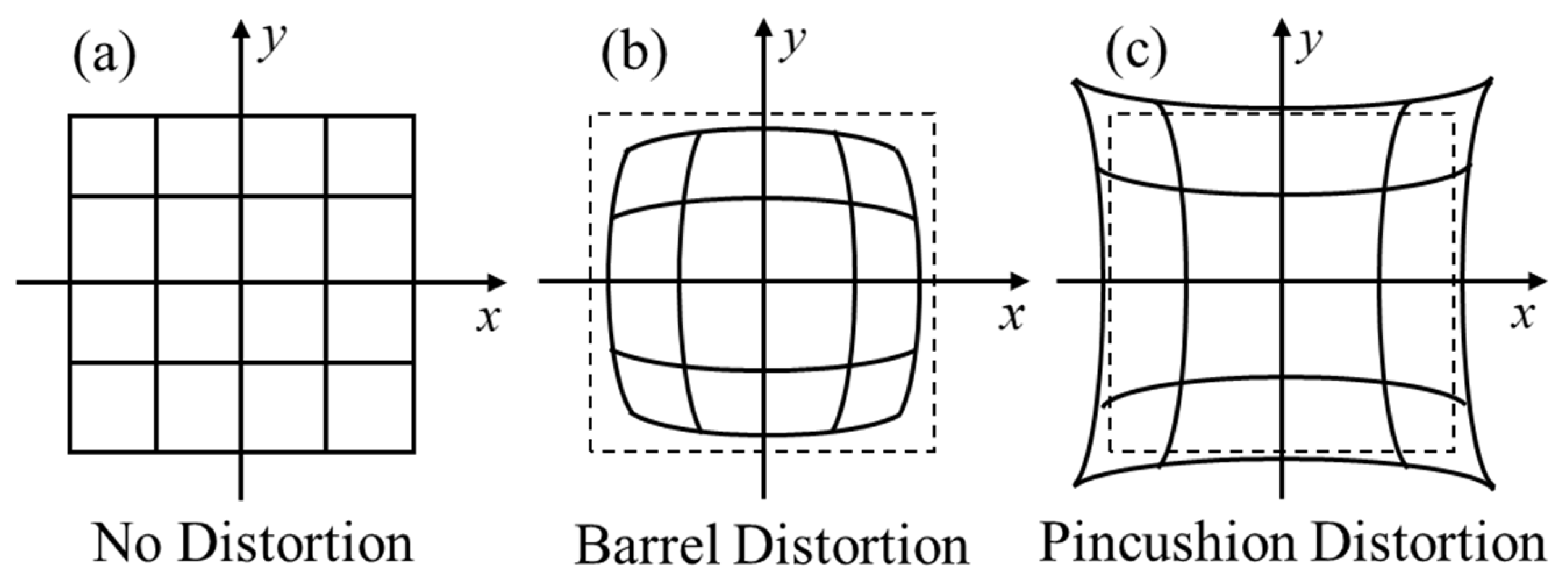
2.1.2. Distortion Correction
2.1.3. Orthorectification
2.2. Principle Analysis of OFV Method
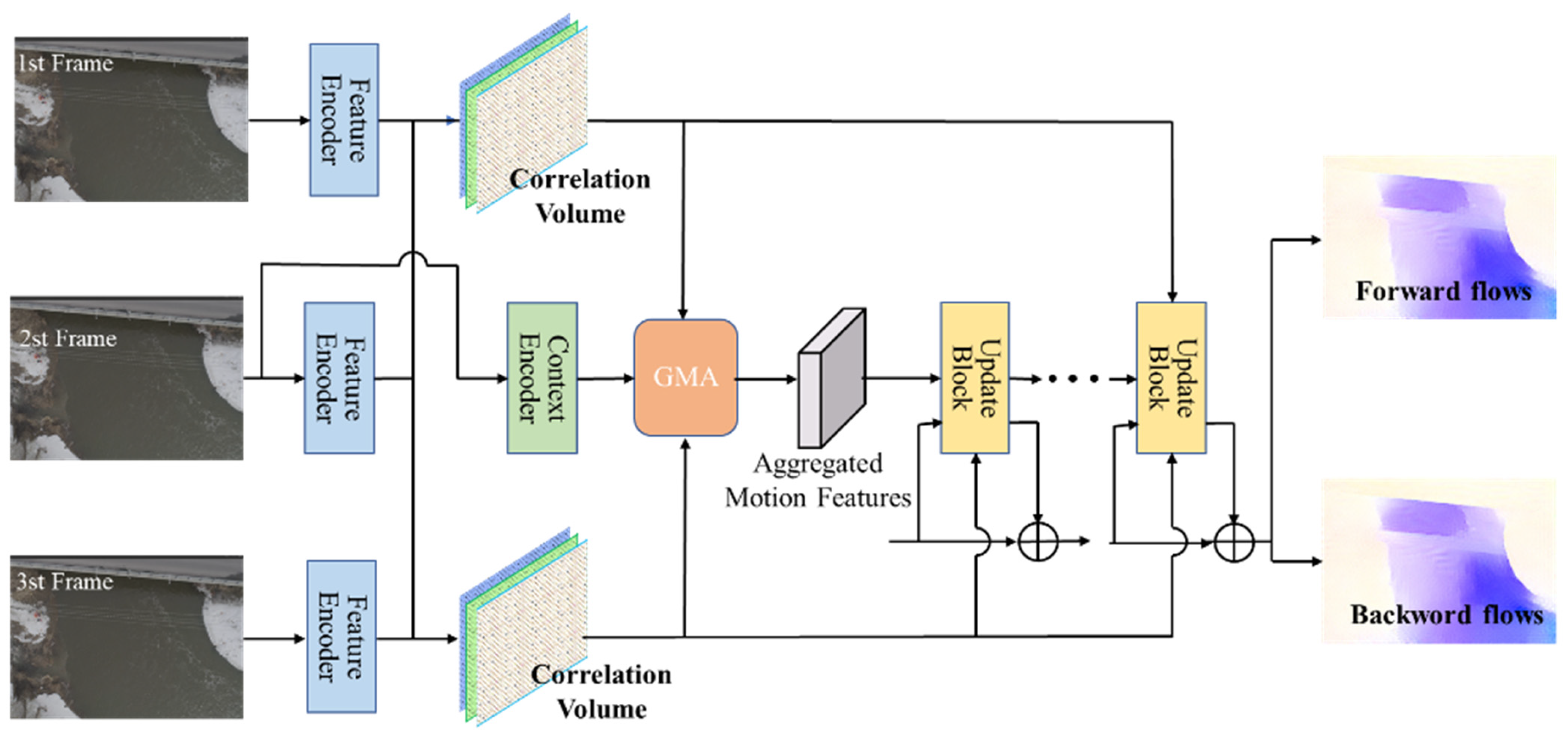
2.3. Model Features and Architectures of VideoFlow
2.3.1. TROF for Tri-Frame Optical Flow Estimation
2.3.2. Motion Propagation for Multi-Frame
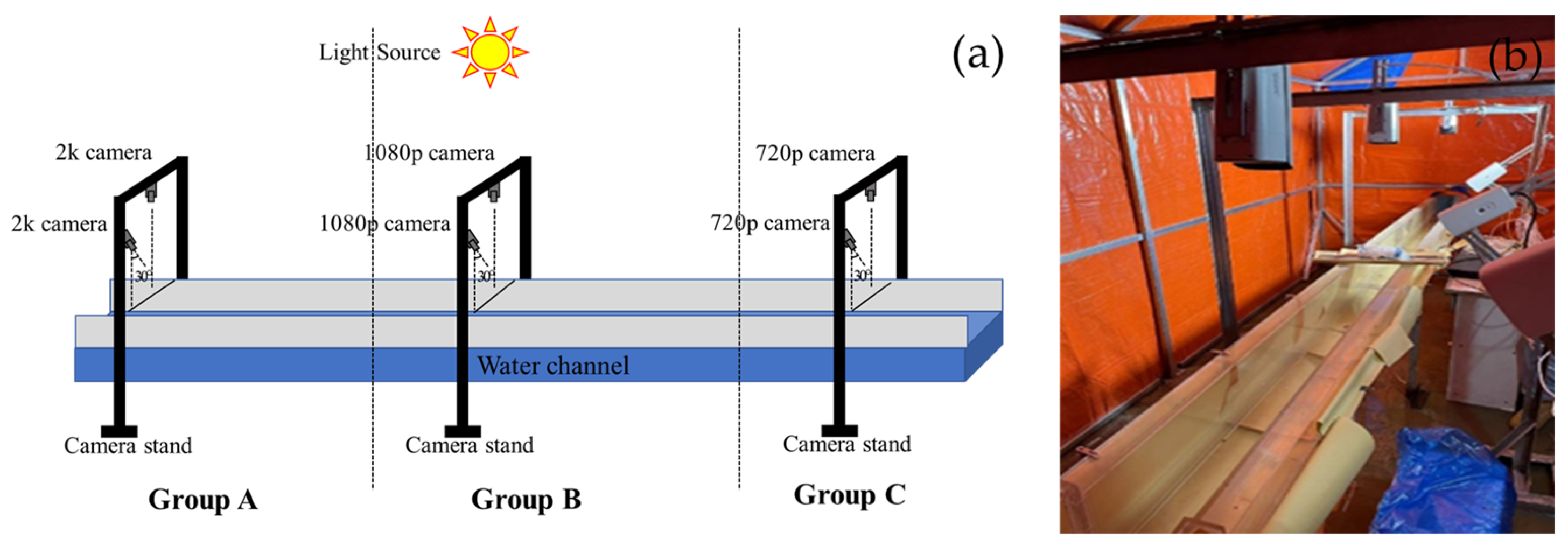
2.4. Video Acquisition and Data Processing
3. Results
3.1. Model Training
3.2. The Simulated River in Laboratory and Analysis of Experimental Results
3.3. Field River Measurements and Algorithm Validation
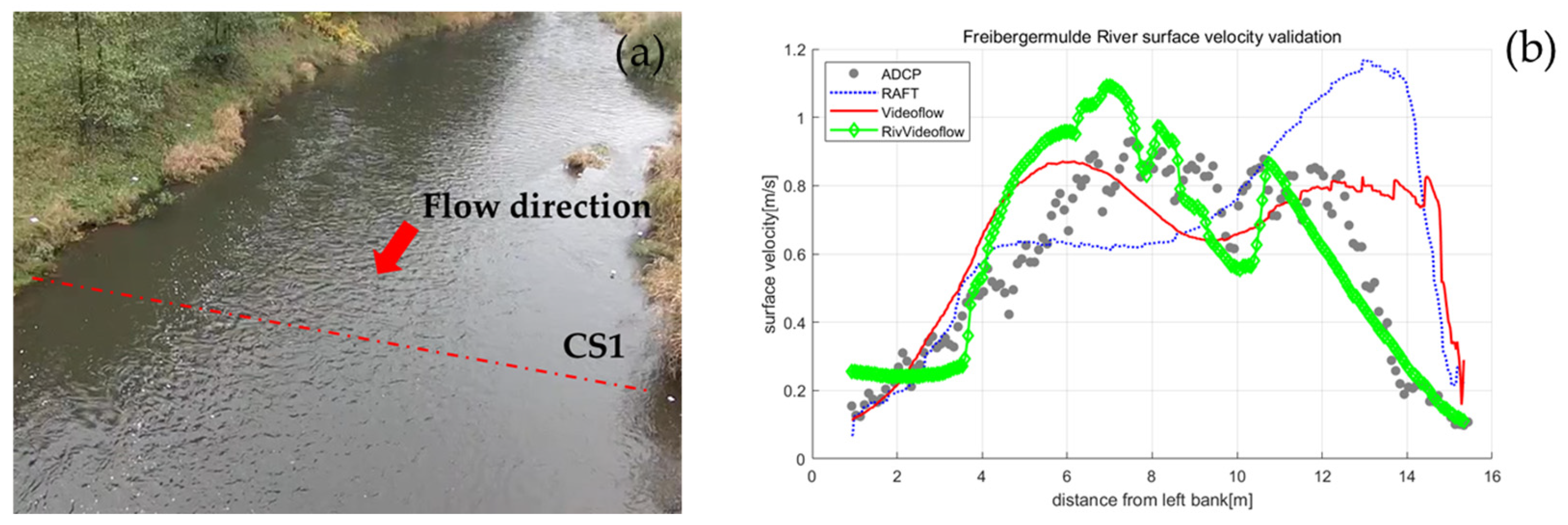
3.3.1. The Freiberger Mulde River in Field
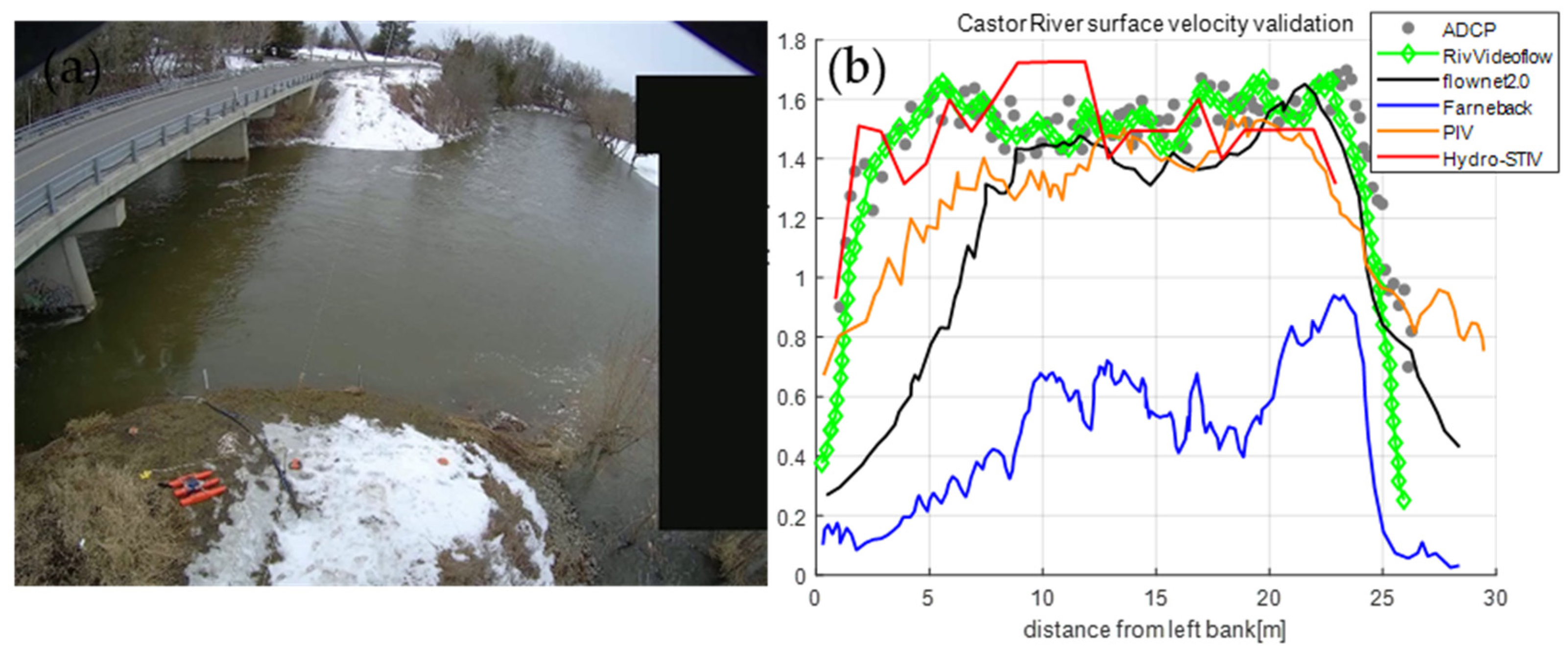
3.3.2. Comparative Analysis of WSV Measurement Techniques
3.3.3. Analysis of RivVideoFlow Algorithm Applicable Velocity Range
3.4. Visualization and Analysis of Experiments on the Synthetic River Datasets
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fernández-Nóvoa, D.; González-Cao, J.; García-Feal, O. Enhancing Flood Risk Management: A Comprehensive Review on Flood Early Warning Systems with Emphasis on Numerical Modeling. Water 2024, 16, 1408. [Google Scholar] [CrossRef]
- Laible, J.; Dramais, G.; Le Coz, J.; Calmel, B.; Camenen, B.; Topping, D.J.; Santini, W.; Pierrefeu, G.; Lauters, F. River suspended-sand flux computation with uncertainty estimation, using water samples and high-resolution ADCP measurements. EGUsphere 2024, 2024, 1–32. [Google Scholar]
- Fujita, I.; Muste, M.; Kruger, A. Large-scale particle image velocimetry for flow analysis in hydraulic engineering applications. J. Hydraul. Res. 1998, 36, 397–414. [Google Scholar] [CrossRef]
- Lemos, B.L.H.D.; de Lima Amaral, R.; Bortolin, V.A.A.; Lemos, M.L.H.D.; de Moura, H.L.; de Castro, M.S.; de Castilho, G.J.; Meneghini, J.R. Dynamic mask generation based on peak to correlation energy ratio for light reflection and shadow in PIV images. Measurement 2024, 229, 114352. [Google Scholar] [CrossRef]
- Tauro, F.; Piscopia, R.; Grimaldi, S. Streamflow observations from cameras: Large-scale particle image velocimetry or particle tracking velocimetry? Water Resour. Res. 2017, 53, 10374–10394. [Google Scholar] [CrossRef]
- Gu, M.; Li, J.; Hossain, M.M.; Xu, C. High-resolution microscale velocity field measurement using light field particle image-tracking velocimetry. Phys. Fluids 2023, 35, 112006. [Google Scholar] [CrossRef]
- Tauro, F.; Noto, S.; Botter, G.; Grimaldi, S. Assessing the optimal stage-cam target for continuous water level monitoring in ephemeral streams: Experimental evidence. Remote Sens. 2022, 14, 6064. [Google Scholar] [CrossRef]
- Fujita, I.; Shibano, T.; Tani, K. Application of masked two-dimensional Fourier spectra for improving the accuracy of STIV-based river surface flow velocity measurements. Meas. Sci. Technol. 2020, 31, 094015. [Google Scholar] [CrossRef]
- Xu, H.; Wang, J.; Zhang, Y.; Zhang, G.; Xiong, Z. Subgrid variational optimized optical flow estimation algorithm for Image Velocimetry. Sensors. 2022, 23, 437. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhu, R.; Zhang, G.; He, X.; Cai, R. Image flow measurement based on the combination of frame difference and fast and dense optical flow. Adv. Eng. Sci. 2022, 54, 195–207. [Google Scholar]
- Ansari, S.; Rennie, C.D.; Jamieson, E.C.; Seidou, O.; Clark, S.P. RivQNet: Deep learning based river discharge estimation using close-range water surface imagery. Water Resour. Res. 2023, 59, e2021WR031841. [Google Scholar] [CrossRef]
- Ilg, E.; Mayer, N.; Saikia, T.; Keuper, M.; Dosovitskiy, A.; Brox, T. Flownet 2.0: Evolution of optical flow estimation with deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2462–2470. [Google Scholar]
- Shi, X.; Huang, Z.; Bian, W.; Li, D.; Zhang, M.; Cheung, K.C.; See, S.; Qin, H.; Dai, J.; Li, H. Videoflow: Exploiting temporal cues for multi-frame optical flow estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023. [Google Scholar]
- Le Coz, J.; Renard, B.; Vansuyt, V.; Jodeau, M.; Hauet, A. Estimating the uncertainty of video-based flow velocity and discharge measurements due to the conversion of field to image coordinates. Hydrol. Process. 2021, 35, e14169. [Google Scholar] [CrossRef]
- Gavin, H.P. The Levenberg-Marquardt Algorithm for Nonlinear Least Squares Curve-Fitting Problems; Department of Civil and Environmental Engineering Duke University: Durham, NC, USA, 2019; Volume 3. [Google Scholar]
- Wang, J.; Shi, F.; Zhang, J.; Liu, Y. A new calibration model of camera lens distortion. Pattern Recognit. 2008, 41, 607–615. [Google Scholar] [CrossRef]
- Patalano, A.; García, C.M.; Rodríguez, A. Rectification of image velocity results (river): A simple and user-friendly toolbox for large scale water surface particle image velocimetry (PIV) and particle tracking velocimetry (PTV). Comput. Geosci. 2017, 109, 323–330. [Google Scholar] [CrossRef]
- Vigoureux, S.; Liebard, L.L.; Chonoski, A.; Robert, E.; Torchet, L.; Poveda, V.; Leclerc, F.; Billant, J.; Dumasdelage, R.; Rousseau, G.; et al. Comparison of streamflow estimated by image analysis (LSPIV) and by hydrologic and hydraulic modelling on the French Riviera during November 2019 flood. In Advances in Hydroinformatics: Models for Complex and Global Water Issues—Practices and Expectations; Springer Nature: Singapore, 2022; pp. 255–273. [Google Scholar]
- Dosovitskiy, A.; Fischer, P.; Ilg, E.; Hausser, P.; Hazirbas, C.; Golkov, V.; Van Der Smagt, P.; Cremers, D.; Brox, T. FlowNet: Learning optical flow with convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; IEEE Press: Piscataway, NJ, USA, 2015; pp. 2758–2766. [Google Scholar]
- Sun, D.; Yang, X.; Liu, M.-Y.; Kautz, J. Pwc-net: Cnns for optical flow using pyramid, warping, and cost volume. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; Volume 2, pp. 8934–8943. [Google Scholar]
- Hui, T.W.; Tang, X.; Loy, C.C. Liteflownet: A lightweight convolutional neural network for optical flow estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8981–8989. [Google Scholar]
- Teed, Z.; Deng, J. RAFT: Recurrent all-Pairs field transforms for optical flow. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Volume 16, pp. 402–419. [Google Scholar]
- Xu, H.; Zhang, J.; Cai, J.; Rezatofighi, H.; Tao, D. Gmflow: Learning optical flow via global matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8121–8130. [Google Scholar]
- Huang, Z.; Shi, X.; Zhang, C.; Wang, Q.; Cheung, K.C.; Qin, H.; Dai, J.; Li, H. Flowformer: A transformer architecture for optical flow. In European Conference on Computer Vision; Springer Nature: Cham, Switzerland, 2022; pp. 668–685. [Google Scholar]
- Chu, X.; Tian, Z.; Wang, Y.; Zhang, B.; Ren, H.; Wei, X.; Xia, H.; Shen, C. Twins: Revisiting spatial attention design in vision transformers. arXiv 2021, arXiv:2104.13840. [Google Scholar]
- Sun, S.; Chen, Y.; Zhu, Y.; Guo, G.; Li, G. Skflow: Learning optical flow with super kernels. Adv. Neural Inf. Process. Syst. 2022, 35, 11313–11326. [Google Scholar]
- Mayer, N.; Ilg, E.; Hausser, P.; Fischer, P.; Cremers, D.; Dosovitskiy, A.; Brox, T. A large dataset to train convolutional networks for disparity, optical flow, and scene flow estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4040–4048. [Google Scholar]
- Butler, D.J.; Wulff, J.; Stanley, G.B.; Black, M.J. A naturalistic open source movie for optical flow evaluation. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2012; pp. 611–625. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The kitti dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Kondermann, D.; Nair, R.; Honauer, K.; Krispin, K.; Andrulis, J.; Brock, A.; Gussefeld, B.; Rahimimoghaddam, M.; Hofmann, S.; Brenner, C.; et al. The hci benchmark suite: Stereo and flow ground truth with uncertainties for urban autonomous driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 27–30 June 2016; pp. 19–28. [Google Scholar]
- Bahmanpouri, F.; Eltner, A.; Barbetta, S.; Bertalan, L.; Moramarco, T. Estimating the average river cross-section velocity by observing only one surface velocity value and calibrating the entropic parameter. Water Resour. Res. 2022, 58, e2021WR031821. [Google Scholar] [CrossRef]
- Biggs, H. Drone Flow User Guide v1. 1-River Remote Sensing and Surface Velocimetry; National Institute of Water and Atmospheric Research (NIWA) Report; National Institute of Water and Atmospheric Research (NIWA): Auckland, New Zealand, 2022. [Google Scholar]
- Bodart, G.; Le Coz, J.; Jodeau, M.; Hauet, A. Synthetic river flow videos for evaluating image-based velocimetry methods. Water Resour. Res. 2022, 58, e2022WR032251. [Google Scholar] [CrossRef]
- Le Coz, J.; Jodeau, M.; Hauet, A.; Marchand, B.; Le Boursicaud, R. Image-based velocity and discharge measurements in field and laboratory river engineering studies using the free FUDAA-LSPIV software. In River Flow; CRC Press: Lausanne, Switzerland, 2014; Volume 2014, pp. 1961–1967. [Google Scholar]
- Farnebäck, G. Two-frame motion estimation based on polynomial expansion. In Image Analysis: 13th Scandinavian Conference, SCIA 2003 Halmstad, Sweden, June 29–July 2, 2003 Proceedings 13; Springer: Berlin/Heidelberg, Germany, 2003; pp. 363–370. [Google Scholar]
- Fujita, I.; Watanabe, H.; Tsubaki, R. Development of a non-intrusive and efficient flow monitoring technique: The space-time image velocimetry (STIV). Int. J. River Basin Manag. 2007, 5, 105–114. [Google Scholar] [CrossRef]

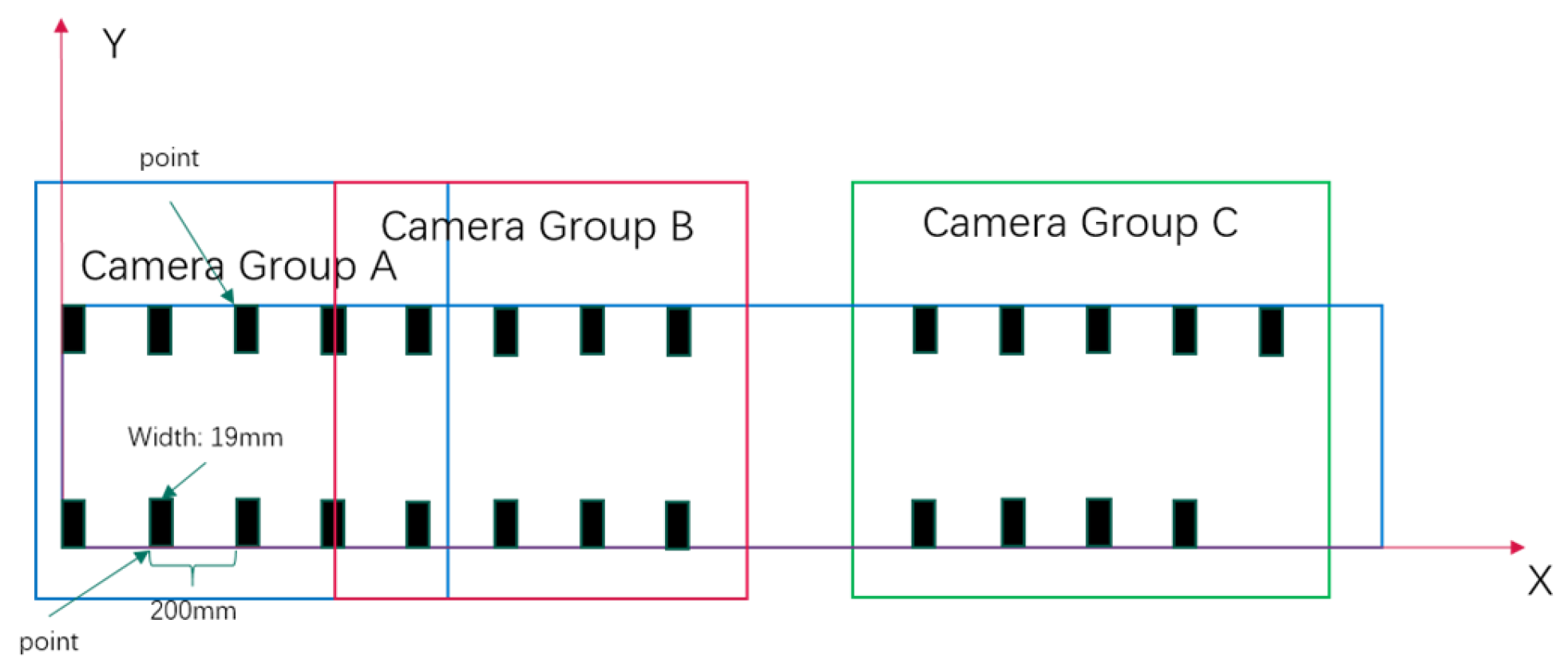




| Velocity-Range | Tracer | Light | Shadow | Resolution | RDV-Velocity | Mid-Velocity | Max-Velocity |
|---|---|---|---|---|---|---|---|
| 0~1 m/s | √ | 1000 W lamp | √ | 2 k/1080 p/720 p | 0.98 m/s | 0.700 m/s | 1.100 m/s |
| √ | 1000 W lamp | X | 2 k/1080 p/720 p | 0.86 m/s | 0.832 m/s | 0.982 m/s | |
| √ | Dark | X | 2 k/1080 p/720 p | 0.86 m/s | - | - | |
| X | 1000 W lamp | √ | 2 k/1080 p/720 p | 0.98 m/s | 0.912 m/s | 1.131 m/s | |
| X | 1000 W lamp | X | 2 k/1080 p/720 p | 0.89 m/s | 0.881 m/s | 1.202 m/s | |
| X | Dark | X | 2 k/1080 p/720 p | 0.86 m/s | - | - | |
| 1~2 m/s | √ | 1000 W lamp | √ | 2 k/1080 p/720 p | 1.30 m/s | 1.222 m/s | 2.959 m/s |
| √ | 1000 W lamp | X | 2 k/1080 p/720 p | 1.30 m/s | 1.139 m/s | 1.529 m/s | |
| √ | Dark | X | 2 k/1080 p/720 p | 1.505 m/s | - | - | |
| X | 1000 W lamp | √ | 2 k/1080 p/720 p | 1.30 m/s | 1.241 m/s | 1.677 m/s | |
| X | 1000 W lamp | X | 2 k/1080 p/720 p | 1.854 m/s | 1.782 m/s | 2.013 | |
| X | Dark | X | 2 k/1080 p/720 p | 1.505 m/s | - | - | |
| 2~3 m/s | √ | 1000 W lamp | √ | 2 k/1080 p/720 p | 2.604 m/s | 1.944 m/s | 2.541 m/s |
| √ | 1000 W lamp | X | 2 k/1080 p/720 p | 2.85 m/s | 1.964 m/s | 2.814 m/s | |
| √ | Dark | X | 2 k/1080 p/720 p | 2.85 m/s | - | - | |
| X | 1000 W lamp | √ | 2 k/1080 p/720 p | 2.85 m/s | 2.132 m/s | 2.769 m/s | |
| X | 1000 W lamp | X | 2 k/1080 p/720 p | 2.85 m/s | 2.412 m/s | 3.072 m/s | |
| X | Dark | X | 2 k/1080 p/720 p | 2.89 m/s | - | ||
| 3~4 m/s | √ | 1000 W lamp | √ | 2 k/1080 p/720 p | 3.61 m/s | 1.262 m/s | 1.784 m/s |
| √ | 1000 W lamp | X | 2 k/1080 p/720 p | 3.61 m/s | 1.597 m/s | 2.205 m/s | |
| √ | Dark | X | 2 k/1080 p/720 p | 3.61 m/s | - | - | |
| X | 1000 W lamp | √ | 2 k/1080 p/720 p | 3.61 m/s | 2.555 m/s | 3.490 m/s | |
| X | 1000 W lamp | X | 2 k/1080 p/720 p | 3.61 m/s | 2.791 m/s | 3.491 m/s | |
| X | Dark | X | 2 k/1080 p/720 p | 3.61 m/s | - | - |
| Dataset Name | Image Pairs | Scene Type | Details |
|---|---|---|---|
| FlyingThings | ~39,000 | synthetic | Scenes with various everyday objects flying along ran-dom 3D trajectories. |
| Sintel | 1040 | synthetic movie scenes | Includes natural scenes and motion challenges such as long-range motion, lighting changes, etc. |
| KITTI-2015 | 400 | real-world driving scenes | Contains real annotations for dynamic scene flow, used for 3D scene flow estimation. |
| HD1K | 1000 | real-world urban driving scenes | Features high-resolution, high-frame-rate, and high-dynamic-range images. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, G.; Du, T.; He, J.; Zhang, Y. Non-Intrusive Water Surface Velocity Measurement Based on Deep Learning. Water 2024, 16, 2784. https://doi.org/10.3390/w16192784
An G, Du T, He J, Zhang Y. Non-Intrusive Water Surface Velocity Measurement Based on Deep Learning. Water. 2024; 16(19):2784. https://doi.org/10.3390/w16192784
Chicago/Turabian StyleAn, Guocheng, Tiantian Du, Jin He, and Yanwei Zhang. 2024. "Non-Intrusive Water Surface Velocity Measurement Based on Deep Learning" Water 16, no. 19: 2784. https://doi.org/10.3390/w16192784
APA StyleAn, G., Du, T., He, J., & Zhang, Y. (2024). Non-Intrusive Water Surface Velocity Measurement Based on Deep Learning. Water, 16(19), 2784. https://doi.org/10.3390/w16192784







