Delineation of the Hydrogeological Functioning of a Karst Aquifer System Using a Combination of Environmental Isotopes and Artificial Tracers: The Case of the Sierra Seca Range (Andalucía, Spain)
Abstract
1. Introduction
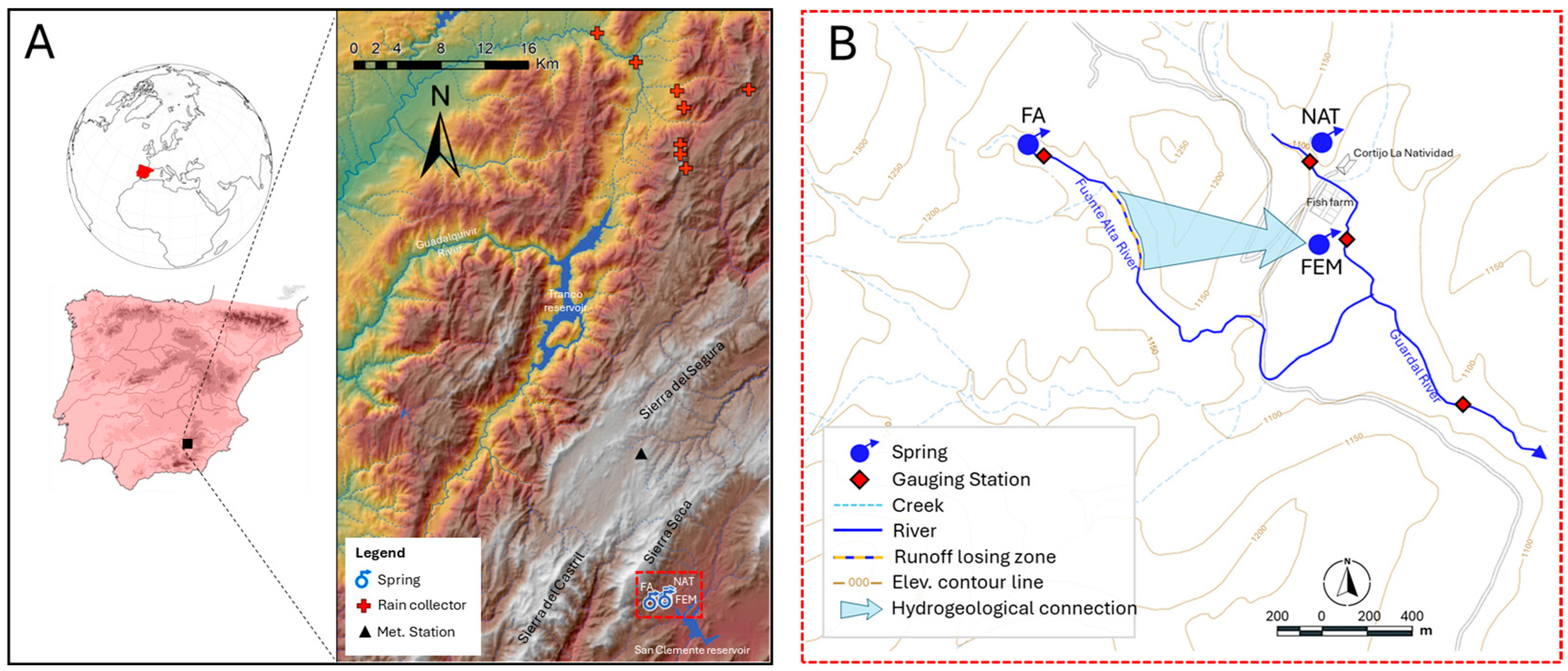
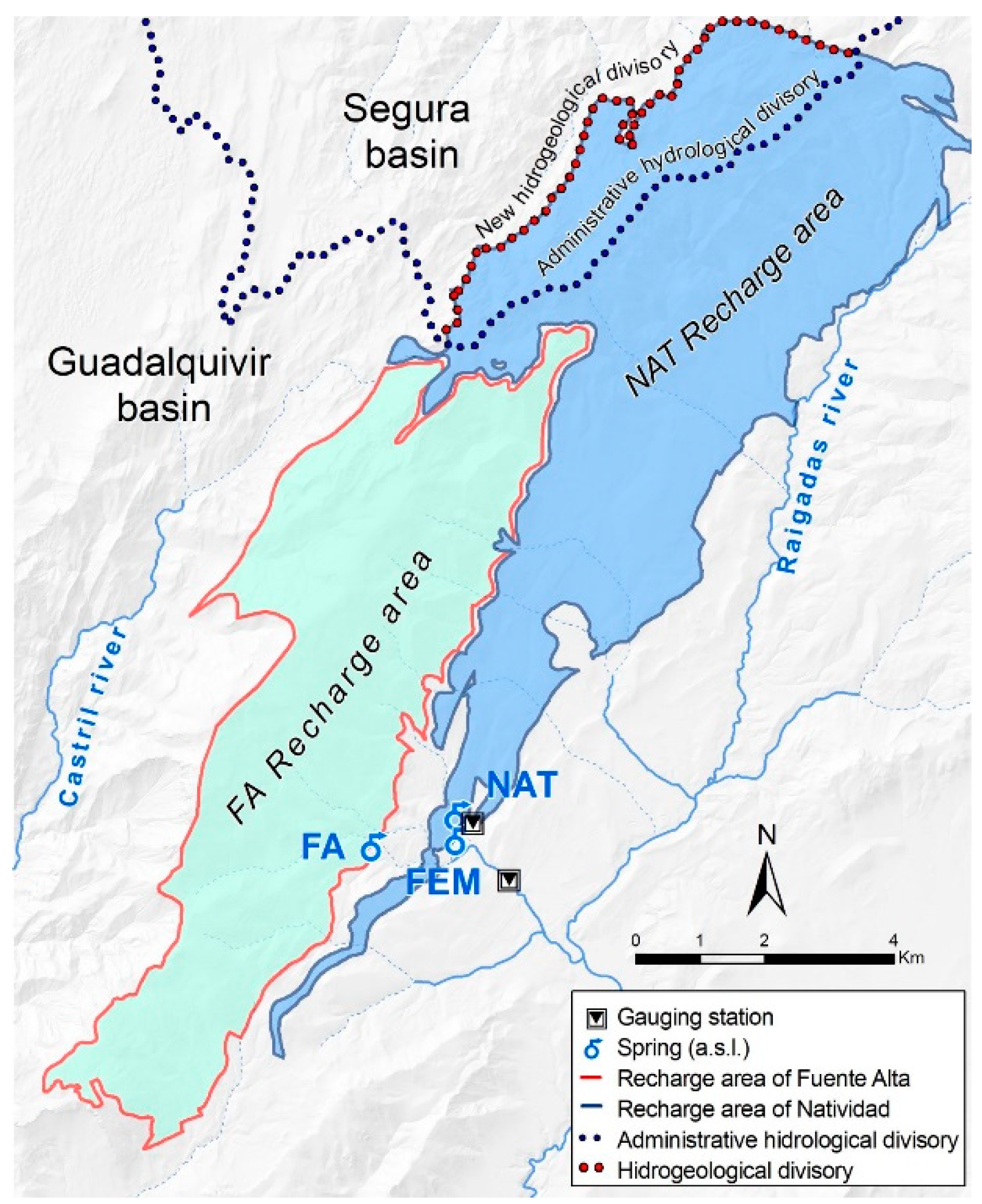
2. Location, Geological, and Hydrogeological Context
- The Lower Cretaceous aquifer developed in carbonate materials, predominantly limestones with rudists, and exhibits a thickness of 400 m. These carbonates are partially sealed at the roof in the slope break zone by a low permeability level of marls and marl limestones of variable thickness [29]. The primary hydrogeological drainage zone of this aquifer is the Fuente Alta (FA) spring, which is situated at the interface between the carbonate aquifer and the sealing low-permeability level.
- The Upper Cretaceous aquifer is formed by limestones with an average thickness of 150 m. This aquifer is drained by two springs, Natividad (NAT) and Fuente de Enmedio (FEM). The former spring drains this aquifer while discharging through a contact between the Upper Cretaceous limestone and the Paleocene marls. FEM drains a small sector of the Upper Cretaceous aquifer, although some of the associated groundwater discharge is probably generated by surface water infiltration along the Fuente Alta riverbed, as suggested by González-Ramón et al. (2024) [25].
3. Methodology and Materials
3.1. Rainfall and Groundwater Sampling
3.2. Estimation of Aquifer Recharge Elevation
- A1.
- All the precipitation samples are considered.where [-] and [L] are isotopic content and precipitation length of the j-th sampled precipitation event, respectively, and N [-] is the total number of precipitation events sampled. This case assumes that .
- A2.
- The same approach as A1 without considering the summer rainfall samples.
- A3.
- The same approach as A2 without considering any water sample from rainfall events lower than 20 mm.
- A4.
- The same approach as A2 without considering any water sample from rainfall events lower than 30 mm.
- A5.
- The same approach as A2 without considering any water sample from rainfall events lower than 40 mm.
3.3. Estimation of Groundwater Transit Times
- Monthly recharge flow to the aquifer. This time series is obtained as one of the terms of the water balance, calculated by numerical modeling of the hydrodynamic behavior of the aquifer. An HBV model has been implemented for both the Lower Cretaceous aquifer and the Upper Cretaceous aquifer drained by FA and NAT springs, respectively, HBV is a conceptual rainfall-runoff model for hydrodynamic modeling of hydrological basins, which solves a general water balance equation. This model has been used in different hydrological research studies in mountain areas [40,41,42,43,44,45].
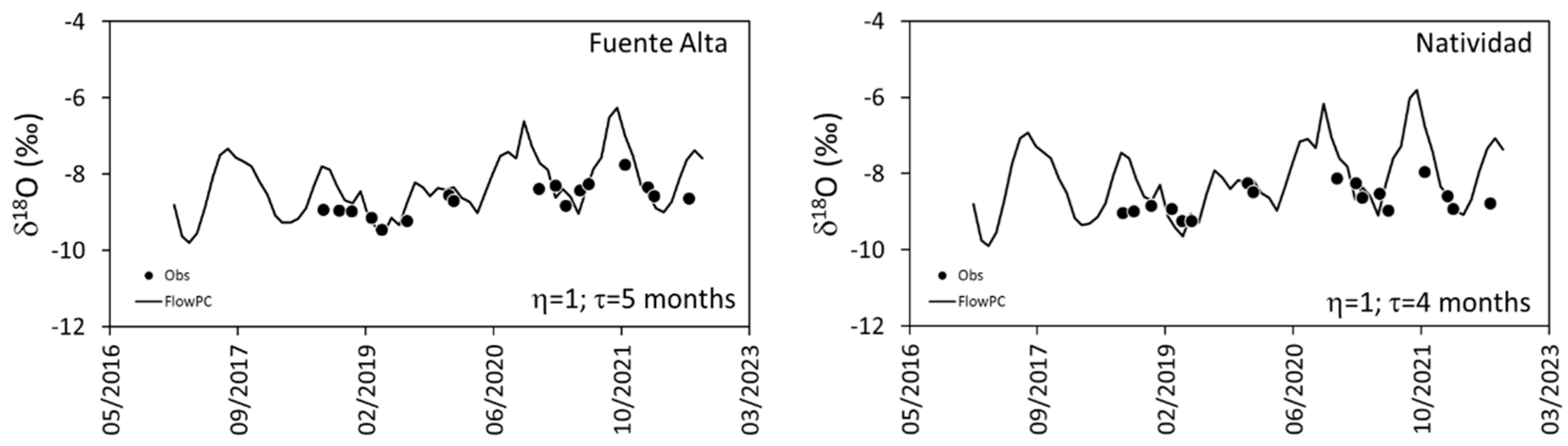
- Average isotopic content of the monthly recharge, which is obtained from the monthly precipitation samples accumulated in the rainfall monitoring stations installed in the study area. For the months in which precipitation samples could not be obtained in the study area, they were estimated using the machine learning model developed by [46], which generates, for any location in Europe, monthly time series of isotope content in precipitation for the period 1950–2019. Outside this period, the monthly values associated with a given month (e.g., January) are estimated as the average of all the time series values associated with that month.
3.4. Artificial Tracers
3.4.1. Instrumentation
3.4.2. Tracer Injection and Transport Modeling
4. Results and Discussion
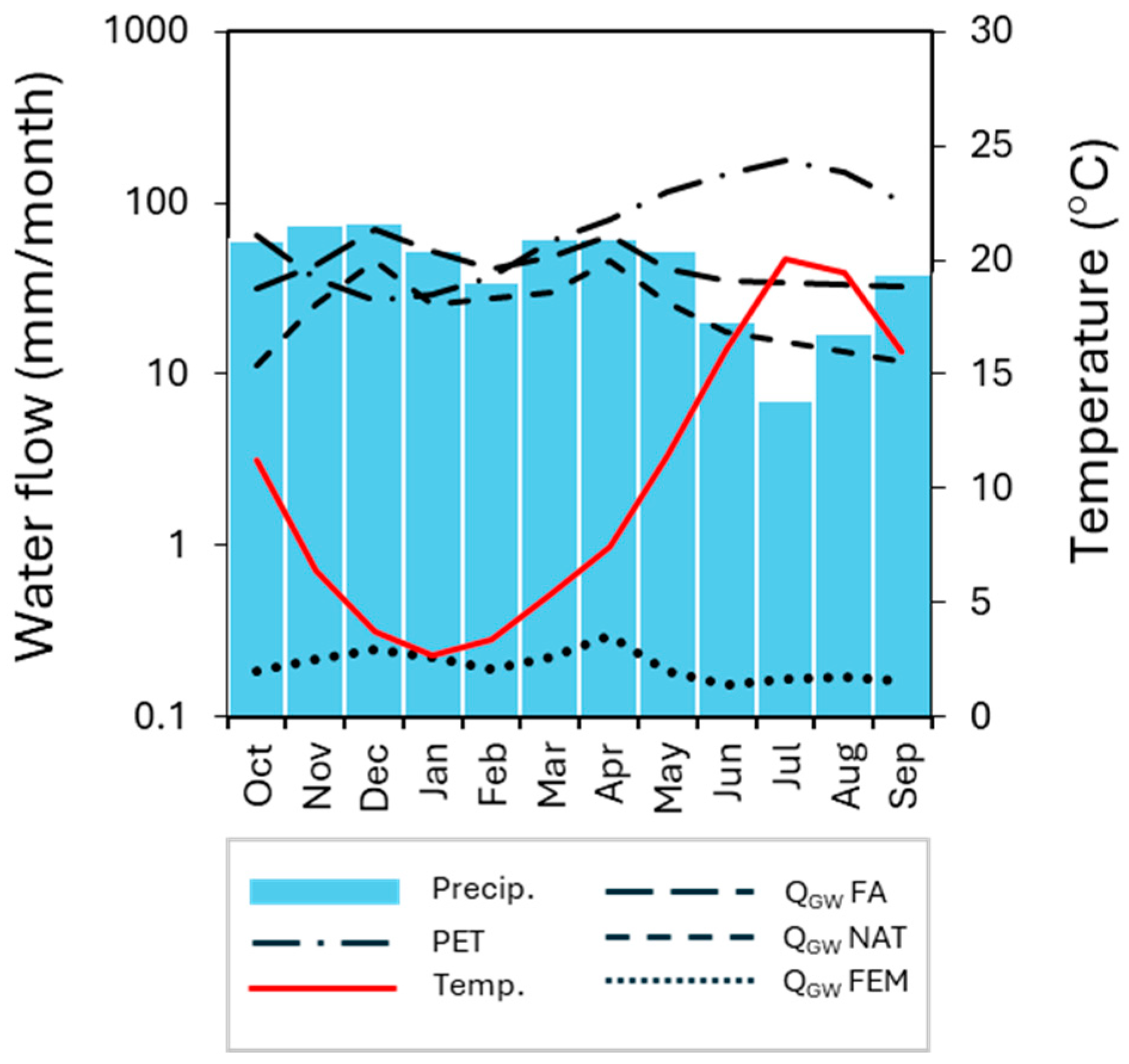
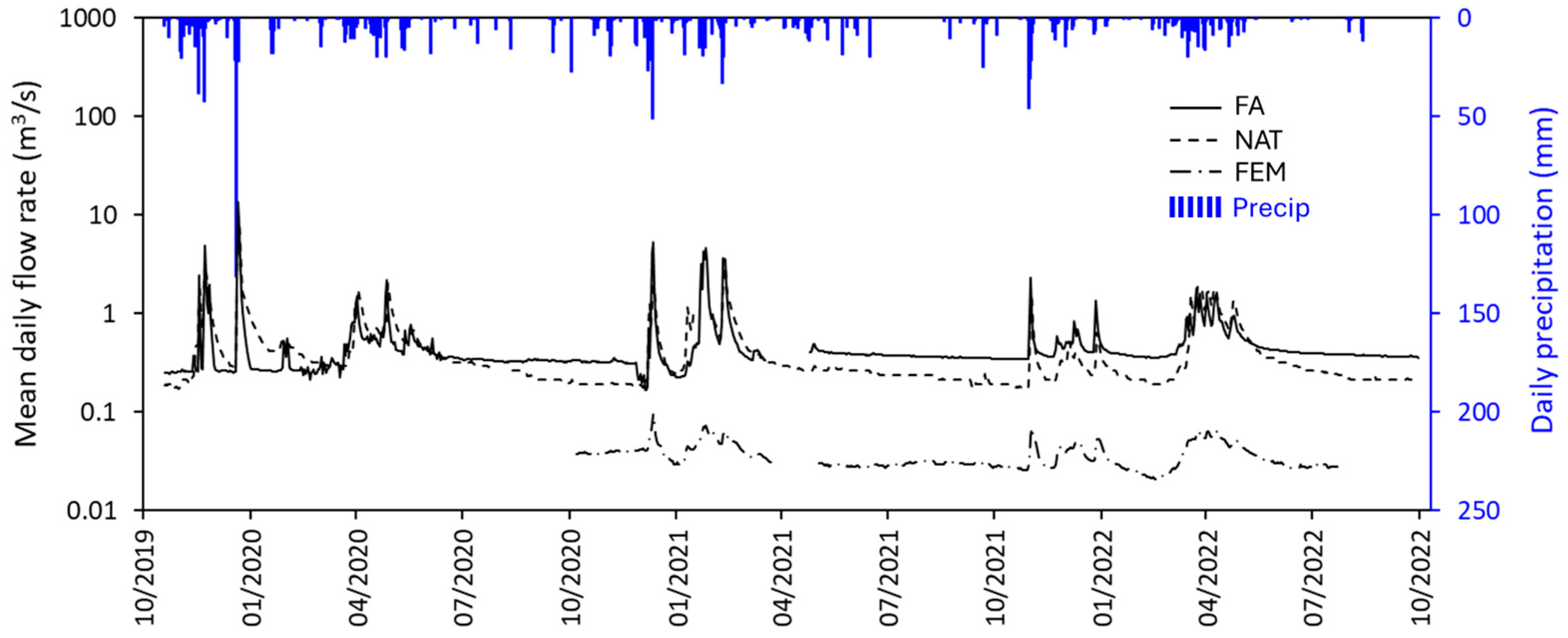
4.1. Hydrodynamic Data
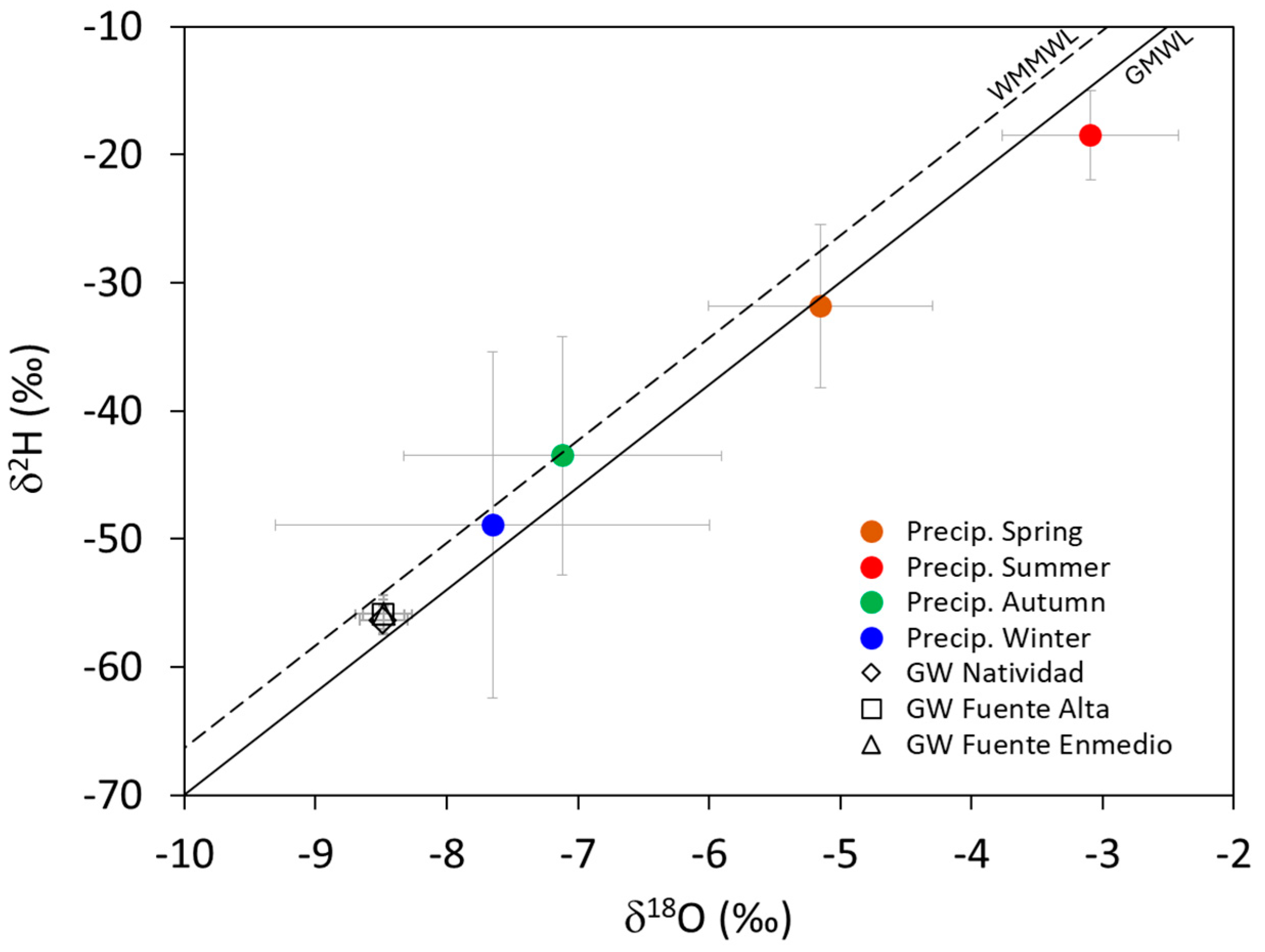
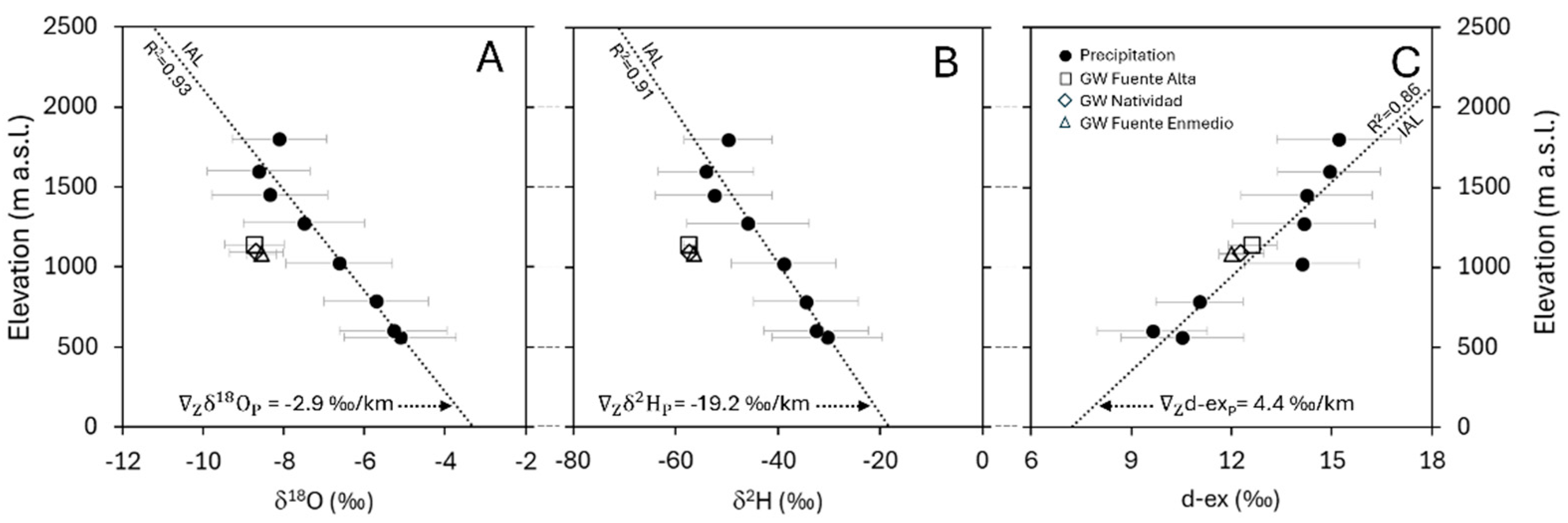
4.2. Environmental Tracers (, and -) in Precipitation and Groundwater
4.3. Groundwater Transit Time
4.3.1. Determination of Using Dye Tracer Tests
4.3.2. Determination of Using Environmental Tracers
4.4. Definition of Hydrogeological Boundaries:
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goldscheider, N.; Chen, Z.; Auler, A.S.; Bakalowicz, M.; Broda, S.; Drew, D.; Hartmann, J.; Jiang, G.; Moosdorf, N.; Stevanovic, Z.; et al. Global Distribution of Carbonate Rocks and Karst Water Resources. Hydrogeol. J. 2020, 28, 1661–1677. [Google Scholar] [CrossRef]
- Stevanović, Z. Karst Waters in Potable Water Supply: A Global Scale Overview. Environ. Earth Sci. 2019, 78, 662. [Google Scholar] [CrossRef]
- Ford, D.; Williams, P.D. Karst Hydrogeology and Geomorphology; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 9780470849965. [Google Scholar]
- Hartmann, A.; Jasechko, S.; Gleeson, T.; Wada, Y.; Andreo, B.; Barbera, J.A.; Brielmann, H.; Bouchaou, L.; Charlier, J.B.; Darling, W.G.; et al. Risk of Groundwater Contamination Widely Underestimated Because of Fast Flow into Aquifers. Proc. Natl. Acad. Sci. USA 2021, 118, e2024492118. [Google Scholar] [CrossRef] [PubMed]
- Andreo, B.; Liñán, C.; Carrasco, F.; Jiménez de Cisneros, C.; Caballero, F.; Mudry, J. Influence of Rainfall Quantity on the Isotopic Composition (18O and 2H) of Water in Mountainous Areas. Application for Groundwater Research in the Yunquera-Nieves Karst Aquifers (S Spain). Appl. Geochem. 2004, 19, 561–574. [Google Scholar] [CrossRef]
- Stroj, A.; Briški, M.; Lukač Reberski, J.; Frangen, T. Regional Analysis of Tracer Tests in the Karstic Basin of the Gacka River (Croatian Dinaric Karst). Hydrology 2023, 10, 106. [Google Scholar] [CrossRef]
- Custodio, E. Recarga Natural a Los Acuíferos, Metodología y Soporte de La Isotopía Del Agua: Aplicación a La Planificación Hidrológica y Conocimiento de Las Aguas Subterráneas En España: Informe RAEMIA; Iniciativa Digital Politècnica; Oficina de Publicacions Acadèmiques Digitals de La UPC: Barcelona, Spain, 2019. [Google Scholar]
- Dansgaard, W. Stable Isotopes in Precipitation. Tellus A Dyn. Meteorol. Oceanogr. 2012, 16, 436–468. [Google Scholar] [CrossRef]
- Allen, S.T.; Jasechko, S.; Berghuijs, W.R.; Welker, J.M.; Goldsmith, G.R.; Kirchner, J.W. Global Sinusoidal Seasonality in Precipitation Isotopes. Hydrol. Earth Syst. Sci. 2019, 23, 3423–3436. [Google Scholar] [CrossRef]
- Liu, F.; Conklin, M.H.; Shaw, G.D. Altitudinal Control of Isotopic Composition and Application in Understanding Hydrologic Processes in the Mid Merced River Catchment, Sierra Nevada, California, USA. Hydrol. Earth Syst. Sci. 2023, 28, 2239–2258. [Google Scholar] [CrossRef]
- Jódar, J.; Custodio, E.; Lambán, L.J.; Martos-Rosillo, S.; Herrera-Lameli, C.; Sapriza-Azuri, G. Vertical Variation in the Amplitude of the Seasonal Isotopic Content of Rainfall as a Tool to Jointly Estimate the Groundwater Recharge Zone and Transit Times in the Ordesa and Monte Perdido National Park Aquifer System, North-Eastern Spain. Sci. Total Environ. 2016, 573, 505–517. [Google Scholar] [CrossRef]
- Jódar, J.; Lambán, L.J.; Medina, A.; Custodio, E. Exact Analytical Solution of the Convolution Integral for Classical Hydrogeological Lumped-Parameter Models and Typical Input Tracer Functions in Natural Gradient Systems. J. Hydrol. 2014, 519, 3275–3289. [Google Scholar] [CrossRef]
- Lambán, L.J.; Jódar, J.; Custodio, E.; Soler, A.; Sapriza, G.; Soto, R. Isotopic and Hydrogeochemical Characterization of High-Altitude Karst Aquifers in Complex Geological Settings. The Ordesa and Monte Perdido National Park (Northern Spain) Case Study. Sci. Total Environ. 2015, 506–507, 466–479. [Google Scholar] [CrossRef] [PubMed]
- Herms, I.; Jódar, J.; Soler, A.; Vadillo, I.; Lambán, L.J.; Martos-Rosillo, S.; Núñez, J.A.; Arnó, G.; Jorge, J. Contribution of Isotopic Research Techniques to Characterize High-Mountain-Mediterranean Karst Aquifers: The Port Del Comte (Eastern Pyrenees) Aquifer. Sci. Total Environ. 2019, 656, 209–230. [Google Scholar] [CrossRef] [PubMed]
- Mudarra, M.; Andreo, B.; Marín, A.I.; Vadillo, I.; Barberá, J.A. Combined Use of Natural and Artificial Tracers to Determine the Hydrogeological Functioning of a Karst Aquifer: The Villanueva Del Rosario System (Andalusia, Southern Spain). Hydrogeol. J. 2014, 22, 1027–1039. [Google Scholar] [CrossRef]
- González-Ramón, A.; Jódar, J.; Samsó, J.M.; Martos-Rosillo, S.; Heredia, J.; Zabaleta, A.; Antigüedad, I.; Custodio, E.; Lambán, L.J. Hydrometeorological Factors Determining the Development of Water Table Cave Patterns in High Alpine Zones. The Ordesa and Monte Perdido National Park, Ne Spain. Int. J. Speleol. 2020, 49, 249–270. [Google Scholar] [CrossRef]
- Jódar, J.; González-Ramón, A.; Martos-Rosillo, S.; Heredia, J.; Herrera, C.; Urrutia, J.; Caballero, Y.; Zabaleta, A.; Antigüedad, I.; Custodio, E.; et al. Snowmelt as a Determinant Factor in the Hydrogeological Behaviour of High Mountain Karst Aquifers: The Garcés Karst System, Central Pyrenees (Spain). Sci. Total Environ. 2020, 748, 141363. [Google Scholar] [CrossRef]
- Chen, Z.; Goldscheider, N. Modeling Spatially and Temporally Varied Hydraulic Behavior of a Folded Karst System with Dominant Conduit Drainage at Catchment Scale, Hochifen–Gottesacker, Alps. J. Hydrol. 2014, 514, 41–52. [Google Scholar] [CrossRef]
- Lauber, U.; Goldscheider, N. Use of Artificial and Natural Tracers to Assess Groundwater Transit-Time Distribution and Flow Systems in a High-Alpine Karst System (Wetterstein Mountains, Germany). Hydrogeol. J. 2014, 22, 1807–1824. [Google Scholar] [CrossRef]
- Luo, M.; Wan, L.; Liao, C.; Jakada, H.; Zhou, H. Geographic and Transport Controls of Temperature Response in Karst Springs. J. Hydrol. 2023, 623, 129850. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Chen, X.; Xie, Y.; Cheng, Q.; He, Q.; Peng, T.; Chen, B.; Soulsby, C. Can Temperature Be a Low-Cost Tracer for Modelling Water Age Distributions in a Karst Catchment? J. Hydrol. 2024, 643, 131947. [Google Scholar] [CrossRef]
- Bergström, S. Development and Application of a Conceptual Runoff Model for Scandinavian Catchments; RHO 7; SMHI: Norrköping, Sweden, 1976. [Google Scholar]
- Seibert, J. HBV Light. User’s Manual; Uppsala University, Institute of Earth Science, Department of Hydrology: Uppsala, Sweden, 1996. [Google Scholar]
- Maloszewski, P.; Zuber, A. Lumped Parameter Models for the Interpretation of Environmental Tracer Data. In Manual on Mathematical Models in Isotope Hydrogeology, TECDOC-910; International Atomic Energy Agency, Ed.; International Atomic Energy Agency Publishing Section: Vienna, Austria, 1996. [Google Scholar]
- González-Ramón, A.; Jódar, J.; Morales-González, A.L.; Moral-Martos, F.; Jiménez-Espinosa, R. Characterising the Discharge of Hillslope Karstic Aquifers from Hydrodynamic and Physicochemical Data (Sierra Seca, SE Spain). Hydrogeol. J. 2024. [Google Scholar] [CrossRef]
- Chazarra Bernabé, A.; Flórez García, E.; Peraza Sánchez, B.; Tohá Rebull, T.; Lorenzo Mariño, B.; Criado Pinto, E.; Moreno García, J.V.; Romero Fresneda, R.; Botey Fullat, R. Mapas Climáticos de España (1981–2010) y ETo (1996–2016); Agencia Estatal de Meteorología: Madrid, Spain, 2018. [Google Scholar]
- Moral, F. Contribución al Conocimiento de Los Acuíferos Carbonáticos de La Sierra de Segura (Alto Guadalquivir y Alto Segura). Doctoral Dissertation, Universidad Pablo de Olavide, Sevilla, Spain, 2005. [Google Scholar]
- Instituto Geológico y Minero de España. Mapa geológico de España, Escala 1:50.000. San Clemente. 2007. Available online: https://info.igme.es/cartografiadigital/datos/magna50/memorias/MMagna0929.pdf (accessed on 27 September 2024).
- García-Hernández, M. El Jurásico Terminal y El Cretácico Inferior En Las Sierras de Cazorla y Del Segura (Zona Prébetica). Doctoral Dissertation, Universidad de Granada, Granada, Spain, 1978. [Google Scholar]
- González-Ramón, A.; Rodríguez-Cerezuela, B. Prospección En Sierra Seca, Sierra de Castril y Buceo Del Sifón Pedro Jiménez (Granada). Andalucía Subterránea. 2023, Volume 36. Available online: https://espeleo.com/publicaciones/andalucia-subterranea-36-2 (accessed on 27 September 2024).
- Steig, E.J.; Gkinis, V.; Schauer, A.J.; Schoenemann, S.W.; Samek, K.; Hoffnagle, J.; Dennis, K.J.; Tan, S.M. Calibrated High-Precision 17O-Excess Measurements Using Cavity Ring-down Spectroscopy with Laser-Current-Tuned Cavity Resonance. Atmos. Meas. Tech. 2014, 7, 2421–2435. [Google Scholar] [CrossRef]
- Giménez, R.; Bartolomé, M.; Gázquez, F.; Iglesias, M.; Moreno, A. Underlying Climate Controls in Triple Oxygen (16O, 17O, 18O) and Hydrogen (1H, 2H) Isotopes Composition of Rainfall (Central Pyrenees). Front. Earth. Sci. 2021, 9, 633698. [Google Scholar] [CrossRef]
- Custodio, E.; Jódar, J. Simple Solutions for Steady–State Diffuse Recharge Evaluation in Sloping Homogeneous Unconfined Aquifers by Means of Atmospheric Tracers. J. Hydrol. 2016, 540, 287–305. [Google Scholar] [CrossRef]
- Matheswaran, K.; Khadka, A.; Dhaubanjar, S.; Bharati, L.; Kumar, S.; Shrestha, S. Delineation of Spring Recharge Zones Using Environmental Isotopes to Support Climate-Resilient Interventions in Two Mountainous Catchments in Far-Western Nepal. Hydrogeol. J. 2019, 27, 2181–2197. [Google Scholar] [CrossRef]
- Morales-González, A.L.; Jódar, J.; Jiménez-Espinosa, R.; González-Ramón, A. Comparison between Two Methodologies for the Determination of the Recharge Heights in Springs of the Sierra de Segura (Jaén) Based on Environmental Isotopes. In Proceedings of the 76th Scientific Session, Segura de La Sierra, Spain, 7–8 June 2024; Available online: https://sociedadgeologica.org/sesiones-cientificas/76-sesion-cientifica-2 (accessed on 27 September 2024).
- Maloszewski, P.; Stichler, W.; Zuber, A.; Rank, D. Identifying the Flow Systems in a Karstic-Fissured-Porous Aquifer, the Schneealpe, Austria, by Modelling of Environmental 18o and 3h Isotopes. J. Hydrol. 2002, 256, 48–59. [Google Scholar] [CrossRef]
- Małoszewski, P.; Zuber, A. Determining the Turnover Time of Groundwater Systems with the Aid of Environmental Tracers. 1. Models and Their Applicability. J. Hydrol. 1982, 57, 207–231. [Google Scholar] [CrossRef]
- Zuber, A. Chapter 1. Mathematical models for the interpretation of environmental radioisotopes in groundwater systems. In Handbook of Environmental Isotope Geochemistry; Fritz, P., Fontes, J.C., Eds.; Elsevier: Amsterdam, Netherlands, 1986; Volume 2. [Google Scholar]
- Amin, I.E.; Campana, M.E. A General Lumped Parameter Model for the Interpretation of Tracer Data and Transit Time Calculation in Hydrologic Systems. J. Hydrol. 1996, 179, 1–21. [Google Scholar] [CrossRef]
- Epting, J.; Page, R.M.; Auckenthaler, A.; Huggenberger, P. Process-Based Monitoring and Modeling of Karst Springs—Linking Intrinsic to Specific Vulnerability. Sci. Total Environ. 2018, 625, 403–415. [Google Scholar] [CrossRef]
- Hottelet, C.; Braun, L.N.; Leibundgut, C.; Rieg, A. Simulation of Snowpack and Discharge in an Alpine Karst Basin. In Snow and Glacier Hydrology. Proceedings of the International Symposium, Kathmandu, 1992; IAHS Publication: Wallingford, UK, 1993. [Google Scholar]
- Barberá, J.A.; Jódar, J.; Custodio, E.; González-Ramón, A.; Jiménez-Gavilán, P.; Vadillo, I.; Pedrera, A.; Martos-Rosillo, S. Groundwater Dynamics in a Hydrologically-Modified Alpine Watershed from an Ancient Managed Recharge System (Sierra Nevada National Park, Southern Spain): Insights from Hydrogeochemical and Isotopic Information. Sci. Total Environ. 2018, 640–641, 874–893. [Google Scholar] [CrossRef]
- Konz, M.; Seibert, J. On the Value of Glacier Mass Balances for Hydrological Model Calibration. J. Hydrol. 2010, 385, 238–246. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. Regionalisation of Catchment Model Parameters. J. Hydrol. 2004, 287, 95–123. [Google Scholar] [CrossRef]
- Staudinger, M.; Stoelzle, M.; Seeger, S.; Seibert, J.; Weiler, M.; Stahl, K. Catchment Water Storage Variation with Elevation. Hydrol. Process. 2017, 31, 2000–2015. [Google Scholar] [CrossRef]
- Nelson, D.B.; Basler, D.; Kahmen, A. Precipitation Isotope Time Series Predictions from Machine Learning Applied in Europe. Proc. Natl. Acad. Sci. USA 2021, 118, e2024107118. [Google Scholar] [CrossRef] [PubMed]
- Richter, D.; Goeppert, N.; Goldscheider, N. New Insights into Particle Transport in Karst Conduits Using Comparative Tracer Tests with Natural Sediments and Solutes during Low-Flow and High-Flow Conditions. Hydrol. Process. 2022, 36, e14472. [Google Scholar] [CrossRef]
- Liñán Baena, C. Hidrología de Acuíferos Carbonatados En La Unidad Yunquera -Nieves (Málaga). Doctoral Dissertation, Universidad de Granada, Granada, Spain, 2003. [Google Scholar]
- Hornero-Díaz, J.E. Contribución de Las Técnicas Hidroquímicas, Isotópicas e Hidrodinámicas a La Caracterización de Acuíferos Carbonatados y Su Relación Con La Red de Flujo Superficial. Aplicación al Acuífero de Alcadozo (Cuenca Del Segura). Doctoral Dissertation, Universidad Politécnica de Cartagena, Cartagena, Spain, 2018. [Google Scholar]
- Yanes, J.L.; Moral, F. Relief and Climate Influence on Isotopic Composition of Atlantic-Mediterranean Karst Spring Waters (Andalusia, Southern Spain). Hydrol. Process. 2022, 36, e14669. [Google Scholar] [CrossRef]
- Poage, M.A.; Chamberlain, C.P. Empirical Relationships between Elevation and the Stable Isotope Composition of Precipitation and Surface Waters: Considerations for Studies of Paleoelevation Change. Am. J. Sci. 2001, 301, 1–15. [Google Scholar] [CrossRef]
- Cruz-Sanjulián, J.; Araguas, L.; Rozanski, K.; Benavente, J.; Cardenal, J.; Hidalgo, M.C.; García-Lopez, S.; Martínez-Garrido, J.C.; Moral, F.; Olías, M. Sources of Precipitation over South-Eastern Spain and Groundwater Recharge. An Isotopic Study. Tellus B 1992, 44, 226–236. [Google Scholar] [CrossRef]
- Vallejos, A.; Díaz-Puga, M.A.; Sola, F.; Daniele, L.; Pulido-Bosch, A. Using Ion and Isotope Characterization to Delimitate a Hydrogeological Macrosystem. Sierra de Gádor (SE, Spain). J. Geochem. Explor. 2015, 155, 14–25. [Google Scholar] [CrossRef]
- Díaz-Teijeiro, M.F.; Rodríguez-Arévalo, J.; Castaño, S. La Red Española de Vigilancia de Isótopos En La Precipitación (REVIP): Distribución Isotópica Espacial y Aportación al Conocimiento Del Ciclo Hidrológico. Ing. Civ. 2009, 155, 87–97. [Google Scholar]
- González-Ramón, A.; Cortés Cortés, M.; López Ramón, I.; Carra Vélez, R.; Ávila Alba, J.B.; Santaella Alba, A.; Rodríguez Saez, D. Evolución Del Relieve y Espeleogénesis. Las Cavidades Del Nacimiento Del Río Guardal, Sierra Seca (Granada); Proceedings Espeleo Meeting Ciudad de Villacarrillo, Caving Congress, 39-44. Grupo de Espeleología de Villacarrillo, 2016; pp. 13–15. Available online: https://www.researchgate.net/profile/Jose-Antonio-Lopez-Saez/publication/330135425_Registro_paleoambiental_del_Pleistoceno_superior_a_partir_del_relleno_sedimentario_de_la_Cueva_del_Cucu_Almeria_SE_de_Espana/links/5c2f43aa458515a4c70b03bd/Registro-paleoambiental-del-Pleistoceno-superior-a-partir-del-relleno-sedimentario-de-la-Cueva-del-Cucu-Almeria-SE-de-Espana.pdf#page=186 (accessed on 27 September 2024).
- Schoenemann, S.W.; Schauer, A.J.; Steig, E.J. Measurement of SLAP2 and GISP δ17O and Proposed VSMOW-SLAP Normalization for δ17O and 17Oexcess. Rapid Commun. Mass Spectrom. 2013, 27, 582–590. [Google Scholar] [CrossRef]
- Angert, A.; Cappa, C.D.; DePaolo, D.J. Kinetic 17O Effects in the Hydrologic Cycle: Indirect Evidence and Implications. Geochim. Cosmochim. Acta 2004, 68, 3487–3495. [Google Scholar] [CrossRef]
- Pešić, V.; Paunović, M.; Kostianoy, A.G. The Rivers of Montenegro; Springer International Publishing: Cham, Switzerland, 2020; Volume 93, ISBN 978-3-030-55711-9. [Google Scholar]
- Commission Directive 2014/80/UE of 20 June 2014 Amending Annex II to Directive 2006/118/EC of the European Parliament and of the Council on the Protection of Groundwater against Pollution and Deterioration. Off. J. Eur. Union L 182/52. 2014. Available online: https://eur-lex.europa.eu/eli/dir/2014/80/oj (accessed on 27 September 2024).


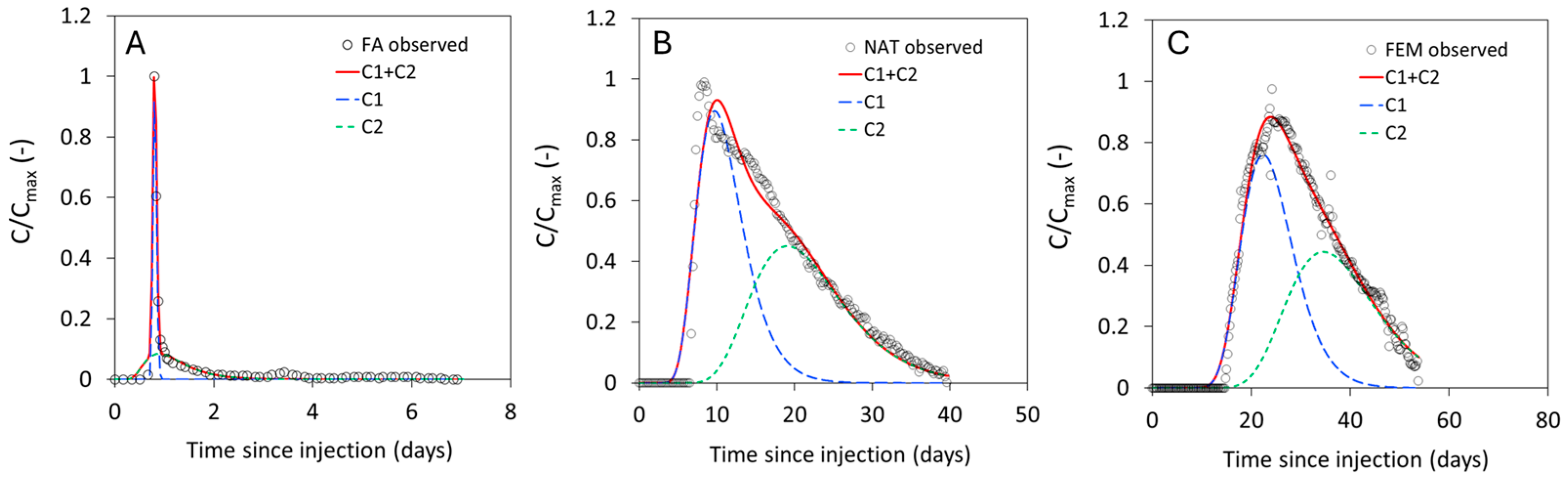
| Tracer Test | Injection Point Lithology a | Injected Tracer | Injected Mass (g) | Tracer Outflow Point | Tracer Test Distance b L (km) | c (m3/s) |
|---|---|---|---|---|---|---|
| 1 | LC | Eosine | 1500 | FA | 6.07 | 3.698 |
| 2 | UC | Uranine | 2500 | NAT | 7.45 | 0.883 |
| 3 | UC | Uranine | 200 | FEM | 0.84 | 0.013 |
| (m a.s.l.) | Isotopic Content Vertical Gradient in Recharge | |||||
|---|---|---|---|---|---|---|
| Case | FA | NAT | FEM | (‰/km) | (‰/km) | - (‰/km) |
| A1 | 1710 | 1698 | 1650 | −2.9 | −19.5 | 4.0 |
| A2 | 1708 | 1696 | 1648 | −2.9 | −19.1 | 4.4 |
| A3 | 1673 | 1662 | 1617 | −3.1 | −20.6 | 4.3 |
| A4 | 1626 | 1616 | 1578 | −3.7 | −25.2 | 4.1 |
| A5 | 1589 | 1580 | 1548 | −4.4 | −31.4 | 4.0 |
| a | 1661 | 1650 | 1608 | −3.4 | −23.2 | 4.2 |
| b | 53 | 51 | 45 | 0.7 | 5.2 | 0.2 |
| (%) c | 7.1 | 6.9 | 6.2 | 61.0 | 10.0 | 51.7 |
| Pe (-) | (d) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Trace Test | a (Days) | b (m) | Mass Recovery (%) | Flow Path 1 | Flow Path 2 | Average | Flow Path 1 | Flow Path 2 | Average |
| 1 | 0.58 | 30.7 | 26.1 | 1000 | 10 | 505 | 0.809 | 1.200 | 1.005 |
| 2 | 3.28 | 33.6 | 4.4 | 22.2 | 21.7 | 22.0 | 11.110 | 21.883 | 16.500 |
| 3 | 14.56 | 20.33 | 75.4 | 37.0 | 30.3 | 38.7 | 24.271 | 38.187 | 31.230 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morales-González, A.L.; Jódar, J.; Moral-Martos, F.; Jiménez-Espinosa, R.; Gázquez, F.; González-Ramón, A. Delineation of the Hydrogeological Functioning of a Karst Aquifer System Using a Combination of Environmental Isotopes and Artificial Tracers: The Case of the Sierra Seca Range (Andalucía, Spain). Water 2024, 16, 2768. https://doi.org/10.3390/w16192768
Morales-González AL, Jódar J, Moral-Martos F, Jiménez-Espinosa R, Gázquez F, González-Ramón A. Delineation of the Hydrogeological Functioning of a Karst Aquifer System Using a Combination of Environmental Isotopes and Artificial Tracers: The Case of the Sierra Seca Range (Andalucía, Spain). Water. 2024; 16(19):2768. https://doi.org/10.3390/w16192768
Chicago/Turabian StyleMorales-González, Antonio Lope, Jorge Jódar, Francisco Moral-Martos, Rosario Jiménez-Espinosa, Fernando Gázquez, and Antonio González-Ramón. 2024. "Delineation of the Hydrogeological Functioning of a Karst Aquifer System Using a Combination of Environmental Isotopes and Artificial Tracers: The Case of the Sierra Seca Range (Andalucía, Spain)" Water 16, no. 19: 2768. https://doi.org/10.3390/w16192768
APA StyleMorales-González, A. L., Jódar, J., Moral-Martos, F., Jiménez-Espinosa, R., Gázquez, F., & González-Ramón, A. (2024). Delineation of the Hydrogeological Functioning of a Karst Aquifer System Using a Combination of Environmental Isotopes and Artificial Tracers: The Case of the Sierra Seca Range (Andalucía, Spain). Water, 16(19), 2768. https://doi.org/10.3390/w16192768







