Study on Valley Shrink Deformation of the High Arch Dam with Large Faults near Dam Area during Initial Impoundment

Abstract

Valley shrink deformation is a common physical and mechanical phenomenon during the reservoir operation of high arch dams. This phenomenon is particularly significant in the initial stages of impoundment and can severely impact the operational safety of the arch dam. This study focuses on the arch dam under construction in the upstream of the Lancang River. By considering the secondary structural planes F115 and F111 at the dam site, a numerical model of valley shrink deformation was established. The study investigates the characteristics of valley shrink deformation during the initial impoundment phase of the arch dam. The results show that during the impoundment process, the valley slopes on both sides of the reservoir shrink towards the center of the valley. The deformation on the right bank is greater than that on the left bank due to the influence of the F115 fault. When the elevation is lower than the exposure position of F115, the deformation on the right bank increases with elevation; when it is higher than this position, the deformation decreases. On the left bank, due to the influence of F111 and the seepage field, the deformation value increases first and then decreases with the increase in elevation. After the water level stabilizes, the deformation rate decreases and approaches zero. This research results provide a reference for addressing valley shrink deformation issues during the initial impoundment of the arch dam.

1. Introduction

In the high mountain and canyon regions, varying degrees of valley deformation have been observed in high arch dam projects during reservoir impoundment operations [1,2,3,4], which may affect the normal operation of hydropower stations. Ultra-high arch dam projects are typically constructed in high mountain and canyon regions, with large-scale construction and complex geological conditions at the dam site. The impoundment of arch dams significantly disturbs the original hydrogeological conditions of the dam area [5]. Changes in hydrogeological conditions lead to significant alterations in the time-dependent mechanical properties, such as deformation and strength, of the reservoir bank rock mass. The characteristics of valley shrink deformation vary among different projects, and a unified understanding has not yet been established.

Therefore, many scholars, both domestic and international, have conducted numerous mechanistic studies on the phenomenon of valley shrink deformation [6,7,8,9]. The Xiluodu Hydropower Project is one of the representative projects where valley shrink deformation of arch dams has been observed. Since reservoir impoundment in 2014, the maximum valley shrink deformation displacement has exceeded 100 mm [10]. Xu [11] and Wang [12] analyzed the correlation between reservoir water level adjustments and valley deformation, confirming the impact of reservoir water levels on valley deformation. Based on monitoring data, similarly, Li [13] examined the complete displacement process before and after impoundment, considering that slope excavation caused valley shrink deformation and subsequent reservoir impoundment accelerated it by altering creep parameters. A poroelastic-creep model with two-stage creep parameters was applied for numerical simulation. Liu [14] used a discrete element model to analyze the deformation of fractured reservoir bank slopes at the Xiluodu Hydropower Station, considering periodic water level changes. The study found that increased water pressure and the weakening of mechanical parameters are the main reasons for shear zone sliding.

Besides the Xiluodu Hydropower Station, the Baihetan Hydropower Station, the second largest in the world, also observed valley shrink deformation during the initial impoundment. Xu [15] conducted finite element calculations for the Baihetan Hydropower Project based on the effective stress principle of fractured rock masses, indicating a certain correlation between initial impoundment valley shrink deformation and rising water levels. Xu [16] studied the valley shrink deformation at Baihetan during the impoundment period based on the effective stress principle, considering changes in the seepage field before and after impoundment. The results showed that upstream valley shrinkage is mainly caused by the reduction of effective stress, steep topography, and weakening of structural planes, while downstream deformation is primarily due to bypass seepage and stress adjustment. The Yalong River Jinping-I Hydropower Station also experienced valley shrink deformation. Yang [17] considered the effect of fracture water pressure, introduced hydrostatic pressure into the yield function of an elastoplastic model, and applied it to the calculation and analysis of the Jinping-I arch dam during the impoundment period. Yang [18] established a model of the unsaturated relative permeability coefficient for rock masses, structural planes, and their fillings. The study found that the development pattern of valley shrink deformation is mainly influenced by the impoundment process, while the shrink magnitude is primarily controlled by the dam construction process. Zhou [19] summarized through multiple hydropower project cases that topography, lithology, geological structures, and hydrogeological conditions are intrinsic factors causing valley shrink deformation, while the reservoir water level and impoundment process are the most important extrinsic factors. Extrinsic factors act through intrinsic factors. Similarly, hydropower projects located in high mountain and canyon areas often have numerous faults and weak structural planes in the mountain slopes on both sides. After reservoir impoundment, the weakening of fault parameters leading to plastic deformation has also become a widely accepted explanation [20,21].

In summary, impoundment, water level regulation, special geological structures, and rock mass rheology have significant impacts on valley shrink deformation during the impoundment period of arch dams. Therefore, this paper focuses on the arch dam under construction in the upper reaches of the Lancang River, where there are two long, large-scale secondary structural planes in the dam site area. The authors have also conducted calculations and analyses on the full life cycle and safety of dam construction at the arch dam [22], but did not focus on considering the impact of valley shrink deformation during the reservoir impoundment period on the construction of the arch dam. To study the impact of initial impoundment on valley shrink deformation, numerical simulation methods were used in combination with the initial impoundment plan to analyze the characteristics of valley shrink deformation during the initial impoundment stage, providing references for the project’s construction.

2. Geological Background

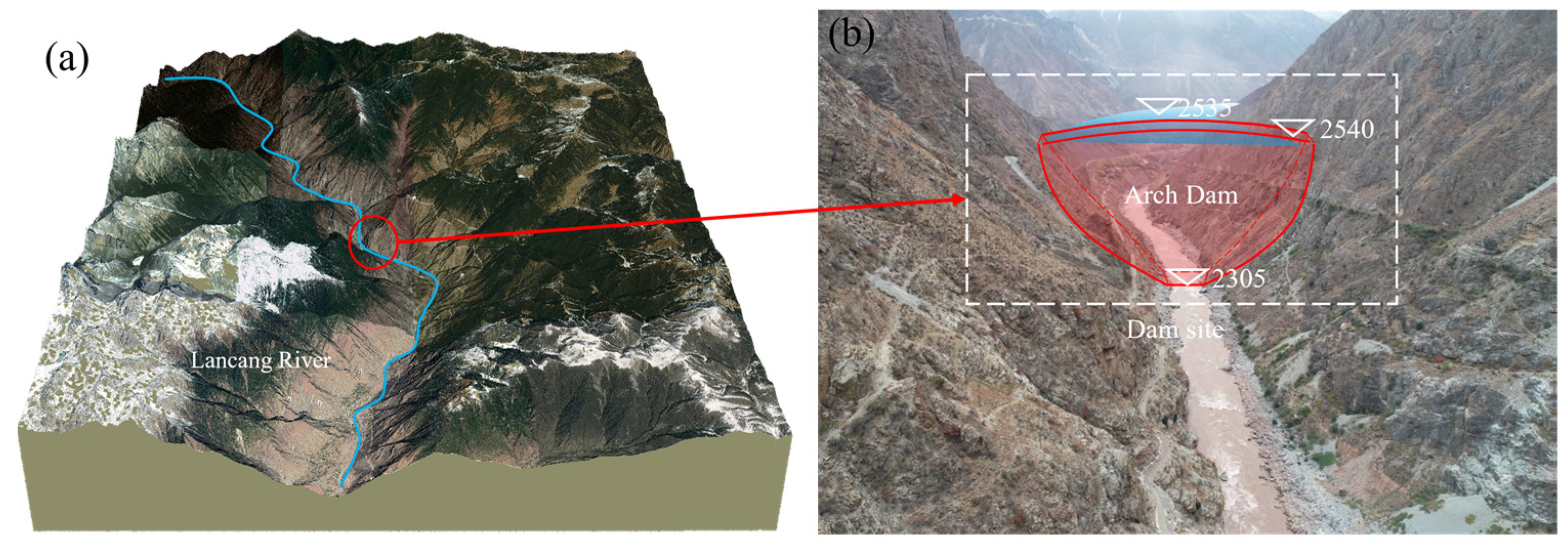
The arch dam is located in the upstream section of the Lancang River (as shown in Figure 1), featuring a double-curved arch dam with a crest elevation of 2540 m, a foundation elevation of 2305 m, a maximum dam height of 235 m, a normal reservoir water level upstream of 2535 m, and a natural water level downstream of 2345 m. The authors conducted two field surveys respectively in January and April 2023, fully understanding the geological conditions of the arch dam. The dam site location is as shown in Figure 1. The natural terrain slope in the dam site area generally exceeds 45°, with relatively neat topography. The direction of the upstream slopes on both banks tends to be north–south, gradually deviating to around 290° downstream. Exposed strata in the dam site area include the Indosinian intrusive rock (γδ51), the Middle Jurassic Hua Kai Formation (J2h), the Upper Jurassic Baozhulu Formation (J3b), the Lower Cretaceous Jingxing Formation (Kj), and Quaternary strata. The intrusive rock is the main bedrock formation in the dam site area, with exposed bedrocks on both banks. Slope debris accumulations are found in gentle slope areas and lower parts of both banks, with residual terrace deposits in some areas and alluvial deposits in riverbeds.

The dam site has dense fault development, with 39 main faults exposed on the surface and in exploratory adits. The F115 fault on the right bank and the F111 fault on the left bank are secondary structural planes The F115 fault extends over 1000 m, exposed in multiple adits and on the surface, trending N80°–85° W, dipping SW at 60°–75°. It is linearly exposed upstream along line 4 and revealed in adits downstream along line 6 (291 m from dam in downstream), trending N50°–55° W. The fault zone is 0.6 m–1.3 m wide, consisting of breccia, rock fragments, debris, and clay bands. The influence zone is 15 m–25 m wide, mainly in the fault’s footwall, consisting of brecciated rock blocks and dense joints. The hanging wall is typically medium- to fine-grained granite with good integrity, while the footwall is a mix of granite and granodiorite. The F111 fault trends 295°–305°/SW with a dip angle of 65°–75°. The fault zone is 20–60 mm wide and is a reverse fault, composed of brownish-yellow and gray-green rock blocks, debris, and yellow and gray-white clay.

3. Numerical Simulation and Impoundment Plan

3.1. Constitutive Model

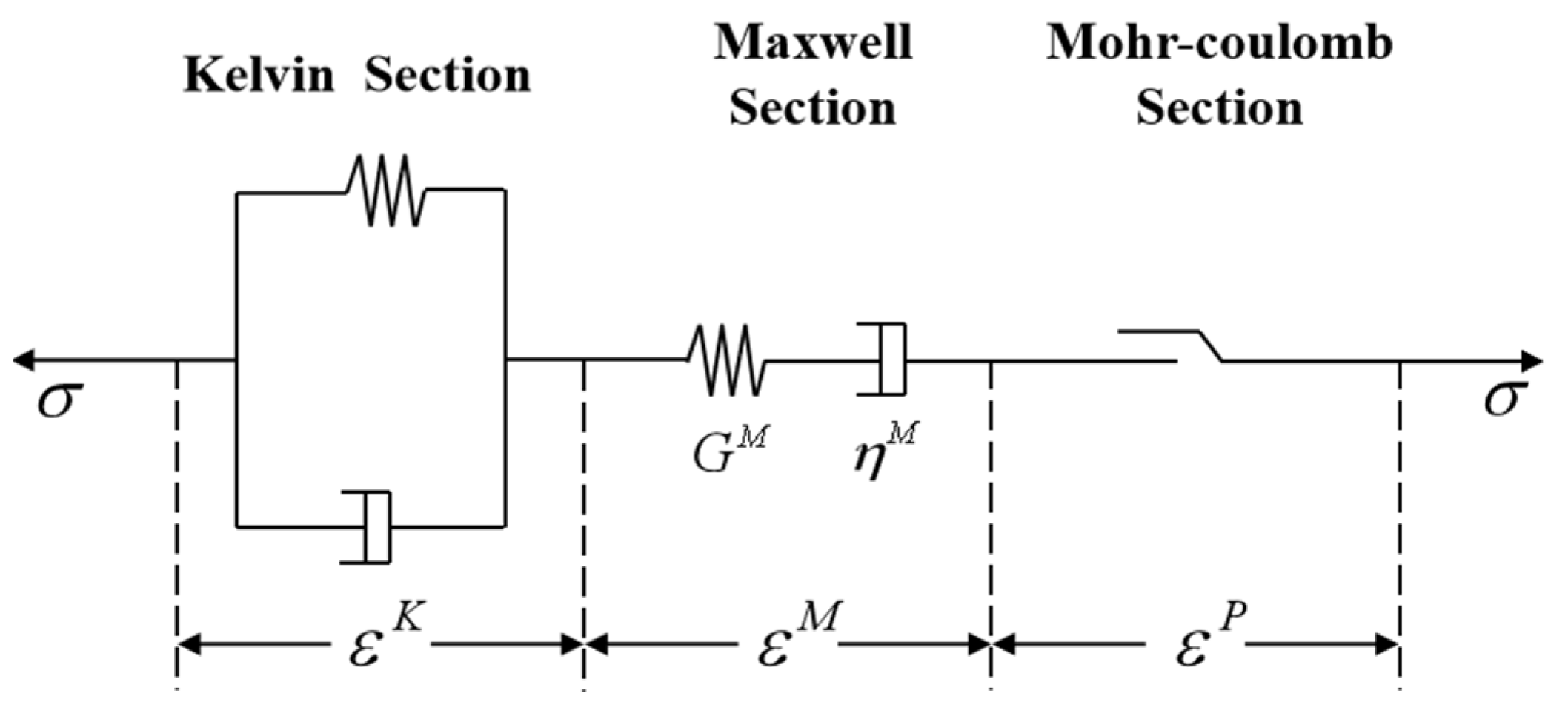
Previous studies have shown [13] that the phenomenon of valley shrink deformation is highly time-dependent. Considering the rheological properties of rocks is significant for studying this phenomenon. The CVISC model can be used to simulate the rheological mechanical properties of rocks and has been applied to relevant engineering and valley shrink deformation issues [23,24,25]. This model exhibits viscoelastic–plastic characteristics, with the viscoelastic constitutive model corresponding to the Burgers model and the plastic constitutive model corresponding to the Mohr–Coulomb model (see Figure 2). It can be expressed as follows:

Kelvin Model:

$$S_{ij}=2{\eta }^K{\dot{e}}_{ij}^K+2G^K{e}_{ij}^K$$

(1)

Maxwell Model:

$${\dot{e}}_{ij}^M={\displaystyle \frac{{\dot{S}}_{ij}}{2G^M}}+{\displaystyle \frac{S_{ij}}{2{\eta }^M}}$$

(2)

M-C Model:

$$\left.\begin{array}{c}{\dot{e}}_{ij}^p={\lambda }^{*}{\displaystyle \frac{\partial g}{\partial {\sigma }_{ij}}}-{\displaystyle \frac{1}{3}}{\dot{e}}_{vol}^p{\delta }_{ij}\\ {\dot{e}}_{vol}^p={\lambda }^{*}\left[{\displaystyle \frac{\partial g}{\partial {\sigma }_{11}}}+{\displaystyle \frac{\partial g}{\partial {\sigma }_{22}}}+{\displaystyle \frac{\partial g}{\partial {\sigma }_{33}}}\right]\end{array}\right\}$$

(3)

In these relations, the superscripts K, M, and p represent the Kelvin, Maxwell, and M-C plastic components of the corresponding variables, respectively. The variables with dot markings indicate their first derivatives with respect to rheological time. K and G are the bulk and shear moduli, and η is the dynamic viscosity. e_ij and S_ij are the deviatoric components derived from the strain tensor and stress tensor, respectively, and e_vol and σ₀ are the volumetric components of the strain tensor and stress tensor.

3.2. Calculation Model and Parameters

3.2.1. Calculation Model

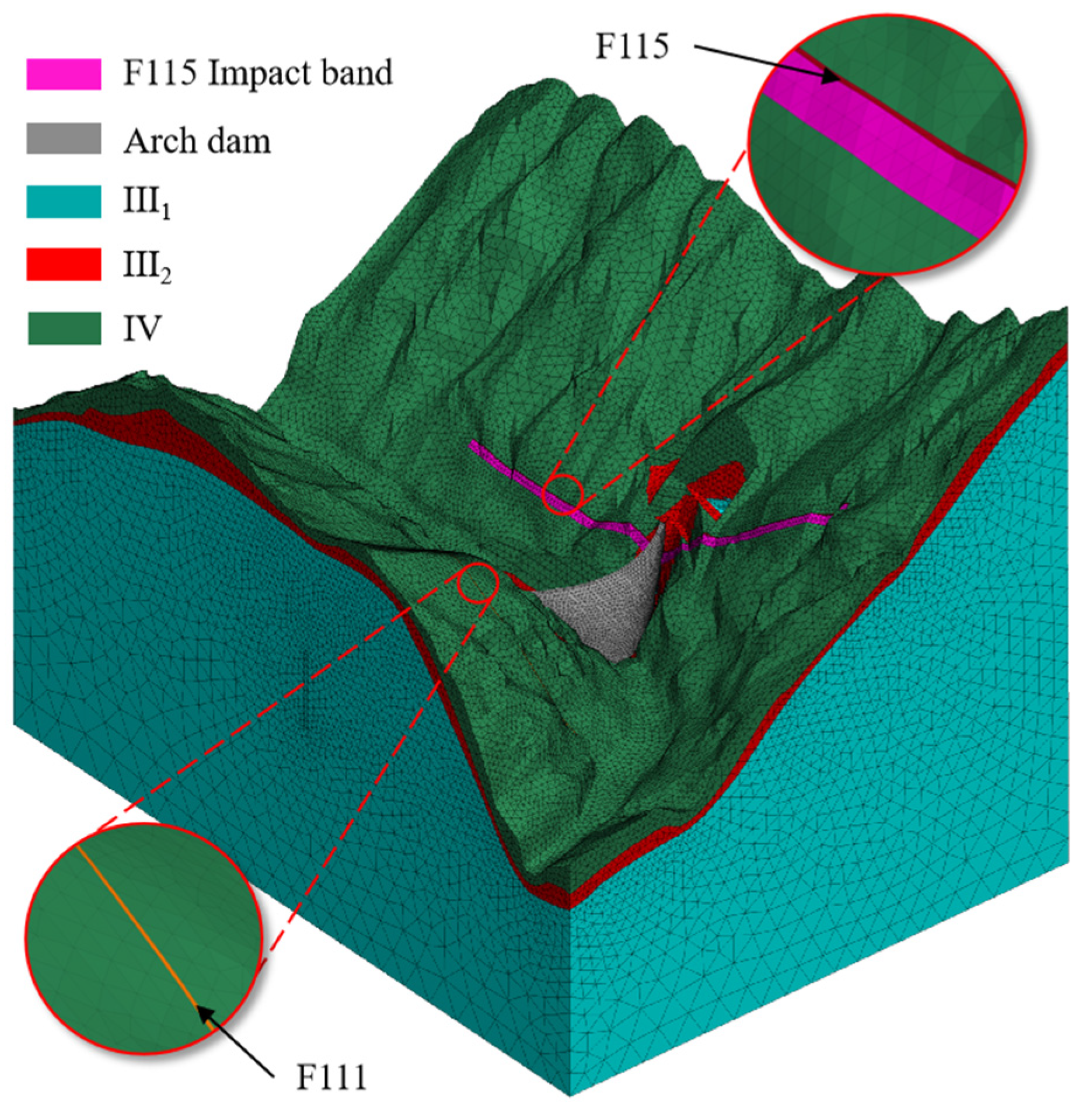
In this section, the FLAC3D 7.0 software developed by Itasca Consulting Group is used for the numerical simulation study of valley shrink deformation in the arch dam. Based on geological cross-section diagrams and field investigation results, the material zoning of the 3D model is appropriately merged and simplified. The model (see Figure 3) extends 1500 m in the X-direction (across the river), 2000 m in the Y-direction (along the river), and from an elevation of 1800 m to the ground surface in the Z-direction. The numerical model considers the anti-seepage grouting curtain. The main strata in the model are classified into three categories based on weathering degree: Category IV rock mass, Category III2 rock mass, and Category III1 rock mass. The model also considers the secondary structural planes F115 and F111, with the influence zone of F115 taken into account. The model uses tetrahedral elements, with a total grid consisting of 1,285,800 elements and 227,246 nodes.

3.2.2. Boundary Conditions and Parameters

Normal constraints are applied to the sides of the model, full constraints to the bottom surface, and the free surfaces of the reservoir bank slope and dam are free deformation boundaries (as in Equation (4)). Based on indoor rock physical and mechanical tests, on-site rigid bearing plate tests, direct shear tests, and geophysical testing, and considering the differences between modeled and actual fault thicknesses, the deformation equivalence principle is used to propose the rock mass physical and mechanical parameters and structural surface mechanical parameters for calculations, as shown in

Table 1. Calculation parameters.

Group	EM (Pa)	Bulk Modulus (Pa)	Sheer Modulus (Pa)	EK (Pa)	ηM (Pa·d)	GK (Pa)	ηK (Pa·d)	Cohesion (kPa)	Friction Angle (°)
III1	2.50 × 1010	1.40 × 1010	1.00 × 1010	5.00 × 1011	2.50 × 1014	8.00 × 1010	6.30 × 1011	1.30 × 106	49.02
III2	9.00 × 109	6.50 × 109	7.60 × 109	1.80 × 1011	1.30 × 1014	6.30 × 1010	2.30 × 1011	9.00 × 105	42.60
IV	4.00 × 109	3.30 × 109	1.50 × 108	8.00 × 1010	4.00 × 1013	3.10 × 1010	1.00 × 1011	6.00 × 105	36.89
F115	2.20 × 108	1.70 × 108	8.50 × 107	4.40 × 109	2.20 × 1012	1.70 × 109	5.50 × 109	5.00 × 104	16.18
Impact band	4.00 × 109	4.00 × 109	1.60 × 109	2.30 × 1011	4.00 × 1013	3.10 × 1010	1.00 × 1011	5.40 × 105	34.23
F111	5.00 × 108	3.80 × 108	2.00 × 108	1.00 × 1010	5.00 × 1012	3.90 × 109	1.30 × 1010	8.00 × 104	17.70
Concrete	6.00 × 1010	2.20 × 1010	1.80 × 1010	6.00 × 1011	4.20 × 1014	2.10 × 1011	9.00 × 1011	2.50 × 106	54.50

.

$$\left.\begin{array}{c}{u}_x=u_y=u_z=0,\forall \left(x,y,z\right)\in {\mathsf{\Gamma }}_{Bottom}\\ u_{normal}=0,\forall (x,y,z)\in {\mathsf{\Gamma }}_{Side}\end{array}\right\}$$

(4)

3.3. Impoundment Plan

The initial impoundment plan of the arch dam is mainly divided into four stages, as shown in Figure 4:

Stage 1: 2361.668–2384.256 m. Close the flat gates of the #1 and #2 holes in diversion tunnel #1; control the discharge flow with the flat gates of the #1 and #2 holes in diversion tunnel #2; close the flat gates of the #1 and #2 holes in diversion tunnel #2. Impoundment duration is 0.4 days.

Stage 2: 2384.256–2458.699 m. Control the discharge flow through the downstream water supply bottom hole until the water level rises to 2458.699 m; close the downstream water supply bottom hole. Impoundment duration is 7.8 days.

Stage 3: 2458.699–2475.000 m. Control the discharge flow through the flood discharge deep hole. Impoundment duration is 5.8 days.

Stage 4: 2475.000–2517.000 m. Control the discharge flow through 4 flood discharge deep holes. Impoundment duration is 33.1 days; 2517.000–2525.000 m, control the discharge flow through 4 deep holes and 3 surface overflow holes. Impoundment duration is 3.0 days.

3.4. Calculation Scheme

This paper conducts a numerical simulation of the narrowing deformation of the valley during the rise of the reservoir water level from 2361 m to 2525 m based on the water storage plan. Following the method in the reference [22] to generate the stress field, a pore pressure corresponding to a water level of 2361 m is applied to the upstream and a pore pressure corresponding to a water level of 2345 m is applied to the downstream. According to the impoundment plan, the water load and pore pressure on both banks of the upstream mountain bodies and the dam body are gradually increased. Rheological calculations are then carried out to obtain the magnitude of the valley narrowing deformation in the reservoir area at different times during the water storage period.

4. Results and Discussion

4.1. Displacement Field Evolution

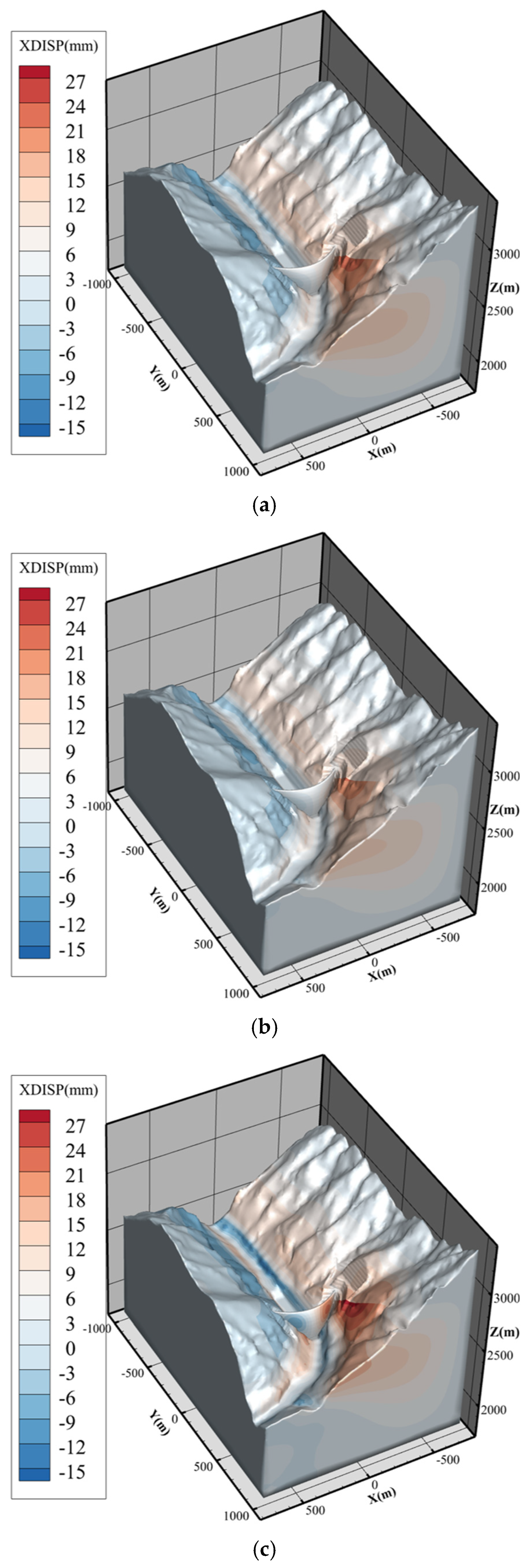
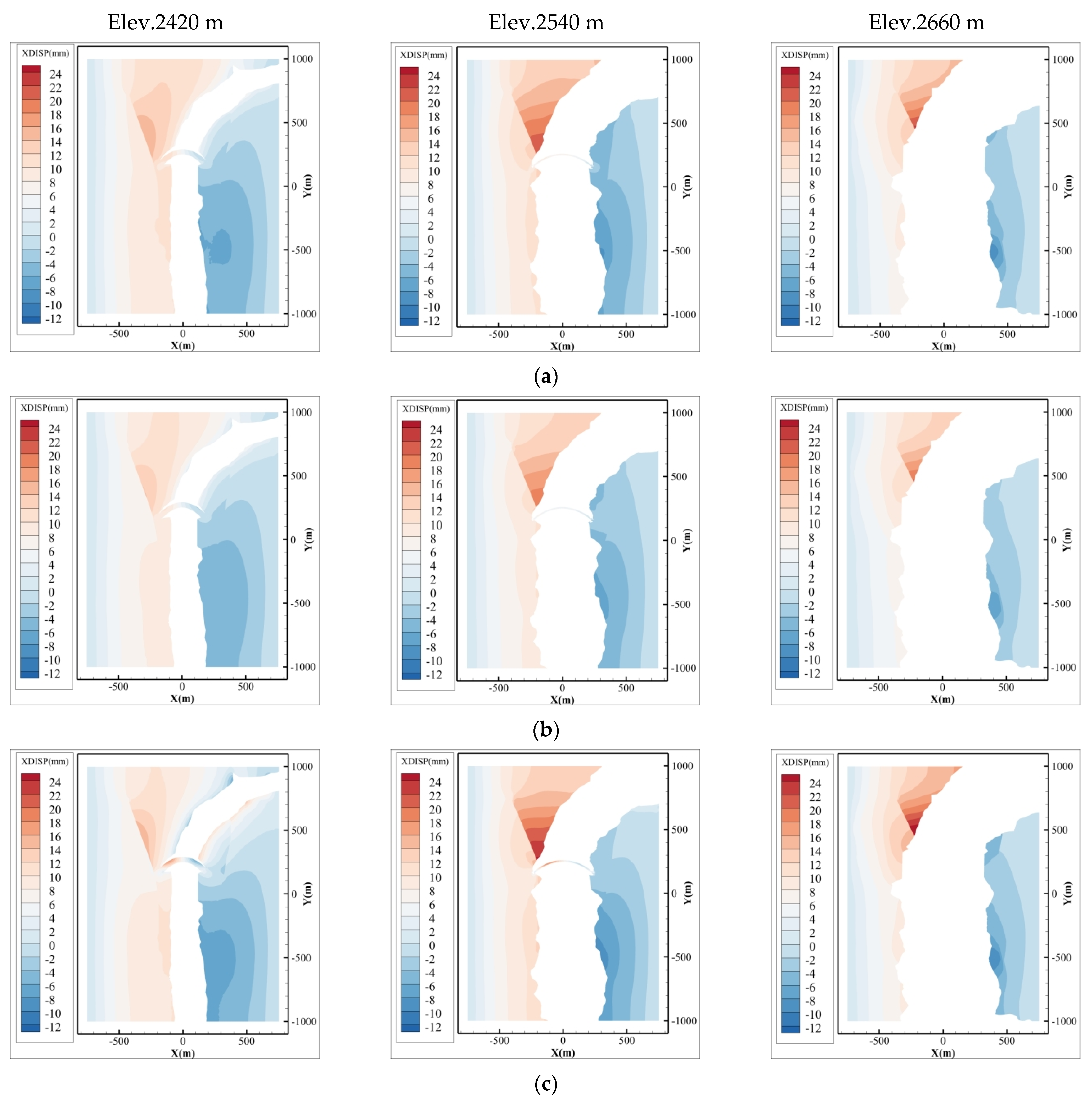
The overall transverse displacement distribution of the dam area under different reservoir water levels and the transverse displacement distribution at different elevations are shown in Figure 5 and Figure 6.

During the impoundment process, the reservoir bank valley slopes generally show a shrinking trend, with the rock masses on both the left and right banks deforming towards the center of the valley. The deformation amount on the right bank slope is greater than that on the left bank. When the reservoir water level is 2475 m, the maximum transverse deformation on the right bank is about 24.0 mm, and on the left bank, it is about 9.5 mm. When the reservoir water level is 2525 m, the maximum transverse deformation on the right bank is about 29.0 mm, and on the left bank, it is about 14.7 mm. The main reason for the greater deformation on the right bank slope is that the F115 fault on the right bank dips towards the left bank. Additionally, the F115 fault has a long extension range and a wide influence zone, exacerbating the deformation of the right bank mountain. After the reservoir water level stabilizes at 2475 m for 155 days, the valley shrink deformation slightly retracts compared to when it had just reached 2475 m. This is because, after the water level stabilizes, the pore water pressure inside the mountain gradually stabilizes, and under the influence of water pressure and gravity, the valley expands towards both sides of the mountain. As the reservoir water level rises, the lower elevation mountain experiences increasing water pressure, and the displacement towards the mountain shrinkage also gradually increases. The pattern of valley shrink deformation varies between upstream and downstream. The upstream right bank is influenced by the F115 fault and its influence zone, resulting in greater transverse displacement on the upstream right bank compared to the downstream. On the upstream left bank, the F111 fault’s direction serves as a major water-conducting pathway and, due to its greater depth, causes higher water pressure within the structural plane, leading to greater valley deformation downstream on the left bank compared to upstream.

The transverse displacement distribution at different elevation cross-sections indicates that the right bank is significantly influenced by the F115 fault. The F115 fault dips towards the left bank, and its dip direction and strike cause the rock masses on the right bank to be compressed towards the valley center under the influence of water pressure, leading to greater displacement at higher elevations, with the maximum transverse displacement occurring near the fault zone. Additionally, the F115 fault outcrops at multiple elevations, especially at higher altitudes, where its influence is more pronounced. When the reservoir water level is at 2475 m, the maximum displacement on the right bank at an elevation of 2420 m is about 16.0 mm, while on the left bank it is only 6.0 mm. This discrepancy is not only related to the outcrop location of the fault on the right bank but also to the steep dip angle of the F115 fault, which results in a stress concentration effect. At an elevation of 2540 m, the right bank displacement increases to 22.0 mm, while the left bank increases to 8.5 mm; at an elevation of 2660 m, the right bank displacement reaches 23.0 mm, and the left bank 8.8 mm. The more pronounced deformation in the higher elevation regions indicates that the higher the fault outcrop, the greater the influence of water pressure and gravity on the transverse displacement. After the reservoir water level stabilizes at 2475 m for 155 days, the maximum displacement at various elevations on both the right and left banks slightly decreases due to the gradual balance of pore water pressure. When the reservoir water level rises to 2525 m, the displacement at all elevations increases significantly. The maximum displacement at three elevations on the right bank from low to high is 15.1 mm, 24.6 mm, and 27.6 mm, respectively, while on the left bank, it is 6.5 mm, 9.2 mm, and 9.4 mm, respectively. It is evident that the deformation on the right bank is much greater than on the left, and this deformation increases with elevation and rising reservoir water levels. The dip and strike of the F115 fault, the different outcrop elevations, and the structural characteristics of the rock masses controlled by the fault all contribute to the more severe deformation on the right bank, which is more affected by water pressure and gravity.

4.2. Spatiotemporal Evolution Characteristics

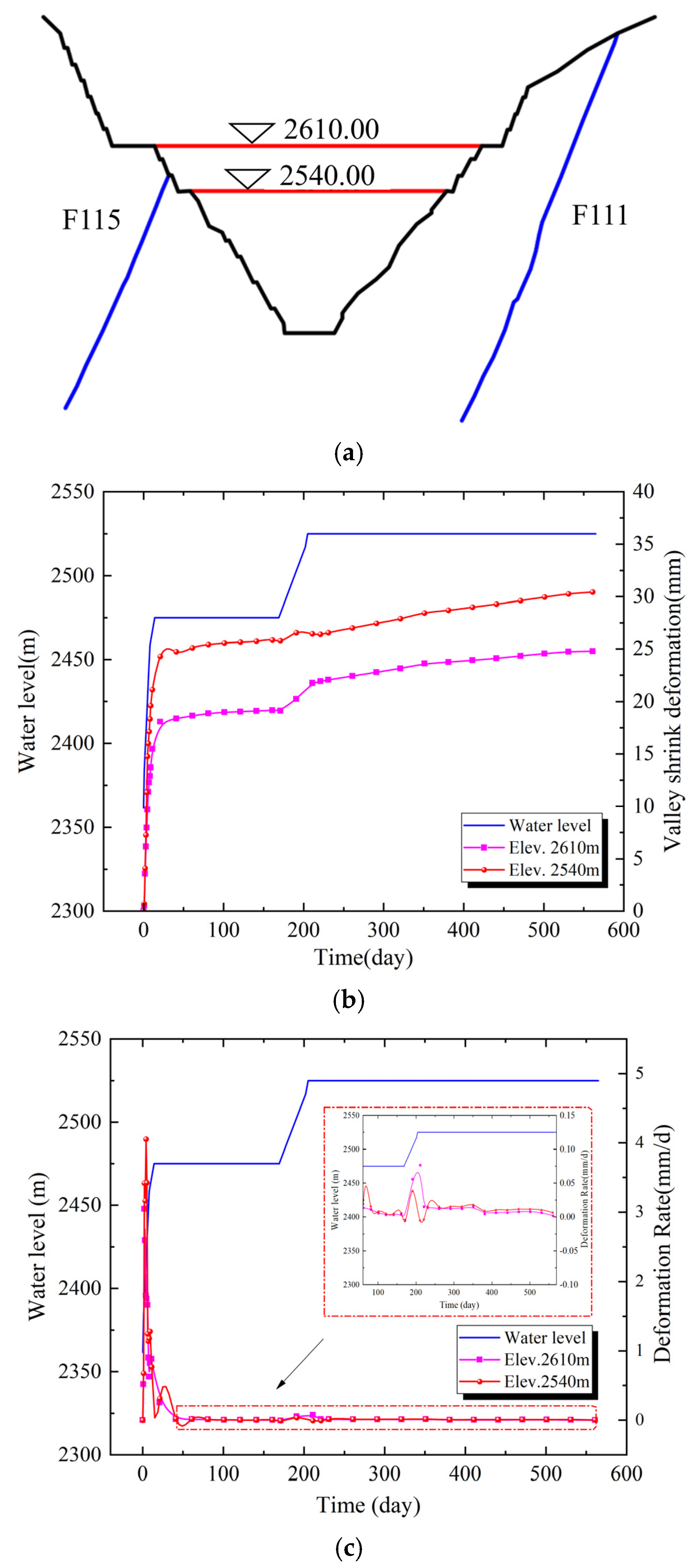
To study the impact of valley shrink deformation with the change in impoundment time, considering the stability at 2525 m water level for 360 days, geological cross-sections 4-4 (30 m from dam in the upstream) and 5-5 (120 from dam in the downstream) were selected to explore the time-varying characteristics of valley shrink displacement.

Two valley shrink deformation monitoring lines were set at elevations 2610 m and 2540 m on cross-section 4-4, as shown in Figure 7a, to monitor the time-varying characteristics of valley shrink deformation at different elevations. Figure 7b shows the time-varying curves of valley shrink deformation along the two monitoring lines on the upstream 4-4 cross-section. It can be seen that the maximum valley shrink deformation value is about 30.44 mm. During the initial impoundment to 2475 m, due to the rapid impoundment rate, the valley shrink deformation increased rapidly, with a shrink value of 24.28 mm, marking the main deformation stage. After 155 days of stability, the valley shrink deformation value was 25.79 mm, with a slight increase. When the water level reached 2525 m, the valley shrink deformation value was 26.45 mm. The valley shrink value at 2540 m elevation slightly decreased during the impoundment from 2475 m to 2525 m. The reason is that the fault dips towards the left bank, and the F115 fault has a long extension range and a wide influence zone, exacerbating the deformation of the right bank mountain. This causes the overall valley shrink deformation to increase first and then decrease, with a lower reduction. For the two monitoring lines on the 4-4 cross-section, the valley shrink deformation value at 2540 m elevation is greater than that at 2610 m. This is because the F115 fault surface exposure elevation on the 4-4 cross-section is 2550 m, and the 2540 m elevation monitoring line is more affected by the fault.

Figure 7c shows the variation of valley shrink deformation rates along the two monitoring lines on the upstream 4-4 cross-section. It can be seen that the deformation rates underwent significant changes during the initial impoundment period. In the initial stage of impoundment, the deformation rates showed considerable fluctuations but quickly tended to stabilize. During this process, due to the presence of the F115 fault, the deformation rate of the monitoring line at an elevation of 2540 m was significantly higher than that of the line at an elevation of 2610 m.

During the impoundment from 2475 m to 2525 m, the valley shrink deformation rate slightly increased, showing a strong correlation with the reservoir water level changes and exhibiting a slight lag effect. During the 360-day period of stable water level, the valley shrink deformation rate gradually decreased, eventually approaching zero.

Four valley shrink deformation monitoring lines were set at elevations 2610 m, 2540 m, 2470 m, and 2400 m on cross-section 5-5, as shown in Figure 8a, to monitor the time-varying characteristics of valley shrink deformation at different elevations. Figure 8b shows the time-varying curves of valley shrink deformation along the four monitoring lines on the downstream 5-5 cross-section.

It can be seen that the maximum valley shrink deformation value is about 16.40 mm. During the initial impoundment to 2475 m, due to the rapid impoundment rate, the valley shrink deformation increased rapidly, with a shrink value of 14.69 mm, marking the main deformation stage. After 155 days of stability, the valley shrink deformation value was 16.03 mm. When the water level reached 2525 m, the valley shrink deformation value was 13.94 mm. Unlike the upstream cross-section, the 2540 m, 2470 m, and 2400 m monitoring lines on the 5-5 cross-section showed a decrease in valley shrink deformation values during the impoundment from 2475 m to 2525 m. This is because the 5-5 cross-section is near the dam area. When the upstream water pressure increases during impoundment, the bank slope moves towards the mountain. Due to the curtain effect, the downstream seepage field cannot balance in time, causing a decrease in valley shrink deformation values for the monitoring lines below the 2540 m elevation during impoundment. The 2470 m elevation valley shrink deformation value was the largest among the four monitoring lines during the initial impoundment. This is because the surface exposure elevation of the F115 fault on the 5-5 cross-section is 2520 m, and the 2470 m elevation monitoring line is the most affected by the fault among the four lines.

Figure 8c shows the variation of valley shrink deformation rates along the four monitoring lines on the downstream 5-5 cross-section. It can be seen that the pattern is similar to that of the 4-4 cross-section. Due to the presence of the F115 fault, the 2470 m elevation monitoring line has the highest valley shrink deformation rate among the four lines, followed by the 2540 m elevation. The deformation rates at 2400 m and 2610 m elevations are similar.

4.3. Dam Displacement

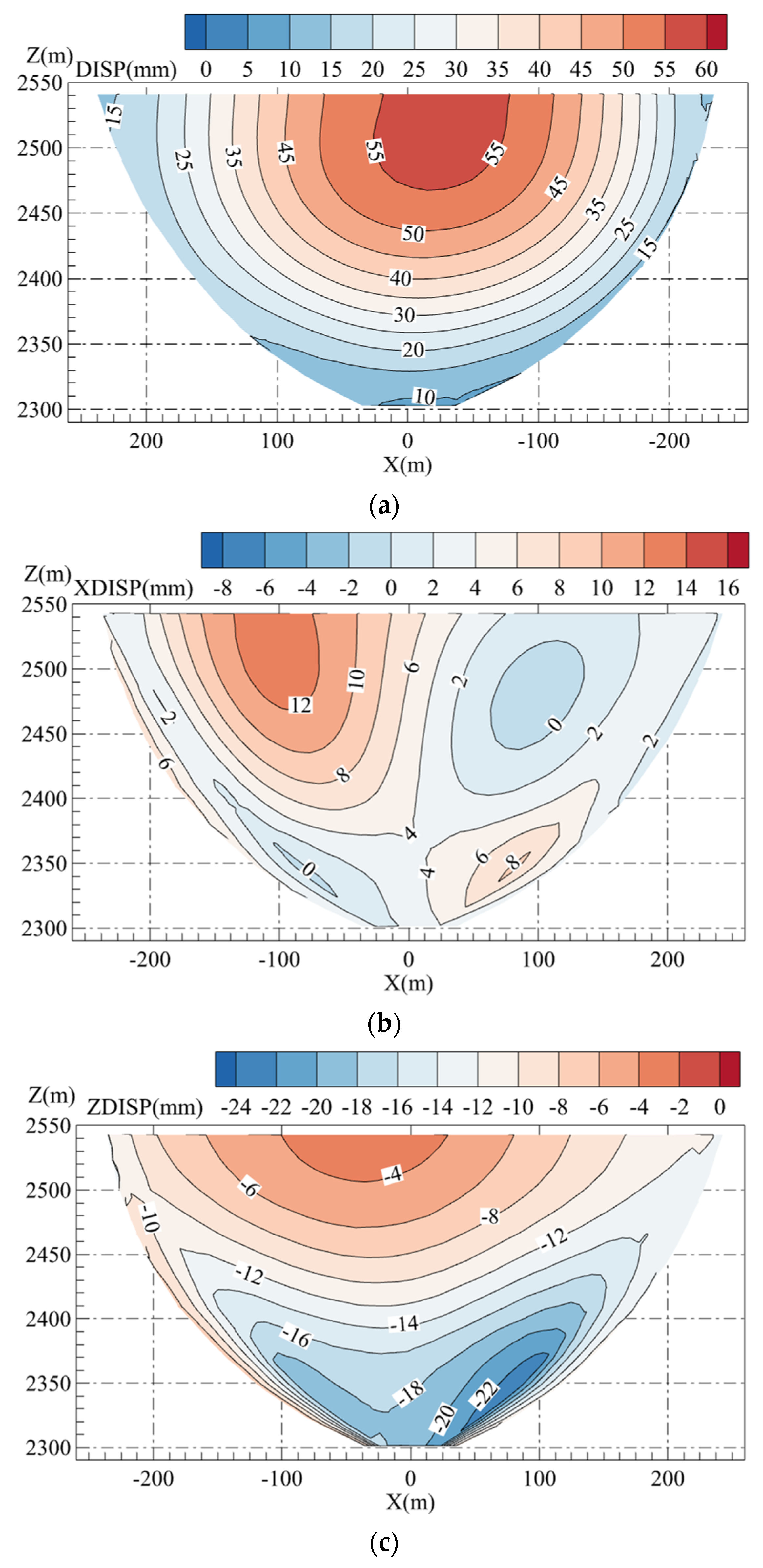
When the water level reaches 2525 m, the combined displacement and the cross-river displacement of the upper and lower dam faces caused by the reservoir water are shown in Figure 9 and Figure 10, respectively. It can be observed that the water load causes the arch dam to displace downstream, and the displacement gradually decreases from the slightly left-of-center position at the top of the dam toward the edges of the arch dam. As shown in Figure 9b, under the influence of the reservoir, the mountain bodies on both sides contract toward the river valley, compressing the dam. The F115 fault in the right bank’s mountain body is larger than that in the left bank, making the compression on the right side of the dam more pronounced. This results in the total displacement of the arch dam downstream being skewed to the left.

Figure 9c and Figure 10c show the vertical displacement of the upstream and downstream faces of the arch dam. The upstream face of the arch dam exhibits upward displacement in the central region and downward displacement in the peripheral areas, with the displacement pattern forming an approximately concentric circular distribution. The downstream face displacement is primarily downward, with a maximum displacement of −22 mm. The displacement gradually decreases as the distance from the central region increases, with the displacement near the edges approaching −10 mm. In contrast, the upper dam face shows some upward displacement, which may be attributed to factors such as buoyant forces from the water and concrete shrinkage. The lower dam face primarily exhibits downward displacement, likely due to the combined effects of the gravity of the arch dam and water pressure.

5. Conclusions

This paper studies the valley shrinkage deformation during the initial impoundment of an arch dam located in the upstream section of the Lancang River, considering the impact of secondary structural planes in the dam site area. The main findings are as follows:

(1) During impoundment, the valley slopes of the reservoir banks show shrinkage, with both the left and right bank rock masses deforming toward the center. The right bank experiences greater deformation than the left, with a maximum transverse deformation of 29.0 mm on the right and 14.7 mm on the left at a water level of 2525 m. The F115 fault on the right bank, which dips toward the left, contributes to the larger deformation.

(2) During impoundment, the valley slopes of the reservoir banks show shrinkage, with both the left and right bank rock masses deforming toward the center. The right bank experiences greater deformation than the left, with a maximum transverse deformation of 29.0 mm on the right and 14.7 mm on the left at a water level of 2525 m. The F115 fault on the right bank, which dips toward the left, contributes to the larger deformation.

(3) As elevation increases, valley shrinkage deformation initially increases and then decreases on both banks. On the right bank, deformation rises with elevation until above the F115 fault’s exposure, where it begins to decrease. On the left bank, the deformation follows a similar trend due to the F111 fault and seepage field.

(4) As the water level stabilizes, the seepage field within the mountain also stabilizes, causing the valley shrinkage deformation rate to decrease and approach zero.

(5) At a water level of 2525 m, the water load displaces the arch dam downstream. The F115 fault causes greater compression on the right side, resulting in the dam’s displacement skewing to the left. Gravity and buoyant forces create an upward vertical displacement in the central region and downward displacement in the outer areas on the upstream face, with primarily downward displacement on the downstream face.