Abstract
Shallow groundwater is an important resource, especially in low- and middle-income countries; however, shallow groundwater is particularly vulnerable to point sources of pollution such as latrines or unlined waste disposal ponds. The objective of this paper is to derive a quantitative criterion for siting an extraction well and an upgradient point source of pollution to ensure that they are hydraulically disconnected, i.e., that no water flows from the point source to the well. To achieve this objective, we modeled the flow of shallow groundwater considering uniform regional flow, a single point source of pollution, and a single extraction well. For any set of flow rates and upgradient point source distance, we sought the minimum “off-center distance” ymin (i.e., the distance in the direction perpendicular to regional flow) that ensures the well and the point source are hydraulically disconnected. For constituencies with access to computing resources and coding expertise, we used a computer-based method for determining ymin that is exact to within the accuracy of a root-finding algorithm; this approach is recommended when computer access is available. For constituencies lacking these resources, we determined a simple, closed-form, approximate solution for ymin that has an average error of less than 3% for the conditions we tested. For a subset of scenarios in which the point source is sufficiently far upgradient of the well (n = 77), the root mean square relative error of the approximate solution is only 0.52%. We found that ymin depends on a length parameter (Qw + Qps)/QR, where Qw is the extraction rate of the well, Qps is the injection rate of the point source, and QR is the regional groundwater flow rate per unit of perpendicular length. Either the exact solution or the closed-form approximation can help to site wells near point sources of pollution, or to site point sources near wells, in a manner that protects the health of the well user. The approximate solution is valuable because many constituencies that rely on shallow wells for water supply and latrines for sanitation also lack access to the computer resources necessary to apply the exact solution.
1. Introduction
As the population of the world grows, more and more people, communities, and countries are relying on groundwater as a reliable source of potable water [1]. In low- and middle-income countries (LMICs), principles such as self-supply and use of appropriate technologies (e.g., suction handpumps) are applied to access shallow groundwater up to 10 m deep [2,3,4,5]. However, shallow groundwater in LMICs is also highly susceptible to contamination from point sources of pollution [6,7]. For example, common sanitation technologies in LMICs are latrines or pit toilets for single-family or multiple-family use [8]. Latrines are designed primarily to physically separate humans from their waste but do not actually destroy or remove microbial and chemical pollutants [9], so a latrine can act as a point source of pollution into the nearby groundwater. Thus, the siting of a shallow groundwater well in the vicinity of a latrine (or the siting of a latrine in the vicinity of a well) threatens the chemical and biological quality of water extracted from the well and thereby threatens the health of people using the well. Other examples of point sources of contamination in shallow groundwater could include waste-disposal injection wells [10,11], infiltration from mine tailing piles [12], cesspools [13], or small unlined ponds/lagoons [14,15]. Therefore, harmful agents introduced into the groundwater by point sources could include bacteria, viruses, nitrate, toxic metals, or other hazardous chemicals.
One way to minimize health risks from these contamination sources is to make sure there is adequate separation distance between a shallow well and any upgradient point source of pollution. For the particular case of latrines, several governmental and nongovernmental organizations have developed guidelines for how far a latrine should be placed from a downgradient well or water receptor. However, Nenninger et al. [16] determined these one-size-fits-all distances need re-evaluation due to the varying transport properties of different pathogen classes that are found in human excrement and due to the limited number of field studies that have supported the recommended guidelines for a “safe” distance.
Another approach to this problem of co-locating water supply and waste-disposal technologies near each other is to account for the groundwater flow hydraulics, ensuring that water from the upgradient point source does not flow to the well. That is, we want to ensure that the latrine or other point source lies outside the capture zone of the extraction well. Equivalently, we want to ensure that the extraction well lies outside the zone of influence of the point source. Put yet another way, we want to ensure that the point source and the extraction well are not hydraulically connected. This could be accomplished using a numerical model such as MODFLOW, but here we instead seek an analytical mathematical equation or criterion that can be applied quickly and easily to a proposed scenario without reliance on specialized computational resources. The advantages of using an analytical solution have been pointed out by Shan [17] and Haitjema [18], among others. Some examples of these advantages are direct and explicit calculations [17] and improved conceptual understanding as compared to more complicated model designs [18].
There are several examples of relevant analytical modeling in previous well-hydraulics literature, but apparently none have addressed the specific question asked here. For example, Javandel and Tsang [19] derived equations for delineating the capture zones of one, two, or three extraction wells in a regional flow field. This work was later expanded by Grubb [20], Shan [17], and Christ and Goltz [21], all of whom overcame some of the limitations of the work by Javandel and Tsang [19]. However, none of those authors considered the presence of a point source, which affects the groundwater hydraulics if the rate of water loading from the point source is appreciable. Cunningham and Reinhard [22] and Cunningham et al. [23] derived analytical equations for the hydraulics of an extraction well near a point source (in the form of an injection well), including the condition under which the wells are hydraulically disconnected; however, those analyses were limited to situations in which the pumping rates of the two wells were equal and the well pair was oriented perpendicular to the regional groundwater flow. Recently, Zhang and Wang [24] overcame the latter of these two limitations, but not the former.
Accordingly, the overall objective of this paper is to quantify the conditions under which an upgradient point source is hydraulically disconnected from a downgradient extraction well. Specifically, we seek (1) an approach or methodology that can exactly determine a minimum offset distance required to ensure that the point source is outside the capture zone of the extraction well, and (2) a convenient, easy-to-use approximate analytical solution or equation that agrees closely with the exact solution but does not require a computer. To advance the work of previous researchers, the solutions derived herein are able to consider the situation in which the hydraulic loading rate of the point source differs from the pumping rate of the extraction well, as well as the situation in which the well and the point source are oriented arbitrarily relative to the regional groundwater flow. Application of the criteria developed herein for siting a well near a point source will protect the quality of the water extracted by the well and hence will protect the health of the users of the well.
The second of our two specific objectives is necessary because 2.9 billion people still live offline, with 96% of those residing in LMICs [25]. In the 46 UN-designated least developed countries (LDCs), 76% of the population is covered by a mobile broadband signal, but only 25% are using the Internet [25]. Furthermore, there is a significant overlap between the 2.9 billion people living offline, the 3.5 billion people lacking access to safely managed sanitation services, and the 2.2 billion people lacking access to safely managed water services [26,27,28]. Water and sanitation solutions that require computer resources may be of limited value to such constituencies, indicating the need for simple but accurate pencil-and-paper solutions such as those presented herein.
2. Materials and Methods
2.1. Conceptual Framework
We consider a situation in which a point source of pollution is located upgradient of an extraction well. Regional groundwater flow is assumed to be steady and uniform. Without loss of generality, we can assign the −x direction as the direction of regional groundwater flow, and we can assign the location of the origin (0, 0) to the extraction well (cf. [19]). The point source is thus located at a location (xps, yps) for which xps > 0. The y-location of the point source, yps, could be either positive or negative, but here we consider only the situation in which yps > 0. This conceptual model is illustrated in Figure 1.
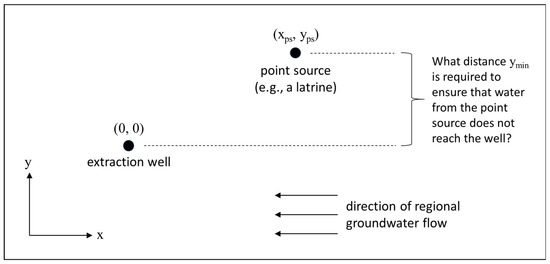
Figure 1.
Conceptual model of the scenario considered in this paper and the key question requiring resolution. Note that Figure 1 is provided as a plan view or “birds-eye view” of the area of interest, not an elevation view. The x- and y-directions represent orthogonal horizontal directions (e.g., east and north). Regional groundwater flow is in the −x direction (e.g., flow to the west).
Important approximations or simplifications that we adopt are the following:
- Regional flow is steady, e.g., the direction and the magnitude of the regional flow do not vary seasonally or with precipitation;
- The shallow aquifer is homogeneous and isotropic in the x- and y-directions;
- Flow can be considered as two-dimensional (depth-integrated);
- The extraction rate of the well is constant over time;
- The rate at which the point source introduces water into the aquifer (which we will hereafter call the hydraulic loading rate) is constant over time.
In most real situations, the extraction rate of the well and the hydraulic loading rate of the point source are not likely to be constant over time; e.g., a latrine introduces water into the aquifer intermittently depending on the usage patterns and flushing mechanism of the latrine. However, to ensure a conservative siting of the well and the point source that is most protective of health, we can assume in the ensuing development that the well and the point source are always operating at their maximum flow rates.
From Figure 1, it is obvious that if the point source is directly upgradient of the well (i.e., if yps = 0), then contaminated water from the point source will always flow into the extraction well. Thus, to create a situation in which the well is protected from the point source, we require that |yps| > 0. We therefore pose the key question as follows: for a given set of conditions, what is the minimum value of yps that ensures that the well and the point source are hydraulically disconnected, i.e., that no water from the point source reaches the well? We call this minimum separation distance ymin. If yps < ymin, then the well and the point source are hydraulically connected, and at least some of the water from the point source will reach the well. However, if yps > ymin, they are hydraulically disconnected, and the well is “safe” from contamination from the point source. These two situations are illustrated graphically in Figure 2.
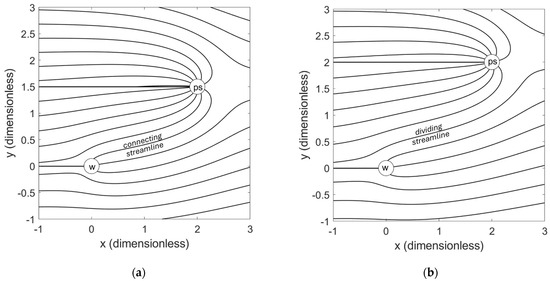
Figure 2.
Streamlines of the groundwater flow in the vicinity of a point source (denoted “ps”) and a downgradient extraction well (denoted “w”): (a) Well and point source are hydraulically connected (as evidenced by the connecting streamline) because yps < ymin; (b) Well and point source are hydraulically disconnected (as evidenced by the dividing streamline) because yps > ymin.
2.2. Mathematical Model and Non-Dimensionalization
To model this situation quantitatively, we employ the analytic element method [29,30,31]. This method relies on the specification of a potential function Φ(x, y) and a stream function Ψ(x, y) that describe the flow of the groundwater. Groundwater flows from regions of high Φ to regions of low Φ; the path of the groundwater is along streamlines (see Figure 2), which are curves along which Ψ is constant. The functions Φ and Ψ can be specified through the superposition of the “analytic elements” pertaining to the situation being modeled; for this paper, the relevant elements are a point source, an extraction well, and regional groundwater flow. The functions Φ and Ψ are known for these elements [29,30,31] and can therefore be employed here without derivation.
Specifically, for the situation illustrated in Figure 1, the potential function Φ(x, y) and the stream function Ψ(x, y) are given by the following:
in which QR is the regional volumetric groundwater flow rate (per unit width in the perpendicular direction) (L2 T−1); Qw is the extraction rate of the well (L3 T−1); Qps is the hydraulic loading rate from the point source into the groundwater (L3 T−1); and Φ0 is an arbitrary constant (L3 T−1) that allows Φ to be set to a desired value at a particular location. For a confined aquifer, QR is equivalent to the product B U of Javandel and Tsang [19], i.e., the product of the vertical aquifer thickness and the specific discharge rate. Curves along a constant value of Ψ are streamlines, i.e., the pathlines of the flowing water; curves along a constant value of Φ are equipotentials; the equipotentials and the streamlines are orthogonal [30]. Strictly speaking, Equation (1) is not mathematically valid because it is not allowable to take the logarithm of a quantity with units; however, we can consider that Φ0 contains the necessary constant terms that combine with the logarithms shown in the equation, making the arguments dimensionless and thus making Equation (1) valid for practical purposes.
Equations (1) and (2) contain five parameters: QR, Qw, Qps, xps, and yps. To reduce the number of parameters, we can non-dimensionalize Equations (1) and (2). Following the non-dimensionalization of Javandel and Tsang [19], we define the following non-dimensional terms as:
This allows Equations (1) and (2) to be rewritten as the following:
Whereas Equations (1) and (2) depended on five parameters, Equations (4) and (5) depend on only three: , , and α. The parameters and are the non-dimensionalized coordinates of the point source. The parameter α is the ratio of the hydraulic loading rate of the point source to the extraction rate of the well. In terms of the dimensionless variables, the key question is now: for any given values of and α, what is the minimum value of that ensures the point source and the well are hydraulically disconnected? We use the notation to denote this minimum acceptable value of . In the sub-sections that follow, we describe two methods for determining ; the first of these makes use of the analytic element method but requires the use of a computer; the second can be implemented simply with nothing more than pencil and paper.
2.3. Exact Determination of for Specified Values of α and
To ensure that the point source and the well are hydraulically disconnected, we must determine for the applicable values of and α. For constituencies that have access to computers and sufficient coding expertise, the value of can be determined exactly (to within machine accuracy) via the following method.
Building on the functions Φ(x, y) and Ψ(x, y) as specified above, we now make use of the (dimensionless) complex location and the complex potential function , as presented by Strack [29,30]. Switching from the real domain (, , , and ) to the complex domain ( and ) facilitates the algebra in the mathematical derivation that follows. We denote the yet-to-be-determined location of the point source as . Equations (4) and (5) can then be rewritten as a single equation in complex notation as follows, making use of known functions derived elsewhere [29,30,31]:
Stagnation points in the flow field are located where the complex discharge function equals 0 [32]. Differentiating Equation (6) and equating to 0 yields the following equation for the location of the stagnation points:
Solving the quadratic Equation (7) provides the locations of two stagnation points in the flow field, and .
When the point source is located at its critical value, i.e., when = , the two stagnation points and both lie on the bounding streamline [32]. This means that the value of the streamfunction must be equal at and (Because of the “branch cut” and the fact that the inverse tangent function is not single-valued, the value of can actually differ by a value of exactly 1 at the two stagnation points). The streamfunction is the imaginary part of the complex function , which can be evaluated at the two stagnation points using Equation (6). Thus, the problem of finding for given values of and α can be reframed as finding the location that enables the following condition to be met:
A root-finding algorithm can be employed to find the value of that enables Equation (8) to be satisfied. This yields for the given values of and α. We wrote short functions in MATLAB® (version 2023a) to compute , , and , then used the “fzero” root-finding function in MATLAB® to find . This yields a value of that is exact to within the tolerance of the root-finding algorithm employed. Our MATLAB® codes are provided in Appendix A. To execute the MATLAB® functions to obtain the exact value of , the three functions from Appendix A should be saved in the same file directory; then, at the MATLAB® command prompt, type “MAIN_find_y_min(x_ps, alpha),” inserting the desired numerical values for x_ps and alpha.
As will be seen later, a point of particular interest is α = 1.0, = 0. For this particular combination, we determined that = 0.5792. The relevance of this value will be discussed subsequently.
2.4. Development of Approximate Analytical Equations = f () and ymin = f (xps)
The sub-section immediately preceding describes a method to determine exactly for any given combination of and α. We recommend application of that method when the user has the necessary computer access and coding expertise to implement it. However, it is also an objective of this paper to find a convenient, easy-to-use, approximate analytical equation for that agrees closely with the exact solution but does not require a computer for the following reasons:
- A simple-but-accurate approximate analytical solution will be deployable by constituencies that do not have adequate computer access to implement the exact solution;
- A suitably simple analytical equation explicitly articulates the dependence of on and α, whereas the “exact” procedure does not. Thus, the analytical equation may yield insights into the physics of the problem and/or may enable estimation of important conditions or criteria;
- As will be seen subsequently, an analytical equation for can be applied to a well-known problem in groundwater hydraulics, enabling a closed-form solution to a problem that previously relied on the solution of a transcendental equation.
There might also be additional advantages beyond these that we have not yet considered.
Thus, to find an approximate analytical equation for , we proceeded as follows: We applied the procedure described in Section 2.3 to find the exact value of for 101 different combinations of and α. We considered eight values of α: 0, 0.1, 0.2, 0.5, 1.0, 2.0, 5.0, and 10.0. For each of these values of α, we considered eleven values of : 0, 0.25, 0.5, 1.0, 1.5, 2, 3, 4, 5, 7, and 10. In addition, we considered the pair of values α = 1.0, = 15. Finally, for each of the three largest values of α (2.0, 5.0, and 10.0), we also considered values of 15, 20, 25, and 30. After obtaining the exact values of for these 101 sets of conditions, we graphed for each of the eight values of α considered. Each of the resultant eight graphs contained between 11 and 15 data points. Each graph exhibited the same general shape, but the particular values on the graph vary with α, i.e., values of are generally higher for a higher value of α. We considered different functions that matched the general shape of the graphs until identifying a function that matched the data closely for all eight values of α. For the dimensionless variables, the function = f () contains one parameter, namely, α. Then, we converted all variables back to their dimensional forms to determine the function ymin = f (xps); this function contains the three parameters QR, Qw, and Qps.
3. Results
3.1. Exact Values of for Specified Values of α and
In Section 2.3, we presented a methodology for determining the (dimensionless) minimum required off-center distance, , exactly (to within the accuracy of a root-finding algorithm). To verify the validity of the method, we applied it to 101 different combinations of and α. For each set of and α, we determined using the method described, and we verified graphically that the determined value of is the minimum required off-center distance. That is, we graphically verified that setting leads to hydraulic connection between the point source and the well, but setting leads to hydraulic disconnection between the point source and the well, as illustrated in Figure 2.
We therefore conclude that the method described in Section 2.3 is valid for determining . Because this procedure is exact to within the accuracy of the root-finding algorithm employed, we recommend this route for determining when the user has access to the computer tools necessary to implement the described procedure.
3.2. Closed-Form Approximation for
For constituencies that lack the computer resources or access required to find exactly, we determined the following approximate analytical solution, which can be applied easily using only pencil and paper:
To demonstrate the suitability of this equation, Figure 3 compares the predictions of Equation (9) to the exact values of . For clarity of presentation, Figure 3 shows the results for only four of the eight values of α considered; thus, Figure 3 contains only 47 of the 101 overall cases considered. However, the agreement between the approximation and the exact values was similar for all eight values of α, including those values not shown in Figure 3. As evidence of that fact, Appendix B provides the estimates of from both the computer-based method and the approximate analytical solution for all 101 cases considered.
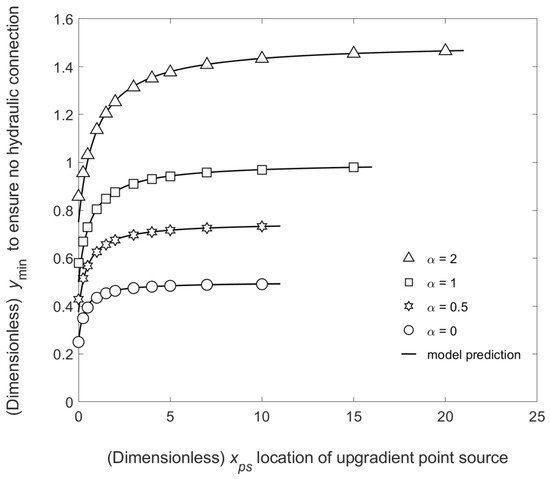
Figure 3.
Comparison of the predictions of Equation (9) with exact values of .
From Figure 3, it is clear that Equation (9) is, overall, in excellent agreement with the exact values, particularly when is relatively large and/or when α is relatively small. For larger values of α and smaller values of , the approximate analytical solution under-predicts the exact value. For instance, for the particular condition that α = 1.0, = 0, the exact value of is 0.5792, but Equation (9) predicts = 0.500, a relative error of about 14%. This is important because siting the point source too close to the well could threaten the quality of the extracted water. We therefore recommend including some margin of safety if using Equation (9) to site the point source or the well, but including some margin of safety is good practice in any case. If we consider all 101 combinations of and α, the average relative error is only 1.3%, and the root mean square relative error (RMSRE) is 2.9%. The RMSRE is calculated as follows:
Furthermore, for values of ≥ 1.0, the RMSRE is only 0.52% (n = 77; see Appendix B). This shows that Equation (9) is nearly perfect except when is small, a conclusion that agrees with visual inspection of Figure 3.
3.3. Dimensional Form of the Approximate Analytical Equation
Using Equation (3) to convert Equation (9) back to dimensional variables, we derive the following approximate analytical equation for ymin, the dimensional form of the minimum required off-center distance:
in which the parameter L has dimensions of length and is given by the following:
Equations (11) and (12) are interesting because, in theory, the function ymin = f (xps) could depend upon three parameters: QR, Qw, and Qps. However, these three parameters appear only as the group L = (Qw + Qps)/QR. Thus, the function ymin = f (xps) depends only on one parameter, L, making Equation (11) quite simple. In fact, Equation (11) has exactly the same functional form as Equation (9), with (1 + α) in Equation (9) replaced by L in Equation (11).
From Equation (11) we can see that, as xps increases (the point source is moved farther upgradient from the well), ymin approaches an asymptotic value of L/2. This gives us a simple way to ensure that a well and a point source are not hydraulically connected: if the “off-center” distance between the well and the point source is at least L/2 = (Qw + Qps)/(2 QR), then they will necessarily be hydraulically disconnected, regardless of the upgradient distance between them.
It is not surprising that the required off-center distance, ymin, scales with the group (Qw + Qps)/QR. This means that if either the extraction rate of the well is high or the hydraulic loading rate of the point source is high—or both—then a large off-center distance is required to ensure that the well and the point source are hydraulically disconnected. That result is rather intuitive. However, despite the unsurprising qualitative nature of the result, Equations (11) and (12) are useful because they present the specific dependence of ymin upon the relevant hydraulic rates. Furthermore, Equations (11) and (12) are simple and easy to apply if the relevant hydraulic rates and groundwater flow rate can be estimated reliably. This is important because our objective was to determine an analytical equation that is simple and easy to apply but still sufficiently accurate.
4. Discussion
Having developed both exact and approximate methods for determining the minimum required off-center distance to ensure hydraulic disconnection, it is worthwhile to consider how the results of this paper are related to the results from relevant prior publications, as well as any limitations that might apply to the results herein.
4.1. Application to the Results of Javandel and Tsang [19]
In their classic paper, Javandel and Tsang [19] derived an analytical equation for the capture zone of a single extraction well in regional flow. Using the notation system of this current paper, Equation (2) of Javandel and Tsang would be written as follows:
This is the dimensionless form of the equation for the boundary of the capture zone. Notably, Equation (13) is a transcendental equation rather than a closed-form expression; that is, appears on both the left- and right-hand sides of the equation. The solution of the equation for a particular value of therefore requires iteration or another numerical solution technique. (It is possible to solve directly for given a specified value of , but it is not possible to solve directly for given a specified value of .)
However, we can realize that the situation considered by Javandel and Tsang [19]—a single extraction well in uniform regional flow—is a special case of the situation considered in this paper. Specifically, as the dimensionless parameter α = Qps/Qw approaches zero, the scenario modeled in this paper becomes the same as that considered by Javandel and Tsang [19]; we want to know if the location of a point source (with a negligible hydraulic loading rate, such that the groundwater hydraulics are not affected) lies inside the capture zone of the extraction well. Therefore, if we set α = 0, Equation (9) in this paper should provide a closed-form approximation to the equation derived by Javandel and Tsang [19]. The boundary of the capture zone of a single extraction well in regional flow can therefore be approximated by the following closed-form equation (in dimensionless form):
To demonstrate the validity of Equation (14), Figure 4 compares the analytical result of Javandel and Tsang [19] to the approximation of Equation (14). From Figure 4, it is clear that the closed-form Equation (14) is a suitable approximation. The x-intercept of the analytical solution is −1/2π ≈ −0.159, and the x-intercept of the approximation is −0.16. For nearly all values of , the difference between the analytical solution and the approximation is less than 1%. We therefore contend that Equation (14) is valuable as an easily applicable closed-form approximation to the classic result of Javandel and Tsang [19]. To the best of our knowledge, this is the first time that a closed-form approximation to Equation (2) of Javandel and Tsang [19] has been presented.
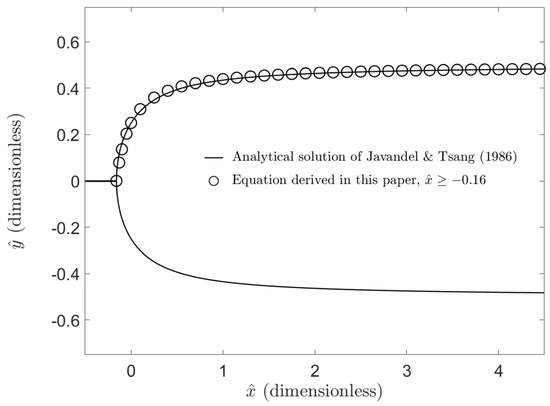
Figure 4.
Boundary of the capture zone of a single extraction well in uniform regional flow; comparison of the transcendental solution from Javandel and Tsang [19] to the closed-form approximation of Equation (14) from this paper.
4.2. Comparison with the Results of Cunningham and Reinhard [22]
Cunningham and Reinhard [22] and Cunningham et al. [23] considered an injection–extraction well pair in uniform regional flow, which is a situation similar to that considered in this current paper. Cunningham and Reinhard [22] found that the injection well and the extraction well are hydraulically connected only if a dimensionless group that they called ξ is greater than 1.1. Converting from the notation system of Cunningham and Reinhard [22] to the notation system of the current paper, this result would imply that the injection well and the extraction well are hydraulically connected only if , which is equivalent to saying that ≈ 0.579.
However, Cunningham and Reinhard [22] and Cunningham et al. [23] only considered the case in which the injection rate and the extraction rate are equal and the well pair is oriented perpendicular to the regional flow. In the notation of the current paper, the first of these conditions means that α = 1; the second of these conditions means that . In this paper, for the case of α = 1 and , we found that = 0.5792. Thus, the results of Cunningham and Reinhard [22] and the results of the current paper are in near-exact agreement ( = 0.579 vs. = 0.5792).
4.3. Comparison with the Results of Zhang and Wang [24]
Zhang and Wang [24] also considered an injection–extraction well pair in uniform regional flow; they termed it their “1e/1i” system. Zhang and Wang [24], like Cunningham and Reinhard [22], considered the particular case that the injection rate and the extraction rate are equal, which, in the notation of this current paper, means α = 1. However, Zhang and Wang [24] expanded upon the work of Cunningham and Reinhard [22] by allowing the well pair to be oriented at any angle relative to the regional groundwater flow. Zhang and Wang [24] determined the conditions under which the wells were hydraulically connected or hydraulically disconnected; in their notation, a value of η = 0 indicates the boundary between connected and disconnected conditions. Therefore, we can consider some of the η = 0 cases of Zhang and Wang [24], and we can see if they agree with this paper’s results for the case that α = 1.
When the well pair is oriented perpendicular to the regional groundwater flow, the notation of Zhang and Wang [24] would say that the angle is π/2. Figure 5 of Zhang and Wang [24] shows that at this angle, η = 0 occurs when their dimensionless group qD is approximately 1.8. Converting to the notation of this current paper, that would correspond to the condition that = (1.8/π) sin(π/2) ≈ 0.573. As noted above, we found in this paper that = 0.5792 for these conditions. The agreement is within 2%, and it might in fact be better than that, because the value of 1.8 was estimated from visual inspection of Figure 5 from Zhang and Wang [24].
When the well pair is oriented at a 45° angle to the regional flow (with the injection well upgradient of the extraction well), the notation of Zhang and Wang [24] would say that the angle is π/4. For this angle, Figure 5 of Zhang and Wang [24] does not show what value of qD would produce η = 0. However, we can extrapolate from Figure 5 and estimate that this condition occurs when their dimensionless group qD is approximately 3.5. Converting to the notation of this current paper, that would correspond to the condition that = (3.5/π) sin(π/4) ≈ 0.788. In this current paper, an angle of 45° means that . For the case that α = 1, the condition that occurs at = 0.7736 (based on Equation (9)). Therefore, this paper agrees with Zhang and Wang [24] to within 2%. Again, the actual agreement might be even better than that, because the value of 3.5 was estimated from extrapolation of Figure 5 from Zhang and Wang [24].
Consideration of additional points from Figure 5 of Zhang and Wang [24] is difficult because they defined their coordinate system differently from the way it is defined in Figure 1 of this paper. Also, much of the analysis of Zhang and Wang [24] is for situations in which the extraction well is upgradient of the injection well (which, in their notation, means that the angle is greater than π/2); we did not consider such situations in this paper, limiting ourselves to situations in which the point source is upgradient of the extraction well. However, based on the two sets of conditions that can be easily compared, it appears that the results of the current analysis agree with those of Zhang and Wang [24] to within 2%, and perhaps even better than that.
A summary of the comparisons discussed above is provided in Table 1.

Table 1.
Comparison of this paper’s results to the corresponding results from Cunningham and Reinhard [22] or Zhang and Wang [24].
4.4. Application of the Methodology and Equations Presented Herein
The primary application we envision for the methodology and equations presented above is the siting of a proposed point source (such as a latrine) near an existing well or the siting of a proposed well near an existing point source. These equations might be particularly useful in low- and middle-income countries where shallow groundwater is an important resource, where latrines are used frequently for sanitation, and where siting entities might not have ready access to computing resources and coding experience, nor to more sophisticated numerical models such as MODFLOW. The method presented here is also applicable to assess the risk of contamination in the vicinity of a leaking underground storage tank or a leaking septic tank. Furthermore, in contexts where more advanced computing resources are available, the methodology and equations presented above could likely be used as screening tools to decide which possible contamination situations need more in-depth investigation with MODFLOW or similar computational tools.
4.5. Limitations to This Analysis
The values and equations derived above are based on certain assumptions or simplifications that can limit their applicability. Specifically, we believe the following are the most important limitations of the analysis presented here:
- Application of Equation (9) or Equation (11) requires the user to have reliable estimates of the magnitude and direction of regional groundwater flow. This knowledge might not be readily available in some contexts;
- Equations are derived by assuming that both the magnitude and direction of the regional flow are steady over time, e.g., any seasonal variations in the regional flow must be small. In some situations, particularly for shallow unconfined aquifers such as those considered here, the direction of regional flow can vary significantly over time. In these situations, Equations (9) and (11) could still be applied to assess the risk of well contamination, but the equations would need to be applied for each of the most “extreme” possible flow directions to ensure that the well is protected regardless of the flow direction;
- The injection rate of the point source and the extraction rate of the well are assumed to be steady in time. This is probably not realistic. However, this limitation can be overcome by assuming that the point source and the well always operate at or near their maximum flow rates. That will result in a conservative estimate of ymin that is protective of health;
- The hydraulic conductivity in the vicinity of the well and the point source are assumed to be sufficiently homogeneous that heterogeneity has negligible effects on the flow field. In environments that exhibit high degrees of heterogeneity even at small scales, the equations derived here might not apply;
- The aquifer is assumed to be isotropic in the x- and y-directions. This limitation can be overcome by applying a coordinate transform, as discussed and demonstrated elsewhere (e.g., Strack [30]; Fienen et al. [33]; Fitts [34]);
- The equations derived here account only for a single point source, a single extraction well, and regional groundwater flow. Therefore, any other features that affect the local flow field (e.g., recharge zones, physical barriers to flow, additional wells) would have to be sufficiently far away that they do not impact the groundwater flow in the vicinity of the point source and the extraction well.
Future work could quantify how sensitive the model results are to violations of these simplifications and assumptions. For instance, how much temporal variability in the regional flow direction and/or how much heterogeneity of conductivity is allowable? However, such analyses are beyond the scope of the current paper. Despite the limitations listed above, we envision the methodology and equations presented here as useful in a variety of contexts, as discussed in the preceding sub-section. As with all models, results will be best when the user has access to reliable input data such as the direction and magnitude of regional flow.
5. Conclusions
The objective of this paper was to quantify the conditions under which an upgradient point source is hydraulically disconnected from a downgradient extraction well. The objective was achieved by developing a methodology for determining ymin, the minimum “off-center” distance required to ensure no hydraulic connection between the well and the point source. Key findings, results, and conclusions are the following:
- For constituencies with adequate computer resources, we have presented a computer-based method capable of finding ymin exactly (to within the tolerance of a computer-based root-finding algorithm);
- For constituencies lacking reliable access to computing resources, we have presented a simple approximate closed-form expression for ymin;
- The simple algebraic solution for ymin was shown to provide an excellent approximation to the exact solution. The average relative error of the approximate solution is less than 3% for the conditions we considered. For a subset of scenarios in which the point source is sufficiently far upgradient of the well (n = 77), the root mean square relative error of the approximate solution is only 0.52%;
- We found that ymin depends on the upgradient separation distance xps between the point source and the latrine, as well as a length parameter that we call L. The length parameter L is easily computed from the hydraulic loading rate of the point source, the extraction rate of the well, and the regional groundwater flow rate, as shown in Equation (12);
- If ymin > L/2, then the well and the point source are guaranteed to be hydraulically disconnected regardless of the upgradient separation distance xps;
- Results obtained herein are in good agreement with the corresponding results from Javandel and Tsang [19], Cunningham and Reinhard [21], and Zhang and Wang [24];
- The methodology and equations presented here enable the siting of a proposed well or a proposed point source at a location that protects the quality of the water extracted by the well and hence protects the health of the users of the well.
Author Contributions
Conceptualization, C.N., J.A.C. and J.R.M.; methodology, J.A.C. and C.N.; software, J.A.C.; validation, J.A.C., C.N. and J.R.M.; formal analysis, C.N.; investigation, C.N. and J.A.C.; resources, J.A.C. and J.R.M.; data curation, C.N.; writing—original draft preparation, C.N.; writing—reviewing and editing, J.A.C., C.N. and J.R.M.; visualization, J.A.C.; supervision, J.R.M.; project administration, J.A.C. and J.R.M.; funding acquisition, J.R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Julia and Samuel Flom Endowment at the University of South Florida and by the Paul D. Coverdell Fellows program.
Data Availability Statement
The original contributions presented in the study are included in the article (Appendix A and Appendix B); further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. MATLAB® Codes for Constituencies with Necessary Computer Access
As described in Section 2.3, we wrote short codes in MATLAB® to determine exactly (to within the tolerance of a root-finding algorithm) for any given values of and α. This method of estimating is recommended for those constituencies that have access to the necessary computing resources and coding expertise. The codes of the three MATLAB® functions we developed are provided in Figure A1.

Figure A1.
Codes of the three MATLAB® functions used to estimate .
Appendix B. Comparison of Computer-Based and Equation-Based Estimates of
Figure 3 compares the near-exact computer-based estimate of and the approximate analytical solution of for 47 of the 101 cases we considered. Table A1, Table A2, Table A3 and Table A4 provide the exact and modeled values of for all 101 cases.

Table A1.
Exact (computer-based) and modeled (from Equation (9)) values of for α = 0 and for α = 0.1.
Table A1.
Exact (computer-based) and modeled (from Equation (9)) values of for α = 0 and for α = 0.1.
| α = 0 | α = 0.1 | |||
|---|---|---|---|---|
| Exact (Computer-Based) Value of | Analytical Estimate of | Exact (Computer-Based) Value of | Analytical Estimate of | |
| 0 | 0.2500 | 0.2500 | 0.2906 | 0.2750 |
| 0.25 | 0.3489 | 0.3596 | 0.3836 | 0.3892 |
| 0.5 | 0.3938 | 0.4024 | 0.4298 | 0.4364 |
| 1 | 0.4347 | 0.4394 | 0.4742 | 0.4784 |
| 1.5 | 0.4533 | 0.4560 | 0.4951 | 0.4977 |
| 2 | 0.4637 | 0.4655 | 0.5071 | 0.5088 |
| 3 | 0.4750 | 0.4759 | 0.5202 | 0.5211 |
| 4 | 0.4810 | 0.4815 | 0.5272 | 0.5278 |
| 5 | 0.4845 | 0.4850 | 0.5316 | 0.5319 |
| 7 | 0.4889 | 0.4891 | 0.5367 | 0.5368 |
| 10 | 0.4913 | 0.4922 | 0.5406 | 0.5406 |

Table A2.
Exact (computer-based) and modeled (from Equation (9)) values of for α = 0.2 and for α = 0.5.
Table A2.
Exact (computer-based) and modeled (from Equation (9)) values of for α = 0.2 and for α = 0.5.
| α = 0.2 | α = 0.5 | |||
|---|---|---|---|---|
| Exact (Computer-Based) Value of | Analytical Estimate of | Exact (Computer-Based) Value of | Analytical Estimate of | |
| 0 | 0.3278 | 0.3000 | 0.4285 | 0.3750 |
| 0.25 | 0.4176 | 0.4183 | 0.5155 | 0.5034 |
| 0.5 | 0.4652 | 0.4697 | 0.5680 | 0.5663 |
| 1 | 0.5130 | 0.5168 | 0.6262 | 0.6284 |
| 1.5 | 0.5363 | 0.5389 | 0.6569 | 0.6591 |
| 2 | 0.5499 | 0.5517 | 0.6757 | 0.6774 |
| 3 | 0.565 | 0.5660 | 0.6972 | 0.6983 |
| 4 | 0.5732 | 0.5737 | 0.7091 | 0.7098 |
| 5 | 0.5782 | 0.5786 | 0.7167 | 0.7172 |
| 7 | 0.5842 | 0.5844 | 0.7257 | 0.7259 |
| 10 | 0.5888 | 0.5889 | 0.7327 | 0.7328 |

Table A3.
Exact (computer-based) and modeled (from Equation (9)) values of for α = 1 and for α = 2.
Table A3.
Exact (computer-based) and modeled (from Equation (9)) values of for α = 1 and for α = 2.
| α = 1 | α = 2 | |||
|---|---|---|---|---|
| Exact (Computer-Based) Value of | Analytical Estimate of | Exact (Computer-Based) Value of | Analytical Estimate of | |
| 0 | 0.5792 | 0.5000 | 0.8570 | 0.7500 |
| 0.25 | 0.6691 | 0.6404 | 0.9560 | 0.9050 |
| 0.5 | 0.7299 | 0.7193 | 1.0311 | 1.0068 |
| 1 | 0.8050 | 0.8049 | 1.1360 | 1.1327 |
| 1.5 | 0.8486 | 0.8505 | 1.2046 | 1.2073 |
| 2 | 0.8767 | 0.8788 | 1.2524 | 1.2568 |
| 3 | 0.9105 | 0.9121 | 1.3139 | 1.3182 |
| 4 | 0.9299 | 0.9310 | 1.3514 | 1.3548 |
| 5 | 0.9424 | 0.9433 | 1.3765 | 1.3792 |
| 7 | 0.9577 | 0.9581 | 1.4079 | 1.4095 |
| 10 | 0.9697 | 0.9699 | 1.4334 | 1.4343 |
| 15 | 0.9795 | 0.9795 | 1.4545 | 1.4549 |
| 20 | 1.4654 | 1.4656 | ||
| 25 | 1.4721 | 1.4723 | ||
| 30 | 1.4767 | 1.4767 | ||

Table A4.
Exact (computer-based) and modeled (from Equation (9)) values of for α = 5 and for α = 10.
Table A4.
Exact (computer-based) and modeled (from Equation (9)) values of for α = 5 and for α = 10.
| α = 5 | α = 10 | |||
|---|---|---|---|---|
| Exact (Computer-Based) Value of | Analytical Estimate of | Exact (Computer-Based) Value of | Analytical Estimate of | |
| 0 | 1.6392 | 1.5000 | 2.9064 | 2.7500 |
| 0.25 | 1.7568 | 1.6728 | 3.0383 | 2.9324 |
| 0.5 | 1.8577 | 1.8099 | 3.1585 | 3.0920 |
| 1 | 2.0211 | 2.0137 | 3.3698 | 3.3584 |
| 1.5 | 2.1469 | 2.1579 | 3.5491 | 3.5717 |
| 2 | 2.2462 | 2.2653 | 3.7030 | 3.7464 |
| 3 | 2.3917 | 2.4146 | 3.9526 | 4.0153 |
| 4 | 2.4922 | 2.5135 | 4.1455 | 4.2128 |
| 5 | 2.5652 | 2.5838 | 4.2984 | 4.3638 |
| 7 | 2.6636 | 2.6771 | 4.5236 | 4.5798 |
| 10 | 2.7497 | 2.7584 | 4.7420 | 4.7840 |
| 15 | 2.8251 | 2.8298 | 4.9510 | 4.9773 |
| 20 | 2.8658 | 2.8686 | 5.0709 | 5.0884 |
| 25 | 2.8912 | 2.8930 | 5.1482 | 5.1606 |
| 30 | 2.9085 | 2.9098 | 5.2021 | 5.2112 |
References
- United Nations World Water Development Report (UN WWDR). Groundwater: Making the Invisible Visible; United Nations Educational, Scientific, and Cultural Organization (UNESCO): Paris, France, 2022. [Google Scholar]
- Smits, S.; Sutton, S. Self Supply: The Case for Leveraging Greater Household Investment in Water Supply; IRC: The Hague, The Netherlands, 2015. [Google Scholar]
- Butterworth, J.; Sutton, S.; Mekonta, L. Self-supply as a complementary water services delivery model in Ethiopia. Water Altern. 2013, 6, 405–423. [Google Scholar]
- MacCarthy, M.F.; Annis, J.E.; Mihelcic, J.R. Unsubsidized self-supply in eastern Madagascar. Water Altern. 2013, 6, 424–438. [Google Scholar]
- Marshall, K.C. An evaluation of the water lifting limit of a manually operated suction pump: Model estimation and laboratory assessment. Master’s Thesis, University of South Florida, Tampa, FL, USA, 2017. [Google Scholar]
- Sorensen, J.P.R.; Lapworth, D.J.; Nkhuwa, D.C.W.; Stuart, M.E.; Goody, D.C.; Bell, R.A.; Chirwa, M.; Kabika, J.; Liemisa, M.; Chibesa, M.; et al. Emerging contaminants in urban groundwater sources in Africa. Water Res. 2015, 72, 51–63. [Google Scholar] [CrossRef] [PubMed]
- Ouedraogo, I.; Defourney, P.; Vanclooster, M. Mapping the groundwater vulnerability for pollution at the pan African scale. Sci. Total Environ. 2016, 544, 939–953. [Google Scholar] [CrossRef] [PubMed]
- Franceys, R.; Pickford, J.; Reed, R. A Guide to the Development of On-Site Sanitation; World Health Organization: Geneva, Switzerland, 1992. [Google Scholar]
- Orner, K.; Naughton, C.; Stenstrom, T.A. Pit toilets (latrines). In Sanitation and Disease in the 21st Century: Health and Microbiological Aspects of Excreta and Wastewater Management, Global Water Pathogen Project, Part Four, Management of Risk from Excreta and Wastewater; Rose, J.B., Jiménez-Cisneros, J., Eds.; UNESCO: East Lansing, MI, USA, 2018. [Google Scholar] [CrossRef]
- Dillon, K.S.; Corbett, D.R.; Chanton, J.P.; Burnett, W.C.; Kump, L. Bimodal transport of a waste water plume injected into saline ground water of the Florida Keys. Ground Water 2000, 38, 624–634. [Google Scholar] [CrossRef]
- Omrcen, B.; Loncaric, B.; Brkic, V. Waste disposal by injection into deep wells. In Proceedings of the ASME 2001 Engineering Technology Conference on Energy, Houston, TX, USA, 5–7 February 2001. [Google Scholar] [CrossRef]
- Tomiyama, S.; Igarashi, T. The potential threat of mine drainage to groundwater resources. Curr. Opin. Environ. Sci. Health 2022, 27, 100347. [Google Scholar] [CrossRef]
- Mezzacapo, M.; Donohue, M.J.; Smith, C.; El-Kadi, A.; Falinski, K.; Lerner, D.T. Hawaii’s cesspool problem: Review and recommendations for water resources and human health. J. Contemp. Wat. Res. Ed. 2020, 170, 35–75. [Google Scholar] [CrossRef]
- Vroblesky, D.A.; Rhodes, L.C.; Robertson, J.F.; Harrigan, J.A. Locating VOC contamination in a fractured-rock aquifer at the ground-water/surface-water interface using passive vapor collectors. Ground Water 1996, 34, 223–230. [Google Scholar] [CrossRef]
- Kanazawa, K.; Miyaji, N.; Kusaba, T.; Ban, K.; Hayakawa, Y.; Hatano, R. Groundwater pollution by cattle slurry stored in unlined lagoon. JARQ 1999, 33, 7–13. [Google Scholar]
- Nenninger, C.R.; Cunningham, J.A.; Mihelcic, J.R. A historical and critical review of latrine-siting guidelines. J. Water Sanit. Hyg. Dev. 2023, 13, 833–846. [Google Scholar] [CrossRef]
- Shan, C. Analytical solution for the capture zone of two arbitrarily located wells. J. Hydrol. 1999, 222, 123–128. [Google Scholar] [CrossRef]
- Haitjema, H. The role of hand calculations in ground water flow modeling. Ground Water 2006, 44, 786–791. [Google Scholar] [CrossRef] [PubMed]
- Javandel, I.; Tsang, C. Capture-zone type curves: A tool for aquifer cleanup. Ground Water 1986, 24, 616–625. [Google Scholar] [CrossRef]
- Grubb, S. Analytical model for estimation of steady-state capture zones of pumping wells in confined and unconfined aquifers. Ground Water 1993, 31, 27–32. [Google Scholar] [CrossRef]
- Christ, J.A.; Goltz, M.N. Hydraulic containment: Analytical and semi-analytical models for capture zone curve delineation. J. Hydrol. 2002, 262, 224–244. [Google Scholar] [CrossRef]
- Cunningham, J.A.; Reinhard, M. Injection-extraction treatment well pairs: An alternative to permeable reactive barriers. Ground Water 2002, 40, 599–607. [Google Scholar] [CrossRef]
- Cunningham, J.A.; Hoelen, T.P.; Hopkins, G.D.; Lebrón, C.A.; Reinhard, M. Hydraulics of recirculation well pairs for ground water remediation. Ground Water 2004, 42, 880–889. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, X. Regional flow influenced recirculation zones of pump-and-treat systems for groundwater remediation with one or two injection wells: An analytical comparison. Water 2023, 15, 2852. [Google Scholar] [CrossRef]
- International Telecommunication Union (ITU) Development Sector. Connectivity in the Least Developed Countries Status Report 2021; ITU Publications: Geneva, Switzerland, 2021. [Google Scholar]
- World Health Organization and the United Nations International Children’s Emergency Fund (WHO/UNICEF). Joint Monitoring Programme (JMP). Available online: https://washdata.org/data/household#!/ (accessed on 3 March 2024).
- UNICEF, UNICEF Data. Available online: https://data.unicef.org/topic/water-and-sanitation/drinking-water/ (accessed on 17 July 2024).
- United Nations Children’s Fund (UNICEF) and World Health Organization (WHO). Progress on Sanitation and Hygiene in Africa 2000–2022; UNICEF and WHO: New York, NY, USA, 2023. [Google Scholar]
- Strack, O.D.L. Analytical Groundwater Mechanics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Strack, O.D.L. Groundwater Mechanics; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Haitjema, H.M. Analytic Element Modeling of Groundwater Flow; Academic Press Inc.: San Diego, CA, USA, 1995. [Google Scholar]
- Bakker, M.; Strack, O.D.L. Capture zone delineation in two-dimensional groundwater flow models. Water Resour. Res. 1996, 32, 1309–1315. [Google Scholar] [CrossRef]
- Fienen, M.N.; Luo, J.; Kitanidis, P.K. Semi-analytical homogenous anisotropic capture zone delineation. J. Hydrol. 2005, 312, 39–50. [Google Scholar] [CrossRef]
- Fitts, C.R. Modeling aquifer systems with analytic elements and subdomains. Water Resour. Res. 2010, 46, 1–10. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).