Enhancing Evapotranspiration Estimations through Multi-Source Product Fusion in the Yellow River Basin, China
Abstract
1. Introduction
2. Materials and Methods
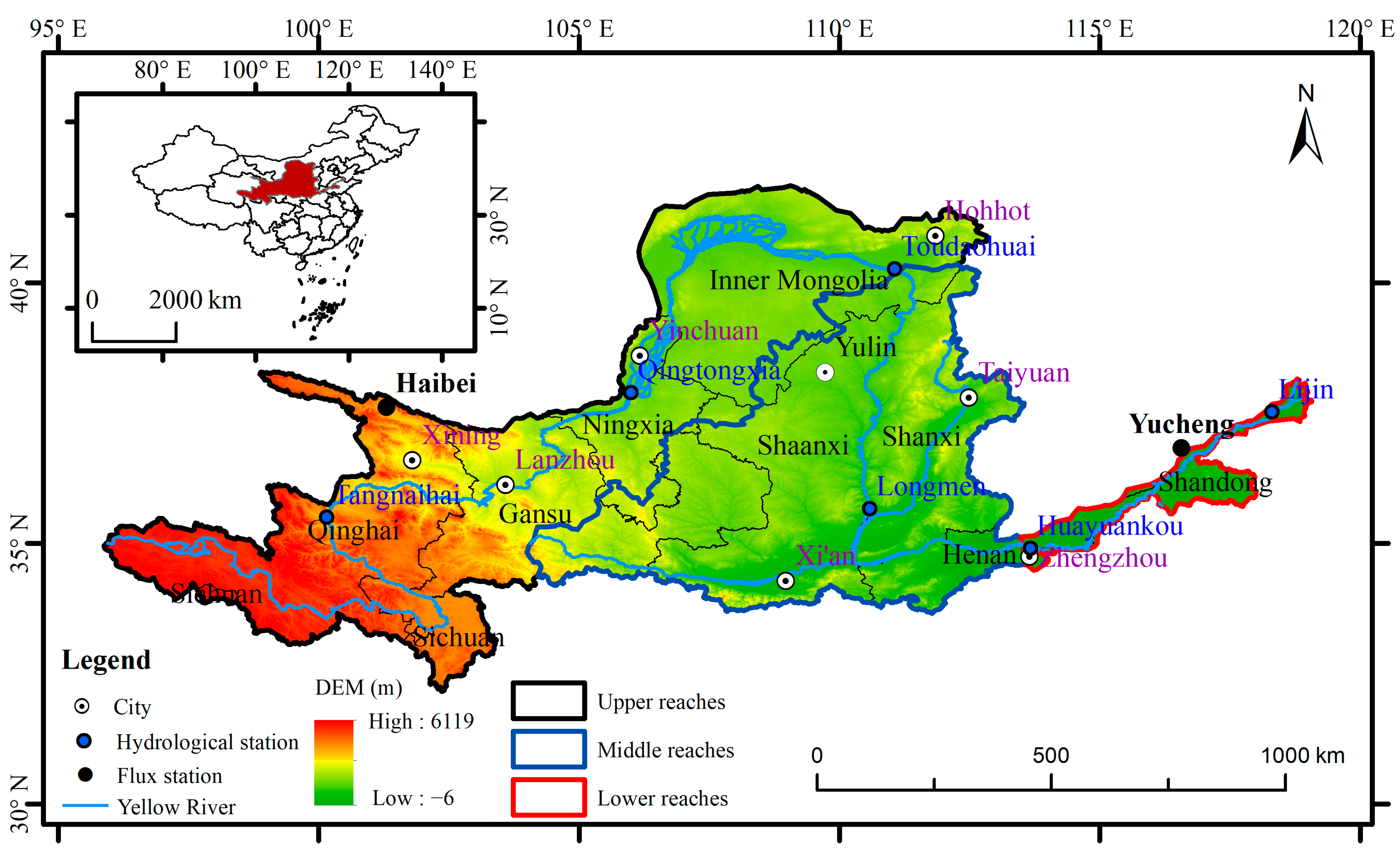
2.1. Study Area
2.2. Data and Processing
2.2.1. Remote Sensing Data and Preprocessing
Evapotranspiration Data Products
GRACE Data
2.2.2. Observed Data
2.3. Methods
2.3.1. Bayesian-Based Three-Cornered Hat Method
2.3.2. Water Balance Method
2.3.3. Surface Energy Balance Closure
2.3.4. Result Evaluation Method
Spatio-Temporal Scale Analysis Method
Mann–Kendall Test
Accuracy Evaluation Index
3. Results
3.1. Uncertainty Analysis of Input Products
3.2. Accuracy Validation
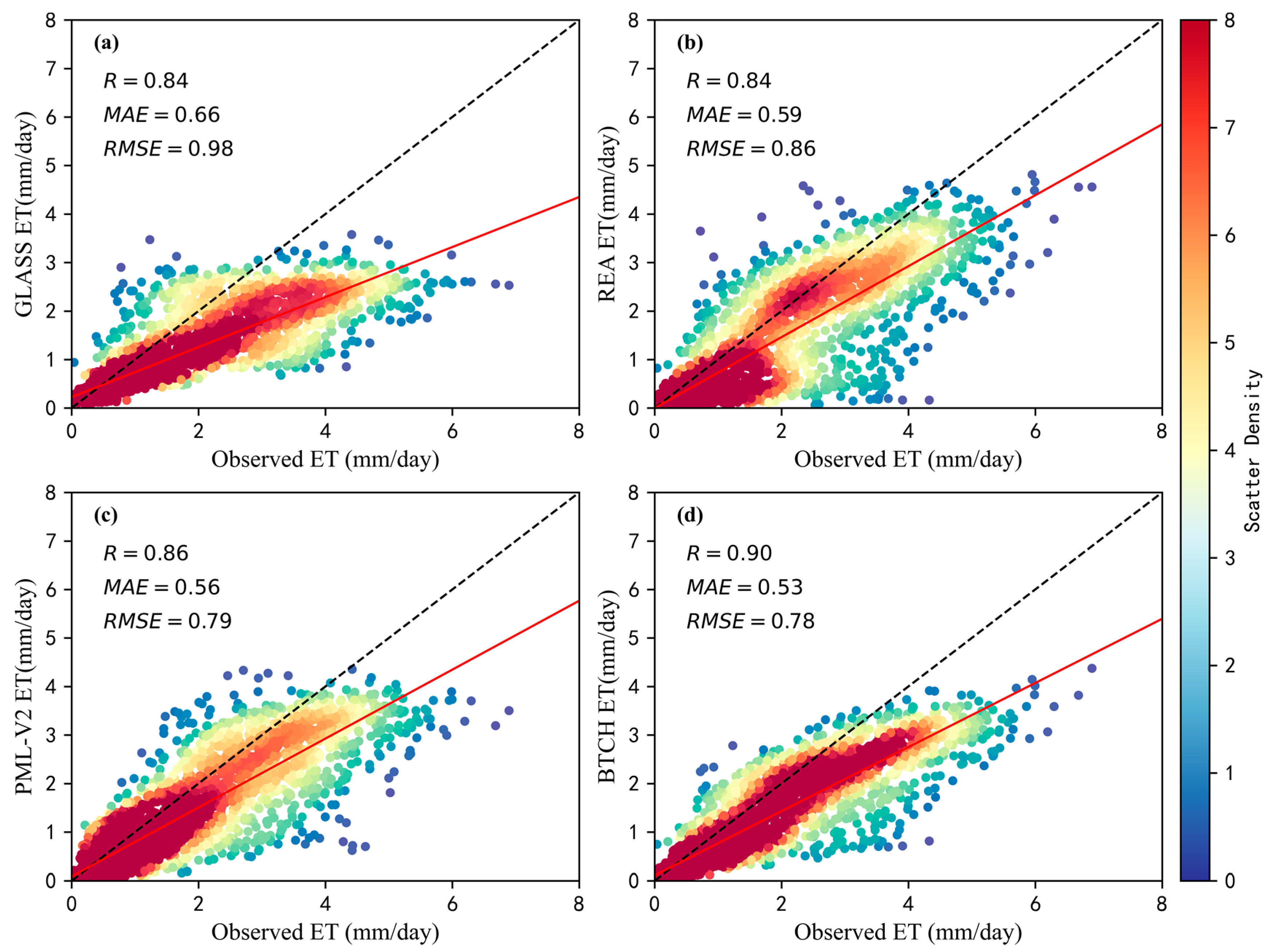
3.2.1. Validation of Site-Measured Data
3.2.2. Validation of Surface Energy Balance
3.2.3. Validation of the Water Balance Method
3.3. Spatiotemporal Variation Trends for Evapotranspiration
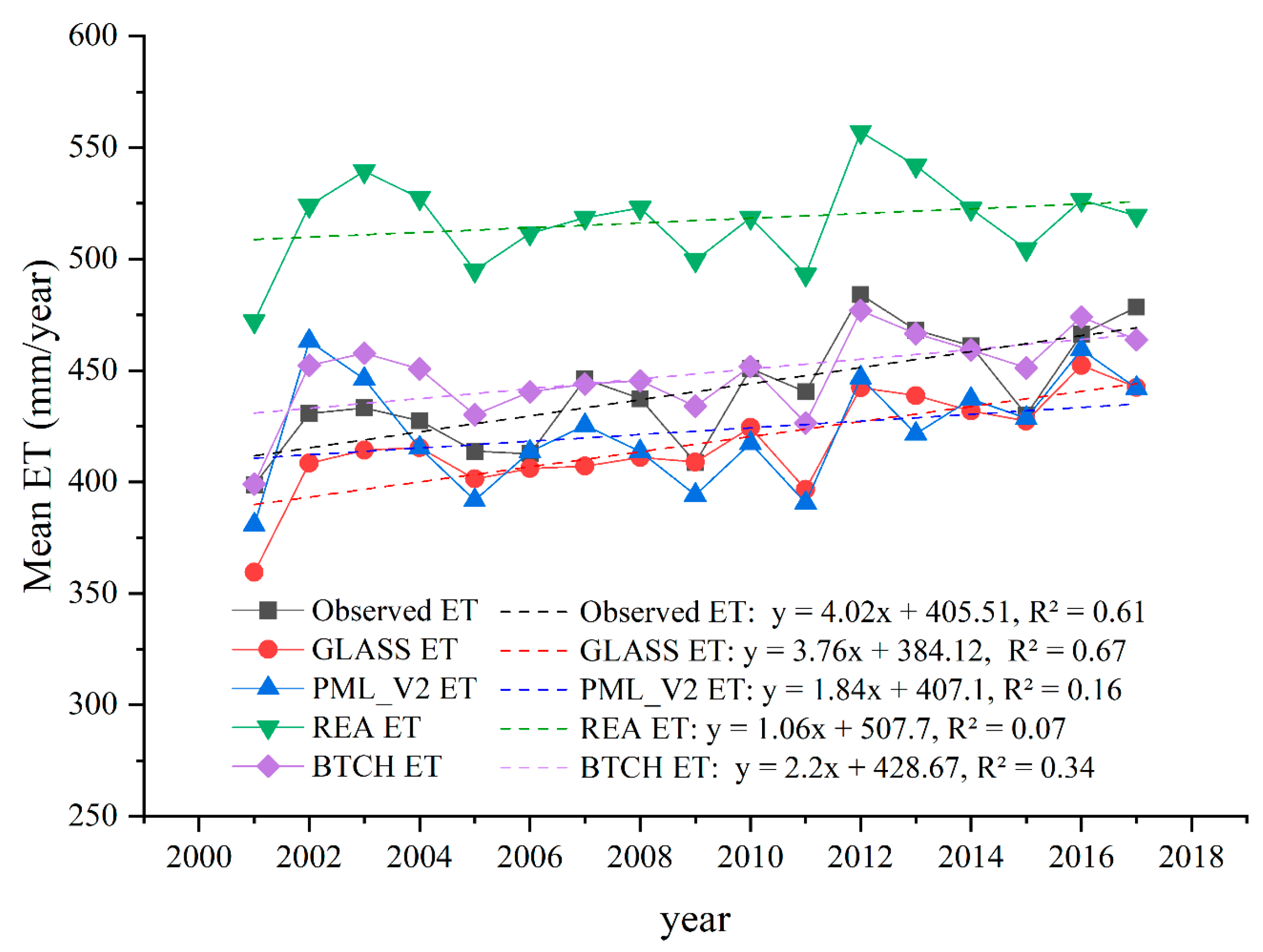
3.3.1. Characteristics of Evapotranspiration Time Variations
3.3.2. Spatial Variation Characteristics of Evapotranspiration
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rodell, M.; Beaudoing, H.K.; L’ecuyer, T.S.; Olson, W.S.; Famiglietti, J.S.; Houser, P.R.; Adler, R.; Bosilovich, M.G.; Clayson, C.A.; Chambers, D.; et al. The observed state of the water cycle in the early twenty-first century. J. Clim. 2015, 28, 8289–8318. [Google Scholar] [CrossRef]
- Huang, Q.; Ma, N.; Wang, P. Faster increase in evapotranspiration in permafrost-dominated basins in the warming Pan-Arctic. J. Hydrol. 2022, 615, 128678. [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2005, 319, 83–95. [Google Scholar] [CrossRef]
- Vergopolan, N.; Fisher, J.B. The impact of deforestation on the hydrological cycle in Amazonia as observed from remote sensing. Int. J. Remote Sens. 2016, 37, 5412–5430. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration evaluation models based on machine learning algorithms—A comparative study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Zhao, F.; Ma, S.; Wu, Y.; Qiu, L.; Wang, W.; Lian, Y.; Chen, J.; Sivakumar, B. The role of climate change and vegetation greening on evapotranspiration variation in the Yellow River Basin, China. Agric. For. Meteorol. 2022, 316, 108842. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 1954, 24, 163–187. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Ser. A 1948, 193, 120–145. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Baldocchi, D. ‘Breathing’ of the terrestrial biosphere: Lessons learned from a global network of carbon dioxide flux measurement systems. Aust. J. Bot. 2008, 56, 1–26. [Google Scholar] [CrossRef]
- Anderson, R.G.; Goulden, M.L. A mobile platform to constrain regional estimates of evapotranspiration. Agric. For. Meteorol. 2009, 149, 771–782. [Google Scholar] [CrossRef][Green Version]
- Wang, K.; Liang, S. An improved method for estimating global evapotranspiration based on satellite determination of surface net radiation, vegetation index, temperature, and soil moisture. J. Hydrometeorol. 2008, 9, 712–727. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S. Estimation of surface evaporation map over southern Great Plains using remote sensing data. Water Resour. Res. 2001, 37, 329–340. [Google Scholar] [CrossRef]
- Caparrini, F.; Castelli, F.; Entekhabi, D. Estimation of surface turbulent fluxes through assimilation of radiometric surface temperature sequences. J. Hydrometeorol. 2004, 5, 145–159. [Google Scholar] [CrossRef]
- Deb, P.; Abbaszadeh, P.; Moradkhani, H. An ensemble data assimilation approach to improve farm-scale actual evapotranspiration estimation. Agric. For. Meteorol. 2022, 321, 108982. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Liu, S.; He, X.; Meng, Y.; Xu, Z.; Xia, Y.; Xiao, J.; Zhang, Y.; Ma, Y.; et al. Evaluating different machine learning methods for upscaling evapotranspiration from flux towers to the regional scale. J. Geophys. Res. Atmos. 2018, 123, 8674–8690. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, Z.; Jiang, H.; Sun, S. Estimating daily reference evapotranspiration based on limited meteorological data using deep learning and classical machine learning methods. J. Hydrol. 2020, 591, 125286. [Google Scholar] [CrossRef]
- Morillas, L.; García, M.; Nieto, H.; Villagarcia, L.; Sandholt, I.; Gonzalez-Dugo, M.; Zarco-Tejada, P.; Domingo, F. Using radiometric surface temperature for surface energy flux estimation in Mediterranean drylands from a two-source perspective. Remote Sens. Environ. 2013, 136, 234–246. [Google Scholar] [CrossRef]
- Kustas, W.P.; Daughtry, C.S.; Van Oevelen, P.J. Analytical treatment of the relationships between soil heat flux/net radiation ratio and vegetation indices. Remote Sens. Environ. 1993, 46, 319–330. [Google Scholar] [CrossRef]
- Jacobsen, A.; Hansen, B.U. Estimation of the soil heat flux/net radiation ratio based on spectral vegetation indexes in high-latitude Arctic areas. Int. J. Remote Sens. 1999, 20, 445–461. [Google Scholar] [CrossRef]
- Dolman, A.J. A multiple-source land surface energy balance model for use in general circulation models. Agric. For. Meteorol. 1993, 65, 21–45. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops-an energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J.; Zhu, G.; Li, H.; Shao, D.; Hao, X. Estimation of surface latent heat fluxes in an oasis utilizing a two-source energy balance model based on land surface temperature decomposition. J. Appl. Remote Sens. 2019, 13, 034504. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Al-Juboori, A.M.; Beyaztas, U.; Al-Ansari, N.; Chau, K.-W.; Qi, C.; Ali, M.; Salih, S.Q.; Shahid, S. Prediction of evaporation in arid and semi-arid regions: A comparative study using different machine learning models. Eng. Appl. Comput. Fluid Mech. 2019, 14, 70–89. [Google Scholar] [CrossRef]
- Jiménez, C.; Martens, B.; Miralles, D.M.; Fisher, J.B.; Beck, H.E.; Fernández-Prieto, D. Exploring the merging of the global land evaporation WACMOS-ET products based on local tower measurements. Hydrol. Earth Syst. Sci. 2018, 22, 4513–4533. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Hong, Y.; Fisher, J.B.; Zhang, N.; Chen, J.; Cheng, J.; Zhao, S.; Zhang, X.; et al. Bayesian multimodel estimation of global terrestrial latent heat flux from eddy covariance, meteorological, and satellite observations. J. Geophys. Res. Atmos. 2014, 119, 4521–4545. [Google Scholar] [CrossRef]
- Khan, M.S.; Liaqat, U.W.; Baik, J.; Choi, M. Stand-alone uncertainty characterization of GLEAM, GLDAS and MOD16 evapotranspiration products using an extended triple collocation approach. Agric. For. Meteorol. 2018, 252, 256–268. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.; Gao, F.; Hain, C.; Kustas, W. Mapping daily evapotranspiration at field scales over rainfed and irrigated agricultural areas using remote sensing data fusion. Agric. For. Meteorol. 2014, 186, 1–11. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Yang, Y.; Anderson, M.C.; Gao, F.; Hain, C.R.; Semmens, K.A.; Kustas, W.P.; Noormets, A.; Wynne, R.H.; Thomas, V.A.; Sun, G. Daily Landsat-scale evapotranspiration estimation over a forested landscape in North Carolina, USA, using multi-satellite data fusion. Hydrol. Earth Syst. Sci. 2017, 21, 1017–1037. [Google Scholar] [CrossRef]
- Yi, Z.; Zhao, H.; Jiang, Y. Continuous daily evapotranspiration estimation at the field-scale over heterogeneous agricultural areas by fusing ASTER and MODIS data. Remote Sens. 2018, 10, 1694. [Google Scholar] [CrossRef]
- Fan, M.; Ma, D.; Huang, X.; An, R. Adaptability Evaluation of the Spatiotemporal Fusion Model of Sentinel-2 and MODIS Data in a Typical Area of the Three-River Headwater Region. Sustainability 2023, 15, 8697. [Google Scholar] [CrossRef]
- He, X.; Xu, T.; Xia, Y.; Bateni, S.M.; Guo, Z.; Liu, S.; Mao, K.; Zhang, Y.; Feng, H.; Zhao, J. A Bayesian three-cornered hat (BTCH) method: Improving the terrestrial evapotranspiration estimation. Remote Sens. 2020, 12, 878. [Google Scholar] [CrossRef]
- Koot, L.; Viron, O.D.; Dehant, V. Atmospheric angular momentum time-series: Characterization of their internal noise and creation of a combined series. J. Geodesy 2006, 79, 663–674. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef]
- Zhu, Y.; Chang, J.; Huang, S.; Huang, Q. Characteristics of integrated droughts based on a nonparametric standardized drought index in the Yellow River Basin, China. Hydrol. Res. 2015, 47, 454–467. [Google Scholar] [CrossRef]
- Chang, J.; Wei, J.; Wang, Y.; Yuan, M.; Guo, J. Precipitation and runoff variations in the Yellow River Basin of China. J. Hydroinform. 2016, 19, 138–155. [Google Scholar] [CrossRef]
- Qiu, M.; Zuo, Q.; Wu, Q.; Yang, Z.; Zhang, J. Water ecological security assessment and spatial autocorrelation analysis of prefectural regions involved in the Yellow River Basin. Sci. Rep. 2022, 12, 5105. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.; Yang, H.; Di, D.; Zhao, Y.; Liang, Q.; Hussain, Z. Comprehensive evaluation of hydrological drought and its relationships with meteorological drought in the Yellow River basin, China. J. Hydrol. 2020, 584, 124751. [Google Scholar] [CrossRef]
- Liang, S.; Cheng, J.; Jia, K.; Jiang, B.; Liu, Q.; Xiao, Z.; Yao, Y.; Yuan, W.; Zhang, X.; Zhao, X.; et al. The Global land surface satellite (GLASS) product suite. Bull. Am. Meteorol. Soc. 2021, 102, E323–E337. [Google Scholar] [CrossRef]
- He, S.; Zhang, Y.; Ma, N.; Tian, J.; Kong, D.; Liu, C. A daily and 500 m coupled evapotranspiration and gross primary production product across China during 2000–2020. Earth Syst. Sci. Data 2022, 14, 5463–5488. [Google Scholar] [CrossRef]
- Lu, J.; Wang, G.; Chen, T.; Li, S.; Hagan, D.F.T.; Kattel, G.; Peng, J.; Jiang, T.; Su, B. A harmonized global land evaporation dataset from model-based products covering 1980–2017. Earth Syst. Sci. Data 2021, 13, 5879–5898. [Google Scholar] [CrossRef]
- Voss, K.A.; Famiglietti, J.S.; Lo, M.-H.; De Linage, C.; Rodell, M.; Swenson, S.C. Groundwater depletion in the Middle East from GRACE with implications for transboundary water management in the Tigris-Euphrates-Western Iran region. Water Resour. Res. 2013, 49, 904–914. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Zhang, X.; Chen, Z. Spatiotemporal changes in China’s terrestrial water storage from GRACE satellites and its possible drivers. J. Geophys. Res. Atmos. 2019, 124, 11976–11993. [Google Scholar] [CrossRef]
- Zheng, H.; Yu, G.; Zhu, X.; Wang, Q.; Zhang, L.; Chen, Z.; Sun, X.; He, H.; Su, W.; Wang, Y.; et al. A Dataset of Actual Evapotranspiration and Water Use Efficiency of Typical Terrestrial Ecosystems in China (2000–2010); China Scientific Data: Beijing, China, 2019. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, W.; Nie, N.; Guo, Y. Long-term groundwater storage variations estimated in the Songhua River Basin by using GRACE products, land surface models, and in-situ observations. Sci. Total. Environ. 2018, 649, 372–387. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Gowda, P.H.; Oâshaughnessy, S.A.; Tolk, J.A.; Kustas, W.P.; Anderson, M.C. Two-source energy balance model: Refinements and lysimeter tests in the southern high plains. Trans. ASABE 2012, 55, 551–562. [Google Scholar] [CrossRef]
- Song, Z.; Yang, H.; Huang, X.; Yu, W.; Huang, J.; Ma, M. The spatiotemporal pattern and influencing factors of land surface temperature change in China from 2003 to 2019. Int. J. Appl. Earth Obs. 2021, 104, 102537. [Google Scholar] [CrossRef]
- Wang, R.; You, X.; Shi, Y.; Wu, C.; Liu, B. Study on air temperature estimation and its influencing factors in a complex mountainous area. PLoS ONE 2022, 17, e0272946. [Google Scholar] [CrossRef]
- Sonali, P.; Kumar, D.N. Review of trend detection methods and their application to detect temperature changes in India. J. Hydrol. 2013, 476, 212–227. [Google Scholar] [CrossRef]
- Bari, S.H.; Rahman, M.T.U.; Hoque, M.A.; Hussain, M. Analysis of seasonal and annual rainfall trends in the northern region of Bangladesh. Atmospheric Res. 2016, 176–177, 148–158. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. B. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Barr, A.; Morgenstern, K.; Black, T.; McCaughey, J.; Nesic, Z. Surface energy balance closure by the eddy-covariance method above three boreal forest stands and implications for the measurement of the CO2 flux. Agric. For. Meteorol. 2006, 140, 322–337. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and drainage paper 56; FAO: Rome, Italy, 1998; pp. 17–64. [Google Scholar]
- Hasan, A.; Mia, B.; Khan, M.R.; Alam, J.; Chowdury, T.; Amin, A.; Ahmed, K.M.U. Temporal changes in land cover, land surface temperature, soil moisture, and evapotranspiration using remote sensing techniques—A case study of Kutupalong rohingya refugee camp in Bangladesh. J. Geovisualization Spat. Anal. 2023, 7, 11. [Google Scholar] [CrossRef]
- Liu, Y.; Gui, D.; Yin, C.; Zhang, L.; Xue, D.; Liu, Y.; Ahmed, Z.; Zeng, F. Effects of Human Activities on Evapotranspiration and Its Components in Arid Areas. Int. J. Environ. Res. Public Health 2023, 20, 2795. [Google Scholar] [CrossRef]
- Cui, Z.; Zhang, Y.; Wang, A.; Wu, J.; Li, C. Uncertainty Analysis and Data Fusion of Multi-Source Land Evapotranspiration Products Based on the TCH Method. Remote Sens. 2023, 16, 28. [Google Scholar] [CrossRef]
- Yin, L.; Tao, F.; Chen, Y.; Liu, F.; Hu, J. Improving terrestrial evapotranspiration estimation across China during 2000–2018 with machine learning methods. J. Hydrol. 2021, 600, 126538. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, Y.; Yinglan, A.; Wang, G.; Zhang, X.; Ma, G.; Duan, L.; Liu, K. Optimizing actual evapotranspiration simulation to identify evapotranspiration partitioning variations: A fusion of physical processes and machine learning techniques. Agric. Water Manag. 2024, 295, 108755. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; You, X.; Shi, Y.; Wu, C. Enhancing Evapotranspiration Estimations through Multi-Source Product Fusion in the Yellow River Basin, China. Water 2024, 16, 2603. https://doi.org/10.3390/w16182603
Wang R, You X, Shi Y, Wu C. Enhancing Evapotranspiration Estimations through Multi-Source Product Fusion in the Yellow River Basin, China. Water. 2024; 16(18):2603. https://doi.org/10.3390/w16182603
Chicago/Turabian StyleWang, Runke, Xiaoni You, Yaya Shi, and Chengyong Wu. 2024. "Enhancing Evapotranspiration Estimations through Multi-Source Product Fusion in the Yellow River Basin, China" Water 16, no. 18: 2603. https://doi.org/10.3390/w16182603
APA StyleWang, R., You, X., Shi, Y., & Wu, C. (2024). Enhancing Evapotranspiration Estimations through Multi-Source Product Fusion in the Yellow River Basin, China. Water, 16(18), 2603. https://doi.org/10.3390/w16182603





